Преподаватель который помогает студентам и школьникам в учёбе.
Электрическое поле заряженного шара в физике – формулы и определение с примерами
Электрическое поле заряженного шара:
Пусть электропроводящий шар радиусом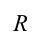 
Определим напряженность поля, создаваемого заряженным шаром (сферой) в его центре, на поверхности и за его пределами. Для этого мы сначала разделим заряд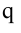 
на несколько зарядов, равномерно распределенных по поверхности шара, т.е. 
.
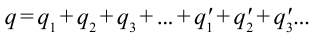Итоговая напряженность поля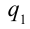 
и 
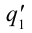любых одинаковых зарядов в центре шара на основе принципа суперпозиции равна нулю. Значит, внутри заряженной сферы напряженность поля будет равна нулю.
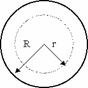
Найдем напряженность поля в произвольной точке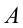 
, расположенной на расстоянии 
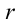от поверхности шара. Выделим пару зарядов 
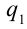и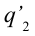 
, расположенных симметрично линии 
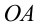. Эти заряды создают напряженность на оси, направленной по оси 
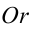. Значит, силовые линии напряженности поля в точке за пределами шара соответствуют силовым линиям положительно заряженного точечного заряда, направленным из центра шара (рис. 7.5 б)
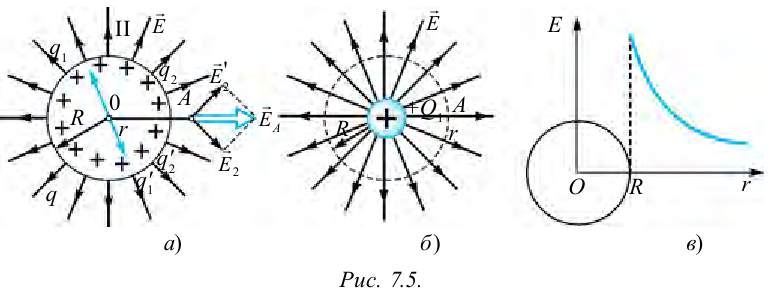
Напряженность электрического поля на поверхности заряженного шара определяется следующей формулой:
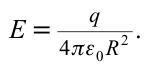
Из-за того, что напряженность поля, созданного в точке за пределами заряженного шара, одинаковы с полем, созданным точечным зарядом, напряженность поля, созданного в точке за пределами шара, определяется по формуле:
Это означает, что напряженность поля уменьшается обратно пропорционально квадрату расстояния (рис. 7.5 в).
Напряженность электрического поля зависит от свойств среды, в которой расположен заряд, создающий поле. Рассмотрим случай, когда между двумя противоположно заряженными пластинами помещен диэлектрик (рис. 7.6).
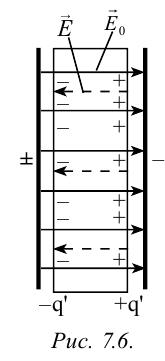
В диэлектрике свободных электронов очень мало. Основные электроны расположены в электронной оболочке атома. Под воздействием поля электрических зарядов пластин электронная оболочка деформируется. В результате центры положительных и отрицательных зарядов атома не накладываются друг на друга. Это явление называется поляризацией диэлектрика.
Напряженность поля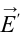 
, создаваемого поляризованными атомами (молекулами), направлена противоположно напряженности основного поля 
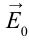. В результате общая напряженность поля снижается 
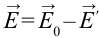. Величина, показывающая во сколько раз уменьшается напряженность поля, называется диэлектрической восприимчивостью диэлектрика:
В таком случае напряженность поля в точке, расположенной на расстоянии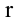 
от точечного заряда, расположенного в диэлектрике, тоже уменьшается в ε раз:
Также сила взаимодействия точечных зарядов, расположенных в однородном диэлектрике, будет в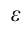 
раз меньше, чем сила их взаимодействия в вакууме, и сила этого взаимодействия вычисляется с помощью следующего выражения:
Диэлектрическая восприимчивость – это безразмерная величина.
- Электрические явления в физике
- Потенциал поля точечного заряда в физике
- Работа электрического поля при перемещении заряда в физике
- Энергия электрического поля
- Изменение агрегатного состояния вещества
- Электродинамика
- Электростатика
- Закон сохранения заряда в физике
Напряженность поля шара
С помощью формул Поверхностная плотность заряда [2], Относительная и абсолютная диэлектрическая проницаемость [3] и [4] можно определить напряженность поля на поверхности проводника. Если заряд распределен равномерно по поверхности проводника, то:
[ E = frac{D}{ε_a} = frac{Q}{S ε_a} ]
Эта формула справедлива только для шара. Из тел другой формы указанная формула применима только к участкам равномерно заряженной поверхности ∆S с зарядом ∆Q.
Если
| E | напряженность электрического поля, | Вольт/метр |
|---|---|---|
| Q | заряд поверхности шара, | Кулон |
| εa | абсолютная диэлектрическая проницаемость, | Кулон/(Вольт·метр) |
| r | радиус шара, | метр |
то
учитывая, формулу Поверхность шара [1], имеем
[ E = frac{Q}{4πε_{a}r^2} ]
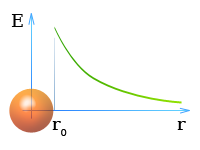
Напряженность поля шара
[ frac{1}{4πε_{0}} = 8.99 cdot 10^9 frac{Вольт cdot Метр}{Кулон} ]
У тел с произвольной формой поверхности напряженность поля особенно велика в местах большой кривизной.
Здесь может происходить самопроизвольное стекание зарядов (разряд с острия).
С металлического острия, имеющего радиус кривизны около 1мкм, электроны стекают уже при напряжении в несколько сотен вольт.
Вычислить найти напряженность поля шара по формуле (2)
Напряженность поля шара |
стр. 629 |
|---|
Напряженность поля шара заряженного
по объему
.Введем понятие объемной плотности
заряда: 
Объемная плотность заряда показывает,
какой заряд содержится в единице объема
заряженного по всему объему тела. 
Объем шара произвольного радиуса 
.
Обозначим q – заряд
шара, q0 – заряд,
находящийся внутри объема произвольного
радиуса.
Тогда
заряд сферы радиуса r ,
будет: 
Следовательно:
.
– Напряженность поля внутри шара, равномерно заряженного по объему. 8)Расчёт электрического поля бесконечно длинной равномерно заряженной нити.
Поле равномерно заряженного бесконечного
цилиндра (нити).
Бесконечный
цилиндр радиуса R
заряжен равномерно с
линейной плотностью
(
=
– заряд, приходящийся на единицу длины).
Из соображений симметрии следует, что
линии напряженности будут направлены
по радиусам круговых сечений цилиндра
с одинаковой густотой во все стороны
относительно оси цилиндра. В качестве
замкнутой поверхности мысленно построим
коаксиальный с заряженным цилиндр
радиуса r
и высотой l.
Поток вектора Е
сквозь торцы коаксиального цилиндра
равен нулю (торцы параллельны линиям
напряженности), а сквозь боковую
поверхность равен 2rlЕ.
По теореме Гаусса (81.2), при r>R
2rlЕ
= l/0,
откуда
(82.5)
Если r<R,
то замкнутая поверхность
зарядов внутри не содержит, поэтому в
этой области E=0.
Таким образом, напряженность поля вне
равномерно заряженного бесконечного
цилиндра определяется выражением
(82.5), внутри же его поле отсутствует.
(В системе СГС ответ: 
).
9)Работа сил электрического поля по перемещению заряда. Циркуляция вектора эдс.(е). Потенциальность электрического поля.
Если в электростатическом поле точечного
заряда Q из точки 1
в точку 2 вдоль произвольной траектории
перемещается другой точечный заряд Q0,
то сила, приложенная к заряду, совершает
работу. Работа силы F
на элементарном перемещении dl
равна
Так как d/cos=dr,
то
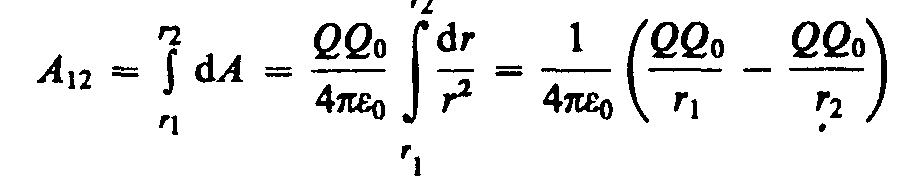
Работа при перемещении заряда Q0
из точки 1 в точку 2 не зависит
от траектории перемещения, а определяется
только положениями начальной 1 и
конечной 2 точек. Следовательно,
электростатическое поле точечного
заряда является потенциальным.
Из формулы (83.1) следует, что работа,
совершаемая при перемещении электрического
заряда во внешнем электростатическом
поле по любому замкнутому пути L,
равна нулю, т.е.
Если в качестве заряда, переносимого в
электростатическом поле, взять единичный
точечный положительный заряд, то
элементарная работа сил поля на пути
dl равна
Е dl
= El
dl, где El
= Ecos
— проекция вектора Е на направление
элементарного перемещения. Тогда формулу
можно записать в виде
(83.3)
Интеграл
называется циркуляцией вектора
напряженности. Следовательно,
циркуляция вектора напряженности
электростатического поля вдоль любого
замкнутого контура равна нулю. Силовое
поле, обладающее свойством (83.3), называется
потенциальным. Из обращения в нуль
циркуляции вектора Е следует, что
линии напряженности электростатического
поля не могут быть замкнутыми, они
начинаются и кончаются на зарядах
(соответственно на положительных или
отрицательных) или же уходят в
бесконечность.
Формула (83.3) справедлива только для
электростатического поля. В дальнейшем
будет показано, что для поля движущихся
зарядов условие (83.3) не выполняется (для
него циркуляция вектора напряженности
отлична от нуля).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этой заметке разберем одну из задачек по электродинамике. Постараюсь привести максимально подробное решение, которое будет полезно учащимся 1-2 курсов физико-математических факультетов. Кто скучал по электродинамике и интегралам – ставим жирный лайк, чтоб я чаще писал про это 🙂 Доброго времени суток, друзья, мы начинаем…
Задача
Шар из однородного изотропного диэлектрика с диэлектрической проницаемостью ε и радиуса R заряжен сторонним зарядом q с объемной плотностью, линейно меняющейся от значения 0 в центре до максимального значения на поверхности шара. Считая, что шар находится в воздухе, определить потенциал во всей области изменения радиуса.
Решение:
Для начала нам нужно сделать рисунок к задаче. К любой задаче надо пытаться делать рисунок. Не потому что это нужно для кого-то или для красоты. Это нужно для того, чтобы наш мозг лучше визуализировал происходящее, строил абстрактные модели и логические цепочки.
1. По условию сказано, что плотность заряда диэлектрического шара меняется линейно, значит функционально мы можем выразить это так ( с проверкой граничных условий):
2. Нам задан именно общий заряд q, а не максимальная плотность. Поэтому эту неизвестную константу попробуем найти из условия нормировки.
3. Для начала найдем напряженность внешнего электрического поля (вне шара), а также потенциал вне шара. Для этого применим теорему Гаусса:
4. Теперь найдем напряженность электрического поля внутри шара. Для этого замкнутой поверхностью выберем сфера с радиусом r < R, центр которой будет совпадать с центром нашего шара. Симметрия подсказывает, что напряженность направленно радиально и одинакова по величине на всей поверхности. Применяем также теорему Гаусса. Учитываем, что внутри шара диэлектрик с заданной диэлектрической проницаемостью.
5. Теперь, зная внешнее и внутреннее поля, найдем потенциал внутри шара.
Первый интеграл в начале нашей формулы имеет смысл работы по переносу единичного положительного заряда из бесконечно удаленной точки в точку на поверхности шара r = R. Второй интеграл имеет смысл работы по переносу единичного положительного заряда с поверхности шара внутрь на радиус r < R. Обратим внимание, что внешний и внутренний потенциал сшиваются на границе при r = R.
Задача решена.
Понравилась заметка? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
Направление линий напряженности,
как мы уже говорили, позволяет определить направление вектора напряженности в
различных точках поля. Густота этих линий говорит нам о том, в каких областях
пространства напряженность больше. Поэтому, мы можем сказать, что линии
напряженности — это непрерывные линии, касательные к которым в каждой точке,
через которую они проходят, совпадают с направлением векторов напряженности.
Если мы отметим точки 1 и
2 так, как показано на рисунке, то можно с уверенностью сказать, что
напряженность в точке 1 будет больше, чем напряженность в точке 2.
Если мы рассмотрим теперь
линии напряженности одноименно заряженных шариков, то они будут выглядеть
несколько иначе:
Также мы можем
рассмотреть линии напряженности положительно и отрицательно заряженного шарика:
Как вы видите, вне шарика
они не отличаются от линий напряженности точечных зарядов.
Рассмотрим еще один
важный пример: электрическое поле, создаваемое параллельными заряженными
пластинами. Одна из пластин заряжена отрицательно, а другая — положительно.
Еще раз напомним, что
линии напряженности направлены от плюса к минусу. Обратите внимание на
центральную часть электрического поля между этими пластинами: линии
напряженности здесь параллельны и расположены с одинаковой густотой. Такое
электрическое поле называется однородным. То есть однородное
электрическое поле — это поле, линии напряженности которого, параллельны друг
другу и расположены с одинаковой густотой. Если в качестве примера мы опять
рассмотрим точки 1 и 2, то можем сказать, что поле в точке 1 однородное, а в
точке 2 — неоднородное.
Вернемся теперь к вопросу
об электрическом поле заряженной сферы.
Обозначим радиус сферы за
R, а заряд сферы за Q,
предполагая, что этот заряд равномерно распределен по всей поверхности сферы.
Очевидно, что если мы расположим множество пробных зарядов вблизи поверхности сферы,
то убедимся, что вне сферы линии напряженности расположены точно так же, как и
линии напряженности точечного заряда. Тем не менее, внутри проводящей сферы
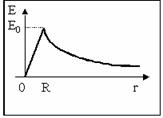
напряженность поля равна нулю. Напряженность внутри заряженного шара линейно
растет с увеличением расстояния от центра шара. О том, почему так происходит,
мы поговорим немного позже. Обозначим произвольное расстояние от центра сферы
за r. Тогда функция
зависимости напряженности заряженной сферы от r
будет такова:
Примеры решения задач.
Задача 1. Пылинка
массой 6
×
10−6 кг
неподвижно висит в однородном поле между параллельными противоположно
заряженными пластинами. Если модуль напряженности электрического поля между
пластинами составляет 300 Н/Кл, то каков заряд пылинки?
Задача 2. Шар
обладает зарядом 0,4 мкКл, который равномерно распределен по всему объёму шара.
На точечный заряд, равный 800 нКл, действует кулоновская сила, модуль которой
равен 0,2 мН. Определите, находится ли данный заряд внутри шара или нет?
Расстояние между центром шара и точечным зарядом составляет 60 см.
