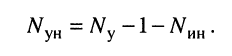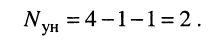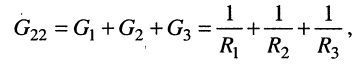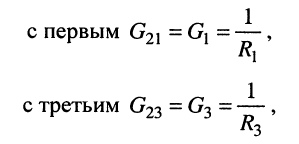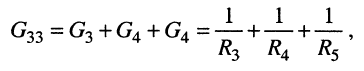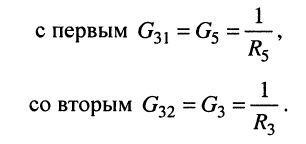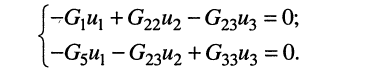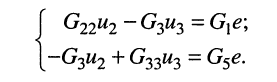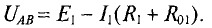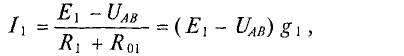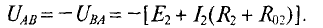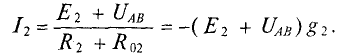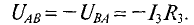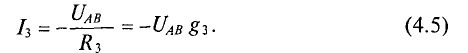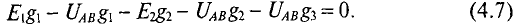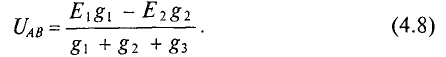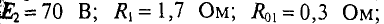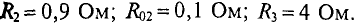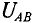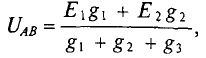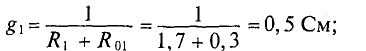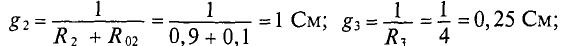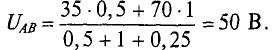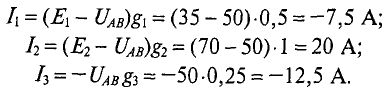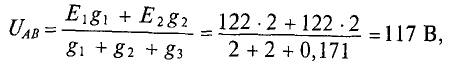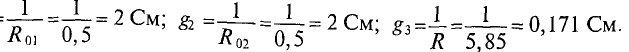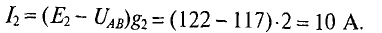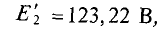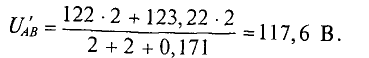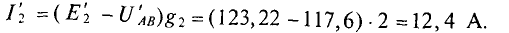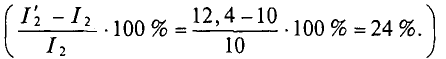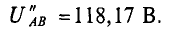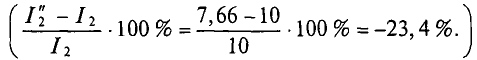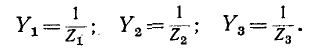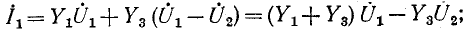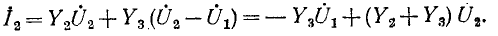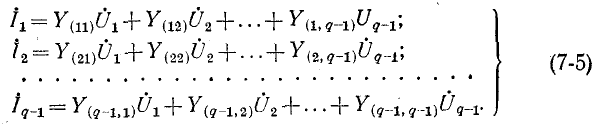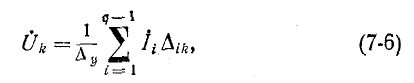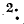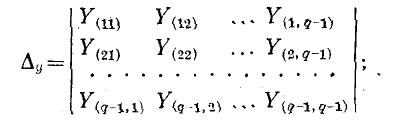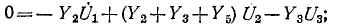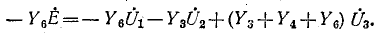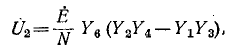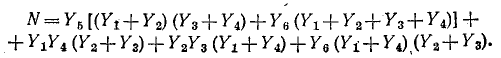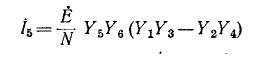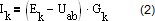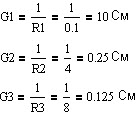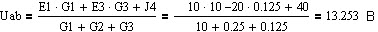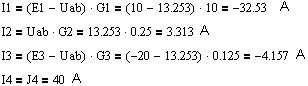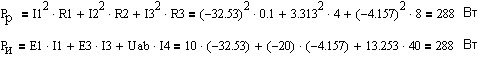Метод узлового напряжения



Этот метод рекомендуется использовать в том случае, если сложную электрическую схему можно упростить, заменяя последовательно и параллельно соединенные резисторы эквивалентными, используя при необходимости преобразование треугольника сопротивлений в эквивалентную звезду. Если полученная схема содержит несколько параллельно соединенных активных и пассивных ветвей, как, например, схема на рис. 1.27, то ее расчет и анализ весьма просто можно произвести методом узлового напряжения.
Пренебрегая сопротивлением проводов, соединяющих ветви цепи, в ее схеме (рис. 1.27) можно выделить два узла: a и b. В зависимости от значений и направлений ЭДС и напряжений, а также значений сопротивлений ветвей между узловыми точками a и b установится определенное узловое напряжение Uab. Предположим, что оно направлено так, как показано на рис. 1.27, и известно. Зная напряжение Uab легко найти токи во всех ветвях.
Выберем положительные направления токов и обозначим их на схеме. Запишем уравнения по второму закону Кирхгофа для контуров (1.4), проходящих по первой и второй ветви, содержащих источники ЭДС, совершая обход контуров по часовой стрелке.
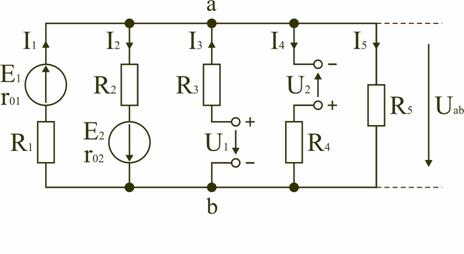
Рис. 1.27
Определим значения токов, возникающих в первой и второй ветвях,
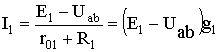
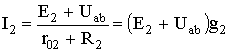
где: 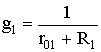
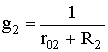
Запишем уравнения по второму закону Кирхгофа для ветвей (1.5), содержащих источники напряжений, совершая обход контуров также по часовой стрелке.
Определим значения токов, возникающих в третьей и четвертой ветвях,
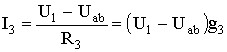
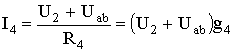
где: 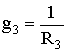
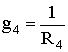
Ток в пятой ветви определим по закону Ома:
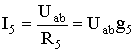
где 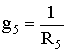
Для вывода формулы, позволяющей определить напряжение Uab, напишем уравнение по первому закону Кирхгофа (1.3) для узла a:
После замены токов их выражениями (1.20) – (1.24) и соответствующих преобразований получим
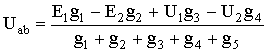
Формула узлового напряжения в общем случае имеет вид
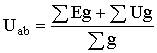
При расчете электрической цепи методом узлового напряжения после определения величины напряжения Uab значения токов в ветвях находят по их выражениям (1.20) – (1.24).
При записи формулы (1.25) следует задаться положительным направлением узлового напряжения Uab. Со знаком «+» в (1.25) должны входить ЭДС, направленные между точками a и b встречно напряжению Uab, и напряжения ветвей, направленные согласно с Uab. Знаки в формуле (1.25) не зависят от направления токов ветвей.
При расчете и анализе электрических цепей методом узлового напряжения рекомендуется выбирать положительные направления токов после определения узлового напряжения. В этом случае при расчете токов по выражениям (1.20) – (1.24) положительные направления токов нетрудно выбрать таким образом, чтобы все они совпадали с их действительными направлениями.
Проверка правильности произведенных расчетов проводится по первому закону Кирхгофа для узла a или b, а также составлением уравнения баланса мощностей (1.8).
Источник
Метод узлового напряжения (двух узлов)
Наиболее простым методом расчета электрической цепи с двумя узлами – является метод узлового напряжения или метод двух узлов.
Важно отличать метод узлового напряжения (метод двух узлов) от метода узловых напряжений.
Метод узлового напряжения (двух узлов)
Определим разность потенциалов между двумя узлами цепи А и B.
Найдём потенциал точки А, перемещаясь по первой ветви от узла B до А.
Исходя из выражения (1) можно записать:
где r1 и g1 – сопротивление и проводимость первой ветви соответственно.
Аналогично составляются уравнения для оставшихся ветвей.
По первому закону Кирхгофа запишем уравнение для узла B
Подставим в вышеуказанное уравнение выражения токов (2-5).
Раскрыв скобки, находим узловое напряжение U:
Общее выражение узлового напряжения
Исходя из вышеизложенного, узловое напряжение равно отношению алгебраической суммы произведений ЭДС на проводимости соответствующих ветвей к сумме проводимостей всех ветвей. ЭДС направленная к узлу A, записывается со знаком «+», если в противоположную сторону, то со знаком «-».
Давайте рассмотрим применения метода на конкретном примере.
Пример решения задач методом двух узлов (метод узлового напряжения)
Пример. Электрическая цепь постоянного тока представлена на рисунке 2. Определить токи в ветвях методом двух узлов, если ЭДС источников равна E1 = 40 В, E2 = 50 В, E3 = 10 В, а сопротивления r1 = 10 Ом, r2 = 20 Ом, r3 = 15 Ом, r4 = 12 Ом.

Порядок расчёта:
- Так как действительные направления токов до расчёта цепи нам неизвестны — произвольно указываем направления токов в ветвях, например, как на Рисунке 3.

- Определим проводимость ветвей.
- Найдем напряжение UAВ. Для этого воспользуемся формулой 6.
В числителе записываем произведения ЭДС на проводимости соответствующих ветвей, причем ЭДС направленная к узлу A, записывается со знаком «+», если в противоположную сторону, то со знаком «-».
В знаменателе указываем сумму проводимостей всех ветвей:
Подставляем раннее найденные значения проводимостей и значения ЭДС указанные в условии задачи:
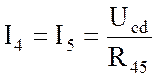
- Определим токи в ветвях. С учетом направления ЭДС
Подставляем численные значения
Токи I3 и I4 получились с отрицательными значениями, следовательно их направление противоположно ранее принятому.

Правильность решения можно проверить при помощи баланса мощностей.
Так же для себя правильность решения задачи можно проверить выполнением первого закона Кирхгофа, а именно:
Источник
Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов , страница 14
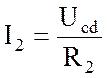
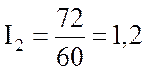
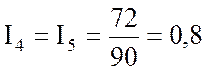
Напряжение Uab можно определить двумя путями:
а) через разность потенциалов
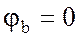
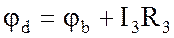
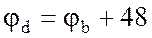
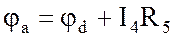
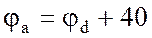
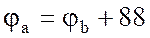
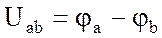
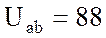
б) по второму закону Кирхгофа, например, для контура аbdа 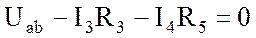
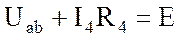
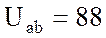
Отдаваемая источником мощность 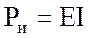
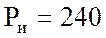
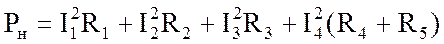
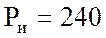
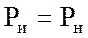
Условие задачи. В цепи (рис.2.38, схемы 1-10) источники ЭДС Е заданы в вольтах, источники тока J – в амперах, сопротивления R – в омах.
2) токи ветвей – методами контурных токов и узловых потенциалов;
3) проверить баланс мощностей.
Ответы приведены в табл.2.2; примеры расчета в разделах 2.7.2, 2.7.3, и 2.5.
Источник
Содержание:
Метод узловых напряжений:
Метод узловых напряжений (узловых потенциалов) является наиболее общим. Он базируется на первом законе Кирхгофа (ЗТК) и законе Ома. В отличие от методов, рассмотренных в лекции 4, метод позволяет уменьшить число уравнений, описывающих схему, до величины, равной количеству рёбер (ветвей) дерева (2.1)
Идея метода состоит в следующем:
- Выбирается базисный узел — один из узлов цепи, относительно которого рассчитываются напряжения во всех узлах; базисный узел помечается цифрой 0.
- Потенциал базисного узла принимается равным нулю.
- Рассчитываются напряжения во всех узлах относительно базисного.
- По закону Ома находятся токи и напряжения в соответствующих ветвях.
Напряжения в узлах цепи, отсчитанные относительно базисного, называют узловыми напряжениями.
Определение:
Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются узловые напряжения, называется методом узловых напряжений.
В дальнейшем будем полагать, что цепь имеет
Предварительно покажем, что при известных узловых напряжениях можно найти напряжения на всех элементах цепи, а потому и все токи. Действительно, напряжение на любой ветви определяется по второму закону Кирхгофа (ЗНК) как разность соответствующих узловых напряжений, а токи в элементах найдутся по закону Ома. Для контура, включающего элементы 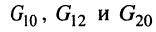
откуда
Аналогично можно записать
что и требовалось показать.
Составление узловых уравнений
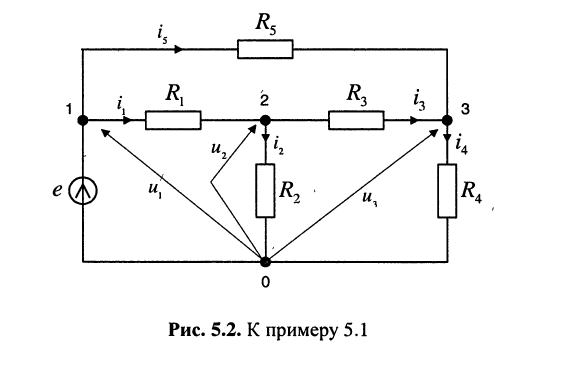
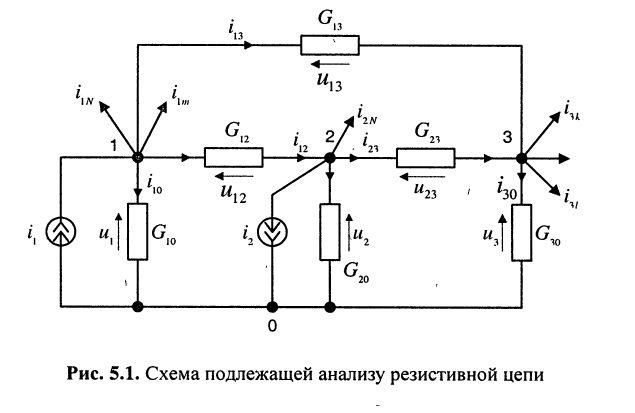
При составлении уравнений для, схемы рис. 5.1 будем полагать, что задающие токи 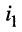
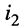
Тогда согласно первому закону Кирхгофа для узлов 1 и 2 в предположении, что в общем случае они связаны со всеми другими узлами, получим:
Выразим токи в уравнениях через узловые напряжения, как показано в разд. 5.1:
Раскрыв скобки и приведя подобные члены, получаем узловые уравнения:
Полученный результат позволяет сделать следующие выводы:

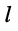
Аналогично записываются узловые уравнения для всех других узлов цепи, в результате чего образуется система узловых уравнений вида:
где:
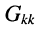


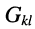

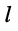

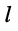
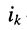



Систему узловых уравнений принято записывать в канонической форме, а именно:
- токи, как свободные члены, записываются в правых частях уравнений;
- неизвестные напряжения записываются в левых частях уравнений с последовательно возрастающими индексами;
- уравнения располагаются в соответствии с порядковыми номерами узлов. Такая запись применена в (5.2).
Система (5.2) является линейной неоднородной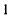
Метод узловых напряжений даёт существенное сокращение необходимого числа уравнений по сравнению с методом токов элементов. Выигрыш оказывается тем значительнее, чем больше независимых контуров имеет цепь.
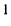
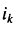
Особенности составления узловых уравнений
Метод узловых напряжений можно применять и в тех случаях, когда в анализируемой цепи имеются источники напряжения. При этом:
- напряжение между любой парой узлов, к которым подключён источник напряжения, известно;
- в качестве базисного желательно выбирать узел, к которому одним из своих зажимов подключён источник напряжения — тогда узловое напряжение, отсчитываемое между базисным узлом и вторым зажимом источника, равно ЭДС источника или отличается от него знаком; кроме того, базисным может быть выбран узел, к которому подключено наибольшее число элементов, если этот выбор не противоречит первой рекомендаций;
- уменьшается число независимых узловых напряжений, а потому понижается и порядок системы, т. е. число входящих в систему независимых уравнений;
- если цепь содержит
источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно
Пример 5.1.
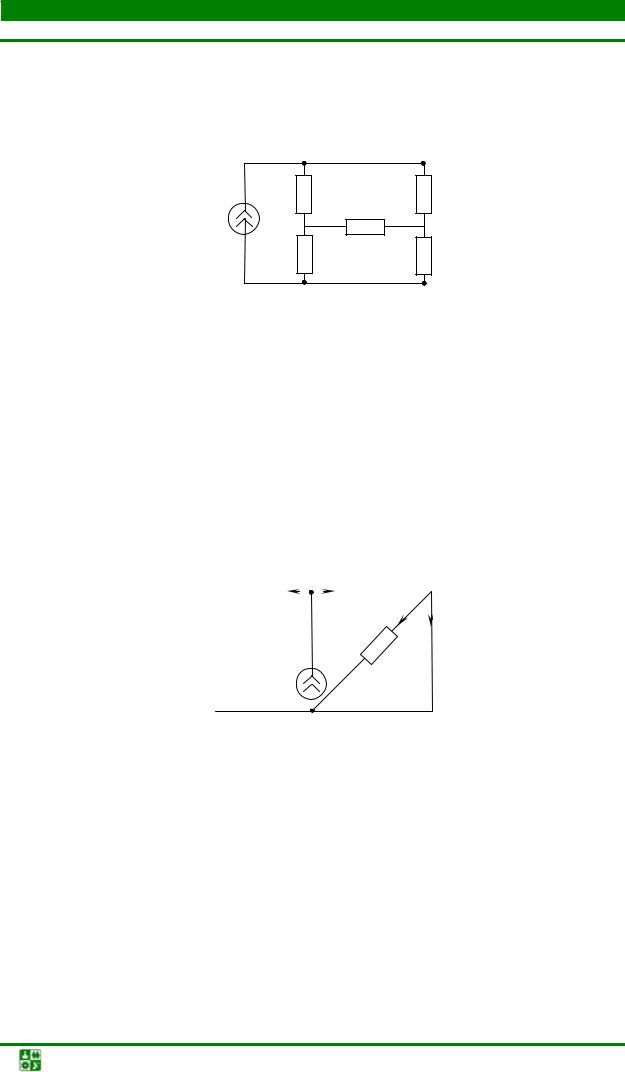
Записать систему узловых уравнений для удлинителя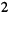
Решение. Удлинитель содержит четыре узла и один источник тока, поэтому согласно (5.3) достаточно составить всего два узловых уравнения
Положим узел 0 базисным, поскольку к нему одним из своих зажимов подключён источник напряжения. Узловое напряжение узла 1 известно и равно. ЭДС источника напряжения 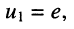
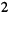
Собственная проводимость второго узла
взаимные проводимости второго узла
собственная проводимость третьего узла
взаимные проводимости третьего узла
Теперь получим систему узловых уравнений, записав узловые уравнения для второго и третьего узлов:
Поскольку 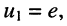
Эта система уравнений и является окончательным результатом решения задачи, поставленной в примере.
Если содержащиеся в цепи источники напряжения не имеют общего зажима, то задачу анализа следует решать или методом узловых напряжений в сочетании с принципом наложения или путём эквивалентных преобразований перейти к другой модели цепи.
При составлении узловых уравнений для цепей, содержащих многополюсники (например, транзисторы, операционные усилители
и т. д), следует прежде всего заменить эти многополюсники их схемами замещения.
Метод узлового напряжения
Расчет сложных разветвленных электрических цепей с несколькими источниками и двумя узлам, можно осуществить методом узлового напряжения. Напряжение межи узлами и называется узловым. UAB R3 узловое напряжение цепи (рис. 4.9) Для различных ветвей (рис. 4.9) узловое напряжение UAB можно опредо лить следующим образом.
1. Поскольку для первой ветви источник работает в режиме генератор:
Величина тока определяется как
где 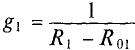
2.Для второй ветви источник работает в режиме потребителя следовательно
Тогда ток
3.Для третьей ветви
(Потенциал точки В для третьей ветви больше, чем потенций точки А, так как ток направлен из точки с большим потенциалом в точку с меньшим потенциалом)
Величину тока 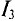
По первому закону Кирхгофа для узловой точки А (или В):
Подставив в уравнение (4.6) значения токов из уравнений (4.3), .4) и (4.5) для рассматриваемой цепи, можно записать
Решив это уравнение относительно узлового напряжения UAB, можно определить его значение
Следовательно, величина узлового напряжения определяется отношением алгебраической суммы произведений ЭДС и проводимости ветвей с источниками к сумме проводимостей всех ветвей:
Для определения знака алгебраической суммы направление токов во всех ветвях выбирают одинаковым, т.е. от одного узла другому (рис. 4.9). Тогда ЭДС источника, работающего в режиме генератора, берется со знаком «плюс», а источника, работающего в режиме потребителя, со знаком «минус». Таким образом, для определения токов в сложной цепи с двумя узлами вычисляется сначала узловое напряжение по выражению 4.9), а затем значения токов по формулам (4.3), (4.4), (4.5). Узловое напряжение UAB может получиться положительным или отрицательным, как и ток в любой ветви.
Знак «минус» в вычисленном значении тока указывает, что реальное направление тока в данной ветви противоположно словно выбранному.
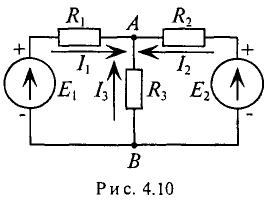
Пример 4.7
В ветвях схемы (рис. 4.10) требуется определить токи, если: 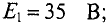
Решение
Узловое напряжение
где
тогда
Токи в ветвях будут соответственно равны
Как видно из полученных результатов, направление токов 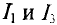
Пример 4.8
Два генератора (рис. 4.11), ЭДС и внутреннее сопротивление которых одинаковы: 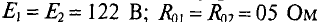
Как изменится ток второго генератора: 1) при увеличении его ЭДС (£2) на 1 %; ” 2) при увеличении узлового напряжения (UAB) на 1 %.
Решение
Определяется узловое напряжение UAB цепи (рис. 4.11)
где
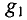
Тогда ток второго генератора
При увеличении Е2 на 1 %, его величина станет равной
тогда
При этом
Следовательно, увеличение ЭДС генератора Е2 на 1 % приводит увеличению тока этого генератора на 24 %.
2. При увеличении узлового напряжения на 1% его величины станет равной
При этом 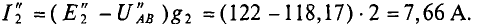
Знак «минус» означает уменьшение, а не увеличение тока 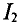
Определение метода узловых напряжений
Метод узловых напряжений заключается в том, что на основании первого закона Кирхгофа определяются потенциалы в узлах электрической цепи относительно некоторого базисного узла. Эти разности потенциалов называются узловыми напряжениями, причем положительное направление их указывается стрелкой от рассматриваемого узла к базисному.
Напряжение на какой-либо ветви равно, очевидно, разности узловых напряжений концов данной ветви; произведение же этого напряжения на комплексную проводимость данной ветви равно току в этой ветви. Таким образом, зная узловые напряжения в электрической цепи, можно найти токи в ветвях.
Если принять потенциал базисного узла равным нулю, то напряжения между остальными узлами и базисным узлом будут равны также потенциалам этих узлов. Поэтому данный метод называется также методом узловых потенциалов.
На рис. 7-7 в виде примера изображена электрическая схема с двумя источниками тока, имеющая три узла: 1, 2 и 3. Выберем в данной схеме в качестве базиса узел 3 и
обозначим узловые напряжения точек 1 и 2 через 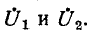
Для заданной электрической цепи с тремя узлами могут быть записаны два уравнения по первому закону Кирхгофа, а именно: для узла 1
для узла 2
Величина 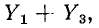
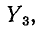
Если заданы токи источников тока и комплексные проводимости ветвей, то узловые напряжения находятся совместным решением уравнений.
В общем случае если электрическая схема содержит q узлов, то на основании первого закона Кирхгофа получается система из q — 1 уравнений (узел q принят за базисный):
Здесь ток источника тока, подходящий к узлу, берется со знаком плюс, а отходящий от узла — со знаком минус;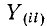
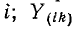
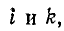
Решив систему уравнений (7-5) при помощи определителей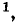
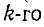
где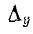
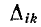
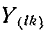
Первый индекс i алгебраического дополнения, обозначающий номер строки, вычеркиваемой в определителе системы, соответствует номеру узла, заданный ток источника тока которого умножается на данное алгебраическое дополнение. Второй индекс 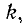
Уравнения (7-5), выражающие первый закон Кирхгофа, записаны в предположении, что в качестве источников электрической энергии служат источники тока. При наличии в электрической схеме источников э. д. с. последние должны быть заменены эквивалентными источниками тока.
Если в схеме имеются ветви, содержащие только э. д, с. (проводимости таких ветвей бесконечно велики), то эти ветви следует рассматривать как источники неизвестных токов, которые затем исключаются при сложении соответствующих уравнений. Дополнительными связями между неизвестными узловыми напряжениями будут являться известные напряжения между узлами, равные заданным э. д. с.
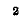
При наличии только одной ветви с э. д. с. и бесконечной проводимостью целесообразно принять за базисный узел один из узлов, к которому примыкает данная ветвь; тогда напряжение другого узла становится известным и число неизвестных сокращается на одно.
Метод узловых напряжений имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа. Если заданная электрическая схема имеет q узлов и р ветвей, то в соответствии со сказанным выше, метод узловых напряжений представляет преимущество при q — 1 < р — q + 1. или, что то же, при 2 (q — 1) < р.
Здесь имеется в виду общий случай, когда число уравнений не сокращается за счет известных контурных токов
или узловых напряжении.
Пример 7-3.
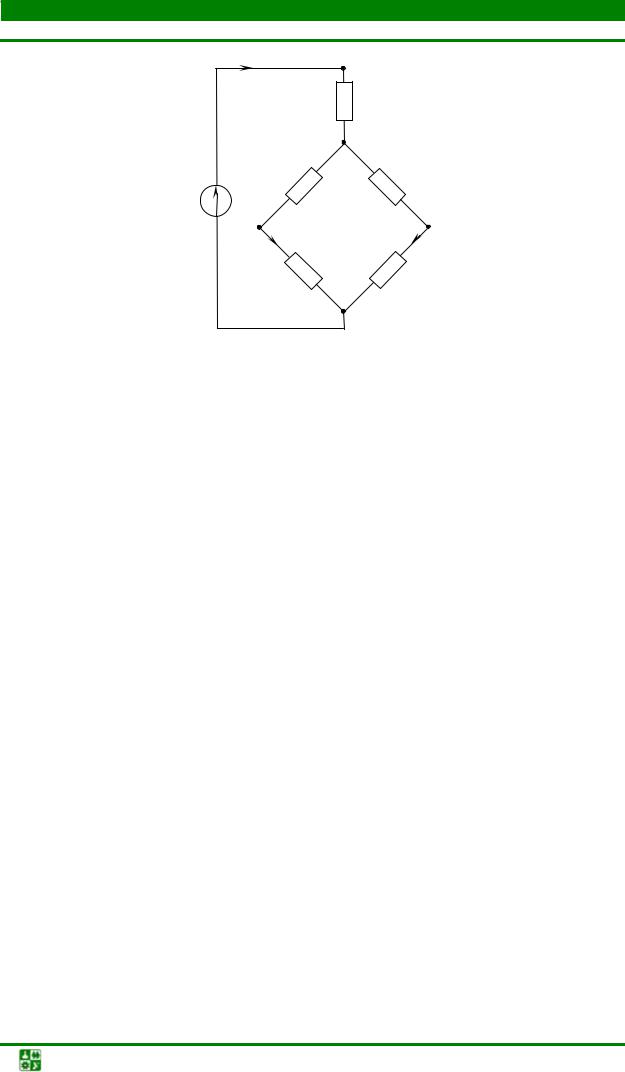
Пользуясь методом узловых напряжений определить ток в диагонали мостовой схемы (см. рис. 7-6).
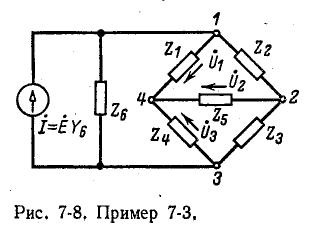
В результате замены заданного источника э. д. с. .эквивалентным источником тока получается схема (рис. 7-8), содержащая четыре узла. Для этой схемы по первому закону Кирхгофа записывают 4—1 = 3 уравнения (по числу независимых узлов). Если выбрать в данной схеме в качестве базиса узел 4 и направить узловые напряжения к базису, то уравнения примут вид:
для узла 1
для узла 2
для узла 3
Решение полученной системы уравнений относительно 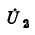
где
Умножив найденное узловое напряжение 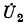
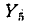
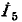
- Метод узловых потенциалов
- Принцип и метод наложения
- Входные и взаимные проводимости
- Преобразование треугольника сопротивлений в эквивалентную звезду
- Электрическая цепь
- Электрический ток
- Электрические цепи постоянного тока
- Методы анализа сложных электрических цепей

Тема1 Метод эквивалентных преобразований
Изучение этой темы очень важно, так как в ней подробно рассматриваются вопросы, необходимые для решения задач всех последующих разделов курса. Учебной программой предусмотрены три практических занятия по данной теме.
Занятие1
Цели занятия:
1.Научиться применять законы Ома и Кирхгофа для расчета цепей
содним источником ЭДС.
2.Научиться рассчитывать эквивалентное сопротивление цепи при последовательно-параллельном соединении приемников.
3.Научиться использовать формулу для определения тока в одной из двух пассивных параллельных ветвей, когда общий ток известен.
Рассмотрим первую целевую задачу занятия.
В настоящее время под законом Ома понимают соотношения, связывающие напряжение и ток. В схемах замещения цепей постоянного тока имеется один вид приемников – резистор, обладающий сопротивлением R. По закону Ома напряжение на резисторе пропорционально току в нем.
Коэффициент пропорциональности и назван сопротивлением: U R = R I .
Первый закон Кирхгофа сформулирован для узла. Узел – это точка в схеме, где сходятся не менее трех ветвей. В настоящее время при использовании ЭВМ для ввода исходных данных узлами выделяют каждый элемент схемы замещения. Эти узлы называют ложными или устранимыми. В дальнейшем речь будет идти о неустранимых узлах.
Алгебраическая сумма токов в узле равна нулю:
n
∑I j = 0.
j=1
Второй закон Кирхгофа относится к контуру. Алгебраическая сумма напряжений на приемниках в любом контуре равна алгебраической сумме ЭДС, действующих в этом же контуре:
|
Теоретические основы электротехники. Практикум |
-6- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
При непосредственном использовании законов Ома и Кирхгофа решение получается громоздким. Расчет схемы с одним источником энергии и несколькими приемниками существенно упрощается при применении метода эквивалентных преобразований. Все приемники заменяют одним с эквивалентным сопротивлением. При этом токи и напряжения в частях схемы, не затронутых преобразованием, должны оставаться неизменными. Находят токи в свернутой схеме. Затем постепенно возвращаются к исходной схеме с определением остальных токов.
Перейдем ко второй целевой задаче.
Преобразование схемы проводят постепенно, выявляя участки с последовательными и параллельными соединениями приемников. Предварительно нужно выявить узлы и ветви. Узел – точка в схеме, где сходятся не менее трех ветвей. Ветвь – участок с одним током между двумя узлами. Элементы, принадлежащие одной ветви, соединены между собой последовательно. В них один ток. Эквивалентное сопротивление последовательно соединенных резисторов равно сумме их сопротивлений:
n
Rэ = i∑=1Ri .
При параллельном соединении элементы схемы замещения находятся под одним напряжением и соединены между собой двумя выходными зажимами. Эквивалентная проводимость параллельно соединенных резисторов равна сумме их проводимостей:
|
1 |
n |
1 |
||
|
= i∑=1 |
||||
|
R |
э |
R |
||
|
i |
При параллельном соединении двух резисторов с сопротивлениями R1 и R2 эквивалентное сопротивление
Rэ = R1 R2
R1 + R2
При параллельном соединении n одинаковых резисторов сопротивлением R эквивалентное сопротивление Rэ = Rn
Если способ соединения резисторов не совсем ясен, нужно перечертить схему, начиная с одного входного зажима и заканчивая другим, изображая узлы с одинаковыми потенциалами (соединенные ветвью с нулевым сопротивлением) как один узел.
|
Теоретические основы электротехники. Практикум |
-7- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
К третьей целевой задаче занятия переходим после того, как схема превращена в одноконтурную с током I, который определяют по закону Ома:
I = Е . Возвращаемся к исходной схеме с определением остальных токов.
Rэ
При этом удобно пользоваться формулой для определения тока в одной из двух параллельно соединенных пассивных ветвей. Ток в одной из двух
|
параллельно соединенных |
пассивных |
ветвей пропорционален току |
|||
|
в неразветвленной |
части |
схемы. |
В |
числителе |
коэффициента |
пропорциональности записываем сопротивление другой пассивной ветви, в знаменателе – сумму сопротивлений двух пассивных параллельных ветвей.
Рассмотрим алгоритм решения на примере конкретных задач.
Задача1
Напряжение между зажимами батареи измеряли три раза разными вольтметрами, отличающимися друг от друга величиной внутреннего
|
сопротивления: |
RV = |
400 Ом, |
RV |
= 2400 |
Ом, RV |
= ∞. ЭДС |
батареи |
|||||||||
|
1 |
2 |
3 |
||||||||||||||
|
Е = 75 В, |
Rвн =100 Ом. |
|||||||||||||||
|
Определить показания вольтметра. |
||||||||||||||||
|
Пояснение к решению |
||||||||||||||||
|
Если в условии задачи не приведена схема замещения цепи, то прежде |
||||||||||||||||
|
всего ее надо составить (рис. 1.1). |
||||||||||||||||
|
Схема одноконтурная, в ней один ток, |
I |
|||||||||||||||
|
направление |
которого |
определяет |
||||||||||||||
|
направление |
ЭДС. |
Стрелка |
источника |
|||||||||||||
|
E |
RV |
|||||||||||||||
|
показывает |
направление |
увеличения |
UV |
|||||||||||||
|
потенциала. Направление тока рекомендуют |
Rвн |
|||||||||||||||
|
указывать стрелкой на линии, обозначающей |
||||||||||||||||
|
провод. |
Ток |
направлен |
в |
сторону |
||||||||||||
|
уменьшения потенциала. |
||||||||||||||||
|
Рис. 1.1 |
||||||||||||||||
|
Знаки плюс и минус на схеме говорят |
||||||||||||||||
|
лишь о |
том, что |
потенциал |
точки, |
отмеченной знаком плюс, выше потенциала точки, отмеченной знаком минус.
Напряжение на вольтметре, равное напряжению на зажимах батареи, покажем стрелкой, параллельной резистору, учитывающему вольтметр. Напряжение направлено по току.
Решение
1. Напряжение вольтметра по закону Ома: UV = RV I .
|
Теоретические основы электротехники. Практикум |
-8- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
2. Ток в цепи по закону Ома: I = E
Rэ
3. В резисторах один ток, следовательно, они соединены
последовательно, Rэ = Rвн + RV .
Сделаем расчет для трех различных вольтметров:
|
а) R |
= 400 |
Ом; R |
э |
=100 + 400 = |
500 Ом; I = |
75 |
= 0,15 |
А; U |
V |
= 60 |
В. |
|||||||||
|
V |
500 |
|||||||||||||||||||
|
1 |
||||||||||||||||||||
|
б) R |
= 2400 Ом; R |
э |
=100 + 2400 = 2500 Ом; I = |
75 |
= 0,03 |
А; U |
V |
= 72 В. |
||||||||||||
|
V |
2500 |
|||||||||||||||||||
|
2 |
||||||||||||||||||||
|
в) R |
= ∞; |
R |
э |
=100 + ∞ = ∞; I = |
75 = 0 ; U |
V |
= ∞ 0 =неопределенность. |
|||||||||||||
|
V |
∞ |
|||||||||||||||||||
|
3 |
||||||||||||||||||||
Предложенный алгоритм не дает возможности определить показания третьего вольтметра. Обсудим результаты, полученные для двух первых вольтметров. ЭДС батареи Е = 75 В, однако первый вольтметр показал 60 В, второй – 72 В. Разница между ЭДС и показаниями вольт метра – падение напряжения на резисторе, учитывающем внутреннее сопротивление источника. Во втором случае оно меньше, следовательно, второй вольтметр лучше первого. Он отличается большим значением внутреннего сопротивления. Идеальным является вольтметр с RV3 = ∞. Ток в цепи равен
нулю, падение напряжения Uвн = Rвн I = 0 , UV3 = E = 75 В. Уравнение по второму закону Кирхгофа имеет вид Uвн +UV = E . После подстановки значений напряжений по закону Ома получим
Rвн I + RV I = E .
Для третьего вольтметра находим следующее значение:
100 0 + ∞ 0 = 75 , т. е. UV3 = ∞ 0 = 75 В.
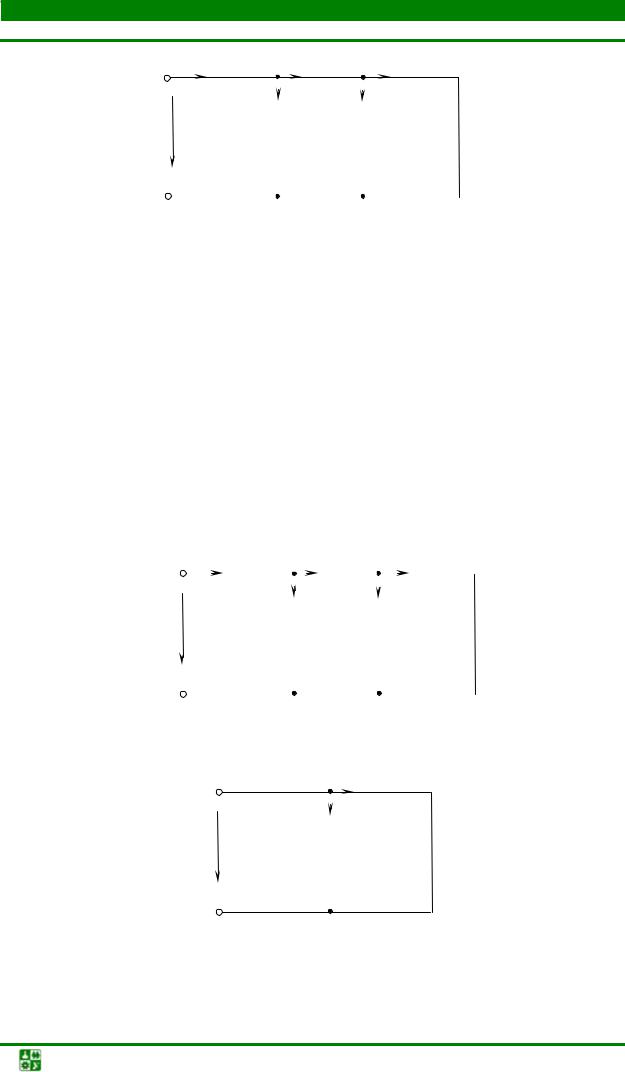
Задача2
Найти эквивалентное сопротивление цепи, схема замещения которой изображена на рис. 1.2.
|
Теоретические основы электротехники. Практикум |
-9- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
I1 |
a I3 |
b |
I 5 |
|||||||||||||||||||||||||||||||||||||
|
I 4 |
||||||||||||||||||||||||||||||||||||||||
|
R1 |
I2 |
R3 |
R5 |
|||||||||||||||||||||||||||||||||||||
|
U |
R2 |
R |
R6 |
|||||||||||||||||||||||||||||||||||||
|
4 |
||||||||||||||||||||||||||||||||||||||||
|
c |
d |
|||||||||||||||||||||||||||||||||||||||
|
Рис. 1.2 |
||||||||||||||||||||||||||||||||||||||||
|
В схеме три узла, потому что точки с и d |
можно рассматривать как |
|||||||||||||||||||||||||||||||||||||||
|
одну. Узлы соединены между собой пятью ветвями. |
||||||||||||||||||||||||||||||||||||||||
|
Решение |
||||||||||||||||||||||||||||||||||||||||
|
В пятой ветви два резистора с сопротивлениями |
R5 |
и R6 |
соединены |
|||||||||||||||||||||||||||||||||||||
|
между собой последовательно. Их |
можно |
заменить |
одним |
резистором |
||||||||||||||||||||||||||||||||||||
|
с эквивалентным сопротивлением |
R56 = R5 + R6 (рис. |
1.3). |
В этой |
схеме |
||||||||||||||||||||||||||||||||||||
|
резисторы с сопротивлениями R4 |
и |
R56 |
соединены |
между |
собой |
|||||||||||||||||||||||||||||||||||
|
параллельно. |
Заменим их |
одним |
с |
эквивалентным |
сопротивлением |
|||||||||||||||||||||||||||||||||||
|
R |
= |
R4 R56 |
(рис. 1.4). |
|||||||||||||||||||||||||||||||||||||
|
bc |
R4 + R56 |
|||||||||||||||||||||||||||||||||||||||
|
I1 |
a I3 |
b |
I 5 |
|||||||||||||||||||||||||||||||||||||
|
I2 |
I |
|||||||||||||||||||||||||||||||||||||||
|
R |
R |
4 |
||||||||||||||||||||||||||||||||||||||
|
U |
1 |
3 |
||||||||||||||||||||||||||||||||||||||
|
R2 |
R |
R56 |
||||||||||||||||||||||||||||||||||||||
|
c |
4 |
|||||||||||||||||||||||||||||||||||||||
|
Рис. 1.3 |
||||||||||||||||||||||||||||||||||||||||
|
a I3 |
||||||||||||||||||||||||||||||||||||||||
|
I2 |
||||||||||||||||||||||||||||||||||||||||
|
R |
R3 |
|||||||||||||||||||||||||||||||||||||||
|
U |
1 |
|||||||||||||||||||||||||||||||||||||||
|
R2 |
R |
|||||||||||||||||||||||||||||||||||||||
|
bc |
||||||||||||||||||||||||||||||||||||||||
c
Рис. 1.4
|
Теоретические основы электротехники. Практикум |
-10- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
Резисторы с сопротивлениями R3 и Rbc соединены между собой
последовательно. Заменяем их одним резистором с эквивалентным сопротивлением, равным R3 + Rbc . Дальнейшие преобразования повторяют
предыдущие. Эквивалентное сопротивление схемы
|
R |
= R |
+ R2 (R3 + Rbc ) |
|||
|
э |
1 |
R2 |
+ R3 + Rbc |
||
Решите следующие задачи самостоятельно.
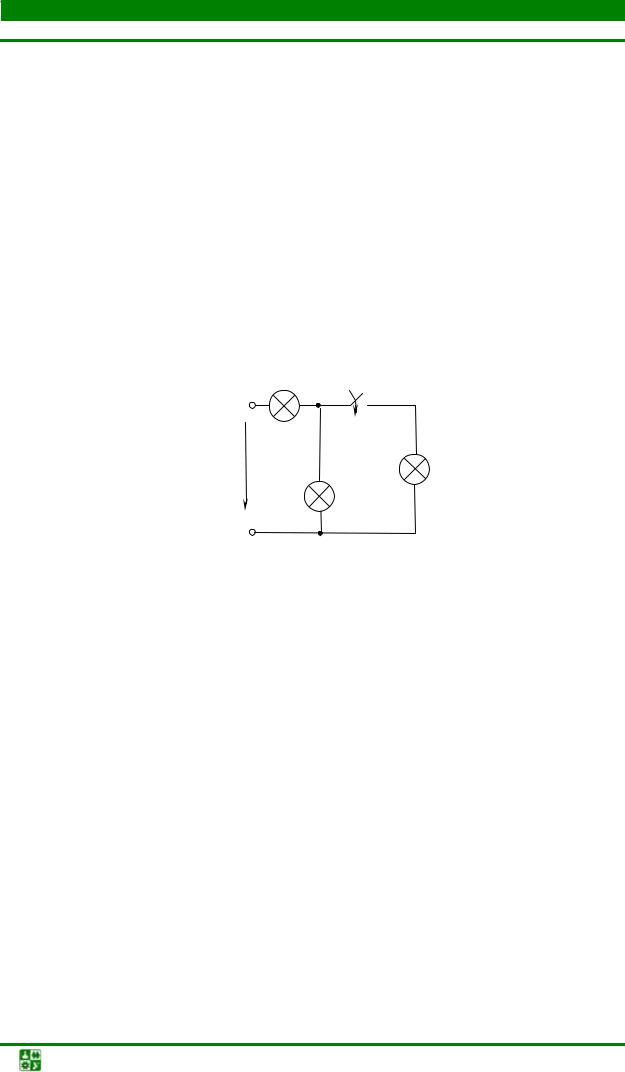
Задача3
Как изменится яркость первой и второй лампочек после подключения третьей лампочки (рис. 1.5).
Рис. 1.5
Сопротивления всех лампочек одинаковы.
Примечание. Если вы получили ответ, в котором говорится, что яркость лампочки Л1 увеличилась, а лампочки Л2 – уменьшилась, переходите к решению следующей задачи. В противном случае (или для самоконтроля) прочтите решение задачи 3.
Решение
Яркость лампочек зависит от напряжения на них. По второму закону Кирхгофа напряжение на входе схемы U до и после замыкания ключа складывается из напряжений на первой и второй лампочках. Так как входное напряжение не изменялось, напряжения на лампочках Л1 и Л2 либо тоже не изменялись, либо изменялись противоположно. Если обозначим сопротивление одной лампочки R, то до замыкания ключа эквивалентное сопротивление последовательно соединенных Л1 и Л2 Rэ1 = 2R . После
замыкания ключа получилась схема со смешанным соединением: лампочки Л2 и Л3 соединены между собой параллельно, лампочка Л1 подключена к ним последовательно. Эквивалентное сопротивление
|
Теоретические основы электротехники. Практикум |
-11- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
Rэ2 = R + R2 =1,5 R .
Эквивалентное сопротивление уменьшилось, поэтому общий ток увеличился, увеличилось напряжение на первой лампочке, следовательно, и ее яркость. Яркость второй лампочки соответственно уменьшится.
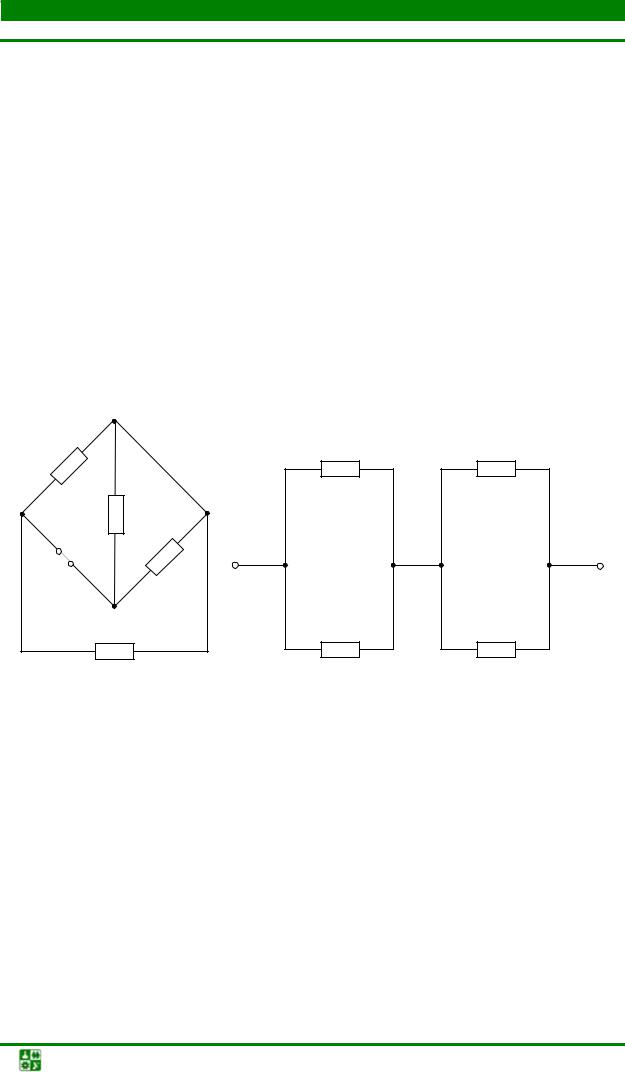
Задача4
Найти входное эквивалентное сопротивление схемы, изображенной на рис. 1.6.
Пояснение к решению
Если перерисовать схему (рис. 1.7) в соответствии с данными рекомендациями, то способ соединения резисторов становится очевидным.
|
R |
R |
R |
|
|
R |
|||
|
a b |
a |
b |
|
|
R |
|||
|
R |
R |
R |
|
|
Рис. 1.6 |
Рис. 1.7 |
Ответ: Rэ = R2 + R2 = R.
Задача5
Найти входное эквивалентное сопротивление схемы рис. 1.8.
|
Теоретические основы электротехники. Практикум |
-12- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
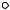
R R
Рис. 1.8
Пояснение к решению
Знак означает, что потенциал данной точки равен нулю. Ответ: Rэ = 2R.
|
Задача6 |
||||||
|
Вычислить токи в схеме |
рис. 1.9, |
если U =120 В, R1 = 18 Ом, |
||||
|
R2 = 30 Ом, R3 = 20 Ом. |
R2 |
|||||
|
I2 |
||||||
|
I1 |
R1 |
b |
||||
|
a |
||||||
|
+ |
I3 |
R3 |
||||
|
U |
||||||
Рис. 1.9
Пояснение к решению
Выявить в схеме узлы ( a и b), найти ветви, их соединяющие, указать направления токов. Цепь на входе не разорвана. Источник ЭДС на схеме часто не изображают, так как он находится на электростанции. Показывают напряжение на его зажимах. Ветвь с током I1 является активной, ветви с
токами I2 и I3 – пассивные.
Решение
|
Теоретические основы электротехники. Практикум |
-13- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
1. Эквивалентное сопротивление цепи
|
R |
э |
= R + |
R2 R3 |
=18 + |
30 20 |
= 30 Ом. |
|
1 |
R2 |
+ R3 |
30 + 20 |
|||
2. Ток в свернутой схеме I1 (так как источник ЭДС не подвергался преобразованиям) вычисляем по закону Ома:
I1 = U = 120 = 4 А.
Rэ 30
3. Вычислим ток в одной из двух пассивных параллельных ветвей:
I2 = R2R+3 R3 I1 = 3020+ 20 4 =1,6 А.
4. Ток I3 можно вычислить по аналогичной формуле либо с помощью первого закона Кирхгофа:
I3 = R2R+2R3 I1 = 3030+ 20 4 = 2,4 А,
либо I3 = I1 − I2 = 4 −1,6 = 2,4 А.
Следующие задачи решите для самоконтроля.
Задача7
Вычислить эквивалентное сопротивление схемы рис. 1.10. Ответ: Rэ =113 R .
R R 
Рис. 1.10
Задача8
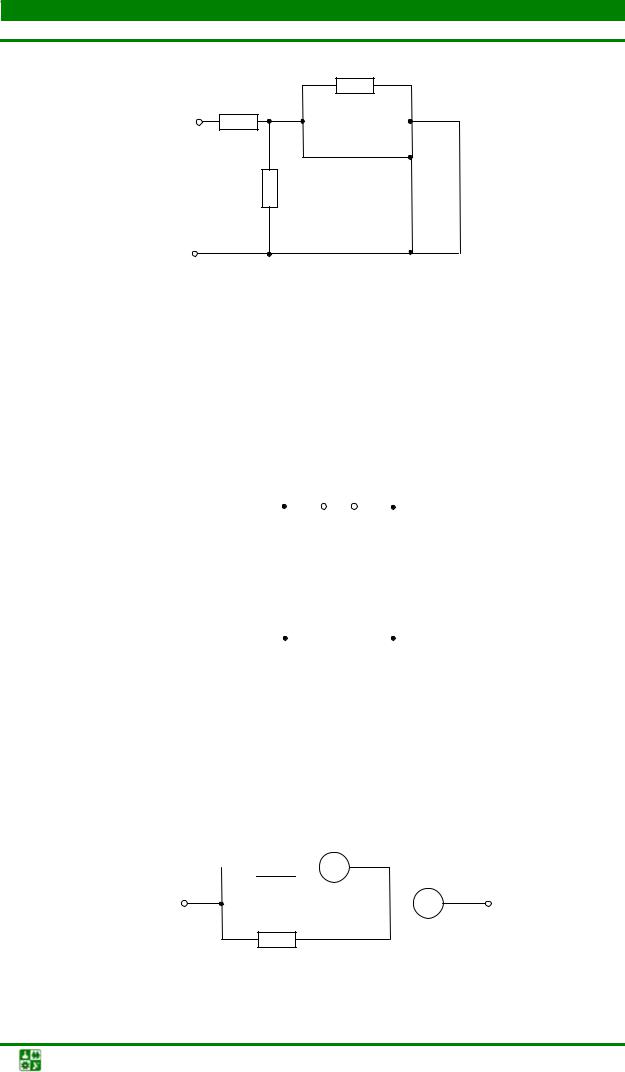
Вычислить эквивалентное сопротивление схемы рис. 1.11.
|
Теоретические основы электротехники. Практикум |
-14- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
2R
R
2R
|
4R |
4R |
4R |
||||||
|
R |
||||||||
|
Рис. 1.11 |
Ответ: Rэ = 3R .
Задача9
Вычислить эквивалентное сопротивление схемы рис. 1.12.
3R
|
2R |
2R |
2R |
2R |
|||||||||||||
|
R |
||||||||||||||||
|
Рис. 1.12 |
||||||||||||||||
|
Ответ: Rэ =1,5R . |
||||||||||||||||
|
Задача10 |
||||||||||||||||
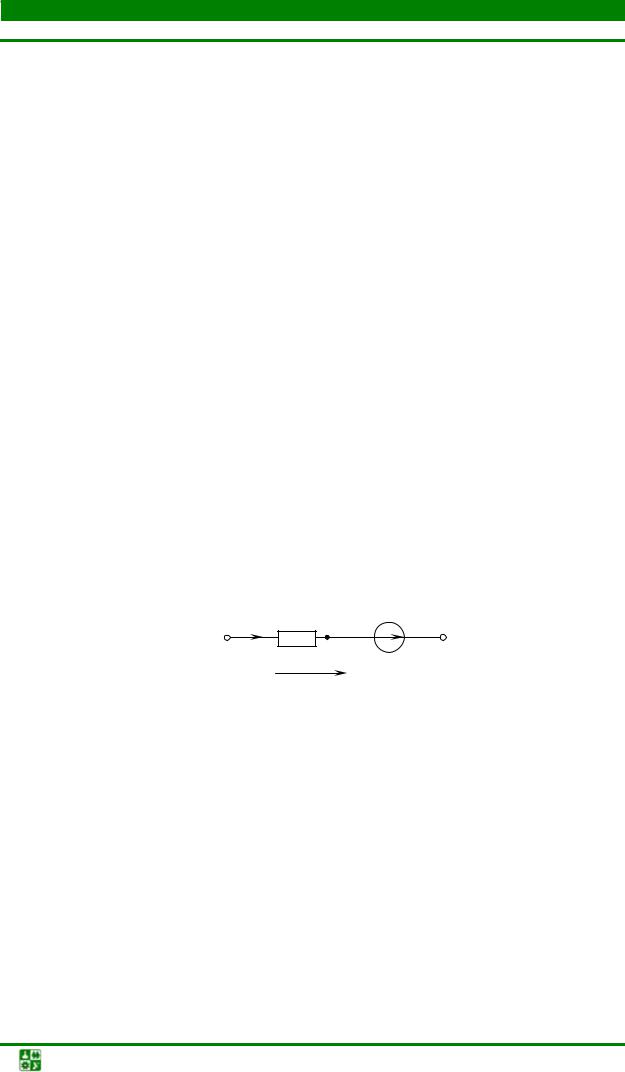
|
Вычислить сопротивление |
R2 в схеме рис. 1.13, если R1 = 3 Ом, |
|||||||||||||||
|
амперметр А показывает ток 25 А, амперметр |
A2 – ток 5 А. |
R2


R1
Рис. 1.13
|
Теоретические основы электротехники. Практикум |
-15- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
Ответ: R2 =12 Ом.
Задача11
Линия передачи электроэнергии расположена на двух опорах, сопротивление изоляции которых составляет 20 кОм. Напряжение на входе U = 480 В. Человек, стоя на земле, взялся одной рукой за провод. Сопротивление человека равно 5 кОм. Погибнет ли человек, если «убойный» ток порядка 0,1 А?
Пояснение к решению
Прежде чем решать задачу, следует составить схему замещения исследуемой цепи.
Ответ: нет, так как ток через человека Iч = 0,016 А.
Занятие2
Цели занятия:
1.Научиться определять напряжение между любыми точками схемы.
2.Научиться проверять правильность расчета токов, составляя уравнение баланса мощностей.
Рассмотрим первую целевую задачу занятия.
Активная ветвь, названная так из-за наличия источника ЭДС, изображена на рис. 1.14.
|
a |
I |
R |
c |
E |
|
|
b |
|||||
|
Uab |
|||||
Рис. 1.14
Между концами ветви возникает напряжение Uab . Индексация
показывает направление ко второму индексу. Напряжение – это разность потенциалов между двумя точками, т. е. Uab =Va −Vb .
Определим потенциал точки а, исходя из потенциала Vb . Рассчитаем изменение потенциала промежуточной точки c (рис. 1.14) по сравнению с Vb .
Между точками b и с расположен источник ЭДС, т. е. потенциал точки с отличается от потенциала точки b на величину E. Стрелка источника показывает направление увеличения потенциала. Следовательно, потенциал точки с ниже потенциала точки b. Между точками с и а находится резистор с сопротивлением R. Потенциал Va отличается от потенциала Vc величиной
напряжения на резисторе RI . Ток направлен от большего потенциала к
|
Теоретические основы электротехники. Практикум |
-16- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
меньшему. Так как на пути от с к а перемещение происходит навстречу току, потенциал Va выше потенциала Vc .
Итак, Va =Vb − E + RI ,
Va −Vb = −E + RI ,
но Va −Vb =Uab , т. е. Uab = −E + RI .
Можно определить напряжение между двумя любыми точками, рассчитав изменение потенциалов между ними. При этом нужно вести расчет в сторону увеличения потенциала, т. е. от второго индекса к первому.
Решим уравнение относительно тока:
I = UabR+ E = G(Uab + E),
где G = R1 – проводимость ветви. Это выражение называют законом
Ома для активной ветви.
Последнее выражение можно составить, исходя из следующих рассуждений. Для появления тока в ветви (рис. 1.14) есть два условия: наличие разности потенциалов между концами ветви и действие источника ЭДС. Если направление ЭДС совпадает с направлением тока, она способствует его появлению и должна быть записана в уравнение со знаком плюс. В противном случае – со знаком минус. Напряжение Uab и ток I
направлены одинаково (от точки а к точке b), поэтому напряжение Uab
должно быть записано в уравнение со знаком плюс. Рассуждая таким образом, получаем для тока ветви прежнее выражение.
Перейдем к рассмотрению второй целевой задачи.
Баланс мощностей – интерпретация закона сохранения энергии в электротехнике. Мощность источников энергии равна мощности потребителей: Pг = Rн, причем
|
n |
m |
||
|
Pг = ∑Ei Ii + ∑U j J j , |
|||
|
i=1 |
j=1 |
||
|
где |
n |
– мощность источников ЭДС; |
m |
|
∑Ei Ii |
∑U j I j – мощность источников |
||
|
i=1 |
j=1 |
тока; J j – токи источников тока.
Эти суммы алгебраические. Источник может вырабатывать и потреблять электрическую энергию (заряд аккумулятора).
Если направления ЭДС и тока через источник ЭДС совпадают, мощность источника записывают в уравнение баланса мощностей с положительным знаком. Он работает в режиме генератора. При
|
Теоретические основы электротехники. Практикум |
-17- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
противоположных направлениях ЭДС и тока мощность в уравнении баланса учитывают с отрицательным знаком (режим потребителя).
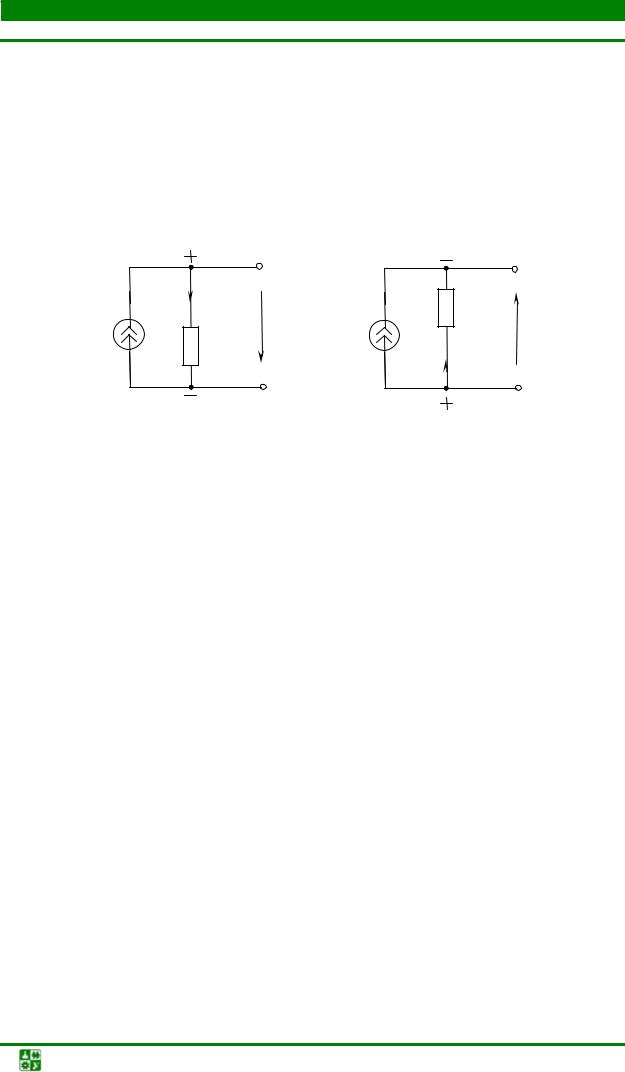
Определение знака мощности источника тока поясняет рис. 1.15, на котором показана разметка зажимов источника тока, вырабатывающего (а) или потребляющего (б) электрическую энергию.
Ток I0 и напряжение U направлены в сторону уменьшения потенциала, что и позволяет разметить зажимы источника.
|
I0 |
R0 |
|||
|
U |
||||
|
J |
J |
U |
||
|
R0 |
||||
|
I0 |
||||
|
а |
б |
Рис. 1.15
Мощность потребителей (нагрузок)
|
1 |
I |
1 |
I 2 . |
||||||
|
P = ∑U |
k |
k |
= ∑R |
k |
|||||
|
н |
k=1 |
k=1 |
k |
||||||
|
Эта сумма арифметическая. Погрешность расчета не |
должна |
||||||||
|
превышать |
|||||||||
|
(1–3) %. |
|||||||||
|
Задача1 |
|||||||||
|
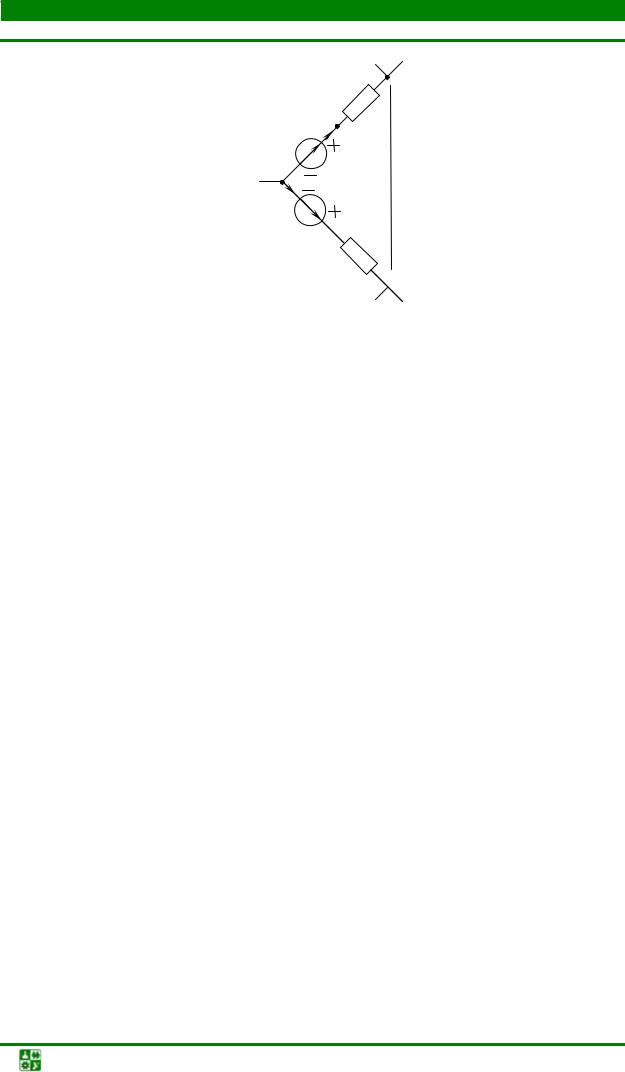
На рис. 1.16 показана часть схемы замещения электрической цепи. |
|||||||||
|
Вычислить напряжение Uab , если |
I1 = 3A, |
I2 = 2,4 А, E1 = 70В, |
R1 = 8Ом, |
||||||
|
R2 = 5Ом, E2 = 20 В. |
|
Теоретические основы электротехники. Практикум |
-18- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
a |
|
|
R1 |
|
|
I1 |
e |
|
E1 |
|
|
d |
Uab |
|
I2 |
E2 
R2 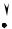
Рис. 1.16
Пояснение к решению
Нужно расставить на схеме промежуточные точки за каждым элементом. Расчет изменения потенциалов ведем от точки b к точке а, т. е. в сторону увеличения потенциала. Разметим зажимы у источников ЭДС.
Решение
Потенциал точки с изменился по сравнению с потенциалом Vb на величину напряжения R2 I2 Так как на пути от b к c перемещение происходит против тока, потенциал Vc выше потенциала Vb . Между точками с и d находится источник ЭДС E2 . Разметка зажимов источника показывает, что потенциал Vd меньше потенциала Vc на величину E2 . Потенциал точки е Ve больше потенциала Vd на величину E1. Потенциал Va меньше потенциала Ve на величину напряжения R1I1 , так как ток I1 направлен от точки е к
точке а.
Таким образом, Uab = R2 I2 − E2 + E1 − R1I1 = 5 2,4 −20 + 70 −8 3 = 38
В.
Задача2
Вычислить напряжение Uab в схеме рис. 1.17, если E = 45 В, R1 = 20 Ом, R2 = 30 Ом, R3 =10 Ом, R4 = 5 Ом.
|
Теоретические основы электротехники. Практикум |
-19- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
a |
R3 |
I3 c |
I2 |
|
I1 |
|||
|
Uab |
R1 |
R2 |
|
|
b |
|||
R4 
d
Рис. 1.17
Пояснение к решению
Сначала нужно разобраться в топологии схемы, т. е. найти узлы и ветви. В схеме два неустранимых узла: с и d. Между ними находятся три ветви. Число токов равно числу ветвей. В схеме с одним источником энергии при последовательно-параллельном соединении приемников направления токов являются очевидными. Если направления токов указаны неверно, то при их расчете методом эквивалентных преобразований напряжение Uab
будет вычислено неправильно. Сначала укажем направление тока в активной ветви I1, которое определено направлением ЭДС источника. В узле с (рис.
1.17) ток I1 разветвляется на токи I2 и I3 .
Решение
1. Запишем выражение напряжения Uab как разность потенциалов Va
и Vb :
Uab = −R1I1 − R3I3,
либо так:
Uab = −E + R4 I3 .
2. Расчет нужных для вычисления напряжения Uab токов проведём
методом эквивалентных преобразований. В резисторах с сопротивлениями R 3 и R4 один ток, значит, они соединены последовательно. Их можно
заменить одним с эквивалентным сопротивлением R34 = R3 + R4.
Резистор с сопротивлением R 34 и резистор с сопротивлением R2 подключены к точкам с и d , т. е. находятся под одним напряжением Ucd ,
следовательно, соединены параллельно. После их замены одним резистором с эквивалентным сопротивлением получаем одноконтурную схему с последовательным соединением элементов. Таким образом,
|
Теоретические основы электротехники. Практикум |
-20- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
R |
э |
= R + |
R2 R34 |
= 20 + |
30 15 |
= 30 Ом. |
|
1 |
R2 |
+ R34 |
30 +15 |
|||
3. Вычислим ток I1 в свёрнутой схеме (ток в источнике ЭДС остался неизменным):
|
I1 = |
E |
= |
45 |
=1,5 |
А. |
|
30 |
|||||
|
Rэ |
4. Вычислим ток I3 по формуле для определения тока в одной из двух пассивных параллельных ветвей:
|
I3 |
= |
R2 |
I1 = |
30 |
=1А. |
||
|
R2 |
+ R34 |
30 +15 |
|||||
Напряжение Uab = −20 1,5 −10 1 = −40 В, либо Uab = −45 +5 1 = −40В.
Обратите внимание! Если ответ получился со знаком минус, это означает, что потенциал точки b выше потенциала точки а. Напряжение направлено противоположно указанному на рис. 1.17. Действительные направления токов и напряжений рекомендуется указывать пунктирными стрелками параллельно выбранным первоначально.
5. Для проверки правильности расчета токов составим уравнение баланса мощностей цепи:
E I1 = R1I12 + R2I22 + R3I32 + R4I32 .
Ток
I2 = I1 − I3 = 0,5 А.
Pг = 45 1,5 = 67,5Вт.
Pн = 20 1,52 +30 0,52 +10 12 +5 12 = 67,5 Вт.
67,5 Вт = 67,5 Вт.
Pг = Pн.
Следующую задачу решите самостоятельно.
Задача3
Вычислить напряжение Uab в схеме рис. 1.18, если E = 90 B,
R1 = 20 Oм, R2 =10 Ом, R3 = 60 Ом, R4 = 40 Ом.
|
Теоретические основы электротехники. Практикум |
-21- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
R1 |
R3 |
R4 |
||||
|
R2 |
E |
||
|
b |
a |
||
|
Uab |
Рис. 1.18
Составить уравнение баланса мощностей. Ответ: Uab = 80 В.
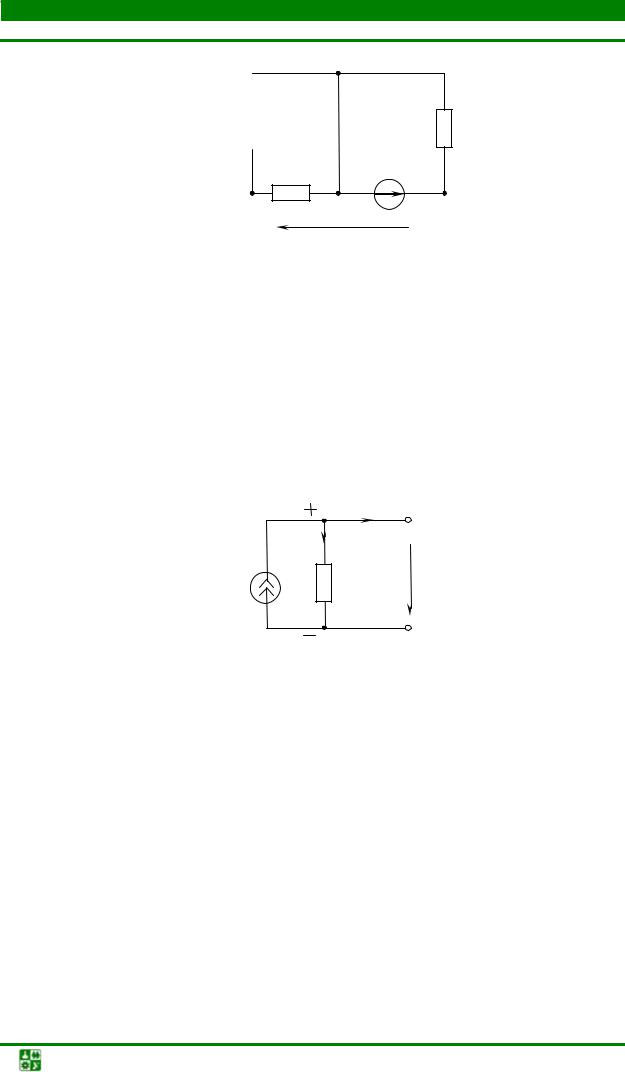
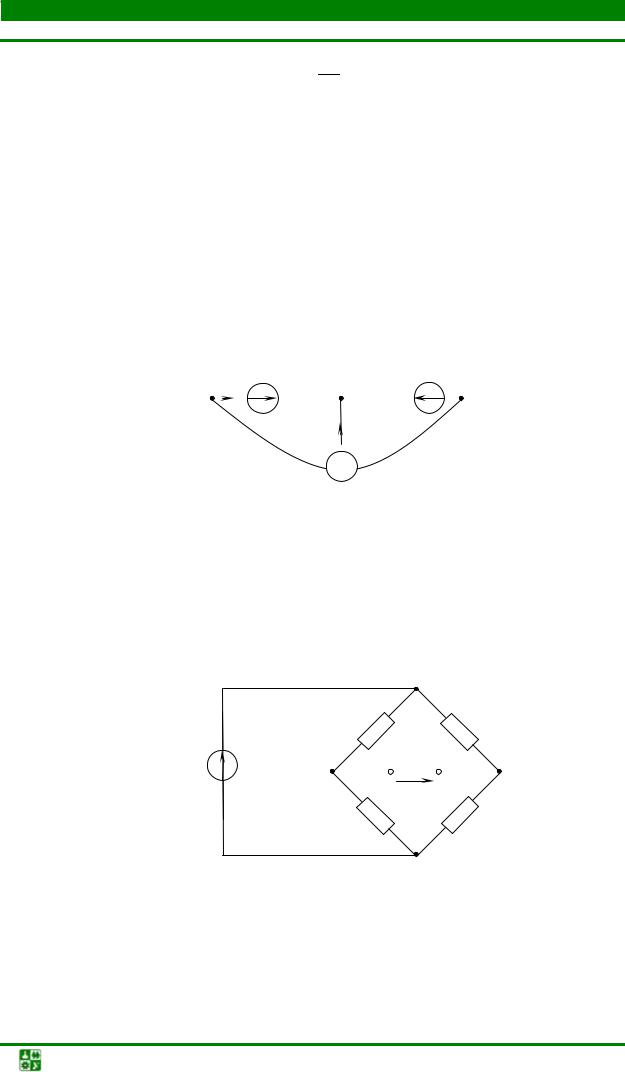
Задача4
Вычислить мощность источника тока на рис. 1.19, если J = 0,1 A, G0 =10−3 Cм, I = 90 мА. Определить, в каком режиме работает источник тока: генератора или нагрузки.
b
Рис. 1.19
Решение
1. Произвольно направим ток I0 и вычислим его по первому закону Кирхгофа:
J − I0 − I = 0.
Отсюда
I0 = J − I = 0,1−0,09 = 0,01 А.
Знак плюс означает, что направление тока I0 выбрано верно.
2. Вычислим напряжение на зажимах источника тока по закону Ома:
|
Теоретические основы электротехники. Практикум |
-22- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
U = R0 I0 = I0 = 0,01 =10 В.
G0 10−3
|
3. Определим |
мощность |
источника |
тока |
по |
формуле |
||||||||||
|
P =U J =10 0,1 =1 Вт. Так как значение тока |
I0 получилось со знаком |
||||||||||||||
|
плюс, то потенциал Va |
выше потенциала Vb , следовательно, источник тока |
||||||||||||||
|
вырабатывает электроэнергию. |
|||||||||||||||
|
Следующие задачи предлагаем для самоконтроля. |
|||||||||||||||
|
Задача5 |
|||||||||||||||
|
Определить показания вольтметра в схеме рис. 1.20, если |
RV → ∞, |
||||||||||||||
|
I1 =1А, I3 = 2 А, R1 = 2Ом, R2 = 2 Ом, E1 =10В, E2 = 5 В. |
|||||||||||||||
|
E |
R1 |
R2 |
E2 |
||||||||||||
|
I1 |
1 |
||||||||||||||
|
I3 |
|||||||||||||||
|
V |
|||||||||||||||
|
Рис. 1.20 |
|||||||||||||||
|
Ответ: UV = 3В. |
|||||||||||||||
|
Задача6 |
|||||||||||||||
|
Вычислить напряжение |
Uab |
в |
схеме рис. 1.21, |
если |
E = 4 В, |
||||||||||
|
R1 = R4 =1Ом, R2 = R3 = 3Ом. |
|||||||||||||||
|
R1 |
R |
||||||||||||||
|
3 |
|||||||||||||||
|
a |
b |
||||||||||||||
|
Uab |
|||||||||||||||
|
R2 |
R4 |
Рис. 1.21
Пояснение к решению
При расчете токов, нужных для вычисления Uab , нет необходимости искать эквивалентное сопротивление. Напряжение между двумя узлами
|
Теоретические основы электротехники. Практикум |
-23- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
равно ЭДС, поэтому токи в пассивных ветвях могут быть найдены сразу по закону Ома.
Ответ: Uab = 2 В.
Задача7
В схеме рис. 1.22 вольтметр показывает напряжение 1 В. Вычислить значение Е, если R1 = R4 = 2 Ом, R2 = R3 = 3Ом, RV → ∞.
Рис. 1.22
Ответ: Е = 5 В.
|
Задача8 |
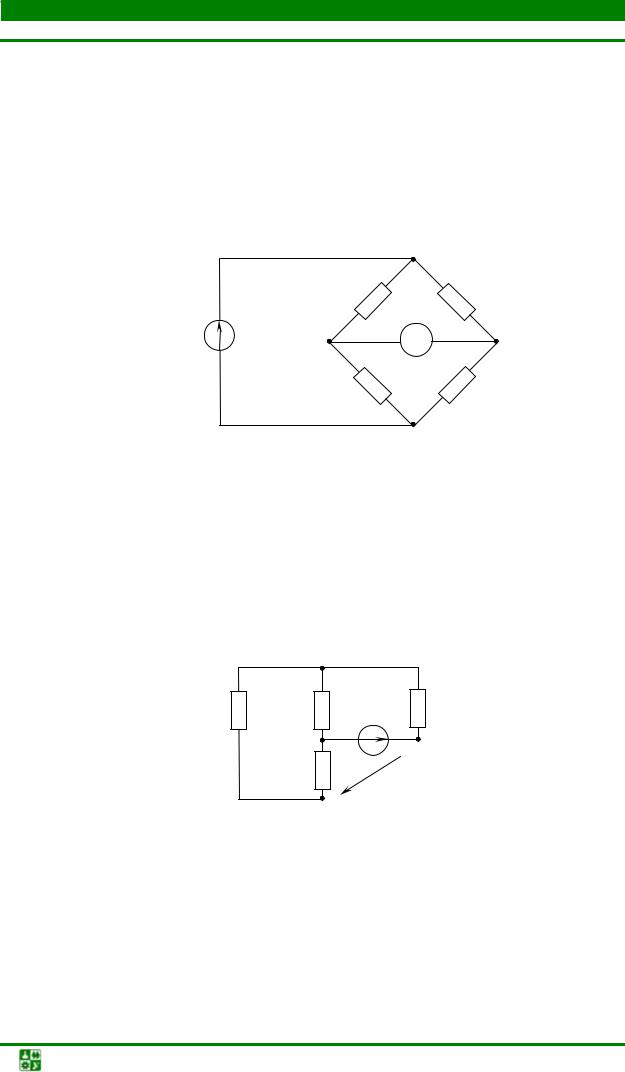
||
|
Вычислить напряжение Uab в схеме рис. 1.23, |
если Е = 27 В, |
R1 = 3 |
|
Ом, R2 = 6 Ом, R3 =18 Ом, R4 =12 Ом. Проверить |
правильность |
расчета |
токов с помощью баланса мощностей.
|
R1 |
R3 |
E |
R4 |
|
a |
|||
|
R2 |
Uab |
||
|
b |
|||
|
Рис. 1.23 |
Ответ: Uab = 21 В.
Занятие3
Цели занятия:
1. Научиться рассчитывать токи методом эквивалентных преобразований в схемах с одним источником тока.
|
Теоретические основы электротехники. Практикум |
-24- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
2. Научиться рассчитывать токи методом эквивалентных преобразований в схемах, не содержащих последовательно-параллельных соединений резисторов.
Рассмотрим первую целевую задачу занятия.
Расчет схем с источником тока проще, чем с источником ЭДС, так как общий ток известен. Свертывание схемы производят до получения трех ветвей: активной с известным током источника и двух пассивных, токи которых находят по рассмотренным нами формулам.
Перейдем к рассмотрению второй целевой задачи.
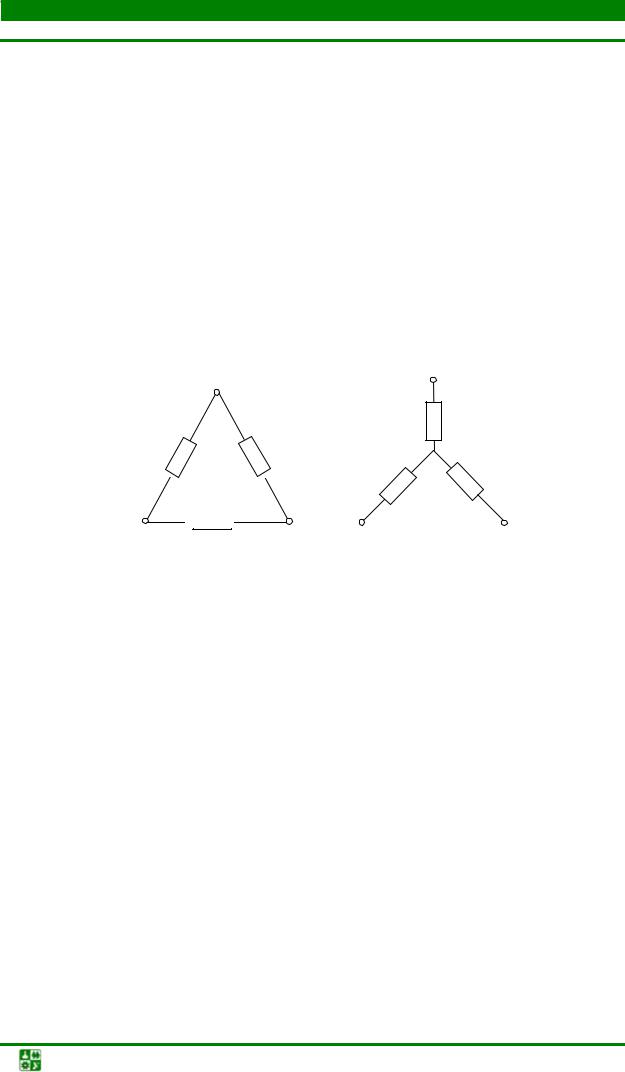
Если схема не содержит последовательно-параллельные соединения резисторов, необходимо соединение треугольником (рис. 1.24, а) заменить эквивалентным соединением звездой (рис. 1.24, б) или выполнить обратную замену.
|
Rca |
Rab |
Ra |
||
|
Rc |
Rb |
|||
|
Rbc |
||||
|
b |
b |
|||
|
c |
a |
c |
||
|
б |
||||
|
Рис. 1.24 |
Структура формул эквивалентных преобразований проста для запоминания:
|
Ra = |
Rab Rca |
, |
||||||
|
Rab + Rbc + Rca |
||||||||
|
Rc = |
Rca Rbc |
; |
||||||
|
Rab + Rbc + Rca |
||||||||
|
R = R + R + |
Rb Rc |
, |
||||||
|
bc b c |
Ra |
|||||||
|
Rb |
= |
Rbc |
Rab |
, |
|||
|
Rab + Rbc + Rca |
|||||||
|
R = R + R + Ra Rb , |
|||||||
|
ab |
a b |
Rc |
|||||
|
R = R + R |
a |
+ |
Rc Ra |
. |
|||
|
ca |
c |
Rb |
|||||
После преобразования резисторы в схеме будут соединены последовательно-параллельно, их можно заменить одним с эквивалентным сопротивлением.
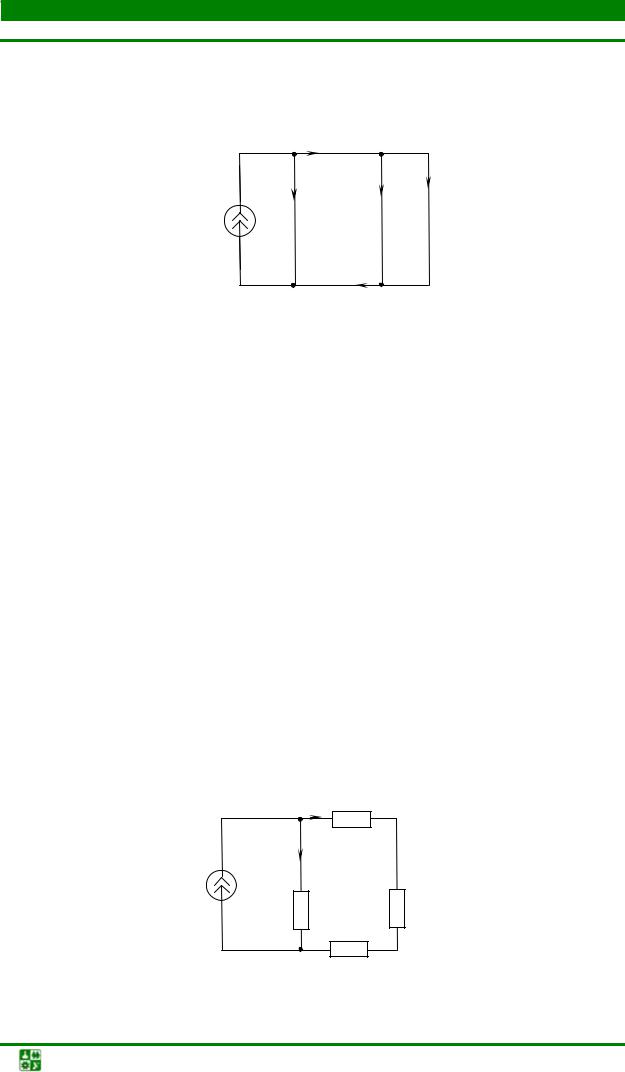
Задача1
|
Теоретические основы электротехники. Практикум |
-25- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
Вычислить |
токи в цепи, схема |
замещения |
которой |
изображена |
||||||||||
|
на рис. 1.25, |
если J =120 мА, R1 =10 кОм, R2 = 0,5 кОм, |
R3 =12 кОм, |
||||||||||||
|
R4 =1,5 кОм, |
R5 = 6 кОм. |
R2 |
||||||||||||
|
a I2 |
b |
|||||||||||||
|
I5 |
||||||||||||||
|
I |
I3 |
|||||||||||||
|
1 |
||||||||||||||
|
J |
||||||||||||||
|
R1 |
R |
R5 |
||||||||||||
|
R4 |
3 |
|||||||||||||
|
c |
I4 |
d |
||||||||||||
|
Рис. 1.25 |
||||||||||||||
|
Пояснение к решению |
||||||||||||||
|
Сначала нужно разобраться в топологии схемы. Она содержит четыре |
||||||||||||||
|
узла (a, b, c, |
d) и шесть ветвей. Направления токов в них вполне |
определенны. Ток в ветви с источником тока известен. Ток I2 = I3 + I5 = I4 . Следовательно, нужно вычислить четыре неизвестных тока.
Решение
1. Для свертывания схемы выявляем последовательные и параллельные соединения резисторов. Ветвей, содержащих более одного резистора, в схеме нет, т. е. нет последовательных соединений. Резисторы с сопротивлениями R3 и R5 соединены параллельно, заменим их одним с эквивалентным
сопротивлением:
|
R R |
12 6 10 |
6 |
||||||
|
R |
= |
3 |
5 |
= |
= 4 |
кОм. |
||
|
35 |
R3 |
+ R5 |
(12 + 6) 103 |
|||||
2. Получившаяся после этого преобразования схема изображена на рис. 1.26. В ней три ветви.
c
Рис. 1.26
|
Теоретические основы электротехники. Практикум |
-26- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
Дальнейшее преобразование схемы не требуется. Наиболее рационально вычислить ток I2 по формуле для определения тока в пассивной
параллельной ветви:
|
I2 |
= |
R1 |
J = 75 мА. |
|||
|
R1 |
+ R2 |
+ R35 + R4 |
||||
3. По первому закону Кирхгофа вычислим ток I1:
I1 = J − I2 = 45мА.
4. Возвращаемся к исходной схеме с определением оставшихся токов. Ток I2 является общим для токов I3 и I5 , поэтому
|
R |
6 |
103 |
−3 |
|||||||||
|
I3 |
= |
5 |
I2 |
= |
103 |
75 10 |
= 25 мА, |
|||||
|
R3 |
6 |
+12 |
||||||||||
|
+ R5 |
I5 = I2 − I3 = 50 мА.
Следующую задачу решите самостоятельно.
|
Задача2 |
||
|
Вычислить напряжение |
Uab в схеме |
рис. 1.27, если J = 4 A, |
|
R1 = R4 =1 Ом, R2 = R3 = 3 Ом. |
||
|
R1 |
R |
|
|
3 |
||
|
J |
a |
b |
Uab
R2 R4
Рис. 1.27
Ответ: Uab = 4 В.
Задача3
Вычислить токи в цепи, схема замещения которой представлена на
рис. 1.28, если Е = 30 В, R1 =180 Ом, R2 = 60 Ом, R3 =120 Ом, R4 = 80 Ом, R5 =120 Ом.
|
Теоретические основы электротехники. Практикум |
-27- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
I |
R1 |
A |
R2 |
|
I1 |
R3 |
I2 |
|
|
E C |
I3 |
||
|
B |
|||
|
R4 |
I4 |
R5 |
|
|
I5 |
D
Рис. 1.28
Пояснение к решению
Найдем узлы, ветви, направим токи. В этой схеме нет резисторов, которые были бы соединены между собой последовательно или параллельно. Резисторы с сопротивлениями R1, R2 и R3 соединены между собой
треугольником. К нему присоединены резисторы с сопротивлениями R4 и R5 .
Можно считать, что треугольником соединены резисторы с сопротивлениями R4 , R3 и R5 . К нему присоединены резисторы с сопротивлениями R1 и R2 .
Нередко студенты делают ошибки, полагая, что в предлагаемой схеме два треугольника. Но схема содержит только пять резисторов. Можно считать
|
соединенными звездой резисторы с сопротивлениями R1, R3 и R4 |
либо с |
|
сопротивлениями R2 , R3 и R5 . Нужно выбрать один из вариантов |
|
|
соединения. |
|
|
Решение |
|
|
1. Заменив соединенные треугольником резисторы с сопротивлениями |
|
|
R1, R2 и R3 эквивалентным соединением звездой, получим |
схему, |
|
изображенную на рис. 1.29. |
|
Теоретические основы электротехники. Практикум |
-28- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
RC RB
E
|
C |
B |
|
|
I4 |
I5 |
|
|
R4 |
D |
R5 |
Рис. 1.29
В этой схеме два узла, соединенных между собой тремя ветвями. Так как источник ЭДС и резисторы с сопротивлениями R4 и R5 не подвергались
преобразованиям, токи в них не изменились.
В схеме рис. 1.29 резисторы соединены последовательно-параллельно, их можно заменить одним с эквивалентным сопротивлением:
|
R |
э |
= |
R |
А |
+ |
(RС + R4 ) (RB + R5 ) |
, |
|||||||||||||||
|
(R |
+ R |
4 |
+ R |
B |
+ R ) |
|||||||||||||||||
|
С |
5 |
|||||||||||||||||||||
|
где |
R |
A |
= |
R1 R2 |
= |
180 60 |
= 30 Ом, |
|||||||||||||||
|
R + R |
2 |
+ R |
180 +60 +120 |
|||||||||||||||||||
|
1 |
3 |
|||||||||||||||||||||
|
RB |
= |
R2 R3 |
= 60 120 |
= 20 |
Ом, |
|||||||||||||||||
|
R1 |
+ R2 + R3 |
|||||||||||||||||||||
|
360 |
||||||||||||||||||||||
|
R = |
R1 R3 |
= 180 120 = 60 Ом. |
||||||||||||||||||||
|
C |
R1 |
+ R2 + R3 |
360 |
|||||||||||||||||||
Тогда
Rэ = 30 + (60 +80) (20 +120)=100 Ом.
60 +80 + 20 +120
2. Вычислим ток в свернутой схеме по закону Ома:
|
Теоретические основы электротехники. Практикум |
-29- |

ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
|
I = |
E |
= |
30 |
= 0,3 А. |
|
|
100 |
|||||
|
Rэ |
3. Определим токи в пассивных параллельных ветвях:
|
I4 |
= |
RB + R5 |
I = 0,15 А, |
|
|
RB + R5 |
+ RC + R4 |
|||
I5 = I − I4 = 0,15 А.
Так как сопротивления пассивных параллельных ветвей оказались одинаковыми, I4 = I5 = I/ 2, хотя сопротивления R4 и R5 не равны друг
другу.
4. Возвращаемся к исходной схеме с определением оставшихся токов.
По закону Ома ток I1 = U АС . Найдем напряжение U АС как изменение
R1
потенциала между точками А и С:
U АС = −R4I4 + E = −80 0,15 +30 =18 В.
Тогда
I1 = 18018 = 0,1 А.
5. Токи I2 и I3 можно найти по первому закону Кирхгофа. Для узла А
I − I1 − I2 = 0.
Отсюда
I2 = I − I1 = 0,2 А.
Для узла С
I1 − I3 − I4 = 0.
Отсюда
I 3 = I1 − I4 = 0,1−0,15 = −0,05 А.
Знак минус показывает, что направление тока I3 выбрано неправильно. Действительное направление тока I3 укажем пунктирной стрелкой.
Следующую задачу решите самостоятельно.
|
Теоретические основы электротехники. Практикум |
-30- |
ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Тема 1 Метод эквивалентных преобразований
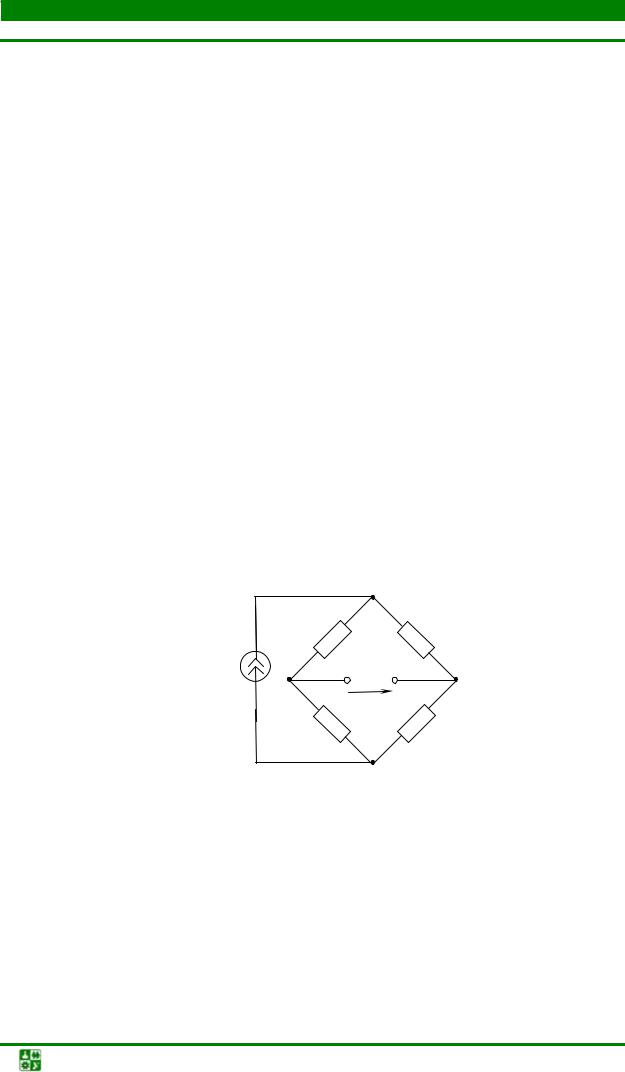
Задача4
Вычислить токи в схеме, представленной на рис. 1.30, если J = 5 А,
R1 = R2 = R3 = R4 = 3Ом, R5 = 5 Ом.
|
R1 |
R3 |
R |
|
J |
2 |
|
|
R4 |
R5 |
|
|
Рис. 1.30 |
Ответ:I1 = 2,67 А, I2 = 2,33 А, I3 = 0,33 А, I4 = 3 А, I5 = 2 А. Для самоконтроля решите задачи 5 и 6.
Задача5
Вычислить все токи в схеме, представленной на рис. 1.31, если J = 2
А, R5 = 20Ом, R1 = R2 = R3 = R4 = R6 = R7 = =10 Ом.
|
R2 |
I2 |
I4 |
R4 |
||||||||||||
|
I5 |
I6 |
||||||||||||||
|
R |
R5 |
||||||||||||||
|
1 |
|||||||||||||||
|
R3 |
R6 |
||||||||||||||
|
J |
|||||||||||||||
|
R7 |
|||||||||||||||
|
Рис. 1.31 |
|||||||||||||||
|
Ответ: I2 =1А, I4 =1А, I5 = 0,5 A, I6 |
= 0,5 А. |
||||||||||||||
|
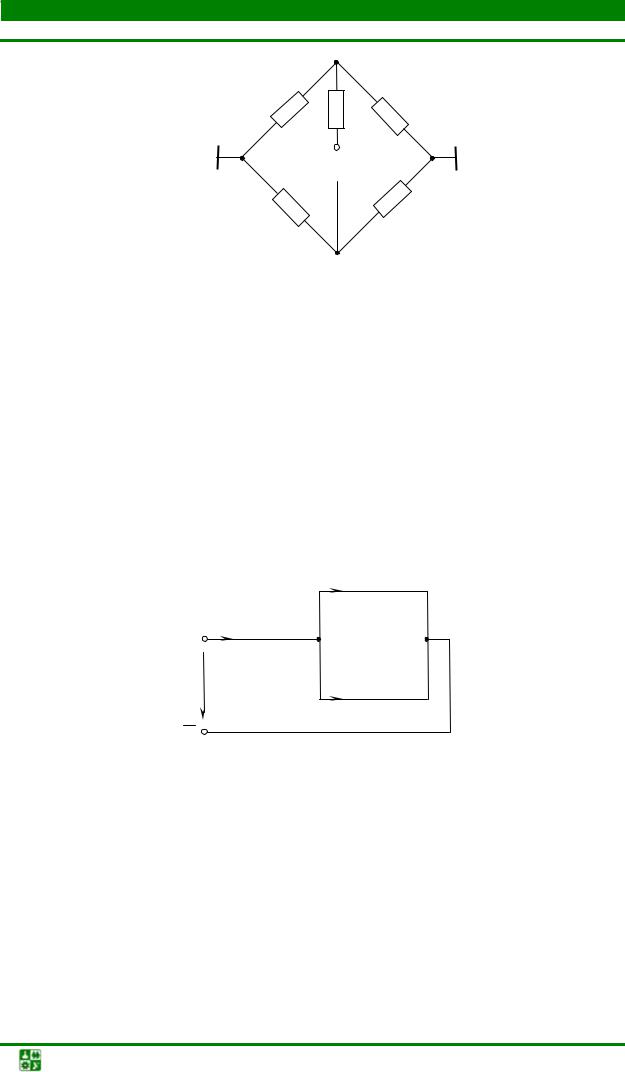
Задача6 |
Рассчитать все токи в схеме, представленной на рис.1.32, если Е = 12
В, R = 3 Ом.
|
Теоретические основы электротехники. Практикум |
-31- |
Метод двух узлов является частным случаем метода узловых потенциалов. Данным методом могут быть рассчитаны цепи содержащие два неустранимых узла. Для расчёта методом двух узлов находят напряжение между зтими узлами Uab по формуле:
Где Ek – напряжение источника ЭДС k-ой ветви, Gk – проводимость k-ой ветви, Jk – ток источника тока k-ой ветви.
Затем находят токи в ветвях без источников тока по формуле:
Ток в ветви с источником тока равен току этого источника.
Рассмотрим расчёт методом двух узлов на примере расчёта схемы на рисунке 1:
Рисунок 1 – Схема для расчёта методом двух узлов
Пусть в этой схеме E1=10 В, R1=0.1 Ом, R2=4 Ом, R3=8 Ом, E3=-20 В, J4=40 А. Найдём проводимости резисторов:
Далее рассчитаем напряжение между узлами а и b по формуле (1):
Затем найдём токи в ветвях по формуле (2):
Рассчтаем мощность выделяющуюся в резисторах Pр и мощность отдаваемую источниками Pи для проверки балланса мощностей:
Мощность выделяющаяся в резисторах, с допустимой погрешностью, равна мощности выделяемой источниками следовательно балланс мощностей выполнен и расчёт произведён верно.
Пример 2
При расчёте схемы методом двух узлов можно применить немного другой подход.
Рассмотрим схему:
Рисунок 2 – Схема 2 для расчёта методом двух узлов
Направления токов в ветвях, кроме тех в которых стоят источники тока, выбраны произвольно. В схеме имеется 2 узла: узел a и узел b. Будем считать что потенциал узла b равен нулю, напряжение Uab, в таком случае, равно потенциалу узла a. Определим проводимости каждой ветви, при этом учтём то что:
сопротивление источника ЭДС (с одинарной стрелочкой в кружке) равно нулю а его проводимость равна бесконечности,
сопротивление источника тока (с двумя стрелочками в кружке) равно бесконечности а его проводимость равна нулю.
Проводимость ветви с током I1 будет равна G1=1/R1, проводимости источников ЭДС равны нулю поэтому они не учитываются (их можно считать перемычками на которых есть напряжение).
Проводимость ветви с током I2 будет равна G2=1/R2 источник опять же не учитывается.
проводимость ветви с током I3 равна нулю (т.к. проводимость источника тока равна нулю (источник тока можно считать разрывом через который течёт ток) ).
Проводимость ветви с током I4 равна нулю т.к. проводимость источника тока равна нулю, можно считать что в этой ветви разрыв и резистор R3 ничего не меняет.
Пусть в этой схеме E1=4 В, R1=10 Ом, R2=5 Ом, R3=2 Ом, E2=6 В, E3=10 В, J1=5 А, J2=4 А. Найдём проводимости резисторов:
Найдём напряжение Uab по формуле (1)
E1 записан со знаком минус т.к. его эдс (стрелочка внутри) направлена от узла а
E2 записано со знаком + т.к. его эдс направлена к узлу а
E3 записано со знаком + т.к. его эдс направлено к узлу а
J1 записан со знаком – т.к. его ток направлен от узла а
J2 записан со знаком + т.к. его ток направлен к узлу а
в знаменателе записана сумма проводимости первой ветви и второй, оставшиеся две ветви имеют проводимость равную нулю поэтому не записываются.
(В первом случае направления источников эдс учитывались а алгебраических знаках перед значениями этих эдс).
Ток I3=J1=5 т.к. источник тока создаёт в ветви ток равный току этого источника,
Ток I4=J2=4 т.к. источник тока создаёт в ветви ток равный току этого источника.
Аналогично можно найти ток I2:
Для составления баланса мощностей необходимо найти напряжение на источнике тока J2 (см. рисунок 2), найдём напряжение UJ2 на источнике тока J2:
Составим баланс мощностей:
Pи- отдаваемая и принимаемая мощность источников, Pп-мощность принимаемая резисторами. Если направление тока совпадает с направлением эдс источника эдс то это эдс записывается со знаком “+” если нет то со знаком “-“. Если напряжение на источнике тока направлено противоположно току этого источника то ток этого источника записывается в уравнение баланса мощностей со знаком “+” если направление напряжения и тока совпадают то со знаком “-“.
На чтение 8 мин. Опубликовано 10.03.2020 Обновлено 10.03.2020
Для того чтобы появился электроток должна быть выполнена работа. Её количественной характеристикой является напряжение. Для участка электрической цепи формула для его расчёта была выведена физиком Симоном Омом. Это базовый закон, позволяющий не только связать фундаментальные величины описывающие ток, но и понять физический смысл разности потенциалов.
Содержание
- Общие сведения
- Вольтов столб
- Эксперимент и закон Ома
- Решение примеров
Общие сведения
После того как Уильям Гильберт установил, что в физическом теле существует некая материя, умеющая взаимодействовать с веществами в другом проводнике, начался бум изучения электричества.
Было установлено, что в материалах существуют частицы, обладающие энергией. В свободном состоянии из-за их хаотического перемещения тело находится в энергетическом равновесии. Но если их движение упорядочить, то возникает явление, названное электрическим током. Вызвать же их направленное движение можно внешней силой. Носители заряда условно разделили на два вида — положительные и отрицательные. Первые назвали протонами, а вторые — электронами.
Для описания движения элементарных частиц вели два понятия:
- сила тока — величина, определяющая количество зарядов, прошедших через поперечное сечение материала за единицу времени;
- напряжение — работа потенциального характера, обеспечивающая перенос элементарной частицы из одной точки тела в другую.
С помощью этих характеристик стало удобно исследовать электричество. Принято считать, что если под действием силы пробный заряд переместится из одно точки в другую, то совершённая работа будет равна изменению энергии частицы, то есть потенциала. Определить который можно как отношение энергии заряда к его величине: φ = W / q. Для однородного поля это значение постоянное.
Так как напряжение — это работа, то равно оно будет разности потенциалов в начальный момент времени и конечный: U = φ 1 — φ2 = A / q. В Международных единицах величина измеряется в вольтах (В) или джоулях, делённых на кулон (Дж / Кл). Следовательно, при движении положительной частицы с зарядом в один кулон в направлении действия силовых линий в 1 Дж напряжение равно вольту.
В зависимости от вида тока изменения потенциала может быть двух видов:
- переменным — амплитуда значения изменяется по синусоидальному закону, носители заряда периодически изменяют своё направление движения;
- постоянным — величина остаётся неизменным на протяжении длительного времени.
Для измерения разности потенциалов используют вольтметр. Этот прибор подключают параллельно к измеряемым точкам. Устройство обладает большим сопротивлением, поэтому не влияет на прохождение тока. Наглядно же увидеть, как изменяется форма сигнала можно с помощью осциллографа. На величину напряжения влияет материал, из которого изготовлен проводник, нагрузка, температура.
Вольтов столб
В 1799 году изучая результаты экспериментов Гальвани итальянский учёный Вольт, предположил о возможности появления электричества при соприкосновении двух металлов. Его теория получила название «контактное электричество». Однако, проводя опыты физик, обнаружил, что простого соприкосновения двух тел недостаточно. Он выяснил, что для возникновения тока необходимо построить замкнутую цепь. При этом нужно использовать два рода проводников и связующий элемент.
Конструкция учёного получила название «вольтов столб».
Состояла она из следующих элементов:
- цинковой пластины;
- медного диска;
- ткани из сукна пропитанной подсоленной водой.
Вольт использовал медь как основу. На неё он уложил ткань, а сверху накрыл цинковой пластинкой. Изготовив несколько таких блоков, он соединил их между собой, используя опять же в качестве разделителя сукно. Из-за круглой формы частей конструкция напоминала собой слоёный пирог в форме столба. К нижней и верхней пластинам Вольт подключил гальванометр Ампера. В итоге он смог наблюдать отклонение стрелки. То есть смог получить напряжение.
Измерить его величину физик не мог, так как существующие на то время приборы не умели определять точное значение потенциала. В своём выступлении перед учёным советом Вольт объяснял появление электротока эффектом возникновения электродвижущих сил, появляющихся при соприкосновении разных материалов. Ткань же была нужна для препятствования образования встречного потока носителей заряда. Так был изобретён первый источник электрической энергии — гальванический.
Творение Вольта получило широкое распространение. На базе его конструкции другие учёные проводили свои эксперименты, применяя различные материалы и разделяющую их жидкость. В дальнейшем было установлено, что ток возникал из-за преобразования химической энергии в электрическую. «Вольтов столб», стал отправной точкой для открытия тепловых, световых и магнитных действий электротока. Изучения изменения потенциала носителей заряда при их движении в электромагнитном поле.
Эксперимент и закон Ома
Георг Симон Ом был экспериментатором. Изучая открытие Вольта, он пришёл к выводу, что в материалах существует что-то, препятствующее прохождению электрического тока. Это величина получила название «потеря силы». Свой закон он вывел эмпирическим путём в 1826 году. Для измерения силы тока физик использовал крутильные веса Кулона, а в качестве источника энергии «вольтов столб».
На базе этих приборов Ом собрал простейшую электрическую цепь. Соединяя устройства проволокой разной длины, он обнаружил изменение характеристик тока. Исследуя, как изменяется электроток от размеров проводника Ом вывел следующую формулу: X = a / (b +L), где:
- x — величина, определяющая изменение тока (сила I);
- L — длина проводника (сопротивление R);
- a — электродвижущая сила (напряжение U);
- b — коэффициент значение которого зависит от источника энергии (внутренний импеданс прибора).
Современная интерпретация закона Ома звучит так: — сила тока в замкнутом контуре прямо пропорциональна падению напряжения на его концах и обратно пропорциональна сопротивлению: I = U / R. Отсюда вытекает, что напряжение на участке цепи будет равно: U = I / R. Таким образом, удалось связать силу тока с разностью потенциалов через сопротивление.
Каков же будет импеданс в том или ином случае зависит от вида кристаллической решётки и геометрических размеров проводника, температуры. Всё дело в том, что при движении носителей заряда происходит их сталкивание с другими частицами. В результате энергия теряется, а значит, снижается сила тока и напряжение. По умолчанию сопротивление определяется так: R = p * (L / S), где: p — постоянная величина, зависящая от рода материала, L — длина проводника, а S — ширина. Измеряется импеданс в омах.
Нахождение зависимости напряжения от других величин позволило вести такое понятие, как вольт-амперная характеристика. По сути, это график зависимости, на котором показывают, как изменяются значения величин. Изображают его в декартовой системе координат. По оси абсцисс откладывают напряжение, а ординат — силу тока.
Следует отметить, что определение напряжения по закону Ома справедливо только для участка цепи. Другими словами, в замкнутом контуре, в котором нет источников тока с ЭДС. То есть на участке описываемым каким-то сопротивлением, но при этом без учёта внутренних параметров генераторов энергии.
Решение примеров
Зная закон Ома, можно найти по формуле как напряжение, так ток или сопротивление. Для заданий начального уровня этого знания будет достаточно. Но для высокой сложности необходимо понимать, как рассчитывается сопротивление активных и реактивных элементов. Вот два примера, для школьников седьмых классов, рекомендуемых к самостоятельному их решению.
Простое задание. Электрическая цепь состоит из источника питания и двух последовательно включённых резисторов 5 Ом и 10 Ом. Найти разность потенциалов на каждом элементе при токе в цепи один ампер. Вычисляться нужное напряжение для каждого элемента будет по простой формуле: U = I * R. Отсюда: U1 = 1 * 5 = 5 В, U2 = 1 * 10 = 10 В.
Пример сложной задачи. Вычислить напряжение Uab на последовательно соединённых конденсаторах С1 = 10мкФ и С2 = 20 мкФ и параллельно подключённому к ним резистору R = 10 Ом если известно, что при замыкании сила тока, возрастает в пять раз. Действующая ЭДС источника питания составляет: E = 50 В.
Решение задачи нужно выполнять в следующей последовательности:
- Найти падение разности потенциалов на реактивных элементах. Так как при последовательном соединении напряжение складывается, то можно записать: U = U1 + U2, где: U1 = C2 * U / (C1 + C2), U2 = C1 * U / (C1 + C2).
- Выполнить вычисление тока, проходящего через конденсаторы. По закону Ома: I = E / (R + r). Так как падение на резисторе можно определить по формуле: U = I * R, то с учётом того, что при токе короткого замыкания сопротивление равняется нулю, можно записать: I0 = E / r.
- По условию сила тока изменилась в эн раз. Значит: (R + r) / r = n. Отсюда R = r * (n — 1).
- Полученное R нужно подставить в формулу для тока: I = E / r * n. Тогда: U = (n — 1) * E / n.
- Выведенные выражения теперь можно подставить в формулу нахождения разности потенциалов на конденсаторе: U1 = E * ((n — 1) * C2 / n * (C1 + C2)) = 50 В * (4 * 20 * 10-6 Ф / 5 (20 * 10-6Ф + 10 * 10-6 Ф)) = 50 В * (80 * 10-6 Ф / 150 * 10-6 Ф = 0,53 * 50 В = 26,5 В и U2 = E * (n — 1) * C1 / n * (C1 + C2) = 50 В * (4 * 10 * 10-6 Ф / 5 (20 * 10-6 Ф + 10 * 10-6 Ф)) = 50 В * (40 * 10-6 Ф / 150 * 10-6 Ф) = 13,3 В.
Следует отметить, что вычислять напряжение можно и в автоматическом режиме. Для этого следует воспользоваться так называемыми онлайн-калькуляторами. Это сайты с интуитивно понятным интерфейсом требующие от пользователя лишь введения исходных данных.


































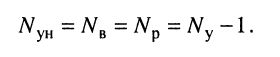
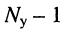
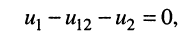
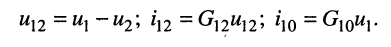
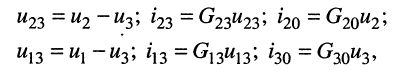
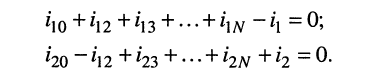
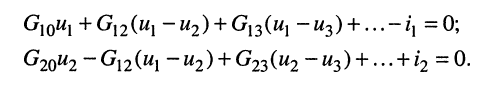
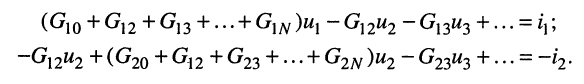
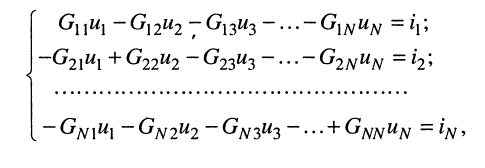
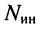 источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно
источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно