Содержание:
Электрические цепи синусоидального тока:
В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.
При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.
Цепь с активным сопротивлением
Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).
Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение 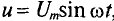
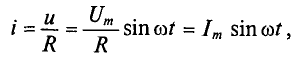
где 
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны (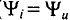 = 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
= 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 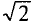 =1,41.
=1,41.
Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.
Активная мощность
Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.
Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.
Количественно мощность в цепи с активным сопротивлением определяется следующим образом:
Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 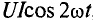 , изменяющейся с двойной частотой.
, изменяющейся с двойной частотой.
Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть
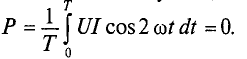
Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:
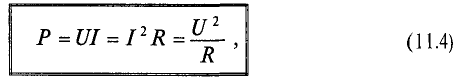
где U- действующее значение напряжения; I— действующее значение тока.
Единицей активной мощности является ватт:
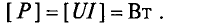
Поверхностный эффект и эффект близости
Сопротивление проводника постоянному току 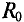 называют омическим сопротивлением и определяют выражением (2.8)
называют омическим сопротивлением и определяют выражением (2.8) 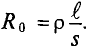 Сопротивление проводника переменному току R называют активным.
Сопротивление проводника переменному току R называют активным.
Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е. 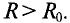
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).
На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.
Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.
Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 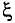 (кси)
(кси)
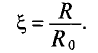
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости 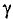 , магнитной проницаемости материала проводника
, магнитной проницаемости материала проводника 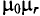 и частоты переменного тока
и частоты переменного тока  , проходящего по проводнику, показан на рис. 11.26.
, проходящего по проводнику, показан на рис. 11.26.
При токах большой частоты  (радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
(радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
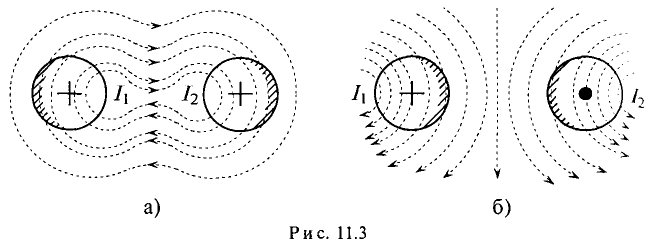
На величину активного сопротивления проводника R оказывает влияние и эффект близости.
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.
Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).
Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.
Цепь с идеальной индуктивностью
Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток 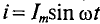 , то этот ток создает в катушке синусоидальный магнитный поток
, то этот ток создает в катушке синусоидальный магнитный поток 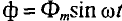 , который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
, который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
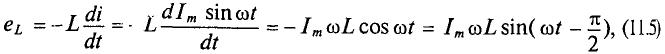
так как 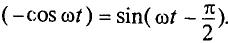
Очевидно, эта ЭДС достигает своего амплитудного значения 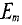 тогда, когда
тогда, когда 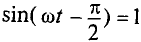 :
:
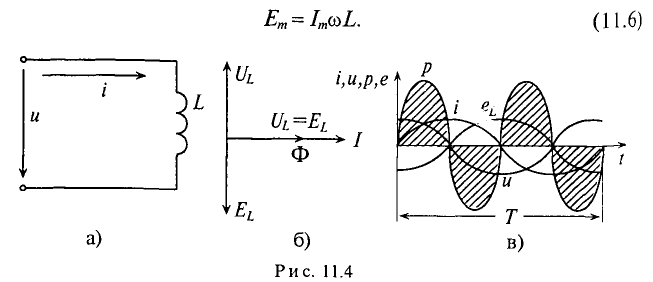
Тогда 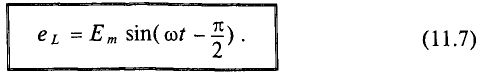
Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 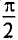 (рис. 11.46, в).
(рис. 11.46, в).
По второму закону Кирхгофа для мгновенных значений можно записать

Откуда 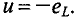
Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):
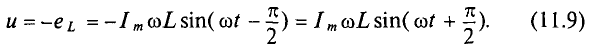
Очевидно, напряжение достигает своего амплитудного значения Um тогда, когда 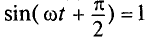 :
:

Следовательно, 
Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 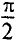 (рис. 11.46, в).
(рис. 11.46, в).
Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).
Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 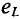 противодействует изменению тока.
противодействует изменению тока.
Если уравнение (11.10) разделить на 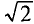 =1,41, то получается
=1,41, то получается 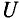 =
=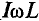 , откуда
, откуда

Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением XL.
Таким образом,

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление XL — это противодействие, которое ЭДС самоиндукции eL оказывает изменению тока.
Реактивная мощность в цепи с индуктивностью
Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока
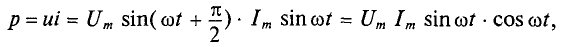
где 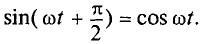
Следовательно, 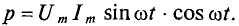
Полученное уравнение умножают и делят на 2:
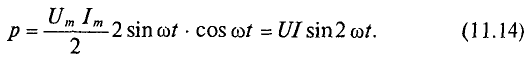
Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.
Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.
Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность ( ) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно
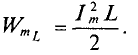
Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.
Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.
Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.
Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).
Величина реактивной мощности в рассматриваемой цепи определяется выражением
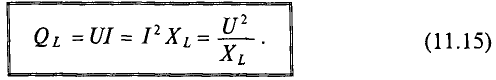
Так как реактивная мощность QL имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. XL.
Цепь с емкостью
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе Uc не станет равным напряжению источника U.
Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).
Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе Uc отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 – конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.
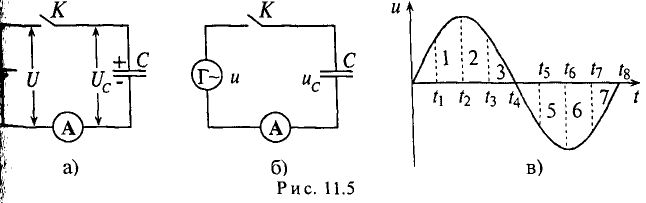
Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 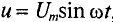 , то в цепи конденсатора проходит ток i (рис. 11.6а):
, то в цепи конденсатора проходит ток i (рис. 11.6а):
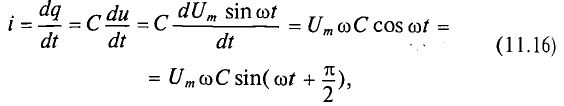
где q= Си согласно (6.3).
Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда 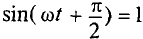 :
:

Тогда 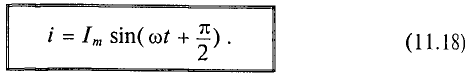
Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=
Следовательно, напряжение отстает по фазе от тока на 90° =  (рис. 11.66).
(рис. 11.66).
Если уравнение (11.17) разделить на 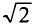 = 1,41, то получится равенство
= 1,41, то получится равенство 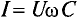 или
или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.
Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:

Когда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление – это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).
Реактивная мощность в цепи с конденсатором
Если в цепи конденсатора емкостью 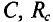 = 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
= 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
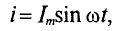
Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно
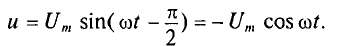
Мгновенная мощность в цепи с конденсатором
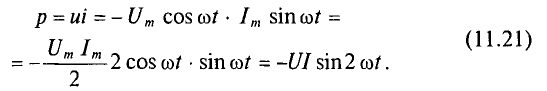
Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).
Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.
Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.
Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно
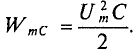
В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.
Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.
Величина реактивной мощности в цепи конденсатора определяется выражением
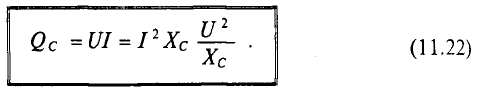
Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) – аналитическом выражении мгновенной мощности в цепи с конденсатором.
Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Хс).
Расчет линейных электрических цепей синусоидального тока
Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.
Цепь с активным сопротивлением и индуктивностью
Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 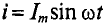 (рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки
(рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки 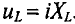
Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением XL (рис. 12.16).
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано 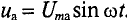 . Индуктивное напряжение
. Индуктивное напряжение 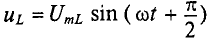 опережает ток на угол 90° =
опережает ток на угол 90° = 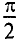 .
.
Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 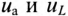 согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
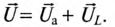
Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).
Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 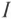 на угол ф. Мгновенное значение этого напряжения может быть записано:
на угол ф. Мгновенное значение этого напряжения может быть записано:
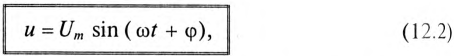
где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.
Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение
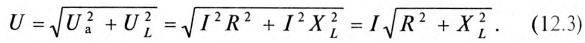
Откуда

Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.
Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:

где Zk — полное, или кажущееся, сопротивление реальной катушки.
Тогда закон Ома для любой цепи переменного тока в общем виде можно записать

где Z — кажущееся сопротивление этой цепи.
Треугольники напряжений, сопротивлений, мощностей
Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).
Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:
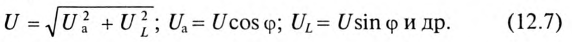
Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:
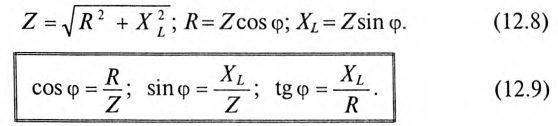
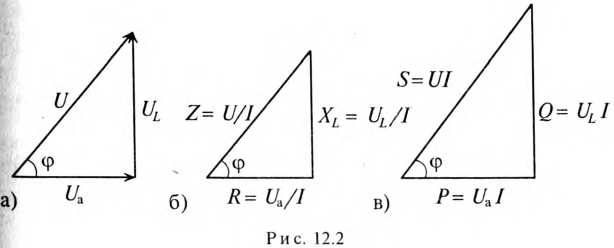
Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).
Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).
Произведение напряжения и тока цепи характеризует полную мощность цепи

которая измеряется в вольт-амперах, т.е. 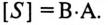
Однако потребляется в цепи только часть полной мощности – активная мощность
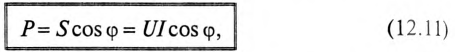
где cos ф показывает, какая часть полной мощности 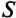 потребляется в цепи, поэтому cos ф называют коэффициентом мощности:
потребляется в цепи, поэтому cos ф называют коэффициентом мощности:

Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:
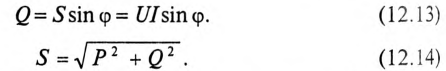
Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.
Цепь с активным сопротивлением и емкостью
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток 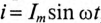 , то он создает падение напряжения на активном сопротивлении
, то он создает падение напряжения на активном сопротивлении 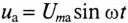 и на емкостном сопротивлении
и на емкостном сопротивлении 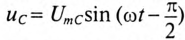 . Векторная диаграмма для этой цепи изображена на рис. 12.36.
. Векторная диаграмма для этой цепи изображена на рис. 12.36.
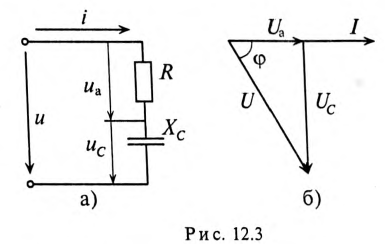
Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф < 90°, т. е.

Действующее значение напряжения U, приложенного к этой цепи, определяется по векторной диаграмме (рис. 12.3):
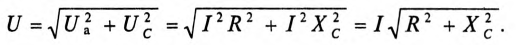
Откуда математическое выражение закона Ома для этой цепи:
Пример 12.1
К цепи с последовательно включенными сопротивлениями R= 8 Ом и Хс= 6 Ом (рис. 12.3а) приложено напряжение U= 220 В. Определить ток цепи I, напряжение на активном 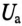 и реактивном Up участках, полную S, активную Р и реактивную Q мощности.
и реактивном Up участках, полную S, активную Р и реактивную Q мощности.
Решение
Для определения тока вычислим полное сопротивление цепи
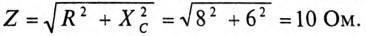
Тогда ток будет равен
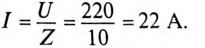
Напряжения на участках:
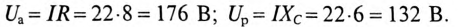
Полная мощность 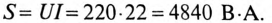
Активная мощность 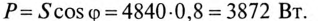
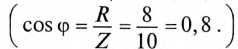
Реактивная мощность 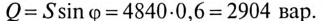
Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью
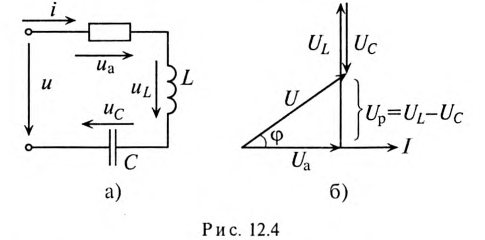
Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток 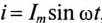 , то он создает падение напряжения на всех участках цепи:
, то он создает падение напряжения на всех участках цепи: 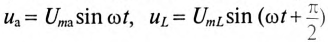 и
и 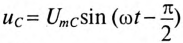 .
.
Мгновенное значение напряжения цепи определяется по формуле
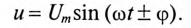
Так как в рассматриваемой цепи включены два реактивных сопротивления XL и Хс, то возможны три режима работы цепи: 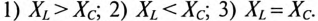
Векторная диаграмма цепи для режима 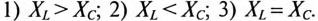 изображена на рис. 12.46.
изображена на рис. 12.46.
Знак перед углом сдвига фаз ф зависит от режима работы цепи Если в рассматриваемой цепи преобладает индуктивное напряжение (сопротивление), т. е. 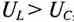 , то цепь имеет индуктивный характер и напряжение U опережает по фазе ток
, то цепь имеет индуктивный характер и напряжение U опережает по фазе ток 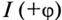 .
.
Если в цепи преобладает емкостное напряжение (сопротивление), т.е. 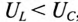 , то цепь имеет емкостной характер и напряжение U отстает по фазе от тока I (—ф).
, то цепь имеет емкостной характер и напряжение U отстает по фазе от тока I (—ф).
Из векторной диаграммы (рис. 12.46) следует:
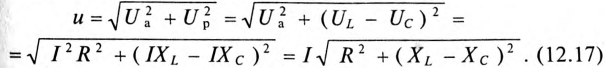
Сопротивление R может включать в себя сопротивление самостоятельного резистора или активное сопротивление реальной катушки и конденсатора.
Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкость:
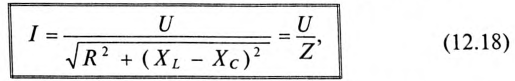
где Z — полное (или кажущееся) сопротивление неразветвленной цепи с R, L и С, т. е.
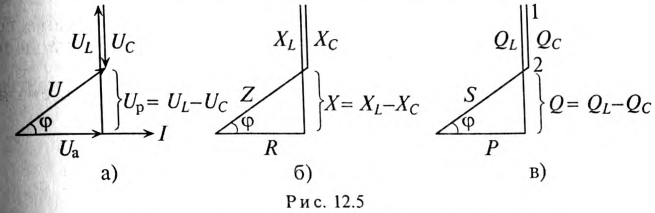
На рис. 12.5 изображены треугольники напряжений, сопротивлений и мощностей для рассматриваемой цепи.
Знак и значение угла ф можно определить из треугольника сопротивлений (рис. 12.56):
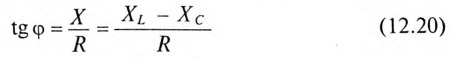
или
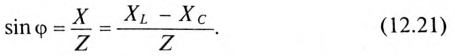
Из выражений (12.20) и (12.21) видно, что если 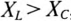 , то угол ф положителен (+ф), если
, то угол ф положителен (+ф), если 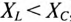 , то угол ф отрицательный (—ф).
, то угол ф отрицательный (—ф).
Из треугольника мощностей (рис. 12.5в) видно, что в цепи с R, L и С кроме активной мощности 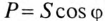 имеется реактивная мощность
имеется реактивная мощность 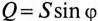 . Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае Uc) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности QL и Qc изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.
. Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае Uc) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности QL и Qc изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.
Из треугольника мощностей (рис. 12.5в) видно, что реактивная мощность, которая загружает источник и провода, Q= QL– Qc. Эта реактивная мощность (энергия) колеблется между источником и магнитным полем катушки индуктивности, так как 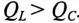
Полная мощность цепи определяется по формуле

Колебательный контур
Электрические цепи, в которых происходят периодические изменения токов, напряжений, энергии называются колебательными.
Для того чтобы исследовать резонансные явления, необходимо иметь представления о процессах в колебательном контуре, состоящем из идеальной катушки и конденсатора без потерь.
Если конденсатор емкостью С зарядить до напряжения Um, то в электрическом поле этого конденсатора накопится энергия, максимальное значение которой согласно выражению (6.21):
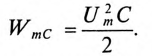
Если к заряженному конденсатору подключить индуктивность L замыканием ключа К (рис. 12.6), то конденсатор будет
разряжаться через индуктивность переменным током i. При этом в индуктивности L создается ЭДС самоиндукции eL, и в магнитном поле ее накапливается энергия, максимальное значение которой (9.12):
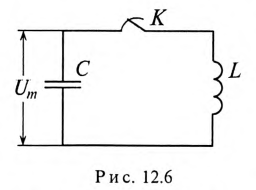
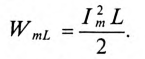
Источником энергии в этом контуре является конденсатор. Ток в контуре, состоящем из индуктивности L и конденсатора С, не прекращается даже когда конденсатор полностью разрядится. За счет ЭДС самоиндукции и энергии, накопившейся в магнитном поле индуктивности, конденсатор будет заряжаться, и энергия магнитного поля индуктивности переходит в электрическое поле конденсатора. При этом источником энергии в этом контуре является индуктивность. Дальше процесс повторяется.
Таким образом, в замкнутом контуре, состоящем из индуктивности и емкости, происходит колебание энергии между электрическим полем конденсатора С и магнитным полем индуктивности L. Поэтому такой замкнутый контур называется колебательным контуром.
Колебание энергии в колебательном контуре происходит с определенной частотой 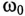 , которую называют частотой собственных колебаний контура. Частоту собственных колебаний со0 определяют из условия равенства энергии электрического и магнитного полей:
, которую называют частотой собственных колебаний контура. Частоту собственных колебаний со0 определяют из условия равенства энергии электрического и магнитного полей:
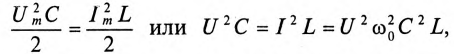
так как из (11.19) в цепи переменного тока с емкостью 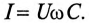
Откуда
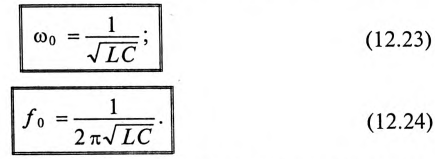
Таким образом, частота собственных колебаний колебательного контура определяется параметрами этого контура L и С.
Если в колебательном контуре отсутствуют потери (идеальный контур), то колебания в нем будут незатухающими с неизменной амплитудой. Если в колебательном контуре имеется активное сопротивление, т.е. возникают потери, то колебания энергии в нем будут затухающие, с уменьшающейся амплитудой, если эти потери не компенсируются.
Резонанс напряжений
Если в цепи синусоидального тока с последовательно соединенными конденсатором емкостью С и катушкой с сопротивлением R И индуктивностью L (рис. 12.7а) равны реактивные сопротивления, то в цепи наступает резонанс напряжений. Равенство реактивных сопротивлений является условием резонанса напряжений.

Из (12.25) следует 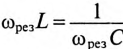 , тогда частота резонанса опреляется выражением
, тогда частота резонанса опреляется выражением

Из (12.26) следует, что резонанс напряжений имеет место в неразветвленной цепи с L и С тогда, когда частота вынужденных колебаний (частота источника) 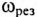 будет равна частоте собственных колебаний резонансного контура
будет равна частоте собственных колебаний резонансного контура 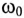 . Следовательно, добиться резонанса напряжений можно изменением частоты источника
. Следовательно, добиться резонанса напряжений можно изменением частоты источника 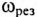 или изменением параметров колебательного контура L или С. т. е. изменением частоты собственных колебаний
или изменением параметров колебательного контура L или С. т. е. изменением частоты собственных колебаний 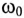 .
.
Полное (кажущееся) сопротивление цепи (рис. 12.7а) при резонансе напряжений определяется по формуле
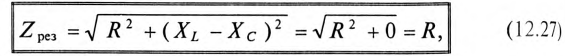
так как XL-Xc=0.
То есть полное сопротивление неразветвленной цепи при резонансе напряжений 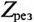 становится минимальным и равным активному сопротивлению цепи R.
становится минимальным и равным активному сопротивлению цепи R.
Следовательно, ток в неразветвленной цепи при резонансе напряжений максимальный:

Реактивные сопротивления при резонансе напряжений равны между собой, т. е.
(12.29)
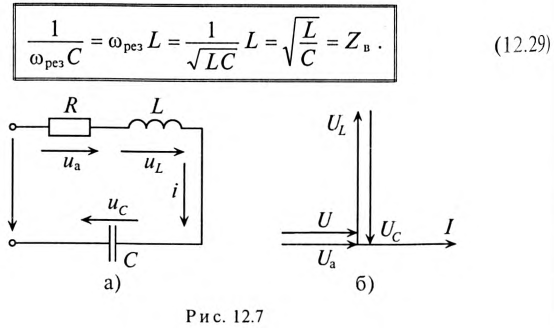
Таким образом, реактивные сопротивления при резонансе напряжений равны (каждое) волновому сопротивлению 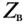 , которое называют характеристическим сопротивлением:
, которое называют характеристическим сопротивлением:
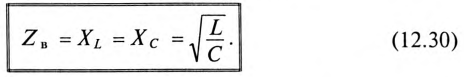
Напряжения на индуктивности UL и на емкости Uc при резонансе напряжений равны между собой, так как равны сопротивления, см. (12.25).
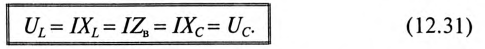
Равенство (12.31) определяет название «резонанс напряжений».
Так как UL и Uc изменяются в противофазе, то напряжение в резонансном режиме равно напряжению на активном сопротивлении 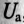 , т. е.
, т. е. 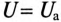 , что видно на векторной диаграмме (рис. 12.76).
, что видно на векторной диаграмме (рис. 12.76).
При резонансе напряжений каждое из реактивных напряжений UL и Uc может оказаться большим, чем напряжение цепи U.
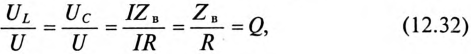
где Q — добротность резонансного контура.
Добротность контура Q показывает, во сколько раз напряжение на индуктивности UL и емкости Uc (каждое) больше напряжения цепи U.
Высокая добротность резонансного контура (при малом активном сопротивлении контура) нашла широкое применение в радиотехнике, в частности в антенном контуре.
Из векторной диаграммы (рис. 12.76) видно, что при резонансе напряжение цепи U совпадает по фазе с током 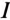 , угол между
, угол между  и U ф = 0 и cos ф = 1. Следовательно, кажущаяся мощность цепи S при резонансе вся потребляется, т. е. является активной:
и U ф = 0 и cos ф = 1. Следовательно, кажущаяся мощность цепи S при резонансе вся потребляется, т. е. является активной:

Колеблющаяся между магнитным полем индуктивности и электрическим полем емкости мощность ( ) не является реактивной, так как не загружает источник и провода.
) не является реактивной, так как не загружает источник и провода.
Из выражения (12.33) следует, что при отсутствии активной Мощности Р (активного сопротивления R) резонансный контур становится при резонансе идеальным колебательным контуром. Следовательно, при наличии активного сопротивления R источник расходует свою мощность на компенсацию потерь в контуре, за счет чего колебания в цепи будут незатухающими.
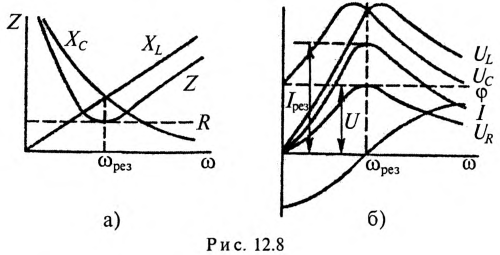
Кроме активного сопротивления R резонансной цепи и напряжения, приложенного к ней, все параметры резонансной цепи ( ) изменяются с изменением частоты сети
) изменяются с изменением частоты сети 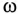 .
.
Эти изменения параметров резонансной цепи наглядно иллюстрируются резонансными кривыми, изображенными на рис. 12.8.
На резонансных кривых четко просматриваются значения этих параметров при частоте резонанса 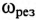 .
.
Общий случай неразветвленной цепи
Для неразветвленной цепи, содержащей несколько активных и реактивных сопротивлений различного характера (рис. 12.9а), справедливо геометрическое равенство напряжений (баланс напряжений)
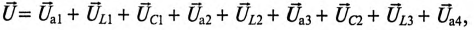
которое лежит в основе построения векторной диаграммы (рис. 12.96).
Таким образом, напряжение цепи равно геометрической сумме напряжений на всех участках этой цепи.
Из векторной диаграммы следует (рис. 12.96)
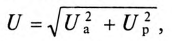
где 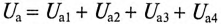 — активное напряжение цепи равно арифметической сумме напряжений на активных участках цепи;
— активное напряжение цепи равно арифметической сумме напряжений на активных участках цепи; 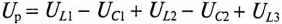 — реактивное напряжение цепи равно алгебраической сумме напряжений на реактивных участках цепи.
— реактивное напряжение цепи равно алгебраической сумме напряжений на реактивных участках цепи.
Те же рассуждения можно отнести и к сопротивлениям:
– полное сопротивление цепи 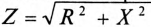 ;
;
– активное сопротивление цепи 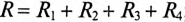 ;
;
– реактивное сопротивление цепи 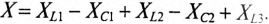
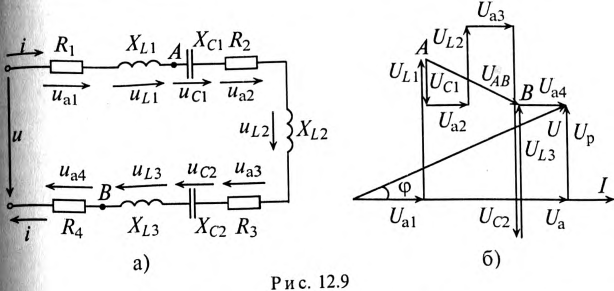
Напряжение на каком-либо участке неразветвленной цепи (рис. 12.9а), например на участке АВ, определяется так:_
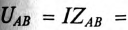
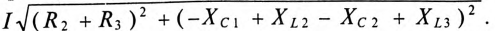
Вектор напряжения UAB показан на векторной диаграмме (рис. 12.96).
Пример 12.2
Напряжение, приложенное к неразветвленной цепи (рис. 12.10) U=220 В, частота тока сети f = 50 Гц. Начальная фаза тока 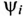 = 0.
= 0.
Сопротивление участков цепи: 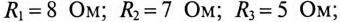
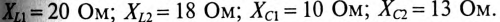
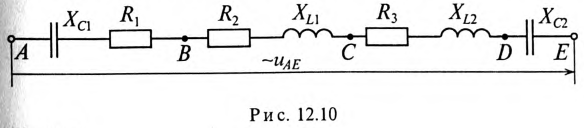
Требуется:
1. Вычислить ток цепи I и записать его мгновенное значение.
2. Записать мгновенное значение напряжения цепи иАЕ, определив предварительно угол ср и характер цепи.
3. Определить напряжение между точками АВ и CD.
4. Построить в масштабе векторную диаграмму цепи, определив едварительно напряжение на каждом сопротивлении.
5. Определить мощности S, Р и Q цепи.
6. Определить частоту, при которой в цепи наступит резонанс напряжений, и ток при резонансе.
7. Определить максимальную энергию, запасенную в магнитном поле катушек WmL и электрическом поле конденсаторов WmC. Как нужно изменить емкость конденсаторов, чтобы в цепи пил резонанс напряжений при частоте f = 50 Гц?
Решение
1. Для определения тока цепи I необходимо вычислить полное сопротивление цепи:
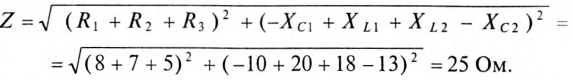
Действующее значение тока 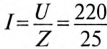 = 8,8 А, а амплитудное значение тока
= 8,8 А, а амплитудное значение тока 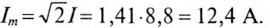
Угловая частота 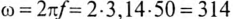 рад/с.
рад/с.
Мгновенное значение тока цепи:
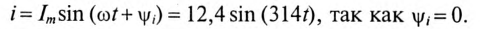
2. Угол сдвига фаз ф и характер цепи определяется через tg ф:
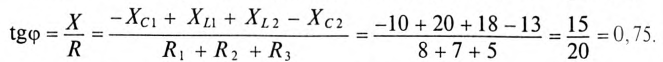
Таким образом, угол ф = 37° (из таблицы), характер цепи индуктивный (+ф).
Тогда мгновенное значение напряжения цепи
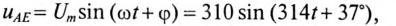
где 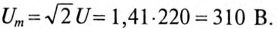
3. Напряжение на участках:
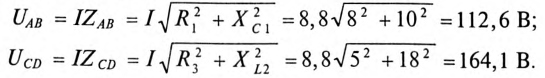
4. Для построения векторной диаграммы определяются напряжения:
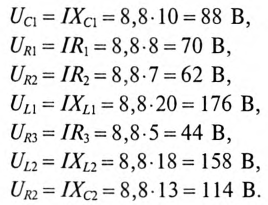
Векторная диаграмма цепи (отображает только характер участков, но не величины напряжений на них) изображена на рис. 12.11.
5. Полная мощность цепи 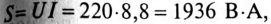 активная мощность Р=
активная мощность Р=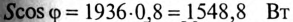 (так как
(так как 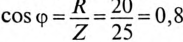 ), реактивная мощность
), реактивная мощность 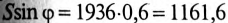 вар, (так как
вар, (так как 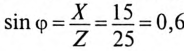 ).
).
6. Для определения частоты резонанса вычисляется индуктивность L и емкость С цепи:
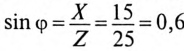
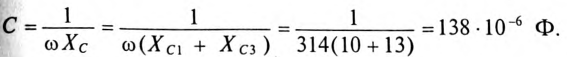
Тогда
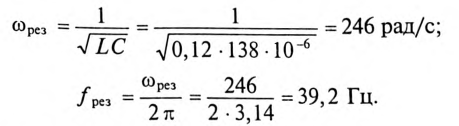
Ток цепи при резонансе 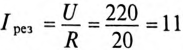 А.
А.
7. Максимальная энергия, запасенная в магнитном поле катушек:
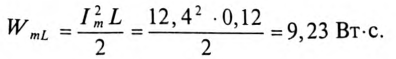
Максимальная энергия, запасенная в электрическом поле конденсаторов:
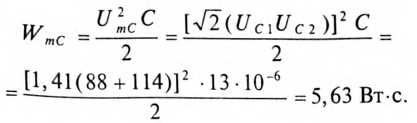
8. Условие резонанса XL = XC.
По условию задачи 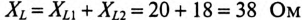 , а
, а 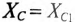
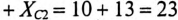 Ом. Этому Хс соответствует емкость С =
Ом. Этому Хс соответствует емкость С = 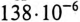 Ф при f = 50 Гц. Для того чтобы выполнить условие резонанса при сохранении частоты 50 Гц, необходимо Хс увеличить до 38 Ом. Чтобы емкостное сопротивление равнялось 38 Ом, величина емкости С должна быть равна
Ф при f = 50 Гц. Для того чтобы выполнить условие резонанса при сохранении частоты 50 Гц, необходимо Хс увеличить до 38 Ом. Чтобы емкостное сопротивление равнялось 38 Ом, величина емкости С должна быть равна
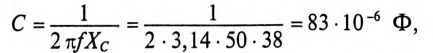
т. е. емкость конденсаторов нужно уменьшить на
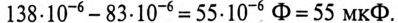
Разветвленная цепь синусоидального тока
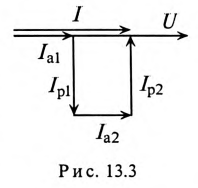
Активный и реактивный токи:
Для расчета разветвленных цепей синусоидального тока вводятся расчетные величины активного и реактивного токов цепи.
Если к цепи, содержащей активное сопротивление R и индуктивное XL (рис. 13.1а), приложено синусоидальное напряжение 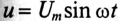 , то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол ф (рис. 12.1 в),
, то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол ф (рис. 12.1 в), 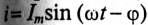 .
.
Векторная диаграмма в этом случае изображена на рис. 13.16.
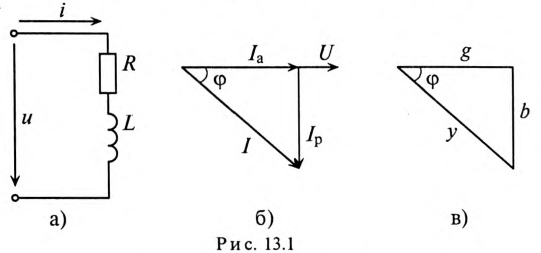
Ток цепи I (рис. 13.16) раскладывается на две составляющие, одна из которых  совпадает по фазе с напряжением, другая
совпадает по фазе с напряжением, другая  — сдвинута на 90°. Составляющая тока
— сдвинута на 90°. Составляющая тока  , совпадающая по фазе с напряжением, называется активной составляющей, или активным током. Составляющая тока
, совпадающая по фазе с напряжением, называется активной составляющей, или активным током. Составляющая тока  , имеющая относительно напряжения сдвиг по фазе на угол 90°, называется реактивной составляющей, или реактивным током.
, имеющая относительно напряжения сдвиг по фазе на угол 90°, называется реактивной составляющей, или реактивным током.
Активный и реактивный токи физического смысла не имеют. Они являются расчетными величинами, так как в неразветвленной цепи (рис. 13.1а) ток на всех участках имеет одинаковое значение. Однако понятия активный  и реактивный
и реактивный  токи значительно облегчают расчет разветвленных цепей синусоидального тока. Соотношения между токами определяются из треугольника токов (рис. 13.16)
токи значительно облегчают расчет разветвленных цепей синусоидального тока. Соотношения между токами определяются из треугольника токов (рис. 13.16)
13.2. Проводимости
Из треугольника токов для рассматриваемой цепи (рис. 13.16) следует: 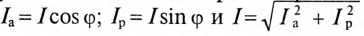 .
.
С другой стороны, известно, что 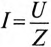 (см. (12.6)), a
(см. (12.6)), a 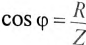 и
и 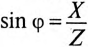 (см. (12.9)).
(см. (12.9)).
Тогда
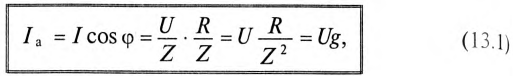
где g — активная проводимость цепи, равная

Величина, на которую умножают напряжение, чтобы получить ток, называют проводимостью.
А так как g определяет активный ток 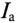 , то ее и называют активной проводимостью.
, то ее и называют активной проводимостью.
Таким образом, активная проводимость g определяется величиной активного сопротивления, деленного на квадрат полного (кажущегося) сопротивления цепи.
Величина реактивного тока определяется выражением
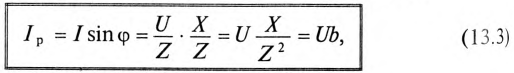
где b — реактивная проводимость цепи, равная

Величина полного тока цепи равна
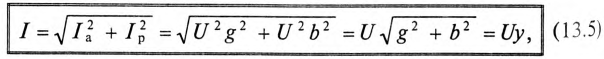
где 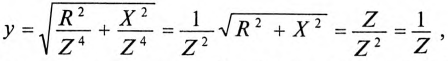 так как для цепи синусоидального тока с
так как для цепи синусоидального тока с  (рис. 13.1а)
(рис. 13.1а) 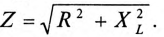
Таким образом, у — полная, или кажущаяся, проводимость цепи:

Полная (кажущаяся) проводимость цепи «у» является обратной величиной полного (кажущегося) сопротивления цепи.
Активная 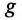 и реактивная
и реактивная 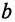 проводимости являются соответственно обратными величинами активного R и реактивного X сопротивлений только в том случае, если эти сопротивления (R и X) являются единственными в цепи или ветви, т. е.
проводимости являются соответственно обратными величинами активного R и реактивного X сопротивлений только в том случае, если эти сопротивления (R и X) являются единственными в цепи или ветви, т. е. 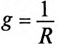 и
и 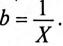
Если же в неразветвленной цепи (или ветви) включены сопротивления  то для определения проводимостей можно воспользоваться выражениями (13.2), (13.4), (13.6). Треугольник проводимостей для рассматриваемой цепи (рис. 13.1а) изображен на рис. 13.1 в. Соотношения между проводимостями определяются из этого треугольника.
то для определения проводимостей можно воспользоваться выражениями (13.2), (13.4), (13.6). Треугольник проводимостей для рассматриваемой цепи (рис. 13.1а) изображен на рис. 13.1 в. Соотношения между проводимостями определяются из этого треугольника.
Параллельное соединение катушки и конденсатора
Если к источнику синусоидального напряжения  подключить параллельно реальную катушку с активным сопротивлением
подключить параллельно реальную катушку с активным сопротивлением 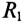 и индуктивным
и индуктивным 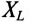 и конденсатор с активным сопротивлением
и конденсатор с активным сопротивлением 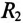 и емкостным
и емкостным 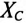 (рис. 13.2а), то токи в параллельных ветвях этой цепи изменяются по синусоидальному закону:
(рис. 13.2а), то токи в параллельных ветвях этой цепи изменяются по синусоидальному закону:
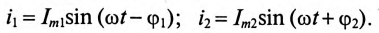
Действующие значения этих токов будут соответственно равны
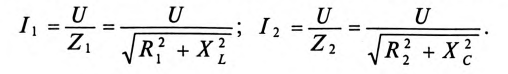
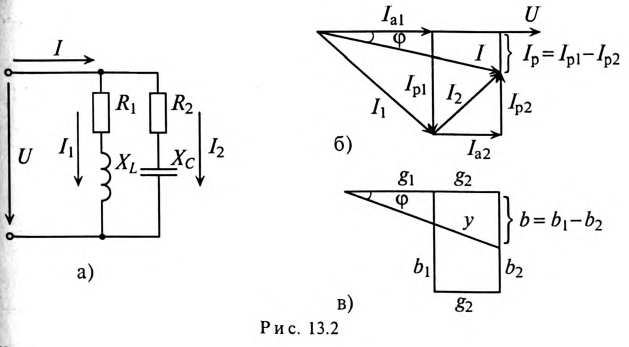
Ток в неразветвленной цепи 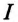 равен геометрической сумме токов в ветвях, так как токи не совпадают по фазе:
равен геометрической сумме токов в ветвях, так как токи не совпадают по фазе:
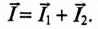
Для определения этого тока строится векторная диаграмма цепи (рис. 13.26), из которой следует:
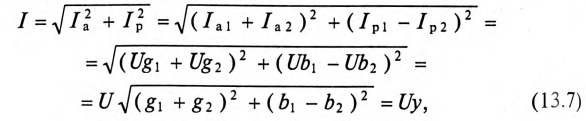
где 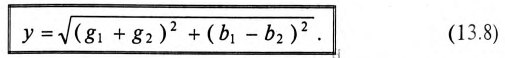
Таким образом, ток в неразветвленной части цепи 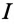 определяется произведением напряжения U и полной проводимости цепи
определяется произведением напряжения U и полной проводимости цепи 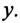
Реактивные проводимости в ветвях имеют различные знаки, так как сопротивления в ветвях различного характера (индуктивное и емкостное).
Треугольник проводимостей рассматриваемой цепи изображен на рис. 13.2в.
Характер разветвленной цепи определяется так же, как и неразветвленной. Если ток цепи 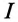 отстает от напряжения
отстает от напряжения 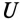 (как в рассматриваемом случае), то цепь индуктивного характера, если же ток
(как в рассматриваемом случае), то цепь индуктивного характера, если же ток 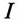 опережает напряжение
опережает напряжение 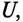 то цепь емкостного характера.
то цепь емкостного характера.
Резонанс токов
Резонанс токов в цепи (рис. 13.2а) с параллельным включением катушки и конденсатора (в различных ветвях) возникает при равенстве реактивных проводимостей в ветвях:
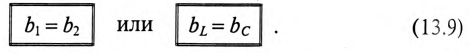
Выражение (13.9) является условием резонанса токов в разветвленных цепях синусоидального тока. Полная (кажущаяся) проводимость при этом условии
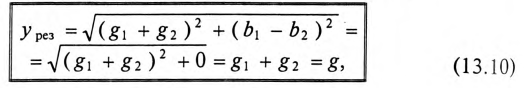
так как 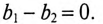
Таким образом, полная проводимость цепи при резонансе токов 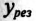 минимальна по величине и равна активной проводимости
минимальна по величине и равна активной проводимости 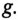 Следовательно, и ток в неразветвленной части цепи при резонансе токов имеет минимальную величину
Следовательно, и ток в неразветвленной части цепи при резонансе токов имеет минимальную величину

Реактивные токи в ветвях при резонансе токов равны между собой

Это равенство и определяет название «резонанс токов».
На основании равенства (13.12) строится векторная диаграмма при резонансе токов (рис. 13.3). Реактивные токи находятся в противофазе, поэтому ток в неразветвленной части цепи 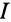 при резонансе токов равен активному току
при резонансе токов равен активному току 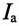 и совпадает по фазе с напряжением, т.е.
и совпадает по фазе с напряжением, т.е. 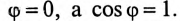 Следовательно, вся мощность цепи 5 при резонансе токов является активной Р:
Следовательно, вся мощность цепи 5 при резонансе токов является активной Р:
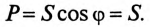
Эта активная мощность компенсирует потери на активном сопротивлении в параллельном резонансном контуре. Мощность (энергия), которая колеблется между электрическим полем конденсатора и магнитным полем индуктивности при резонансе, не является реактивной, так как не загружает источник и провода.
Частота резонанса токов в параллельном резонансном контуре может быть определена из условия резонанса токов, т. е. равенства реактивных проводимостей в ветвях 
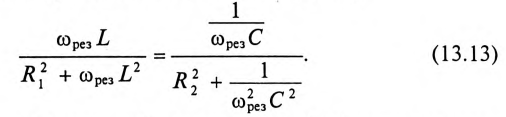
После ряда преобразований равенства (13.13) определяется частота резонанса токов
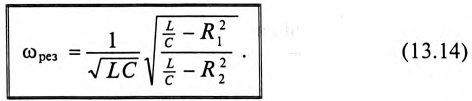
Резонансная частота зависит не только от параметров колебательного контура 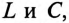 но и от активных сопротивлений в ветвях реального резонансного контура.
но и от активных сопротивлений в ветвях реального резонансного контура.
Если в резонансном контуре отсутствуют активные сопротивления в ветвях, то частота резонанса токов 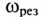 становится равной частоте собственных колебаний идеального резонансного контура
становится равной частоте собственных колебаний идеального резонансного контура
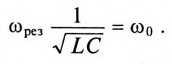
Если в резонансном контуре 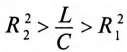 или
или 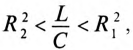 то резонанса токов добиться невозможно.
то резонанса токов добиться невозможно.
Резонанс токов нашел широкое применение в радиотехнике и выпрямительной технике (в резонансных фильтрах) и др.
Пример 13.1
Напряжение, приложенное к параллельно включенным катушке и конденсатору (рис. 13.4а), 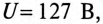 частота сети
частота сети 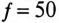 Гц. Параметры цепи:
Гц. Параметры цепи: 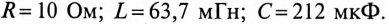 Определить:
Определить:
1) токи всех участков цепи: 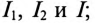
2) углы сдвига фаз этих токов относительно напряжения: 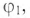
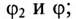
3) полную S, активную Р и реактивную Q мощности цепи;
4) частоту, при которой наступит резонанс токов в этой цепи. Построить векторную диаграмму.
Решение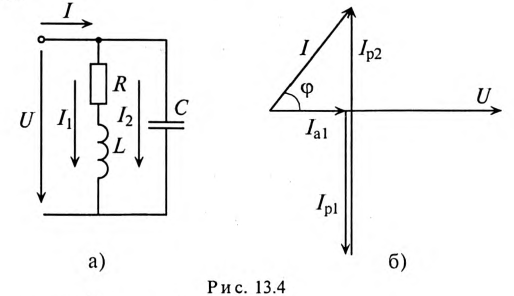
1. Сопротивление участков цепи:
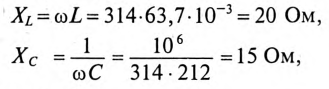
где 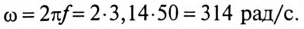
Сопротивление 1-й ветви:
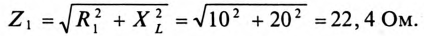
Токи в ветвях соответственно равны
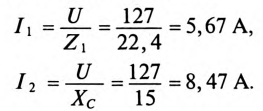
Для определения тока 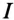 в неразветвленной части цепи определяются проводимости:
в неразветвленной части цепи определяются проводимости:
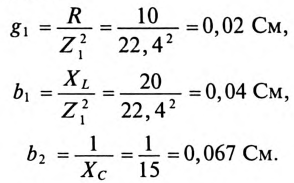
Тогда полная проводимость цепи будет равна
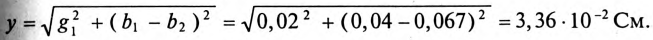
Ток в неразветвленной части цепи
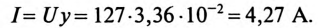
2. Углы сдвига фаз:
.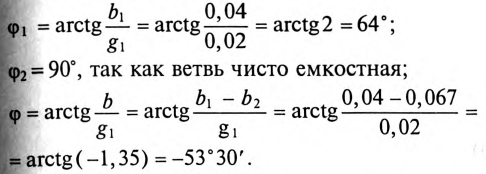
Знак «минус» перед значением угла  параллельного контура означает, что цепь имеет емкостной характер, так как
параллельного контура означает, что цепь имеет емкостной характер, так как 
3. Полная мощность цепи 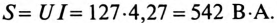
Активная мощность цепи 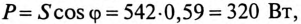 так как
так как 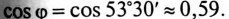
Реактивная мощность цепи 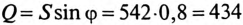 вар, так как
вар, так как 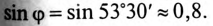
4. Угловая частота резонанса токов в цепи равна
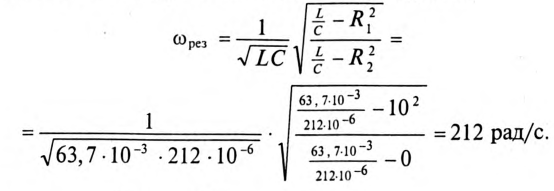
Откуда 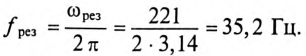
Для построения векторной диаграммы определяют активные и реактивные токи в ветвях:

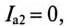 так как в ветви с емкостью отсутствует активное сопротивление, т.е.
так как в ветви с емкостью отсутствует активное сопротивление, т.е. 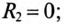
Векторная диаграмма для рассматриваемой цепи изображена на рис. 13.46.
На векторной диаграмме видно, что ток I опережает напряжение U на угол 53°30′ (цепь емкостного характера).
Коэффициент мощности
Номинальные параметры, т.е. мощность источника 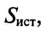 мощность потребителя
мощность потребителя 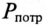 и коэффициент мощности
и коэффициент мощности 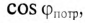 связаны следующим соотношением
связаны следующим соотношением

Из (13.15) следует, что чем меньше 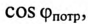 тем большую мощность
тем большую мощность 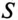 должен иметь источник для питания этого потребителя, т. е. тем больше его габариты, вес, расход материалов, стоимость и др.
должен иметь источник для питания этого потребителя, т. е. тем больше его габариты, вес, расход материалов, стоимость и др.
Ток в цепи потребителя с определенным 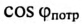 согласно выражению (12.11) равен
согласно выражению (12.11) равен
Из (13.16) видно, что чем меньше 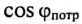 , тем больше ток потребителя
, тем больше ток потребителя 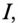 тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД ее и всей системы (3.11). Кроме того, увеличение тока требует для его передачи проводов большего сечения, т. е. большего расхода цветных металлов.
тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД ее и всей системы (3.11). Кроме того, увеличение тока требует для его передачи проводов большего сечения, т. е. большего расхода цветных металлов.
Таким образом, низкий коэффициент мощности потребителя 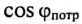 приводит к увеличению мощности источника, питающего этот потребитель, уменьшению КПД линии электропередачи и к увеличению сечения проводов линий электропередачи. 4В России установлен минимально допустимый коэффициент мощности не менее 0,93, т.е.
приводит к увеличению мощности источника, питающего этот потребитель, уменьшению КПД линии электропередачи и к увеличению сечения проводов линий электропередачи. 4В России установлен минимально допустимый коэффициент мощности не менее 0,93, т.е.  должен быть равен или больше 0,93
должен быть равен или больше 0,93 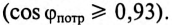
Однако  большинства электрических потребителей переменного тока меньше этой нормы. Так, например,
большинства электрических потребителей переменного тока меньше этой нормы. Так, например,  асинхронных двигателей, в зависимости от нагрузки, составляет
асинхронных двигателей, в зависимости от нагрузки, составляет 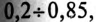 трансформаторов –
трансформаторов – 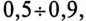 выпрямителей –
выпрямителей – 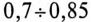 и т.д. Следовательно, коэффициент мощности этих потребителей необходимо повышать.
и т.д. Следовательно, коэффициент мощности этих потребителей необходимо повышать.
Так как большинство потребителей представляет собой нагрузку индуктивного характера, то для улучшения 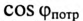 параллельно с ним подключаются конденсаторы (рис. 13.5а).
параллельно с ним подключаются конденсаторы (рис. 13.5а).
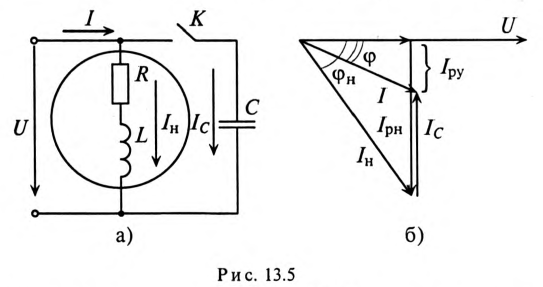
Из векторной диаграммы (рис. 13.56) видно, что с подключением конденсатора С (ключ К замкнут) появляется 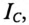 за счет которого уменьшается угол
за счет которого уменьшается угол 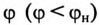 и увеличивается
и увеличивается 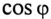 установки. При этом уменьшается ток цепи
установки. При этом уменьшается ток цепи 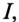 который до подключения конденсатора был равен току нагрузки
который до подключения конденсатора был равен току нагрузки 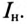
Для повышения коэффициента мощности 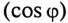 конденсатор можно включить последовательно с потребителем индуктивного характера. Однако при этом нарушается режим работы (напряжение) потребителя. Поэтому для улучшения
конденсатор можно включить последовательно с потребителем индуктивного характера. Однако при этом нарушается режим работы (напряжение) потребителя. Поэтому для улучшения 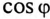 конденсатор подключают параллельно с нагрузкой (рис. 13.5а).
конденсатор подключают параллельно с нагрузкой (рис. 13.5а).
Коэффициент мощности можно повысить, увеличив активную нагрузку. При этом увеличивается потребляемая энергия, что экономически нерационально (уменьшается КПД установки).
Пример 13.2
Асинхронный двигатель, включенный в сеть с напряжением 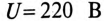 и частотой
и частотой 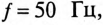 развивает на валу мощность
развивает на валу мощность 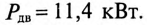 КПД двигателя
КПД двигателя 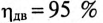 при
при 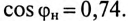 Определить емкость конденсатора С, который необходимо включить параллельно с двигателем (рис. 13.5а), чтобы повысить
Определить емкость конденсатора С, который необходимо включить параллельно с двигателем (рис. 13.5а), чтобы повысить 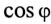 установки до 0,95.
установки до 0,95.
Решение
Мощность, потребляемая двигателем из сети:
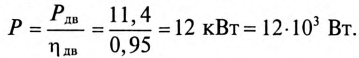
Ток нагрузки 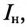 т.е. ток двигателя (рис. 13.5а), равен
т.е. ток двигателя (рис. 13.5а), равен
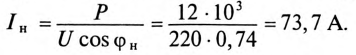
Реактивная составляющая тока двигателя 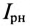 (рис. 13.56)
(рис. 13.56)
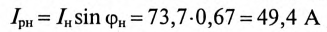
(по таблице 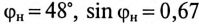 ).
).
Ток установки 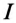 при подключении конденсатора, т. е. при
при подключении конденсатора, т. е. при 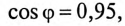 будет равен
будет равен

При 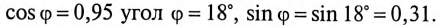 Реактивная составляющая тока установки (рис. 13.56)
Реактивная составляющая тока установки (рис. 13.56)
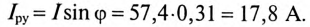
Ток конденсатора 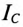 (рис. 13.56)
(рис. 13.56)
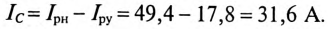
Емкостное сопротивление конденсаторов
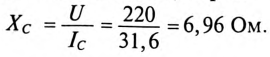
Емкость конденсаторов, которые нужно подключить параллельно двигателю для улучшения 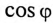 до 0,95:
до 0,95:
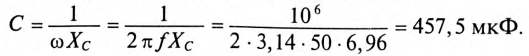
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
- Резистивные электрические цепи и их расчёт
- Резонанс токов
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
- Вращающееся магнитное поле
Пример расчета однофазной цепи синусоидального тока
Д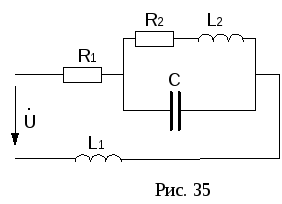 ля
ля
электрической цепи рис. 35 известны:
действующее значение приложенного
напряжения
![]() В,
В,
частота питающей сетиf=50
Гц, резисторыR1=3
Ом, R2=2
Ом, индуктивностиL1=3,185мГн,L2=12,75мГн, емкостьС=254,8мкФ.
Определить
токи, напряжения, мощности на всех
участках и во всей цепи.
1.
Определяем индуктивные и емкостное
сопротивления цепи:
![]()
![]()
![]()
2. Запишем
комплексы сопротивлений участков цепи:
![]() Ом
Ом
![]()
![]()
![]()
-
Эквивалентное сопротивление двух
параллельных ветвей:
![]() Ом;
Ом;
-
Эквивалентное сопротивление всей цепи:
![]() Ом.
Ом.
-
Ток в неразветвленной части цепи
определим по закону Ома. Для этого
зададим направление приложенного
напряжения и представим это напряжение
в комплексной форме.
Пусть
вектор приложенного напряжения совпадает
с положительным направлением оси
действительных чисел (рис. 36). Тогда
![]()
![]()
-
Падение напряжения на резисторе R1:
![]()
7. Падение
напряжения на индуктивности L1:
![]()
8.
Напряжение на параллельном участке
определяются по второму закону Кирхгофа.
Так как
![]() ,
,
то
![]()
Токи в
параллельных ветвях находятся по закону
Ома:

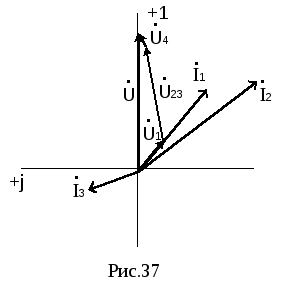
-
Векторная
диаграмма токов и напряжений приведена
на рис. 37. -
Р
 асчет
асчет
мощностей:
а) мощность, вырабатываемая источником
питания:
![]() ВА;
ВА;
![]() Вт;
Вт;![]() Вар.
Вар.
б) мощности, потребляемые нагрузкой:
– мощность сопротивления R1:

(нагрузка
этого участка цепи носит активный
характер);
– мощность участка цепи, содержащего
активное сопротивление R2и индуктивностьL2:
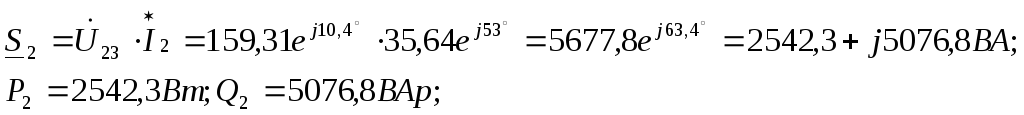
-
мощность участка цепи, содержащего
емкость С:
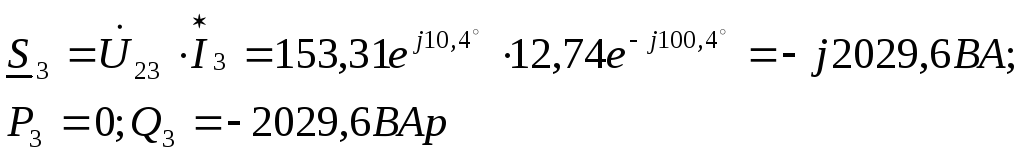
(нагрузка
участка цепи емкостная);
– мощность участка цепи, содержащего
индуктивность L1:

(нагрузка
участка цепи индуктивная);
в) уравнение баланса мощностей:

Погрешность
в расчетах не превышает 5%, следовательно,
задача решена верно.
11. Модель
заданной электрической цепи (рис. 38).

Рис. 38
Полученные
при моделировании показания приборов
немного отличаются от расчетных, так
как измерительные приборы имеют
внутренние сопротивления, которые
моделирующая система учитывает.
Цепи периодического несинусоидального тока Основные характеристики несинусоидальных периодических токов и напряжений
Большинство периодических
функций, с которыми имеют дело в
электротехнике и электронике, удовлетворяют
условиям Дирихле, поэтому их можно
представить в виде ряда Фурье:
![]()
![]()
![]()
![]()
где E0,
U0, I0– постоянные составляющие несинусоидальных
ЭДС, напряжения, тока;
Em1,
Um1,
Im1– амплитуды гармоник ЭДС, напряжения,
тока основной частоты;
Em2,
Um2,
Im2– амплитуды гармоник ЭДС, напряжения,
тока двойной и других кратных частот;
1 –
циклическая частота гармоник основной
частоты;
u1,
u2,
e1,
e2,,i1,
i2
– начальные фазы гармоник основной
и кратных частот напряжения, ЭДС, тока.
Действующее значение
любой периодической функции –
среднеквадратичное значение:
 ,
,
т.е.
![]()
![]()
![]()
Таким
образом, действующее значение
периодического несинусоидального тока
(напряжения, ЭДС) равно корню квадратному
из суммы квадратов постоянной
составляющей![]()
![]()
![]()
![]() и квадратов действующих значений всех
и квадратов действующих значений всех
гармонических составляющих![]()
Действующее
значение несинусоидальных периодических
величин не зависит от начальных фаз
гармоник, а зависит только от их
действующих значений (амплитуд).
Среднее
значение периодической несинусоидальной
величины
![]() за
за
период:![]()
Оно равно
постоянной составляющей, так как
суммарная площадь, ограниченная кривой
за период любой гармонической составляющей,
равна нулю.
![]() .
.
Сравнивать
несинусоидальные периодические величины
можно при помощи трех коэффициентов:
формы
![]() амплитуды
амплитуды![]() ,
,
искажения![]() .
.
![]()
где
![]() –
–
амплитудное, среднее, действующее
значения величины;
![]() – действующее значение основной гармоники.
– действующее значение основной гармоники.
Соседние файлы в папке Все что скинул препод
- #
- #
- #
25.03.20169.01 Кб111Задача 1.xlsx
- #
25.03.201610.02 Кб63зАДАЧА 2.xlsx
- #
25.03.20168.97 Кб42Звезда с нулем.xlsx
- #
- #
- #
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Параметры цепей синусоидального электрического тока
Определение 1
Переменный ток – это электрический ток, который изменяется во времени по какому-либо закону.
В том случае, когда форма кривых величины переменного тока и напряжения повторяется через одинаковые промежутки времени, то они являются периодическими. Наименьшее время, через которое повторяется форма кривых величины переменного тока и напряжения называется периодом. Количество периодов за одну секунду называется частотой, она может быть рассчитана по следующей формуле:
$f = 1 / T$
где, Т – период.
Самыми простыми периодическими переменными напряжения и величины тока являются токи и напряжения синусоидальной формы:
$u(t) = Um*sin(wt+фu)$
$i(t) = Im*sin(wt+фi)$
где, u(t), i(t) – мгновенные значения напряжения и тока; Im, Um – амплитудные значения тока и напряжения; фu, фi – начальные фазы напряжения и тока; w – угловая скорость.
Определение 2
Угол сдвига фаз – это разница начальных фаз тока и напряжения.
Угол сдвига фаз обозначается следующим образом:
$О = фu – фi$
Известно, что комплексное число можно представить в виде вектора на комплексной плоскости, а мнимая и действительная часть части комплексного числа являются проекциями вектора на мнимую и вещественную оси.
Рисунок 1. График. Автор24 — интернет-биржа студенческих работ
«Расчет однофазной цепи синусоидального тока» 👇
В электротехнике за мнимую единицу принята буква j.
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
где, А – модуль; ф – фаза или аргумент
Допустим, что вектор А на комплексной плоскости вращается против часовой стрелки с угловой скоростью, то комплексное число запишется следующим образом
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
Рисунок 4. Оператор вращения. Автор24 — интернет-биржа студенческих работ
Таким образом видно, что мгновенные значения синусоидального тока и напряжения похожи на мнимую часть вращающегося комплексного числа:
Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ
где, Im – комплексная амплитуда тока; Um – комплексная амплитуда напряжения.
Допустим, что
$i(t)=5sin(wt + 30)$
Тогда максимальное значение в комплексной форме будет выглядеть следующим образом
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Действующее значение в комплексной форме можно записать так:
Рисунок 7. Формула. Автор24 — интернет-биржа студенческих работ
Если
Рисунок 8. Формула. Автор24 — интернет-биржа студенческих работ
То мгновенное значение можно записать в следующем виде:
Рисунок 9. Формула. Автор24 — интернет-биржа студенческих работ
Получается, что мгновенные реальные значения синусоидального тока и напряжения могут быть заменены комплексной амплитудой или комплексным действующим значением напряжения и тока.
Расчет однофазной цепи синусоидального тока
Рассмотрим схему электрической цепи однофазного синусоидального тока, которая представлена на рисунке ниже
Рисунок 10. Схема цепи однофазного синусоидального тока. Автор24 — интернет-биржа студенческих работ
Допустим, что нам известны следующие значения:
Рисунок 11. Формулы. Автор24 — интернет-биржа студенческих работ
В данном случае расчет будет производиться методом контурных токов. Значение контурного тока I22 принимается равным значению источника тока J1, уравнение для контурного тока I11 будет выглядеть следующим образом:
$I11 * (R3 + jx2) – I22 * jx2 = E3$
Отсюда
$I11 = (I22jx2 – E3) / (R3 + jx2) = (j1 *j10 – j10) / (10 + j10) = –1 A$
Ток в третьей ветви рассматриваемой цепи равен контурному току I11, который в показательной форме комплексного числа будет выглядеть следующим образом:
Рисунок 12. Формула. Автор24 — интернет-биржа студенческих работ
Электрический ток во второй ветви цепи представляет собой алгебраическую сумму контурных токов, проходящих через эту ветвь:
Рисунок 13. Формула. Автор24 — интернет-биржа студенческих работ
Полная мощность приемников может быть рассчитана следующим образом:
$Sпр = Рпр + Qпр$
где: Р – активная мощность приемников; Q – реактивная мощность приемников
Для расчета активной мощности рассматриваемой электрической цепи используется следующая формула:
Рисунок 14. Формула. Автор24 — интернет-биржа студенческих работ
Реактивная мощность может быть определена следующим образом:
Рисунок 15. Формула. Автор24 — интернет-биржа студенческих работ
Таким образом, полная мощность, выделяемая источниками в схему определяется по формуле:
Рисунок 16. Формула. Автор24 — интернет-биржа студенческих работ
Рассмотрим схему на рисунке ниже
Рисунок 17. Схема. Автор24 — интернет-биржа студенческих работ
Нам известны следующие величины:
- U(t) = 10sin(wt+90)
- R1 = 2 Ом
- х1 = 2 Ом
- R2 = 2 Ом
- R3 = 2 Ом
- х3 = 4 Ом
Нам необходимо рассчитать I1 в неразветвленной части выше представленной схемы.
Функция времени U(t) = 10sin(wt + 90) в виде показательной комплексного числа будет выглядеть следующим образом:
Рисунок 18. Формула. Автор24 — интернет-биржа студенческих работ
Сначала необходимо рассчитать входное сопротивление рассматриваемой схемы относительно зажимов источника напряжения:
$Z = R1 + x1 + (R2 * (R3 – jx3)) / (R2 + R3 + jx3) = 2 + j2 + ((4 – j8) / 4 – j4)) = 2 + j2 + ((4 – j8) * (4 + j4)) / 16 + 16 = 2 + j2 + ((16 – j32 + j16 + 32) / 16 + 16) = 2 + j2 + ((48 – j16) / 32) = 2 + j2 + 1.5 – j0.5 = 3.5 – j1.5$
Теперь можно рассчитать ток I1 по закону Ома
Рисунок 19. Формула. Автор24 — интернет-биржа студенческих работ
Рассмотрим схему на рисунке ниже
Рисунок 20. Схема. Автор24 — интернет-биржа студенческих работ
Известны следующие значения
Рисунок 21. значения. Автор24 — интернет-биржа студенческих работ
Необходимо определить напряжение U31
Принимаем за базисный узел – первый, то есть ф1 = 0. Потенциалы второго и четвертого узлов рассматриваемой схемы определяются следующим образом:
$ф2 = Е5$
$ф4 = –Е4$
Уравнение для третьего потенциала будет выглядеть следующим образом:
$ф3 * ((1 / –jx2) + (1 / (R3 – jx3))) – ф2 * (1 / (R3 + jx3)) + ф4 * (1 / –jx2) = –J1$
Если мы подставим в получившееся уравнение численные значения, то получим:
Рисунок 22. Формула. Автор24 — интернет-биржа студенческих работ
Из последнего выражения можно выразить потенциал третьего узла
Рисунок 23. Формула. Автор24 — интернет-биржа студенческих работ
Так как ф3 = U31, то мгновенное значение напряжения можно записать следующим образом:
Рисунок 24. Формула. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
























