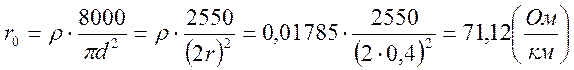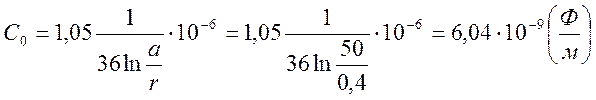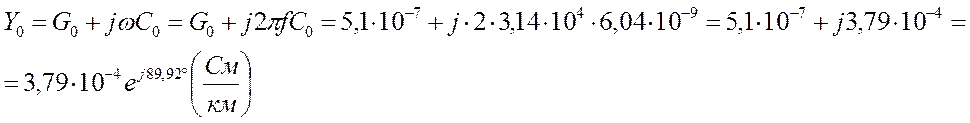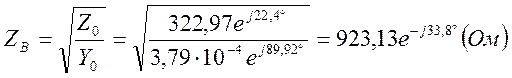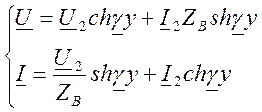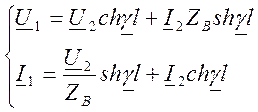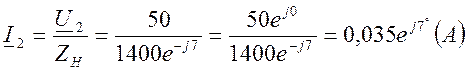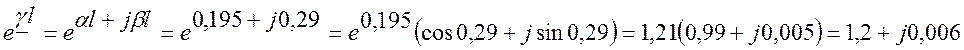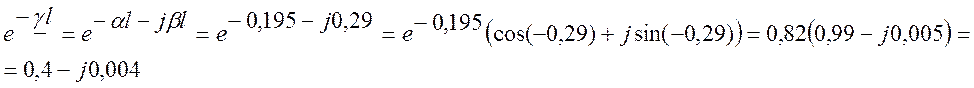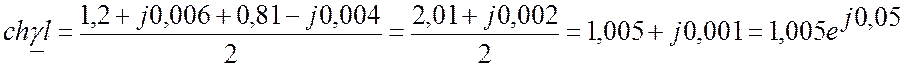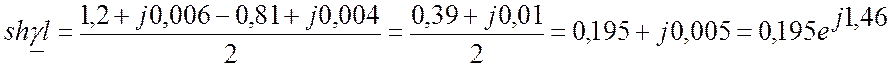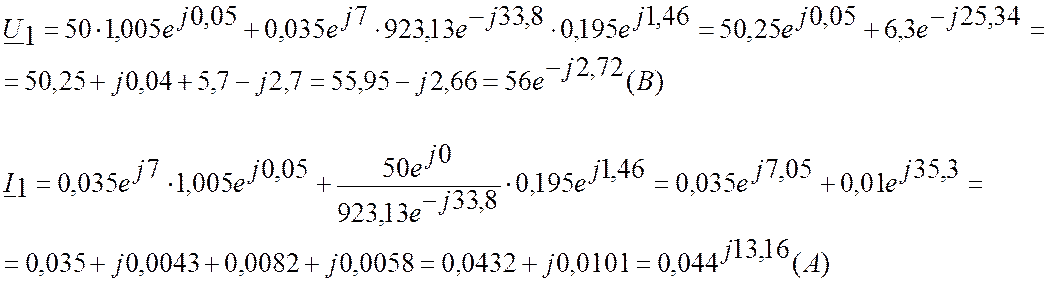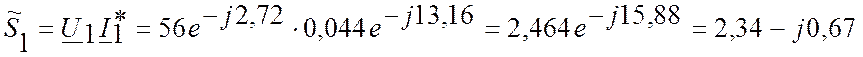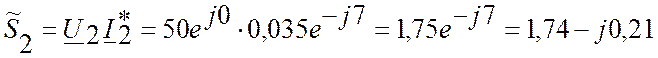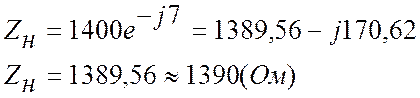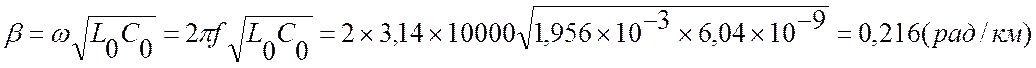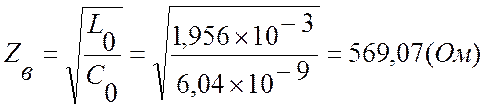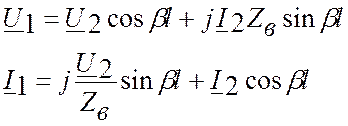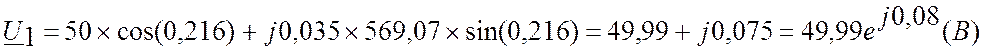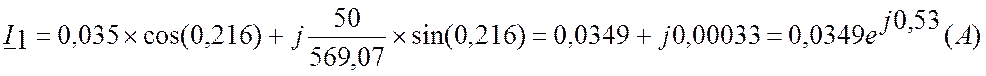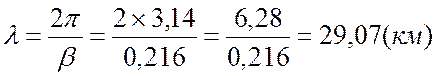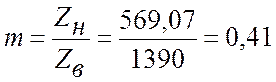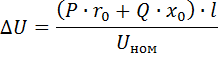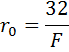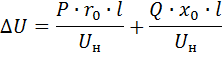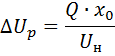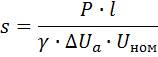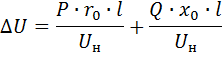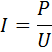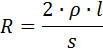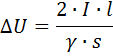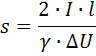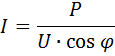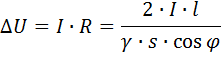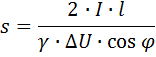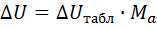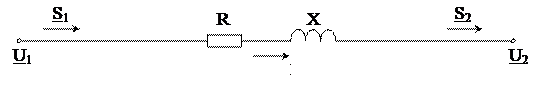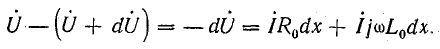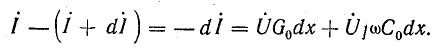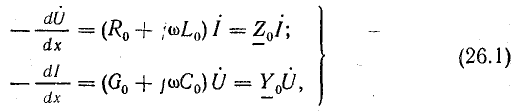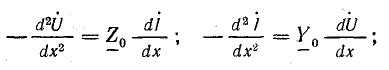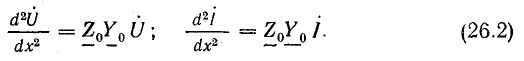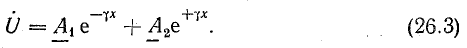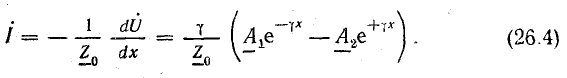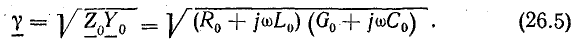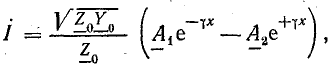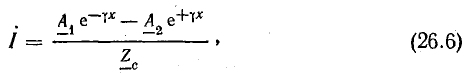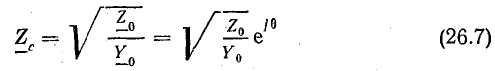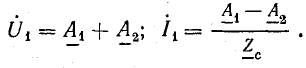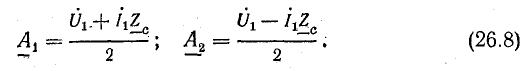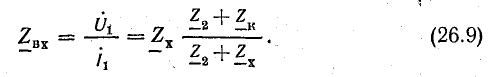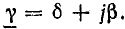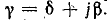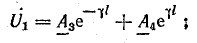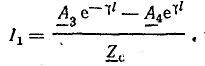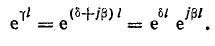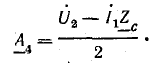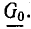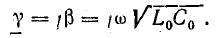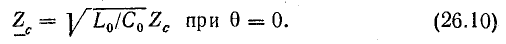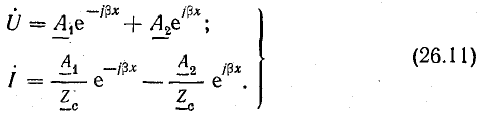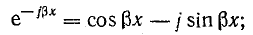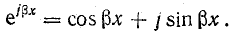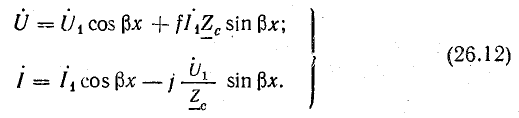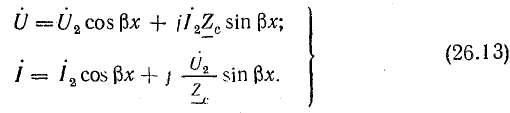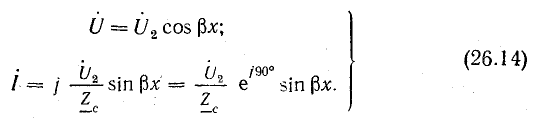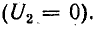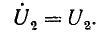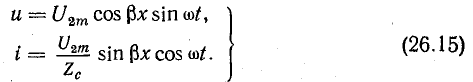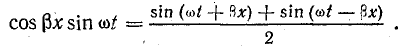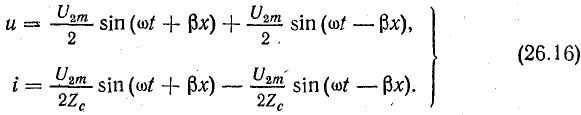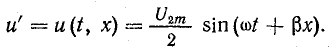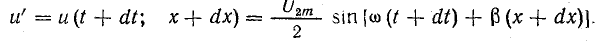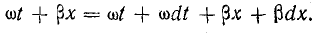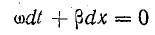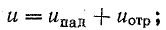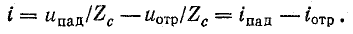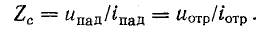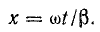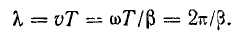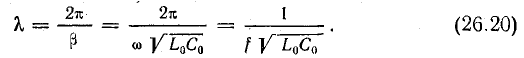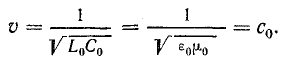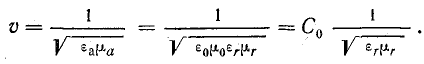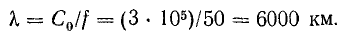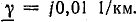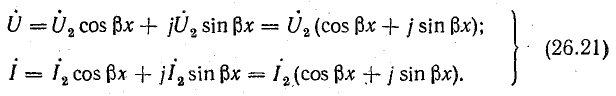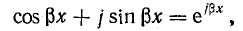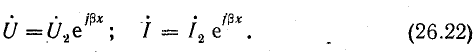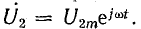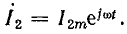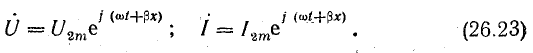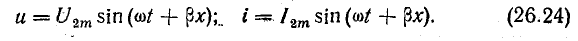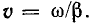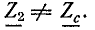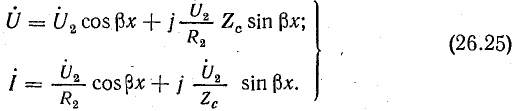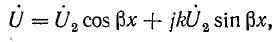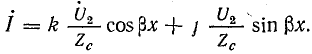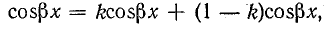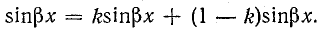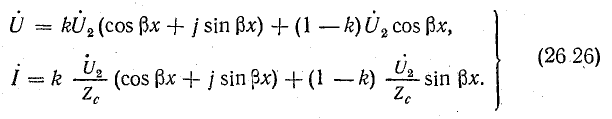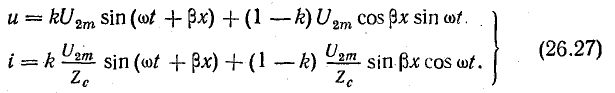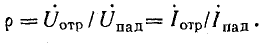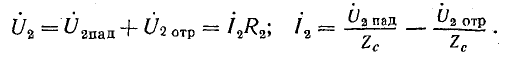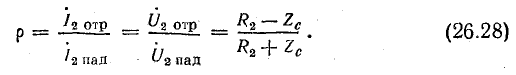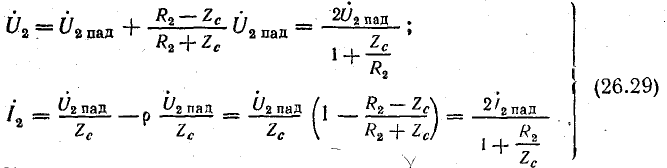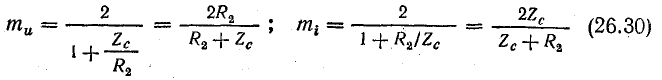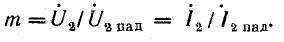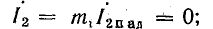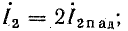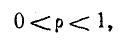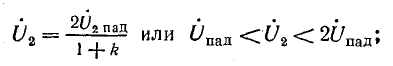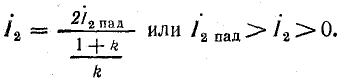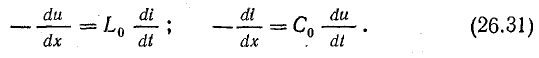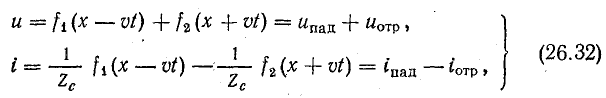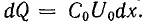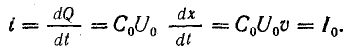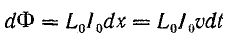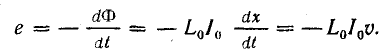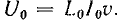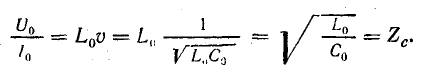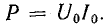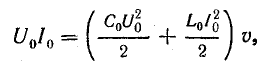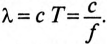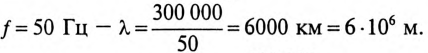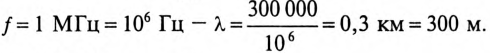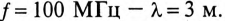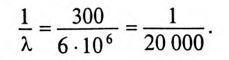Выпишем комплексное представление волн
напряжения и тока вдоль линии, и определим
константы интегрирования входящие в
эти выражения, используя граничные
условия в начале линии:

Пусть в начале линии при
напряжении
и
,
тогда можно получить:

Просуммируем первое, и второе уравнения
в системе (4), в результате получим
выражение для константы
:
.
Вычитая второе уравнение из первого в
системе (4), получим выражение для
константы
:
.
Поставим найденные константы в выражения
для напряжения:

Напомним, что в скобках находятся
гиперболические функции синус и косинус:
|
|

Приведём графический вид функций
,
.
ch(x)
Теперь выражения для напряжения и
тока можно переписать в виде:
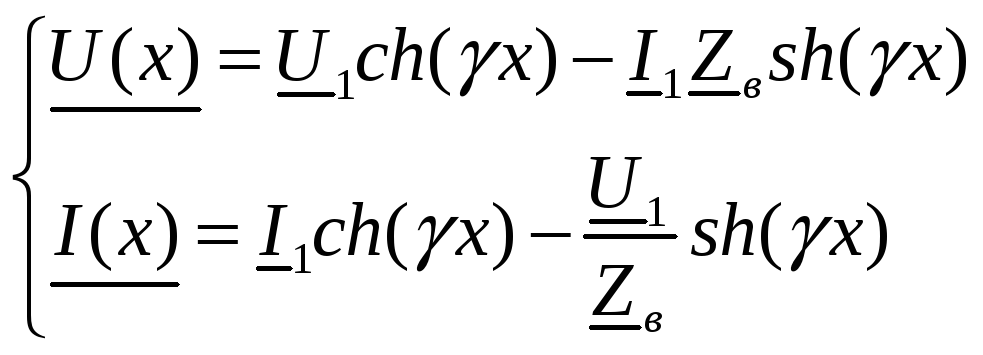
sh(x)
Используя это выражение можно
получить связь между величинами в начале
и в конце линии. Поставим
в выражения (5), здесь
длина линии:
(6)
Решим уравнения (6) относительно
и
,
получим систему уравнений позволяющую
определять ток и напряжения в начале
линии при известных значения в конце
линии.

(7)
Если ввести обозначения
то мы получаем уравнение четырехполюсника

(8)
Для всякого пассивного четырехполюсника
выполняется:
.
(9)
§5.2 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии
Обозначим расстояние от текущей точки
на линии до конца линии
,
а длину всей линии
:
. (10)
Пусть известны напряжения и ток в конце
линии
и
.
Будем использовать эти значения
как граничные условии при
.
На основании системы уравнений (4)
получаем:
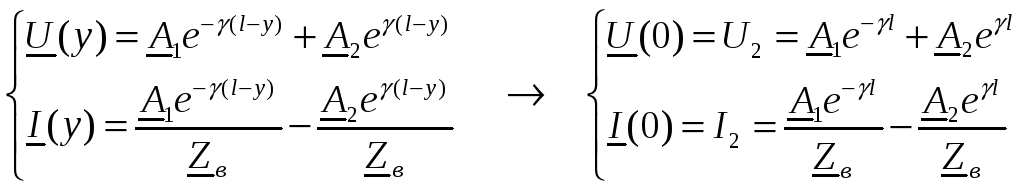
Решая систему относительно констант
и
:

Подставив найденные значения постоянных
и
в систему (4) получаем:

(13)
§5.3 Линии без потерь
Строго говоря, линии без потерь не
существует. Однако можно создать линию
с очень малыми потерями (с очень малыми
и
по сравнению с
и
соответственно). В ряде случаев, в
особенности при высоких частотах, когда
>>
и
>>
,
можно пренебречь наличием потерь в
линии и принять
и
.
В этом случае коэффициент затухания
,
и коэффициент распространения становится
чисто мнимой величиной
,
,
а волновое сопротивление является чисто
активным:
. (15)
Для определения напряжения и тока в
любой точке линии обратимся к системе
уравнений (13)

(16)
и учтем,
что
,
и перепишем уравнения (16):

Используя те же выражения для системы
(5) можно записать уравнения линий без
потерь через ток и напряжения в начале
линии:

§5.4 Коэффициент отражения
Отношение напряжения отраженной волны
в конце линии к напряжению падающей
волны в конце линии называют коэффициентом
отражения по напряжению и обозначают
.
В соответствии с формулой (12)можно
получить:

Из этого выражение видно, что при
согласованной нагрузке мы получаем
,
и следовательно нет отражённой волны,
а при
холостом ходе мы получаем
то есть волна полностью отражается.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Страницы работы
Содержание работы
Исходные данные (16 вариант):
f = 10 кГц U2 = 50 В
l = 1 км Zн = 1400e–j7º Ом
a = 50 мм Тип
– ВЛ
r = 0,4 мм
1. Определяем первичные параметры
линии:
– сопротивление проводов двухпроводной
медной линии на постоянном токе:
ρ – удельное сопротивление
проводов при t=20º; для меди ρ=0,01785 Ом*мм2/м;
– поправочный коэффициент F(x), учитывающий увеличение активного сопротив ления за счёт
поверхностного эффекта:
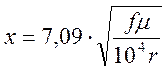
для меди µ=1; 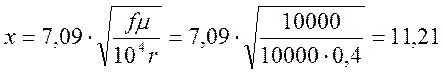
По таблице определяем F(x):
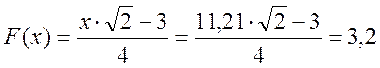
R0=r0(1+F(x))=71,12(1+3,2)=298,7
(Ом/км)
Индуктивность двухпроводной линии
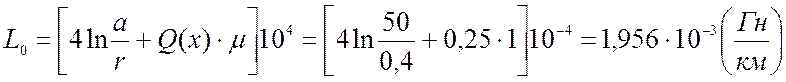
;
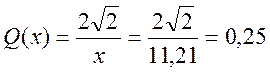
Ёмкость двухпроводной воздушной линии
на единицу длины:
Проводимость единицы длины линии:
G0=G’+nf=1×10-8+5×10-11×104=5,1×10-7
(См/км), где
G’ – проводимость изоляции
на постоянном токе, равная 1×10-8 (См/км) при
сухой погоде.
n – коэффициент диэлектрических
потерь, равный 5×10-11 (См/км×Гц) при сухой
погоде.
2. Определяем напряжение U1, ток I1,
мощности в начале и конце линии, КПД линии
а) Определяем вторичные параметры
линии:
– полное комплексное сопротивление
единицы длины линии:
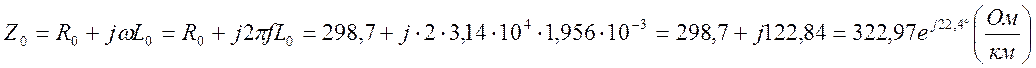
полная комплексная проводимость единицы длины линии:
– волновое сопротивление линии:
– комплексный коэффициент распространения:
γl = αl+jβl = (0,195+j0,29)×1 = 0,195+j0,29
затухание сигнала αl = 0,195 (Нп)
изменение фазы βl = 0,29 (рад)
б) Запишем уравнения для линии с
потерями через параметры конца линии:
Для расчёта напряжения и тока в
начале линии U1и I1 вместо y подставляем l,
тогда:
Так как ток I2 в конце линии неизвестен, но известны нагрузка и
напряжение в конце линии, то найдём его:
Рассчитываем и
, для этого воспользуемся следующими соотношениями:
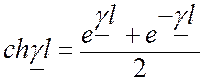
; 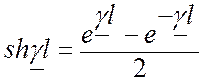
Рассчитаем U1 и I1 в начале
линии:
в) Рассчитаем полную комплексную
мощность в начале и конце линии и КПД линии
Полная мощность S1=2,464 (BA)
Активная мощность P1=2,34
(Вт)
Реактивная мощность Q1=-0,67
(вар)
Полная мощность S2=1,75
(BA)
Активная мощность P2=1,74
(Вт)
Реактивная мощность Q2=-0,21
(вар)
Определяем КПД линии:
η=(Р1/Р2)×100%=(1,74/2,34)×100%=74,36%
3. Для линии без потерь определяем
напряжение U1 и ток I1
в начале линии, а также длину электромагнитной волны λ:
а) Для линии без потерь R0=0,
G0=0
Нагрузка стала активной
Коэффициент фазы
Определяем изменение фазы сигнала по
всей длине линии
Определяем волновое сопротивление
б) Напряжение и ток в начале линии
без потерь
тогда
Длина электромагнитной волны λ:
4. Построим график U=f(βy) для линии без потерь:
|
|
0 |
|
|
2,16 |
|
|
0 |
3,634 |
7,258 |
1 |
|
|
1 |
|
0 |
0,976 |
|
|
1 |
0,5 |
0 |
0,952 |
|
|
0 |
|
1 |
0,214 |
|
|
0 |
|
1 |
0,0458 |
|
|
0 |
0,084 |
0,1681 |
0,0077 |
|
|
50 |
38,21 |
20,5 |
48,98 |
Похожие материалы
- Определение тока и закона изменения во времени тока во второй ветви, приведённой схемы, интегралом Дюамеля
- Переходные процессы в линейных электрических цепях с сосредоточенными параметрами
- Переходные процессы при заряде и разряде конденсатора
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Расчет сетей по потерям напряжения

Понижение напряжения у потребителя по сравнению с нормальным сказывается на работе токоприемника, будь то силовая или осветительная нагрузка. Поэтому при расчете любой линии электропередачи отклонения напряжений не должны превышать допустимых норм, сети, выбранные по току нагрузки и рассчитанные на нагрев, как правило, проверяют по потере напряжения.
Потерей напряжения Δ U называют разность напряжений в начале и конце линии (участка линии) . ΔU принято определять в относительных единицах — по отношению к номинальному напряжению. Аналитически потеря напряжения определена формулой:
где P — активная мощность, кВт, Q — реактивная мощность, квар, ro — активное сопротивление линии, Ом/км, xo — индуктивное сопротивление линии, Ом/км, l — длина линии, км, U ном — номинальное напряжение, кВ.
Значения активного и индуктивного сопротивлений (Ом/км) для воздушных линий, выполненных проводом марки А-16 А-120 даны в справочных таблицах. Активное сопротивление 1 км алюминиевых (марки А) и сталеалюминевых (марки АС) проводников можно определить также по формуле:
где F — поперечное сечение алюминиевого провода или сечение алюминиевой части провода АС, мм 2 (проводимость стальной части провода АС не учитывают).
Согласно ПУЭ («Правилам устройства электроустановок»), для силовых сетей отклонение напряжения от нормального должно составлять не более ± 5 %, для сетей электрического освещения промышленных предприятий и общественных зданий — от +5 до — 2,5%, для сетей электрического освещения жилых зданий и наружного освещения ±5%. При расчете сетей исходят из допустимой потери напряжений.
Учитывая опыт проектирования и эксплуатации электрических сетей, принимают следующие допустимые величины потери напряжений: для низкого напряжения — от шин трансформаторного помещения до наиболее удаленного потребителя — 6%, причем эта потеря распределяется примерно следующим образом: от станции или понизительной трансформаторной подстанции и до ввода в помещение в зависимости от плотности нагрузки — от 3,5 до 5 %, от ввода до наиболее удаленного потребителя — от 1 до 2,5%, для сетей высокого напряжения при нормальном режиме работы в кабельных сетях — 6%, в воздушных— 8%, при аварийном режиме сети в кабельных сетях – 10 % и в воздушных— 12 %.
Считают, что трехфазные трехпроводные линии напряжением 6—10 кВ работают с равномерной нагрузкой, т. е что каждая из фаз такой линии нагружена равномерно. В сетях низкого напряжения из-за осветительной нагрузки добиться равномерного ее распределения между фазами бывает трудно, поэтому там чаще всего применяют 4-проводную систему трехфазного тока 380/220 В. При данной системе электродвигатели присоединяют к линейным проводам, а освещение распределяется между линейными и нулевым проводами. Таким путем уравнивают нагрузку на все три фазы.
При расчете можно пользоваться как заданными мощностями, так и величинами токов, которые соответствуют этим мощностям. В линиях, которые имеют протяженность в несколько километров, что, в частности, относится к линиям напряжением 6—10 кВ, приходится учитывать влияние индуктивного сопротивления провода на потерю напряжения в линии.
Для подсчетов индуктивное сопротивление медных и алюминиевых проводов можно принять равным 0,32—0,44 Ом/км, причем меньшее значение следует брать при малых расстояниях между проводами (500—600 мм) и сечениях провода выше 95 мм2, а большее — при расстояниях 1000 мм и выше и сечениях 10—25 мм2.
Потеря напряжения в каждом проводе трехфазной линии с учетом индуктивного сопротивления проводов подсчитывается по формуле
где первый член в правой части представляет собой активную, а второй — реактивную составляющую потери напряжения.
Порядок расчета линии электропередачи на потерю напряжения с проводами из цветных металлов с учетом индуктивного сопротивления проводов следующий:
1. Задаемся средним значением индуктивного сопротивления для алюминиевого или сталеалюминевого провода в 0,35 Ом/км.
2. Рассчитываем активную и реактивную нагрузки P, Q.
3. Подсчитываем реактивную (индуктивную) потерю напряжения
4. Допустимая активная потеря напряжения определяется как разность между заданной потерей линейного напряжения и реактивной:
5. Определяем сечение провода s, мм2
где γ — величина, обратная удельному сопротивлению ( γ = 1/ro — удельная проводимость).
6. Подбираем ближайшее стандартное значение s и находим для него по справочной таблице активное и индуктивное сопротивления на 1 км линии ( ro, хо ).
7. Подсчитываем уточненную величину потери напряжения по формуле.
Полученная величина не должна быть больше допустимой потери напряжения. Если же она оказалась больше допустимой, то придется взять провод большего (следующего) сечения и произвести расчет повторно.
Для линий постоянного тока индуктивное сопротивление отсутствует и общие формулы, приведенные выше, упрощаются.
Расчет сетей п остоянного тока по потерям напряжения.
Пусть мощность P, Вт, надо передать по линии длиной l, мм, этой мощности соответствует ток
где U — номинальное напряжение, В.
Сопротивление провода линии в оба конца
где р — удельное сопротивление провода, s — сечение провода, мм2.
Потеря напряжения на линии
Последнее выражение дает возможность произвести проверочный расчет потери напряжения в уже существующей линии, когда известна ее нагрузка, или выбрать сечение провода по заданной нагрузке
Расчет сетей однофазного переменного тока по потерям напряжения.
Если нагрузка чисто активная (освещение, нагревательные приборы и т. п.), то расчет ничем не отличается от приведенного расчета линии постоянного тока. Если же нагрузка смешанная, т. е. коэффициент мощности отличается от единицы, то расчетные формулы принимают вид:
потери напряжения в линии
а необходимое сечение провода линии
Для распределительной сети 0,4 кВ, питающей технологические линии и другие электроприемники лесопромышленных или деревообрабатывающих предприятий, составляют ее расчетную схему и расчет потери напряжения ведут по отдельным участкам. Для удобства расчетов в таких случаях пользуются специальными таблицами. Приведем пример такой таблицы, где приведены потери напряжения в трехфазной ВЛ с алюминиевыми проводами напряжением 0,4 кВ.
Потери напряжения определены следующей формулой:
где Δ U — потеря напряжения, В, Δ U табл — значение относительных потерь, % на 1 кВт•км, Ма — произведение передаваемой мощности Р (кВт) на длину линии, кВт•км.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
№10 Линия электропередачи постоянного тока.
Если линия электропередачи имеет небольшую длину, при которой можно пренебречь утечкой тока через изоляцию, то ее электрическую схему можно представить в виде последовательного соединения сопротивления линии RЛ, равного суммарному сопротивлению прямого и обратного проводов, и сопротивления нагрузки RН (рис. 10.1).
Рис. 10.1 — Линия электропередачи постоянного тока
При анализе работы линии нас интересуют, главным образом, три вопроса: напряжение на нагрузке, величина передаваемой мощности и коэффициент полезного действия передачи. Режимы работы линии удобно рассматривать в виде зависимостей различных величин от тока в линии, равного :
Падение напряжения в линии ΔU и напряжение на нагрузке U2 определяются следующими выражениями:
Если U1 и RЛ постоянны, то оба выражения представляют собой линейные функции тока (рис. 10.2). В режиме холостого хода (при I = 0) ΔU = 0, а U2 = U1. С ростом тока падение напряжения в линии возрастает, а напряжение на нагрузке уменьшается, и в режиме короткого замыкания (при RН = 0)
Все входное напряжение гасится на сопротивлении линии.
Рис. 10.2 — Режимы работы линии
Мощность на входе линии линейно зависит от тока: P1 = U1*I. При холостом ходе она равна нулю, а при коротком замыкании вычисляется по формуле
Потери мощности в линии ΔP=I2Rл представляют собой квадратичную функцию тока. Ее график – парабола, проходящая через начало координат.
т.е. в режиме короткого замыкания мощность, поступающая в цепь, полностью теряется в линии.
Мощность, поступающая в нагрузку, равна разности мощности в начале линии и мощности, теряемой в проводах:
Последнее выражение представляет собой уравнение параболы со смещенной вершиной и с обращенными вниз ветвями, проходящими через точки I = 0 и I = IK.
Мощность нагрузки представляет собой довольно сложную зависимость от сопротивления RН:
При RН =0: Р2 = 0; при возрастании RН мощность Р2 сначала возрастает, достигает максимального значения и начинает убывать, стремясь к нулю при RН→∞ (рис. 1.25).
Выясним, при каком сопротивлении нагрузки передаваемая ей мощность максимальна. Для этого продифференцируем функцию (1.15) по RН и приравняем ее к нулю:
Приравняв к нулю числитель производной, получим:
То есть мощность, получаемая нагрузкой, максимальна, когда сопротивление нагрузки равно сопротивлению линии.
Ток, протекающий при этом по линии составляет половину тока короткого замыкания, а мощность в конце линии равна:
Коэффициент полезного действия равен отношению мощностей в начале и конце линии:
Из данной формулы следует, что коэффициент полезного действия передачи определяется отношением сопротивлений линии и нагрузки.
При их равенстве, когда нагрузке передается максимальная мощность, η = 0,5 = 50 %. Этот режим, при котором теряется половина передаваемой энергии, на практике, естественно, не пригоден. В реальных линиях при передаче больших мощностей КПД составляет примерно 0,94–0,97. При этом сопротивление нагрузки значительно больше сопротивления линии.
Для анализа режимов электропередачи полезной оказывается еще одна формула. Так как
То есть при одной и той же мощности нагрузки Р2, потери ΔР пропорциональны сопротивлению линии и обратно пропорциональны квадрату напряжения. Для увеличения коэффициента полезного действия передачи необходимо повышение напряжения и снижение электрического сопротивления проводов линии путем увеличения их сечения и применения материалов с меньшим удельным сопротивлением.
Пример 1.6. Линия электропередачи с проводами марки А-120 длиной l = 1000 км питает нагрузку мощностью Р2 = 50 МВт. Каким должно быть напряжение в начале линии, чтобы КПД передачи был не ниже 90 %?
Р е ш е н и е. Сопротивление одного километра провода марки А-120 R0 = 0,27 Ом/км. Суммарное сопротивление прямого и обратного проводов линии составляет RЛ = 2lR0 = 540 Ом.
Принимая η = 0,9, из формулы (1.17) получаем:
Для выполнения условий задачи напряжение в начале линии должно быть не ниже 548 кВ.
Источник
Зависимости между напряжениями и мощностями начала и конца элемента электрической сети



Под элементом электрической сети понимают участок (звено) ее схемы замещения, например, линии электропередачи или трансформатора (рис. 4.3). Так, в случае линии электропередачи звеном будет являться участок ее П-образной схемы замещения между проводимостями. Поскольку в звене сети присутствует только сопротивление Z=R+jX, ток в начале и в конце звена остается неизменным. Расчет будем вести в линейных напряжениях.
Схема замещения элемента электрической сети
Рассмотрим наиболее характерные для практики случаи.
Случай 1 (Расчет по данным конца):известны мощность и напряжение в конце звена: S2=P2 — jQ2; U2. Требуется определить мощность S1 и напряжение U1 в начале.
Этот случай встречается в практике, например, если задана нагрузка потребителя и требуется найти напряжение источника питания, при котором будет обеспечено требуемое напряжение у потребителя.
Потери мощности определим по данным конца звена:
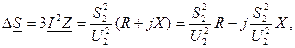
т.е. потери активной мощности:
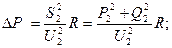
потери реактивной мощности:
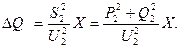
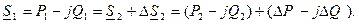
В этом случае потокораспределение находится точно, т.к. мощность и напряжение заданы в одной точке (в конце).
Совмещая вектор напряжения U2 с вещественной осью, запишем:
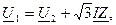
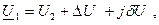
где продольная составляющая падения напряжения:
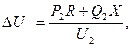
поперечная составляющая падения напряжения:
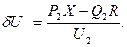
Модуль напряжения в начале звена определяется по выражению (4.15).
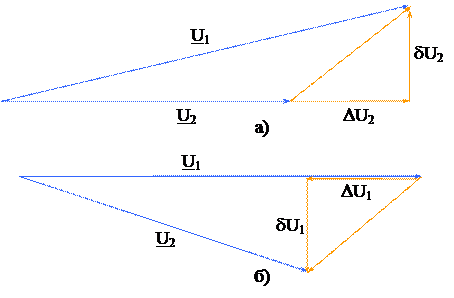
Векторная диаграмма напряжений для этого случая показана на рис. 4.4, а.
Случай 2 (Расчет по данным начала):известны мощность и напряжение в начале звена: S1=P1— jQ1; U1. Требуется определить мощность S2 и напряжение U2 в конце. На практике этот случай имеет место тогда, когда возникает необходимость передачи заданной мощности источника (электростанции) при фиксированном напряжении на его шинах в центр потребления. При этом следует выяснить, каково будет напряжение у потребителей.
Потери мощности, выраженные через параметры начала:
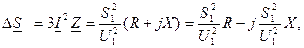
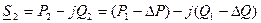
В этом случае потокораспределение также находится точно, т.к. мощность и напряжение заданы в одной точке (в начале).
Совмещая вектор напряжения U1 с вещественной осью, запишем:
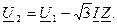
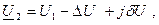
где продольная составляющая падения напряжения:
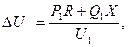
поперечная составляющая падения напряжения:
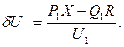
Модуль напряжения в конце звена определяется по выражению (4.16).
Векторная диаграмма напряжений для этого случая показана на рис. 4.4, б.
Векторные диаграммы для звена сети: а – по данным конца; б – по данным начала
Случай 3:известны мощность в конце звена S2=P2 — jQ2 и напряжение в начале U1. Требуется найти мощность в начале звена S1=P1— jQ1 и напряжение в конце U2. Этот случай наиболее типичный, так как обычно известно напряжение на шинах источника питания (электростанции, понижающей подстанции), от которого отходят линии с заданными нагрузками потребителей в конце.
Здесь сразу вычислить напряжение U2 не представляется возможным, так как не известна мощность в начале звена. Поэтому расчет ведут методом последовательных приближений напряжения 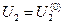
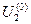
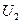
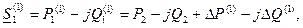
где потери мощности определяют как:
Теперь можно найти первое приближение напряжения:
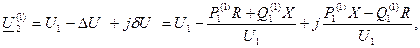
модуль которого подставляют в формулу (4.33) для вычисления потерь мощности и снова находят мощность в начале звена (второе приближение). Расчет заканчивают в том случае, если разность между модулями напряжений U2 i-го и (i-1)-го приближений не больше заданной точности расчета:
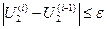
При расчетах без применения ЭВМ обычно ограничиваются расчетом первого приближения напряжения 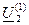
Источник
Лекция 2. Параметры электрических сетей
Электрическая сеть состоит из разных элементов имеющих каждый свое назначение и конструктивное выполнение. Каждый из участков электрической сети характеризуется одинаковым набором параметров (r, x, g, b, Kt ).
r – активное сопротивление, Ом;
x – реактивное сопротивление, Ом;
g – активная проводимость, См;
b – реактивная проводимость, См;
Kt – коэффициент трансформации.
Параметры отражают характерные свойства элементов сети и различаются только количественно.
Для количественного определения свойств элементов электрической сети составляется схема замещения. На ней указывают все параметры, определяющие состояние электрической сети. Схемы замещения сети составляются из схем замещения отдельных элементов, они отличаются от принципиальных схем соединения этих элементов.
Рекомендуемые материалы
Принципиальные схемы соединений (схемы коммутации) нужны только для определения направления передачи электрической энергии и степени резервирования питания потребителей. В них каждый элемент сети имеет изображение, отражающее его действие в решении задачи электроснабжения.
Схема замещения сети составляется для выполнения расчетов рабочих режимов. Каждый элемент сети в ней может отражаться несколькими подэлементами.
При характеристике симметричных рабочих режимов схемы замещения составляются на одну фазу трехфазной сети, общей является нейтраль цепи.
Потери активной мощности отражаются активными сопротивлениями (r) или проводимостями (g). Потери реактивной мощности отражаются реактивными (индуктивными) сопротивлениями или проводимостями. Генерация реактивной мощности отражается отрицательными реактивными емкостными сопротивлениями или проводимостями.
Различают продольные и поперечные ветви схем замещения. Продольными называются ветви, по которым проходит ток нагрузки. Потери мощности в этих ветвях определяются нагрузочным током.
Поперечными называются ветви, которые включены на полное напряжение (непосредственно соединены с нейтралью схемы). Потери мощности в этих ветвях определяются подведенным напряжением.
Особо отражается на схемах замещения явление трансформации. Это относится к сетям, состоящим из участков разных номинальных напряжений и рассматриваемых вместе.
Элемент трансформации отражает факт изменения параметров режима – напряжений и токов. Значения полной мощности при этом не изменяются (потери в трансформаторах отражаются другими элементами схемы).
Особыми являются и элементы, отражающие работу потребителей и пунктов питания. Они отражают факт потребления и генерации мощности, их представляют активными элементами схемы – нагрузками. При этом генерация мощности рассматривается как отрицательная нагрузка. Совокупность нагрузок определяет режим сети.
Линия электропередачи как элемент электрической сети
Передача электрической энергии по линиям обусловлена распространением электромагнитного поля в проводах и окружающим их пространстве. При действии переменного напряжения возникают переменное магнитное поле вокруг проводов и переменное электростатическое поле между фазными проводами и между каждым из проводов и землей. Условное изображение элементов этих полей показано на рисунке для одного провода ВЛ.
Возникновение переменного электрического поля приводит к появлению токов смещения (зарядных токов), величины которых зависят как от свойств диэлектрика, окружающего проводник, так и от разности потенциалов между проводом и землей, а для трехфазной линии также и между фазными проводами. Зарядные токи, накладываясь на нагрузочный ток, определяют постепенное изменение тока вдоль длины линии. Электромагнитное поле характеризуется напряженностью, также изменяющейся вдоль длины линии. Это приводит к наведению эдс самоиндукции и взаимоиндукции, неравных для различных элементов длины линии. Неравенство этих эдс определяет сложный закон изменения напряжения по линии и изменение токов смещения (зарядных токов) вдоль длины линии.
Погонные (удельные) параметры линий
Погонное (удельное) (на единицу длины) активное сопротивление rо при частоте 50 Гц и обычно применяемых сечениях алюминиевых или медных проводов и жил кабелей можно принять равным погонному омическому сопротивлению. Явление поверхностного эффекта начинает заметно сказываться только при сечениях порядка 500 мм2.
Активное сопротивление – это сопротивление при протекании по проводнику переменного тока, омическое – это сопротивление при протекании по тому же проводнику постоянного тока. Для сталеалюминиевых проводов явление поверхностного эффекта также незначительно и может не учитываться.
Значительное влияние на активное сопротивление оказывает температура материала проводников, которая зависит от температуры окружающей среды и тока нагрузки.
Погонные (удельные) реактивные (индуктивные) сопротивления фаз линий в общем случае получаются разными. Они определяются взаимным расположением фаз и геометрическими параметрами. При расчетах симметрических рабочих режимов пользуются средними значениями (независимо от транспозиции фаз линии).
Схемы замещения ЛЭП
Линия электрической сети теоретически рассматривается состоящей из бесконечно большого количества равномерно распределенных вдоль нее активных и реактивных сопротивлений и проводимостей.
Точный учет влияния распределенных сопротивлений и проводимостей сложен и необходим при расчетах очень длинных линий, которые в этом курсе не рассматривается.
На практике ограничиваются упрощенными методами расчета, рассматривая линию с сосредоточенными активными и реактивными сопротивлениями и проводимостями.
Для проведения расчетов принимают упрощенные схемы замещения линии, а именно: П-образную схему замещения, состоящую из последовательно соединенных активного (rл) и реактивного (xл) сопротивлений. Активная (gл) и реактивная (емкостная) (bл) проводимости включены в начале и конце линии по 1/2.
П-образная схема замещения характерна для воздушных ЛЭП напряжением
110-220 кВ длиной до 300-400 км.
 |
П – образная схема замещения ЛЭП напряжением 110-220 кВ длиной до 300-400 км.
Активное сопротивление определяется по формуле: 
где rо – удельное сопротивление Ом/км при tо провода + 20о,
l – длина линии, км
Активное сопротивление проводов и кабелей при частоте 50 Гц обычно примерно равно омическому сопротивлению. Не учитывается явление поверхностного эффекта.
Удельное активное сопротивление rо для сталеалюминиевых и других проводов из цветных металлов определяется по таблицам в зависимости от поперечного сечения.
Для стальных проводов нельзя пренебрегать поверхностным эффектом. Для них rо зависит от сечения и протекающего тока и находится по таблицам.
При температуре провода, отличной от 20о С сопротивление линии уточняется по соответствующим формулам.
Реактивное сопротивление определяется: 
где xо – удельное реактивное сопротивление Ом/км. Удельные индуктивные сопротивления фаз ВЛ в общем случае различны (об этом уже говорилось).
При расчетах симметричных режимов используют средние значения xо : 
где rпр – радиус провода, см;
Дср – среднегеометрическое расстояние между фазами, см, определяется следующим выражением:

Где Дав, Двс, Дса – расстояния между проводами соответствующих фаз А, В, С.
Например, при расположении фаз по углам равностороннего треугольника со стороной Д, среднегеометрическое расстояние равно Д.
 |
Дав=Двс=Дас=Д
 |
При расположении проводов ЛЭП в горизонтальном положении:
Дав=Двс=Д
Дас=2Д
При размещении параллельных цепей на двухцепных опорах потокосцепление каждого фазного провода определяется токами обеих цепей. Изменение Х0 из-за влияния второй цепи зависит от расстояния между цепями. Отличие Х0 одной цепи при учете и без учета влияния второй цепи не превышает 5-6% и не учитывается в практических расчетах.
В линиях электропередач при 
220 кВ) провод каждой фазы расщепляется на несколько проводов. Это соответствует увеличению эквивалентного радиуса. В выражении для Х0:

вместо rпр используется

где rэк – эквивалентный радиус провода, см;
аср – среднегеометрическое расстояние между проводами одной фазы, см;
nф– число проводов в одной фазе.
Для линии с расщепленными проводами последнее слагаемое в формуле 1 уменьшается в nф раз, т.е. имеет вид 
Удельное активное сопротивление фазы линии с расщепленными проводами определяются так : r0= r0пр / nф ,
Где r0пр – удельное сопротивление провода данного сечения, определенное по справочным таблицам. Для сталеалюминиевых проводов Х0 определяется по справочным таблицам, в зависимости от сечения, для стальных в зависимости от сечения и тока.
Активная проводимость (gл) линии соответствует двум видам потерь активной мощности:
1) от тока утечки через изоляторы;
2) потери на корону.
Токи утечки через изоляторы малы и потерями в изоляторах можно пренебречь. В воздушных линиях (ВЛ) напряжением 110 кВ и выше при определенных условиях напряженность электрического поля на поверхности провода возрастает и становится больше критической. Воздух вокруг провода интенсивно ионизируется, образуя свечение – корону. Короне соответствуют потери активной мощности. Наиболее радикальными средствами уменьшения потерь мощности на корону является увеличение диаметра провода, для линий высокого напряжения (330 кВ и выше) использование расщепления проводов. Иногда можно использовать так называемый системный способ уменьшения потерь мощности на корону. Диспетчер уменьшает напряжение в линии до определенной величины.
В связи с этим задаются наименьшие допустимые сечения по короне:
110 кВ – 70 мм2 (сейчас рекомендуется использовать сечение 95 мм2);
150 кВ – 120 мм2;
220 кВ – 240 мм2.
Коронирование проводов приводит: к снижению КПД; к усиленному окислению поверхности проводов; к появлению радиопомех.
При расчете установившихся режимов сетей до 220 кВ активная проводимость практически не учитывается.
В сетях с 
Емкостная проводимость (вл) линии обусловлена емкостями между проводами разных фаз и емкостью провод – земля и определяется следующим образом:

где в0 – удельная емкостная проводимость См/км, которая может быть определена по справочным таблицам или по следующей формуле:

где Дср – среднегеометрическое расстояние между проводами фаз; rпр – радиус провода.
Для большинства расчетов в сетях 110-220 кВ ЛЭП (линия электропередачи) представляется более простой схемой замещения:
 |
 |
Иногда в схеме замещения вместо емкостной проводимости 
Половина емкостной мощности линии, МВАр, равна:

где:
Uф и U – соответственно фазное и междуфазное (линейное) напряжения, кВ;
Iс – емкостный ток на землю
Из выражения для Qс (*) следует, что мощность Qс, генерируемая линий сильно зависит от напряжения. Чем выше напряжение, тем больше емкостная мощность.
Для воздушных линий напряжением 35 кВ и ниже емкостную мощность (Qс) можно не учитывать, тогда схема замещения примет следующий вид:
Для линий с 
 |
Кабельные линии электропередачи представляют такой же П-образной
схемой замещения
как и ВЛ.
Удельные активные и реактивные сопротивления r0, х0 определяют по справочным таблицам, так же как и для ВЛ.
Из выражения для х0 и в0
видно, что х0 уменьшается, а в0 растет при сближении разных проводов.
Для кабельных линий расстояние между проводами фаз значительно меньше, чем для ВЛ и Х0 очень мало.
При расчетах режимов КЛ (кабельных линий) напряжением 10кВ и ниже можно учитывать только активное сопротивление.
 |
Емкостный ток и Qс в кабельных линиях больше чем в ВЛ. В кабельных линиях (КЛ) высокого напряжения учитывают Qс, причем удельную емкостную мощность Qc0 кВАр/км можно определить по таблицам в справочниках.
Активную проводимость (gл )учитывают для кабелей 110 кВ и выше.
Удельные параметры кабелей х0, а также Qс0 приведенные в справочных таблицах ориентировочны, более точно их можно определить по заводским характеристикам кабелей.
Характерные соотношения между параметрами линий
Активное сопротивление проводов и кабелей определяется материалом токоведущих жил и их сечениями.
С изменением сечения проводов и кабелей значительно изменяются их активные сопротивления.
Активное сопротивление обратно пропорционально сечению провода или кабеля.
Магнитное поле возникающее вокруг и внутри проводов ВЛ и жил кабелей определяет их индуктивное сопротивление. Индуктивное сопротивление зависит от взаимного расположения проводов.
Индуктивные сопротивления фазных проводов ВЛ будут одинаковыми, если они расположены по вершинам равностороннего треугольника, и будут отличаться друг от друга, если фазные провода подвешиваются в горизонтальной плоскости. Чтобы избежать нежелательной несимметрии применяют транспозицию проводов, которая заключается в том, что в нескольких точках линии фазные провода на опорах меняются местами. При этом каждый провод поочередно занимает все три возможные положения при примерно одинаковой протяженности.
Благодаря транспозиции, эдс, наводимые в фазных проводах выравниваются и индуктивные сопротивления становятся одинаковыми.
Для иллюстрации приведем пример индуктивных сопротивлений трех напряжений для средних сечений проводов и расстояний между проводами:
1) линия 6,10 кВ х0=0,362 Ом/км;
2) линия 35 кВ х0=0,401 Ом/км;
3) линия 110 кВ х0=0,433 Ом/км.
При выполнении ВЛ одиночными (нерасщепленными проводами) их индуктивное сопротивление: х0 »0,4 Ом/км.
Индуктивное сопротивление расщепленных проводов, вследствие увеличения эквивалентного радиуса, будет меньше и при расщеплении на три провода будет х0 »0,29 Ом/км.
Малая зависимость от конструктивных характеристик ВЛ также присуща и емкостной проводимости.
Среднее значение проводимости для ВЛ , выполненной одиночными проводами
во ср »2,75´10-6 См/км.
Для линий с расщепленными проводами емкостная проводимость увеличивается и при расщеплении на три провода: в0 »3,8´10-6См/км.
Для линий 110кВ при характерной для них протяженности зарядная мощность QC »10% от передаваемой;
Для линий 220кВ 30% от передаваемой;
Для линий 500кВ может быть соизмерима с передаваемой активной мощностью.
Для линий 35кВ и более низким направлением зарядную мощность можно не учитывать.
Режимы и параметры системы и сети
Состояние системы в любой момент времени или на некотором интервале времени называется режимом системы.
Режим определяется показателями, которые называются параметрами режима к их числу относятся:
1)частота,
2)активная и реактивная мощность в элементах системы,
3)напряжение в различных точках сети у потребителей,
4)величины токов,
5)величины углов расхождения векторов ЭДС и напряжения.
Различают три основных вида режимов электроэнергетических систем:
1. Нормальный установившейся режим, применительно к которому проектируется элкктрическая сеть и определяются ее технико–экономические характеристики;
2. Послеаварийный установившийся режим, наступающий после аварийного отключения какого – либо элемента сети или ряда элементов (в этом режиме система и соответственно сеть могут работать с несколько ухудшенными технико– экономическими характеристиками);
3. Переходный режим, во время которого система переходит из одного состояния к другому.
Любой режим состоит из множества различных процессов.
Различают параметры режима и параметры сети.
Параметры режима электрической сети связаны между собой определенными зависимостями, в которые входят некоторые коэффициенты, зависящие от физических свойств элементов сети, от способа соединения этих элементов между собой, а также от некоторых допущений расчетного характера.
К ним относятся полное сопротивление, активное и реактивное сопротивление, проводимости элементов, собственная и взаимная проводимости, коэффициент трансформации, коэффициент усиления.
Например, ток на участке ЛЭП определяется зависимостью: I=
Ряд параметров сети зависит от характера изменений ее режима, т.е. является нелинейной системой. Однако во многих практических задачах параметры сети можно полагать не изменяющимися и считать сеть линейной.
Другой вид нелинейности сети обусловлен характером соотношений между параметрами ее режима. Так, мощность, связана квадратичной зависимостью с напряжением и т.д.( S=



Нелинейность такого вида надо учитывать.
Электрическую сеть рассматривают применительно к неизменному режиму системы, но в действительности такого режима не существует, и говоря об установившемся режиме имеют в виду режим малых возмущений. Отклонения параметров режима, происходит около некоторого устойчивого состояния.
Система должна быть устойчива при этих малых возмущениях. Иначе говоря, она должна обладать статической устойчивостью.
Аварийные переходные процессы возникают при резких аварийных изменениях режима, например, при к.з. элементов системы и последующем их отключении, при изменении схемы электрических соединений элементов системы.
Большие возмущения в системе при аварийных переходных процессах приводят к значительным отклонениям параметров режима к большим возмущениям, устойчивость по отношению к которым определяют как динамическую.
При этом под динамической устойчивостью понимают способность системы восстанавливать после больших возмущений свое состояние, практически близкое к исходному.
Необходимо учитывать изменения параметров режима, которые возникают при 1)увеличении передаваемых мощностей, 2)росте нагрузок и 3)изменении схемы электрических соединений в результате повреждений в сети.
Расчет режимов линий электропередач и электрических сетей
Связь между изменяющимися величинами определяется с помощью диаграмм, в которых каждая из величин характеризуется вектором. Построим диаграмму, показывающую соотношения между токами и напряжениями П-образной схемы замещения.
Расчет режима ЛЭП при заданном токе нагрузки и напряжении
в конце линии
Будем считать, что режим конца линии задан фазным напряжением Uф=сonst и отстающим током нагрузки I2. Также заданы Z12=r12+jx12, в12.
Необходимо определить 1) напряжение в начале линии – U1,2) ток в продольной части – I12, 3) потери мощности – DS12 4) ток в начале линии – I1.
 |
Расчет состоит в определении неизвестных токов и напряжений, последовательно от конца линии к началу.
Емкостный ток в конце линии 1-2, по закону Ома:
 |
Ток в продольной части линии 1-2, по первому закону Кирхгофа: I12=I2+Iкс12: (2)
Напряжение в начале линии по закону Ома: U1ф=U2ф+I12´Z12: (3)
Емкостный ток в начале линии:
Ток в начале линии по первому закону Кирхгофа:
Потери мощности в линии (в трех фазах): DS12=3I212´Z12: (6)
Векторная диаграмма токов и напряжений строится в соответствии с выражениями 1-5.
 |
Вначале строим известные U2ф и I2.
Полагаем что U2ф=U2ф, т.е. напряжение U2ф направлено по действительной оси. Емкостный ток 

Затем строим отдельно два слагаемых в правой части (3) [U1ф=U2ф+I12´Z12]. I12´Z12=I12´r12+I12´jx12 (7)
Вектор I12´r12 êê I12, вектор I12´jx12 опережает на 90о ток I12
Напряжение U1ф соединяет начало и конец суммируемых векторов U2ф, I12´r12, I12´jx12.
Ток 
I1 соответствует (5) I1=I12+
В линии с нагрузкой напряжение в конце линии по модулю меньше, чем в начале U2ф<U1ф.
На линии на холостом ходу (I2=0), течет только емкостной ток, т.к. в соответствии с формулой I12=I2+Iкс12 (2) I12=Iкс12
 |
В этом случае напряжение в конце линии
повышается
U2ф>U1ф
Векторная диаграмма для такой линии:
Падение и потеря напряжения в линии
Различие в напряжениях U2ф и U1ф в П-образной схеме определяется падением напряжения на сопротивлении Z12 (Z12+jx12), вызванным током I12. Определяется это падением напряжения как сумма вектора I12r12, совпадающего по фазе с вектором I12 и вектора I12´jx12, опережающего вектор I12 на 90о.
Падение напряжения – геометрическая (векторная) разность между комплексами напряжений начала и конца линий.
 |
На рис. падение напряжения это вектор 
разность комплексных значений по концам линий, используется для характеристики режима линии.
Продольной составляющей падения напряжения DUк12 называют проекцию падения напряжения на действительную ось или на напряжение U2, DUк12=АС. Индекс “к” означает , что Uк12 – проекция на напряжение конца линии U2.
Обычно DUк12 выражается через данные в конце линии: U2, Pк12, Qк12.
Поперечная составляющая падения напряжения dUк12 – это проекция падения напряжения на мнимую ось, jdUк12=СВ. Т. о. U1-U2=
Величина dUк12 определяет сдвиг вектора напряжения в начале линии (U1) на угол d по отношению к вектору напряжения в ее конце (U2).
Часто используют понятие потеря напряжения – это алгебраическая разность между модулями напряжений начала (U1) и конца (U2) линий.
На рис. çU1ê– êU2ê=АД.
Если поперечная составляющая dUк12 мала (например, в сетях Uном £ 110кВ), то можно приближенно считать, что потеря напряжения равна продольной составляющей падения напряжения.
Потеря напряжения является показателем изменения относительных условий работы потребителей в начале и в конце линии.
Расчет режимов линий электропередач и электрических сетей
при заданной мощности нагрузки
При подаче энергии по линии от начала к ее концу имеют место потери реактивной мощности. Они обусловлены реактивным сопротивлением линии и соответствующим ему реактивным сопротивлением схемы замещения этой линии. При передаче энергии имеют место и потери активной мощности, расходуемой на нагревание проводов. Поэтому в схеме замещения следует различать полную мощность до сопротивления Z12(r12+jx12), Sн12 и после него Sк12.
Расчет режима ЛЭП при заданной мощности нагрузки и напряжении
в конце линии
Задано напряжение в конце линии U2=сonst. Известна мощность нагрузки S2, напряжение U2, сопротивление и проводимость линии Z12=r12+jx12, в12.
 |
Необходимо определить напряжение U1, мощности в конце и в начале продольной части линии Sк12, Sн12, потери мощности DS12, мощность в начале линии S1. Для проверки ограничений по нагреву иногда определяют ток в линии I12.
Расчет аналогичен расчету при заданном токе нагрузке (I2), и состоит в последовательном определении от конца линии к началу неизвестных мощностей и напряжений при использовании I закона Кирхгофа и закона Ома. Будем использовать мощности трех фаз и линейные напряжения.
Зарядная (емкостная) мощность трех фаз в конце линии:
–jQкс12=3I*кс12´U2ф=
Мощность в конце продольной части линии по I закону Кирхгофа: Sк12=S2 – jQкс12
Потери мощности в линии: DS12=3I212Z12=
Ток в начале и в конце продольной ветви линии одинаков.
Мощность в начале продольной ветви линии больше, чем мощность в конце, на величину потерь мощности в линии, т.е. Sн12=Sк12+DS12
Линейное напряжение в начале линии по закону Ома равно:
U1=U2+
Емкостная мощность в начале линии: –jQнc12=
Мощность в начале линии: S1=Sн12 – jQнс12
Под влиянием зарядной мощности Qс реактивная мощность нагрузки Q2 в конце, схема замещения уменьшается. Аналогичное явление имеет место и в начале схемы замещения, где реактивная мощность Qс уменьшает реактивную мощность в начале линии.
Это свидетельствует о том, что зарядная мощность сокращает реактивную мощность, поступающую от станции в линию для питания нагрузки. Поэтому зарядная мощность условно может рассматриваться как “генератор” реактивной мощности.
В линии электрической сети имеют место как потери, так и генерация реактивной мощности.
От соотношения потерь и генерации реактивной мощности зависит различие между реактивными мощностями в начале и конце линии.
Расчет режима ЛЭП при заданной мощности нагрузки и напряжении
в начале линии
Задано напряжение в начале линии.
Схема замещения:
 |
U1=сonst. Известны S2, U1 ,Z12=r12+jx12, в12.
Необходимо определить U2, Sк12, Sн12, DS12, S1
Т.к. U2 неизвестно, то невозможно определить последовательно от конца линии к началу определить неизвестные токи и напряжения по I закону Кирхгофа и закону Ома.
1-й способ.
Нелинейное уравнение узловых напряжений для узла 2 имеет вид:
Y22U2+Y12U1=I2(U)=S*2/U*2
Это уравнение можно решить и найти неизвестное напряжение U2, а затем найти все мощности по выражениям:
Но можно осуществить приближенный расчет в два этапа.
2-й способ.
1 этап:
Предположим, что U2=Uном (7) и определим потоки и потери мощности аналогично выражениям (1)-(4), используя (7) получим:
Если Вам понравилась эта лекция, то понравится и эта – 2 Электродвижущие силы обмоток переменного тока.
2 этап:
Определим напряжение U2 по закону Ома, используя поток мощности Sн12, найденный на 1 этапе. Для этого используем закон Ома в виде: 
но выразим ток I12 через Sн12 и U1:
Потоки мощности на 1 этапе определены приближенно, поскольку в формулах вместо U2 использовали Uном.
Соответственно напряжение U2 на 2 этапе также определено приближенно, т.к. в последней формуле для U2 используется приближенное значение Sн12, определенное на 1 этапе.
Возможно итерационное повторение расчета, т.е. повторение 1-го и 2-го этапов для получения более точных значений мощности и напряжений. При проведении расчетов вручную, а не на ЭВМ, такое уточнение не требуется.
Содержание:
Электрические цепи с распределенными параметрами:
Каждый элемент электрической цепи (резистор, катушка, конденсатор) имеет конечные размеры, и его можно представить как совокупность малых однородных частей, в которых совершаются интересующие нас электромагнитные процессы — преобразование энергии в тепло, накопление энергии в магнитном и электрическом полях. Иначе говоря, все устройства имеют распределенные параметры — сопротивление, индуктивность, емкость.
При изучении электрических цепей до сих пор мы не учитывали размеры устройств, предполагая, что параметры R, L, C сосредоточены, т. е. представляли в расчетной схеме каждый элемент в целом.
Такой подход к анализу электрических цепей принимают тогда, когда рассматривают и изучают внешние связи между элементами. В тех случаях, когда требуется выявить соотношения внутри устройства, соответствующий элемент рассматривается как объект с распределенными параметрами. Таким объектом может быть обмотка электрической машины, трансформатора, антенна радиотехнического устройства и др.
Электрическая цепь с распределенными параметрами
Электрическая цепь с распределенными параметрами — это цепь, в которой сопротивления, проводимости, индуктивности и емкости распределены вдоль цепи.
Наглядным примером цепи с распределенными параметрами является электрическая длинная линия.
Уравнения длинной линии
Длинные линии строят для передачи электрической энергии, для электросвязи (передачи информации). Их рассматривают как объекты с распределенными параметрами при низких частотах и длине в десятки и сотни километров.
В радиотехнике при высоких частотах распределение параметров по длине учитывают в более коротких участках проводов (единицы и доли метра), например в антеннах.
Схемы замещения длинных линий
На рис. 26.1 изображена схема электрической цепи, состоящей из источника и приемника электрической энергии, связанных двухпроводной линией. Эту цепь можно рассматривать неразветвленной, с одинаковым током во всех ее элементах, если не учитывать двух обстоятельств: скорость распространения электромагнитных возмущений конечна; имеются токи, обусловленные емкостью между проводами (емкостный ток) и проводимостью изоляции (ток утечки через изоляцию).
В данном случае первое обстоятельство можно не учитывать, так как скорость распространения электромагнитных возмущений действительно велика (в вакууме равна скорости света). Емкостные токи и токи утечки пропорциональны напряжению между проводами; кроме того, емкостный ток увеличивается с ростом частоты, так как уменьшается емкостное сопротивление. Поэтому при высоком напряжении или большой частоте, а также при большой длине линии емкостные токи и токи утечки становятся значительными по величине и их нельзя исключить из расчета.
Токи между проводами существуют на сколь угодно малом отрезке линии, поэтому ток в проводах уменьшается по мере удаления от начала линии.
Вдоль линии напряжение между проводами тоже неодинаково. Оно уменьшается в направлении от начала к концу линии, так как растет падение напряжения, обусловленное активным и индуктивным сопротивлениями проводов.
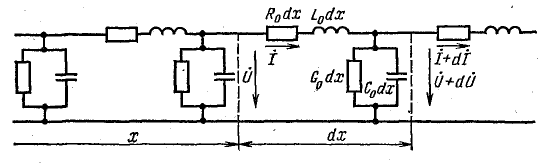
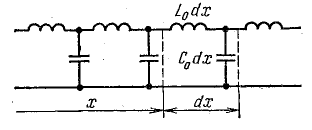
Для расчета можно составить схему замещения линии, изображенную на рис. 26.2. На схеме замещения бесконечно малый участок двухпроводной линии длиной dx представлен ячейкой с активным сопротивлением R0dx прямого и обратного проводов, индуктивностью L0dx, проводимостью G0dx и емкостью C0dx между проводами. Вся линия изображается электрической схемой последовательного соединения таких ячеек. Активное сопротивление, индуктивность, проводимость и емкость считают равномерно распределенными вдоль линии, а R0, L0, G0, C0 — величины этих параметров на единицу длины.
Рис. 26.3. Схема замещения однородной линии без потерь
Линия с равномерным распределением параметров называется однородной. Реальные линии можно считать однородными лишь приближенно, так как параметры их все же распределены неравномерно. Например, проводимость воздушной линии сосредоточена в основном на опорах, а благодаря провесу проводов емкость по отношению к земле вдоль пролета неодинакова.
В зависимости от целей и требуемой точности расчета можно учитывать все четыре параметра или некоторые из них. Так, при рассмотрении линии электропередачи с напряжением до 35 кВ и при частоте 50 Гц часто не учитывают емкостные токи и токи утечки, т. е. считают равными нулю параметры C0 и G0.
При высокой частоте (например, в радиотехнических устройствах) или при коротких импульсах напряжения в линиях, возникающих от грозовых разрядов, емкостные токи между проводами могут быть сравнительно большими и ими пренебрегать нельзя.
Вместе с тем при высокой частоте и малой длине линии в отдельных случаях можно пренебречь активным сопротивлением R0 и проводимостью G0.
При таком упрощении получается линия без потерь, схема замещения которой показана на рис. 26.3.
Основные уравнения длинной линии
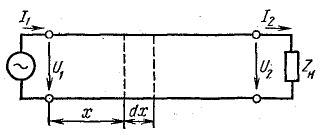
При синусоидальном напряжении источника питания напряжение и ток в линии на любом расстоянии x от ее начала изменяются во времени. Вместе с тем напряжение и ток изменяются вдоль линии. Установившийся режим в длинной линии представляется довольно сложной пространственно-временной картиной, для изучения которой необходимо получить аналитическую зависимость напряжения и тока от двух независимых переменных — времени и расстояния.
Решить такую задачу можно, используя схему замещения однородной линии (см. рис. 26.2). На схеме кроме параметров некоторого элемента длины линии dx обозначены напряжение и ток в начале и конце этого элемента, расположенного на расстоянии x от начала линии.
Падение напряжения в элементе длины dx линии
Разность токов в начале и конце того же элемента равна сумме тока утечки и емкостного тока:
Из этих выражений получают дифференциальные уравнения однородной линии, в которые входят комплексы токов и напряжений, изменяющихся во времени по синусоидальному закону, а также их производные по переменной координате х:
где 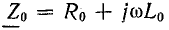
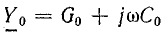
Продольные R0, L0 и поперечные G0, C0 параметры линии характеризуют совершенно различные физические явления, поэтому между собой не связаны.
Далее можно составить уравнения, в которых переменными будут напряжение или ток. Для этого продифференцируем по х уравнения (26.1):
учитывая выражения (26.1), получим линейные дифференциальные уравнения второго порядка с постоянными коэффициентами:
Решением первого уравнения из (26.2) является выражение
Уравнение тока получим из (26.1) и (26.3):
Характеристики длинной линии
В выражениях (26.3) и (26.4) 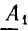
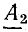
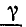
Учитывая формулу (26.5), запишем другое уравнение тока:
или
где величина
имеет размерность сопротивления и называется волновым сопротивлением линии.
Постоянные коэффициенты 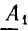
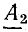
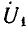
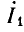
Из уравнений (26.3) и (26.6) при x = 0
Отсюда
Отношение комплекса напряжения к комплексу тока в начале линии называется входным сопротивлением линии.
Входное сопротивление линии при нагрузке 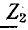
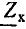
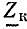
Коэффициент распространения электромагнитной волны 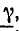
Этот коэффициент, имея два слагаемых, характеризует две стороны электромагнитного процесса в линии: затухание амплитуд и изменение фазы напряжения и тока в зависимости от расстояния от начала линии.
В соответствии с этим действительная часть комплекса δ называется коэффициентом затухания, а мнимая часть β — коэффициентом фазы.
Коэффициент затухания δ показывает степень затухания амплитуды колебаний при распространении волны на единицу длины.
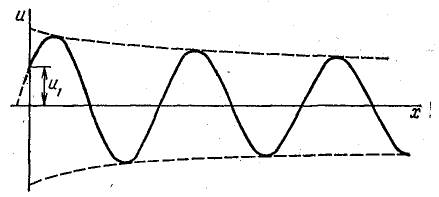
Рис. 26.4. График распределения напряжения вдоль линии
На рис. 26.4 показан график распределения напряжения вдоль линии в некоторый фиксированный момент времени. Из графика видно, что напряжение вдоль линии распределено по периодическому закону, а амплитуды напряжения затухают по экспоненциальному закону в направлении от начала к концу линии.
Задача 26.1.
Трехфазная линия электропередачи длиной l = 900 км имеет первичные параметры: R0 = 0,08 Ом/км; Z0 = 1,336 • 10-3 Гн/км; С0 = 8,6 x 10-9 Ф/км; G0 = 3,75 • 10-8 См/км.
Нагрузка в конце линии Р2 = 300 МВт; U2 = 380 кВ; соsφ2 = 1; частота f = 50 Гц.
Определить вторичные параметры линии (Zc, γ), напряжение и ток на ее входе.
План решения:
1. Комплексы «продольного» сопротивления и «поперечной» проводимости [см. формулы (26.1)].
2. Волновое сопротивление линии — по формуле (26.7).
3. Коэффициент распространения — по формуле (26.5).
4. Коэффициент затухания и коэффициент фазы — по формуле
5. Ток в конце линии — по формуле (20.9).
6. Напряжение и ток в начале линии — по формулам (26.3) и (26.6), которые следует записать при условии, что расстояния вдоль линии отсчитываются от конца линии:
При этом
Коэффициенты 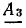
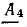
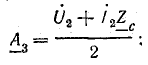
Выполнить вычисления по данному плану.
Установившийся режим в длинной линии без потерь
Линия без потерь, как уже было отмечено, не имеет активных сопротивления R0 и проводимости
В радиотехнике длинные линии с малыми потерями встречаются часто, поэтому рассмотрение линии при R0 = 0 и G0 = 0 имеет практическое значение.
Уравнения длинной линии без потерь
Согласно формулам (26.5) и (26.9), для линии без потерь коэффициент затухания 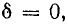
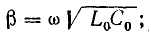
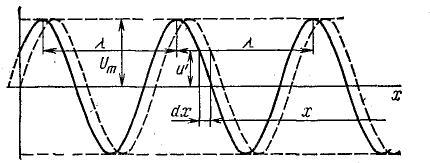
Поэтому график распределения напряжения вдоль линии в некоторый фиксированный момент времени представляет собой синусоиду. Амплитуда напряжения вдоль линии остается постоянной (рис. 26.5). Волновое сопротивление [см. формулу (26.7)]
Уравнения напряжения и тока в линии без потерь, согласно уравнениям (26.3), (26.6),
Вместо коэффициента 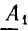
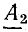
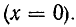
После преобразования из уравнений (26.11) получим
Рис. 26.5. Распределение волны напряжения вдоль линии без потерь
Из этих уравнений можно также получить выражения напряжения и тока в любой точке линии, если известны напряжение U2 и ток I2 в конце линии, при условии отсчета расстояния от конца линии:
С помощью уравнений (26.12) и (26.13) можно исследовать различные режимы длинной линии без потерь.
Холостой ход
При холостом ходе линии (I2 = 0)
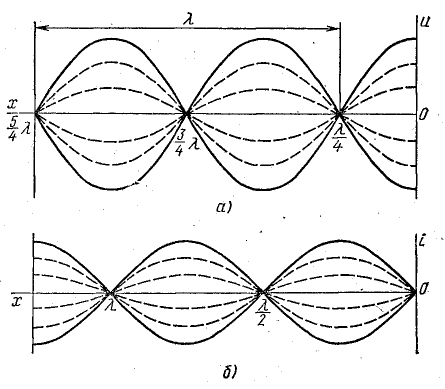
Напряжение и ток вдоль линии в любой момент времени распределены по синусоидальному закону, причем в пунктах, где напряжение равно нулю, ток имеет наибольшую величину, а в пунктах с наибольшим напряжением ток равен нулю (рис. 26.6, а, б).
Точки линии, в которых напряжение или ток равны нулю, называются узлами, а точки с наибольшей величиной напряжения или тока — пучностями.
Таким образом, узлы напряжения по месту расположения на линии совпадают с пучностями тока, а пучности напряжения — с узлами тока.
Положение узлов напряжения и пучностей тока найдем, приравняв нулю напряжение в первом уравнении (26.14): U = 0 при 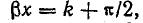
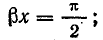
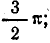
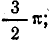
Рис. 26.6. Графики напряжения и тока стоячей электромагнитной волны в длинной линии без потерь
Положение на линии узлов тока и пучностей напряжения определяется из второго уравнения (26.14) при I = 0.
Напряжение и ток, распределяясь вдоль линии по синусоидальному закону без затухания, по такому же закону изменяются во времени.
Короткое замыкание
Аналогичная картина наблюдается и при коротком замыкании конца линии без потерь. Отличие электромагнитных процессов в линии без потерь в режимах холостого хода и короткого замыкания состоит лишь в том, что изменяется расположение пучностей и узлов напряжения и тока по длине линии: в тех пунктах, где при холостом ходе находятся пучности напряжения и узлы тока, при коротком замыкании обнаруживаются пучности тока и узлы напряжения. В частности, в конце разомкнутой линии имеется пучность напряжения и узел тока 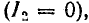
Стоячая волна
Пусть вектор напряжения в конце разомкнутой линии направлен по действительной оси комплексной плоскости, т. е. начальная временная фаза напряжения равна нулю:
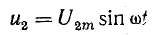
В этом случае мгновенные значения напряжения и тока в линии можно выразить уравнениями
При 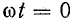
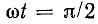
Но эта амплитуда напряжения во всех пунктах линии разная. В месте пучности напряжение достигает наибольшей величины U2m, а в узле она всегда равна нулю.
Электромагнитный процесс, подчиняющийся уравнениям (26.15), называется стоячей волной, характерной особенностью которой является неподвижность узлов и пучностей на линии.
Бегущая волна
Из тригонометрии известно, что
Следовательно, напряжение и ток в линии можно представить суммой двух составляющих, каждая из которых является уравнением бегущей волны:
Первое слагаемое в этих уравнениях — прямая волна, распространяющаяся от начала к концу линии; второе — обратная волна с такой же амплитудой.
В этом можно убедиться, рассмотрев подробно одну из составляющих, например первую в уравнении напряжения.
Предположим, что некоторая величина напряжения u’ в момент времени t имеет место в пункте, пространственное положение которого определяется расстоянием x от конца (или начала) линии (см. рис. 26.5):
Распространение волны напряжения означает, что через бесконечно малый промежуток времени dt такое же напряжение u’ возникает в другом пункте линии, отстоящем от первого на бесконечно малое расстояние dx:
Равенство напряжений в моменты времени, отстоящие на dt, возможно при равенстве аргументов синусов в обоих уравнениях, т. е. при
Отсюда
или
Отношение 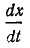
Знак минус указывает на то, что волна движется от начала к концу линии (расстояние x уменьшается).
Аналогично можно показать, что вторая составляющая напряжения в уравнении (26.16) представляет собой волну, распространяющуюся в обратном направлении (x увеличивается).
Волна, распространяющаяся от начала к концу линии, называется прямой или падающей, а волна, распространяющаяся в обратном направлении (от конца линии к началу), — обратной или отраженной.
Те же рассуждения можно отнести к составляющим тока во втором уравнении (26.16).
Таким образом, стоячая волна напряжения представляет собой сумму, а волна тока — разность прямой (падающей) и обратной (отраженной) волн одинаковой амплитуды.
Волновое сопротивление. Длина волны
Уравнения (26.16) запишем в таком виде:
Отсюда
Волновое сопротивление линии выражается отношением напряжения к току падающих волн или аналогичным отношением для отраженных волн.
Волновое сопротивление линии можно определить через входные сопротивления при холостом ходе и коротком замыкании:
Большой интерес представляет также расстояние, на которое бегущая волна распространяется за время одного периода синусоидально изменяющегося напряжения или тока.
Из формулы (26.17) видно, что фазовая скорость постоянна, поэтому
Путь, пройденный волной за время периода 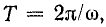
В линии без потерь фазовая скорость
а длина волны
Найдем величину фазовой скорости для воздушной линии без потерь, подставляя в формулу (26.19) L0 и С0 двухпроводной линии, определенные ранее [см. формулы (7.31), (8.29)]:
Фазовая скорость электромагнитной волны в воздушной линии без потерь равна скорости света.
Если среда, в которой распространяется электромагнитная волна, характеризуется величинами диэлектрической 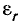
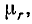
Принимая 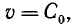
Нетрудно заметить, что при частоте 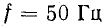
В линиях дальних передач с номинальным напряжением 500 кВ и более изменения величины напряжения вдоль линии становятся заметными и приходится принимать меры к его выравниванию. С увеличением частоты длина волны уменьшается. В технике связи, где применяются высокие частоты, длина волны может быть во много раз меньше длины линии.
Задача 26.3.
В конце двухпроводной линии без потерь напряжение U2 = 600 В при холостом ходе. Определить напряжение и ток в начале линии, если известны: волновое сопротивление 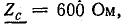
План решения.
1. Напряжение в начале линии по первой формуле (26.13) при I2 = 0.
2. Ток в начале линии по второй формуле (26.13).
Выполнить подсчеты по данному плану.
Дополнительное задание: определить напряжение и ток в начале линии при коротком замыкании на конце, где ток I = 4 А.
Нагрузочные режимы длинной линии без потерь
Кроме крайних режимов холостого хода и короткого замыкания для практики еще более интересными являются нагрузочные режимы, когда в конце линии включается приемник электромагнитной энергии. Из различных нагрузочных режимов рассмотрим режимы с согласованной и несогласованной активными нагрузками.
Режим с согласованной нагрузкой
Режим в линии называется согласованным, если сопротивление нагрузки в конце линии равно ее волновому сопротивлению: 
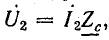
Учитывая, что
уравнения (26.21) можно записать в виде
Предположим, что синусоидальное напряжение в конце линии имеет начальную фазу ψ = 0, тогда
Если нагрузка линии активная (R2 = Zc), ток и напряжение совпадают по фазе:
Уравнения напряжения и тока в линии:
В этом случае мгновенные величины напряжения и тока в любом пункте линии на расстоянии x от ее концов определяются уравнениями
Это уравнения бегущих волн напряжения и тока, распространяющихся от начала к концу линии (прямые волны) с фазовой скоростью
При согласованной нагрузке отраженных волн в линии нет, следовательно, энергия, которую несет падающая электромагнитная волна, полностью поглощается в нагрузке.
Режим с несогласованной нагрузкой
Нагрузка линии называется несогласованной, если нагрузочное сопротивление в конце линии 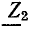
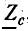
Рассмотрим случай, когда линия замкнута на активное сопротивление 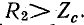
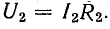
Отношение 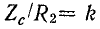
С введением этого коэффициента уравнения (26.25) принимают следующий вид:
Вместо 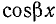
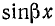
После подстановки получим
Первые слагаемые в этих уравнениях аналогичны уравнениям (26.21). Анализ их ранее показал, что они выражают бегущие волны напряжения и тока. Вторые слагаемые аналогичны уравнениям (26.14), которые являются уравнениями стоячих волн. Опуская промежуточные выводы, выполненные ранее для бегущих и стоячих волн, напишем уравнения для мгновенных величин напряжения и тока при несогласованной нагрузке:
Таким образом, режим в линии без потерь при несогласованной нагрузке можно рассматривать как наложение бегущих и стоячих волн напряжения и тока.
Наличие бегущих волн в направлении от начала к концу линии указывает на потребление энергии в нагрузке. Однако потребляется лишь часть энергии электромагнитной волны, другая часть отражается от конца линии.
Режимы холостого хода и с согласованной нагрузкой линии без потерь являются частными случаями, соответствующими значениям коэффициента бегущей волны k = 0 (холостой ход) и k = 1 (согласованная нагрузка).
Коэффициенты отражения и преломления
Представление электромагнитного процесса в линии как наложение прямых (падающих) и обратных (отраженных) волн напряжения и тока возможно не только в рассмотренных частных случаях. Оно соответствует общим уравнениям напряжения и тока в линии (26.12), в правой части которых записана сумма (разность) двух составляющих.
При анализе электромагнитных процессов в длинных линиях вводится понятие о коэффициенте отражения р, который равен отношению комплекса напряжения отраженной волны к комплексу напряжения падающей волны или аналогичному отношению комплексов токов:
Выразим напряжение и ток в конце линии их падающими и отраженными составляющими в соответствии с уравнениями (26.11):
При совместном решении этих уравнений найдем коэффициент отражения:
Подставим найденное выражение ρ в уравнения напряжения U2 и тока I2:
Множители
называются коэффициентами преломления волн напряжения (тока).
Согласно выражениям (26.29), коэффициент преломления равен отношению комплексов напряжения (тока) в рассматриваемом пункте линии к комплексу напряжения (тока) падающей волны:
Анализ этих формул показывает:
1) при холостом ходе линии 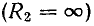

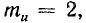
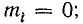
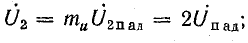
2) при коротком замыкании линии 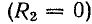
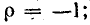
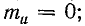
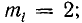
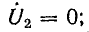
3) при согласованной нагрузке 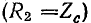
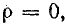
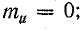
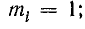
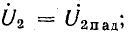
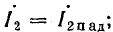
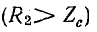
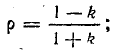
где k — коэффициент бегущей волны;
Распространение электромагнитной волны с прямоугольным фронтом по линии без потерь
Как было показано в предыдущих параграфах, установившийся режим в длинной линии при синусоидальном изменении напряжения и тока удобно представить наложением прямых и обратных электромагнитных волн.
Переходные процессы в цепях с распределенными параметрами тоже рассматриваются как движение прямых и отраженных волн, возникающих после включения или отключения какого-либо участка, при передаче телемеханических или телефонно-телеграфных сигналов по линиям связи т. п.
Переходные процессы могут быть также следствием изменения внешних магнитных и электрических полей, связанным с грозовыми явлениями.
Электромагнитная волна с прямоугольным фронтом
В цепи с сосредоточенными параметрами переходный процесс начинается и протекает одновременно во всех ее элементах. Особенностью переходного процесса в длинной линии является то, что появившееся в некоторой точке возмущение распространяется по линии с определен-ной скоростью, поэтому переходный процесс в данном пункте линии начинается тем позднее, чем он дальше от места возмущения.
При переходных процессах в цепях с распределенными параметрами (линии, обмотки электрических машин и трансформаторов) могут возникать электромагнитные волны различной формы.
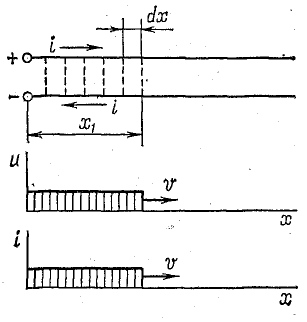
Качественную сторону явления распространения электромагнитной волны рассмотрим на примере волны с прямоугольным фронтом (рис. 26.7) в линии без потерь.
Рис. 26.7. Распределение электромагнитной волны с прямоугольным фронтом вдоль линии без потерь
Для такой волны характерно то, что во всех пунктах линии, расположенных до фронта волны, напряжение и ток равны нулю, а в пунктах линии, расположенных за фронтом волны, напряжение и ток постоянны.
Распространение электромагнитной волны с прямоугольным фронтом означает, что напряжение и ток последовательно в каждом пункте линии изменяются скачком. Как было показано ранее, такое изменение напряжения и тока в цепях, обладающих емкостью и индуктивностью, невозможно, так как требует источника бесконечно большой мощности. Таких источников не существует, поэтому волну с прямоугольным фронтом нужно рассматривать как некоторую идеализацию реального процесса.
Электрические и магнитные явления в линии — это две стороны единого электромагнитного процесса. Однако эти явления удобно рассматривать отдельно, т. е. выделять из электромагнитной волны волну напряжения и волну тока.
Были записаны в комплексной форме уравнения (26.1) для синусоидального изменения напряжения и тока. Те же уравнения для мгновенных величин напряжения и тока в однородной линии без потерь имеют вид
Решением этих уравнений в общем виде являются функции
где 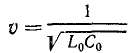
Уравнения (26.32) по своей структуре подобны уравнениям (26.16), поэтому любой электромагнитный переходный процесс в линии можно рассматривать как наложение прямых и обратных волн напряжения и тока. Физический смысл переходных процессов в линии удобно выяснить на простейших примерах.
Подключение источника постоянного напряжения U0 к бесконечно длинной линии
После включения источника вдоль линии будет распространяться волна с прямоугольным фронтом, заряжающая ее последовательно (от одного пункта к другому) до напряжения U0. На поверхности проводов появляется заряд, величина которого на единице длины Q0 = C0U0.
Если за время dt волна переместилась на расстояние dx, линия получает дополнительный заряд
Этот заряд как бы распространяется по проводам от источника вдоль линии до точки х1, в которой находится в данный момент фронт волны; при этом образуется ток
Один провод заряжается положительно, а другой (обратный) — отрицательно, что соответствует противоположному направлению токов в них (рис. 26.7).
На отрезке линии длиной dx, около фронта волны, возникновение электрического поля сопровождается током смещения между проводами. Таким образом, цепь оказывается замкнутой. При движении волны она удлиняется, но ток остается постоянным, равным I0.
Контур, по которому замыкается ток, пронизывается магнитным потоком, направленным, согласно правилу буравчика, в плоскостях, перпендикулярных осям проводов.
Перемещение волны на dx сопровождается увеличением магнитного потока на величину
и наведением в контуре э. д. с. самоиндукции
Э. д. с. самоиндукции направлена против тока, т. е. у фронта волны она направлена навстречу напряжению U0 и равна ему по величине
Отношение напряжения к току дает величину волнового сопротивления линии
Энергия, отдаваемая источником в линию за единицу времени,
На отрезке линии длиной, равной единице, запасается энергия 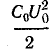
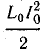
Согласно закону сохранения энергии, мощность источника должна быть равна энергии, запасаемой в электромагнитном поле линии за 1 с:
где 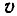
Включение источника постоянного напряжения на линию конечной длины
Пользуясь выводами, полученными ранее, рассмотрим движение волн с учетом возможных отражений от конца линии.
Если линия разомкнута на конце, то коэффициенты отражения ρ и преломления m, согласно формулам (26.28) и (26.30), оказываются равными: ρ = 1; mu = 2; mi = 0. Следовательно, u2 = 2Uпад; i2 = 0.
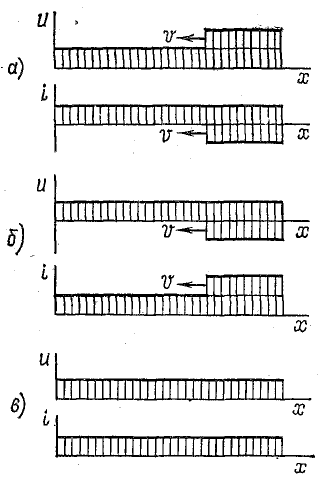
Отраженная волна напряжения накладывается на падающую, в результате чего напряжение на линии удваивается (рис. 26.8, а).
При этом энергия электромагнитной волны преобразуется в энергию электрического поля.
При коротком замыкании конца линии ρ = —1; mu = 0; mi = 2.
Отраженная волна напряжения компенсирует падающую волну (u2 = 0), а ток в линии удваивается (рис. 26.8, б). Этот процесс сопровождается переходом всей энергии волны в энергию магнитного поля.
При согласованной нагрузке (R2 = Zс) ρ = 0; u2 = Uпад; i2 = Iпад.
Отраженных волн нет, а энергия волны полностью поглощается нагрузкой (рис. 26.8, в).
Рис. 26.8. Различные случаи отражения электромагнитной волны с прямоугольным фронтом от конца линии
Электрические цепи с распределенными параметрами
Электрические цепи, параметры которых (сопротивления, индуктивности и емкости) распределены по всей длине, называются цепями с распределенными параметрами.
В неразветвленных цепях с распределенными параметрами токи в разных сечениях неодинаковы. Это происходит вследствие токов утечки между проводами, токов смещения через межпроводные емкости и по ряду других причин. Так как токи утечки пропорциональны напряжению, а токи смещения пропорциональны частоте и напряжению, то с ростом напряжения и частоты их влияние становится более заметным. Кроме того, токи утечки и смещения увеличиваются с увеличением протяженности линии.
К цепям с распределенными параметрами относятся линии электропередачи.
Любая электрическая линия, например двухпроводная линия электропередачи или электросвязи, характеризуется четырьмя первичными параметрами, отнесенными к единице ее длины: активным сопротивлением проводов 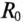
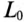
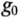
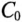
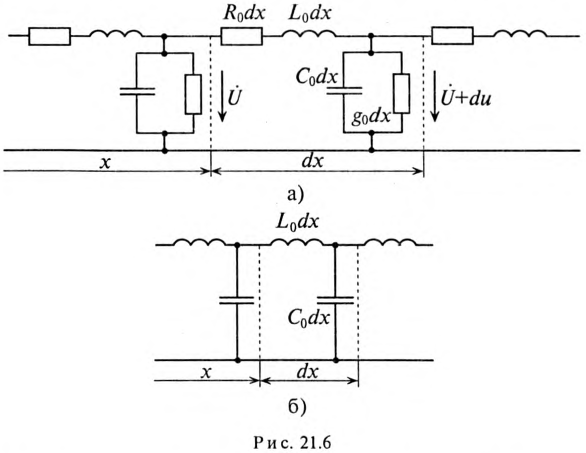
Для исследования длинные линии с распределенными параметрами заменяют схемами замещения (рис. 21.6).
На схеме замещения однородной линии с потерями (рис. 21.6а) рассматривается длинная линия, состоящая из бесконечно большого числа элементарных ячеек длиной dx с параметрами: активным сопротивлением 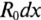
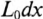
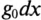
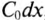
В зависимости от целей и требуемой точности выполненного расчета можно учитывать все четыре параметра или некоторые из них. Например, при исследовании линии электропередачи напряжением 35 кВ и частотой f=50 Гц часто не учитываются токи смещения и утечки, т.е. принимается g0 = 0 и С0 = 0.
При высокой частоте или при коротких импульсах напряжения токи смешения могут быть значительно большими и ими пренебречь нельзя. Но при высокой частоте и малой длине линии можно пренебречь активным сопротивлением R0 и проводимостью g0. При этом получается схема замещения однородной линии без потерь (рис. 21.66).
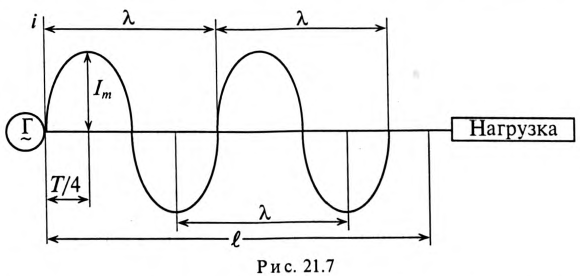
Исследуя длинную линию электропередачи как цепь с распределенными параметрами, в которой имеются токи утечки и смещения, передачу энергии следует рассматривать как движение электромагнитных волн, или волн тока и напряжения.
При включении генератора в начале линии возникают волны тока и напряжения, которые движутся от генератора (начало линии) к нагрузке (конец линии). Когда электромагнитная волна достигает конца линии, ее энергия лишь частично поглощается нагрузкой. При этом возникают отраженные волны тока и напряжения, перемещающиеся от нагрузки к генератору.
Только при специально подобранном сопротивлении нагрузки вся энергия поглощается нагрузкой и отраженные волны отсутствуют.
Если сопротивление нагрузки в конце линии равно волновому сопротивлению линии, то такая нагрузка называется согласованной. Если же сопротивление нагрузки в конце линии отличается от волнового сопротивления, то нагрузка называется несогласованной. Волновое сопротивление выражается отношением напряжения к току падающих (прямых) или отраженных волн. При согласованной нагрузке отраженных волн в линии нет, т. е. энергия, которую несет падающая электромагнитная волна, полностью поглощается в нагрузке.
При исследовании различных режимов работы длинных линий необходимо учитывать коэффициент отражения р и коэффициент преломления m.
Коэффициент отражения характеризует соотношение между падающими (прямыми) и отраженными волнами напряжения и тока:
Коэффициент преломления в рассматриваемом пункте линии n:
То есть коэффициент преломления m равен отношению комплексов напряжения (тока) в рассматриваемой точке n к комплексу напряжения (тока) падающей волны.
Если на каждую падающую (прямую) волну напряжения и тока накладывается отраженная волна с амплитудой, равной амплитуде падающей волны, то результирующий процесс называют стоячей волной.
Скорость распространения электромагнитных волн в проводах воздушной линии в первом приближении можно считать равной скорости распространения электромагнитных волн в вакууме, т.е. с = 300ООО км/сек.
Расстояние, на которое распространяется электромагнитная волна, или волна тока и напряжения, в течение периода Т, называется длиной волны 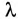
При частоте
При частоте
При частоте
При известной длине волны легко показать распределение тока или напряжения вдоль линии в любой момент времени и без вычислений токов утечки и смещения. Например, при частоте f = 1 МГц и 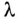
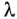
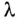
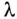
В следующий момент времени характер распределения тока будет таким же, но нулевые и амплитудные значения тока будут наблюдаться в других сечениях линии.
Неодинаковость тока наблюдается только в линиях, длина которых i соизмерима или больше длины волны 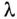
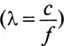
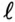
Следовательно, величина тока, проходящего через каждое сечение линии в любой выбранный момент времени, практически одна и та же, т. е. линия слишком «коротка», чтобы в ней можно было заметить неравномерное распределение тока.
При частоте же f = 1 МГц, как показано на рис. 21.7, в той же линии (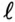
- Резистивные электрические цепи и их расчёт
- Гармонические напряжения и токи
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Вращающееся магнитное поле
- Электрические цепи синусоидального тока
- Электрические цепи несинусоидального тока
- Несинусоидальный ток