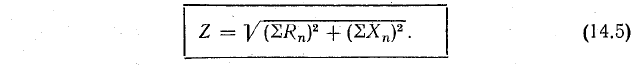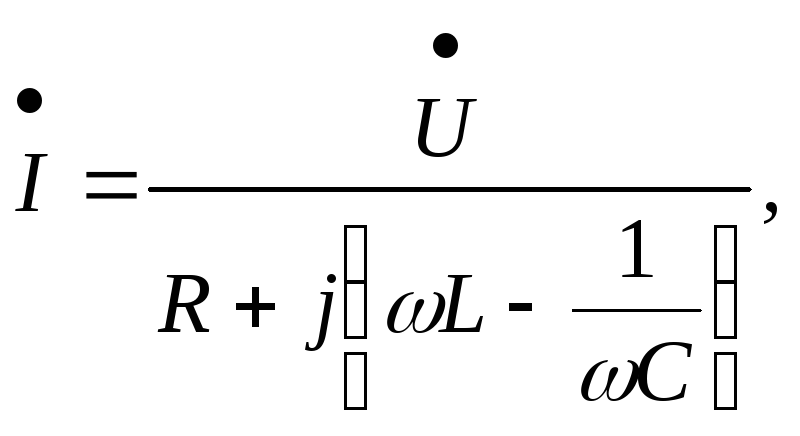Как найти напряжение в неразветвленной цепи

Порядок расчета, установленный для цепи при последовательном соединении катушки и конденсатора, можно применить и для цепи, содержащей произвольное число катушек и конденсаторов, соединенных последовательно.

На рис. 14.7, а для примера дана схема неразветвленной цепи, состоящей из пяти участков: конденсатора (R1 Х1) и катушки (R2, Х2), представленных активными и реактивными сопротивлениями; резистора R3; идеальных конденсатора Х4 и катушки Х5.

Предположим, что кроме сопротивлений известен ток в цепи i = I_msinωt. Требуется найти напряжения на участках, общее напряжение в цепи и мощность.

Векторная диаграмма

Произвольно выберем условно-положительное направление тока i, в данном случае по часовой стрелке. Для мгновенных величин в соответствии со вторым законом Кирхгофа уравнение напряжений (а — падение напряжение на активном сопротивлении; р — падение напряжения на реактивном элементе )

u = u_1a + u_1p + u_2a + u_2p + u_3a  + u_4p + u_5p;

Для действующих величин необходимо записать векторную сумму:

U = U_1a + U_1p + U_2a + U_2p + U_3a + U_4p + U_5p;

Численно векторы напряжений определяются произведением тока и сопротивления соответствующего участка. На рис. 14.7, б построена векторная диаграмма, соответствующая этому уравнению. За исходный, как обычно при расчете неразветвленных цепей, принят вектор тока, а затем проведены векторы падения
напряжения на каждом участке схемы, причем направления их относительно веrтора тока выбраны в соответствии с характером сопротивления участков.

При построении диаграммы напряжений выбрана начальная точка 6 совпадающая с началом вектора тока i. Из этой точки проведен вектор U_5.2 реактивного напряжения индуктивности (по фазе опережает ток на 90°) между точками 5 и 6 цепи. Из конца его проведен вектор U_4р реактивного напряжения емкости (по фазе отстает от тока на 90° ) между точками 4 и 5 цепи. Затем отложен вектор U3a активного напряжения на резисторе (совпадает по фазе с током) между точками
3 и 4 цепи и т. д., если следовать по цепи против направления тока.Точки векторной диаграммы, где сходятся начало следующего вектора с концом предыдущего, обозначены теми же номерами, какими на схеме обозначены точки, отделяющие одни элемент от другого.

При таком, построении напряжение между любыми двумя точками цепи можно найти по величине и фазе, проведя вектор на диаграмме между точками с теми же номерами. Например, напряжение U_5.2 между точками 5 и 2 выражается вектором, проведенным из точки 2 в точку 5 (вектор  U_2.5 направлен в обратную сторону); напряжение U_3.1 между точками 3 и 1 выражается вектором, проведенным из точки
1 в точку 3.

Векторная диаграмма, построенная в соответствии с чередованием элементов цепи, называется топографической, так как точки, отделяющие векторы друг от друга, соответствуют точкам, разделяющим элементы схемы.

Расчетные формулы

Из векторной диаграммы видно, что все активные составляющие векторов напряжений направлены одинаково — параллельно вектору тока, поэтому векторное сложение их можно заменить арифметическим и найти активную составляющую напряжения цепи: Ua = U_1a + U_2a + U_3a

Реактивные составляющие векторов напряжений перпендикулярны вектору тока, причем индуктивные напряжения направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая напряжения цепи Up определяется их алгебраической суммой, в которой индуктивные напряжения считаются положительными, а емкостные — отрицательными: U_p = — U_1р + U_2p — U_4p + U_5p.

Векторы активного, реактивного и полного напряжений цепи образуют прямоугольный треугольник, из которого следует

Подставив падения напряжения, выраженные через ток и соответствующие сопротивления, получим:

Таким образом снова получена знакомая уже формула, связывающая ток, напряжение и полное сопротивление цепи [ср. (14.4) и (14.1)].

В этой формуле ∑R_n—общее активное сопротивление, равное арифметической сумме всех активных сопротивлений, входящих в неразветвленную цепь; ∑X_n — общее реактивное сопротивление, равное алгебраической сумме всех реактивных сопротивлений, входящих в неразветвленную цепь. В этой сумме индуктивные сопротивления считаются положительными, а емкостные — отрицательными. Полное сопротивление неразветвленной цепи

В общем случае полное сопротивление цепи определяется как гипотенуза прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активное и реактивное сопротивления всей цепи. Из треугольника сопротивлений следует:

От треугольника напряжений можно перейти также к треугольнику мощностей и получить уже известные формулы для определения мощностей в цепи:

Вместе с тем активную мощность цепи можно представить как арифметическую сумму активных мощностей в элементах с активным сопротивлением. Реактивная мощность цепи равна алгебраической сумме мощностей реактивных элементов.

В этой сумме мощность индуктивных элементов считается положительной, а емкостных — отрицательной:

Формулы (14.2)—(14.7) являются общими; из них можно получить конкретное выражение для любой неразветвленной цепи.

Задачи по теме с решением.

синусоидального
тока

Для
расчета режима неразветвленной
электрической цепи применим комплексный
метод. Представим все синусоидальные
величины их комплексами:

Порядок
расчета такой же, как на постоянном
токе. Во-первых, стрелками
изображаем условные положительные
направления тока, ЭДС и напряжений.
Во-вторых, выбираем направление обхода
контура по направлению движения часовой
стрелки и записываем уравнение по
второму закону Кирхгофа:

(3.45)

Выражения

,,
отражают особенности проявления закона
Ома для резистивного, индуктивного и
емкостногоэлементов
электрической цепи:

Здесь
умножение на


означает,
что напряжение


опережает
по
фазе ток
на 90^º
, умножение на

означает,
что напряжение

отстает
по
фазе от тока
на
90°.

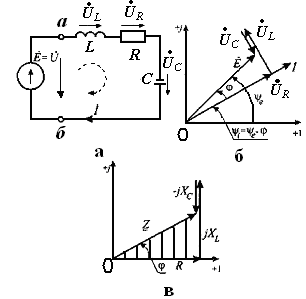
Рис.
3.7. Расчет неразветвленной электрической
цепи синусоидального
тока: а) схема электрической цепи; б)
векторная
диаграмма тока и напряжений; в) изображение
комплексных
сопротивлений на комплексной плоскости

Из (3.45) находим
комплексный ток в цепи:

(3.46)

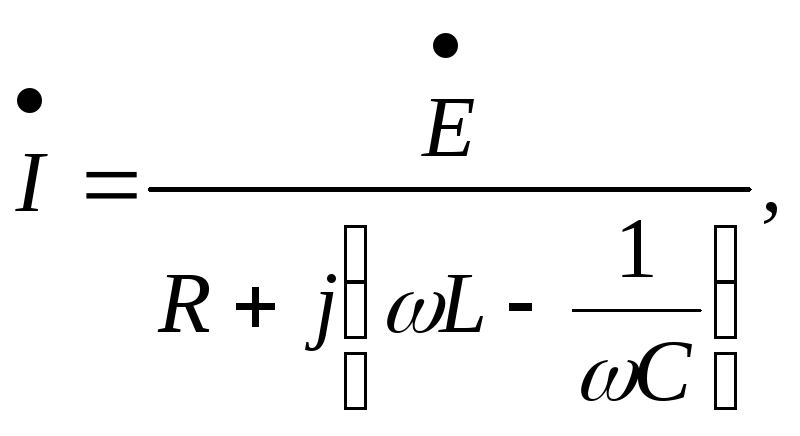
или
(так как

)

(3.47)

где
–
напряжение между выводами
_аб
неразветвленной
цепи (рис. 3.7,а). Величина,
стоящая в знаменателе и равная

(3.48)

называется
комплексным
сопротивлением (неразветвленной
цепи).

Величина,
обратная комплексному сопротивлению,
называется комплексной
проводимостью:

На
рис. 3.7,б построена векторная диаграмма
тока и напряжений неразветвленной
цепи для случая:
.

Обычно
векторная диаграмма строится в конце
расчета по полученным
значениям тока и напряжений. При этом
проверяется правильность расчета.

Поделив
все составляющие векторной диаграммы
на отрезок,
определяем значения
комплексных сопротивлений и изображаем
комплексные сопротивления

,

,

,

на
комплексной плоскости (рис.
3.7,в), тогда получаем
диаграмму, подобную диаграмме тока и
напряжений.

Обратим
внимание на «треугольник сопротивлений»
(заштрихованная
площадь), стороны которого соответствуют
сопротивлениям
,

и

.
Треугольник сопротивлений подобен
треугольнику напряжений
(рис.3.7,б)

Анализ
диаграммы сопротивлений позволяет
перейти от алгебраической формы записи
комплексного сопротивления к
тригонометрической и показательной
формам:

;
(3.49)

(3.50)

где

–
модуль комплексного сопротивления или
полное
сопротивление;

–аргумент
комплексного сопротивления.

В
зависимости от знака величины ()
аргумент
комплексного
сопротивления может быть либо положительным
(индуктивный характер), либо отрицательным
(емкостный характер).

Подставив
(3.50) в (3.46) или в (3.47), получим закон Ома
для неразветвленной
цепи:

(3.51)

или

(3.52)

то есть

(3.53)

При
нескольких последовательно соединенных
элементах комплексное
сопротивление

(3.54)

где

–
активное сопротивление цепи;

–
реактивное
сопротивление цепи.

В
активном сопротивлении происходит
необратимое
преобразование
электрической энергии в другие виды
энергии, а в реактивном сопротивлении
– не происходит.

Полное
сопротивление и аргумент комплексного
сопротивления можно
рассчитывать по формулам:

(3.55)

(3.56)

Соседние файлы в предмете Теоретические основы электротехники

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

  02.05.20141.14 Mб47Примеры решения задач – Линейные цепи. Автоматизированный метод рассчета.mcd

• #

Векторная диаграмма

Пример простейшей неразветвленной электрической цепи изображен на рисунке ниже.

Рассмотрим схему неразветвленной электрической цепи переменного тока, которая представлена на рисунке ниже.

Вышепредставленная электрическая сеть состоит из следующих участков:

1. Конденсатор (R1 X1).
2. Катушки (R2 X2).
3. Резистора (К3).
4. Двух идеальных конденсаторов (Х4 и Х5).

Допустим, что нам, кроме сопротивлений, известен ток в цепи:

$i = Imsinwt$

Произвольно выбираем условно-положительное направление тока, по часовой стрелке. Для мгновенных величин, согласно второму закону Кирхгофа, уравнение напряжений, в векторном виде, будет выглядеть следующим образом:

«Расчет неразветвленной цепи переменного тока» 👇

$U = U1a+U1p+U2a+U2p+U3a+U4p+U5p$

Численно, векторы напряжений определяются, как произведение сопротивления соответствующего участка цепи и тока. На рисунке ниже изображена векторная диаграмма, которая соответствует данному уравнению.

За исходный принимается вектор тока, а потом проводятся векторы падения напряжений для каждого участка цепи, направления векторов которых выбираются в соответствии с характером сопротивления. При построении векторной диаграммы напряжений выбирается точка б, которая совпадает с началом вектора тока. Затем из этой точки проводится вектор U5.2, представляющий собой вектор реактивного напряжения индуктивности и опережающий по фазе вектор тока на 90 градусов, между точками 5 и 6 на схеме. Из его конца проводится вектор реактивного напряжения емкости (U4p), который отстает от тока на 90 градусов, между точками 4 и 5 на схеме. После этого откладывается вектор активного напряжения на резисторе, совпадающий с вектором тока (U3a), между точками 3 и 4 на схеме и т.д., если следовать по цепи противоположно направлению тока. Те точки, в которых сходятся начало следующего и конец предыдущего векторов, обозначаются такими же номерами, каким обозначены на схеме.

При данном построении векторной диаграммы, напряжение между двумя любыми точками рассматриваемой цепи возможно определить по фазе и величине, посредством проведения вектора на диаграмме между точками с такими же номерами. Например, напряжение между точками 5 и 2 можно выразить вектором, который проводится из точки 2 в точку 5 и т.д.

Расчетные формулы

Из векторной диаграммы видно, что активные элементы векторов напряжений направлены одинаково, то есть параллельно по отношению к вектору тока, поэтому их векторное сложение можно заменить арифметическим. Реактивные составляющие векторов напряжений перпендикулярны к вектору тока, при этом емкостные направлены в противоположную сторону, а индуктивные в ту же. Таким образом Up определяется их алгебраической суммой, где емкостные напряжение считаются отрицательными, а индуктивные положительными:

$Up = -U1p+U2p-U4p+U5p$

Векторы полного, реактивного и активного напряжений образуют треугольник, откуда следует, что:

Если подставить падения напряжений, которые были выражены через ток и соответствующие напряжения, то получается:

Данная формула связывает между собой полное сопротивление, ток и напряжение. В этой формуле Rn – общее активное сопротивление, представляющее собой арифметическую сумму активных сопротивлений, которые входят в состав неразветвленной электрической цепи. Xn – общее реактивное сопротивление, равняющееся алгебраической сумме всех реактивных сопротивлений, которые являются частью неразветвленной цепи. Здесь емкостные сопротивления отрицательны, а индуктивные положительны, а формула для расчета полного сопротивления цепи будет иметь следующий вид:

В общем случае полное сопротивление неразветвленной электрической цепи переменного тока может быть определено, как гипотенуза прямоугольного треугольника, у которого катеты, выраженные в определенном масштабе, представляют собой активное и реактивное сопротивления, таким образом получается, что:

От треугольника напряжений возможно перейти к треугольнику мощностей и получить формулы для их определение:

Активную мощность рассматриваемой неразветвленной электрической цепи можно также представить в виде арифметической суммы активных мощностей в составляющих с активными сопротивлениями. А реактивная мощность является алгебраической суммой мощностей реактивных элементов. В данной сумме мощность индуктивных элементов – положительна, а емкостных – отрицательна:

Задание для обучающихся с применением
дистанционных образовательных технологий и электронного обучения

Дата 07.10

Группа Э-17

Общепрофессиональная дисциплина: ОП.02 ЭЛЕКТРОТЕХНИКА
И ЭЛЕКТРОНИКА

Тема занятия: Неразветвленная цепь с активным сопротивлением,
емкостью и индуктивностью

Форма: лекция

ПЛАН

1 Неразветвленная цепь с активным сопротивлением,
емкостью и индуктивностью

2 Расчет неразветвленной цепи переменного тока с
произвольным числом активных и реактивных элементов.

3. Общий случай неразветвленной цепи.
Построение топографической диаграммы

ЛЕКЦИЯ

1 Неразветвленная цепь с активным
сопротивлением, емкостью и индуктивностью

Электрическая цепь с активным сопротивлением,
индуктивностью и емкостью представляет собой общий случай последовательного
соединения активных и реактивных сопротивлений и является последовательным
колебательным контуром.

Принимаем фазу тока нулевой, т.е. ток в этой цепи
изменяется по закону:

  .

Тогда напряжение на активном сопротивлении будет
изменяться как  , а напряжение на
индуктивности  , напряжение на емкости –  .

Выведем закон Ома для рассматриваемой цепи. Так как
модуль вектора U_L + U_C рассчитывают как
разность действующих значений U_L–U_C,

то из диаграммы следует, что  .
Но  ;  ,  ;
следовательно,  ,откуда

Рисунок 1 – Электрическая схема
последовательного соединения элементов

.

Введя обозначение  ,

где Z–полное
сопротивление цепи, найдем, что полный ток рассматриваемой цепи определится
как:

 .

Разность между индуктивным и емкостным
сопротивлениями  называют реактивным
сопротивлением цепи.

2 Расчет неразветвленной цепи переменного
тока с произвольным числом активных и реактивных элементов

Задача 1

Последовательная цепь (рисунок 2) подключена к
источнику переменного напряжения U=36В. Параметры выбраны следующие:
R=10Ом,L=10мГн,C=1мкФ. Определить характеристики полного
сопротивления и тока цепи при частоте 7961,8Гц.

Дано: U=36В

R=10Ом

L=10мГн

C=1мкФ

F=7961,8Гц

————————

Определить: I, Z                                                 

Рисунок 2 – Электрическая схема

Решение задачи

Находим полное сопротивление: ;

=10 Ом;

Находим ток: I=U/Z;

I=36/10=3,6А.

Задача 2

В сеть синусоидального тока с частотой f=
50 Гц включены последовательно реостат с сопротивлением R=5 Ом,
индуктивность L и емкость C. Вычислить индуктивность L и
емкость C, если напряжения на R, L и C одинаковы.

Дано: f= 50 Гц

R=5 Ом

U_L=U_C=U_R

———————–

Определить: L, C;

Рисунок 3 – Электрическая схема

Решение задачи

Так как в неразветвленной цепи ток на всех участках
(сопротивлениях) имеет одинаковое значение, то и падение напряжения на всех
участках цепи имеет одинаковое значение при одинаковых сопротивлениях участков.

R=5 Ом,X_L=5
Ом,X_C=5 Ом.

Схема цепи изображена на рисунке 3

-индуктивное
сопротивление;

–
емкостное сопротивление;

Напряжения на индуктивности и емкости при резонансе
равны между собой и могут оказаться больше по значению напряжения цепи. Понятие
добротности имеет важное практическое значение (например, для антенн).

3 Общий случай неразветвленной цепи

В неразветвленной цепи в общем случае может быть
включено несколько активных, несколько реактивных сопротивлений. Такие цепи
рассчитываются аналогично цепям, содержащим активное, емкостное и индуктивное
сопротивления. Находим эквивалентные сопротивления: активное, емкостное,
индуктивное, как суммы соответствующих сопротивлений.

Задача 3

На рисунке 4 в однофазную электрическую цепь
переменного синусои­дального тока напряжением U=50В включены активные R₁=9
Ом и R₂=11 Ом и реактивные элементы, обладающие сопротивления­ми Х_L= 12 Ом, X_C=27 Ом.

Определить: ток I в цепи;напряжение на каждом
элементе цепи; активные, реактивные и полное сопротивления; угол сдвига фаз
между напряжением и током ( по величине и знаку); активные и реактивные
мощности элементов; активную, реактивную и полную мощности цепи.

Построить в масштабе векторную диаграмму напряжений.
После построения диаграммы измерить вектор суммарного напряжения и убедиться в
том, что с учетом масштаба его величина равна напряжению, подведенному к
зажимам цепи

Рисунок 4 – Электрическая схема

Решение

1. Определяем полное сопротивление цепи

2. Определяем ток цепи 

3. Определяем падение напряжения:

на активном сопротивлении R₁  

на активном сопротивлении R₂  

на индуктивном сопротивлении 

на емкостном сопротивлении     

4. Определяем угол сдвига фаз между напряжением и
током

;  

5. Определяем активную мощность цепи

6. Определяем реактивную мощность цепи

7. Определяем  полную мощность цепи 

8. Построение векторной диаграммы начинаем с выбора
масштаба для тока и напряжения. Задаемся масштабом по току и по напряжению ; 

Здесь и  – масштабные коэффициенты. Они показывают,
сколько ампер или вольт содержится в 1 см. Масштаб можно задавать и графически
(см. рис. 5).

Порядок построения

От точки 0 горизонтально вправо проводим вектор тока I
общий для всей цепи. В выбранном масштабе его длина будет  

Рисунок 5 – Векторная диаграмма

Вектор активного напряжения совпадает по фазе с током,
угол сдвига фаз между ними равен 0, поэтому откладываем его вдоль вектора тока
от точки 0 вправо. В выбранном масштабе его длина будет

От конца вектора U_R1,
откладываем вправо вдоль вектора тока вектор активного напряжения U_R2.  Его
длина будет

От конца вектора U_R2  откладываем
вертикально вверх вектор падения напряжения на индуктивном сопротивлении U_L так как
он опережает ток на угол 90°.  Его длина будет

От конца вектора U_L
откладываем вертикально вниз вектор падения напряжения U_С на
емкостном сопротивлении, т.к. он отстает от тока угол 90°. Его длина будет

Геометрическая сумма векторов U_R1, U_R2, U_L и U_С должна
быть равна полному напряжению U, приложенному к зажимам цепи, т.е. 

Измерив длину этого вектора, убеждаемся, что она l_U = 5 см.
Это значит, что с учетом масштаба его величина будет:

По условию задачи именно такое напряжение приложено к
зажимам

цепи.

Примечание:

Если в выбранном масштабе вектор суммарного напряжения
не будет равен приложенному к зажимам цепи напряжению, то это будет говорить об
ошибке, допущенной в решении задачи или в построении векторной диаграммы. Ее
нужно найти и устранить:

Чаще всего наблюдаются ошибки, связанные с искажение
масштабов при построении векторной диаграммы. Учтите это, при построении
векторной диаграммы пользуйтесь чертежным инструментом. Выполняйте диаграмму
точно и аккуратно.

Задача 4

Напряжение, приложенное к цепи (рисунок 6) U=
220 В, частота тока сетиf=50 Гц. Начальная фазаψ=0. Сопротивление
участков цепиR1=8Ом,R2=7Ом,R3=5Ом,X_L1=20Ом,X_L2=18Ом,X_C1=10
Ом,X_C2=13Ом. Требуется определить ток цепи и записать его
мгновенное значение, построить векторную диаграмму цепи, полную, активную,
реактивную мощности цепи.

Дано: U= 220 В;

f=50 Гц;

ψ=0;

R1=8Ом;

R2=7Ом;

R3=5Ом;

X_L1=20Ом;

X_L2=18Ом;

X_C1=10 Ом;                                                
Рисунок 6 – Электрическая схема

X_C2=13Ом;

————————  

Определить: I, P, Q, S,
записать мгновенное значение тока, построить векторную диаграмму цепи.

Решение задачи

Вычислим полное сопротивление цепи:

;

Z = =25Ом

Находим действующее значение тока:  I=U/Z;     I=220/25=8,8
А;

Найдем значение амплитуды тока :  I_m=I;     I_m=*8,8=12,4А;

Угловая частота: ω=2πf=2π∙50=314;

Определим коэффициент мощности:

;     ;     φ=arccos 0,8=
37⁰

Мгновенное значение тока цепи:

;      i=12,4sin(314t+37⁰);

Определим полную мощность:

S=U∙I;

S=220∙8,8=1936 ВА;

Определим активную мощность:

;

Р=1936∙0,8=1548,8Вт;

Определим реактивную мощность:

;

Q=1936∙0,6=1161,6
Вар;

Для построения векторной диаграммы находим напряжения
на каждом элементе цепи:

U_C1 =IX_C1;    U_C1 =8,8∙10=88В;

U_R1 =IX_R1;  U_R1 =8,8∙8=70В;

U_R2 =IX_R2;   U_R2 =8,8∙7=62В;

U_L1 =IX_L1;   U_L1 =8,8∙20=176В;

U_R3 =IX_R3;   U_R3 =8,8∙5=44В;

U_L2 =IX_L2;   U_L2 =8,8∙18=158В;

U_C2 =IX_C2;   U_C2 =8,8∙13=114В.

Строим векторную (топографическую) диаграмму (рисунок 7):

Рисунок 7 – Топографическая диаграмма

Задание 1 Проработать
материал лекции.

Цель: закрепить знания методов расчета параметров неразветвленных электрических цепей переменного тока.

Теоретические сведения

Реактивное сопротивление цепи рано разности индуктивных и емкостных сопротивлений:

Формула для полного сопротивление цепи имеет вид:

Эту формулу нужно привести в соответствие со своей схемой, следуя указаниям:

– если одно из этих сопротивлений в схеме отсутствует, то брать его за ноль;

– если каких-то сопротивлений два, то при их подставке в формулу складывают; причем XL всегда берут с «плюсом», а ХC – с «минусом».

Ток в цепи можно найти несколькими способами:

Напряжения в цепи также можно найти по нескольким формулам:

Коэффициент мощности равен отношению активного сопротивления к полному:

sinφ находят как отношение реактивного сопротивления к полному:

Формулы для мощности цепи имеют вид:

Для построения векторной диаграммы необходимо:

1. Составить уравнение

(векторно сложить в порядке схемы соответствующие напряжения).

2. Выбрать масштаб, т.е. поделить все значения напряжений на одно число, чтобы результат деления было удобно строить в сантиметрах.

3. После этого построить векторную диаграмму по масштабу и в соответствии с уравнением.

ПРИМЕЧАНИЕ:

a) первым всегда строят ток I;

b) вектор UR всегда идет параллельно току;

c) вектор UL перпендикулярно току вверх;

d) UC перпендикулярно току вниз;

e) итоговый вектор U соединяет начало первого вектора с концом последнего.

Проверка: длина вектора U в сантиметрах, измеренная по линейке, должна совпадать с расчетной величиной.

Задание

Неразветвленная цепь переменного тока содержит активные и реактивные сопротивления, величины которых заданы в таблице. Кроме того, известна одна из дополнительных величин. Определить следующие величины, если они не заданы в таблице вариантов: полное сопротивление цепи; напряжение, приложенное к цепи: силу тока в цепи; активную, реактивную и полную мощности; cosφ; sinφ.

Порядок выполнения расчета

1. Начертить исходную схему.

2. Найти реактивное сопротивление:

3. Найти полное сопротивление цепи:

4. Найти ток:

5. Найти напряжения:

6. Найти cosφ и sinφ:

7. Найти мощности:

активная

реактивная

полная

8. Построить векторную диаграмму:

a) Векторно сложить соответствующие напряжения в порядке схемы

b) Выбрать масштаб, т.е. поделить все значения напряжений на одно число, чтобы результат деления было удобно строить в сантиметрах.

c) Построить векторную диаграмму по масштабу и в соответствии с уравнением.

Описание:

1. Первым строят ток I, горизонтально, длиной 5 см;

2. Вектор UR1 идет параллельно току, длиной 1 см;

3. Вектор UL перпендикулярно току вверх, от конца вектора UR1, длиной 6 см;

4. Вектор UR2 идет параллельно току, от конца вектора UL, длиной 3 см;

5. UC перпендикулярно току вниз, от конца вектора UR2 , длиной 3 см;

6. Итоговый вектор U соединяет начало первого вектора UR1 с концом последнего UC.

Проверка: длина вектора U в сантиметрах, измеренная по линейке, равна 5 см, что совпадает с расчетной величиной.