Напряжение цепи переменного тока

Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде).
Где u = u(t) — мгновенное значение переменного напряжения [В].
Um — максимальное значение напряжения (амплитудное значение) [В].
f — частота равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с -1 )
ω — угловая частота (омега) (единица угловой частоты — рад/с или с -1 )
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
U — Действующее значение напряжения [В]:
Рассмотрим параметры напряжения в бытовой электросети.
Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.).
Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения.
- Действующее значение напряжения U = 220 В.
- Амплитудное значение напряжения цепи переменного токаUm = U*√2 = 220 *√2 = 311 В.
- Угловая частота ω = 2πf = 3,14*2*50 = 314рад/с.
- Начальная фаза Ψ = 0град.
- Мгновенное значениеu= 311sin(314t)В.
Источник
Расчет электрических цепей переменного тока
Для электрической цепи, схема которой соответствует варианту задания и изображена на рис. 1.1-1.50, по заданным в табл. 1 параметрам и приложенному к цепи напряжению, определить токи во всех ветвях цепи. Определить активную, реактивную и полную мощности цепи. Построить в масштабе векторную диаграмму токов и напряжений.
Методические указания
Для правильного решения поставленной задачи необходимо изучить теорию электрических цепей однофазного синусоидального тока, усвоить основные формулы сопротивлений, проводимостей токов, напряжений; научиться применять для анализа и расчета закон Ома, уравнения Кирхгофа, метод проводимостей.
Все предлагаемые заданием электрические цепи являются смешанными, т.е. содержат последовательную ветвь и две параллельные. В каждой ветви имеются различные сопротивления, величины которых заданы.
Для примера рассмотрим обобщенную цепь, представленную на рис. 1.
 Общий ход решения задач подобного типа следующий. Необходимо преобразовать последовательно-параллельную цепь в простую последовательную цепь, заменив разветвленный участок цепи эквивалентной последовательной цепочкой.
Общий ход решения задач подобного типа следующий. Необходимо преобразовать последовательно-параллельную цепь в простую последовательную цепь, заменив разветвленный участок цепи эквивалентной последовательной цепочкой.
Прежде всего, необходимо методом проводимости определить параметры эквивалентной цепочки, которой может быть замещен разветвленный участок цепи.
В эквивалентной цепочке реактивное сопротивление будет индуктивным или емкостным в зависимости от знака эквивалентной реактивной проводимости. Дальнейшее решение сводится к определению активного и реактивного сопротивления цепи, а по ним полного сопротивления цепи.
По каждому сопротивлению цепи и заданному напряжению определяется общий потребляемый ток в цепи  . Чтобы определить ток в отдельных ветвях разветвленного участка, находим сначала напряжение между узловыми точками
. Чтобы определить ток в отдельных ветвях разветвленного участка, находим сначала напряжение между узловыми точками  , а затем и токи в ветвях
, а затем и токи в ветвях  .
.
После чего находим напряжение на указанном участке, активную, реактивную и полную мощности в цепи. Заканчиваем расчет построением векторной диаграммы токов и напряжений.
Возможно вам будут полезны данные страницы:
Алгоритм расчета
1. Вычисляем величины сопротивлений отдельных элементов цепи:

где 
 — в Генри (Гн),
— в Генри (Гн),  — в Фарадах (Ф).
— в Фарадах (Ф).
ВНИМАНИЕ: в задании L дается в мГн, С — в мкФ.
2. Вычисляем полные сопротивления ветвей:
 где
где 
3. Вычисляем активные проводимости параллельных ветвей:

4. Вычисляем общую эквивалентную активную проводимость  :
:

5. Вычисляем реактивные проводимости ветвей и общую эквивалентную проводимость  :
:

6. Изобразим эквивалентную схему, на которой сопротивления заменим проводимостями (рис.2).
 7. Заменим эквивалентные проводимости эквивалентными сопротивлениями, включенными последовательно (рис.З).
7. Заменим эквивалентные проводимости эквивалентными сопротивлениями, включенными последовательно (рис.З).
 8. Найдем общее сопротивление всей цепи: при сложении (реактивных сопротивлений учитывать знаки).
8. Найдем общее сопротивление всей цепи: при сложении (реактивных сопротивлений учитывать знаки).

9. Найдем общий потребляемый ток:

10. Найдем напряжение, приложенное к параллельному участку цепи:


12. Найдем напряжение на сопротивлении  :
:

13. Вычисляем мощности цепи:
 где
где 
Строим векторную диаграмму токов и напряжений, предварительно определив масштаб для векторов напряжений и векторов тока (рис.4).
 В качестве исходного вектора удобно принимать вектор напряжения, приложенного к параллельным ветвям, вектор
В качестве исходного вектора удобно принимать вектор напряжения, приложенного к параллельным ветвям, вектор  .
.
Относительно вектора  откладываем вектора токов ветвей
откладываем вектора токов ветвей  , предварительно определив углы
, предварительно определив углы  из уравнений:
из уравнений:

Ток в неразветвленной части цепи  (общий ток), находим векторным сложением токов
(общий ток), находим векторным сложением токов  . При построении векторов учитывать, что опережающий ток откладывается против часовой стрелки относительно вектора напряжения U
. При построении векторов учитывать, что опережающий ток откладывается против часовой стрелки относительно вектора напряжения U  а отстающий по фазе — по часовой стрелке.
а отстающий по фазе — по часовой стрелке.
Строим треугольник напряжений (масштабы для векторов токов и напряжений выбираем разные, выбирая их согласно полученных значений).
Так как  , необходимо определить угол (
, необходимо определить угол (  из уравнения:
из уравнения: 
Для построения вектора  из конца вектора
из конца вектора  проводим пунктирную линию параллельно
проводим пунктирную линию параллельно  , под углом
, под углом  к ней откладываем вектор
к ней откладываем вектор 
Если  положительная величина, вектор откладывается против часовой стрелки, если отрицательная величина — по часовой стрелке. Соединяем начало вектора
положительная величина, вектор откладывается против часовой стрелки, если отрицательная величина — по часовой стрелке. Соединяем начало вектора  с концом вектора
с концом вектора  и находим вектор
и находим вектор  , т.е.
, т.е. 
Пример с решением № 2
Для электрической цепи, схема которой изображена на рис. 2.1 — 2.17 (СМ. ВАРИАНТ ЗАДАНИЯ), по заданным в табл. 2 параметрам, определить фазные и линейные токи, ток в нейтральном проводе (для четырехпроводной схемы), активную мощность всей цепи и каждой фазы отдельно. Построить векторную диаграмму токов и напряжений.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Прежде чем приступить к расчету задания № 2, необходимо изучить теорию трехфазных цепей при соединении потребителей электрической энергии по схеме «звезда» и «треугольник». При этом надо особо обратить внимание на соотношение фазных и линейных напряжений при соединении потребителей звездой и соотношение фазных и линейных токов при соединении треугольником.

Для соединения потребителей треугольником:

Рассмотрим примеры расчета трехфазной цепи при соединении потребителей звездой и треугольником.
Электрическая цепь при соединении «звездой».
 Алгоритм расчета
Алгоритм расчета
1. Находим полное сопротивление фаз:

2. Находим фазные (линейные) токи:
 где
где 
3. Находим углы сдвига по фазе из выражений:

4. Находим активные мощности фаз:

5. Находим полную активную мощность цепи:

Строим с учетом масштаба векторную диаграмму токов относительно фазных напряжений (рис.6) и находим графически ток в нейтральном проводе:
 Диаграмму строим посредством отметок циркулем, предварительно задавшись масштабом, начав построение с фазных напряжений, например, из точки 0 (угол между направлением векторов 120°). Вычислив фазные токи, задавшись масштабом для токов, откладываем фазные токи под соответствующим углом сдвига по фазе относительно одноименного фазного напряжения.
Диаграмму строим посредством отметок циркулем, предварительно задавшись масштабом, начав построение с фазных напряжений, например, из точки 0 (угол между направлением векторов 120°). Вычислив фазные токи, задавшись масштабом для токов, откладываем фазные токи под соответствующим углом сдвига по фазе относительно одноименного фазного напряжения.
Проводим сложение векторов токов по правилам силового многоугольника и находим ток в нейтральном проводе  , измерив длину вектора в выбранном масштабе.
, измерив длину вектора в выбранном масштабе.
Пример 2. Электрическая цепь при соединении треугольником.
 Алгоритм расчета
Алгоритм расчета
1. Находим полное сопротивление каждой фазы:


где 
1. Находим значение углов сдвига по фазе из выражений:

4. Находим активные мощности каждой фазы:

5. Находим активную мощность всей цепи:
 Вт.
Вт.
6. Строим векторную диаграмму токов относительно векторов фазных напряжений для этой цепи, используя полученные цифровые данные (рис.8). Откладываем значения вычисленных фазных токов с учетом сдвига по отношению к своим фазным напряжениям.
 7. Определяем линейные токи.
7. Определяем линейные токи.
Линейные токи определяются графически с учетом масштаба. Каждый из линейных токов равен геометрической разности фазных токов согласно приведенных ранее уравнений для соединения потребителей энергии треугольником.
Вектор линейного тока соединяет концы векторов фазных токов, отложенных из точки О и направленных к уменьшаемому.
На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Источник
3.1. Задание для самостоятельной работы
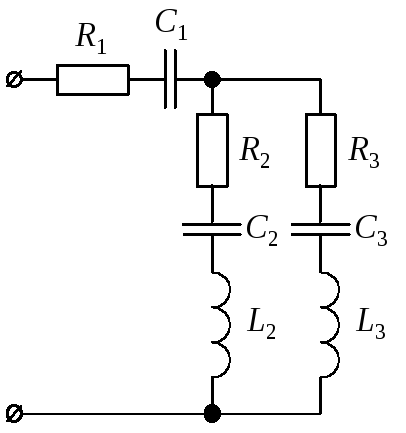
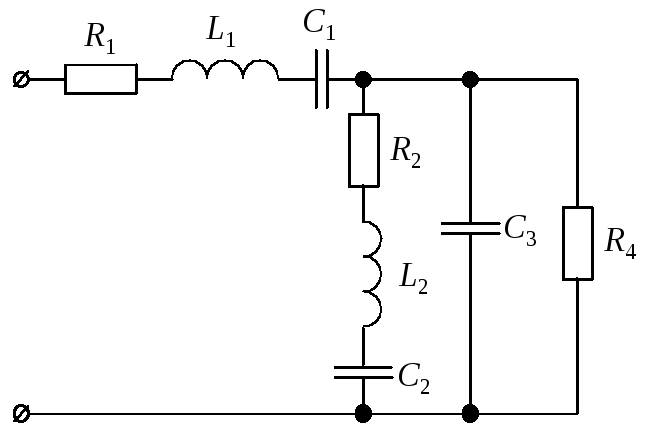
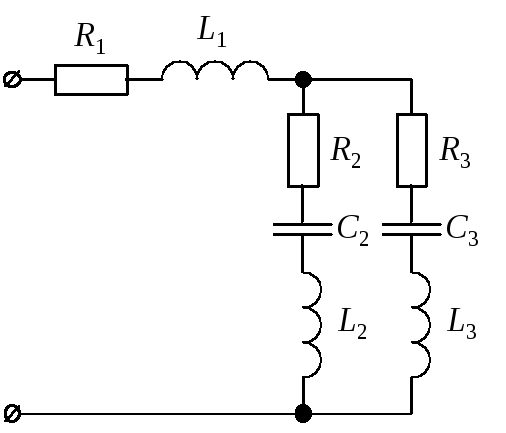
Для цепи
синусоидального тока заданы параметры
(табл. 8) включенных в нее элементов (рис.
10) и действующее значение напряжения
на ее зажимах; частота питающего
напряжения f = 50 Гц. Необходимо:
1) определить
действующие значения тока в ветвях и
неразветвленной части цепи символическим
методом;
2) по полученным
комплексным изображениям записать
выражения для мгновенных значений тока
в ветвях и напряжения на участке цепи
с параллельным соединением;
3) построить
упрощенную векторную диаграмму;
4) составить баланс
мощности;
5) определить
характер (индуктивность или емкость) и
параметры элемента, который нужно
добавить в неразветвленную часть схемы,
чтобы в цепи имел место резонанс
напряжений;
6) выполнить
моделирование режима работы цепи при
заданных параметрах и в режиме резонанса
напряжений с помощью системы
схемотехнического моделирования
Electronics Workbench.
3.2. Методические указания к выполнению аналитического расчета
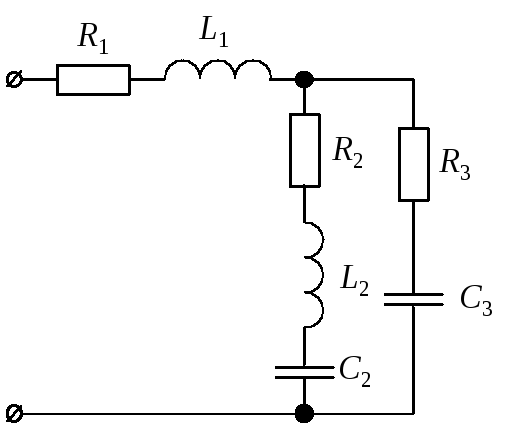
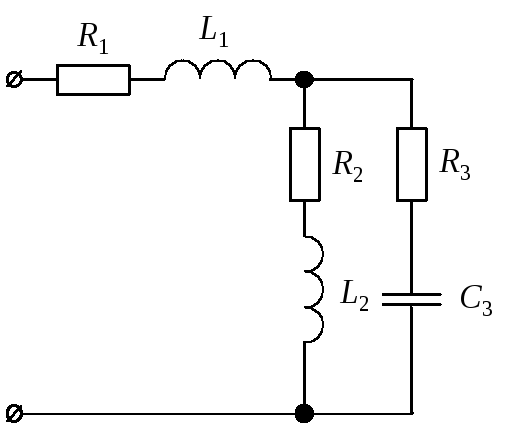
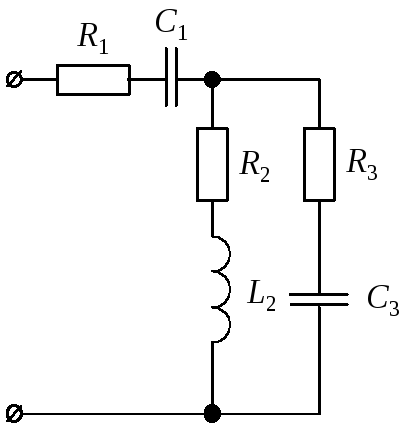
3.2.1. Рассмотрим
порядок расчета однофазной цепи
переменного тока на примере анализа
схемы, представленной на рис. 11, а.
Числовые значения параметров указаны
в табл. 9.
Расчет однофазной
цепи с одним источником выполняют
методом эквивалентных преобразований
(«сворачиванием» – «разворачиванием»)
схемы, который рассмотрен в разд. 1.
Перед выполнением
расчетов необходимо значения всех
параметров привести к международной
системе единиц СИ (1 мГн = 10-3 Гн; 1 мкФ =
10-6 Ф). Расчет ведется символическим
методом с помощью аппарата комплексных
чисел.
 1
1
2
3
4 5
6
7
 EMBED Word.Picture.8
EMBED Word.Picture.8
 EMBED Word.Picture.8
EMBED Word.Picture.8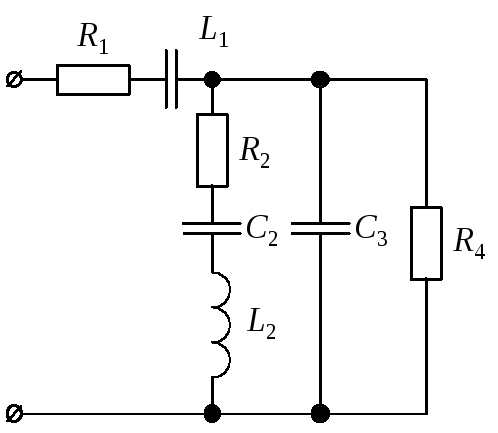
8
9
0
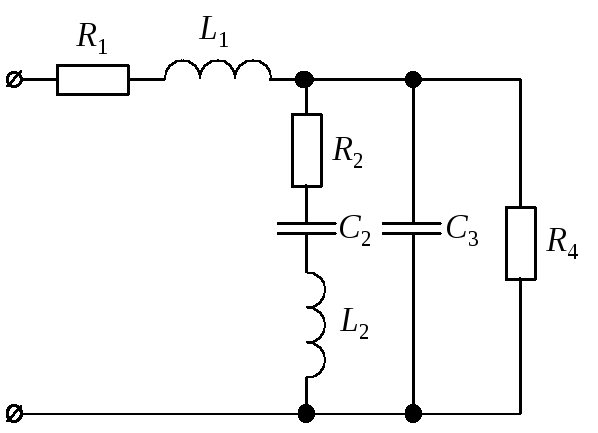
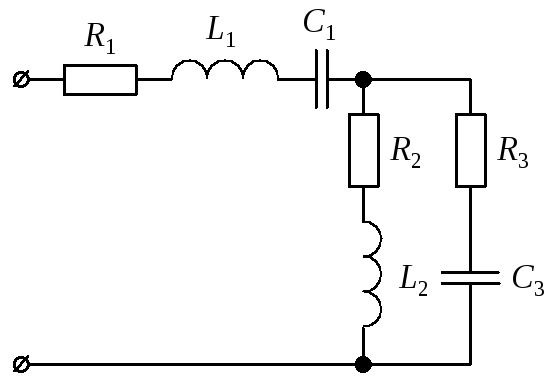
Рис. 10
Таблица 8
Числовые значения
параметров элементов схемы
|
Вариант |
Напряжение, В |
Параметры |
||||||||
|
R1, |
L1, |
С1, |
R2, |
L2, |
С2, |
R3, |
L3, |
С3, |
||
|
0 |
220 |
9 |
15 |
800 |
9 |
17 |
1000 |
5 |
14 |
800 |
|
1 |
127 |
6 |
20 |
200 |
8 |
18 |
800 |
6 |
10 |
700 |
|
2 |
380 |
8 |
25 |
400 |
7 |
20 |
600 |
7 |
8 |
450 |
|
3 |
380 |
5 |
16 |
600 |
6 |
48 |
400 |
8 |
13 |
600 |
|
4 |
127 |
7 |
10 |
500 |
5 |
13 |
500 |
9 |
11 |
500 |
|
5 |
220 |
4 |
14 |
1000 |
12 |
31 |
700 |
10 |
9 |
400 |
|
6 |
220 |
3 |
18 |
700 |
6 |
20 |
900 |
7 |
21 |
300 |
|
7 |
127 |
6 |
12 |
300 |
7 |
16 |
450 |
8 |
18 |
200 |
|
8 |
380 |
5 |
26 |
650 |
6 |
18 |
650 |
6 |
15 |
900 |
|
9 |
127 |
8 |
24 |
480 |
8 |
26 |
800 |
4 |
12 |
600 |
Таблица 9
Числовые значения
параметров элементов схемы для примера
расчета
|
Вариант |
Напряжение, В |
Параметры |
||||
|
R1, |
R2, |
L2, |
С2, |
С3, |
||
|
– |
127 |
5 |
10 |
20 |
200 |
300 |
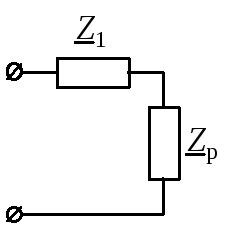
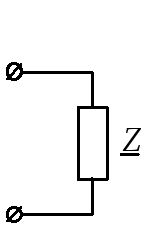
Для расчета полных
комплексных сопротивлений ветвей
определим реактивные составляющие
сопротивлений (рис. 11, б), которые создают
реактивные элементы, находящиеся в
ветвях. Реактивное сопротивление
индуктивного элемента
![]() ,
,
емкостного –![]() ,
,
общее сопротивление ветви, содержащей
индуктивный и емкостный элементы, –![]() ,
,
где![]() рад; f = 50 Гц – частота питающего
рад; f = 50 Гц – частота питающего
напряжения.
Первая ветвь цепи
не содержит реактивного элемента,
поэтому реактивная составляющая
сопротивления ветви будет равна нулю:
![]() Ом.
Ом.
Вторая ветвь
содержит два реактивных элемента. Общее
реактивное сопротивление ветви равно
алгебраической сумме индуктивного и
емкостного сопротивлений. Знак «плюс»
ставится у индуктивного сопротивления,
«минус» – у емкостного:
-
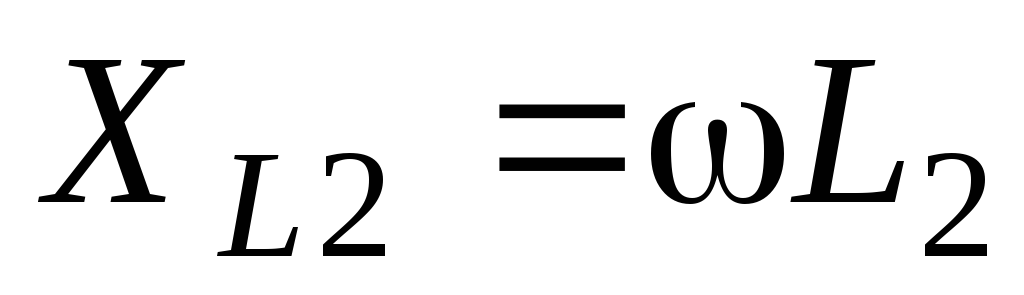 ;
;
(55)
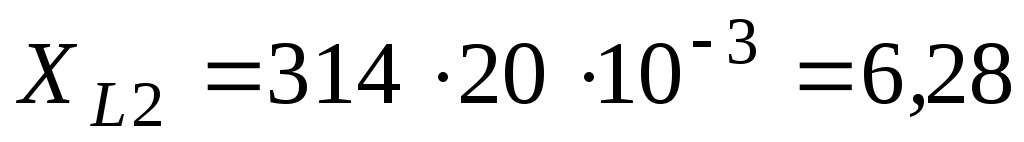 Ом;
Ом;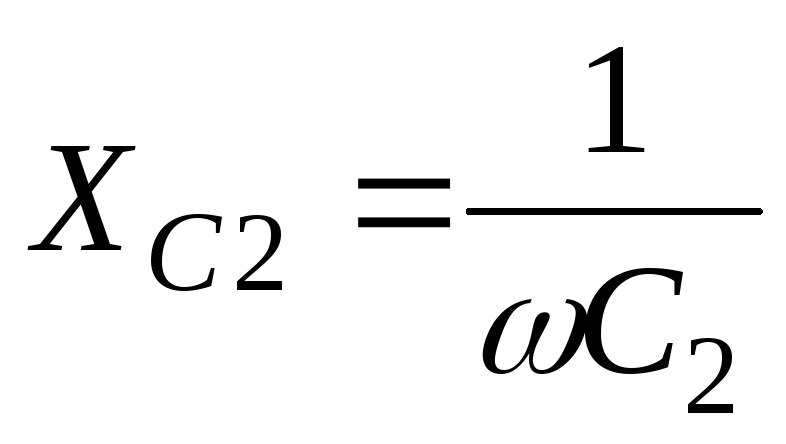 ;
; (56)
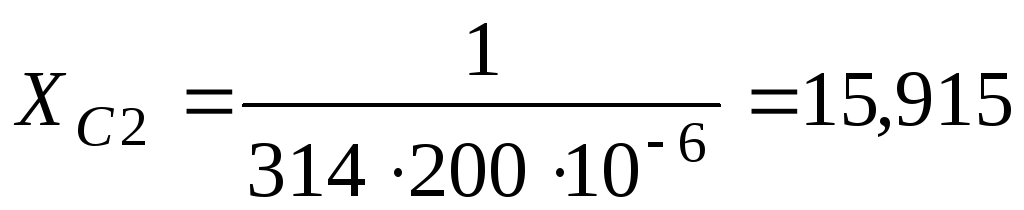 Ом;
Ом;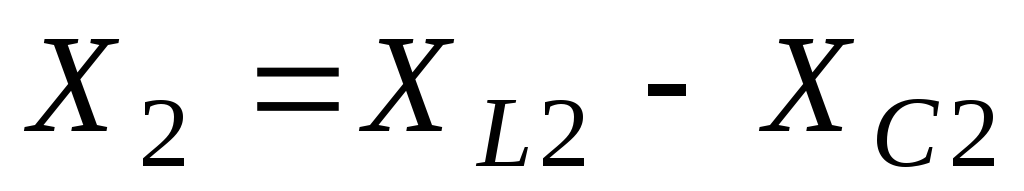 ;
;(57)
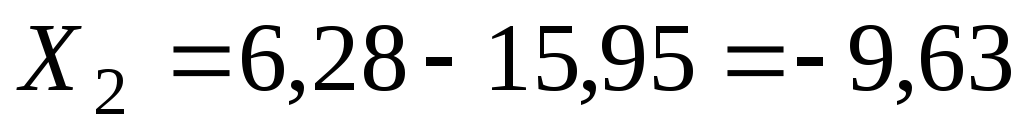 Ом.
Ом.
Знак «минус» перед
общим реактивным сопротивлением ветви
указывает на его емкостный характер.
Этот знак сохраняется и при записи
полного комплексного сопротивления
(см. ниже).
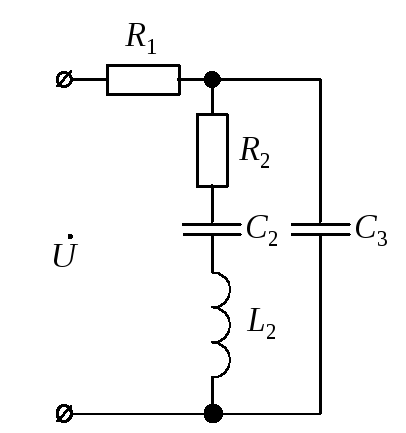
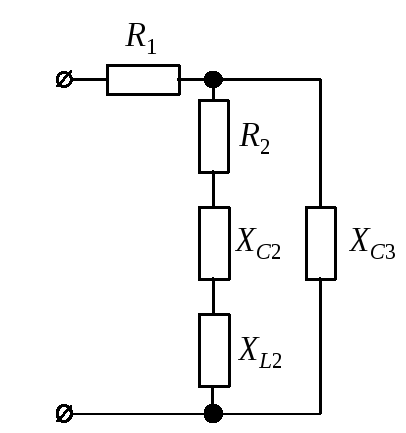
а
б
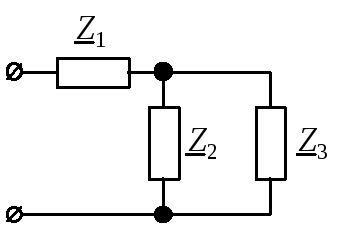
в
г д
Рис. 11
Реактивное
сопротивление третьей ветви
-
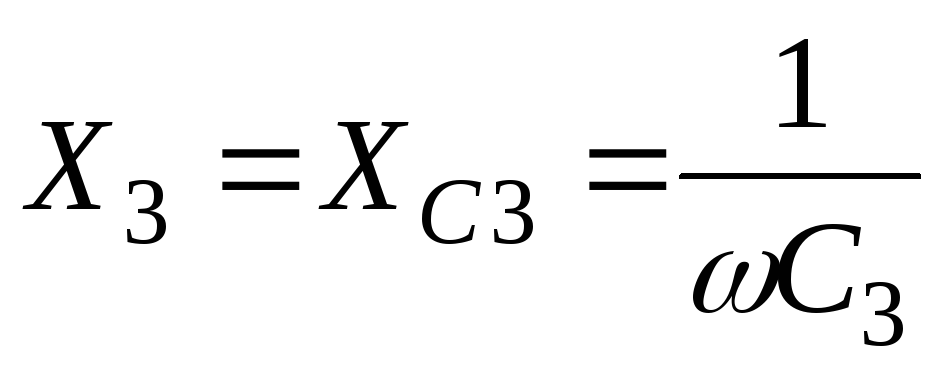 ;
;(58)
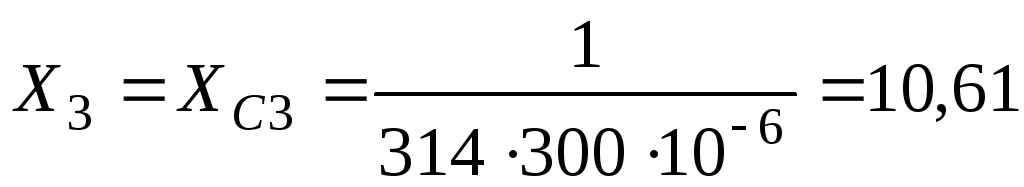 Ом.
Ом.
Полные комплексные
сопротивления ветвей в алгебраической,
показательной и тригонометрической
форме (см. рис. 11) имеют вид:
![]() ,
,
(59)
где R – действительная
составляющая комплексного сопротивления;
Х – мнимая
составляющая комплексного сопротивления;
![]() –модуль комплексного
–модуль комплексного
сопротивления;
![]() –аргумент
–аргумент
комплексного сопротивления, знак
аргумента зависит от знака реактивного
сопротивления ветви.
Для ветвей
рассматриваемой электрической цепи
![]() ;
;
(60)
![]() Ом;
Ом;
![]() ;
;
(61)
![]() Ом;
Ом;
![]() ;
;
(62)
![]() Ом.
Ом.
Эквивалентная
схема с учетом выполненных расчетов
представлена на рис. 11, в.
Последующие
операции «сворачивания» электрической
схемы основаны на рассмотренных в первом
разделе свойствах параллельного и
последовательного соединений. Нужно
помнить, что сложение и вычитание
комплексных чисел выполняется в
алгебраической форме записи, а умножение
и сложение – в показательной, если
расчеты ведутся на калькуляторе.
Заменим параллельный
участок на эквивалентное сопротивление
(рис. 11, г):
![]() ;
;
(63)
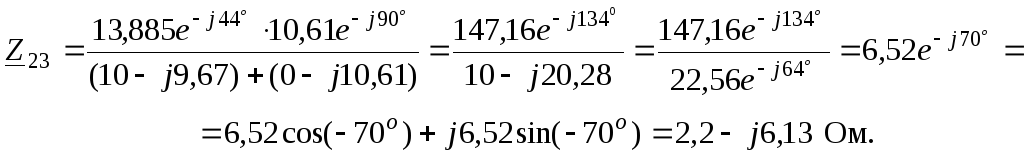
Последовательное
соединение двух сопротивлений преобразуем
в простейшую цепь (рис. 11, д):
![]() ;
;
(64)
![]() Ом.
Ом.
Полученная
элементарная цепь рассчитывается по
закону Ома для цепей переменного тока:
-
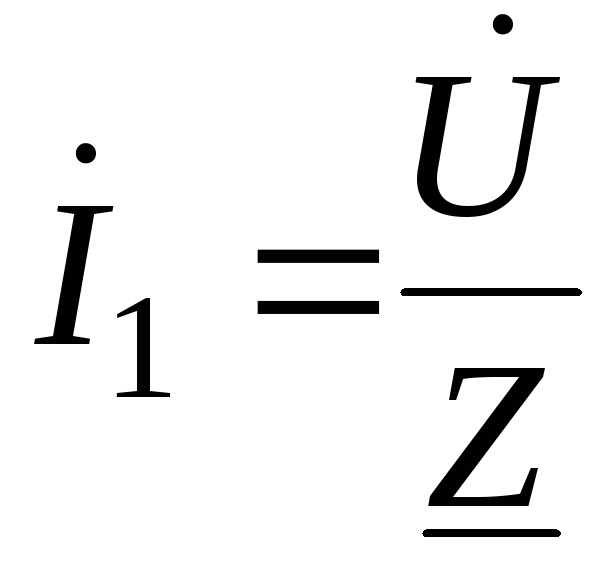 ;
; (65)
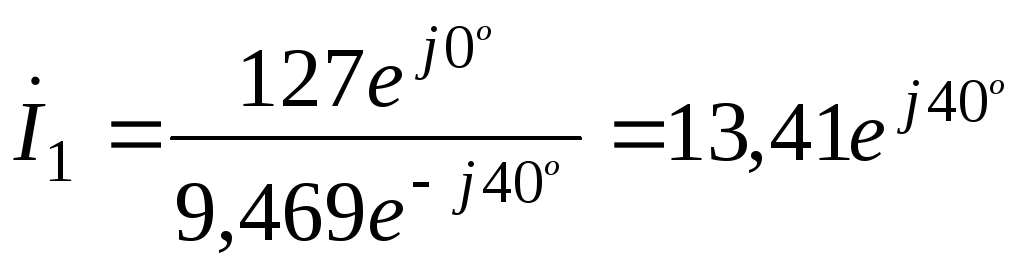
 А.
А.
Напряжение на
параллельном участке
-
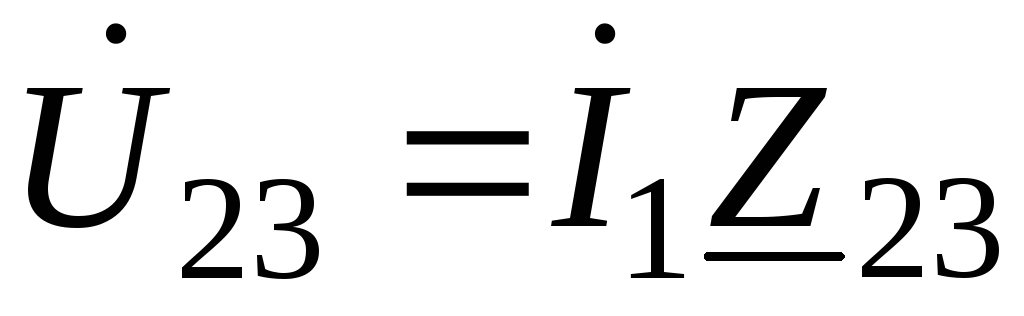 ;
;(66)
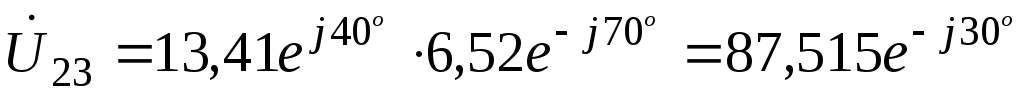 В.
В.
Токи в параллельных
ветвях рассчитываются по выражениям:
-
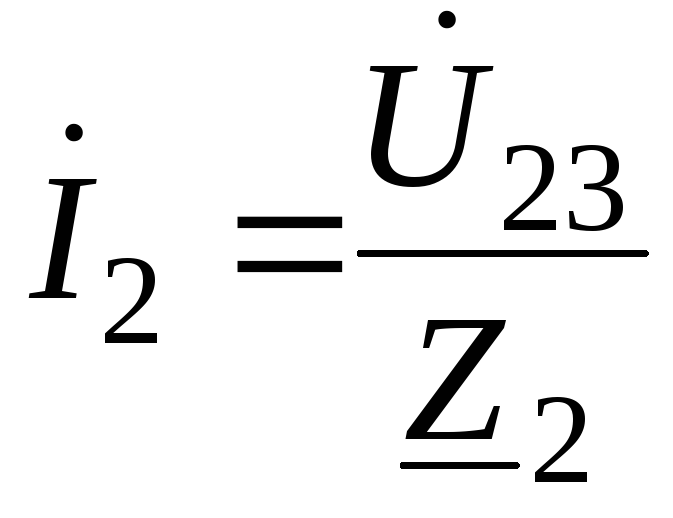 ;
;(67)
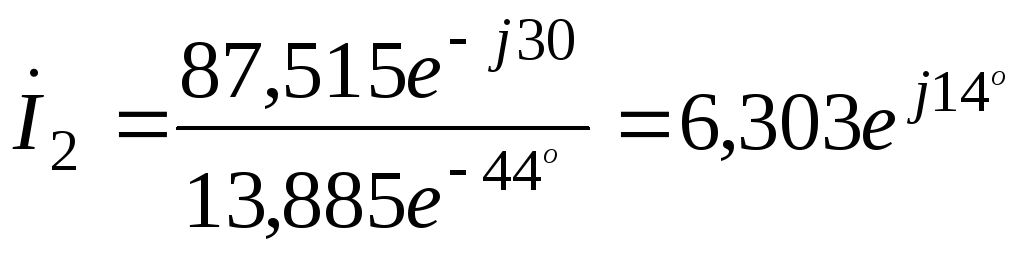 А;
А;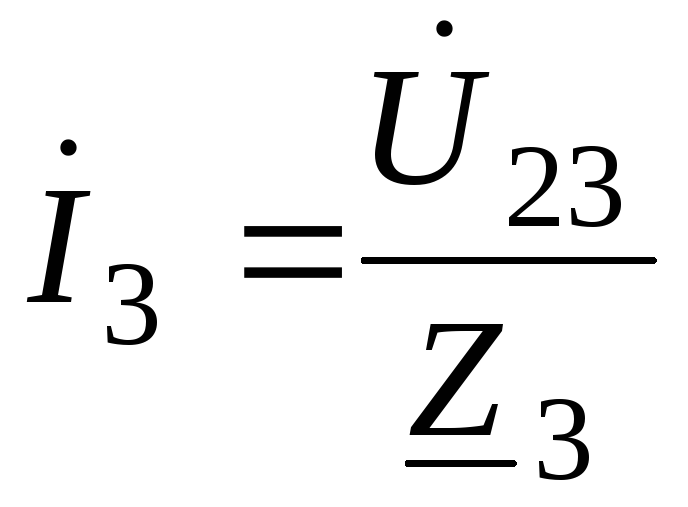 ;
;
(68)
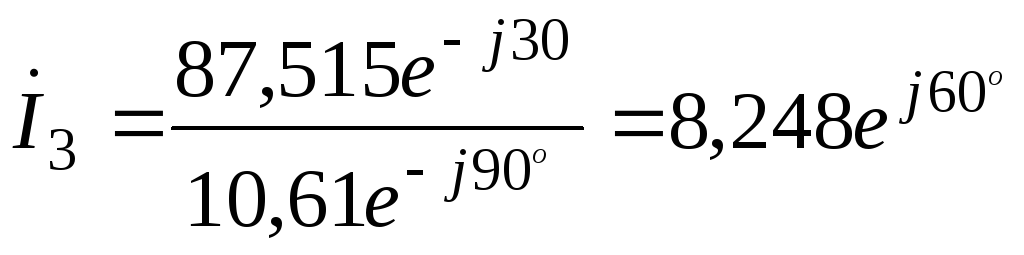 А.
А.
Для построения
векторной диаграммы необходимо также
определить напряжение на неразветвленной
части цепи:
-
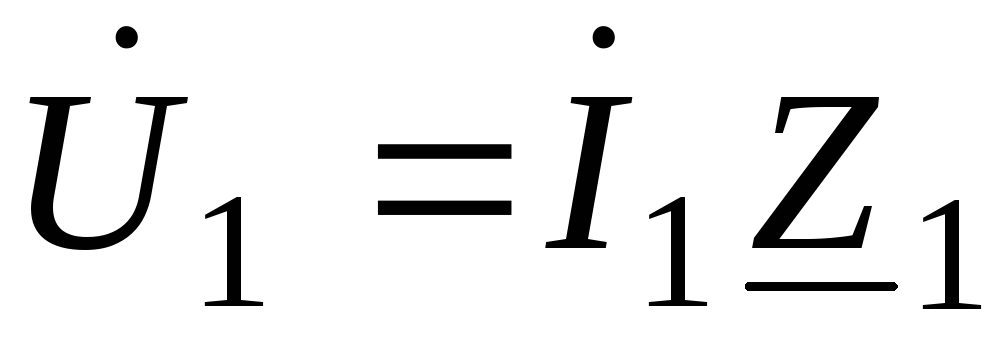 ;
;
(69)
 В.
В.
Расчет однофазной
цепи с помощью математического редактора
Mathсad представлен в прил. 3. Нужно заметить,
что в Mathсad операции с комплексными
числами выполняют в алгебраической
форме записи. Для определения модулей
и аргументов комплексных чисел нужно
выполнить дополнительные команды. Углы
в Mathсad вычисляются в радианах. Для
перехода в градусную меру измерения
углов необходимо дополнительно указать
оператор: «deg» (см. прил. 3).
Результаты расчетов
занесите в графу «Расчет» табл. 10.
Таблица 10
Полученные значения
токов и напряжений для рассматриваемой
цепи
|
Параметр |
Действующие |
Моделирование резонанса |
|
|
расчет |
моделирование |
||
|
I1, |
13,44 |
13,46 |
17,57 |
|
I2, |
6,32 |
6,352 |
8,290 |
|
I3, |
8,26 |
8,300 |
10,83 |
|
U23, |
87,62 |
86,96 |
113,5 |
|
φ, |
40,41 |
40,05 |
0 |
3.2.2. Мгновенные
значения тока в ветвях и напряжения
можно записать с учетом того, что
амплитудное значение тока в
![]() раз больше действующего значения,
раз больше действующего значения,
которое равно модулю полученного
комплексного числа:
|
|
(70) |
|
|
|
(71) |
|
|
|
(72) |
|
|
|
(73) |
|
|
|
(74) |
|
3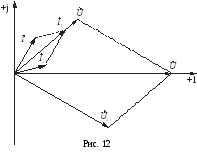
Рис. 12
.2.3. Для проверки правильности
расчетов строят векторную диаграмму
токов и напряжений электрической цепи.
Необходимо выбрать масштаб по току![]() ,
,
А/мм, и по напряжению![]() ,
,
В/мм, построить систему ортогональных
осей комплексной плоскости (+1, +j). Векторы
тока и напряжения строят из начала
координат так, чтобы длина вектора была
равна модулю комплексного числа
(действующему значению) с учетом масштаба,
а угол наклона к действительной оси
(+1) – аргументу комплексного числа
(начальной фазе), причем положительные
углы откладываются против часовой
стрелки, отрицательные – по часовой.
Векторная диаграмма для рассматриваемого
примера приведена на рис. 12.
Если на векторной
диаграмме сумма векторов токов
параллельных ветвей равна вектору тока
в неразветвленной части цепи в соответствии
с первым законом Кирхгофа для узловой
точки, а сумма векторов напряжения –
напряжению источника, то считается, что
диаграмма сходится, и это обязательное,
но не достаточное условие для вывода о
правильности расчетов.
3.2.4. Окончательно
о правильности полученных результатов
можно судить по балансу мощности, который
для цепей переменного тока может быть
составлен для комплексов полной мощности
источника и потребителей:
![]() ,
,
(75)
или для активной
и реактивной мощностей как составляющих.
Выполним проверку по балансу активной
и реактивной мощностей:
|
|
(76) |
где
![]() ,
,![]() – угол сдвига фаз между приложенным
– угол сдвига фаз между приложенным
напряжением и током в неразветвленной
части цепи, он зависит от нагрузки цепи
и равен аргументу полного комплексного
сопротивления![]() ;
;
![]() ;
;
![]() ,
,
где
![]() – действующие значения токов, т. е.
– действующие значения токов, т. е.
модули комплексных чисел, изображающих
соответствующие токи;
![]() ,
,
реактивное сопротивление берется с
учетом знака.
Активная мощность
всегда положительна, реактивная может
быть и отрицательной. Знак «минус»
указывает на то, что реактивная мощность
отдается цепью в сеть, а не потребляется
из сети.
Для рассматриваемого
примера:
![]() Вт;
Вт;
![]() Вт;
Вт;
![]() вар;
вар;
![]()
В результате баланс
активной мощности:
1297 Вт = 1297 Вт,
а реактивной:
– 1105 вар = – 1105
вар.
Баланс активной
и реактивной мощности выполняется,
следовательно, расчет однофазной цепи
выполнен верно.
3.2.5. Резонанс
напряжений в цепи наступает тогда, когда
реактивное сопротивление цепи равно
нулю. Если реактивное сопротивление
цепи носит индуктивный характер (![]() ),
),
то необходимо в неразветвленную часть
цепи добавить емкостное сопротивление,
значение которого равно индуктивной
составляющей сопротивления:
![]() (77)
(77)
![]() .
.
(78)
Если реактивное
сопротивление цепи носит емкостный
характер (![]() ),
),
то необходимо в неразветвленную часть
цепи добавить индуктивное сопротивление:
![]() (79)
(79)
![]() .
.
(80)
В рассматриваемом
примере
![]() ;
;
реактивная составляющая сопротивления
– емкостная. Рассчитаем индуктивное
сопротивление, которое обеспечит в цепи
резонанс напряжений:
-
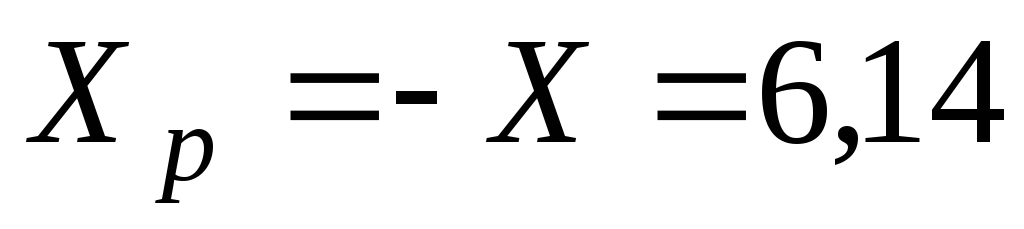 Ом;
Ом;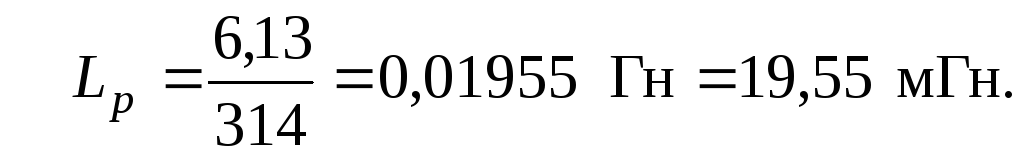
Содержание:
Однофазные электрические цепи переменного тока:
Для получения, передачи и распределения электрической энергии применяются в основном устройства переменного тока: генераторы, трансформаторы, линии электропередачи и распределительные цепи переменного тока.
Постоянный ток, необходимый в некоторых областях народного хозяйства (транспорт, связь, электрохимия и др.), получают выпрямлением переменного тока.
Переменным электрическим током называют ток, периодически изменяющийся по величине и направлению.
Основное достоинство переменного тока заключается в возможности трансформировать напряжение. Кроме того, электрические машины переменного тока надежней в работе, проще по устройству и эксплуатации.
Говоря о переменном токе, обычно имеют в виду синусоидальный переменный ток, т. е. ток, изменяющийся по синусоидальному закону. При синусоидальном токе ЭДС электромагнитной индукции, самоиндукции и взаимоиндукции изменяются по синусоидальному закону.
Синусоидальный переменный ток проходит в замкнутой линейной электрической цепи под действием синусоидальной ЭДС.
Рассмотрим получение синусоидальной ЭДС. Если в однородном магнитном поле с индукцией В равномерно со скоростью V вращается рамка (рис. 10.1), то в каждой активной стороне этой рамки длиной 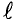
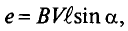
где а – угол, под которым активный проводник рамки пересекает магнитное поле (угол между 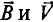 ), или угол поворота рамки относительно нейтральной плоскости
), или угол поворота рамки относительно нейтральной плоскости 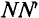 как углы со взаимно перпендикулярными сторонами.
как углы со взаимно перпендикулярными сторонами.
Плоскость 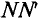 называется нейтральной, т. к. ЭДС в рамке, расположенной в этой плоскости, равна нулю (а = 0, следовательно, sin а = 0).
называется нейтральной, т. к. ЭДС в рамке, расположенной в этой плоскости, равна нулю (а = 0, следовательно, sin а = 0).
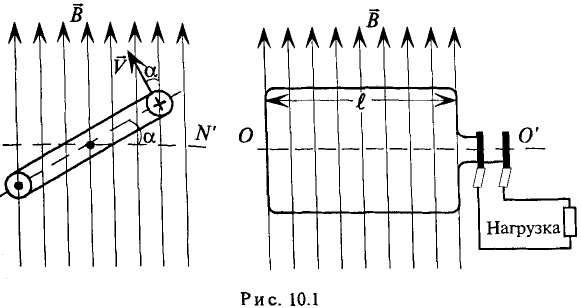
как 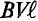 — величина постоянная по условию, то е пропорциональна sin а, т. е. ЭДС в этой рамке, при вращении ее вокруг оси изменяется по синусоидальному закону. Если к этой рамке включить нагрузку (потребитель), то в замкнутой цепи (рис. 10.1) идет ток, который, как и ЭДС, изменяется по синусоидальному ну. Поэтому такой ток и называется синусоидальным.
— величина постоянная по условию, то е пропорциональна sin а, т. е. ЭДС в этой рамке, при вращении ее вокруг оси изменяется по синусоидальному закону. Если к этой рамке включить нагрузку (потребитель), то в замкнутой цепи (рис. 10.1) идет ток, который, как и ЭДС, изменяется по синусоидальному ну. Поэтому такой ток и называется синусоидальным.
Синусоидальная ЭДС 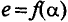 изображена на графике рис. 10.2. график принято называть «волновая диаграмма». (Если изменяющаяся величина изображена в зависимости от времени то ее называют «временная диаграмма».) На этой диаграмме синусоида ограничивает величины ЭДС (ординаты) при раз-личных углах поворота рамки относительно нейтральной плоскости NN”. Как видно, синусоидальная ЭДС изменяется по величине и направлению.
изображена на графике рис. 10.2. график принято называть «волновая диаграмма». (Если изменяющаяся величина изображена в зависимости от времени то ее называют «временная диаграмма».) На этой диаграмме синусоида ограничивает величины ЭДС (ординаты) при раз-личных углах поворота рамки относительно нейтральной плоскости NN”. Как видно, синусоидальная ЭДС изменяется по величине и направлению.
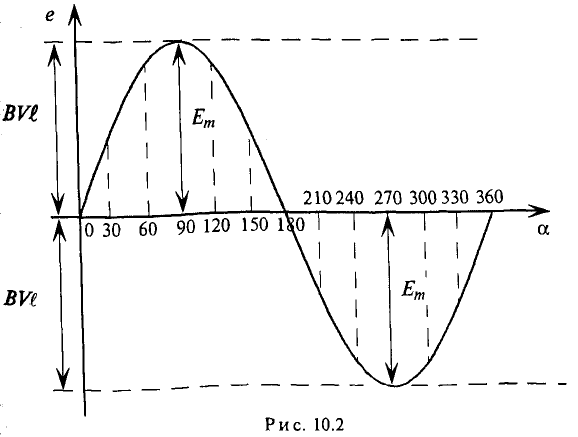
Величины, характеризующие синусоидальную ЭДС
Амплитуда — это максимальное значение периодически изменяющейся величины.
Обозначаются амплитуды прописными буквами с индексом m, т. е. 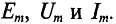
Нетрудно видеть (рис. 10.2), что ЭДС достигает своих амплитудных значений тогда, когда рамка повернется на угол а = 90° или на угол а = 270°, так как 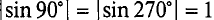 . Следовательно,
. Следовательно, 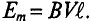
Тогда 
Период – это время, в течение которого переменная величина делает полный цикл своих изменений, после чего изменения повторяются в той же последовательности.
Обозначается период буквой Т и измеряется в секундах, с (сек) т.е. 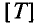 = с.
= с.
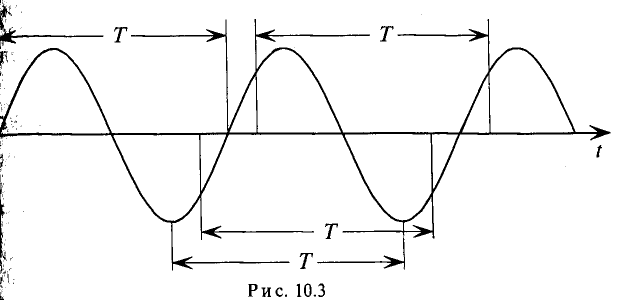
Значение ЭДС через каждый период определяется следующим равенством (рис. 10.3):
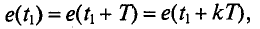
где к – целое число.
На рис. 10.3 изображена временная диаграмма синусоидальной ЭДС при вращении рамки в магнитном поле.
Частота – число периодов в единицу времени, т. е. величина, обратная периоду.
Обозначается частота буквой 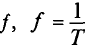 , и измеряется в герцах (Гц):
, и измеряется в герцах (Гц):
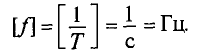
Стандартной частотой в электрических сетях России является частота 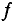 = 50 Гц. Для установок электронагрева пользуются частотами
= 50 Гц. Для установок электронагрева пользуются частотами 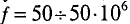 Гц (
Гц (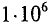 Гц = 1 МГц – мегагерц).
Гц = 1 МГц – мегагерц).
При частоте 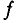 =50 Гц, т.е. 50 периодов в секунду, период
=50 Гц, т.е. 50 периодов в секунду, период
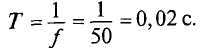
Угловая частота (угловая скорость) характеризуется углом поворотом рамки в единицу времени.
Обозначается угловая частота буквой 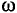 (омега):
(омега):

Измеряется угловая частота в единицах радиан в секунду, так как угол измеряется в радианах (рад).
Так, время одного периода Т рамка повернется на угол 360° = рад. Следовательно, угловую частоту можно выразить следующим образом:

Мгновенное значение — это значение переменной величины в й конкретный момент времени.
Мгновенные значения обозначаются строчными буквами..
Из выражения (10.2) следует, что угол поворота рамки 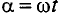 , мгновенные значения синусоидальных величин можно записать так:
, мгновенные значения синусоидальных величин можно записать так:
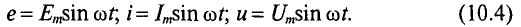
Таким образом, любая синусоидальная величина характеризуется амплитудой и угловой частотой, которые являются постоянными для данной синусоиды. Следовательно, по формулам (10.4) можно определить синусоидальную величину в любой конкретный момент времени t, если известны амплитуда и угловая частота.
Фаза и сдвиг фаз
Если в магнитном поле вращаются две жестко скрепленные между собой под каким-то углом одинаковые рамки (рис. 10.4а), т.е. амплитуды ЭДС 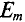 и угловые частоты со их одинаковы, то мгновенное значение их ЭДС можно записать в виде
и угловые частоты со их одинаковы, то мгновенное значение их ЭДС можно записать в виде
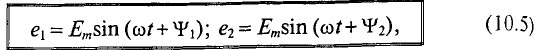
где 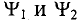 — углы, определяющие значения синусоидальных величин
— углы, определяющие значения синусоидальных величин 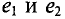 в начальный момент времени (t = 0), т.е.
в начальный момент времени (t = 0), т.е.
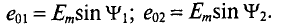
Поэтому эти углы 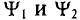 называют начальными фазами синусоид.
называют начальными фазами синусоид.
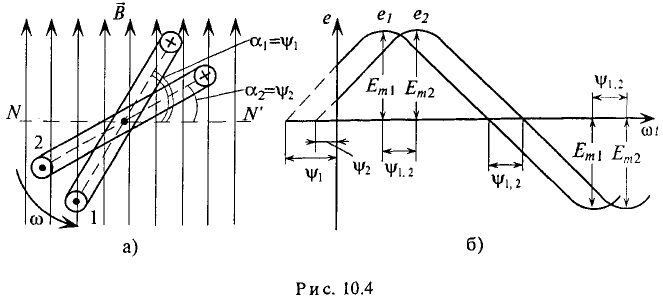
Начальные фазы 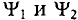 этих ЭДС различны.
этих ЭДС различны.
Таким образом, согласно (10.5) каждая синусоидальная величина характеризуется амплитудой 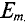 , угловой частотой со и начальной фазой
, угловой частотой со и начальной фазой  . Для каждой синусоиды эти величины
. Для каждой синусоиды эти величины 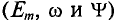 являются постоянными. В выражениях (10.4) начальные фазы
являются постоянными. В выражениях (10.4) начальные фазы  синусоид равны нулю (
синусоид равны нулю ( = 0).
= 0).
Величина 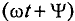 называется фазой синусоиды.
называется фазой синусоиды.
Разность начальных фаз двух синусоидальных величин одинаковой частоты определяет угол сдвига фаз этих величин:

При вращении против часовой стрелки (рис. 10.4а) ЭДС в первой рамке достигает амплитудного и нулевого значения раньше, чем во второй, т. е. 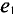 опережает по фазе
опережает по фазе 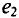 или
или 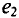 отстает по фазе
отстает по фазе 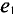 (рис. 10.46). Угол сдвига фаз
(рис. 10.46). Угол сдвига фаз 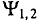 показывает, на какой угол синусоидальная величина опережает или отстает от другой, достигает своих амплитудных и нулевых значений раньше позже).
показывает, на какой угол синусоидальная величина опережает или отстает от другой, достигает своих амплитудных и нулевых значений раньше позже).
Две синусоидальные величины одинаковой частоты, достигаю-одновременно своих амплитудных (одного знака) и нулевых сечений, считаются совпадающими по фазе (рис. 10.5а).
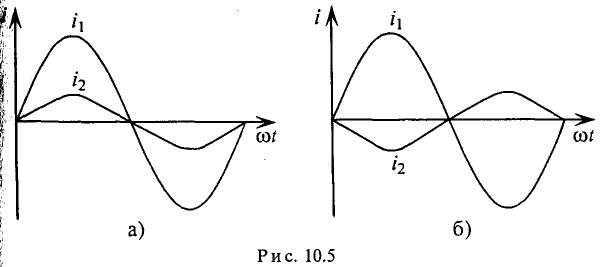
Если две синусоиды одинаковой частоты достигают одновременно своих нулевых и амплитудных значений разных знаков (рис. 10.56), то они находятся в противофазе.
Время, на которое одна синусоидальная величина опережает и отстает от другой, характеризует время сдвига фаз 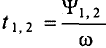 , которое можно выразить через период Т и частоту
, которое можно выразить через период Т и частоту 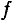 синусоиды следующим образом:
синусоиды следующим образом:
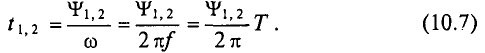
Среднее и действующее значения переменного тока
Кроме амплитудных и мгновенных значений переменный ток, напряжение, ЭДС характеризуются еще средними и действующими (эффективными) значениями.
Среднее значение переменного тока
Среднее значение переменного тока равно величине такого постоянного тока, при котором через поперечное сечение провод-проходит то же количество электричества Q, что и при переменном токе.
Таким образом, среднее значение переменного тока эквивалентно постоянному току по количеству электричества Q, проходящему через поперечное сечение проводника в определенный промежуток времени.
Средние значения переменных величин обозначаются прописными буквами с индексом «с», т. е. 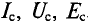 .
.
Если ток изменяется по синусоидальному закону, то за половину периода через поперечное сечение проводника проходит определенное количество электричества Q в определенном направлении, а за вторую половину периода через то же сечение проходит то же количество электричества в обратном направлении. Таким образом, среднее значение синусоидального тока за период равно нулю, т. е. 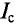 = 0.
= 0.
Поэтому для синусоидального переменного тока определяется его среднее значение за половину периода Т/2, т. е.
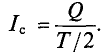
Из выражения (2.1) значение переменного тока 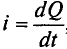 , откуда
, откуда 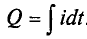 . Следовательно, среднее значение синусоидального тока
. Следовательно, среднее значение синусоидального тока 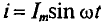 с начальной фазой
с начальной фазой 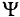 = 0 за полупериод определяется (рис. 10.6) выражением
= 0 за полупериод определяется (рис. 10.6) выражением
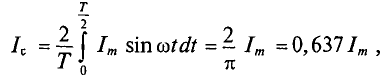
где 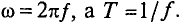
Графически среднее за полупериод значение синусоидального тока равно высоте прямоугольника с основанием, равным Т/2, и площадью, равной площади, ограниченной кривой тока и осью абсцисс за половину периода (рис. 10.6).
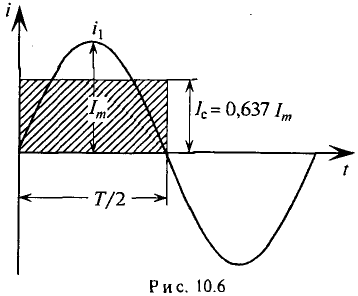
Под средним значением переменной величины понимают постоянную составляющую этой величины.
Средние значения синусоидального напряжения и ЭДС за полупериод можно определить по аналогии с током.
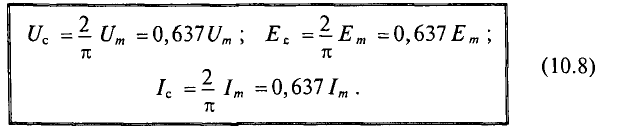
Действующее значение переменного тока
Действующее (или эффективное) значение переменного тока — значение переменного тока, эквивалентное постоянному току тепловому действию.
Действующее значения переменных величин обозначается прочими буквами без индексов: I, U, Е.
Действующее значение переменного тока I равно величине такого постоянного тока, которое за время, равное одному периоду первого тока Т, выделит в том же сопротивлении R такое же количество тепла, что и переменный ток i:
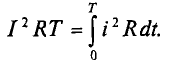
Откуда действующее значение переменного тока
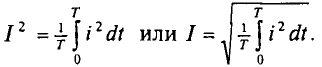
Если переменный ток изменяется по синусоидальному закону с начальной фазой, равной нулю, т.е. 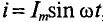 , то действующее сечение такого синусоидального тока будет равно
, то действующее сечение такого синусоидального тока будет равно
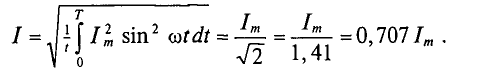
Действующее значение синусоидального тока в 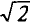 =1 ,41 раза меньше его амплитудного значения. Так же можно определить действующие значения синусоидального напряжения и ЭДС.
=1 ,41 раза меньше его амплитудного значения. Так же можно определить действующие значения синусоидального напряжения и ЭДС.
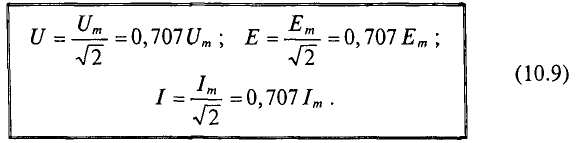
Номинальные значения тока и напряжения в электрических цепей и устройствах выражаются их действующими значениями.
Так, например, стандартные напряжения электрических сетей U= 127 В или U = 220 В выражают действующие значения этих напряжений. А изоляцию необходимо рассчитывать на амплитудное значение этих напряжений, т. е.
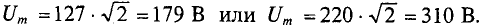
При расчете цепей переменного тока и их исследованиях чаще всего пользуются действующими (эффективными) значениями тока, напряжения и ЭДС.
На шкалах измерительных приборов переменного тока указывается действующие значение переменного тока или напряжения.
Именно действующие значения тока, напряжения и ЭДС указываются в технической документации, если нет специальных оговорок.
Коэффициенты формы и амплитуды
Отклонения кривых тока, напряжения и ЭДС от синусоиды характеризуются коэффициентами формы 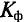 и амплитуды
и амплитуды 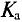 .
.
Коэффициент формы 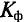 определяется отношением действующего значения переменной величины к ее среднему значению:
определяется отношением действующего значения переменной величины к ее среднему значению:

Коэффициент формы необходимо учитывать при проектировании и изучении выпрямительных устройств и электрических машин.
Для синусоидальных величин коэффициент формы будет равен
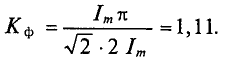
Коэффициент амплитуды 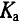 определяется отношением амплитудного значения переменной величины к ее действующему значению:
определяется отношением амплитудного значения переменной величины к ее действующему значению:

Для синусоидальных величин коэффициент амплитуды равен
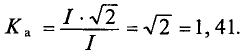
Чем больше коэффициент формы и коэффициент амплитуды отличается от значений 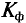 = 1,11 и
= 1,11 и 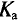 = 1,41, тем больше рассматриваемая кривая отличается от синусоиды. Так, например, если
= 1,41, тем больше рассматриваемая кривая отличается от синусоиды. Так, например, если 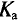 = 1,41, то исследуемая кривая имеет более острую форму, чем синусоида, а если
= 1,41, то исследуемая кривая имеет более острую форму, чем синусоида, а если 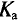 < 1,41, то более тупую.
< 1,41, то более тупую.
График прямоугольной формы имеет коэффициент амплитуды 1.
Векторные диаграммы
Для наглядности синусоидальные величины изображают векторами, вращающимися против часовой стрелки со скоростью, равной угловой частоте со этих синусоид. Так как эти векторы изображают синусоиды в начальный момент времени (t = 0), то они подвижны. Длина вектора в выбранном масштабе определяется амплитудой синусоиды, а угол поворота вектора против часовой стрелки относительно положительного направления оси абсцисс начальной фазе синусоиды. Таким образом, вектор учитывают все значения, характеризующие синусоидальную величину – амплитуду, угловую частоту и начальную фазу, пример, три синусоидальные ЭДС одинаковой частоты
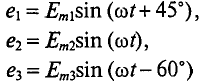
можно изобразить векторами (рис. 10.7).
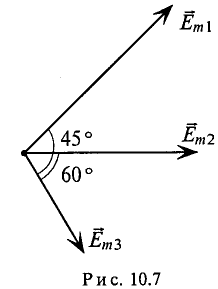
Совокупность нескольких векторов, изображающих синусоидальные величины одинаковой частоты в начальный момент времени, называется векторной диаграммой.
На векторной диаграмме (рис. 10.7) на-ю видны величины синусоид (ампли-), их начальные фазы и углы сдвига между ними. Очевидно, наибольшую амплитуду имеет ЭДС 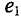 , а наименьшую ЭДС
, а наименьшую ЭДС 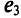 ЭДС
ЭДС 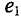 опережает по фазе
опережает по фазе 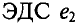 угол 45°, а ЭДС
угол 45°, а ЭДС 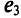 отстает от ЭДС
отстает от ЭДС 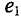 по фазе на угол 105° и т. д. Начало отсчета времени можно выбирать произвольно, т. е. один из векторов векторной диаграммы направляется произвольно, а остальные векторы (соответствующих длин) изображаются отношению к нему под углами, равными углам сдвига фаз между ними (рис. 10.8). При указанном ЭДС могут быть записаны так:
по фазе на угол 105° и т. д. Начало отсчета времени можно выбирать произвольно, т. е. один из векторов векторной диаграммы направляется произвольно, а остальные векторы (соответствующих длин) изображаются отношению к нему под углами, равными углам сдвига фаз между ними (рис. 10.8). При указанном ЭДС могут быть записаны так:

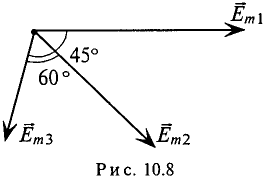
При этом амплитуды ЭДС и углы сдвига фаз остаются неизменными (как и угловая частота), а меняются только начальные фазы синусоид, изображенных на векторной диаграмме (рис. 10.7). В расчетах, если специально не оговорено, начальные фазы не играют роли.
Сложение синусоидальных величин
Сложение и вычитание синусоидальных величин одинаковой частоты можно осуществлять аналитически и графически. В результате такого сложения (вычисления) получается синусоида с той же частотой, с определенной амплитудой и определенной начальной фазой.
Аналитическое сложение предусматривает сложение мгновенных значений синусоидальных величин, выраженных аналитически, т. е.
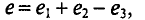
где 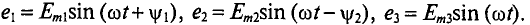
Тогда
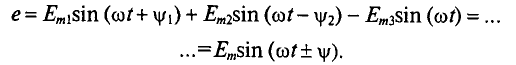
Математический анализ позволяет определить суммарную ЭДС е и ее аналитическое выражение.
Графическое сложение можно осуществлять по: 1) волновым (временном) диаграммам и 2) векторным диаграммам.
1. Графическое сложение по временным диаграммам (рис. 10.9) осуществляется следующим образом: ординаты суммарной синусоиды определяются сложением ординат слагаемых синусоид в различные моменты времени.
Как видно, в рассматриваемом примере амплитуда суммарной синусоиды не равна алгебраической сумме амплитуд слагаемых синусоид. Начальная фаза суммарной синусоиды также не является результатом арифметических действий, т.е. по временным диаграммам производятся только графические действия.
2. Графическое сложение по векторным диаграммам осуществляется в следующей последовательности. Прежде всего необходимо построить векторную диаграмму слагаемых синусоидальных величин (рис. 10.10а).
Определение вектора, изображающего суммарную синусоиду, осуществляется сложением векторов слагаемых синусоид по правилу многоугольника, т. е. из какой-либо точки О изображают вектор, соответствующий первой слагаемой синусоиде 10.106), из конца этого вектора изображают вектор, соответствующий второй слагаемой синусоиде, и т.д.
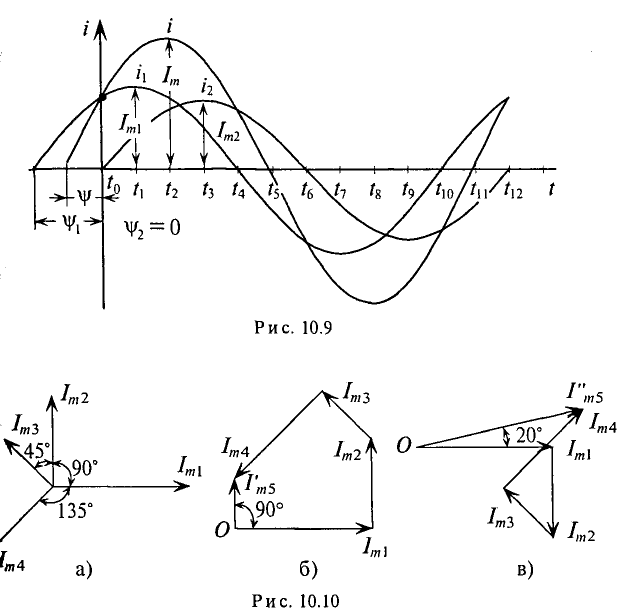
Вектор, соответствующий суммарной синусоиде, проводят из и О к концу последней слагаемой синусоиды.
Тот вектор (рис. 10.106), в масштабе изображения слагаемых синусоид, соответствует амплитуде суммарной синусоиды 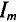 . Угол поворота этого вектора против часовой стрелки относительно положительного направления оси абсцисс соответствует положительному значению начальной фазы
. Угол поворота этого вектора против часовой стрелки относительно положительного направления оси абсцисс соответствует положительному значению начальной фазы 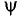 суммарной синусоиды, угловая частота суммарной синусоиды равна частоте слагаемых синусоид.
суммарной синусоиды, угловая частота суммарной синусоиды равна частоте слагаемых синусоид.
Вычитание синусоидальной величины равносильно умножение этой величины на отрицательную единицу (—1), что соответствует повороту вектора этой величины на 180″ (рис. 10.10 в).
Сложение и вычитание синусоидальных величин по векторный диаграммам рассматривается в примере 10.1.
Пример 10.1
Заданы мгновенные значения четырех токов:

Определить:
1)суммарный ток при условии 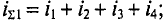
2)суммарный ток при условии 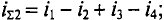
3)частоту f всех синусоид.
Решение
Для построения векторной диаграммы слагаемых токов задаются определенным масштабом токов 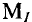 (например,
(например, 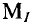 = 1 А/см). В этом масштабе построена векторная диаграмма токов на рис. 10.10а.
= 1 А/см). В этом масштабе построена векторная диаграмма токов на рис. 10.10а.
1. Для определения суммарного тока производится сложение векторов по правилу многоугольника (рис. 10.106). Суммарный ток в результате сложения будет равен 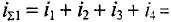
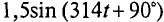 . Амплитуда суммарного тока
. Амплитуда суммарного тока 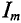 = 1,5 А определена из многоугольника в выбранном масштабе, а начальная фаза его измерена транспортиром
= 1,5 А определена из многоугольника в выбранном масштабе, а начальная фаза его измерена транспортиром 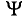 = 90°.
= 90°.
2. Построение многоугольника для заданного условия показано на рис. 10.10в. Из многоугольника определяется результирующий ток
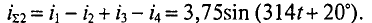
3. Частота слагаемых и результирующих токов будет равна
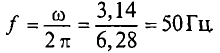
В заключение можно сделать вывод, что самым удобным и, следовательно, распространенным методом сложения синусоидальных величин является метод графического сложения по векторным диаграммам. Этот метод и будет использован при расчете электрических цепей однофазного и трехфазного тока, изменяющегося по синусоидальному закону.
Так как действующие значения синусоидальных величин пропорциональны их амплитудным значениям (см. (10.9)), то вектор, отражающий в определенном масштабе амплитудное значение, в этом масштабе представляет действующее значение той же вены. Исходя из этого, в дальнейшем на векторных диаграммах будут изображаться векторы, в определенном масштабе представляющие не амплитудное, а действующее значение синусоидальной вены, которое чаще всего используется при расчетах цепей переменного тока.
- Однофазные цепи синусоидального тока
- Законы и правила Кирхгофа для электрических цепей
- Линии с распределенными параметрами
- Идеализированные пассивные элементы
- Закон Ома для замкнутой цепи
- Энергия и мощность электрического тока
- Закон Джоуля — Ленца для тока
- Режимы работы электрических цепей
Мощность ток напряжение, общие сведения
Электроэнергия давно используется человеком для удовлетворения своих потребностей, но она невидима, не воспринимается органами чувств, потому сложна для понимания. Мощность ток напряжение, все эти характеристики электроэнергии исследованы известными учеными, которые дали им определения и описали математическими методами взаимные связи между ними.
Мощность ток напряжение сопротивление
Так же следует помнить, на величину электрического сопротивления влияет несколько факторов:
- строение вещества, определяющее наличие свободных электронов в проводнике и влияющее на удельное сопротивление
- площадь поперечного сечения и длина токовода
- температура
В приведенной таблице показаны общие соотношения для цепей постоянного и переменного тока, которые можно применять для анализа работы схем электроснабжения.
Расчёт сечения питающего кабеля и проводки
Для обеспечения безопасности при эксплуатации бытовых электроприборов необходимо верно вычислить сечение питающего кабеля и проводки. Поскольку ошибочно выбранное сечение жил кабеля способно привести к перегреву провода, плавление его изоляции и в итоге, возгоранию, из-за короткого замыкания.
Мощность ток напряжение, удобная шпаргалка
Основным параметром, по которому производят расчет сечения провода, является его продолжительная допустимая токовая нагрузка. Т.е, это такая номинальная величина тока, которую проводник способен через себя пропускать на протяжении длительного времени. Для определения величины номинального тока, необходимо знать приблизительную мощность всех подключаемых электроприборов и оборудования в квартире.
И так, что мы имеем:
- От значения величины тока зависит выбор питающего кабеля (провода), по которому могут быть подключены приборы энергопотребления к сети
- Зная напряжение электрической сети и полную нагрузку электроприборов, можно по формуле вычислить силу тока, который потребуется пропускать по проводнику(проводу, кабелю). По его величине выбирают площадь сечения жил.
Расчет тока, выполняем самостоятельно
Если известны электро-потребители в квартире или доме, необходимо выполнить несложные расчёты, чтобы правильно смонтировать схему электроснабжения.
Аналогичные расчёты выполняются для производственных целей: определения необходимой площади сечения жил кабеля при осуществлении подключения промышленного оборудования (различных промышленных электрических двигателей и механизмов).
Мощность ток напряжение, расчёты для однофазной сети 220 В
Сила тока I (в амперах, А) подсчитывается по формуле:
I = P / U,
где
P – электрическая полная нагрузка (обязательно указывается в техническом паспорте устройства), Вт (ватт)
U – напряжение электрической сети, В (вольт)
Ниже в таблице представлены величины нагрузки типичных бытовых электроприборов и потребляемый ими ток (для напряжения 220 В).
| Электроприбор | Потребляемая мощность, Вт | Сила тока, А |
| Стиральная машина | 2000 – 2500 | 9,0 – 11,4 |
| Джакузи | 2000 – 2500 | 9,0 – 11,4 |
| Электроподогрев пола | 800 – 1400 | 3,6 – 6,4 |
| Стационарная электрическая плита | 4500 – 8500 | 20,5 – 38,6 |
| СВЧ печь | 900 – 1300 | 4,1 – 5,9 |
| Посудомоечная машина | 2000 — 2500 | 9,0 – 11,4 |
| Морозильники, холодильники | 140 — 300 | 0,6 – 1,4 |
| Мясорубка с электроприводом | 1100 — 1200 | 5,0 — 5,5 |
| Электрочайник | 1850 – 2000 | 8,4 – 9,0 |
| Электрическая кофеварка | 6з0 — 1200 | 3,0 – 5,5 |
| Соковыжималка | 240 — 360 | 1,1 – 1,6 |
| Тостер | 640 — 1100 | 2,9 — 5,0 |
| Миксер | 250 — 400 | 1,1 – 1,8 |
| Фен | 400 — 1600 | 1,8 – 7,3 |
| Утюг | 900 — 1700 | 4,1 – 7,7 |
| Пылесос | 680 — 1400 | 3,1 – 6,4 |
| Вентилятор | 250 — 400 | 1,0 – 1,8 |
| Телевизор | 125 — 180 | 0,6 – 0,8 |
| Радиоаппаратура | 70 — 100 | 0,3 – 0,5 |
| Приборы освещения | 20 — 100 | 0,1 – 0,4 |
Различные потребители электроэнергии подключаются через соответствующие автоматы к электросчётчику и далее общему автомату, который должен быть рассчитан на нагрузку приборов, которыми будет оборудована квартира. Провод, который подводит питание также должен удовлетворять нагрузке энергопотребителей.
Как рассчитать ток защитного автомата
Для группы розеток, предназначенных для питания бытовых электроприборов на кухне, необходимо подобрать защитный автоматический выключатель. Мощности приборов по паспортным данным составляют 2,0, 1,5 и 0,6 кВт.
Решение. В квартире используется однофазная переменная сеть 220 вольт. Общая мощность всех приборов, подключенных в работу одновременно, составит 2,0+1,5+0,6=4,1 кВт=4100 Вт.
По формуле I = P / U определим общий ток группы потребителей: 4100/220=18,64 А.
Ближайший по номиналу автоматический выключатель имеет величину срабатывания 20 ампер. Его и выбираем. Автомат меньшего значения на 16 А будет постоянно отключаться от перегрузки.
Ниже приводится таблица для скрытой проводки при однофазной схеме подключения квартиры для подбора провода при напряжении 220 В
| Сечение жилы провода, мм2 | Диаметр жилы проводника, мм | Медные жилы | Алюминиевые жилы | ||
| Ток, А | Мощность, Вт | Ток, А | Мощность, кВт | ||
| 0,50 | 0,80 | 6 | 1300 | ||
| 0,75 | 0,98 | 10 | 2200 | ||
| 1,00 | 1,13 | 14 | 3100 | ||
| 1,50 | 1,38 | 15 | 3300 | 10 | 2200 |
| 2,00 | 1,60 | 19 | 4200 | 14 | 3100 |
| 2,50 | 1,78 | 21 | 4600 | 16 | 3500 |
| 4,00 | 2,26 | 27 | 5900 | 21 | 4600 |
| 6,00 | 2,76 | 34 | 7500 | 26 | 5700 |
| 10,00 | 3,57 | 50 | 11000 | 38 | 8400 |
| 16,00 | 4,51 | 80 | 17600 | 55 | 12100 |
| 25,00 | 5,64 | 100 | 22000 | 65 | 14300 |
Как видно из таблицы сечение жил зависит кроме нагрузки и от материала, из которого изготовлен провод.
Мощность ток напряжение, расчёты для трёхфазной сети 380 В
При трёхфазном электроснабжении сила тока I (в амперах, А) вычисляется по формуле:
I = P /1,73 U,
где P -потребляемая мощность, Вт;
U — напряжение в сети, В,
так как напряжение при трёхфазной схеме электроснабжения 380 В, формула примет вид:
I = P /657, 4.
Сечение жил в питающем кабеле при различной нагрузке при трёхфазной схеме напряжением 380 В для скрытой проводки представлена в таблице.
| Сечение жилы провода, мм2 | Диаметр жилы проводника, мм | Медные жилы | Алюминиевые жилы | ||
| Ток, А | Мощность, Вт | Ток, А | Мощность, кВт | ||
| 0,50 | 0,80 | 6 | 2250 | ||
| 0,75 | 0,98 | 10 | 3800 | ||
| 1,00 | 1,13 | 14 | 5300 | ||
| 1,50 | 1,38 | 15 | 5700 | 10 | 3800 |
| 2,00 | 1,60 | 19 | 7200 | 14 | 5300 |
| 2,50 | 1,78 | 21 | 7900 | 16 | 6000 |
| 4,00 | 2,26 | 27 | 10000 | 21 | 7900 |
| 6,00 | 2,76 | 34 | 12000 | 26 | 9800 |
| 10,00 | 3,57 | 50 | 19000 | 38 | 14000 |
| 16,00 | 4,51 | 80 | 30000 | 55 | 20000 |
| 25,00 | 5,64 | 100 | 38000 | 65 | 24000 |
Для расчёта тока в цепях питания нагрузки, характеризующейся большой реактивной полной мощностью, что характерно применению электроснабжения в промышленности:
- электрические двигатели
- дроссели приборов освещения
- сварочные трансформаторы
- индукционные печи
В мощных приборах и оборудовании, доля реактивной нагрузки выше и поэтому для таких приборов в расчетах коэффициент мощности принимают равным 0,8.
На практике принято считать, что при подсчёте электрических нагрузок для бытовых целей запас мощности принимают 5%. В случае расчёта электрических сетей для промышленного производства запас мощности принимают 20%.
Будем рады, если подпишетесь на наш Блог!
[wysija_form id=»1″]
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Параметры цепей синусоидального электрического тока
Определение 1
Переменный ток – это электрический ток, который изменяется во времени по какому-либо закону.
В том случае, когда форма кривых величины переменного тока и напряжения повторяется через одинаковые промежутки времени, то они являются периодическими. Наименьшее время, через которое повторяется форма кривых величины переменного тока и напряжения называется периодом. Количество периодов за одну секунду называется частотой, она может быть рассчитана по следующей формуле:
$f = 1 / T$
где, Т – период.
Самыми простыми периодическими переменными напряжения и величины тока являются токи и напряжения синусоидальной формы:
$u(t) = Um*sin(wt+фu)$
$i(t) = Im*sin(wt+фi)$
где, u(t), i(t) – мгновенные значения напряжения и тока; Im, Um – амплитудные значения тока и напряжения; фu, фi – начальные фазы напряжения и тока; w – угловая скорость.
Определение 2
Угол сдвига фаз – это разница начальных фаз тока и напряжения.
Угол сдвига фаз обозначается следующим образом:
$О = фu – фi$
Известно, что комплексное число можно представить в виде вектора на комплексной плоскости, а мнимая и действительная часть части комплексного числа являются проекциями вектора на мнимую и вещественную оси.
Рисунок 1. График. Автор24 — интернет-биржа студенческих работ
«Расчет однофазной цепи синусоидального тока» 👇
В электротехнике за мнимую единицу принята буква j.
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
где, А – модуль; ф – фаза или аргумент
Допустим, что вектор А на комплексной плоскости вращается против часовой стрелки с угловой скоростью, то комплексное число запишется следующим образом
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
Рисунок 4. Оператор вращения. Автор24 — интернет-биржа студенческих работ
Таким образом видно, что мгновенные значения синусоидального тока и напряжения похожи на мнимую часть вращающегося комплексного числа:
Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ
где, Im – комплексная амплитуда тока; Um – комплексная амплитуда напряжения.
Допустим, что
$i(t)=5sin(wt + 30)$
Тогда максимальное значение в комплексной форме будет выглядеть следующим образом
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Действующее значение в комплексной форме можно записать так:
Рисунок 7. Формула. Автор24 — интернет-биржа студенческих работ
Если
Рисунок 8. Формула. Автор24 — интернет-биржа студенческих работ
То мгновенное значение можно записать в следующем виде:
Рисунок 9. Формула. Автор24 — интернет-биржа студенческих работ
Получается, что мгновенные реальные значения синусоидального тока и напряжения могут быть заменены комплексной амплитудой или комплексным действующим значением напряжения и тока.
Расчет однофазной цепи синусоидального тока
Рассмотрим схему электрической цепи однофазного синусоидального тока, которая представлена на рисунке ниже
Рисунок 10. Схема цепи однофазного синусоидального тока. Автор24 — интернет-биржа студенческих работ
Допустим, что нам известны следующие значения:
Рисунок 11. Формулы. Автор24 — интернет-биржа студенческих работ
В данном случае расчет будет производиться методом контурных токов. Значение контурного тока I22 принимается равным значению источника тока J1, уравнение для контурного тока I11 будет выглядеть следующим образом:
$I11 * (R3 + jx2) – I22 * jx2 = E3$
Отсюда
$I11 = (I22jx2 – E3) / (R3 + jx2) = (j1 *j10 – j10) / (10 + j10) = –1 A$
Ток в третьей ветви рассматриваемой цепи равен контурному току I11, который в показательной форме комплексного числа будет выглядеть следующим образом:
Рисунок 12. Формула. Автор24 — интернет-биржа студенческих работ
Электрический ток во второй ветви цепи представляет собой алгебраическую сумму контурных токов, проходящих через эту ветвь:
Рисунок 13. Формула. Автор24 — интернет-биржа студенческих работ
Полная мощность приемников может быть рассчитана следующим образом:
$Sпр = Рпр + Qпр$
где: Р – активная мощность приемников; Q – реактивная мощность приемников
Для расчета активной мощности рассматриваемой электрической цепи используется следующая формула:
Рисунок 14. Формула. Автор24 — интернет-биржа студенческих работ
Реактивная мощность может быть определена следующим образом:
Рисунок 15. Формула. Автор24 — интернет-биржа студенческих работ
Таким образом, полная мощность, выделяемая источниками в схему определяется по формуле:
Рисунок 16. Формула. Автор24 — интернет-биржа студенческих работ
Рассмотрим схему на рисунке ниже
Рисунок 17. Схема. Автор24 — интернет-биржа студенческих работ
Нам известны следующие величины:
- U(t) = 10sin(wt+90)
- R1 = 2 Ом
- х1 = 2 Ом
- R2 = 2 Ом
- R3 = 2 Ом
- х3 = 4 Ом
Нам необходимо рассчитать I1 в неразветвленной части выше представленной схемы.
Функция времени U(t) = 10sin(wt + 90) в виде показательной комплексного числа будет выглядеть следующим образом:
Рисунок 18. Формула. Автор24 — интернет-биржа студенческих работ
Сначала необходимо рассчитать входное сопротивление рассматриваемой схемы относительно зажимов источника напряжения:
$Z = R1 + x1 + (R2 * (R3 – jx3)) / (R2 + R3 + jx3) = 2 + j2 + ((4 – j8) / 4 – j4)) = 2 + j2 + ((4 – j8) * (4 + j4)) / 16 + 16 = 2 + j2 + ((16 – j32 + j16 + 32) / 16 + 16) = 2 + j2 + ((48 – j16) / 32) = 2 + j2 + 1.5 – j0.5 = 3.5 – j1.5$
Теперь можно рассчитать ток I1 по закону Ома
Рисунок 19. Формула. Автор24 — интернет-биржа студенческих работ
Рассмотрим схему на рисунке ниже
Рисунок 20. Схема. Автор24 — интернет-биржа студенческих работ
Известны следующие значения
Рисунок 21. значения. Автор24 — интернет-биржа студенческих работ
Необходимо определить напряжение U31
Принимаем за базисный узел – первый, то есть ф1 = 0. Потенциалы второго и четвертого узлов рассматриваемой схемы определяются следующим образом:
$ф2 = Е5$
$ф4 = –Е4$
Уравнение для третьего потенциала будет выглядеть следующим образом:
$ф3 * ((1 / –jx2) + (1 / (R3 – jx3))) – ф2 * (1 / (R3 + jx3)) + ф4 * (1 / –jx2) = –J1$
Если мы подставим в получившееся уравнение численные значения, то получим:
Рисунок 22. Формула. Автор24 — интернет-биржа студенческих работ
Из последнего выражения можно выразить потенциал третьего узла
Рисунок 23. Формула. Автор24 — интернет-биржа студенческих работ
Так как ф3 = U31, то мгновенное значение напряжения можно записать следующим образом:
Рисунок 24. Формула. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме