
Опасным называют сечение балки, в котором под действием внешних нагрузок ожидаются максимальные напряжения. Чаще всего, оно определяется по построенной эпюре изгибающих моментов.
При расчетах на прочность необходимо определять значения внутренних силовых факторов в опасном сечении бруса.
Опасным называют сечение, в котором напряжения вызываемые действием внешних усилий максимальны.
Другие видео
Для определения опасного сечения балки необходимо построить эпюры внутренних поперечных сил и изгибающих моментов.
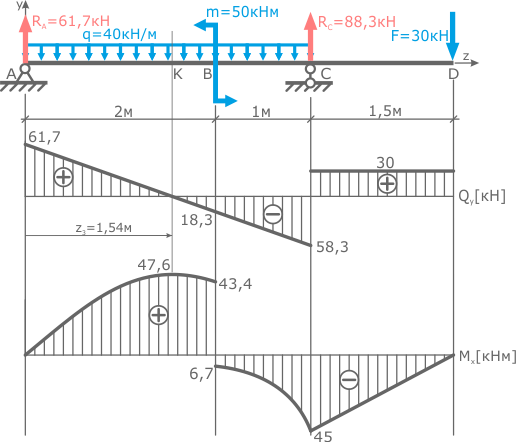
Из них определяющей является эпюра M, так как изгибающие усилия для балки опаснее поперечных сил.
В данном случае по ранее построенным эпюрам Q и M видно, что балка имеет два опасных сечения:
- Сечение в точке K где наблюдается максимальное значение изгибающего момента Mx max=47,6 кНм, при этом поперечная сила в данном сечении отсутствует (Qy=0).
- Сечение в точке C несмотря на то, что момент в нем несколько меньше (Mx=45кНм) тоже является опасным, так как тут одновременно с изгибающим моментом имеет место значительная величина поперечной силы Qy=58,3кН.
Какое из сечений балки более нагружено могут показать дополнительные расчеты.
В таких случаях:
- При проверке на прочность
Рассчитывается величина главных напряжений во всех опасных сечениях, после чего большее из них (по абсолютной величине) сравнивается с соответствующим допустимым значением напряжения для данной задачи. - При проектировочном расчете (подборе размеров сечения балки)
Размеры сечения подбираются по максимальному изгибающему моменту, затем выполняется проверка подобранного сечения на прочность по главным напряжениям в опасных сечениях.
Примеры построения эпюр >
Другие примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Полная проверка прочности. Опасные сечения и опасные точки.
Для
проверки на прочность при изгибе по
действующим на балку внешним нагрузкам
строят эпюры изменения внутренних
усилий по ее длине и определяют опасные
сечения балки, для каждого из которых
необходимо провести проверку прочности.
При
полной проверке прочности таких сечений
будет, как минимум, три (иногда они
совпадают):
1.
сечение, в котором изгибающий момент
Мх
– достигает своего максимального по
модулю значения, – именно по этому сечению
подбирают сечение всей балки;
2.
сечение, в котором поперечная сила Qy,
достигает своего максимального по
модулю значения;
3.
сечение, в котором и изгибающий момент
Мx
и поперечная сила Qy
достигают по модулю достаточно
больших величин.
В
каждом из опасных сечений необходимо,
построив эпюры нормальных и касательных
напряжений, найти опасные точки сечения
(проверка прочности проводится для
каждой из них), которых также будет, как
минимум, три:
1.
точка, в которой нормальные напряжения
![]()
,
достигают своего максимального
значения, – то есть точка на наружной
поверхности балки наиболее удаленная
от нейтральной оси сечения;
2.
точка, в которой касательные напряжения
достигают
своего максимального значения, –
точка, лежащая на нейтральной оси
сечения;
3.
точка, в которой и нормальные напряжения,
и касательные напряжения, достигают
достаточно больших величин (эта проверка
имеет смысл для сечений типа тавра или
двутавра, где ширина резко изменяет
свое значение).
Пример
11.
Для
заданных двух схем балок (рис.6.39) требуется
написать выражения
,
для
каждого участка в общем виде, построить
эпюры
,
,
найти
![]()
и
подобрать: для схемы а) деревянную балку
круглого поперечного сечения при
![]()
МПа;
для схемы б) стальную балку двутаврового
поперечного сечения при
![]()
МПа.
При М
= 20 кН/м, Р
= 20 кН, q
=
8 кН/м,
![]()
м,
![]()
м,
![]()
,
![]()
,
![]()
.
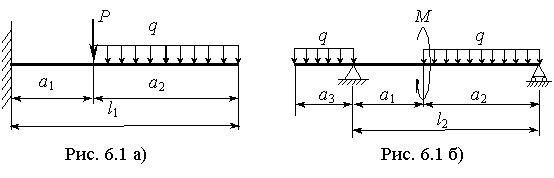
а)
б)
Рис.6.39
Решение.
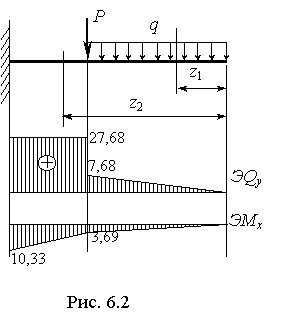
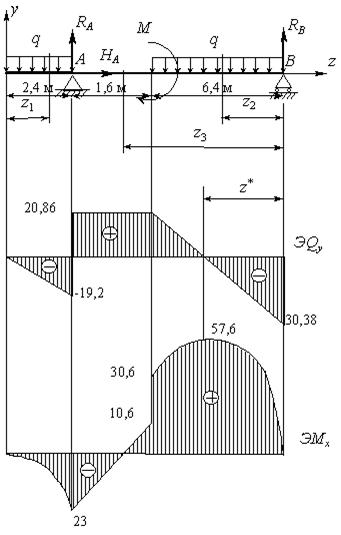
а)
б)
Рис.6.40
Схема
а).
1.
Для определения внутренних
усилий
,
используем
метод сечений. Определим количество
участков: граничными точками участков
являются точки приложения сосредоточенных
сил и моментов, а также точки начала и
конца распределенной нагрузки. В данной
задаче консольная балка имеет два
участка. Рассечем последовательно со
свободного конца каждый из
них.
Отбрасывая
часть балки, включавшую защемление,
определим внутренние силовые факторы
в сечении. Поперечная сила равна
алгебраической сумме проекций сил,
приложенных к отсеченной части на
поперечную ось (ось у),
изгибаюший момент равен алгебраической
сумме моментов, возникающих на отсеченной
части относительно оси х
в сечении. При определении знаков,
используем следующее правило: поперечная
сила положительна, если отсеченная
часть стремится повернуться по часовой
стрелке относительно, точки сечения,
изгибающий момент положителен, если
балка становится вогнутой.
Запишем
выражения для внутренних силовых
факторов и сосчитаем
их
значения в граничных точках участков
(рис.6.40,а).
1
участок:
![]()
м
![]()
кН;
![]()
.
![]()
,
![]()
кН;
![]()
,
![]()
кНм.
II
участок:
![]()
м
![]()
;
![]()
,
![]()
кН,
![]()
кН;
![]()
кНм,
![]()
кНм.
2.
Построим эпюры внутренних силовых
факторов, откладывая вычисленные
значения на графике (рис.6.40,а).
Соединим полученные точки прямыми
линиями на участках, где аргумент z
входит в первой степени и параболами,
где z
входит во второй степени. Таким образом,
эпюра изгибающего момента на первом
участке будет криволинейной, остальные
участки эпюр будут прямолинейными.
Определим опасное сечение балки, т.е.
сечение, в котором изгибающий момент
достигает наибольшего по модулю значения.
Опасным сечением будет сечение на опоре,
где
![]()
кН/м.
3.
Диаметр круглого сечения найдем из
условия прочности
![]()
,
![]()
,
![]()
,
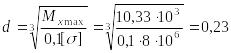
м.
Схема
б).
1.
Для балки, лежащей на двух шарнирных
опорах (рис.6.40,б),
найдем опорные реакции RА,
НА,
RВ
. Запишем уравнения равновесия статики:
![]()
;
![]()
;
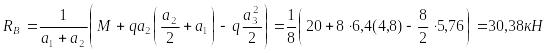
.
![]()
;
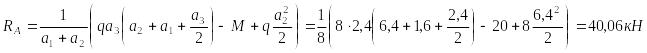
.
Для
проверки правильности определения
реакций запишем еще одно уравнение
равновесия, которое должно тождественно
удовлетвориться при правильно найденных
значениях реакций.
![]()
,
![]()
.
Балка
имеет три участка, рассечем каждый
из
них.
I
участок:
![]()
![]()
кН;
![]()
.
,
![]()
кН;
,
![]()
кНм.
II
участок:
![]()
м
![]()
;
![]()
,
![]()
кН,
![]()
кН;
![]()
,
![]()
кНм.
2.
Построим эпюры, соединяя полученные
значения
и
.
На втором участке эпюра
имеет
максимум при
![]()
.
Для определения величины максимального
момента приравняем нулю выражение
поперечной силы на участке, определим
величину
и
подставим ее в выражение изгибающего
момента:
![]()
,
![]()
м,
![]()
кНм.
Двутавровое
сечение найдем
из
условия прочности, определив необходимую
величину момента сопротивления
![]()
,
![]()
.
Из
сортамента прокатной стали (ГОСТ 8239-72)
выберем двутавр с
![]()
см3,
![]()
,
![]()
см3.
Перемещения
при изгибе балок
Дифференциальное
уравнение изогнутой оси упругой
балки
При
расчете балок на изгиб инженер интересуется
не только напряжениями, возникающими
от действия внешних сил, но и перемещениями
от действия тех же сил. Одно из требований
к элементам конструкций, чтобы перемещение
не превосходило некоторого допустимого
значения, обусловленного требованиями
эксплуатации. Это условие называется
условием жесткости либо конструктивной
прочности.
При
расчете строительных и машиностроительных
конструкций на жесткость
(в
большинстве случаев по прогибам, по
углам поворота) должно соблюдаться
условие
![]()
т.е.
относительный
прогиб
f/l,
подсчитанный при действии нормативных
нагрузок, не должен превышать установленный
нормами предельный прогиб 1/no
для данного вида конструкции.
Для
обеспечения нормальной работы подшипников
скольжения и роликовых подшипников
качения иногда ставится дополнительное
условие жесткости – ограничение угла
поворота
![]()
опорных
сечений:
![]()
.
Допускаемый
угол поворота
![]()
берется
из соответствующих справочников. В
среднем
составляет
0,001 рад.
Рассмотрим
плоский чистый изгиб балки (рис. 6.41, а).
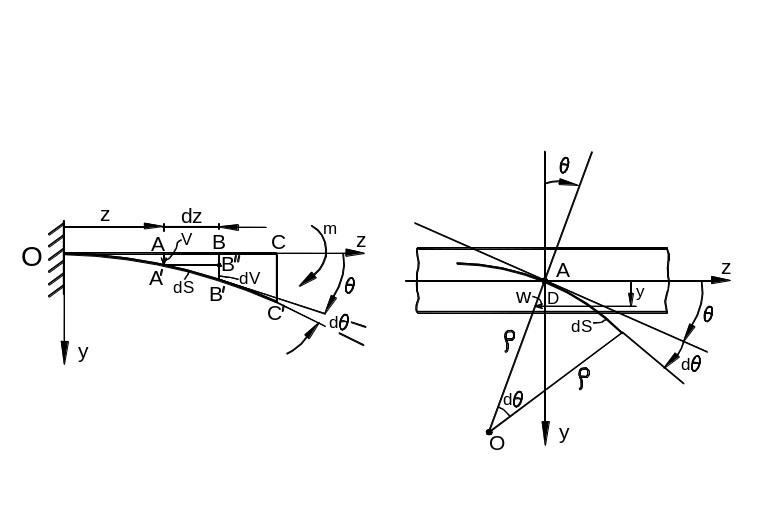
а)
б)
Рис.
6.41
В
результате действия изгибающего момента
m
ось балки ОС
изгибается
и занимает некоторое положение ОС’.
Произвольная точка
А
оси балки, характеризуемая координатой
,
перемещается в новое положение А‘.
Перемещение, изображаемое направленным
отрезком
![]()
,
назовем прогибом балки для точки
А
с координатой
и
обозначим v.
Проведем в точке А‘
касательную к изогнутой оси балки. Она
образует с осью
угол
![]()
.
Из
рис. 6.41,б
видно, что этот угол в силу взаимной
перпендикулярности сторон в точности
равен углу поворота поперечного сечения.
При изменении
,
т.е. при переходе к другим точкам оси
балки, прогиб
v
и угол поворота
поперечного
сечения изменяется. Следовательно, они
являются функциями
:
![]()
(19)
Горизонтальное
перемещение w произвольной точки
D
поперечного сечения на расстоянии
![]()
от
оси балки равно:
![]()
(20)
Из
треугольника А’В’В”
следует, что первая производная от
функции прогиба
![]()
:
![]()
(21)
равна
тангенсу угла наклона касательной к
изогнутой оси балки в точке А
с координатой
.
Из этого же треугольника получаем
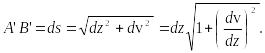
(22)
Из
рис. 6.41,б
находим
![]()
где
–
радиус кривизны дуги
![]()
.
Следовательно, кривизна изогнутой оси
в точке А
равна:
![]()
(23)
Дифференцируя
(21) по
и
учитывая (19), (22), (23), получаем:
![]()
откуда
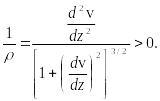
(24)
Формула
для кривизны балки
![]()
для
положительных значений
.
В нашем примере на рис. 6.41 изгибающий
момент
![]()
.
Поэтому эту формулу мы должны использовать
в виде:
![]()
(25)
Приравнивая
(24), (25), получаем точное дифференциальное
уравнение изогнутой оси балки:
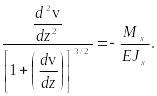
(26)
Если
прогибы
![]()
балки
малы по сравнению с ее линейными
размерами, то и углы поворота сечений
–
малые величины и, согласно (21)-(24), можно
считать:
![]()
,
![]()
,
![]()
Тогда
дифференциальное уравнение (26) упрощается
и принимает вид
![]()
(27)
Уравнение
(27) носит название приближенного
дифференциального уравнения изогнутой
оси упругой балки.
Оно получено для случая чистого
изгиба, но может быть использовано и
при поперечном, когда момент
![]()
является
функцией
.
Интегрируя
(27), получаем:
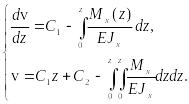
(28)
Произвольные
постоянные C1,
С2
в (28) имеют простой геометрический смысл.
Обозначим через
![]()
прогиб
и угол поворота cечения
соответственно в начале координат при
.
Тогда при
из
(10) получаем:
![]()
Величины![]()
называют
начальными
параметрами
задачи по определению перемещений в
балках.
Соотношения
(28) запишем в виде
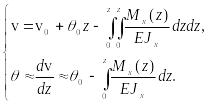
(29)
Так
как
![]()
то
решение (29) можно записать в виде:
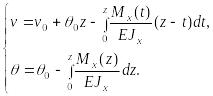
В
соответствии с дифференциальными
зависимостями Журавского
![]()
(30)
Дифференцируя
(27) дважды по
и
используя зависимости (30), находим
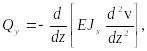
(31)
![]()
.
(32)
При
постоянной жесткости
![]()
получаем
![]()
(33)
![]()
(34)
Уравнения
(32), (34) представляют собой вторую форму
дифференциальных уравнений изогнутой
оси балки четвертого порядка.
Общее
решение неоднородного уравнения (34)
имеет вид
![]()
(35)
где![]()
–
его частное решение. Постоянные
![]()
находятся
из условий на опорах балки. Эти условия
называют граничными или краевыми.
Рассмотрим
типичные условия закрепления или
опирания балок (рис. 6.42). Изогнутая ось
балки изображена тонкой линией.
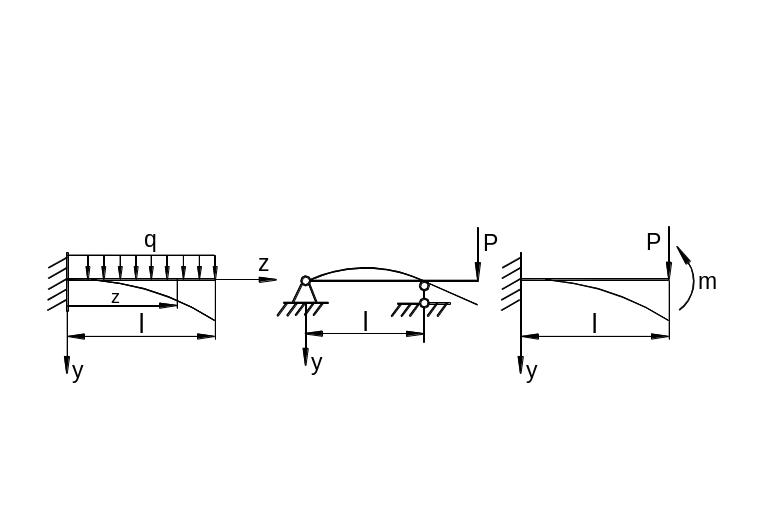
а)
б) в)
Рис.
6.42
а)
Край балки жестко защемлен (рис. 6.42,а).
При z
=
0 на защемленном крае прогиб и угол
поворота сечения равны нулю, т.е.
![]()
б)
Край балки свободен от закрепления и
нагрузки (рис.6.42,а).
В этом случае при
![]()
равны
нулю: момент и перерезывающая сила:
![]()
![]()
в)
Край балки шарнирно закреплен либо
свободно опёрт (рис. 6.42,б).
При z
= 0 край балки шарнирно закреплен. Здесь
прогиб
и
момент
равны
нулю, т.е.
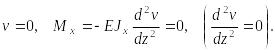
При
балка
свободно лежит на опоре. Прогиб равен
нулю, но изгибающий момент в сечении
балки отличен от нуля. Поэтому здесь
только одно граничное условие
![]()
.
г)
Незакрепленный край балки с действующими
сосредоточенными силой и моментом (рис.
6.42,в).
В
этом случае при
имеем
статические граничные условия:
![]()
![]()
Пределы
применимости приближенной теории
изгиба балок
При
выводе дифференциального уравнения
изогнутой оси балки (28) выражение для
кривизны
![]()
балки
было выбрано приближенно. Выясним
степень точности приближенного уравнения
(27). Для этого рассмотрим задачу о чистом
изгибе консольной балки (рис. 6.43).
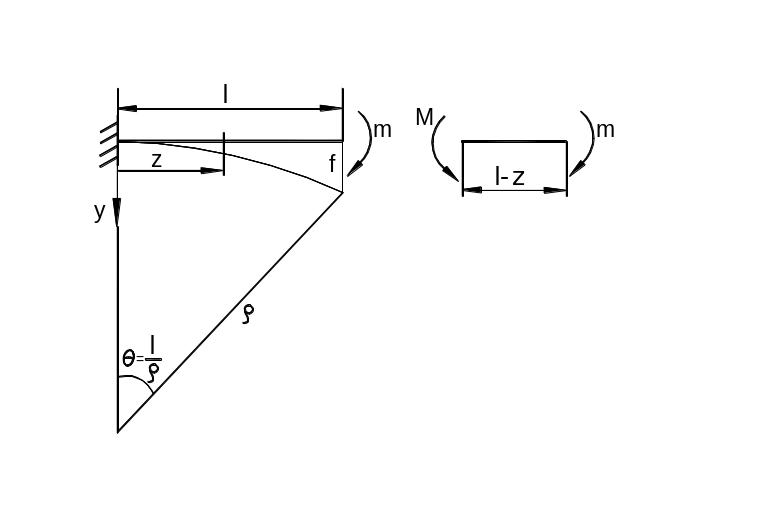
Рис.
6.43
В
этом случае
![]()
и
поэтому![]()
Из
рис. 6.43 прогиб на конце консоли:
![]()
Разложим
косинус в ряд и ограничимся тремя первыми
элементами:
![]()
Выражение
для прогиба f принимает вид:
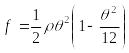
или
с учетом
![]()
и
(7):
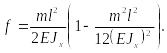
(36)
Дадим
теперь приближенное решение задачи.
Интегрируя уравнение
![]()
при
![]()
получаем:
![]()
Так
как при
![]()
прогиб![]()
,
угол поворота![]()
,
то
![]()
При
на
конце консоли прогиб:
![]()
(37)
Сравнивая
решения (36), (37), находим:
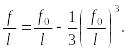
Удовлетворимся
при определении прогибов по приближенной
теории точностью в 3%. Полагая
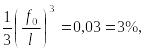
получаем:
![]()
Таким
образом, приближенное дифференциальное
уравнение (27) изогнутой оси упругой
балки дает достаточную точность решения
задачи даже в том случае, когда прогиб
составляет 30% от длины стержня. Такие
прогибы возможны только у очень гибких
балок большой длины или очень малой
толщины типа гибкой стальной линейки.
Интегрирование
дифференциального уравнения изогнутой
оси балки методом начальных параметров
А. Н. Крылова
Рассмотрим
балку, нагруженную силами и моментами
![]()
(рис.
6.44). Силы
,
считаем
положительными, если они направлены в
положительном направлении координатной
оси у,
т.е. вниз. Момент
![]()
считаем
положительным, если он вращает сечение
балки против часовой стрелки, когда мы
смотрим на него с конца положительной
оси
![]()
,
ортогональной к плоскости
![]()
.
В этом случае прогибы
любой
точки оси стержня с координатой z
направлены
вниз по оси у.
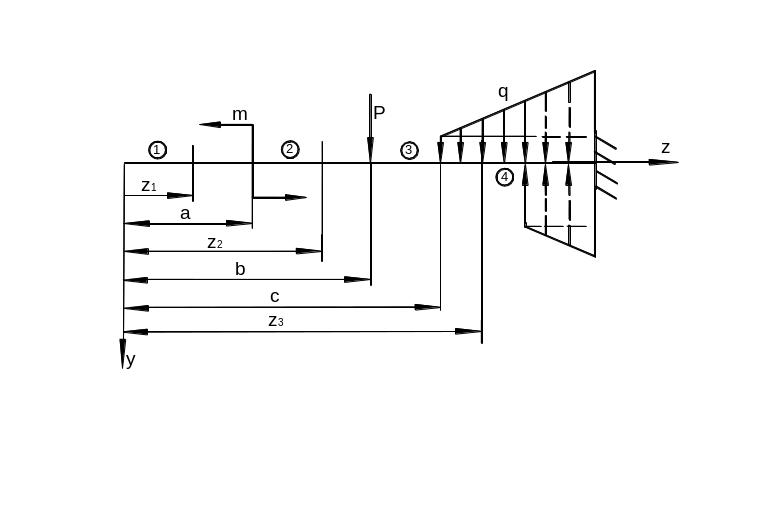
Рис.
6.44
Балку
по длине можно разбить на несколько
участков, на которых аналитические
выражения изгибающих моментов
будут
различны.
Границей
этих участков являются те сечения, над
которыми к балке приложены сосредоточенные
силы Р,
момент m
либо меняется характер нагружения так,
как в сечении
![]()
,
с которого начинается действие
распределенной нагрузки
![]()
.
Интегрируем
дважды дифференциальное уравнение
изогнутой оси балки (27):
![]()
В
результате получаем:
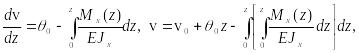
(38)
где
–
прогиб и угол поворота сечения в начале
координат при
,
называемые начальными
параметрами задачи
по определению перемещений. Вычислим
в (38) интеграл:
![]()
при
одновременном действии![]()
считая
жесткость
при
изгибе постоянной величиной. Для этого
найдем аналитические выражения момента
для
двух сечений от каждого внешнего силового
воздействия. Пусть первое сечение z
лежит левее рассматриваемой внешней
силы или момента, а второе – правее. Тогда
получаем (см. рис. 6.44):
![]()
![]()
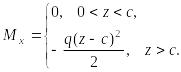
Полагая
последовательно при почленном
интегрировании
![]()
,
получаем:
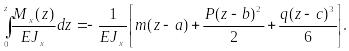
Интегрируя
полученное выражение еще раз, найдем:
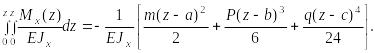
Подставляя
полученные выражения интегралов в (38),
получим формулы:
![]()
(39)
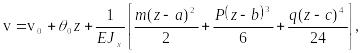
(40)
называемые
универсальными для угла поворота сечения
и прогиба точки оси балки.
Если
распределенная нагрузка
не
является постоянной, то ее можно разложить
в ряд Тейлора в окрестности значения
:
![]()
где![]()
–
факториал числа
![]()
.
В
этом случае после интегрирования (38)
получаем:
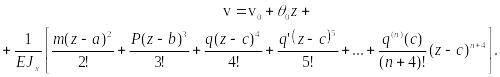
(41)
При
наличии в балке внутреннего шарнира
К
в сечении
![]()
первая
производная от прогиба
по
претерпевает
в этом случае скачок на величину
![]()
(рис.
6.45) так, что:
![]()
(42)
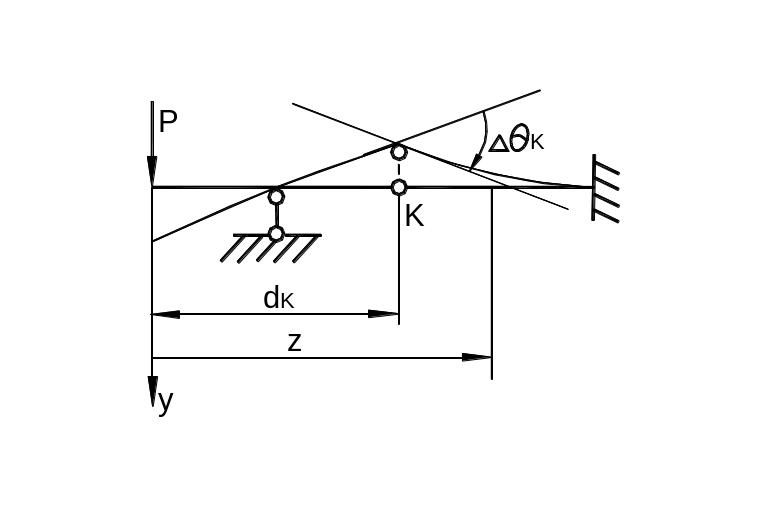
Рис.
6.45
Интегрируя,
получаем:
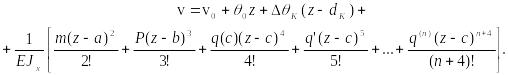
(43)
Обобщенные
силы
,
,
в
(41), (43) повторяются столько раз, сколько
они рассматриваются в рассматриваемой
задаче. Если распределенная нагрузка
не доходит до рассматриваемого сечения
с координатой
,
то ее следует продолжить до этого сечения
и добавить точно такую же, но противоположного
знака (см. рис. 6.44).
Примечание:
Начало
отсчета координаты
z
необходимо брать только на левом конце
балки.
Порядок
расчета по методу начальных параметров:
Чтобы
определить перемещения методом начальных
параметров надо:
1.
Определить опорные реакции.
2.
Выбрать начало отсчета.
3.
Определить начальные параметры из
условий закрепления.
4.
Подсчитать перемещения линейные или
угловые, пользуясь формулами методов
начальных параметров.
Простейшие
статически неопределимые задачи при
изгибе. Метод сравнения (наложения)
перемещений
Рассмотрим
простейшую один раз статически
неопределимую балку (рис. 6.46).
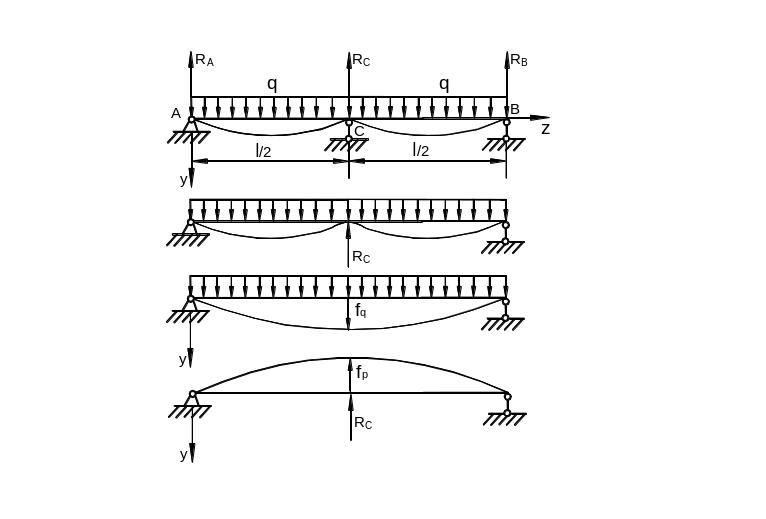
Рис.
6.46
Прогиб
балки над опорой С
равен нулю и его можно, в силу принципа
независимости действия сил, представить
как сумму перемещений от распределенной
нагрузки и сосредоточенной силы
![]()
:
![]()
Используя
известные решения, имеем:
![]()
![]()
Следовательно,
![]()
откуда
![]()
Из
уравнений равновесия:
![]()
находим
опорные реакции
![]()
В
поперечном сечении
![]()
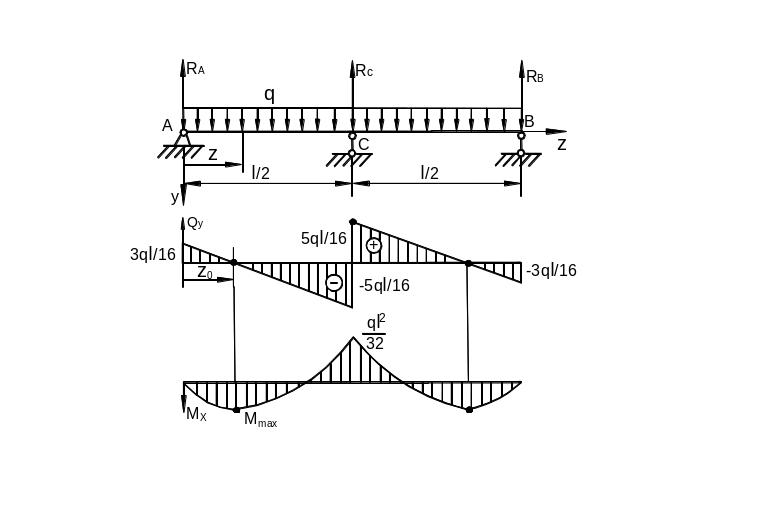
Рис.
6.47
Экстремальный
момент возникает в сечении с координатой
![]()
,
которая находится из условия:
![]()
откуда
![]()
Максимальный
момент
![]()
Он
меньше, чем момент над средним сечением
при
![]()
:
![]()
На
рис. 6.47 построены эпюры
![]()
.
Расчет
на прочность простейших статически
неопределимых балок методом допускаемых
нагрузок
Рассмотрим
простейшую статически неопределимую
балку (рис. 6.48,а).
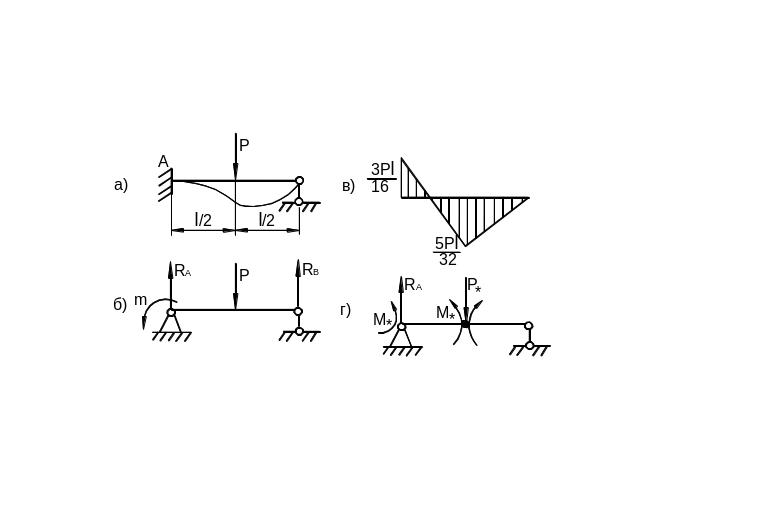
Рис.
6.48
Расчет
на прочность по допускаемым напряжениям
состоит в том, чтобы найти
![]()
и
потребовать![]()
.
Для этого сначала необходимо раскрыть
статическую неопределимость задачи.
На рис. 6.48,б
изображена эквивалентная балка, в
которой момент m
должен
быть подобран так, чтобы угол поворота
в опоре
А
обращался в нуль как и в исходной схеме
балки (рис. 6.48,а).
Вычислим
угол поворота в опоре
А:
![]()
откуда
находим:
![]()
Максимальный
момент возникает в защемлении (рис.
6.48, в):
![]()
Таким
образом, условие прочности по допускаемым
напряжениям (или расчетному сопротивлению)
дает:
![]()
откуда
![]()
Предельная
нагрузка
![]()
упругого
состояния, при которой впервые в балке
возникает пластическая деформация,
равна:
![]()
Первый
пластический шарнир образуется в
защемлении. В этом пластическом шарнире
![]()
.
Однако балка будет испытывать стеснённую
пластическую деформацию, пока в середине
пролета под силой Р
момент также не будет равным
![]()
и
балка превратится в механизм (рис. 6.48,
г). Для предельного состояния имеем
уравнения равновесия:
![]()
откуда
следует
![]()
![]()
Допускаемое
значение внешней нагрузки:
![]()
Сравнивая
![]()
и
![]()
либо
![]()
и
![]()
получим,
что их отношение:
![]()
Статическая
неопределимость задачи повышает
допустимую нагрузку на 12,5%. Для балки
прямоугольного сечения
![]()
.
В случае прямоугольника
![]()
Для
данной задачи обнаруживается резерв
прочности в 69% по сравнению с расчетом
по допускаемым напряжениям.
В
рассматриваемом примере пластические
шарниры образуются в за- щемлении и в
сечении под сосредоточенной силой. В
случае распределенной нагрузки
указать сразу сечения, где возникнут
пластические шарниры, не всегда
удается. Рассмотрим простейшую
двухпролетную статически неопределимую
балку (рис. 6.49). Выше эта задача была
решена для случая упругого поведения
балки и построена эпюра моментов (рис.
6.47).
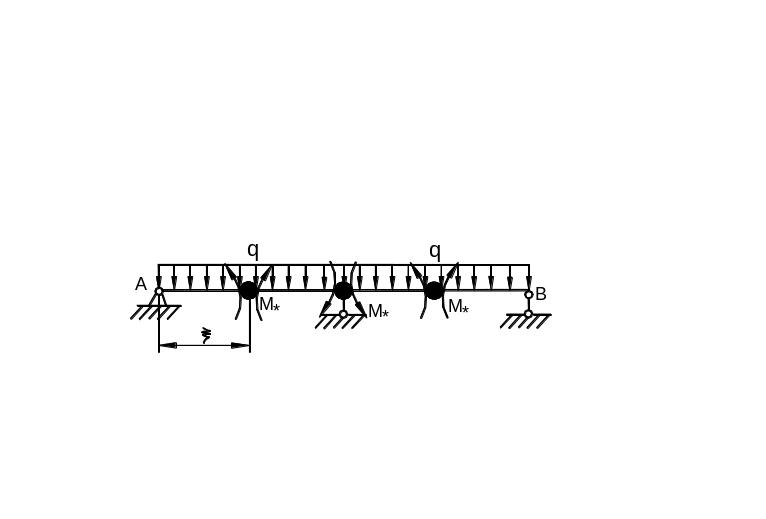
Рис.
6.49
Момент
![]()
в
среднем сечении, при котором в крайних
волокнах возникают пластические
деформации:
![]()
откуда
соответствующая предельная нагрузка
равна:
![]()
Рассмотрим
предельное состояние балки. Первый
пластический шарнир образуется над
средней опорой. Два других – в сечениях,
строго говоря, не совпадающих с сечениями,
где действуют максимальные моменты.
Обозначим расстояние от левой опоры до
первого шарнира в пролете через
![]()
.
Тогда уравнение равновесия балки левее
первого и второго шарниров будет иметь
вид:
![]()
откуда
после исключения
следует:
![]()
Разрушающая
предельная нагрузка оказывается
зависящей от величиины
![]()
,
т.е. местоположения пластического
шарнира в пролете. Дифференцируя данное
выражение для
по
и
приравнивая производную нулю, получим:
![]()
откуда
![]()
Так
как
![]()
,
то перед радикалом следует сохранить
знак плюс. Тогда
![]()
В
результате получим:
![]()
Сравнивая
выражения для
![]()
и
![]()
,
находим:
![]()
Следовательно,
в данной задаче статическая неопределимость
повышает допустимую нагрузку на 45,7%.
Если балка имеет прямоугольное сечение,
то
.
Поэтому в данной задаче полное увеличение
допускаемой нагрузки составляет
![]()
т.е.
118,6%. Если заменить в каждом из пролетов
распределенную нагрузку q
их равнодействующими
![]()
приложенными
в их середине, т.е. при
![]()
,
то получим:
![]()
Величина
![]()
что
отличается от точного решения всего на
2,94%. Для прямоугольного сечения получаем
k
= 2,25 вместо 2,186.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
21.05.2015540.67 Кб326.doc
- #
- #
- #
- #
- #
- #
- #
- #
Перед разбором примеров еще раз обратим внимание на то, что
вычисления направлены на получение характеристик рабочего состояния,
необходимых для проведения оценки прочности. Поэтому во всех случаях
нас будут интересовать значения усилий и напряжений в опасных
сечениях и в опасных точках.
П р и м е р 4.1. Короткий прямоугольный стержень сечением 20х40
см сжимается центрально приложенной силой P = 27000 кН (рис. 4.11).
Определить напряжения в опасных точках.
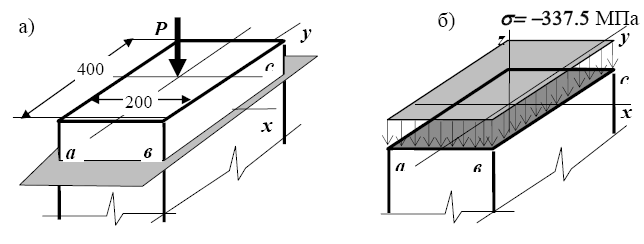
Рис. 4.11. Сжатие стержня силой, направленной по его оси а – схема загружения;
б – эпюра нормальных напряжений;
Р е ш е н и е. При центральном сжатии все связи в сечениях
оказываются в одинаковых условиях. Действующая постоянная по длине
стержня продольная сжимающая сила
N = – P = – 27000 кН
укорачивает все связи по сечению в равной степени. Возникающие при
этом силы в каждой связи – нормальные напряжения – равны
σ = -N/A = – 27000/(40·20) = -33.75 кН/см2 = – 337.5 МПа.
П р и м е р 4.2. Такая же сила P = 27000 кН (см. предыдущий
пример) прикладывается к тому же стержню, но со смещением на e = 5 см
по оси x и на ey = 10 см по оси y (рис 4.12). Определить напряжения в
опасных точках.
Р е ш е н и е. Как и в предыдущем примере, внутренние усилия по
длине стержня не меняются, но в каждом сечении за счет смещения точки
приложения нагрузки кроме продольной силы
N = – P = – 27000 кН
появятся изгибающие моменты
Mx = P·ey = 27000·10 = 270000 кН·см,
My = P·ex = 27000·5 = 135000 кН·см.
Значение напряжения при одновременном действии N, Mx и My вычисляется по формуле (см. табл.4.4)
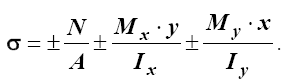
Определим необходимые для вычисления напряжений
геометрические характеристики сечения (см. табл. 4.1)
A = 20·40 = 800 см2,
Ix = b·h3 /12 = 20·40 /12 = 106666.7 см4,
Iy = h·b3 /12 = 40·20 /12 = 26666.7 см·4.
Знак первого слагаемого в формуле определения напряжений
обуславливается знаком продольной силы. В данном случае продольная
сила отрицательна.
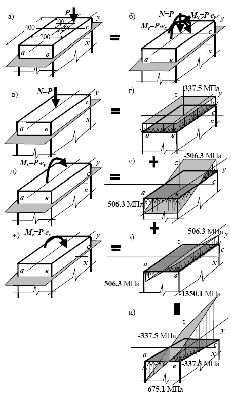
Рис. 4.12. Сжато-изогнутый стержень а – схема загружения;
б – равнодействующая система сил,
приведенная к оси стержня;
в, д, ж – действие составляющих
системы сил в отдельности;
г, е, з – нормальные напряжения от
действия каждой из системы сил в
отдельности;
и – суммарные напряжения
Поэтому наибольшее значение напряжения получится в точке, для
которой второе и третье слагаемое так же будут отрицательными (под
действием моментов Mx и My продольные связи будут сжиматься). Эта
точка наиболее удалена от центра сечения (xmax = 10 см, ymax= 20 см).
Значение напряжения в ней
σ = – 27000/800 – 270000·20/106666.7 – 135000·10 / 26666 =
-135.01 кН/см2 = -1350.1 МПа.
Графическое нахождение положения опасной точки показано на
рисунке 4.12. Из приведенного построения следует, что такой точкой
будет угловая точка с.
Обратите внимание, что по сравнению с предыдущим примером
изменилась только точка приложения нагрузки. Смещение нагрузки
привело к увеличению напряжения в три с лишним раза.
П р и м е р 4.3. Определить напряжения в опасных точках опасных
сечений, если задан закон распределения внутренних усилий,
представленный эпюрами M, Q, N, размеры стержня, форма и размеры
поперечного сечения (рис. 4.13). Размеры сечения по длине стержня не
меняются.
Р е ш е н и е. По таблице 4.4 определяем, что при действии на
стержень M, Q, N (изгиб со сжатием) напряжения в его сечениях будут
равны:
нормальные σ = N/A + Mx·y/Ix ,
касательные τ = Qy·Sx /(Ix ·b).
Опасными мы называем такие сечения, в которых возникают
максимальные усилия. Если размеры сечения по длине стержня не
меняются, то положение такого сечения определяется по эпюрам
усилий. По приведенным эпюрам определяем, что в данном случае
имеют место три опасных сечения: 2, 4 и 3. В сечении 3 изгибающий
момент максимальный и, следовательно, появятся максимальные
нормальные напряжения, но касательные при этом будут равны нулю. Из
всех сечений с одинаковыми значениями поперечной силы выберем
такое, где действует еще и изгибающий момент, так как их совместное
действие может оказаться неблагоприятным. Чтобы получить
представление о работе опасных сечений, построим для них эпюры
напряжений.
Вычислим необходимые для определения напряжений
геометрические характеристики:
площадь сечения A = b·h = 10·20 =200 см2 ,
момент инерции Ix = b·h /12 = 10·20 /12 = 6666.67 см4 ,
статический момент
половины сечения Sx = b· (h/2)·(h/4) = 10·10·5 = 500 см3
четверти сечения Sx = b·(h/4)·(3h/8) = 10·5·7.5 = 375 см3 .
Напряжения в сечении 3. Эпюру нормальных напряжений можно
получить путем графического сложения эпюр (по табл.4.4) σz1 = N / A и
σz2 = Mx·y / Ix (рис. 4.14).
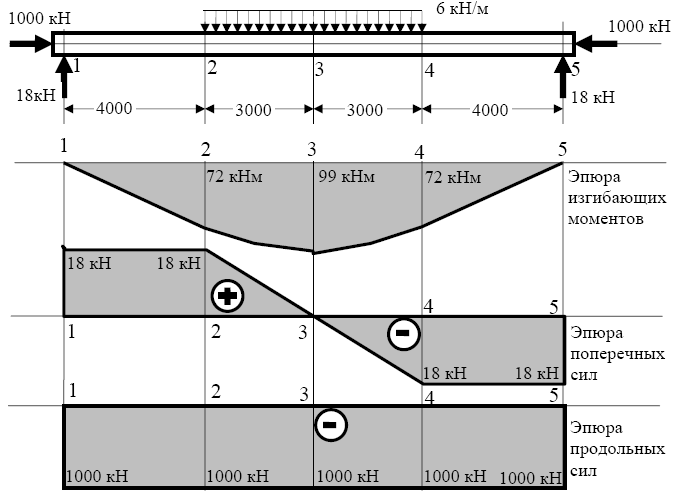
Рис. 4.13. Сжато-изогнутый стержень с эпюрами усилий
σz1 = N/A = – 1000/200 = – 5 кН/см2 = – 50 МПа – сжимающее
напряжение, равномерно распределенное по сечению;
σz2 = Mx·y/ Ix – зависит от y:
при y = 0 σz2 = 0,
при y = ±h/2 имеют наибольшие значения
σz2 = ±99 100·10/6666.67 = ±14.85 кН/см2 = ± 148.5 МПа.
По эпюре моментов определяем знаки напряжений. Так как верхние
волокна сжаты, а нижние растянуты, то соответственно напряжения σz2 по верхней грани сечения – σ в отрицательные, по нижней – σ н положительные
σ в= – 5 – 14.85 = -19.85 кН/см2 = -198.5 МПа,
σ н= – 5 + 14.85 = 9.85 кН/см2 = -98.5 МПа.
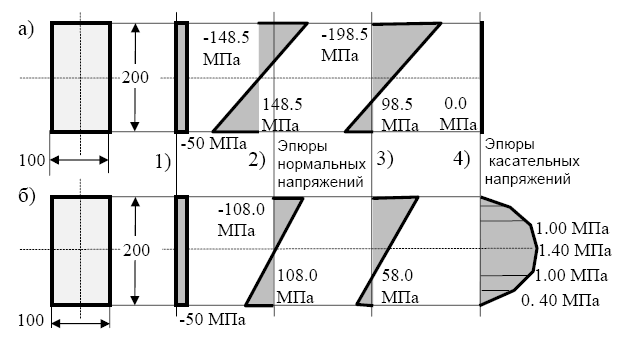
Рис. 4.14. Эпюры напряжений в сечениях 3 и 2 (см. рис. 4.13) а – сечение 3, б – сечение 2.
1, 2, 3 – соответственно напряжения от продольных сил, изгибающих моментов,
суммарные, 4- касательные напряжения
Наибольшие нормальные напряжения в сечении 3 сжимают верхние
волокна.
Напряжения в сечении 2 (рис 4.13в)
нормальные σ = (- 1000/200 ±7200·10/6666.67) кН/см2 ,
на верхней грани σ в = – 5 – 10.80 = -15.80 кН/см2 = -158 МПа,
на нижней σ н = – 5 + 10.80 = 5.80 кН/см2 = – 58 МПа.
Касательные напряжения распределяются по криволинейному
закону.
Эпюру напряжений построим по точкам
в середине сечения τ = 18·500/(6666.67·10) = 0.14 кН/см2 = 1.4 МПа,
в четверти сечения τ = 18·375/(6666.67·10) = 0.10 кН/см2 = 1.0 МПа,
в крайних точках τ = 0.
П р и м е р 4.4 (для самостоятельного решения). Проверить, как
изменятся напряжения в стержне, рассмотренном в предыдущем примере,
если сечение повернуть на 90о, т. е. принять b = 20 см, h = 10 см.
Если внутренние усилия известны, то вычисление напряжений по
формулам таблице 4.2 затруднений обычно не вызывает. Но для анализа
работы сооружения от инженера требуется не только уметь определять
значения внутренних усилий и напряжений, но и хорошо (и это, пожалуй,
главное) представлять, от чего зависят их величины и характер
распределения. Для приобретения навыков в решении таких вопросов
предлагаем самостоятельно решить следующие примеры.
Опасное сечение – балка
Cтраница 1
Опасное сечение балки совпадает с сечением в заделке.
[1]
Установив опасное сечение балки, в котором возникает максимальный изгибающий момент, выбирают наиболее удаленные точки ( точки / и 3 по рис. 186) от нейтральной оси, в которых и следует ожидать экстремальных значений напряжений.
[2]
Определяем опасное сечение балки. Наиболее вероятно это будет сечение С или D, в каждом из которых в одной из плоскостей действует максимальный изгибающий момент. Для того чтобы определить, какое сечение является опасным, определим максимальные напряжения в каждом из этих сечений.
[3]
Для опасного сечения балки, испытывающей косой изгиб, напряжение в точке А равно нулю. В каких точках возникают наибольшие нормальные напряжения.
[4]
В опасном сечении балки возникает изгибающий момент Мх ЗОкН-м. При найденных размерах сравнить их массы, если длины всех балок одинаковы.
[5]
В опасном сечении балки прямоугольного поперечного сечения высоты 26 и ширины b действует изгибающий момент М, изменяющийся по симметричному циклу. Определить предельное значение М в двух вариантах: 1 – плоскость изгиба балки совпадает с плоскостью максимальной жесткости сечения; 2 – плоскость изгиба балки перпендикулярна плоскости максимальной жесткости сечения.
[6]
Где находится опасное сечение балки.
[7]
Для отыскания опасного сечения балки определяем опорные реакции и строим эпюры Q и Ми ( фиг.
[8]
Таким образом, опасное сечение балки из пластичного материала определяется наибольшим изгибающим моментом.
[9]
Таким образом, опасное сечение балки из пластичного материала определяется наибольшим изгибающим моментом, который выявляется построением эпюры изгибающих моментов.
[10]
Таким образом, опасное сечение балки из пластичного материала определяется наибольшим изгибающим моментом.
[11]
Проводим проверку прочности опасного сечения балки по касательным напряжениям.
[12]
Наибольшие напряжения в опасном сечении балки возникнут тогда, когда груз будет приложен в середине пролета.
[13]
Находим напряжение в опасном сечении балки при наличии пружины на правой опоре.
[14]
На установленных в опасном сечении балки тензометрах А и В ( см. рисунок), с базой 20мм и увеличением в 1000 раз, при этом отмечены такие изменения отсчетоз – А-уменьшение на 7мм, В – увеличение на 10 мм.
[15]
Страницы:
1
2
3
Определение наиболее опасного сечения бруса при деформации растяжение — сжатие
NovaInfo 56, с.336-341, скачать PDF
Опубликовано 1 декабря 2016
Раздел: Педагогические науки
Просмотров за месяц: 18
Аннотация
Расчет многоступенчатого бруса является важной и актуальной задачей, поскольку аналогичные элементы часто встречаются в строительных конструкциях. Умение быстро определить слабые места таких конструкций должно способствовать инженеру пожарной безопасности при проведении инспекций объектов, а также при тушении пожаров.
Ключевые слова
РАСТЯЖЕНИЕ, ОЦЕНКА ПРОЧНОСТИ, СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Текст научной работы
Расчет многоступенчатого бруса является важной и актуальной задачей, поскольку аналогичные элементы часто встречаются в строительных конструкциях. Умение быстро определить слабые места таких конструкций должно способствовать инженеру пожарной безопасности при проведении инспекций объектов, а также при тушении пожаров.
Постановка задачи: провести расчет многоступенчатого бруса на прочность, определить критическую температуру нагрева при пожаре, построить эпюры внутренних силовых факторов.
Допускаемое напряжение на растяжение для материала бруса 180 МПа, а модуль упругости 200000 МПа. Материал бруса — сталь.
Исходные данные:

Решение данной задачи может быть выполнено в несколько этапов.
- Построение эпюры продольных сил.
Для построения эпюры требуется, чтобы один из концов стержня был свободным, поэтому отбрасываем одну заделку, заменив ее действие реакцией (рис. 2).

Далее составляется уравнение деформаций для приведенной выше схемы. Из полученного выше уравнения определяем значение реакции N. Если значение реакции получится положительным, то ее направление на рис. 2 верное.
Для построения эпюры разбиваем брус на участки и определяем внутренние силы.
Найденные значения сил на каждом из участков используем для построения эпюры продольных сил (рис. 4).
2. Построение эпюры нормальных напряжений.
Для построения эпюры разбиваем брус вновь на участки и согласно правилу построения эпюр определяем значения напряжений.
Если проверка покажет, что на каком-либо участке эпюры напряжений, прочность бруса будет недостаточной, то необходимо будет увеличить соответствующую площадь.
Найденные значения напряжений на каждом из участков используем для построения эпюры нормальных напряжений (рис. 4).
3. Определение критической температуры.
По величине максимального значения нормального напряжения определяем значение предельной температуры равномерного нагрева бруса. Например, если значение напряжения получилось равным 178 МПа, то по графику (рис. 4) можно определить, что предельная температура нагрева бруса t = 390°C.


Наиболее опасный участок деталей или элементов конструкций, работающих на растяжение, всегда располагается в том сечении, где нормальное напряжение достигает максимального значения.
Читайте также
-
Значение курсового проектирования по механике при изучении дисциплины
- Киселев В.В.
-
Изучение конструкции цилиндрического зубчатого редуктора на занятиях по механике
- Киселев В.В.
-
Индивидуальная работа со слабоуспевающими обучающимися по техническим дисциплинам
- Киселев В.В.
-
Роль куратора в организации учебной и воспитательной работы обучающихся
- Киселев В.В.
-
Особенности проведения лабораторных работ по прикладной механике
- Киселев В.В.
Список литературы
- Киселев В.В. Использование интерактивных форм обучения для формирования профессионально-значимых качеств обучающихся // NovaInfo.Ru (Электронный журнал.) – 2016 г. – № 54; URL: http://novainfo.ru/article/8655.
- Киселев В.В. Актуальность разработки электронных учебников по дисциплине механика // NovaInfo.Ru (Электронный журнал.) – 2016 г. – № 53; URL: http://novainfo.ru/article/8091.
- Киселев В.В. Разработка электронных учебных изданий по дисциплине механика для реализации дистанционных образовательных технологий // NovaInfo.Ru (Электронный журнал.) – 2016 г. – № 53; URL: http://novainfo.ru/article/8090.
- Топоров А.В., Топорова Е.А. Использование магнитоэластоменрного материала для удержания магнитожидкостной смазки в области трения. /
- NovaInfo.Ru. – 2016. – Т. 2. – № 52. – С. 20-25.
- Топоров А.В. Анализ конструкций бесконтактных уплотнений. / NovaInfo.Ru. – 2016. – Т. 2. – № 54. – С. 53-55.
- Топоров А.В. Анализ конструкций контактных уплотнений. / NovaInfo.Ru. – 2016. – Т. 2. – № 54. – С. 55-57.
- Киселев В.В. Исследования по выявлению оптимальной концентрации разработанного медно-оловянного комплекса в масле. / Депонированная рукопись № 836-В2003 29.04.2003.
- Киселев В.В. К проблеме улучшения триботехнических свойств смазочных материалов. / Известия высших учебных заведений. Серия: Химия и химическая технология. – 2006. – Т. 49. – № 12. – С. 115-116.
- Киселев В.В. Меры по снижению износа деталей пожарной техники. / NovaInfo.Ru. – 2016. – Т. 1. – № 51. – С. 37-40.
- Киселев В.В., Пучков П.В. Проведение экспресс оценки качества смазок, используемых в спасательной технике. / Фундаментальные и прикладные исследования в современном мире. – 2015. № 12-1. – С. 105-107.
- Киселев В.В. Роль смазочных материалов в процессе трения и изнашивания // NovaInfo.Ru (Электронный журнал.) – 2016 г. – № 54; URL: http://novainfo.ru/article/8437
- Киселев В.В. Влияние механо-химических процессов при трении на образование поверхностных пленок // NovaInfo.Ru (Электронный журнал.) – 2016 г. – № 53; URL: http://novainfo.ru/article/8206.
- Киселев В.В. К вопросу надежности деталей тормозных механизмов пожарных автомобилей. // NovaInfo.Ru (Электронный журнал.) – 2016 г. – № 54; URL: http://novainfo.ru/article/8439
- Киселев В.В. Повышение долговечности узлов трения строительной техники. // NovaInfo.Ru (Электронный журнал.) – 2016 г. – № 55; URL: http://novainfo.ru/article/8687
Цитировать
Киселев, В.В. Определение наиболее опасного сечения бруса при деформации растяжение — сжатие / В.В. Киселев. — Текст : электронный // NovaInfo, 2016. — № 56. — С. 336-341. — URL: https://novainfo.ru/article/9052 (дата обращения: 18.05.2023).
