
Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде).
u = Umsin(2πt + Ψ ) = Umsin(ωt + Ψ )
Где u = u(t) — мгновенное значение переменного напряжения [В].
Um — максимальное значение напряжения (амплитудное значение) [В].
f — частота равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с-1)
ω — угловая частота (омега) (единица угловой частоты — рад/с или с-1)
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
U — Действующее значение напряжения [В]:![]()
Рассмотрим параметры напряжения в бытовой электросети.
Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.).
Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения.
- Действующее значение напряжения U = 220 В.
- Амплитудное значение напряжения цепи переменного тока Um = U*√2 = 220 *√2 = 311 В.
- Угловая частота ω = 2πf = 3,14*2*50 = 314 рад/с.
- Начальная фаза Ψ = 0 град.
- Мгновенное значение u = 311sin(314t) В.
Что показывает вольтметр, или математика розетки
Время на прочтение
7 мин
Количество просмотров 106K

О чем эта статья
Сегодня я ненадолго отступлю от своей обычной темы о визуальном программировании контроллеров и обращусь к теме измерений напряжения прямо в ней, в розетке!
Родилась эта статья из дискуссий за чаем, когда разразился спор среди «всезнающих и всеведающих» программистов о том, чего многие из них не понимают, а именно: как измеряется напряжение в розетке, что показывает вольтметр переменного напряжения, чем отличается пиковое и действующие значения напряжений.
Скорее всего, это статья будет интересна тем, кто начинает творить свои устройства. Но, возможно, поможет и кому-то опытному освежить память.
В статье рассказано о том, какие напряжения есть в сети переменного тока, как их измеряют и о том, что следует помнить при проектировании электронных схем.
Всему дано краткое и упрощённое математическое обоснование, чтобы было ясно не только «как», но и «почему».
Кому не интересно читать про интегралы, ГОСТы и фазы — могут сразу переходить к заключению.
Вступление
Когда люди начинают говорить о напряжении в розетке, очень часто стереотип «в розетке 220В» скрывает от их взора реальное положение дел.
Начнем с того, что согласно ГОСТ 29322-2014, сетевое напряжение должно составлять 230В±10% при частоте 50±0,2Гц (межфазное напряжение 400В, напряжение фаза-нейтраль 230В). Но в том же ГОСТ имеется примечание: «Однако системы 220/380 В и 240/415 В до сих пор продолжают применять».
Согласитесь, что это уже совсем не то однозначное «в розетке 220В», к которому мы привыкли. А когда речь начинает идти о «фазном», «линейном», «действующем» и «пиковом» напряжениях — вообще каша получается знатная. Так сколько же вольт в розетке?
Чтобы ответить на этот вопрос начнем с того, как измеряется напряжение в сети переменного тока.
Как измерять переменное напряжение?
Прежде, чем углубиться в дебри цепей переменного тока и напряжения, вспомним школьную физику цепей тока постоянного.
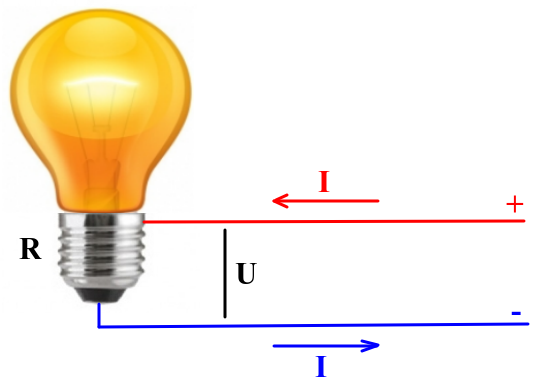
Цепи постоянного тока — вещь простая. Если мы возьмем некоторую активную нагрузку (пусть это будет обычная лампа накаливания, как на рисунке) и воткнем ее в цепь постоянного тока, то все, что происходит в нашей цепи будет характеризоваться всего двумя величинами: напряжением на нагрузке U и током, протекающим через нагрузку I. Мощность, которая потребляется нагрузкой однозначно вычисляется по формуле, известной со школы:
.
Или, если учесть, что по закону Ома
, то мощность P, потребляемую нагрузкой-лампочкой, можно вычислить по формуле
.
С переменным напряжением все куда сложнее: в каждый момент времени — оно может иметь разное мгновенное значение. Следовательно, в разные моменты времени, на нагрузке, подключенной к источнику переменного напряжения (например, на лампе накаливания, воткнутой в розетку) будет выделяться разная мощность. Это очень неудобно с точки зрения описания электрической цепи.
Но нам повезло: форма напряжения в розетке синусоидальная. А синусоида, как известно, полностью описывается тремя параметрами: амплитудой, периодом и фазой. В однофазных сетях (а обычная розетка с двумя дырочками именно и есть однофазная сеть) про фазу можно забыть. На рисунке подробно показаны два периода сетевого однофазного напряжения. Того самого, что в розетке.
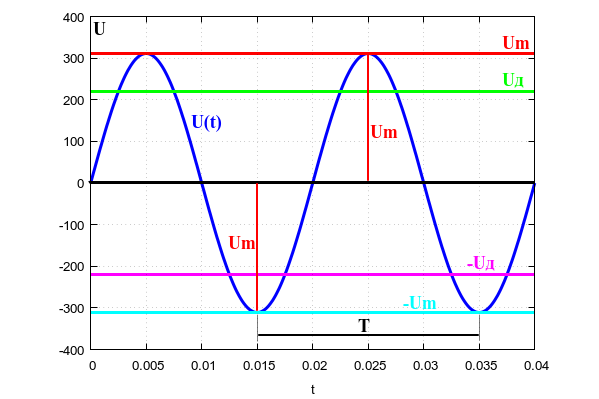
Рассмотрим, что означают все эти буковки на рисунке.
Период T — это время между двумя соседними минимумами или соседними максимумами синусоиды. Для осветительной сети РФ этот период составляет 20 миллисекунд, что соответствует частоте 50Гц. Частота колебаний напряжения электрической сети выдерживается очень точно, до долей процента.
Очевидно, что в любых двух точках синусоиды, отстоящих друг от друга на целое число периодов, напряжения всегда равны между собой.
Амплитуда Um — это максимальное напряжение, пик синусоиды. Про действующее напряжение Uд поговорим чуть ниже.
Напряжение в розетке (или однофазной сети) описывается формулой
где t — текущий момент времени, Um — амплитуда (или пиковое значение) напряжения, T — период сетевого напряжения.
Если с однофазным переменным напряжением более или менее все ясно, то попробуем посчитать мощность, которая выделяется на нашей любимой лампе накаливания, при втыкании ее прямо в розетку.
Так как лампа накаливания является активной нагрузкой (а это значит, что ее сопротивление не зависит от частоты напряжения и тока), то мгновенная мощность, выделяемая на лампе накаливания, воткнутой в розетку, будет вычисляться по формуле
где t — текущий момент времени, а R — сопротивление лампы накаливания при нагретой спирали. Зная амплитуду переменного напряжения Um, можно записать:
Понятно, что мгновенная мощность — неудобный параметр, да и на практике не особо нужный. Поэтому практически обычно применяется мощность, усредненная за период.
Именно усредненная мощность указана на лампочках, нагревателях и прочих бытовых утюгах.
Рассчитывается усредненная мощность в общем случае по формуле:
А для нашей синусоиды — по гораздо более простой формуле:
Можете сами подставить вместо
функцию
и взять интеграл, если не верите.
Не думайте, что про мощность я вспомнил просто так, из вредности. Сейчас поймете, зачем она нам была нужна. Переходим к следующему вопросу.
Что же показывает вольтметр?
Для цепей постоянного тока, тут все однозначно — вольтметр показывает единственное напряжение между двумя контактами.
С цепями переменного тока все опять сложнее. Некоторые (и этих некоторых не так мало, как я убедился) считают, что вольтметр показывает пиковое значение напряжения Um, но это не так!
На самом деле, вольтметры обычно показывают действующее или эффективное, оно же среднеквадратичное, напряжение в сети Uд.
Разумеется, речь идет о вольтметрах переменного напряжения! Поэтому, если будете измерять вольтметром напряжение сети, обязательно убедитесь, что он находится в режиме измерения переменного напряжения.
Оговорюсь, что «пиковые вольтметры», показывающие амплитудные значения напряжения, тоже существуют, но на практике при измерении напряжения питающей сети в быту обычно не применяются.
Разберемся, почему такие сложности. Почему бы не измерять просто амплитуду? Зачем выдумали какое-то «действующее значение» напряжения?
А все дело в потребляемой мощности. Я ведь не просто так писал о ней. Дело в том, что действующее (эффективное) значение переменного напряжения равно величине такого постоянного напряжения, которое за время, равное одному периоду этого переменного напряжения, произведет такую же работу, что и рассматриваемое переменное напряжение.
Или, по-простому, лампочка накаливания будет светить одинаково ярко, воткнем ли мы ее в сеть постоянного напряжения 220В или в цепь переменного тока с действующим значением напряжения 220В.
Для тех, кто уже знаком с интегралами или еще не забыл математику, приведу общую формулу расчета действующего напряжения произвольной формы:
Из этой формулы также становится ясно, почему действующее (эффективное) значение переменного напряжения также называют «среднеквадратичным».
Заметим, что подкоренное выражение и есть та самая «усредненная за период мощность», стоит только поделить это выражение на сопротивление нагрузки R.
Применительно к синусоидальной форме напряжения, страшный интеграл после несложных преобразований превратится в простую формулу:
где Uд — действующее или среднеквадратичное значение напряжение (то самое, которое обычно показывает вольтметр), а Um — амплитудное значение.
Действующее напряжение хорошо тем, что для активной нагрузки, расчет усредненной мощности полностью совпадает с расчетом мощности на постоянном токе:
Это и не удивительно, если вспомнить определение действующего значения напряжения, которое было дано чуть выше.
Ну и, наконец, посчитаем, чему же равна амплитуда напряжения в розетке “на 220В“:
В худшем случае, если у вас сеть на 240В, да еще и с допуском +10%, амплитуда будет аж
!
Поэтому, если хотите, чтобы ваши устройства, питающиеся от сети, работали стабильно и не сгорали, выбирайте элементы, которые выдерживают пиковые напряжения не менее 400В. Разумеется, речь идет об элементах, на которые непосредственно подаётся сетевое напряжение.
Отмечу, что для не-синусоидальной формы сигнала действующее значение напряжения рассчитывается по иным формулам. Кому интересно — могут сами взять интегралы или обратиться к справочникам. Нас же интересует питающая сеть, а там всегда должна быть синусоида.
Фазы, фазы, фазы…
Помимо обычной однофазной осветительной сети ~220В все слышали и о трехфазной сети ~380В. Что такое 380В? А это межфазное эффективное напряжение.
Помните, я сказал, что в однофазной сети про фазу синусоиды можно забыть? Так вот, в трехфазной сети этого делать нельзя!
Если говорить по простому, то фаза — это сдвиг во времени одной синусоиды относительно другой. В однофазной сети мы всегда могли принять за начало отсчета любой момент времени — на расчеты это не влияло. В трехфазной сети необходимо учитывать насколько одна синусоида отстоит от другой. В трехфазных сетях переменного тока каждая из фаз отстоит от другой на треть периода или на 120 градусов. Напомню, что период измеряется также в градусах и полный период равен 360 градусов.
Если мы возьмем осциллограф с тремя лучами и прицепимся к трем фазам и одному нулю, то увидим такую картину.
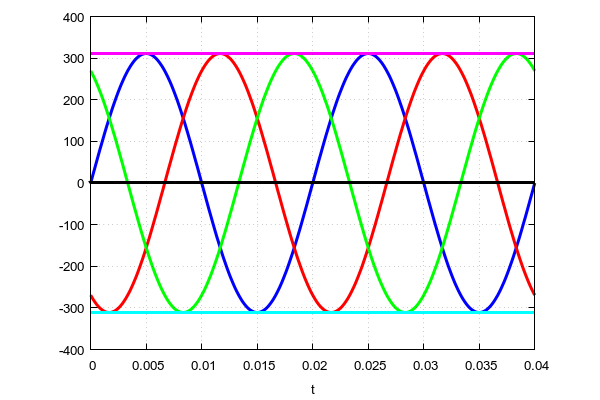
«Синяя» фаза — начинается от нуля отсчета. «Красная» фаза — на треть периода (120 градусов) позже. И, наконец «зеленая» фаза начинается на две трети периода (240 градусов) позже «синей». Все фазы абсолютно симметричны друг относительно друга.
Какую именно фазу брать за точку отсчета — не важно. Картина будет одинаковой.
Математически можно записать уравнения всех трех фаз:
«Синяя» фаза:
«Красная» фаза:
«Зеленая» фаза:
Если измерить напряжение между любой из фаз и нулем в трехфазной сети — то получим обычные 220В (или 230В или 240В — как повезет, см. ГОСТ).
А если измерить напряжение между двумя фазами — то получим 380В (или 400В или 415В — не забываем об этом).
То есть трехфазная сеть — многолика. Ее можно использовать как три однофазные сети с напряжением 220В или как одну трехфазную сеть с напряжением 380В.
Откуда взялось 380В? А вот откуда.
Если мы подставим в формулу расчета действующего напряжения наши данные о двух любых фазах, то получим:
или, упрощая:
Uдф — действующее межфазное, оно же линейное напряжение.
Учитывая, что амплитуда каждой фазы
получим, что
для межфазного напряжения. На рисунке наглядно показано, как образуется межфазное напряжение, которое обозначено F1-F2 из двух фазных напряжений фаз F1 и F2. Напряжение фаз F1 и F2 измеряется относительно нулевого провода. Линейное напряжение F1-F2 измеряется между двумя разными фазными проводами.
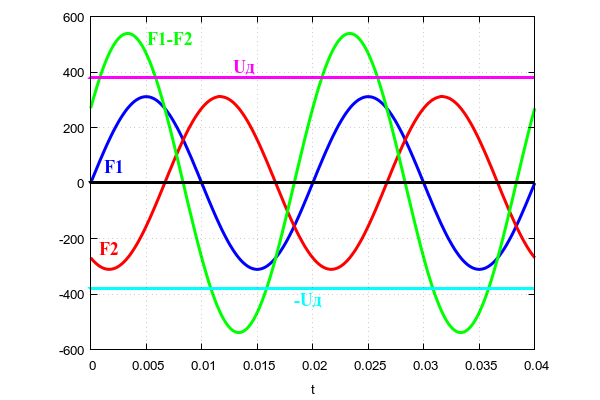
Как видим, что действующее межфазное напряжение больше амплитуды синусоидального напряжения одной фазы.
Амплитуда межфазного напряжения составляет:
Для наихудшего случая (сеть 240В и межфазное напряжение 415В, да еще 10% сверху) амплитуда межфазного напряжения составит:
Учтите это при работе в трехфазных сетях и выбирайте элементы, рассчитанные не менее, чем на 650В, если им предстоит работать между двумя фазами!
Надеюсь, теперь понятно что показывает вольтметр переменного тока?
Заключение
Итак, очень кратко, почти на пальцах, мы ознакомились с тем какие напряжения действуют в бытовых сетях переменного тока. Подведем краткие итоги всего, изложенного выше.
- Фазное напряжение — это напряжение между фазой и нулевым проводом.
- Линейное или межфазное напряжение — это напряжение между двумя разными фазными проводами одной трехфазной сети.
- В сетях переменного тока РФ действуют три, хоть и близких, но разных стандарта (фазное/линейное): 220В/380В, 230В/400В и 240В/415В переменного тока с частотой 50Гц.
- Вольтметр переменного тока обычно показывает действующее (оно же среднеквадратичное, оно же эффективное) напряжение, которое в
раза меньше, чем пиковое (амплитудное) напряжение в сети.
- В наихудшем с точки зрения стандартов случае пиковое фазное напряжение составляет примерно 373В, а пиковое линейное напряжение — 645B. Это следует учитывать при разработке электронных схем.
Надеюсь эта статья помогла кому-то разобраться в теме и ответить для себя на некоторые вопросы.
Отправлять предложения и пожелания, замеченные опечатки и просто мнения можно в комментарии или на почту: shiotiny@yandex.ru.
Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.
Что такое переменное напряжение?
Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.
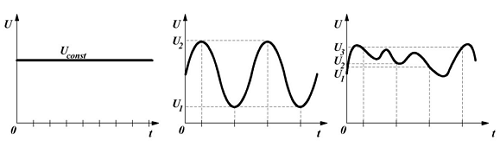
Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.
Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид
![]()
где Т – период.
Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда
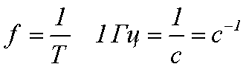
Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже
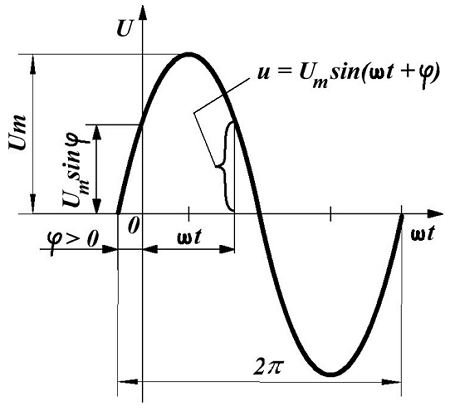 Синусоидальное переменное напряжение.
Синусоидальное переменное напряжение.
Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.
Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением
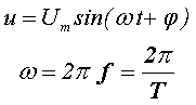
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла),
φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.
Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.
Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.
Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда
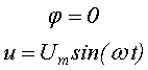
В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.
Что такое действующее напряжение переменного тока?
Как я писал выше, одним из основных параметров переменного напряжения является амплитуда Um, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному Um ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?
Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения
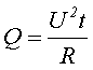
Для переменного напряжения мгновенное значение выделяемой энергии составит
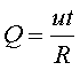
где u – мгновенное значение напряжения
Тогда количество энергии за полный период от t0 = 0 до t1 = T составит
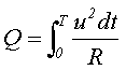
Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения
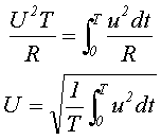
Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.
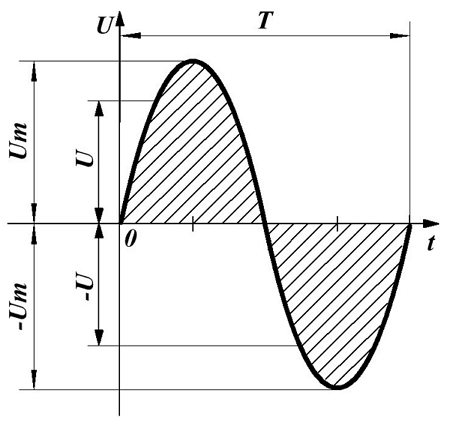
Действующее значение синусоидального напряжения.
Вычислим действующее значение синусоидального напряжения
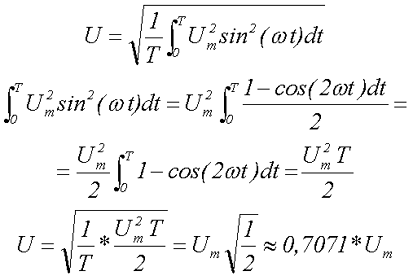
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.
Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение
![]()
Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения
![]()
Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.
С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.
Что такое среднее значение переменного напряжения?
Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением
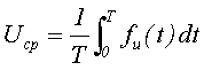
где Т – период переменного напряжения,
fu(t) – функциональная зависимость напряжения от времени.
Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.
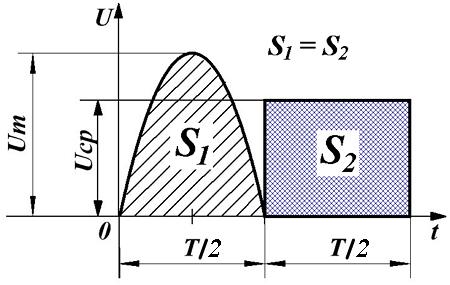
Среднее значение переменного напряжения.
В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.
Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно
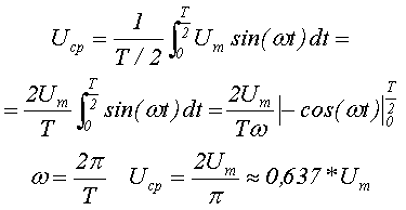
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла).
Какие коэффициенты, характеризуют переменное напряжение?
Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:
1. Коэффициент формы переменного напряжения kф – показывает как относится действующее значение переменного напряжения U к его среднему значению Ucp.
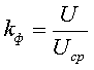
Так для синусоидального напряжения коэффициент формы составит
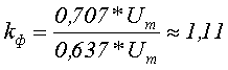
2. Коэффициент амплитуды переменного напряжения kа – показывает как относится амплитудное значение переменного напряжения Um к его действующему значению U
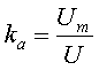
Так для синусоидального напряжения коэффициент амплитуды составит
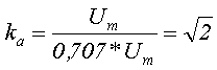
На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.
Что такое действующее, среднеквадратичное, эффективное напряжение или ток
Среднее значение переменного синусоидального напряжения или тока
Говоря о величине, изменяющейся по синусоидальному (гармоническому) закону, можно за половину периода определить ее среднее значение. Поскольку ток в сети у нас в подавляющем большинстве случаев синусоидальный, то для этого тока также легко может быть найдена средняя его величина (за половину периода), достаточно прибегнуть к операции интегрирования, установив пределы от 0 до Т/2. В результате получим:
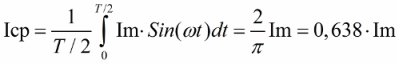
Подставив Пи = 3,14, найдем среднюю, за половину периода, величину синусоидального тока в зависимости от его амплитуды. Аналогичным образом находится среднее значение синусоидальной ЭДС или синусоидального напряжения U:
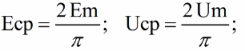
Действующее значение тока I или напряжения U
Однако среднее значение не так широко применяется на практике, как действующее значение синусоидального тока или напряжения. Действующее значение синусоидально меняющейся во времени величины — есть среднеквадратичное, другими словами — эффективное ее значение.
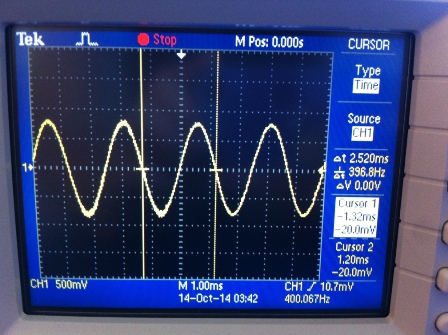
Эффективное (или действующее) значение тока или напряжения находится так же, путем интегрирования, но уже по отношению к квадратам, и с последующим извлечением квадратного корня, причем пределы интегрирования теперь — целый период синусоидальной функции.
Итак, для тока будем иметь:
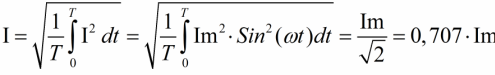
Подставив значение корня из 2, получим формулу для нахождения эффективного (действующего, среднеквадратичного) значения тока, напряжения, ЭДС — по отношению к амплитудному значению. Эту формулу можно встретить очень часто, ее используют всюду в расчетах, связанных с цепями переменного синусоидального тока:
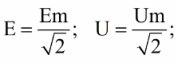
С практической точки зрения, если сравнить тепловое действие тока переменного синусоидального с тепловым действием тока постоянного непрерывного, на протяжении одного и того же периода времени, на одной и той же активной нагрузке, то выяснится, что выделенная за период синусоидального переменного тока теплота окажется равна выделенной за это же время теплоте от тока постоянного, при условии, что величина постоянного тока будет меньше амплитуды тока переменного в корень из 2 раз:
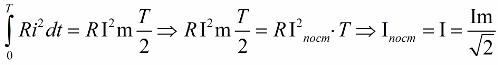
Это значит, что действующее (эффективное, среднеквадратичное) значение синусоидального переменного тока численно равно такому значению постоянного тока, при котором тепловое действие (выделяемое количество теплоты) этого постоянного тока на активном сопротивлении за один период синусоиды равно тепловому действию данного синусоидального тока за тот же период.
Аналогичным образом находится действующее (эффективное, среднеквадратичное) значение синусоидального напряжения или синусоидальной ЭДС.

Подавляющее большинство современных портативных измерительных приборов, измеряя переменный ток или переменное напряжение, показывают именно действующее значение измеряемой величины, то есть среднеквадратичную величину, а не ее амплитуду и не среднее значение за полпериода.
Если других уточняющих настроек на приборе нет, а стоит значок
U – измерены будут действующие значения тока и напряжения. Обозначения для конкретно амплитуды или конкретно действующего — Im (m — maximum – максимум, амплитуда) или Irms (rms — Root Mean Square – среднеквадратичное значение).
Источник
Напряжение цепи переменного тока

Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде).
Где u = u(t) — мгновенное значение переменного напряжения [В].
Um — максимальное значение напряжения (амплитудное значение) [В].
f — частота равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с -1 )
ω — угловая частота (омега) (единица угловой частоты — рад/с или с -1 )
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
U — Действующее значение напряжения [В]:
Рассмотрим параметры напряжения в бытовой электросети.
Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.).
Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения.
- Действующее значение напряжения U = 220 В.
- Амплитудное значение напряжения цепи переменного токаUm = U*√2 = 220 *√2 = 311 В.
- Угловая частота ω = 2πf = 3,14*2*50 = 314рад/с.
- Начальная фаза Ψ = 0град.
- Мгновенное значениеu= 311sin(314t)В.
Источник
Переменный ток

Господа, в прошлой статье мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока. Сегодня про него и поговорим!
Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.
Итак, действующее (или среднеквадратичное) значение переменного тока – это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток. Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.
Итак, у нас есть переменный ток. Допустим, синусоидальный. У него своя амплитуда Аm и период Tпериод (ну или частота f). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R и на этом резисторе выделяется энергия. За один период Tпериод нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз . Допустим, мы насчитали, что за один период Tпериод синусоидального тока выделится Q джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время Tпериод выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли? 
Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье , закон изменения мощности переменного тока равен

Количество выделившейся энергии при работе тока за время Tпериод – соответственно, равно интегралу за время периода Tпериод:

Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками  .
.
Итак, как его нам брать? Ну, величины Im 2 и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени из курса тригонометрии. Надеюсь, вы ее помните  . А если нет, то напомню еще раз:
. А если нет, то напомню еще раз:


Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл – это площадь.

Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!

Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.
Итак, отбрасывая интеграл с косинусом, получаем

Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен

И, таким образом, получаем ответ

Это мы получили количество джоулей, которое выделится на резисторе R при протекании через него синусоидального тока амплитудой Im в течении периода Tпериод. Теперь, чтобы найти чему в данном случае равен действующий ток нам надо исходить из того, что на том же самом резисторе R за то же самое время Tпериод выделится то же самое количество энергии Q. Поэтому мы можем записать

Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца . А мы тем временем выразим действующее значение тока I действ. из этого выражения, предварительно сократив все, что можно

Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения. Хорошо запомните этот результат, это важный вывод.
Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения. При этом у нас зависимость мощности от времени примет вот такой вид

Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно

Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.
Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.
Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина – амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках – это действующее значение! Вольтметры и амперметры , включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать


Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.

Рисунок 1 – Закон изменения напряжения в розетках
И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа. Смотрел я его через делитель напряжения 1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.
ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно! Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления, на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.

Рисунок 2 – Осциллограмма напряжения в розетке (делитель 1:5)
На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота – ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна

Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.
На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Источник
Свободные электромагнитные колебания в контуре быстро затухают. Поэтому они практически не используются. Наиболее важное практическое значение имеют незатухающие вынужденные колебания.
Определение
Переменный ток — вынужденные электромагнитные колебания.
Ток в осветительной сети квартиры, ток, применяемый на заводах и фабриках, представляет собой переменный ток. В нем сила тока и напряжение изменяются со временем по гармоническому закону. Колебания легко обнаружить с помощью осциллографа. Если на вертикально отклоняющие пластины осциллографа подать напряжение от сети, то временная развертка на экране будет представлять сбой синусоиду:
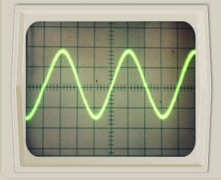
Зная скорость движения луча в горизонтальном направлении (она определяется частотой пилообразного напряжения), можно определить частоту колебаний.
Определение
Частота переменного тока — это количество колебаний за 1 с.
Стандартная частота переменного промышленного тока составляет 50 Гц. Это значит, что на протяжении 1 секунды ток 50 раз течет в одну сторону и 50 раз — в другую. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц.
Если напряжение на концах цепи меняется по гармоническому закону, то напряженность электрического поля внутри проводника будет также меняться гармонически. Эти гармонические изменения напряженности поля вызовут гармонические колебания скорости упорядоченного движения заряженных частиц, и, следовательно, гармонические колебания силы тока.
Внимание!
При изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменение поля происходит с большой скоростью, но она не бесконечно большая. Она равна скорости света (3∙108 м/с).
Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока (см. рисунок ниже).
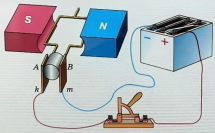
Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла α между нормалью к рамке и вектором магнитной индукции.
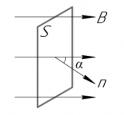
Численно магнитный поток определяется формулой:
Φ=BScosα
При равномерном вращении рамки угол α увеличивается пропорционально времени:
α=2πnt
где n — частота вращения. Поэтому поток магнитной индукции меняется гармонически:
Φ=BScos2πnt
Здесь множитель 2πn представляет собой число колебаний магнитного потока за 2π секунд. Это не что иное, как циклическая частота колебаний:
ω=2πn
Следовательно:
Φ=BScosωt
Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «минус» скорости изменения потока магнитной индукции, т.е. производной потока магнитной индукции по времени:
e=−Φ´=−BS(cosωt)´=BSωsinωt=εmaxsinωt
εmax — амплитуда ЭДС индукции, равная:
εmax=BSω
Напряжение в цепи переменного тока может меняться по закону синуса или по закону косинуса:
u=Umaxsinωt
u=Umaxcosωt
где Umax — амплитуда напряжения (максимальное по модулю значение напряжения).
Сила тока меняется с той частотой, что и напряжение — ω. Но колебания тока необязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока i в любой момент времени определяется по формуле:
i=Imaxsin(ωt+φс)
где Imax — амплитуда силы тока (максимальное по модулю значение силы тока), φс — разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Пример №1. Найти напряжение в цепи переменного тока в момент времени t = π, если циклическая частота электромагнитных колебаний равна 300,25 Гц, а амплитуда напряжения составляет 12В. Считать, что напряжения меняется по закону косинуса.
u=Umaxcosωt=12cos300,25π=12√22≈8,5 (В).
Активное сопротивление в цепи переменного тока
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (см. рисунок ниже).
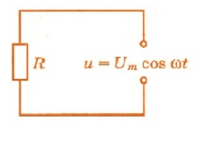
Внимание! Ранее под величиной R мы понимали электрическое сопротивление. Но правильно его называть сопротивлением активным. Дело в том, что в цепи переменного тока могут быть сопротивления иного характера. Сопротивление же R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Будем считать, что напряжение на зажимах цепи меняется по закону косинуса:
u=Umaxcosωt
Для нахождения мгновенного значения силы тока мы можем воспользоваться законом Ома, так как эта величина прямо пропорционально мгновенному значению напряжения:
i=uR=UmaxcosωtR=Imaxcosωt
В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством:
Imax=UmaxR
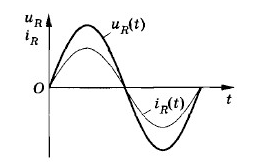
Мощность в цепи с резистором
В цепи переменного тока сила тока и напряжения меняются быстро, поэтому количество выделяемой энергии меняется так же быстро. Но заметить эти изменения невозможно. Чтобы найти среднюю мощность на участке цепи за много периодов, достаточно найти среднюю мощность за один период.
Определение
Средняя за период мощность переменного тока — отношение суммарной энергии, поступающей в цепь за период, к этому периоду.
Мощность постоянного тока определяется формулой:
P=I2R
Следовательно, мгновенная мощность в цепи переменного тока на участке с активным сопротивлением R равна:
p=i2R
Подставим в это выражение полученное ранее значение мгновенной силы переменного тока и получим:
p=(Imaxcosωt)2R
Вспомним из курса математики:
cos2α=1+cos2α2
Отсюда:
p=I2max2R(1+cos2ωt)=I2maxR2+I2maxR2cos2ωt
График зависимости мгновенной мощности от времени:
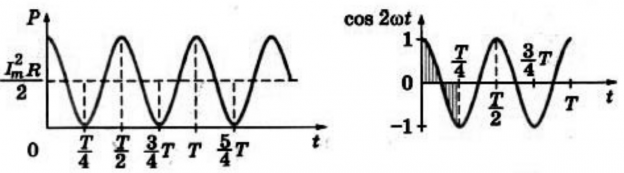
На протяжении первой четверти периода, когда cos2ωt>0, мощность в любой момент времени больше величины I2maxR2. На протяжении второй четверти периода, когда cos2ωt<0, мощность в любой момент времени меньше этой величины. Среднее за период значение cos2ωt=0, следовательно, средняя за период мощность равна I2maxR2.
Средняя мощность −p равна:
−p=I2maxR2=−i2R
Пример №2. Сила переменного тока в цепи меняется по закону i=Imaxcosωt. Определить мгновенную мощность в момент времени t = 1 с, если циклическая частота колебаний ω = 100π Гц при сопротивлении R = 10 Ом. Амплитуда силы тока равна 1 А.
p=(Imaxcosωt)2R=10(1·cos(100π·1)2=10 (Дж)
Действующие значения силы тока и напряжения
Из предыдущей формулы видно, что среднее значение квадрата силы тока равно половине квадрата амплитуды силы переменного тока:
−i2=I2max2
Определение
Действующее значение силы переменного тока — величина, равная квадратному корню, взятому из среднего значения квадрата тока. Обозначается как I.
I=√−i2=Imax√2
Смысл действующего значения силы переменного тока заключается в том, что оно равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за это же время.
Аналогично определяется действующее значение напряжения U:
U=√−u2=Umax√2
Именно действующие значения силы тока и напряжения определяют мощность P переменного тока:
P=I2R=UI
Пример №3. Найти мощность переменного тока, если амплитуда силы тока равна 2 А, а сопротивление цепи равно 5 Ом.
P=I2R
I=Imax√2
P=(Imax√2)2R=I2max2R=222·5=10 ⎛⎝Дж⎞⎠
Задание EF22720
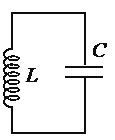 В идеальном колебательном контуре (см. рисунок) напряжение между обкладками конденсатора меняется по закону UC = U0cos ωt, где U0 = 5 В, ω = 1000π с–1. Определите период колебаний напряжения на конденсаторе.
В идеальном колебательном контуре (см. рисунок) напряжение между обкладками конденсатора меняется по закону UC = U0cos ωt, где U0 = 5 В, ω = 1000π с–1. Определите период колебаний напряжения на конденсаторе.
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу Томсона.
3.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• Закон изменения напряжения между обкладками конденсатора: UC=U0cosωt.
• Амплитуда напряжения: U0=5 В.
• Циклическая частота колебаний: ω = 1000π с–1.
Запишем формулу Томсона:
T=2πω=2π1000π=21000=0,002 (с)
Ответ: 0,002
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18735
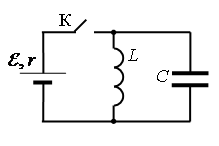 В электрической цепи, показанной на рисунке, ключ К длительное время замкнут, E=6 В, r = 2 Ом, L = 1 мГн. В момент t = 0 ключ К размыкают. Амплитуда напряжения на конденсаторе в ходе возникших в контуре электромагнитных колебаний равна ЭДС источника. В какой момент времени напряжение на конденсаторе в первый раз достигнет значения E? Сопротивлением проводов и активным сопротивлением катушки индуктивности пренебречь. Ответ запишите в мкс.
В электрической цепи, показанной на рисунке, ключ К длительное время замкнут, E=6 В, r = 2 Ом, L = 1 мГн. В момент t = 0 ключ К размыкают. Амплитуда напряжения на конденсаторе в ходе возникших в контуре электромагнитных колебаний равна ЭДС источника. В какой момент времени напряжение на конденсаторе в первый раз достигнет значения E? Сопротивлением проводов и активным сопротивлением катушки индуктивности пренебречь. Ответ запишите в мкс.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Описать, что происходит в момент замыкания и размыкания цепи.
3.Выполнить решение задачи в общем виде.
4.Вычислить искомую величину, подставив известные данные.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε=5 В.
• Амплитуда колебаний напряжения на конденсаторе: UCmax=5 В.
• Сопротивление ЭДС источника тока: r = 2 Ом.
• Индуктивность катушки: L = 1 мГн.
1 мГн = 10–3 Гн
Перед размыканием ключа К ток через конденсатор не идет, по катушке течёт ток:
I0=εr
Напряжение на конденсаторе в начальный момент времени равно нулю, так как оно равно нулю на катушке: U0C=0 В.
После размыкания ключа К в контуре возникают гармонические колебания напряжения между обкладками конденсатора и тока в контуре. Благодаря начальному условию (U0C=0 В) потенциал верхней обкладки конденсатора относительно нижней начинает меняться по закону:
u=−UCmaxsinωt
Знак «–» в формуле связан с тем, что сразу после размыкания ключа К ток приносит положительный заряд на нижнюю обкладку конденсатора.
Циклическую частоту выразим из формулы Томсона:
ω=2πT=1√LC
Энергия электромагнитных колебаний в контуре сохраняется. Она определяется формулой:
W=Li22+Cu22=CU2Cmax2=LI202
Выразим максимальное напряжение на конденсаторе:
CU2Cmax=LI20
UCmax=I0√LC
Учтем, что амплитуда напряжения на конденсаторе равна напряжению источника тока, а I0=εr. Тогда получим:
UCmax=ε=I0r=I0√LC
Отсюда:
√LC=r
C=Lr2
Период колебаний в контуре определим через формулу Томсона:
T=2π√LC=2π√LLr2=2πLr
Вспомним зависимость напряжения от времени:
u=−UCmaxsinωt
Подставим известные данные для искомого момента времени:
5=−5sinωt
Синус должен быть равен «–1» Это возможно, если с начального момента времени пройдет четверть периода:
t=T4=2π4Lr=π210−32≈7,85·10−6(с)=7,85 (мкс)
Ответ: 7,85
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18116
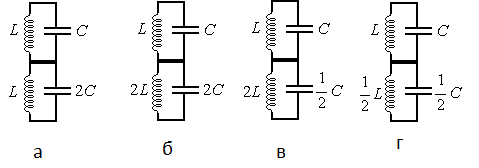
Ученик изучает зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Какие два контура он должен выбрать для этого исследования?
Алгоритм решения
- Выделить цель эксперимента.
- Установить, какие величины для достижения цели эксперимента должны меняться, а какие — оставаться постоянными.
- Выбрать верную пару контуров
Решение
Цель эксперимента — изучить зависимость периода электромагнитных колебаний в контуре от ёмкости конденсатора. Следовательно, емкости конденсатора должна быть единственной меняющейся величиной. При этом все другие величины должны оставаться постоянными. Поэтому катушки индуктивности должны быть одинаковыми, но конденсаторы — разные. Этому условию соответствует рисунок «а».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18656
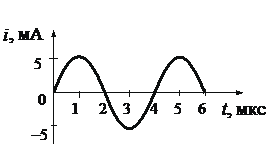 На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.
На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.
Алгоритм решения
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.5k
