Содержание:
Расчет электрических цепей постоянного тока:
Основная цель расчета электрической цепи заключается в определении токов в ее ветвях. Зная токи, нетрудно найти напряжения и мощности ветвей и отдельных элементов цепи.
Величины токов, напряжений, мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования и приборов во всех участках электрической цепи.
Связь между э.д.с., напряжениями и токами линейных электрических цепей выражается линейными уравнениями, т. е. уравнениями первой степени, поэтому для расчета их применяются аналитические методы с обычными алгебраическими преобразованиями.
Законы Кирхгофа
Для расчета электрических цепей наряду с законом Ома применяются два закона Кирхгофа, являющиеся следствиями закона сохранения энергии.
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлам электрических цепей:
в ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю:

В эту сумму токи входят с разными знаками в зависимости от направления их по отношению к узлу. На основании первого закона Кирхгофа для каждого узла можно составить уравнение токов. Например, для точки 3 схемы рис. 3.16 такое уравнение имеет вид
I1 + I2 — I4 — I7 = 0.
В этом уравнении токи, направленные к узлу, условно взяты положительными, а токи, направленные от узла, — отрицательными:
I1 + I2 = I4 + I7. (4.2)
Уравнение (4.2) позволяет дать другую формулировку первого закона Кирхгофа:
сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла.
Этот закон следует из принципа непрерывности тока. Если допустить преобладание в узле токов одного направления, то заряд одного знака должен накапливаться, а потенциал узловой точки непрерывно изменяться, что в реальных цепях не наблюдается.
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрических цепей:
в контуре электрической цепи алгебраическая сумма напряжений на его ветвях равна нулю:

Для доказательства второго закона Кирхгофа обойдем контур 1-2-3-4-5-6-1 в схеме рис. 3.16 по часовой стрелке и запишем выражения потенциалов точек контура при указанных направлениях токов в ветвях (выбраны произвольно). Обход начнем от точки 1, потенциал которой V1. Потенциал каждой последующей точки выразим относительно точки предыдущей: V2 = V1 + Е1; V3 = V2 — I1R1; V4 = V3 — I4R4; V5 = V4 — E3; V6 = V5 + I6R6; V1 = V6 — I3R3.
Изменение потенциала по выбранному контуру должно быть равно нулю, так как оно выражает работу, затраченную на перемещение частиц, обладающих вместе единицей заряда, по замкнутому пути в электрических полях источников и приемников энергии. Таким образом, в замкнутом контуре
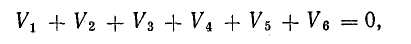
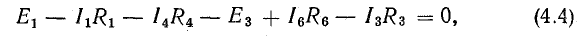
или
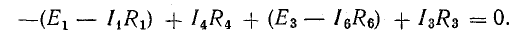
В этом уравнении напряжения ветвей
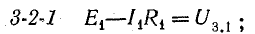
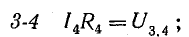
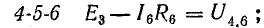
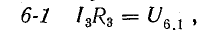
поэтому 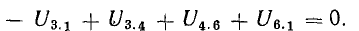
В уравнении (4.4) напряжения, направленные по обходу контура, считаются положительными, а направленные против обхода — отрицательными.
Уравнение (4.4) перепишем в следующем виде:
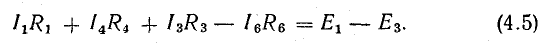
Уравнение (4.5) позволяет дать другую формулировку второго закона Кирхгофа:
в контуре электрической цепи алгебраическая сумма падений напряжения на пассивных элементах равна алгебраической сумме э. д. с. этого контура:

Другим контурам соответствуют другие уравнения, которые нетрудно написать, не прибегая к выражениям потенциалов точек контура.
Для этого можно пользоваться следующим правилом. В левую часть уравнения следует записать алгебраическую сумму падений напряжения в пассивных элементах контура, а в правую—алгебраическую сумму э.д.с., встречающихся при обходе контура.
При этом положительными считаются токи и э. д. с., направление которых совпадает с направлением обхода.
Согласно этому правилу, запишем уравнения для двух других контуров схемы, представленной на рис. 3.16:
для 1-2-3-6-1
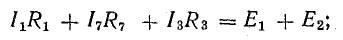
для 3-4-6-3
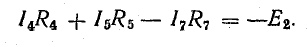
Неразветвленная электрическая цепь
Элементы неразветвленной электрической цепи соединены между собой последовательно.
Отличительной особенностью последовательного соединения является то, что электрический ток во всех участках цепи один и тот же.
Общий случай последовательного соединения
Рассмотрим общий случай последовательного соединения источников и приемников электрической энергии (рис. 4.1), пренебрегая внутренними сопротивлениями источников. Составим уравнение по второму закону Кирхгофа, произвольно задавшись направлением тока в цепи и направлением обхода контура (например, по часовой стрелке):
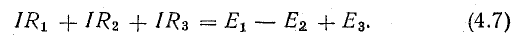
Ток в цепи

При обходе контура видно, что относительно направления обхода э. д. с. Е1 и Е3 направлены одинаково, т. е. согласно, а э. д. с. Е2 — им навстречу.
Ток в цепи определяется действием всех трех э.д.с., и при заданных направлениях э. д. с. и тока нетрудно установить, что элементы с э. д. с. E1 и Е3 вырабатывают электрическую энергию, а элемент с э. д. с. Е2 ее потребляет. Если в качестве источников э. д. с. в данном случае предположить аккумуляторы, то источники Е1 и Е3 разряжаются, а источник Е2 заряжается.
В элементах цепи, характеризующихся сопротивлениями R1, R2 и R3, электрическая энергия преобразуется в тепловую. Рассматривая в качестве примера схему рис. 4.1, нетрудно убедиться в том, что второй закон Кирхгофа является следствием закона сохранения энергии в применении его к контуру электрической цепи.
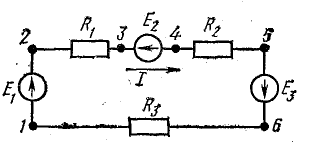
Рис. 4.1. Схема неразветвленной электрической цепи
Для этого достаточно умножить уравнение (4.7) на I, перенеся предварительно Е2 в левую часть:
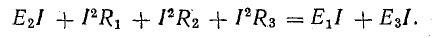
Получим уравнение баланса мощности – для рассматриваемой цепи: сумма мощностей источников электрической энергии равна сумме мощностей приемников.
Ток в цепи с последовательным соединением элементов (рис. 4.1) не изменится и баланс мощностей сохранится, если произвести перестановку элементов цепи, сгруппировав э. д. с. и сопротивления, как показано на рис. 4.2, а.
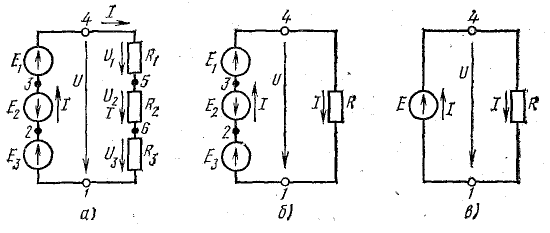
Рис. 4.2. Преобразование схемы неразветвленной электрической цепи
Последовательное соединение пассивных элементов
Участок цепи 4-5-6-1 представляет собой последовательное соединение резисторов. На рассматриваемом участке действует напряжение U, равное алгебраической сумме э. д. с. левой части схемы [см. правую часть уравнения (4.7)]. Это напряжение равно также сумме падений напряжения в правой части схемы [см. левую часть уравнения (4.7)].
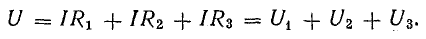
Вынеся I за скобку, получим
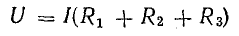
или
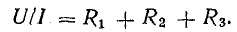
Отношение U/I = R есть некоторое сопротивление, эквивалентное по своему действию всем трем сопротивлениям:
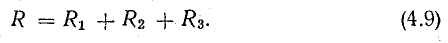
Это равенство позволяет на участке 4-5-6-1 три сопротивления заменить одним (эквивалентным) и получить более простую схему (рис. 4.2, б) при условии неизменности тока в цепи и сохранении того же баланса мощностей. Этот вывод можно распространить на любое число последовательно включенных пассивных элементов:

т. е. общее сопротивление неразветвленной цепи равно сумме сопротивлений ее участков.
Последовательное соединение источников э.д.с.
Участок 1-2-3-4 цепи на рис. 4.2, а представляет собой последовательное соединение источников э. д. с. Напряжение между точками 4-1 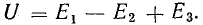
Последнее равенство позволяет на участке 1-2-3-4 три э. д. с. заменить одной (эквивалентной)

и получить более простую схему (рис. 4.2, в), в которой только одна (эквивалентная) э. д. с. Е.
Этот вывод можно распространить на любое число последовательно включенных источников. Если э. д. с. всех источников равны и направлены согласно, как это имеет место при включении аккумуляторных элементов в батарее, то общая э. д. с. может быть определена по формуле

где Еn — э. д. с. одного элемента; n — число элементов в батарее.
Согласно составленной эквивалентной схеме (рис. 4.2, в),
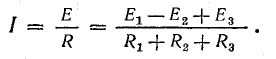
Потенциальная диаграмма
В схеме, представленной на рис. 4.1, при переходе от точки 1 к точке 2 потенциал повышается на величину Е1, а при переходе от точки 2 к точке 3 — снижается на величину U2.3 = IR1. При переходе от точки 3 к точке 4 потенциал понижается на величину U3.4 = —E2.
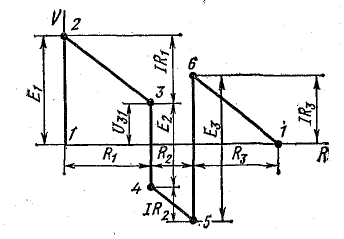
Рис. 4.3. Потенциальная диаграмма электрической цепи
Изменение потенциалов в электрической цепи можно наглядно изобразить графически в виде потенциальной диаграммы.
Потенциальная диаграмма представляет собой график изменения потенциала при обходе цепи, построенный в прямоугольной системе координат, в которой по оси абсцисс откладываются в определенном масштабе сопротивления участков цепи, а по оси ординат — потенциалы соответствующих точек. Потенциальная диаграмма цепи, изображенной на рис. 4.1, показана на рис. 4.3.
Потенциалы точек цепи найдены согласно равенствам
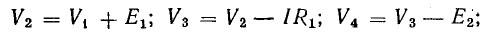
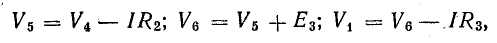
причем потенциал точки 1 принят равным нулю.
Поскольку внутренние сопротивления источников э. д. с. приняты равными нулю, при переходе через эти элементы потенциалы изменяются скачком.
Задача 4.3.
Генератор постоянного тока, аккумуляторная батарея и два резистора с постоянным сопротивлением составляют неразветвленную цепь Э. д. с. генератора Eг = 120 В; внутреннее сопротивление rг = 1,0 Ом, э. д. с. батареи Еа = 72 В, внутреннее сопротивление rа = 3 Ом, R1 = 16 Ом, R2 = 12 Ом.
Определить ток в цепи, составить баланс мощностей и построить потенциальную диаграмму цепи.
Решение. По условию задачи составлена схема (рис 4.4), из которой видно, что генератор и аккумуляторная батарея включены согласно: относительно произвольно выбранного направления обхода цепи обе э. д. с. направлены одинаково.
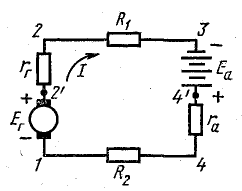
Рис. 4.4. К задаче 4.3
Эквивалентная э. д. с. цепи
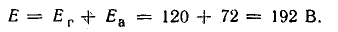
Эквивалентное внутреннее сопротивление
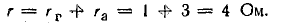
Эквивалентное сопротивление нагрузки
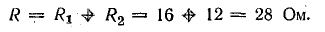
Ток в цепи
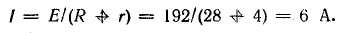
Для составления баланса мощностей найдем мощность каждого элемента цепи:
генератора
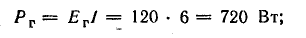
аккумуляторной батареи
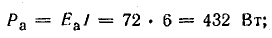
потерь внутри генератора
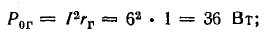
потерь внутри аккумуляторной батареи
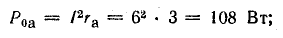
потребления в резисторе R1
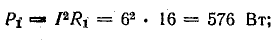
потребления в резисторе R2
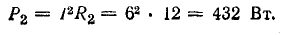
Баланс мощностей (общая мощность источников энергии равна суммарной мощности потребления)

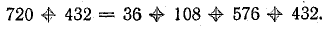
Для построения потенциальной диаграммы найдем потенциалы точек цепи, полагая потенциал точки 1 V1 = 0:
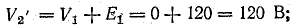
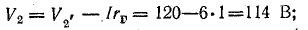
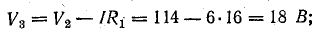
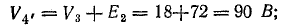
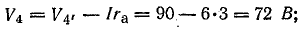
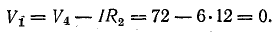
Потенциальная диаграмма показана на рис. 4.5.
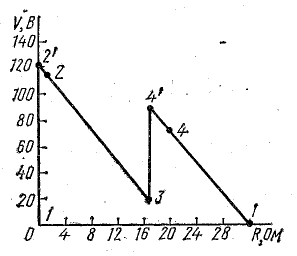
Рис. 4.5. Потенциальная диаграмма.
Разветвленная электрическая цепь с двумя узлами
Разветвленная электрическая цепь, как видно из названия, состоит из нескольких ветвей.
Ветви, присоединенные к одной паре узлов, включены параллельно (рис. 4.7, а). Отличительной особенностью параллельного соединения является то, что ко всем ветвям приложено одно и то же напряжение.
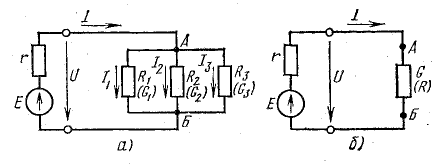
Рис. 4.7. Преобразование схемы с параллельным соединением приемников
Параллельное соединение пассивных элементов
Приемники электрической энергии, представленные на схеме рис.4. 7, а сопротивлениями R1, R2, R3 и источник электрической энергии Е с внутренним сопротивлением r подключены к одной паре узлов (точки А и Б). Составим уравнение токов для узла А в соответствии с первым законом Кирхгофа: 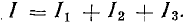
Токи приемников можно выразить, используя напряжение между узлами и проводимости ветвей:
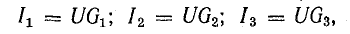
где
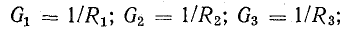
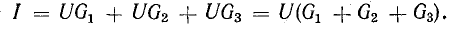
Разделим это уравнение на U:
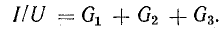
Отношение UU есть проводимость G, соответствующая общему току цепи и общему напряжению:

Этот вывод можно распространить на любое число n параллельно соединенных приемников:

При параллельном соединении пассивных ветвей общая проводимость между двумя узлами равна сумме проводимостей всех ветвей.
Исходя из формул (4.13) и (4.14), можно заменить три проводимости (в общем случае n проводимостей) одной (эквивалентной) проводимостью GО и получить более простую схему (рис. 4.7, б).
Эквивалентное сопротивление при параллельном соединении нескольких ветвей определяется из равенства
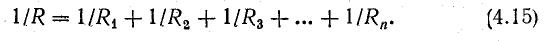
Очень часто встречается параллельное соединение двух ветвей. В этом случае эквивалентное сопротивление определяется по формуле
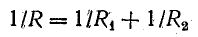
или

Схема на рис. 4.7, б, полученная после замены трех проводимостей одной (эквивалентной), представляет собой простейшую схему электрической цепи.
Ток в этой схеме, равный току в неразветвленной части (рис. 4.7,а), определяется по формуле 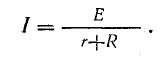
Целью расчета электрической цепи является не только определение общего тока, но и тока в каждой ветви.
Если заданы э.д.с. и все сопротивления, то после определения общего тока по формуле (3.15) нужно определить напряжение между узловыми точками и токи в ветвях по закону Ома:
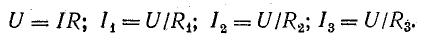
Параллельное соединение источников энергии
В практике часто встречаются случаи параллельного включения источников электрической энергии, работающих совместно на один или несколько приемников (рис. 4.8).
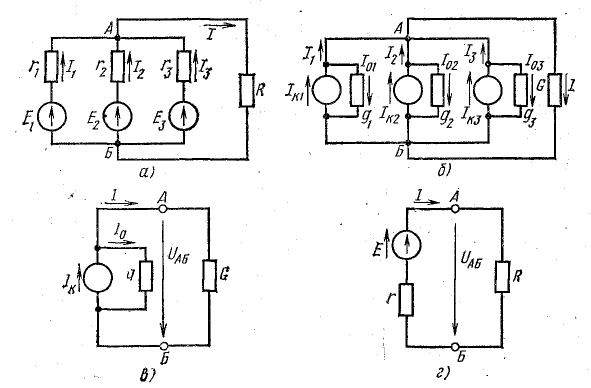
Рис. 4.8. Преобразование схемы с параллельным соединением источников
В таких случаях определением токов в источниках решается важная задача распределения нагрузки между ними.
Представим источники энергии в схеме рис. 4.8, а эквивалентными схемами источников тока, а сопротивление приемника заменим проводимостью G (рис. 4.8, б):

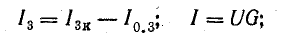


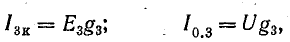
где U = Uаб — напряжение между узловыми точками А и Б.
По первому закону Кирхгофа, для узла А
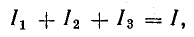
или
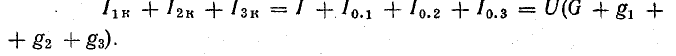
Это равенство дает основание три источника тока заменить одним (эквивалентным), а схему рис. 4.8, б заменить более простой (рис. 4.8, в). Эквивалентный источник тока характеризуется током короткого замыкания
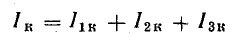
и внутренней проводимостью
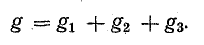
Для схемы рис. 4.8, в
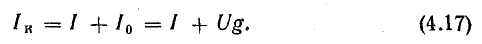
Напряжение между узлами
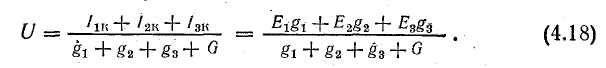
Токи в ветвях можно определить по следующим формулам:
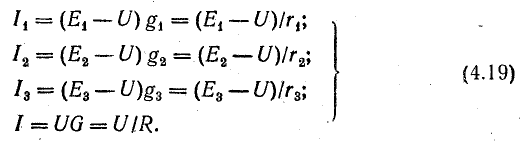
Из этих выражений следует, что источники с относительно большей э. д. с. и меньшим внутренним сопротивлением имеют больший ток, т. е. принимают на себя большую нагрузку. Если э. д. с. и внутренние сопротивления источников одинаковы, нагрузка между ними распределяется поровну.
Общий ток в этом случае определяется произведением тока одного источника In на число параллельно включенных источников:

Величина тока каждого источника ограничена его номинальным значением Iном, сверх которого нагружать источник нельзя. Параллельное соединение источников применяется для увеличения общего тока, благодаря чему достигается увеличение мощности потребления энергии без изменения напряжения.
От схемы с эквивалентным источником тока можно перейти к схеме с эквивалентным источником э. д. с. (рис. 4.8, г), разделив уравнение (4.17) на g:
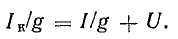
Так как l/g = r — внутреннее сопротивление эквивалентного источника э. д. с., то Iкr = Ir + U.
Но Iкr — Е — э. д. с. эквивалентного источника; Ir — падение напряжения во внутреннем сопротивлении, поэтому Е = U + Ir.
Рассматривается метод расчета разветвленных электрических цепей, предусматривающий замену всех источников э.д.с. одним (эквивалентным), который принято называть эквивалентным генератором.
Общий случай параллельного соединения источников и приемников электрической энергии
Выводы и формулы, полученные ранее, могут быть применены для расчета электрических цепей с двумя узловыми точками, между которыми содержится любое число параллельных ветвей с источниками и приемниками энергии, в том числе и такие ветви, которые имеют несколько элементов, соединенных последовательно (например, схема рис. 4.9).
Порядок расчета таких цепей, предусматривающий предварительное определение напряжения между узловыми точками, называется методом узлового напряжения.
Для применения этого метода должны быть заданы э.д.с. источников и проводимости ветвей (последние можно определить, если заданы сопротивления элементов каждой ветви).
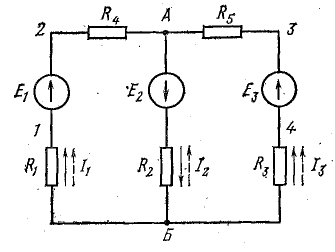
Рис. 4.9. Схема с двумя узлами
В общем случае токи в ветвях и э. д. с. могут иметь различное направление, поэтому при определении узлового напряжения нужно взять алгебраическую сумму произведений ЕG и формула (4.18) примет вид

Знак э. д. с. устанавливается в соответствии с положительным направлением токов в ветвях, которое выбирается произвольно, но одинаково для всех ветвей (например, от Б к А).
Э. д. с. ветви считается положительной, если ее направление совпадает с положительным направлением тока. В противном случае э. д. с. подставляют со знаком минус в формулу (4.21) и также при определении токов по формулам (4.19).
Задача 4.8.
Для схемы, изображенной на рис. 4.7, а, известны: Е = 130 В, r = 0,5 Ом, R1 = 30 Ом, R2 = 20 Ом, R3 = 12 Ом. Определить токи в схеме, мощность передачи энергии приемникам и к. п. д. источника.
Решение. Вначале определим эквивалентное сопротивление между точками А и Б:
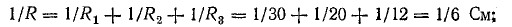
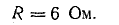
Ток в неразветвленной части цепи
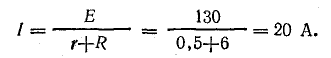
Для определения токов в параллельных ветвях между узловыми точками определим напряжение на зажимах источника, которое в данном случае равно напряжению на приемниках:
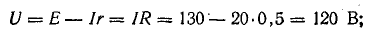
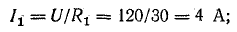
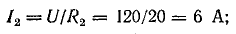
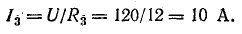
Проверим правильность определения токов по уравнению (4.1):
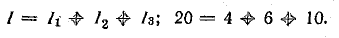
Мощность передачи энергии приемникам
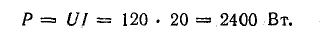
К. п. д. источника
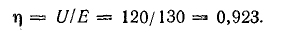
Задача 4.10.
Для схемы, изображенной на рис. 4.7, а, известны: R1 = 10 Ом; R2 = 15 Ом; R3 = 6 Ом, r = 0,5 Ом, l3 = 10 А. Определить токи в схеме, мощность и к. п. д. источника.
Решение. Используя данные условия, относящиеся к третьей ветви, определим напряжение между узлами А и Б по закону Ома:
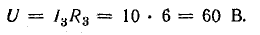
Напряжение U является общим для всех ветвей, присоединенных к точкам А и Б. Это дает возможность использовать ту же формулу для определения токов в двух ветвях:
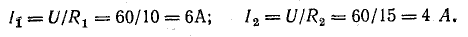
Ток в неразветвленной части цепи
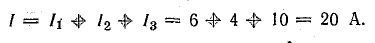
Э. д. с. источника
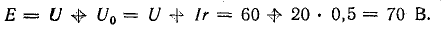
Мощность источника
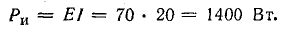
Мощность потребления энергии приемниками
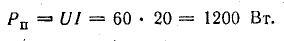
К. п. д. источника
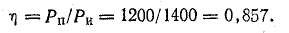
Задача 4.12.
Определить токи и составить баланс мощностей для схемы, изображенной на рис. 4.9, если известны: E1 = 120 В; E2 = 80 В; E3 = 60 В; r1 = 0,5 Ом; r2 = 0,4 Ом; r3 = 0,2 Ом; R1 = 2 Ом; R2 = 15,6 Ом; R3 = 12,4 Ом; R4 = 7,5 Ом; R5 = 7,4 Ом.
Решение. Применяя метод узлового напряжения, найдем UАБ по формуле (4.21). Предварительно зададим положительное направление токов от Б к А и подсчитаем проводимости ветвей:
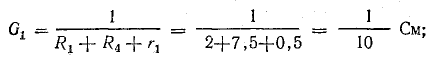
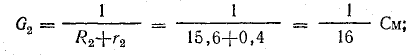
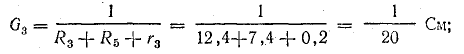
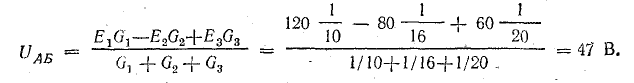
Токи в ветвях:
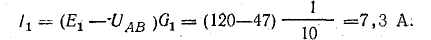
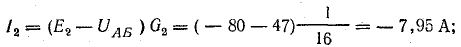
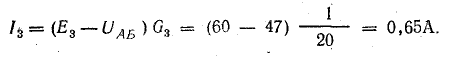
Токи l1 и l3 положительны. Их направление совпадает с выбранным ранее условно-положительным направлением от узла Б к узлу А. Направление тока l2 противоположно положительному направлению; в результате расчета этот ток получился отрицательным. На схеме рис. 4.9 пунктиром показано положительное направление токов в ветвях, а сплошной стрелкой — их действительное направление.
Для составления баланса мощностей необходимо подсчитать мощность каждого элемента схемы, в том числе и мощность потерь внутри источников. Заметим, что направления э. д. с. и токов во всех ветвях совпадают — источники Э. д. с. являются источниками энергии.
Мощности источников: P1.1 = E1I1 = 120 • 7,3 = 876 Вт; P1.2 = Е2I2 = 80 • 7,95 = 636 Вт; Р1.3 = E3I3 = 60 • 0,65 = 39 Вт.
Общая мощность источников 1551 Вт.
При определении мощности источников можно не задумываться над тем, в каком режиме работает тот или другой источник. Ответ на этот вопрос дает знак полученной мощности, если токи и э. д. с. подставлять с теми знаками, какие были приняты или получены в расчете. Например, мощность второго источника положительна: P1.2 = —80 • (—7,95) = 636 Вт. Это указывает на то, что в данной ветви работает источник энергии. Раньше Е2 и I2 сразу были взяты положительными, так как отмечено совпадение направлений напряжения и тока.
Мощность потерь внутри источников: 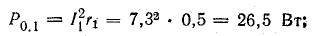
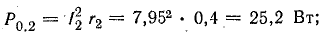
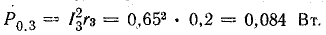
Общая мощность потерь внутри источников приблизительно 52 Вт. Мощность приемников:
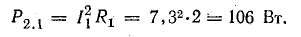
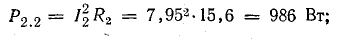
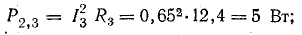
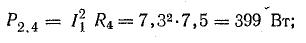
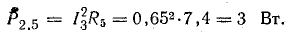
Общая мощность приемников 1499 Вт.
Баланс мощностей (мощность источников равна мощности приемников плюс мощность потерь внутри источников) 1551 Вт = 1499 + 52 Вт.
Расчет электрических цепей методом эквивалентных сопротивлений (метод «свертывания» цепи)
Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивные элементы, включенные между собой последовательно, параллельно или по смешанной схеме.
Определение эквивалентных сопротивлений
На схеме рис. 4.10, а сопротивления R3 и R4 включены последовательно: между ними (в точке 3) нет ответвления с током, поэтому I3 = I4. Эти два сопротивления можно заменить одним (эквивалентным), определив его как сумму 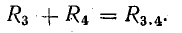
После такой замены получается более простая схема (рис. 4.10, б). Сопротивления R2 и R3.4 соединены параллельно, их можно заменить одним (эквивалентным), определив его по формуле (4.16):
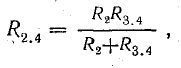
и получить более простую схему (рис. 4.10, в).
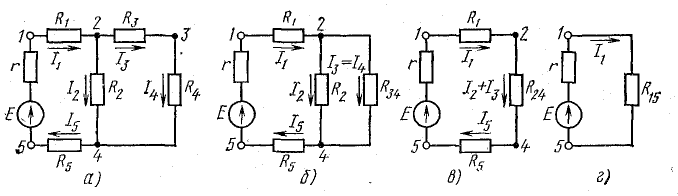
Рис. 4.10. К методу эквивалентных сопротивлений
В схеме рис. 4.10, в сопротивления R1, К2.4, К5 соединены последовательно. Заменив эти сопротивления одним (эквивалентным) сопротивлением между точками 1 и 5, получим простейшую схему (рис. 4.10, г).
Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме. В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает расчет.
Определение токов
В простейшей схеме (рис. 4.10, г) ток I определяется по закону Ома с использованием формулы (3.15). Токи в других ветвях первоначальной схемы определяют, переходя от схемы к схеме в обратном порядке.
Из схемы рис. 4.10, в видно, что
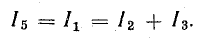
Кроме того, напряжение между точками 2 и 4
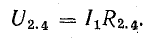
Зная это напряжение, легко определить токи I2 и I3 = I4:
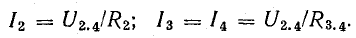
После определения токов I1 и I5 напряжение U2.4 можно найти как разность потенциалов между точками 2 и 4. Для этого положим V4 известным (например, равным нулю), а V2 найдем так же, как при построении потенциальной диаграммы, обойдя от точки 4 неразветвленный участок цепи с током I1 =I5:
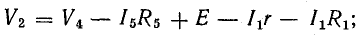
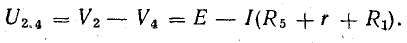
Метод преобразования треугольника и звезды сопротивлений
Пассивные элементы в электрических цепях соединяются не только последовательно или параллельно. Во многих схемах можно выделить группы из трех элементов, образующих треугольник или звезду сопротивлений.
При расчете подобных цепей упрощение схем выполняют известным методом эквивалентных сопротивлений, но предварительно проводят преобразование треугольника сопротивлений в эквивалентную звезду или наоборот.
Треугольник и звезда сопротивлений
Рассмотрим в качестве примера схему рис. 4 .11, а, которая применяется для измерения сопротивлений (схема моста Уитстона).
В этой схеме нет элементов, соединенных последовательно или параллельно, но имеются замкнутые контуры из трех сопротивлений (треугольники сопротивлений), причем точки, разделяющие каждую пару смежных сопротивлений, являются узловыми.
К узловым точкам a, b, c присоединен треугольник сопротивлений Rab, Rbc, Rca. Его можно заменить эквивалентной трехлучевой звездой сопротивлений Ra, Rb, Rc (на рисунке изображены штриховыми линиями), присоединенных с одной стороны к тем же точкам a, b, c, а с другой — в общей (узловой) точке e.
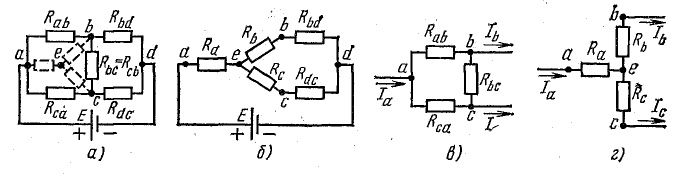
Рис. 4.11. Преобразование треугольника сопротивлений в эквивалентную звезду
Смысл замены становится понятным при рассмотрении эквивалентной схемы 4.11, б, где сопротивления Rb и Rbd соединены между собой последовательно, так же как b сопротивления Rc и Rdc.
Две ветви между узловыми точками e и d с этими парами сопротивлений соединены параллельно. Соответствующими преобразованиями схему можно привести к простейшему виду.
Преобразование треугольника сопротивлений в эквивалентную звезду
Замена треугольника сопротивлений эквивалентной звездой и наоборот осуществляется при условии, что такая замена не изменяет потенциалов узловых точек a, b, c, являющихся вершинами треугольника и эквивалентной звезды.
Одновременно предполагают, что в остальной части схемы, не затронутой преобразованием, режим работы не изменяется (не меняются токи, напряжения, мощности). Для доказательства возможности перехода от треугольника к звезде и наоборот рассмотрим схемы рис. 4.11, в, г.
Эти схемы остаются эквивалентными для всех режимов, в том числе и для режима, при котором Ia = 0, что соответствует обрыву общего провода, ведущего к точке а. В этом случае в схеме треугольника между точками b и c включены параллельно две ветви с сопротивлениями Rbc и Rab + Rca
Общее сопротивление между этими точками
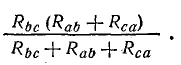
В схеме звезды между точками b и c включены последовательно сопротивления Rb и Rc. Общее сопротивление между этими точками Rb + Rc.
По условиям эквивалентности напряжение между точками b и c и токи Ib и Ic в обеих схемах должны быть одинаковыми. Следовательно, и сопротивления между точками b и c в обеих схемах одинаковы, т. е.
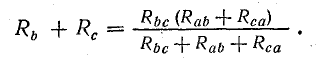
Полагая Ib =0, а затем Ic = 0, получим:
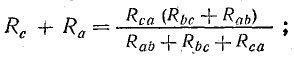
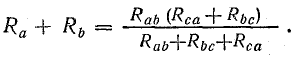
Совместное решение трех полученных уравнений приводит к следующим выражениям, которые служат для определения сопротивлений трехлучевой звезды по известным сопротивлениям эквивалентного треугольника:
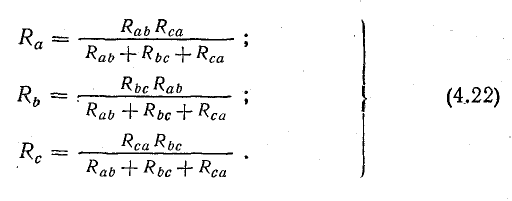
Преобразование звезды сопротивлений в эквивалентный треугольник
Для расчета некоторых схем применяется преобразование трехлучевой звезды в эквивалентный треугольник, которое показано на рис. 4.12, а, где схема взята такой же, как на рис. 4.11, а.
При этом для определения параметров треугольника по заданным параметрам звезды пользуются формулами, которые записаны применительно к схемам рис. 4.12, а, б:
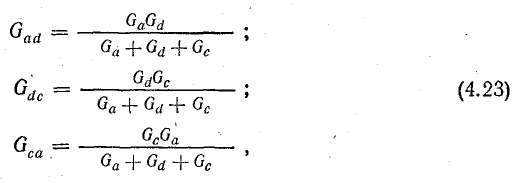
где Gad; Gdc; Gca — проводимости сторон треугольника; Ga; Gd; Gc — проводимости лучей звезды.
Зная проводимости, нетрудно определить сопротивления треугольника, если это необходимо.
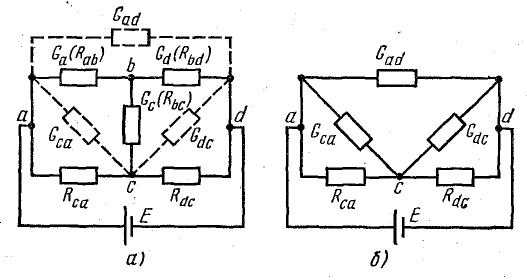
Рис. 4.12. Преобразование трехлучевой звезды в эквивалентный треугольник
- Методы анализа сложных электрических цепей
- Метод узловых напряжений
- Метод узловых потенциалов
- Принцип и метод наложения
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Электрическая цепь
- Электрический ток
Метод узлового напряжения (двух узлов)

Наиболее простым методом расчета электрической цепи с двумя узлами – является метод узлового напряжения или метод двух узлов.
Важно отличать метод узлового напряжения (метод двух узлов) от метода узловых напряжений.
Метод узлового напряжения (двух узлов)
Определим разность потенциалов между двумя узлами цепи А и B.

Найдём потенциал точки А, перемещаясь по первой ветви от узла B до А.

Исходя из выражения (1) можно записать:



где r1 и g1 – сопротивление и проводимость первой ветви соответственно.
Аналогично составляются уравнения для оставшихся ветвей.



По первому закону Кирхгофа запишем уравнение для узла B

Подставим в вышеуказанное уравнение выражения токов (2-5).

Раскрыв скобки, находим узловое напряжение U:

Общее выражение узлового напряжения

Исходя из вышеизложенного, узловое напряжение равно отношению алгебраической суммы произведений ЭДС на проводимости соответствующих ветвей к сумме проводимостей всех ветвей. ЭДС направленная к узлу A, записывается со знаком «+», если в противоположную сторону, то со знаком «-».
Давайте рассмотрим применения метода на конкретном примере.
Пример решения задач методом двух узлов (метод узлового напряжения)
Пример. Электрическая цепь постоянного тока представлена на рисунке 2. Определить токи в ветвях методом двух узлов, если ЭДС источников равна E1 = 40 В, E2 = 50 В, E3 = 10 В, а сопротивления r1 = 10 Ом, r2 = 20 Ом, r3 = 15 Ом, r4 = 12 Ом.
 Рисунок 2 – Электрическая цепь
Рисунок 2 – Электрическая цепь
Порядок расчёта:
- Так как действительные направления токов до расчёта цепи нам неизвестны — произвольно указываем направления токов в ветвях, например, как на Рисунке 3.
 Рисунок 3
Рисунок 3
- Определим проводимость ветвей.





- Найдем напряжение UAВ. Для этого воспользуемся формулой 6.

В числителе записываем произведения ЭДС на проводимости соответствующих ветвей, причем ЭДС направленная к узлу A, записывается со знаком «+», если в противоположную сторону, то со знаком «-».

В знаменателе указываем сумму проводимостей всех ветвей:

Подставляем раннее найденные значения проводимостей и значения ЭДС указанные в условии задачи:

- Определим токи в ветвях. С учетом направления ЭДС





Подставляем численные значения




Токи I3 и I4 получились с отрицательными значениями, следовательно их направление противоположно ранее принятому.
 Рисунок 4 – Реальные направления токов.
Рисунок 4 – Реальные направления токов.
Правильность решения можно проверить при помощи баланса мощностей.
Так же для себя правильность решения задачи можно проверить выполнением первого закона Кирхгофа, а именно:
Источник
Метод узловых (потенциалов) напряжений

При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.
Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие.
В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.
Метод узловых потенциалов примеры решения задач
Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.
 Рис.1. Схема постоянного тока
Рис.1. Схема постоянного тока





Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.
Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ1, φ2, φ3. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.
В общем виде система имеет вид:

Использованные в этой системе уравнений буквенно-цифровые обозначения
 – сумма проводимостей ветвей, сходящихся в узле 1. В данном случае
– сумма проводимостей ветвей, сходящихся в узле 1. В данном случае

 – сумма проводимостей ветвей, сходящихся в узле 2. В данном случае
– сумма проводимостей ветвей, сходящихся в узле 2. В данном случае

 – сумма проводимостей ветвей, сходящихся в узле 3. В данном случае
– сумма проводимостей ветвей, сходящихся в узле 3. В данном случае

 – сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:
– сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:

 – сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:
– сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:

Аналогично находятся и остальные проводимости:

J11 – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае


В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:

Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:

В результате получены следующие значения потенциалов в узлах цепи:

Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.
В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что


Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.
Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.
 Рис.2. Моделирование в Multisim
Рис.2. Моделирование в Multisim
Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.
Источник
Как найти напряжение в ветвях цепи
2. Метод токов ветвей
Метод токов ветвей
Первый и самый простой метод анализа цепей постоянного тока называется методом токов ветвей. В этом методе нам сначала нужно определить направления токов в цепи, а затем написать уравнения, описывающие их отношения друг с другом через законы Кирхгофа и Ома. Как только мы получим уравнения для каждого из неизвестных токов, мы сможем решить систему уравнений, рассчитав тем самым все токи, а затем и все напряжения в цепи.
Для рассмотрения метода мы будем использовать следующую схему:

Первое что нам нужно сделать — это выбрать узел цепи (место соединения проводов), который будет использоваться в качестве точки отсчета для поиска неизвестных токов. Мы выберем узел, соединяющий резистор R1 справа, R2 снизу и R3 слева.

Теперь нам нужно проставить направления токов в примыкающих к этому узлу проводах, обозначив их I1, I2 и I3 соответственно. Имейте ввиду, эти направления будут только предполагаемыми. Если выяснится, что наши предположения оказались ошибочными, то мы это увидим в процессе математического расчета (любые «неправильные» направления токов отобразятся в виде отрицательных чисел).

Согласно Первому Закону Кирхгофа, алгебраическая сумма токов входящих в узел и выходящих из него должна быть равна нулю, поэтому мы можем связать все токи нашей схемы (I1, I2 и I3) друг с другом при помощи одного уравнения. Все входящие в узел токи мы обозначим знаком «плюс», а выходящие из него — знаком «минус»:

На следующем шаге нам нужно промаркировать полярности напряжений всех резисторов в соответствии с предполагаемыми направлениями токов. Конец резистора, в который ток втекает — будет отрицательным, а из которого вытекает — будет положительным (электрон заряжен отрицательно, и течет от минуса к плюсу):

Полярность батареи проставляется в соответствии со стандартом (короткий конец — отрицательный, длинный конец — положительный). В некоторых случаях вы можете обнаружить, что полярность резисторов не соответствует полярности батареи, а ток течет обратно через батарею. Ничего страшного, это только предполагаемое направление тока. Здесь важно помнить, что простановку полярности напряжений на резисторах и последующие расчеты нужно производить по изначально предполагаемым направлениям токов. Как отмечалось ранее, если ваши предположения окажутся неверными, то вы увидите это по окончательным результатам расчетов (они будут отрицательными). Сами же полученные величины все равно будут правильными.
Согласно Второму Закону Кирхгофа, алгебраическая сумма всех напряжений цепи должна равняться нулю. Исходя из этого, мы сможем создать несколько уравнений для нашей системы, подставив в них неизвестные значения токов (I1, I2 и I3). Для получения уравнений Второго Закона Кирхгофа нам нужно знать количество и полярность напряжений в каждой из ветвей цепи. В целях облегчения данной задачи давайте представим, что мы измерили все напряжения реальным вольтметром, обозначив неизвестные значения как положительное или отрицательное напряжение. Сначала мы создадим уравнение для левой ветви схемы, взяв за точку отсчета верхний левый угол, и двигаясь против часовой стрелки (выбор точки отсчета и направление — произвольны). Результат будет выглядеть следующим образом:




Закончив исследование левой ветви схемы, мы можем применить к полученным значениям Второй Закон Кирхгофа (сумма всех напряжений цепи равна нулю):

Нам еще неизвестны значения напряжений на резисторах R1 и R2, поэтому мы не можем вставить их в уравнение в виде числовых величин. Однако, мы знаем, что сумма этих трех напряжений равна нулю, поэтому уравнение верно. Теперь пойдем дальше, и выразим неизвестные напряжения как произведение неизвестных токов и соответствующих им сопротивлений (применив Закон Ома: U = IR), а так же уберем все нулевые значения из левой части уравнения:

Поскольку нам известны сопротивления всех резисторов, давайте подставим в уравнение конкретные числовые значения:

У вас наверняка возник вопрос: зачем мы произвели все эти манипулирования с первоначальным видом уравнения (-28 + ER2 + ER1)? Какая разница в чем будет выражено уравнение, в напряжении или в токе (умноженном на сопротивление), если в обоих случаях последние два члена до сих пор неизвестны? Ответ на данные вопросы прост. Целью всех выше приведенных преобразований является получение уравнения Второго Закона Кирхгофа с использованием тех же неизвестных переменных, что и в уравнении Первого Закона Кирхгофа, так как это является необходимым условием для решения любой системы уравнений. Чтобы найти значения трех неизвестных токов (I1, I2 и I3), у нас должно быть три уравнения, связывающих их вместе.
Применив те же самые действия к правой ветви схемы (начиная с выбранного узла и двигаясь против часовой стрелки), мы получим еще одно уравнение Второго Закона Кирхгофа:





Зная, что напряжение на каждом из резисторов может и должно быть выражено как произведение соответствующих токов и сопротивлений (величина которых известна), мы можем переписать это уравнение следующим образом:

Теперь у нас есть система из трех уравнений (одно уравнение Первого и два уравнения Второго Законов Кирхгофа) с тремя неизвестными:

Далее нам нужно перенести все известные величины в правые части уравнений, а неизвестные оставить в левой, дополнив их отсутствующими нулевыми значениями:

Решив эту систему уравнений мы получим следующий результат:

Таким образом, ток I1 равен 5 амперам, ток I2 равен 4 амперам и ток I3 равен минус 1 амперу. Отрицательное значение тока I3 означает что наше предположение по его направлению оказалось неверным. Давайте вернемся к первоначальной схеме и перерисуем стрелку этого тока на противоположное направление (исправив соответственно полярность напряжения на резисторе R3):

Обратите внимание на тот факт, что в правой ветви схемы ток течет обратно через батарею 2. Это происходит благодаря более высокому напряжению батареи 1 (в которой ток течет «как обычно» — через цепь от минуса к плюсу). Означает ли это, что более «сильная» батарея всегда будет «побеждать» более слабую. Вовсе нет! Данный фактор зависит как от относительных напряжений батарей, так и от сопротивлений резисторов цепи. Единственным способом установления происходящих в цепи процессов является математический анализ.
Итак, величины всех токов данной цепи нам известны. Теперь, при помощи Закона Ома (U = IR), можно рассчитать напряжения на всех ее резисторах:

Давайте теперь проанализируем эту схему при помощи программы PSPICE, проверив тем самым полученные результаты для напряжений. Данная программа, конечно, сможет рассчитать и токи, но тогда нам потребуется включить в схему дополнительные компоненты. Принимая во внимание этот факт, мы с вами пойдем по пути наименьшего сопротивления (если выданные программой значения напряжений совпадут с нашими расчетами, то и токи мы рассчитали правильно). Схема с номерами узлов для программы представлена ниже:

Как видите, результаты работы программы совпадают с нашими рассчетами: 20 вольт на резисторе R1 (узлы 1 и 2), 8 вольт на резисторе R2 (узлы 2 и 0) и 1 вольт на резисторе R3 (узлы 2 и 3). Обратите внимание на знаки всех этих напряжений: они имеют положительные значения! PSPICE основывает свою полярность на порядке, в котором перечислены узлы: первый узел должен быть положительным, а второй — отрицательным. Например, положительное (+) напряжение 20 вольт между узлами 1 и 2 означает, что узел 1 является положительным по отношению к узлу 2. Если бы число получилось отрицательным, то то ошибку следовало бы искать в порядке перечисления узлов.
Источник
3.1. Модель цепи постоянного тока
Если в электрической цепи действуют
постоянные напряжения и протекают
постоянные токи, то модели реактивных
элементов LиCсущественно упрощаются.
Модель сопротивления
![]() остается прежней и связь между напряжением
остается прежней и связь между напряжением![]() и током
и током![]() определяется законом Ома в виде
определяется законом Ома в виде
![]() .
.
(3.1)
В идеальной индуктивности мгновенные
значения напряжения и тока связаны
соотношением
![]() .
.
(3.2)

Аналогично в емкости связь между
мгновенными значениями напряжения и
тока определяется в виде
![]() .
.
(3.3)

53
Таким образом, в модели цепи постоянного
тока присутствуют только сопротивления
(модели резисторов) и источники сигнала,
а реактивные элементы (индуктивности
и емкости) отсутствуют.
3.2. Расчет цепи на основе закона Ома
Этот метод удобен для расчета сравнительно
простых цепей с одним источником
сигнала. Он предполагает вычисление
сопротивлений участков цепи, для которых
известна величина тока (или напряжения),
с последующим определением неизвестного
напряжения (или тока). Рассмотрим пример
расчета цепи, схема которой приведена
на рис. 3.1, при токе идеального источника![]() А
А
и сопротивлениях![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом.
Ом.
Необходимо определить токи ветвей![]() и
и![]() ,
,
а также напряжения на сопротивлениях![]() ,
,![]() и
и![]() .
.
 Известен
Известен
ток источника![]() ,
,
тогда можно вычислить сопротивление
цепи![]() относительно зажимов источника тока
относительно зажимов источника тока
(параллельного соединения сопротивления![]() и последовательно соединен-
и последовательно соединен-
Рис. 3.1. ных
сопротивлений
![]() и
и![]() ),
),
![]() .
.
Тогда напряжение
![]() на источнике тока (на сопротивлении
на источнике тока (на сопротивлении![]() )
)
равно
![]() В.
В.
54
Затем можно найти токи ветвей
![]() А,
А,
![]() А.
А.
Полученные результаты можно проверить
с помощью первого закона Кирхгофа в
виде
![]() .
.
Подставляя вычисленные значения, получим![]() А,
А,
что совпадает с величиной тока источника.
Зная токи ветвей, нетрудно найти
напряжения на сопротивлениях (величина
![]() уже найдена)
уже найдена)
![]() В,
В,
![]() В.
В.
По второму закону Кирхгофа
![]() .
.
Складывая полученные результаты,
убеждаемся в его выполнении.
3.3. Общий метод расчета цепи на основе
законов Ома
и Кирхгофа
Общий метод расчета токов и напряжений
в электрической цепи на основе законов
Ома и Кирхгофа пригоден для расчета
сложных цепей с несколькими источниками
сигнала.
Расчет начинается с задания обозначений
и положительных направлений токов и
напряжений для каждого элемента
(сопротивления) цепи.
Система уравнений включает в себя
подсистему компонентных уравнений,
связывающих по закону Ома токи и
напряжения в каждом элементе
(сопротивлении) и подсистему
55
топологических уравнений, построенную
на основе первого и второго законов
Кирхгофа.
Рассмотрим расчет простой цепи из
предыдущего примера, показанной на рис.
3.1, при тех же исходных данных.
Подсистема компонентных уравнений
имеет вид
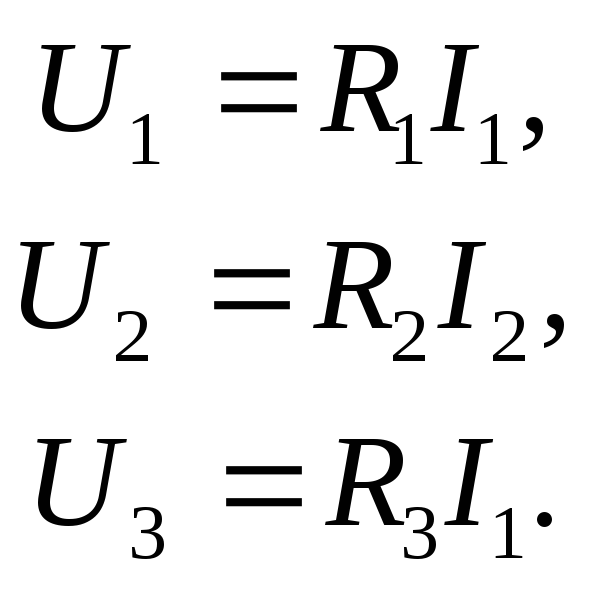 (3.4)
(3.4)
В цепи имеется два узла (![]() )
)
и две ветви, не содержащие идеальных
источников тока (![]() ).
).
Следовательно, необходимо записать
одно уравнение (![]() )
)
по первому закону Кирхгофа,
![]() ,
,
(3.5)
и одно уравнение второго закона Кирхгофа
(![]() ),
),
![]() ,
,
(3.6)
которые и образуют подсистему
топологических уравнений.
Уравнения (3.4)-(3.6) являются полной
системой уравнений цепи. Подставляя
(3.4) в (3.6), получим
![]() ,
,
(3.7)
а, объединив (3.5) и (3.7), получим два
уравнения с двумя неизвестными токами
ветвей,
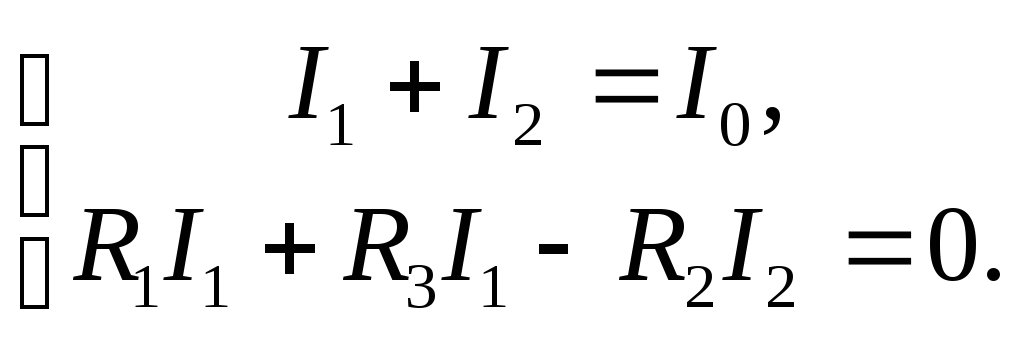 (3.8)
(3.8)
56
Выражая из первого уравнения (3.8) ток
![]() и подставляя его во второе, найдем
и подставляя его во второе, найдем
значение тока![]() ,
,
![]() А,
А,
(3.9)
а затем найдем
![]() А.
А.
По вычисленным токам ветвей из компонентных
уравнений (3.4) определим напряжения.
Результаты расчета совпадают с полученными
ранее в подразделе 3.2.
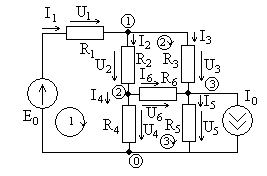
Рассмотрим более сложный пример расчета
цепи в схеме, показанной на рис. 3.2, с
параметрами
![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом,
Ом,
![]()
 В,
В,![]() А.
А.
Цепь содержит
![]() узла (их номера указаны в кружках) и
узла (их номера указаны в кружках) и![]() ветвей, не содержащих идеальные источники
ветвей, не содержащих идеальные источники
тока. Система компонентных уравнений
цепи имеет вид
Рис. 3.2

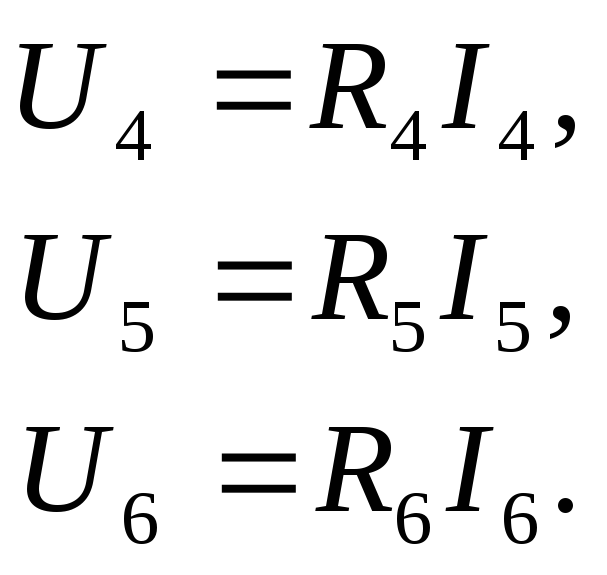 (3.10)
(3.10)
По первому закону Кирхгофа необходимо
записать
![]() уравнения (узел 0 не используется),
уравнения (узел 0 не используется),
57
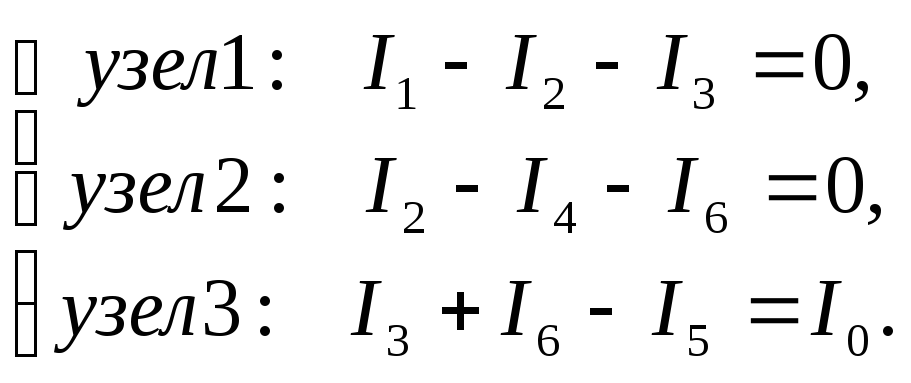 (3.11)
(3.11)
По второму закону Кирхгофа составляется
![]() уравнения для трех независимых контуров,
уравнения для трех независимых контуров,
отмеченных на схеме окружностями со
стрелками (внутри указаны номера
контуров),
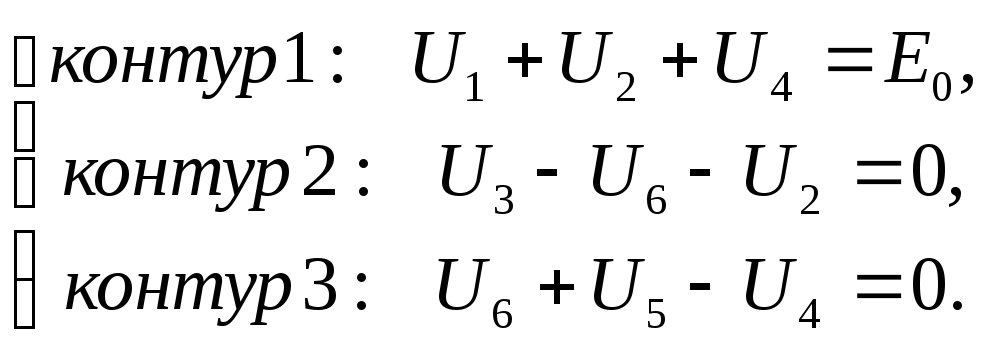 (3.12)
(3.12)
Подставляя (3.11) в (3.13), совместно с (3.12)
получим систему шести
![]() уравнений вида
уравнений вида
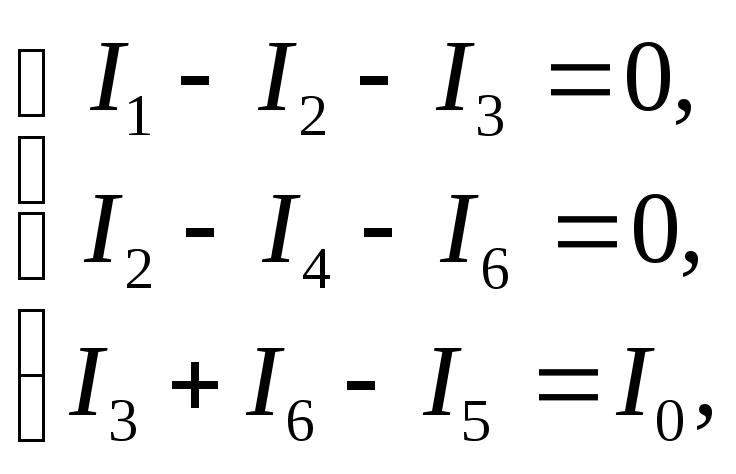 (3.13)
(3.13)
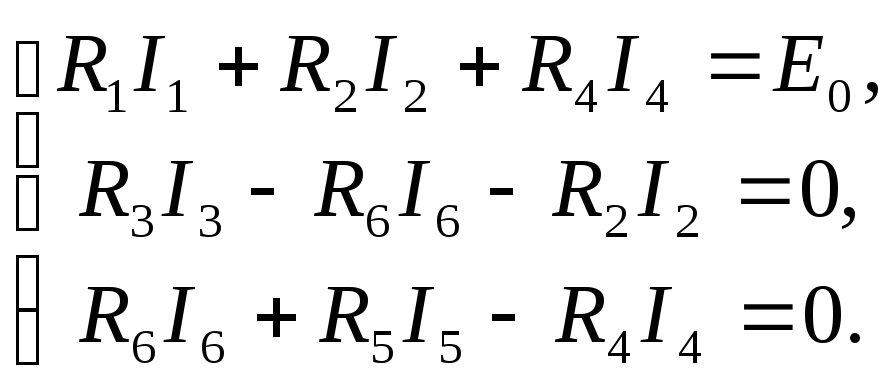
Из второго и третьего уравнений выразим
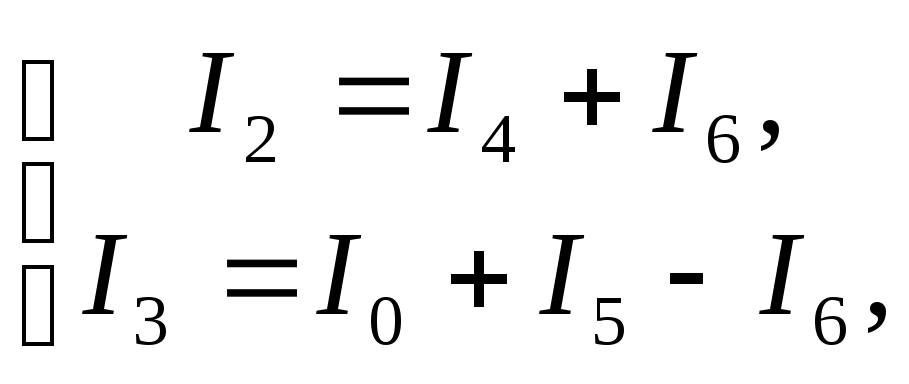 (3.14)
(3.14)
а из первого
![]() ,
,
тогда подставив![]() и
и![]() ,
,
получим![]() .
.
Подставляя токи![]() ,
,![]() и
и![]() в уравнения второго закона Кирхгофа,
в уравнения второго закона Кирхгофа,
запишем систему из трех уравнений
58
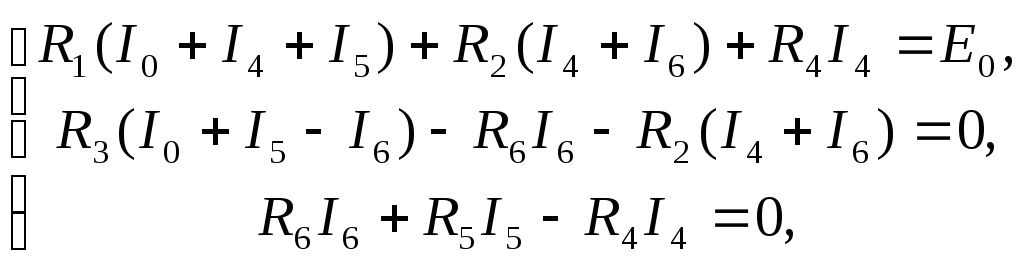
которую после приведения подобных
запишем в виде
 (3.15)
(3.15)
Обозначим
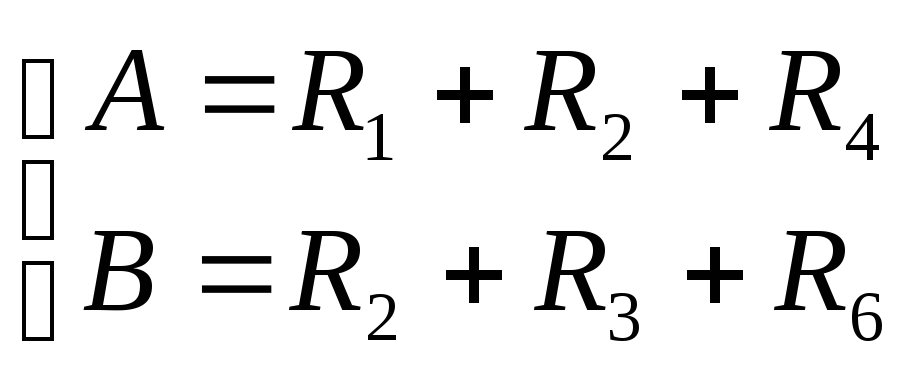 ,
,
(3.16)
и из третьего уравнения системы (3.15)
запишем
![]() .
.
(3.17)
Подставляя полученное значение
![]() в первые два уравнения (3.15), получим
в первые два уравнения (3.15), получим
систему из двух уравнений вида
 (3.18)
(3.18)
Из второго уравнения (3.18) получим
59
![]() ,
,
(3.19)
тогда из первого уравнения найдем ток
![]()
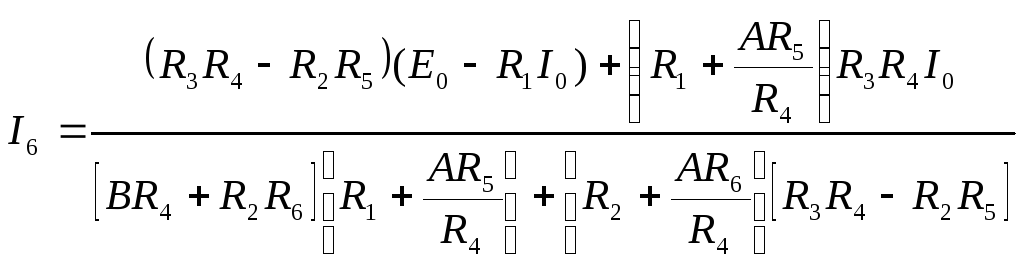 .
.
(3.20)
Вычислив
![]() ,
,
из (3.19) найдем![]() ,
,
из (3.17) вычислим![]() ,
,
а затем из уравнений подстановки найдем
токи![]() ,
,![]() ,
,![]() .
.
Как видно, аналитические вычисления
достаточно громоздки, и для численных
расчетов целесообразней использовать
современные программные пакеты, например,
MathCAD2001. Пример программы
показан на рис. 3.3.
Матрица – столбец
![]() содержит значения токов
содержит значения токов![]() А,
А,![]() А,
А,![]() А.
А.
Остальные
токи вычисляются согласно уравнениям
(3.14) и равны
![]() А,
А,![]() А,
А,![]() А.
А.
Вычисленные значения токов совпадают
с полученными по приведенным выше
формулам.
Общий метод расчета цепи по уравнениям
Кирхгофа приводит к необходимости
решения
![]() линейных алгебраических уравнений. При
линейных алгебраических уравнений. При
большом числе ветвей![]() возникают математические и вычислительные
возникают математические и вычислительные
трудности. Это означает, что целесообразно
искатьметоды расчета, требующие
составления и решения меньшего числа
уравнений.
60

Рис. 3.3
3.4. Метод контурных токов
Метод контурных токов базируется
на уравненияхвторого закона
Кирхгофаи приводит к необходимости
решения![]() уравнений,
уравнений,![]() –
–
число всех ветвей, в том числе и содержащих
идеальные источники тока.
В цепи выбираются
![]() независимых контуров и для каждого
независимых контуров и для каждого![]() -го
-го
из них вводится кольцевой (замкнутый)
контурный ток![]() (двойная индексация позволяет отличать
(двойная индексация позволяет отличать
кон-
61
турные токи от токов ветвей). Через
контурные токи можно выразить все токи
ветвей и для каждого независимого
контура записать уравнения второго
закона Кирхгофа. Система уравнений
содержит
![]() уравнений, из которых определяются все
уравнений, из которых определяются все
контурные токи. По найденным контурным
токам находятся токи или напряжения
ветвей (элементов).
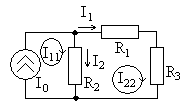 Рассмотрим
Рассмотрим
пример цепи на рис. 3.1. На рис 3.4 приведена
схема с указанием обозначений и
положительных направлений двух контурных
токов![]() и
и![]() (
(![]() ,
,![]() ,
,![]() ).
).
Рис. 3.4 Через
ветвь
![]() проте-
проте-
кает только
контурный ток
![]() и его направление совпадает с
и его направление совпадает с![]() ,
,
поэтому ток ветви![]() равен
равен
![]() .
.
(3.21)
В ветви
![]() протекают два контурных тока, ток
протекают два контурных тока, ток![]() совпадает по направлению с
совпадает по направлению с![]() ,
,
а ток![]() имеет противоположное направление,
имеет противоположное направление,
следовательно
![]() .
.
(3.22)
Для контуров, не содержащих идеальные
источники тока, составляем уравнения
второго закона Кирхгофа с использованием
закона Ома, в данном примере записывается
одно уравнение
![]() .
.
(3.23)
Если в контур включен идеальный
источник тока, то для него
62
уравнение второго закона Кирхгофа не
составляется, а его контурный ток
равен току источника с учетом их
положительных направлений, в рассматриваемом
случае
![]() .
.
(3.24)
Тогда система уравнений принимает вид
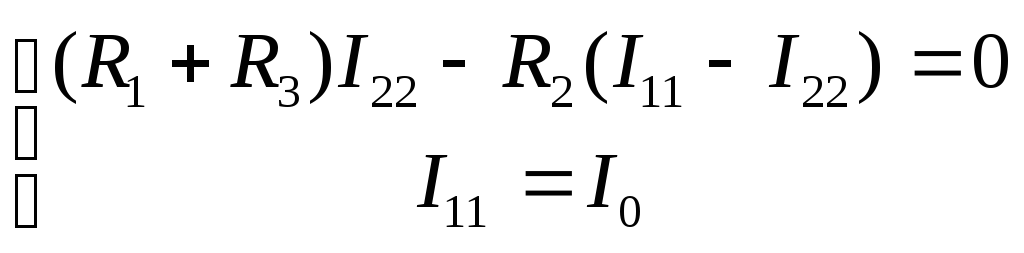 .
.
(3.25)
В результате подстановки второго
уравнения в первое получим
![]() ,
,
(3.26)
тогда ток
![]() равен
равен
![]() А,
А,
(3.27)
а ток
![]() А.
А.
Из (3.21)![]() А,
А,
а из (3.22) соответственно![]() А,
А,
что полностью совпадает с полученными
ранее результатами. При необходимости
по найденным значениям токов ветвей по
закону Ома можно вычислить напряжения
на элементах цепи.
Рассмотрим более сложный пример цепи
на рис. 3.2, схема которой с заданными
контурными токами показана на рис. 3.5.
В этом случае число ветвей
![]() ,
,
количество узлов![]() ,
,
тогда число независимых контуров и
уравнений по методу контурных токов
равно![]() .
.
Для токов ветвей можно записать
63
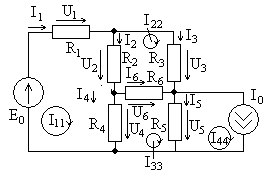
Рис. 3.5
 (3.28)
(3.28)

Первые три контура не содержат идеальных
источников тока, тогда с учетом (3.28) и
использованием закона Ома для них можно
записать уравнения второго закона
Кирхгофа,
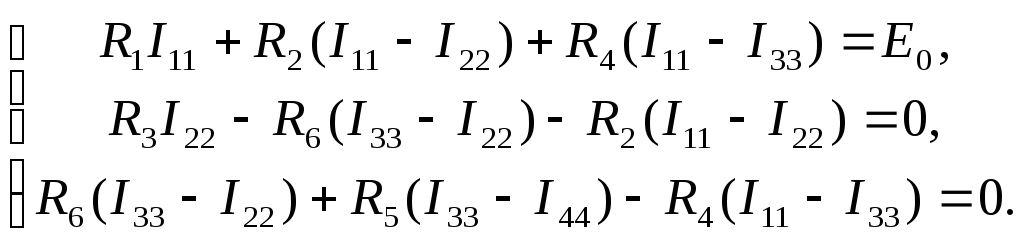 (3.29)
(3.29)
В четвертом контуре присутствует
идеальный источник тока, поэтому для
него уравнение второго закона Кирхгофа
не составляется, а контурный ток равен
току источника (они совпадают по
направлению),
![]() .
.
(3.30)
Подставляя (3.30) в систему (3.29), после
преобразования получим три уравнения
для контурных токов в виде
64
 (3.31)
(3.31)
Систему уравнений (3.31) можно решить
аналитически (например, методом
подстановки – проделайте это),
получив формулы для контурных токов, а
затем из (3.28) определить токи ветвей.
Для численных расчетов удобно использовать
пакет программMathCAD, пример
программы показан на рис. 3.6. Результаты
вычислений совпадают с расчетами,
приведенными на рис. 3.3. Как видно, метод
контурных токов требует составления и
решения меньшего числа уравнений по
сравнению с общим методом расчета по
уравнениям Кирхгофа.

Рис. 3.6
65
3.5. Метод узловых напряжений
Метод узловых напряженийбазируется
на первом законе Кирхгофа, при этом
число уравнений равно![]() .
.
В цепи выделяются все
![]() узлов и один из них выбирается в качествебазисного, которому присваивается
узлов и один из них выбирается в качествебазисного, которому присваивается
нулевой потенциал. Потенциалы (напряжения)![]() …
…![]() остальных
остальных![]() узлов отсчитываются от базисного, их
узлов отсчитываются от базисного, их
положительные направления обычно
выбираются стрелкой в базисный узел.
Через узловые напряжения с использованием
закона Ома и второго закона Кирхгофа
выражаются токи всех ветвей
и для
![]() узлов записываются уравнения первого
узлов записываются уравнения первого
закона Кирхгофа.
 Рассмотрим
Рассмотрим
пример цепи, показанной на рис. 3.1, для
метода узловых напряжений ее схема
показана на рис. 3.7. Нижний узел обозначен
как базисный (для этого используется
символ «земля» – точка нулевого
потенциала), напряжение верхнего узла
относительно базисного обо-
Рис. 3.7 значено как
![]() .
.
Выразим через
него токи
ветвей
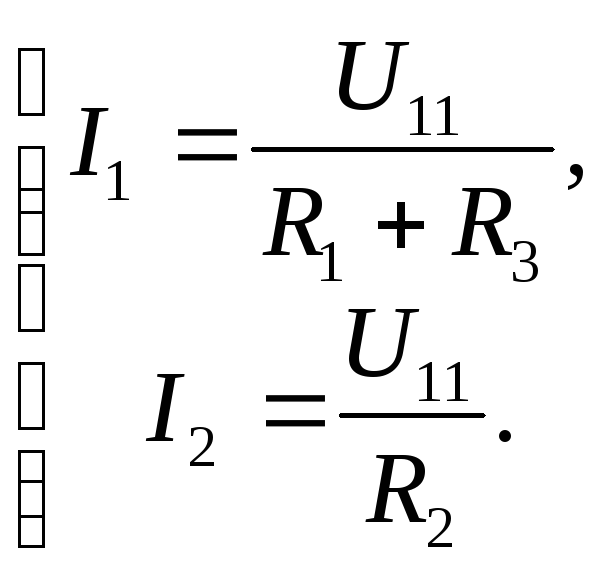 (3.32)
(3.32)
По первому закону Кирхгофа с учетом
(3.32) запишем единственное уравнение
метода узловых напряжений (![]() ),
),
66
![]() .
.
(3.33)
Решая уравнение, получим
![]() ,
,
(3.34)
а из (3.32) определим токи ветвей
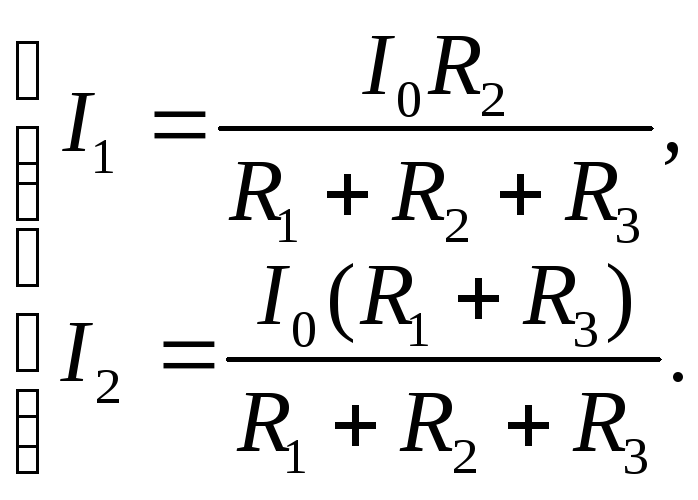 (3.35)
(3.35)
Полученные результаты совпадают с
полученными рассмотренными ранее
методами.
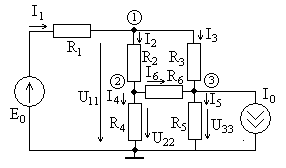 Рассмотрим
Рассмотрим
более сложный пример цепи, показанной
на рис. 3.2 при тех же исходных данных, ее
схема показана на рис. 3.8. В цепи![]() узла, нижний выбран базисным, а три
узла, нижний выбран базисным, а три
остальные обозначены номерами в кружках.
Введены
положительные на- Рис.
3.8
правления и обозна-
чения узловых напряжений
![]() ,
,![]() и
и![]() .
.
По Закону Ома с использованием второго
закона Кирхгофа определим токи ветвей,
67
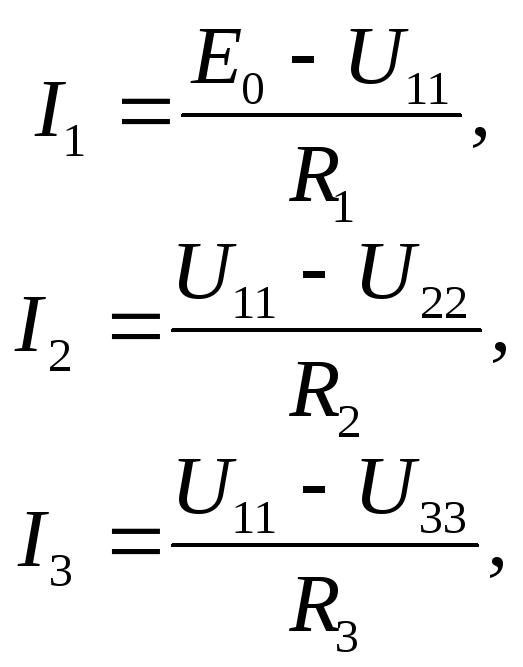
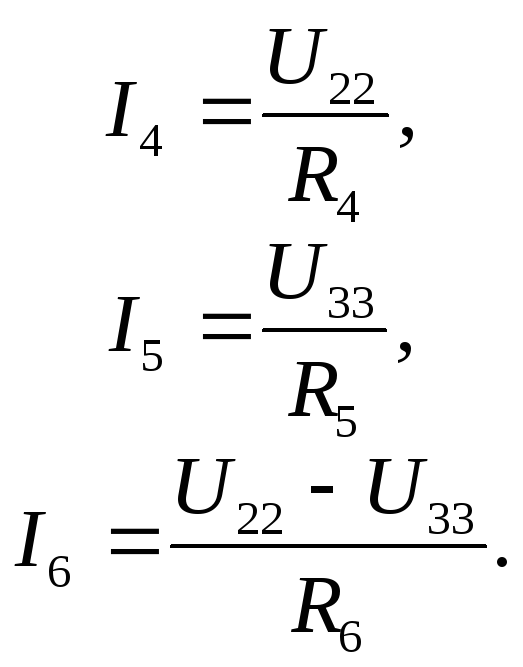 (3.36)
(3.36)
По первому закону Кирхгофа для узлов
с номерами 1, 2 и 3 необходимо составить
три уравнения,
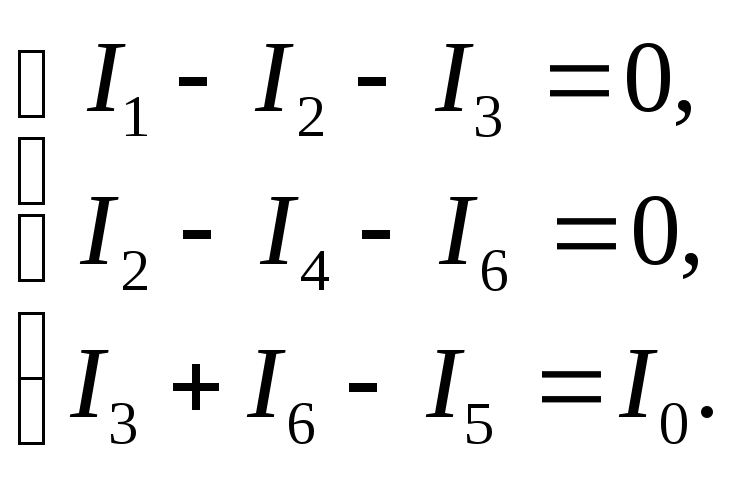 (3.37)
(3.37)
Подставляя (3.36) в (3.37), получим систему
уравнений метода узловых напряжений,
 (3.38)
(3.38)
После преобразования и приведения
подобных получим
 (3.39)
(3.39)
68
Программа расчета узловых напряжений
и токов ветвей приведена на рис. 3.9. Как
видно, полученные результаты совпадают
с полученными ранее другими методами
расчета.
Проведите аналитический расчет узловых
напряжений, получите формулы для токов
ветвей и вычислите их значения.

Рис. 3.9
69
3.6. Метод наложения
Метод наложениязаключается в
следующем.

Расчет проводится следующим образом.
В цепи, содержащей несколько источников,
поочередно выбирается каждый из них, а
остальные отключаются. При этом образуются
цепи с одним источником, число которых
равно количеству источников в исходной
цепи. В каждой из них проводится расчет
искомого сигнала, а результирующий
сигнал определяется их суммой. В качестве
примера рассмотрим расчет тока
![]() в цепи, показанной на рис. 3.2, ее схема
в цепи, показанной на рис. 3.2, ее схема
показана на рис. 3.10а.
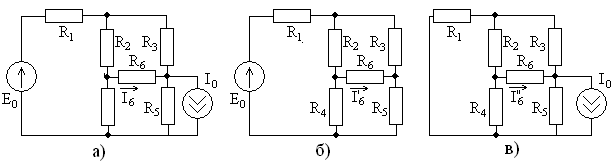
Рис. 3.10
70
При выключении идеального источника
тока (его цепь разрывается) получается
цепь, показанная на рис. 3.9б, в которой
любым из рассмотренных методов
определяется ток
![]() .
.
Затем выключается идеальный источник
напряжения (он заменяется коротким
замыканием) и получается цепь, показанная
на рис. 3.9а, в которой находится ток
![]() .
.
Искомый ток![]() равен
равен
![]() .
.
Проведите аналитические и численные
расчеты самостоятельно, сравните с
полученными ранее результатами, например,
(3.20).
3.7. Сравнительный анализ методов расчета
Метод расчета, основанный
на законе Ома, пригоден для сравнительно
простых цепей с одним источником. Его
нельзя использовать для анализа цепей
сложной структуры, например, мостового
типа вида рис.3.9.
Общий метод расчета цепи на основе
уравнений законов Ома и Кирхгофа
универсален, но требует составления и
решения системы из
![]() уравнений, которая легко преобразуется
уравнений, которая легко преобразуется
в систему из![]() уравнений. При большом числе ветвей
уравнений. При большом числе ветвей
резко возрастают вычислительные затраты,
особенно при необходимости аналитических
расчетов.
Методы контурных токов и узловых
напряжений более эффективны, так как
приводят к системам с меньшим числом
уравнений, равным соответственно
![]() и
и![]() .
.
При условии
![]() или
или![]() (3.40)
(3.40)
метод контурных токов эффективнее, а
иначе целесообразно применять метод
узловых напряжений.
71
Метод наложения удобен, когда при
отключении источников происходит резкое
упрощение цепи.
В системах схемотехнического моделирования
цепей, например, MicroCAPилиOrCADв основном применяют
метод узловых напряжений.
3.8. Задания для самостоятельного решения
Задание 3.1 С помощью
закона Ома определите напряжение![]() в цепях, схемы которых показаны на рис.
в цепях, схемы которых показаны на рис.
3.11 при![]() В,
В,![]() мА,
мА,![]() кОм,
кОм,![]() кОм,
кОм,![]() кОм.
кОм.
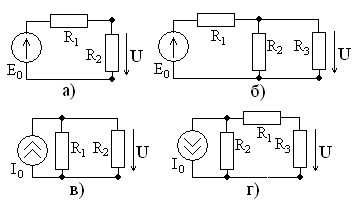
Рис. 3.11
Задание 3.2Общим методом расчета
на основе законов Ома и Кирхгофа
определите ток![]() в цепях, схемы которых показаны на рис.
в цепях, схемы которых показаны на рис.
3.11 при![]() В,
В,![]() В,
В,![]() мА,
мА,![]() мА,
мА,![]() кОм,
кОм,![]() кОм,
кОм,![]() кОм.
кОм.
Задание 3.3Методами контурных токов,
узловых напряжений и наложения определите
ток![]() в цепях, схемы которых показаны на рис.
в цепях, схемы которых показаны на рис.
3.12, параметры цепи возьмите из задания
3.1, сравните полученные результаты.
72

Рис. 3.12
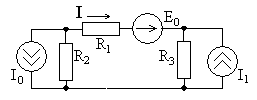 Задание
Задание
3.4.Методами контурных токов и узловых
напряжений определите ток![]() в цепи, схема которой показана на рис.
в цепи, схема которой показана на рис.
3.13 при![]() В,
В,![]() мА,
мА,![]() мА,
мА,![]() кОм,
кОм,![]() кОм,
кОм,
![]() кОм.
кОм.
Рис. 3.13

Задание 3.5. Общим методом расчета,
методами контурных токов и узловых
напряжений определите в цепи рис. 3.14
напряжение![]() при
при![]() мА
мА![]() кОм,
кОм,![]() кОм,
кОм,![]() кОм,
кОм,![]() кОм,
кОм,![]() кОм.
кОм.
Проведите сравнительный анализ
методов расчета.
Рис. 3.14
73
4. ГАРМОНИЧЕСКИЕ ТОКИ И НАПРЯЖЕНИЯ
В ЛИНЕЙНЫХ ЦЕПЯХ
4.1. Гармонические ток и напряжение в
элементах цепи
В элементах цепи R,L,
иCвзаимосвязь произвольных
мгновенных значений тока и напряжения
определяется законом Ома, необходимые
соотношения приведены в табл. 1.1.
 Рассмотримгармоническиеток и напряжение на
Рассмотримгармоническиеток и напряжение на
элементе Э (рис. 4.1) в виде
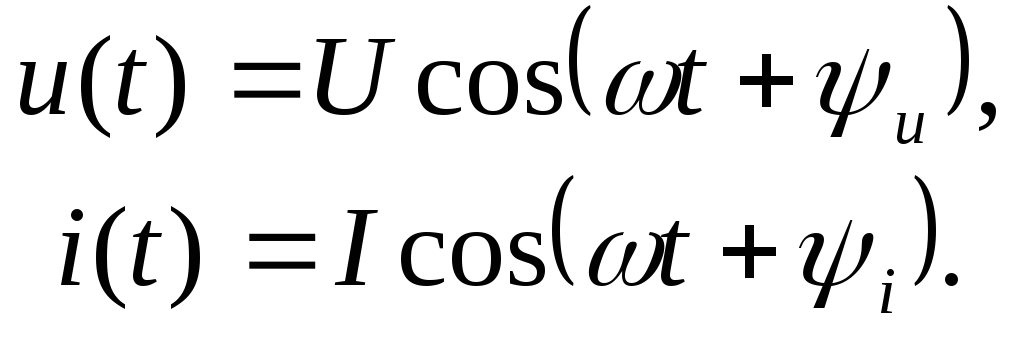 (4.1)
(4.1)
Рис. 4.1
Для сопротивления Rможно записать
![]() .
.
(4.2)
Сравнивая полученный результат с
выражением для напряжения из (4.1), получим
выражение закона Ома для амплитуд тока
и напряжения.
![]() ,
,
(4.3)
и соотношение для начальных фаз
![]() .
.
(4.4)
Как видно из (4.3), амплитуды
(и действующие значения) гармонических
тока и напряжения в сопротивлении
связанызаконом Омав классической
формулировке прямой пропорциональности.
74
Начальные фазы тока
![]() и напряжения
и напряжения![]() в сопротивленииодинаковы, сдвиг
в сопротивленииодинаковы, сдвиг
фаз![]() между напряжением и током равен нулю,
между напряжением и током равен нулю,
![]() .
.
(4.5)
Мгновенная мощность (1.6) гармонических
сигналов в сопротивлении равна
![]() ,
,
(4.6)
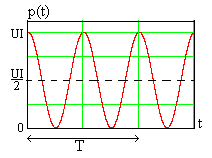
где
![]() .
.
Ее зависимость от времени показана на
рис. 4.2. Величина![]() всегда положительна, то есть
всегда положительна, то есть
сопротивление толькопотребляет
мощностьот источника сигнала. Это
гармоническая функция времени с
периодом по-
вторения в два раза меньше пе-
Рис. 4.2
риода сигнала.
Средняя мощность (1.8) гармонических
сигналов в сопротивлении определяется
выражением
![]() ,
,
(4.7)
где
![]() и
и![]() – действующие значения тока и напряжения,
– действующие значения тока и напряжения,
![]() .
.
(4.8)
75
Это значение показано пунктирной линией
на временной диаграмме рис. 4.2.
В емкости Cмгновенные значения тока и напряжения
связаны соотношением (табл.1.1)
![]() .
.
(4.9)
После преобразования тригонометрической
функции к канонической форме гармонического
сигнала получим
![]() .
.
(4.10)
Сравнивая (4.10) с формулой тока из (4.1),
можно записать
![]() ,
,
(4.11)
![]() .
.
(4.12)
Введем обозначения
![]() ,
,
(4.13)
![]() ,
,
(4.14)
где
![]() –модуль реактивного сопротивления
–модуль реактивного сопротивления
емкости (Ом), а![]() –реактивная проводимость емкости
–реактивная проводимость емкости
(См=1/Ом). Позднее увидим, что реактивное
сопротивление емкостиотрицательно.
Из (4.11) получим уравнения связи амплитуд
(и действующих значений) гармоническихтока и напряжения в емкости
76
![]() ,
,
(4.15)
которые представляют собой выражение
закона Омадля емкости в классической
формулировке прямой пропорциональности.
Из (4.12) следует, что гармонический ток
в емкости опережает по фазе приложенное
к ней напряжение(напряжение отстает
по фазе от тока) на угол![]() радиан или 900. Сдвиг фаз между
радиан или 900. Сдвиг фаз между
напряжением и током в емкости равен
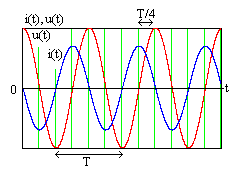
![]() .
.
(4.16)
На рис. 4.3 показаны временные диаграммы
тока и напряжения в емкости. Ток
![]() опережает по фазе напряжение на 900,
опережает по фазе напряжение на 900,
что отражается навременной
диаграмме смещением
кривой тока влево на чет-
Рис. 4.3
верть периода.
Мгновенная мощность в емкости из (4.1) и
(4.9) равна
![]() ,
,
а после тригонометрических преобразований
получим
![]() .
.
(4.17)
Временная диаграмма мгновенной мощности
показана на рис. 4.4
77
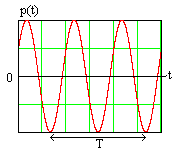 Мгновенная
Мгновенная
мощность электрических сигналов в
емкости может быть положительной
(емкость накапливает энергию электрического
поля) и отрицательной (емкость отдает
во внешнюю цепь ранее накопленную
энергию).Средняя мощность гармонических
сигналов в емкости равна нулю, то
Рис. 4.4 есть емкость
не потребляет мощ-
ность
от гармонического источника.
Для индуктивности Lмгновенные значения тока и напряжения
связаны соотношением закона Ома из
табл.1.1, тогда с учетом выражения для
тока из (4.1) получим
![]() ,
,
а после преобразований
![]() .
.
(4.18)
Сравнивая (4.18) с выражением для напряжения
(4.1), получим уравнения связи для амплитуд
(действующих значений) тока и напряжения
![]() (4.19)
(4.19)
и их начальных фаз
![]() .
.
(4.20)
Введем обозначения
78
![]() ,
,
(4.21)
![]() ,
,
(4.22)
где
![]() –реактивное сопротивление индуктивности
–реактивное сопротивление индуктивности
(Ом), а![]() –модуль реактивной проводимости
–модуль реактивной проводимости
индуктивности (См=1/Ом). Позднее увидим,
что реактивная проводимость индуктивностиотрицательна.
Тогда получим выражения закона Омадля амплитуд (действующих значений)
тока и напряжения в индуктивности
![]() .
.
(4.23)
Согласно (4.20) гармонический ток в
индуктивности отстает по фазе от
напряжения(напряжение опережает по
фазе ток) на угол![]() радиан или 900. Сдвиг фаз между
радиан или 900. Сдвиг фаз между
напряжением и током в индуктивности
равен
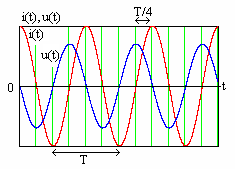
![]() .
.
(4.24)
Временные диаграммы тока и напряжения
в индуктивности показаны на рис. 4.5. В
отличие от аналогичных графиков для
емкости на рис. 4.3 ток и напряжение
меняются
местами, кривая напряже-
Рис. 4.5
ния смещена вправо отно-
сительно тока на четверть периода, что
соответствует опережению по фазе на
900.
79
Мгновенная мощность гармонических
сигналов в индуктивности равна
![]() ,
,
(4.25)
а после тригонометрических преобразований
получим
![]() .
.
(4.26)
Временная диаграмма мгновенной мощности
в индуктивности совпадает с показанной
на рис. 4.4 для емкости.
Средняя мощность гармонических
сигналов в индуктивности (как и в емкости)
равна нулю, то есть индуктивность не
потребляет мощность
от гармонического источника.
В табл. 4.1 приведены сводные результаты
для гармонических сигналов в элементах
цепи.
Таблица 4.1
|
Элемент |
Ток |
Напряжение |
Средняя мощность |
|
R |
|
|
|
|
C |
|
|
|
|
L |
|
|
|
4.2. Средняя мощность гармонических
сигналов в
линейном двухполюснике
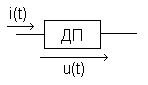
Рассмотрим двухполюсник
(ДП) на рис. 4.6, через который протекает
гармонический ток![]() и к которому приложе-
и к которому приложе-
80
но напряжение
![]() вила (4.1).
вила (4.1).
 Мгновенная
Мгновенная
мощность равна
![]() (4.27)
(4.27)
а после тригонометрических преобра-
Рис.4.6
зований получим
![]() .
.
(4.28)
Как видно, мгновенная мощность изменяется
по гармоническому закону с частотой
![]() и содержит постоянную составляющую.
и содержит постоянную составляющую.
Средняя мощность равна
![]() ,
,
(4.29)
где
![]() – сдвиг фаз между напряжением и током.
– сдвиг фаз между напряжением и током.
Величину![]() называюткоэффициентом мощности.
называюткоэффициентом мощности.
Как видно, потребляемая двухполюсником
мощность определяется амплитудами
(действующими значениями) тока и
напряжения и коэффициентом мощности.
Для максимизации потребляемой мощности
(например, электродвигателем) необходимо
обеспечить условие
![]() ,
,
то есть нулевой сдвиг фаз между напряжением
и током (![]() ).
).
Это означает, что двухполюсник должен
вести себя как сопротивление![]() .
.
В чисто реактивной цепи, содержащей
только индуктивности и емкости, сдвиг
фаз
![]() ,
,
при этом потребляемая мощность будет
рана нулю при любых амплитудах тока и
81
напряжения.
Полученное выражение (4.29) для средней
мощности полностью согласуется со
значениями
![]() в элементах цепиR,LиC(табл. 4.1), так как в
в элементах цепиR,LиC(табл. 4.1), так как в
сопротивлении![]() ,
,
а в индуктивности и емкости![]() .
.

4.3. Тригонометрический метод расчета
Тригонометрический метод
расчета гармонических токов и напряжений
в линейной цепи базируется на законах
Ома и Кирхгофа для мгновенных значений
сигналов в тригонометрической форме.
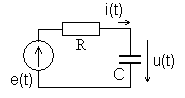 В
В
качестве примера рассмотрим цепь на
рис. 4.7 при![]() ,
,![]() В,
В,![]() рад/с,
рад/с,![]() ,
,![]() кОм
кОм
и![]() нФ.
нФ.
Обозначим гармонический ток![]() в виде
в виде
Рис. 4.7
![]() ,
,
(4.30)
тогда с учетом свойств гармонических
напряжений в сопротивлении и емкости
на основе второго закона Кирхгофа
получим
![]() .
.
(4.31)
82
Левая часть (4.31) может быть преобразована
в тригонометрическую функцию,
![]() ,
,
(4.32)
тогда, уравнивая коэффициенты в правой
и левой частях уравнения, получим
![]() ,
,
(4.33)
![]() .
.
(4.34)
Из полученных выражений нетрудно
определить амплитуду и начальную фазу
тока в цепи,
 А,
А,
![]() .
.
При найденном токе нетрудно определить
напряжение
![]() на емкости (проведите расчет
на емкости (проведите расчет
самостоятельно).
Как видно, тригонометрический метод
требует суммирования гармонических
функций с неизвестными параметрами,
что приводит к громоздким расчетам,
если число слагаемых функций более
двух. Этот метод применим для расчета
очень простых цепей.
83
4.4. Векторная диаграмма цепи
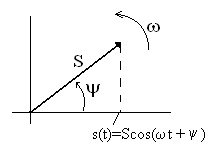 Гармонический
Гармонический
сигнал![]() можно представить проекцией на
можно представить проекцией на
горизонтальную ось вектора, вращающегося
против часовой стрелки вокруг начала
координат с круговой (угловой) частотой![]() ,
,
как показано на рис. 4.8. Длина (модуль)
вектора равна амплитуде гармонического
сигнала![]() и в момент начала вращения (при
и в момент начала вращения (при![]() )
)
угол его наклона к горизонтальной
Рис. 4.8 оси равен
начальной фазе сиг-
нала
![]() (отсчет положительных значений проводится
(отсчет положительных значений проводится
против часовой стрелки).
Все гармонические токи и напряжения в
цепи с одинаковой частотой, равной
частоте источников сигнала, можно
представить совокупностью синхронно
вращающихся векторов вида рис. 4.8. Так
как все векторы вращаются синхронно и
между ними сохраняются амплитудные и
угловые соотношения, то вращение можно
остановить и рассматривать неподвижную
совокупность векторов. Если вращение
остановлено в момент времени
![]() ,
,
то угол наклона каждого вектора к
горизонтальной оси равен начальной
фазе соответствующего вектору
гармонического сигнала.

84
Для векторного представления гармонических
сигналов выполняются законы Кирхгофав классической формулировке.
В качестве примера рассмотрим векторную
диаграмму цепи, показанной на рис. 4.7.
Результаты ее расчета тригонометрическим
методом приведены в табл. 4.2 (проведите
соответствующие расчеты).
Таблица 4.2
|
Сигнал |
Амплитуда |
Начальная фаза |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
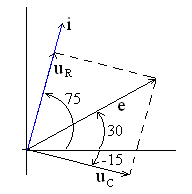 Векторная
Векторная
диаграмма цепи приведена на рис. 4.9.
Векторы тока и напряжений построены по
данным табл. 4.2, длина вектора равна
амплитуде сигнала, а угол отклонения
от горизонтальной оси равен начальной
фазе (отсчет положительных значений
угла против часовой стрелки). Вектор
тока![]() совпадает по направлению с вектором
совпадает по направлению с вектором
напряжения![]() на сопротивлении, их длины (модули)
на сопротивлении, их длины (модули)
не одинаковы, так как масштабы
Рис. 4.9
штабы (например, В/см и мА/см)
токов и напряжений различны (ток и
напряжение не сравнимы между собой).
Напряжение на сопротивлении
![]() опережает по фазе напряжение на емкости
опережает по фазе напряжение на емкости![]() на 900. Это обусловлено тем, что в
на 900. Это обусловлено тем, что в
85
последовательной цепи рис. 4.7 через
сопротивление и емкость протекает один
и тот же ток, причем напряжение на
сопротивлении совпадает по фазе с током,
а на емкости – отстает по фазе от тока
на 900.
Сумма векторов напряжений на сопротивлении
и емкости в цепи рис. 4.7 по второму закону
Кирхгофа (в векторной форме) равна ЭДС
источника, что и показано на векторной
диаграмме рис. 4.9.
Как видно, векторная диаграмма цепи
может быть построена по результатам
расчета всех гармонических токов и
напряжений. Однако ее можно построить
«качественно» (без знания точных
параметров векторов, но с правильными
соотношениями между ними) и не проводя
численных расчетов.
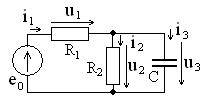 Рассмотрим
Рассмотрим
примерRCцепи, показанной
на рис. 4.10, в которой заданы положительные
направления и условные обозначения
всех токов и напряжений.
Прежде всего, необходимо проанализироватьструктуру цепи. В ней присутствует
Рис. 4.10 параллельный
фрагмент (со-
единение
элементов CиR2),
который соединен последовательно с
сопротивлениемR1и источником напряжения![]() .
.
Тогда построение необходимо начать с
напряжения на параллельном фрагменте,
при этом![]() ,
,
этот вектор проведем произвольно по
модулю и направлению, например,
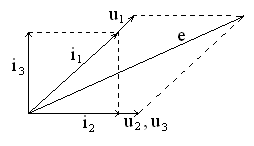
горизонтально, векторная диаграмма
показана на рис. 4.11.
Ток
![]() совпадает по фазе с напряжениями
совпадает по фазе с напряжениями![]() ,
,
а ток![]() опережает их по фазе на 900.
опережает их по фазе на 900.
Соответствующие векторы изображены на
диаграмме рис. 4.11 с произвольной длиной
и указанными угловыми соотношениями
относительно вектора
86
![]()
 .
.
Векторная сумма этих токов по первому
закону Кирхгофа равна току![]() ,
,
то есть этот вектор строится исходя из
векторов![]() и
и![]() .
.
Вектор напряжения![]() на сопротивленииR1совпадает по направлению с вектором
на сопротивленииR1совпадает по направлению с вектором
тока![]() и имеет произвольную длину, а вектор
и имеет произвольную длину, а вектор
ЭДС![]() по второму закону Кирхгофа Кирхгофа
по второму закону Кирхгофа Кирхгофа
равен Рис. 4.11
сумме векторов
![]() и
и
![]() .
.
На этом построение «качественной»
векторной диаграммы цепи заканчивается.
Если цепь содержит последовательный
фрагмент, входящий в смешанное соединение,
то построение целесообразно начинать
с вектора тока этого фрагмента.
Векторная диаграмма электрической
цепи может использоваться для иллюстрацииамплитудных и фазовых соотношений между
токами и напряжениями, и для формированияаналитических выражений, связывающих
их амплитуды (действующие значения) и
начальные фазы.
Например, для диаграммы рис. 4.11 амплитуды
(действующие значения) токов
![]() ,
,![]() и
и![]() по теореме Пифагора связаны выражением
по теореме Пифагора связаны выражением![]() .
.
Для других соотношений можно использовать
теорему косинусов (пример приведите
самостоятельно).
Для сложной цепи построение «качественной»
векторной диаграммы требует вдумчивого
подхода при выборе начального вектора
и способов построения остальных векторов.
87
4.5. Особенности расчета цепи с
гармоническими
сигналами
Мгновенные значения токов и напряжений
в электрической цепи связаны между
собой уравнениями законов Ома и Кирхгофа.
Последние предполагают суммирование
гармонических функций времени с
неизвестными амплитудами и начальными
фазами, например, с помощью теоремы
косинусов, а это приводит к громоздким
расчетам даже в относительно простых
цепях.
Существенно упростить расчеты можно,
отказавшись от описания сигналов с
помощью тригонометрических функций
времени и заменив его числами, на
зависящими от времени. На эту возможность
указывает векторная диаграмма цепи,
которая полностью отражает свойства
гармонических сигналов и не зависит от
времени.
Известно, что вектор, выходящий из
начала координат, можно представить
комплексным числом. Таким образом, в
теории электрических цепей при расчете
гармонических процессов возникает
метод комплексных амплитуд.
4.6. Расчет средней (потребляемой) мощности
По результатам расчета гармонических
токов и напряжений можно определить
мощность, потребляемую цепью от источника
сигнала.
В качестве примера используем цепь на
рис. 4.7, результаты расчета приведены в
табл. 4.2. Рассматривая цепь относительно
зажимов источника как двухполюсник,
при амплитуде напряжения
![]() В,
В,
тока![]() мА
мА
и сдвиге фаз между ними![]() ,
,
получим
![]() мВт.
мВт.
88
С другой стороны, в рассматриваемой
цепи емкость не потребляет мощность
гармонического сигнала, и она может
выделяться только в сопротивлении.
Тогда получим
![]() мВт.
мВт.
Как видно результаты совпадают.
Если в цепи имеется несколько
сопротивлений, то общая потребляемая
цепью мощность будет равна сумме
мощностей, потребляемых каждым
сопротивлением в отдельности.
4.7. Задания для самостоятельного решения
Задание 4.1. Тригонометрическим
методом определите амплитуды и начальные
фазы токов и напряжений на элементах
цепей, показанных на рис. 4.12, при![]() В,
В,![]() мА,
мА,![]() кОм,
кОм,![]() мГн
мГн
и![]() нФ.
нФ.
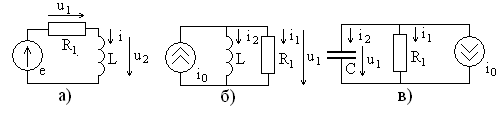
Рис. 4.12
По результатам расчета постройте полные
векторные диаграммы цепей, проверьте
выполнимость законов Кирхгофа.
Задание 4.2.Постройте «качественные»
векторные диаграммы цепей, показанных
на рис. 4.12. Сравните их с расчетными
диаграммами из задания 4.1.
89
Задание 4.3.Определите мощность,
потребляемую от источника сигнала в
цепях, показанных на рис. 4.12. Проведите
расчеты, рассматривая цепь как двухполюсник
или выделив в ней энергопотребляющие
элементы.
Задание 4.4.Постройте «качественные»
полные векторные диаграммы цепей,
показанных на рис. 4.13.
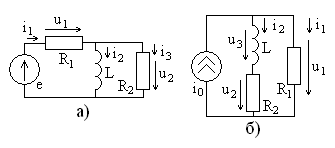
Рис. 4.13
Задание 4.5.Тригонометрическим
методом определите амплитуды и начальные
фазы токов и напряжений на элементах
цепи, показанной на рис. 4.10, при![]() кОм,
кОм,![]() нФ
нФ
и![]() В.
В.
Постройте полную векторную диаграмму
цепи, сравните ее с приведенной на рис.
4.11. Определите мощность, потребляемую
цепью от источника.
90
Расчет простых цепей постоянного тока
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1
Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.
 Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.
Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
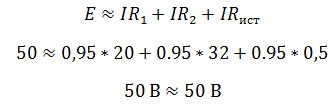
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
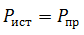
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
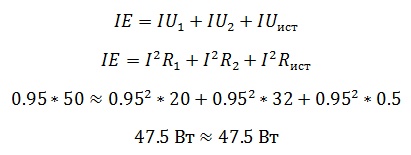
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2
Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах 
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если у вас возникли затруднения, прочтите статью законы Кирхгофа.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи
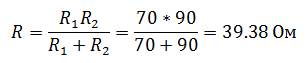
А затем напряжение

Зная напряжения, найдем токи, протекающие через резисторы
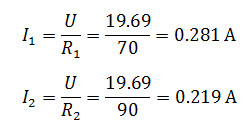
Как видите, токи получились теми же.
Пример 3
В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом. Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.
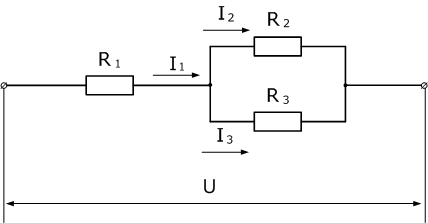
Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Эквивалентное сопротивление и ток в цепи
 Отсюда мощность, выделяемая на R1
Отсюда мощность, выделяемая на R1
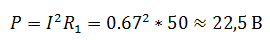 Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
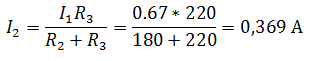
Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2
![]()
Таким образом производится расчет простых цепей постоянного тока.

Наиболее простым методом расчета электрической цепи с двумя узлами – является метод узлового напряжения или метод двух узлов.
Важно отличать метод узлового напряжения (метод двух узлов) от метода узловых напряжений.
Содержание
- Методика расчёта
- Пример решения задач методом двух узлов
- Онлайн программа для расчета электрических цепей постоянного тока методом двух узлов.
Метод узлового напряжения (двух узлов)

Определим разность потенциалов между двумя узлами цепи А и B.
![]()
Найдём потенциал точки А, перемещаясь по первой ветви от узла B до А.
![]()
Исходя из выражения (1) можно записать:
![]()
![]()
Выразим ток первой ветви

где r1 и g1 – сопротивление и проводимость первой ветви соответственно.
Аналогично составляются уравнения для оставшихся ветвей.
![]()
![]()
![]()
По первому закону Кирхгофа запишем уравнение для узла B
![]()
Подставим в вышеуказанное уравнение выражения токов (2-5).
![]()
Раскрыв скобки, находим узловое напряжение U:

Общее выражение узлового напряжения

Исходя из вышеизложенного, узловое напряжение равно отношению алгебраической суммы произведений ЭДС на проводимости соответствующих ветвей к сумме проводимостей всех ветвей. ЭДС направленная к узлу A, записывается со знаком «+», если в противоположную сторону, то со знаком «-».
Давайте рассмотрим применения метода на конкретном примере.
Пример решения задач методом двух узлов (метод узлового напряжения)
У нас есть бесплатная онлайн программа для расчета электрических цепей методом двух узлов.
Пример. Электрическая цепь постоянного тока представлена на рисунке 2. Определить токи в ветвях методом двух узлов, если ЭДС источников равна E1 = 40 В, E2 = 50 В, E3 = 10 В, а сопротивления r1 = 10 Ом, r2 = 20 Ом, r3 = 15 Ом, r4 = 12 Ом.

Порядок расчёта:
- Так как действительные направления токов до расчёта цепи нам неизвестны — произвольно указываем направления токов в ветвях, например, как на Рисунке 3.

- Определим проводимость ветвей.





- Найдем напряжение UAВ. Для этого воспользуемся формулой 6.

В числителе записываем произведения ЭДС на проводимости соответствующих ветвей, причем ЭДС направленная к узлу A, записывается со знаком «+», если в противоположную сторону, то со знаком «-».

В знаменателе указываем сумму проводимостей всех ветвей:

Подставляем раннее найденные значения проводимостей и значения ЭДС указанные в условии задачи:

- Определим токи в ветвях. С учетом направления ЭДС





Подставляем численные значения
![]()
![]()
![]()
![]()
Токи I3 и I4 получились с отрицательными значениями, следовательно их направление противоположно ранее принятому.

Правильность решения можно проверить при помощи баланса мощностей.
Так же для себя правильность решения задачи можно проверить выполнением первого закона Кирхгофа, а именно:

![]()
![]()
С учетом погрешности, условие выполняется.
Бесплатная онлайн программа.

