Как найти напряжение второго вольтметра

Лабораторная
работа №2

Тема.
Измерение
напряжения в цепях постоянного тока

Цель.
Провести измерение напряжения в цепи
постоянного тока прямым методом.
Ознакомится со способам расширения
верхних пределов измерений вольтметров
постоянного тока, с методам расчета
добавочных сопротивлений.

Задание
к работе

1. Определить
   внутренне сопротивление вольтметра.

2. Определить
   сопротивление добавочного резистора.

3. Сделать
   выводы по результатам работы.

Теоретические
сведения

Для
измерения напряжения U,
действующего между какими-либо двумя
точками электрической цепи, вольтметр
2 (рис. 1, а) присоединяют к этим точкам,
т. е. параллельно источнику 1 электрической
энергии или приемнику 3.

Для
того чтобы включение вольтметра не
оказывало влияния на работу электрических
установок и он не создавал больших
потерь энергии, вольтметры выполняют
с большим сопротивлением. Поэтому
практически можно пренебрегать проходящим
по вольтметру током.

Для
расширения пределов измерения вольтметров
последовательно с обмоткой прибора
включают добавочный резистор 4 (R_Д)
(рис. 1, б). При этом на прибор приходится
лишь часть U_V измеряемого
напряжения U,
пропорциональная сопротивлению прибора
R_V.

Зная
сопротивление добавочного резистора
и вольтметра, можно по значению напряжения
U_V,
фиксируемого вольтметром, определить
напряжение, действующее в цепи:

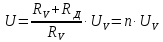
(1)

Величина
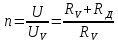 показывает,
во сколько раз измеряемое напряжение
U
больше напряжения U_V,
приходящегося на прибор, т. е. во сколько
раз увеличивается предел измерения
напряжения вольтметром при применении
добавочного резистора.

Сопротивление
добавочного резистора, необходимое для
измерения напряжения U,
в n
раз большего напряжения прибора U_V,
определяется по формуле

(2)

Добавочный
резистор может встраиваться в прибор
и одновременно использоваться для
уменьшения влияния температуры окружающей
среды на показания прибора. Для этой
цели резистор выполняется из материала,
имеющего малый температурный коэффициент,
и его сопротивление значительно превышает
сопротивление катушки, вследствие чего
общее сопротивление прибора становится
почти независимым от изменения
температуры. По точности добавочные
резисторы подразделяются на те же классы
точности, что и шунты.

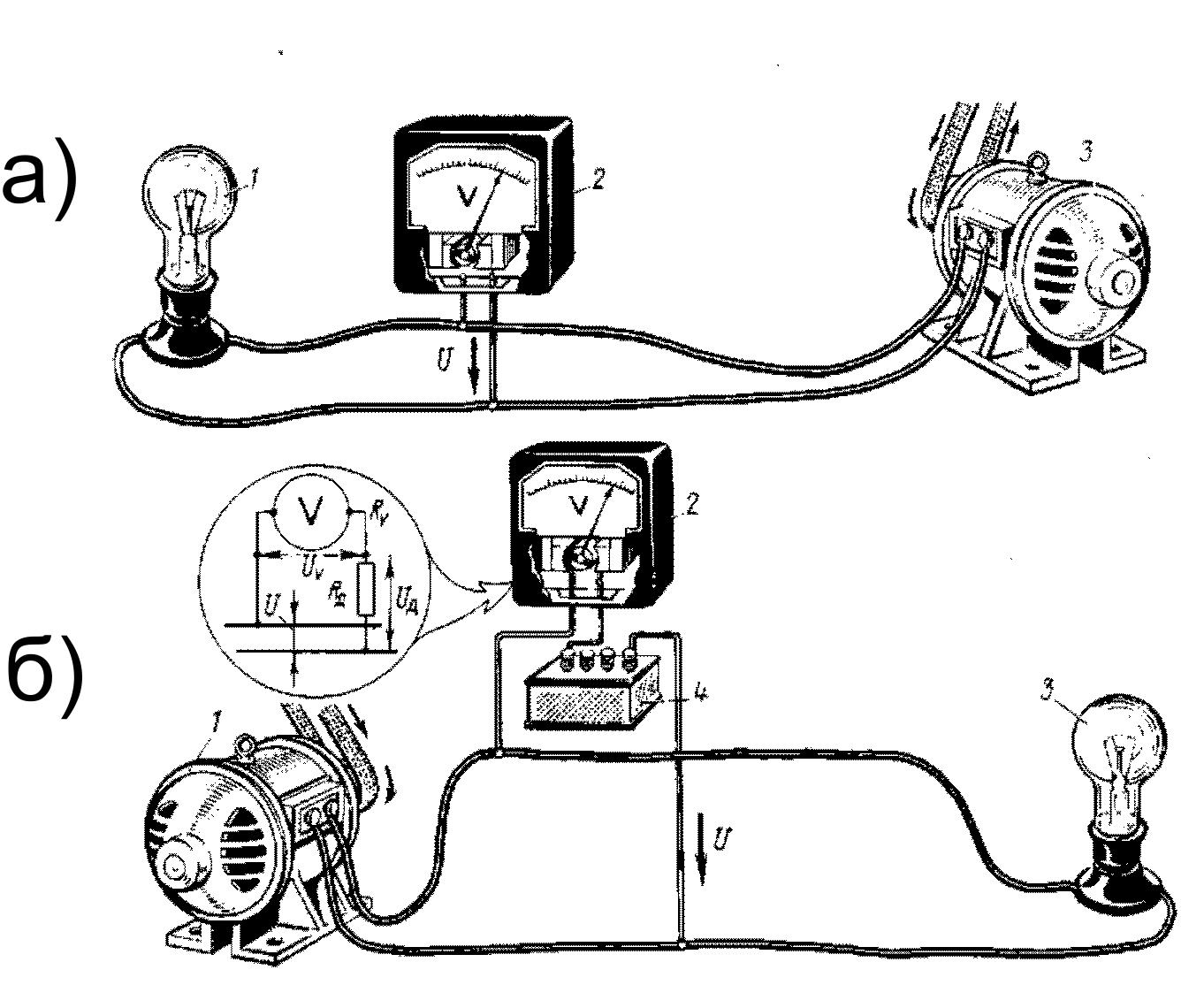
Рис.
1. Схемы для измерения напряжения

Внутреннее
сопротивление вольтметра. Для
определения внутреннего сопротивления
вольтметра его необходимо подключить
последовательно с резистором (с
)
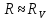к источнику напряжения (рис. 2) . Напряжение
источника поделится между резистором
и вольтметром пропорционально их
сопротивлениям

(3)

Откуда

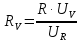
(4)

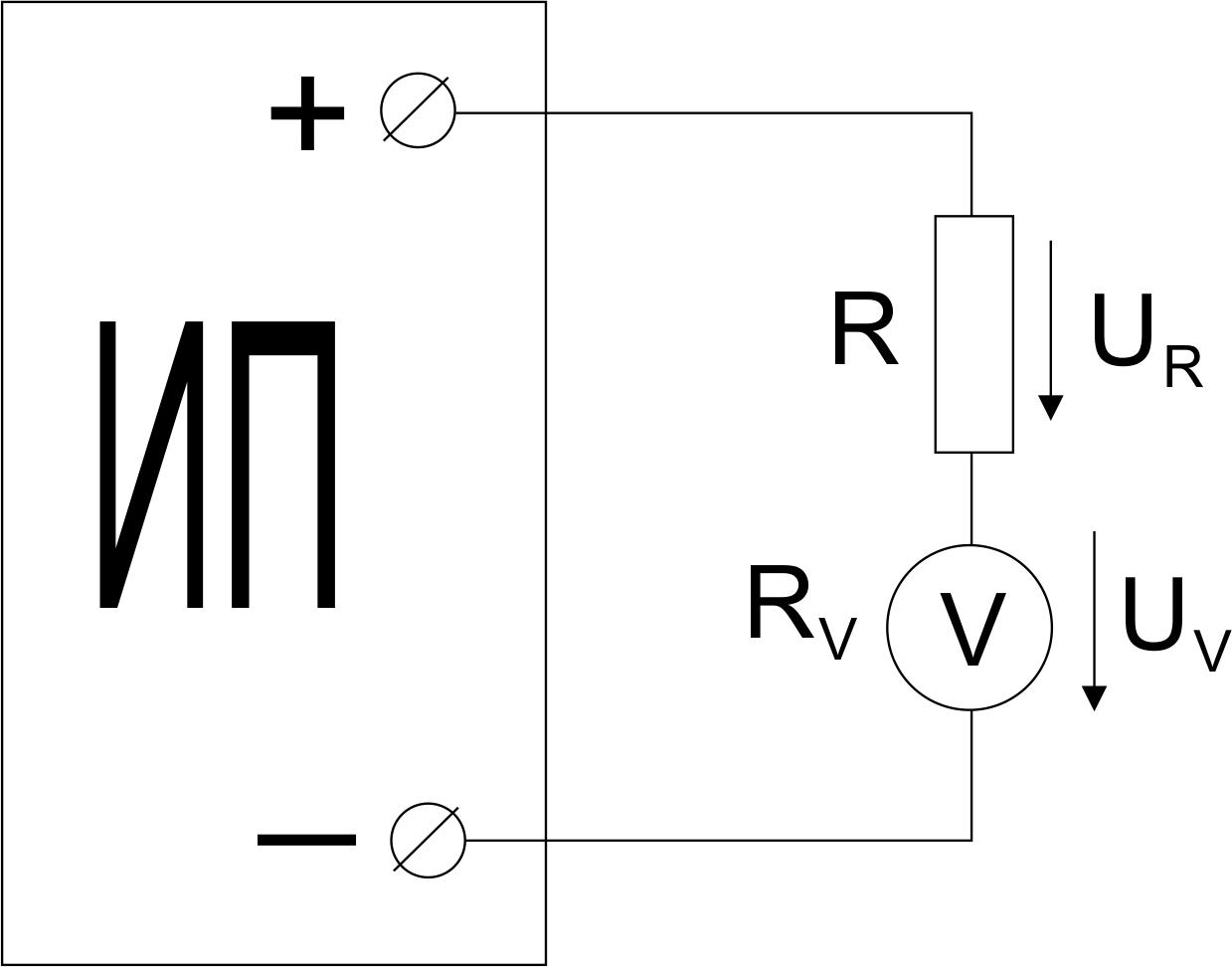
Рис.
2. Схема для определения внутреннего
сопротивления вольтметра

Указания
по проведению работы.

1. Собрать
   схему, как на рис. 2.

2. Сопротивления
   R
   выбрать с помощью магазинов сопротивлений
   так, чтобы напряжения U_R
   и U_V
   были приблизительно равнями ().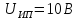

3. Измерив
   цифровым вольтметром напряжения U_R
   и
   U_V,
   по формуле (4) определить сопротивление
   вольтметра R_V.

4. Собрать
   схему, как на рис. 3 (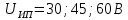
   ).

5. Рассчитать
   значение добавочного сопротивления
   R_Д
   (2) для каждого из значений U_ИП
   и
   коэффициент n.

6. Используя
   показание вольтметра 15
   В
   и
   значение коэффициента n,
   определить напряжение U_ИП
   (1). Убедиться, что его значение совпадает
   с действительным.

7. Заполнить
   таблицу 1.

Рис.
3. Использование добавочного сопротивления

Таблица
1

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Условие задачи:

Два вольтметра, подключенные последовательно к ненагруженной батарее, показывают соответственно (U_{11}=5) В и (U_{12}=15) В. Если подключить к батарее только первый вольтметр, он покажет 19 В. Определить ЭДС батареи.

Задача №7.5.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(U_{11}=5) В, (U_{12}=15) В, (U_2=19) В, (rm E-?)

Решение задачи:

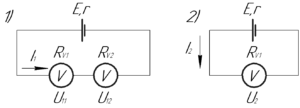В задаче рассмотрено два случая, схемы для которых приведены на рисунке. Очевидно, что в первом случае напряжение во внешней цепи равно сумме напряжений (U_{11}) и (U_{12}), то есть:

[{U_1} = {U_{11}} + {U_{12}}]

[{U_1} = 5 + 15 = 20;А]

Должно быть понятно, что внутренние сопротивления вольтметров (R_{v1}) и (R_{v2}) различны, поскольку в противном случае напряжения (U_{11}) и (U_{12}) были бы равны. В первом случае через вольтметры, соединенные последовательно, течёт одинаковый ток, поэтому верно равенство:

[frac{{{U_{11}}}}{{{R_{v1}}}} = frac{{{U_{12}}}}{{{R_{v2}}}}]

Откуда имеем:

[{R_{v2}} = {R_{v1}}frac{{{U_{12}}}}{{{U_{11}}}}]

Учитывая, что (U_{11}=5) В, а (U_{12}=15) В, получим:

[{R_{v2}} = 3{R_{v2}}]

Тогда в первом случае суммарное сопротивление двух вольтметров равно (4R_{v1}). Запишем закон Ома для полной цепи для двух случаев:

[left{ begin{gathered}
{I_1} = frac{{rm E}}{{4{R_{v1}} + r}} hfill \
{I_2} = frac{{rm E}}{{{R_{v1}} + r}} hfill \
end{gathered} right.]

Тогда напряжения во внешней цепи (U_1) и (U_2) в обоих случаях можно найти по формулам:

[left{ begin{gathered}
{U_1} = frac{{{rm E} cdot 4{R_{v1}}}}{{4{R_{v1}} + r}} ;;;;(1)hfill \
{U_2} = frac{{{rm E} cdot {R_{v1}}}}{{{R_{v1}} + r}} ;;;;(2)hfill \
end{gathered} right.]

Разделим (1) на (2):

[frac{{{U_1}}}{{{U_2}}} = frac{{4left( {{R_{v1}} + r} right)}}{{4{R_{v1}} + r}}]

Учтем, что (U_1=20) В, а (U_2=19) В:

[frac{{20}}{{19}} = frac{{4left( {{R_{v1}} + r} right)}}{{4{R_{v1}} + r}}]

Перемножим “крест-накрест” и сразу же раскроем скобки:

[80{R_{v1}} + 20r = 76{R_{v1}} + 76r]

[4{R_{v1}} = 56r]

[{R_{v1}} = 14r]

Полученное выражение подставим в (2):

[{U_2} = frac{{{rm E} cdot 14r}}{{15r}}]

[{U_2} = frac{{14{rm E}}}{{15}}]

Откуда окончательно получим:

[{rm E} = frac{{15{U_2}}}{{14}}]

Численный ответ равен:

[{rm E} = frac{{15 cdot 19}}{{14}} approx 20,4;В]

Ответ: 20,4 В.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

7.5.27 К источнику тока подключены последовательно амперметр и резистор. Параллельно резистору
7.5.29 В цепь, состоящую из источника ЭДС и сопротивления 2 Ом, включают амперметр сначала
7.5.30 Каково удельное сопротивление проводника, если его длина 10 км, площадь поперечного

2.9. Добавочное сопротивление к вольтметру

Если вольтметр рассчитан на максимальное напряжение `U_max`, а с его помощью необходимо измерять напряжение, в `n` раз большее, то, подключив последовательно с вольтметром добавочное сопротивление `R_2` (рис. 10), разделим напряжение `n*U_max` на два слагаемых: одно из них – это напряжение $$ {U}_{mathrm{max}}$$ на вольтметре, второе – напряжение $$ left(n-1right){U}_{mathrm{max}}$$ на добавочном сопротивлении.

Поскольку добавочное сопротивление включено последовательно с вольтметром, то через вольтметр и добавочное сопротивление течёт одинаковый ток, т. е. справедливо равенство

Отсюда                                     

2017-11-06   

Два одинаковых вольтметра показывают в схемах а) и б) (см. рис.) одинаковые напряжения U = 10 В. Определить напряжение источника питания $U_{0}$.

Примечание: показание вольтметра равно произведению величины протекающего через него тока на его сопротивление.

Решение:

Обозначим сопротивление вольтметра через $r$. Тогда токи через сопротивление $R$ согласно закону Ома в схемах а) и б) (см. рис.) будут:

$I_{1} = frac{U_{0}}{R + 2r}, I_{2} = frac{U_{0}}{R + frac{r}{2}}$.

Поскольку сопротивления вольтметров одинаковы, то ток, протекающий по каждому из них во второй схеме, равен $I_{2}/2$. Так как показание вольтметра равно произведению величины протекающего через него тока на его сопротивление, можем записать:

$V = frac{U_{0}}{R + 2r} r, V = frac{1}{2} frac{U_{0}}{ left ( R + frac{r}{2} right )} r$,

откуда $R + 2r = 2R + r$, т.е. $r = R$ и $U_{0} = 3V = 30 В$.