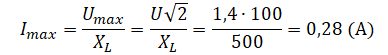При последовательном соединении катушки и конденсатора на расчетной схеме каждый из этих элементов электрической цепи может быть представлен активным и реактивным сопротивлениями или активной и реактивной проводимостями.
Для расчета более простой является схема рис. 14.1, а, где элементы соединены последовательно, а в схеме рис. 14.1, б они соединены смешанно.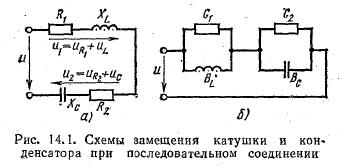 
Предположим известными параметры катушки R1, L и конденсатора R2, C; ток в цепи i = Imsinωt.
Требуется определить напряжение на участках цепи и мощность.
Мгновенную величину общего напряжения можно представить суммой мгновенных напряжений на отдельных элементах схемы:
Имея в виду несовпадение по фазе активных и реактивных напряжений, общее напряжение получим векторным сложением:
В зависимости от соотношения величин реактивных сопротивлений индуктивности и емкости можно отметить три случая:
1. ХL>ХC . Для этого случая векторная диаграмма представлена на рис. 14.2. На диаграмме построены треугольники напряжений для катушки и конденсатора и найдены векторы напряжения U1 и U2 на этих элементах.
Векторная сумма напряжений U1 + U2 = U дает общее напряжение в цепи. Вместе с тем вектор U является гипотенузой прямоугольного треугольника напряжений, катеты которого — активное и реактивное напряжения цепи (Uа и Uр). Так как векторы активных составляющих напряжения направлены в одну сторону, их численные значения складываются: Ua = U1R + U2R.
Векторы реактивных составляющих напряжения направлены по одной прямой в противоположные стороны, поэтому им придают разные знаки: реактивное напряжение индуктивности считают положительным, а напряжение емкости — отрицательным: Uр = UL — UC .
При одинаковом токе во всех элементах цепи UL>UC . Ток отстает от общего напряжения по фазе на угол φ. Из треугольника напряжений следует
где R = R1 + R2 и X = XL — XC общее и активное и реактивное сопротивление цепи. Полное сопротивление цепи — Z.
Эти сопротивления графически можно изобразить сторонами прямоугольного треугольника сопротивлений, который получают уже известным способом из треугольника напряжений.
Полное сопротивление цепи Z является коэффициентом пропорциональности между действующими величинами тока и общего напряжения цепи:
U = IZ; I = U/Z; Z = U/I.
Угол сдвига по фазе между напряжением и током в цепи положительный (φ>0) (фазовые токи отсчитываются от вектора тока).
2. ХL Векторная диаграмма изображена на рис. 14.3, где UL емкостный характер.
Расчетные формулы для первого случая остаются без изменения и для второго случая.
3. XL = ХC . В этом случае реактивные составляющие напряжения катушки и конденсатора равны по величине и взаимно компенсированы: UL = UC (рис. 14.4). Поэтому реактивная составляющая общего напряжения и общее реактивное сопротивление равны нулю, а полное сопротивление цепи Z = R.
Угол φ сдвига фаз между током и общим напряжением равен нулю.
U = IR, или I = U/R.
В случае XL = ХC в цепи имеет место явление резонанса напряжений.
Из треугольника напряжений легко получить треугольник мощностей из которого следуют уже известные формулы:
Реактивные мощности входят в расчеты также с разными знаками: индуктивная мощность положительна, а емкостная — отрицательна.
В соответствии с этим знак реактивной мощности всей цепи может быть тем или другим, что следует и из формул (14.2).
При φ>0 Q>0; при φ
Источник
Конденсатор, катушка и резонанс в цепи переменного тока
теория по физике 🧲 колебания и волны
Опишем колебания, которые происходят в цепи переменного тока при включении в нее конденсатора и катушки индуктивности. А также рассмотрим условия, при выполнении которых в цепи переменного тока наступает резонанс. Получим формулы для вычисления амплитуд напряжений, введем понятия емкостного и индуктивного сопротивления и выясним, какую роль играют эти величины.
Конденсатор в цепи переменного тока
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).
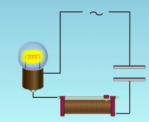
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
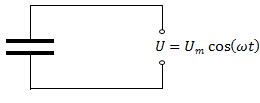
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
Следовательно, заряд конденсатора меняется по гармоническому закону:
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i = q ´ = − C U m a x sin . ω t = C U m a x cos . ( ω t + π 2 . . )
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π 2 . . (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
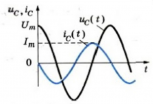
Амплитуда силы тока равна:
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
Величина X C , равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура q m a x = 10 − 6 Кл. Амплитудное значение силы тока в контуре I m a x = 10 − 3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q 2 m a x 2 C . . = L I 2 m a x 2 . .
T = 2 π √ L C = 2 π q m a x I m a x . . = 2 · 3 , 14 10 − 6 10 − 3 . . ≈ 6 , 3 · 10 − 3 ( с )
Катушка индуктивности в цепи переменного тока
Соберем две электрических цепи, состоящих из лампы накаливания, катушки индуктивности и источника питания: в первом случае постоянного, во втором — переменного (см. рисунки «а» и «б» ниже).
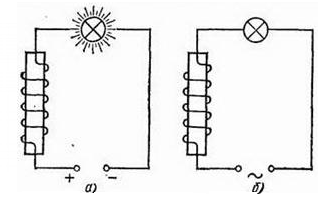
Опыт покажет, что в цепи постоянного тока лампа светится ярче по сравнению с той, что включена в цепь переменного тока. Это говорит о том, что сила тока в цепи постоянного тока выше действующего значения силы тока в цепи переменного тока.
Результат опыта легко объясняется явлением самоиндукции. При подключении катушки к постоянному источнику тока сила тока нарастает постепенно. Возрастающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь спустя какое-то время сила тока достигает наибольшего значения, соответствующему данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не успевает достигнуть максимального значения. Поэтому максимальное значение силы тока в цепи переменного тока с катушкой индуктивности ограничивается индуктивность. Чем больше индуктивность и чем больше частота приложенного напряжения, тем меньше амплитуда силы переменного тока.
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (см. рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.
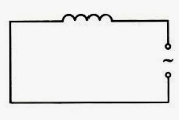
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна равняться нулю. Иначе, согласно закону Ома, сила тока была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля → E i , порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля → E к , создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства → E i = − → E к следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции e i ) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Учитывая, что удельная работа кулоновского поля равна напряжения на концах катушки, можно записать:
Напомним, что сила переменного тока изменяется по гармоническому закону:
Тогда ЭДС самоиндукции равна:
e i = − L i ´ = − L ω I m a x cos . ω t
Так как u = − e i , то напряжение на концах катушки оказывается равным:
u = L ω I m a x cos . ω t = L ω I m a x sin . ( ω t + π 2 . . ) = U m a x ( ω t + π 2 . . )
Амплитуда напряжения равна:
Следовательно, колебания напряжения на катушке опережают колебания силы тока на π 2 . . , или колебания силы тока отстают от колебаний напряжения на π 2 . . , что одно и то же.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (см. график ниже).
Но в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Амплитуда силы тока в катушке равна:
Также будем использовать вместо амплитуд действующие значения силы тока и напряжения. Тогда получим:
Величина X L , равная произведению циклической частоты на индуктивность, называется индуктивным сопротивлением. Индуктивное сопротивление зависит от частоты. Поэтому в цепи постоянного тока, в котором отсутствует частота, индуктивное сопротивление катушки равно нулю.
Пример №2. Катушка с индуктивным сопротивлением X L = 500 Ом присоединена к источнику переменного напряжения, частота которого ν = 1000 Гц. Действующее значение напряжения U = 100 В. Определите амплитуду силы тока I m a x в цепи и индуктивность катушки L. Активным сопротивлением пренебречь.
Индуктивное сопротивление катушки выражается формулой:
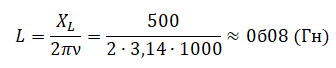
Так как амплитуда напряжения связана с его действующим значением соотношением U m a x = U √ 2 , то для амплитуды силы тока получаем:
Резонанс в электрической цепи
Механические и электромагнитные колебания имеют разную природу, но процессы, происходящие при этом, идентичны. Поэтому можно предположить, что резонанс в электрической цепи так же реален, как резонанс в колебательной системе, на которую действует периодическая сила.
Напомним, что в механической системе резонанс тем более заметен, чем меньше в колебательной системе трение между ее элементами. Роль трения в электрической цепи играет активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника, который при этом нагревается. Следовательно, резонанс в электрической цепи будет отчетливо наблюдаться при малом активном сопротивлении R.
Если активное сопротивление мало, то собственная частота колебаний в колебательном контуре определяется формулой:
Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру равна собственной частоте колебательного контура:
Резонанс в электрическом колебательном контуре — явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
После включения внешнего переменного напряжения резонансное значение силы тока в цепи устанавливается не моментально, а постепенно. Амплитуда колебаний силы тока возрастает до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
I 2 m a x R 2 . . = U m a x I m a x 2 . .
Упростив это уравнение, получим:
Следовательно, амплитуда установившихся колебаний силы тока при резонансе определяется уравнением:
При сопротивлении, стремящемся к нулю, сила тока возрастает до бесконечно больших значений. При большом сопротивлении сила тока возрастает незначительно. Это хорошо видно на графике ниже.
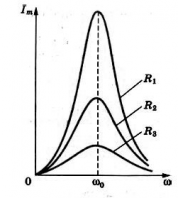
Пример №3. В цепь переменного тока с частотой ν = 500 Гц включена катушка индуктивностью L = 10 мГн. Какой емкости конденсатор надо включить в эту цепь, чтобы наступил резонанс?
Электрическая цепь, описываемая в условии, представляет собой колебательный контур. Резонанс в этой цепи наступит, когда частота переменного тока будет равна собственной частоте колебательного контура (ν = ν0).
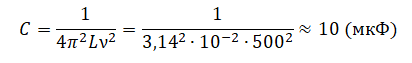
К колебательному контуру подсоединили источник тока, на клеммах которого напряжение гармонически меняется с частотой ν.
Индуктивность L катушки колебательного контура можно плавно менять от максимального значения Lmax до минимального Lmin, а ёмкость его конденсатора постоянна.
Ученик постепенно уменьшал индуктивность катушки от максимального значения до минимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.
Алгоритм решения
В колебательном контуре источником тока возбуждаются вынужденные колебания. Частота этих колебаний равна частоте источника — ν. Амплитуда колебаний зависит от того, как соотносятся между собой внешняя частота и частота собственных электромагнитных колебаний, которая определяется формулой:
По мере увеличения внешней частоты от нуля до ν0 амплитуда растет. Она достигает максимума тогда, когда происходит резонанс. При этом внешняя частота равна частоте собственных электромагнитных колебаний: ν = ν0. Затем амплитуда начинает убывать.
В данном случае, ученик меняет не внешнюю частоту, а частоту собственных электромагнитных колебаний. При плавном уменьшении индуктивности контура от максимального значения Lmax до минимального Lmin частота возрастает от ν0min до ν0max. Причем:
ν 0 m i n = 1 2 π √ L m i n C . .
ν 0 m a x = 1 2 π √ L m a x C . .
Из того факта, что амплитуда всё время увеличивалась, можем сделать вывод, что частота ν0 всё время приближалась к частоте источника тока, при этом ν > ν0max. В противном случае наблюдалось бы уменьшений амплитуды силы тока.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания.
Из приведённого ниже списка выберите две величины, которые остаются постоянными при этих колебаниях.
а) период колебаний силы тока в контуре
б) фаза колебаний напряжения на конденсаторе
г) энергия магнитного поля катушки
д) амплитуда колебаний напряжения на катушке
Алгоритм решения
- Определить, от чего зависит каждая из перечисленных величин.
- Установить, какие величины меняются, а какие нет.
В колебательном контуре происходят гармонические колебания. Поэтому период колебаний силы тока в контуре — величина постоянная.
Фаза — это величина, которая определяет положение колебательной системы в любой момент времени. Поскольку в системе происходят колебания, фаза меняется.
Заряд конденсатора — колебания происходят за счет постоянной перезарядки конденсатора. Следовательно, эта величина тоже меняется.
Энергия магнитного поля катушки — в колебательном контуре происходят взаимные превращения энергии магнитного поля катушки в энергию электрического поля конденсатора, и обратно. Поэтому энергия магнитного поля катушки постоянно меняется.
В условии задачи сказано, что колебания незатухающие. Это значит, что полная механическая энергия колебательной системы сохраняется. Поскольку именно от нее зависит амплитуда колебаний напряжения на катушке, то эта величина также остается постоянной.
pазбирался: Алиса Никитина | обсудить разбор | оценить
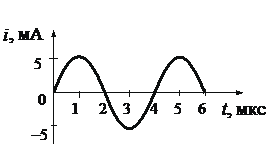На рисунке приведён график зависимости силы тока i от времени t при свободных гармонических колебаниях в колебательном контуре. Каким станет период свободных колебаний в контуре, если конденсатор в этом контуре заменить на другой конденсатор, ёмкость которого в 4 раза меньше? Ответ запишите в мкс.
Источник
Лекция № 4 Резистор, индуктивная катушка и конденсатор в цепи синусоидального тока.
Термин «сопротивление» для цепей переменного тока, оказывается недостаточно полным, поскольку сопротивление переменному току оказывают не только те элементы цепи, в которых выделяется энергия в виде теплоты (их называют активными сопротивлениями), но и те элементы цепи, в которых энергия периодически запасается в электрическом или магнитном полях. Такие элементы цепи называют реактивными сопротивлениями. Реактивными сопротивлениями обладают индуктивности и емкости.
Активное сопротивление в цепи синусоидального тока.
Если по активному сопротивлению 
течет ток 
тогда
по закону Ома
или
где 
Т. е. в активном сопротивлении элемента цепи комплекс тока 
совпадает с комплексом напряжения 
Рис. 4.1 – Графики мгновенных значений 
Мгновенная мощность
=
или 
т. е. мгновенная мощность имеет постоянную составляющую 
и переменную составляющую 
меняющуюся с частотой равной 
(на рис. 4.1)
Индуктивность в цепи переменного синусоидального тока.
Практически любая обмотка (катушка) обладает некоторой индуктивностью 
и активным сопротивлением .
Схема замещения катушки может быть представлена в виде последовательного соединения индуктивности и активного сопротивления 
.
Выделим из схемы одну индуктивность
Рис. 4.2
Если через индуктивность течет ток , то в катушке наводится ЭДС самоиндукции – 
.
Для прохождения переменного тока через индуктивность необходимо, чтобы на ее зажимах было напряжение 
, равное и противоположно направленное 
.
,
где 
– индуктивное сопротивление 
где 
– частота, Гц,
– индуктивность, Гн.
Движению переменного тока через индуктивность оказывается сопротивление за счет накопления энергии 
, это сопротивление называется индуктивным.
Размерность индуктивного сопротивления
.
Значение тока в цепи с индуктивностью опережает ЭДС самоиндукции на 90°, но т. к. вектор напряжения на катушке индуктивности направлен в противоположную сторону ЭДС.
т. е. 
т. о. в цепи с индуктивностью вектор тока отстает от вектора напряжения на угол 90°.
Действующее значение тока в цепи с индуктивностью равно действующему значению напряжения, деленному на индуктивное сопротивление.
т. е. 
Приведенная формула похожа на закон Ома. Это внешнее сходство позволяет определить ток в цепи с индуктивностью, подобно тому, как в цепи с активным сопротивлением. Но нужно помнить, что индуктивное сопротивление с физической точки зрения с обычным сопротивлением ничего общего не имеет.
Понятие об индуктивном сопротивлении формально введено для облегчения расчета.
Оно заменяет фактическое влияние ЭДС самоиндукции на ток в цепи.
Мгновенная и реактивная мощность
Мгновенное значение мощности 
или
График изменения мощности представляет собой синусоиду двойной частоты с амплитудой
.
Наибольшее значение мощности в цепи с индуктивностью равно произведению действующих значений напряжения и тока.
В первую четверть периода, когда ток в цепи увеличивается, энергия накапливается в магнитном поле катушки за счет энергии источника. Катушка в это время является приемником энергии: ток направлен против ЭДС самоиндукции.
Во вторую четверть периода, когда ток уменьшается, энергия возвращается в сеть (источнику). Направление ЭДС самоиндукции и тока совпадают. Катушка является источником энергии.
В следующую половину периода процесс повторяется.
Средняя активная мощность за период равна нулю 
, т. к. в цепи с индуктивностью преобразования электрической энергии в другие виды энергии не происходит.
Цепь с емкостью – 
К конденсатору с идеальным диэлектриком, т. е. в нем нет потерь энергии, подведено напряжение
Определим ток и мощность
Ток в цепи.
Заряд конденсатора пропорционален напряжению между его обкладками, поэтому изменение напряжения сопровождается изменением заряда.
Скорость изменения заряда пропорциональна скорости изменения напряжения.
но скорость изменения заряда равна электрическому току
т. к. 
то 
Сопоставляя: 
получаем, что ток через конденсатор по фазе опережает напряжение на конденсаторе на угол 90°. На векторной диаграмме вектор тока 
опережает вектор напряжения 
на угол 90°.
Амплитуда тока 
Действующее значение тока
или 
где 
– реактивное сопротивление конденсатора
Построение графика мгновенной мощности конденсатора выполняют также как и для индуктивной катушки.
т. к. 
В первую четверть периода, когда напряжение на конденсаторе возрастает, энергия накапливается в электрическом поле конденсатора за счет работы источника, конденсатор в это время заряжается, т. е. является приемником энергии. Направления тока и напряжения совпадают.
Во вторую четверть периода, когда напряжение уменьшается, энергия в том же количестве возвращается в сеть к источнику. Ток направлен против напряжения сети – конденсатор является источником энергии ( разряжается ) и так в 3й и 4й части периода.
Активная мощность равна нулю, а реактивная
Установившийся режим в простейшей неразветвленной цепи с сосредоточенными параметрами.
Электрические цепи характеризуются двумя режимами: переходным и установившимся.
Переходные режимы возникают в результате перераспределения энергии электрических и магнитных полей в 
и 
при резком изменении параметров электрической цепи.
Простейшая электрическая цепь переменного тока с 
Общее сопротивление такой цепи
где 
– реактивное сопротивление
или 
где 
Если по цепи протекает ток, то:
или 
в комплексной форме
Отсюда 
или
– закон Ома в комплексной форме
где 
– комплексное сопротивление
– модуль комплексного сопротивления
Величина обратная комплексному сопротивлению называется комплексной проводимостью.
(сименс)
Умножая на сопряженный комплекс получаем
где 
– активная проводимость,
– реактивная проводимость.
, 
по модулю 
Умножив 
сопротивление на ток 
получим треугольник U.
Напряжение можно представить в виде двух составляющих
Цепь 
Пусть 
По второму закону Кирхгофа
где 
и 
– синусоидальные напряжения
В комплексной форме
тогда 
или 
где 
– комплекс полного сопротивления индуктивной катушки (цепи )
Показательная форма записи
где 
– модуль комплекса полного сопротивления цепи
– аргумент.
Если 
, а 
,
тогда 
где 
, а 
Если ток , то 
.
– Комплекс тока в цепи с 
равен комплексу напряжения деленному на комплекс полного сопротивления катушки.
Умножив треугольники 
на получим:
– полная мощность (ВА)
– реактивная мощность (ВАp)
– активная мощность (Вт)
или 
– коэффициент мощности, зависит от соотношения
и
по его величине судят о том, какую часть полной мощности цепи составляет активная мощность.
Активную мощность измеряют ваттметром.
Цепь 
Пусть 
.
По второму закону Кирхгофа
, т. к. напряжение 
отстает от тока
или 
– комплекс полного сопротивления
– модуль комплекса
– аргумент
Напряжение на входе цепи 
отстает от тока на угол сдвига фаз 
т. о. 
, т. к. 
Аналогично цепи 
или 
Сложные цепи, состоящие из последовательных и параллельных участков
Расчет
1. При расчете цепи определяют активные 
и реактивные 
проводимости параллельных ветвей
; 
; 
; 
.
2. Далее определяют активную и реактивную проводимость разветвления аb
3.Преобразуют схему в эквивалентную
4.Определяют активное и реактивное сопротивление всей цепи
тогда 
; 
; 
; 
,
где 
, а 
.
Построение векторной диаграммы (по активным и реактивным составляющим).
Лучше построение векторной диаграммы начать с последней ветви и идти к началу цепи, т. е.к общему току и напряжению.
В нашем случае построение начнем с напряжения 
– откладываем его произвольно в масштабе.
Топографическая диаграмма:
при последовательном соединении напряжений и параллельных токов.
Топографическая диаграмма – такая векторная диаграмма, каждая точка которой соответствует определенной точке электрической цепи.
Резонанс при последовательном и параллельном соединении элементов 
Резонанс – такой режим цепи содержащей 
, индуктивность и емкость, при котором ее входное сопротивление (или проводимость) имеет активный характер.
В зависимости от вида цепи (последовательное или параллельное соединение) существует резонанс напряжений и токов.
1. Последов. соединение R, L,C.
Условие резонанса:
или 
т. к. 
, а 
, т. о.
, т. е. 
или 
где 
– резонансная угловая частота.
при резонансе 
При последовательном соединении 
и 
в резонансном режиме 
, т. е. имеется резонанс напряжений.
При резонансе значения 
и 
могут значительно превышать напряжения на зажимах.
Ток при резонансе 
или 
, т. к. 
, а 
т. о. 
, делим на 
, сокращаем
,
где 
– характеристическое (волновое) сопротивление контура имеет размерность сопротивления.
т. к. 
; 
; 
.
Отношение напряжения на индуктивности (или емкости) к напряжению на зажимах цепи при резонансе называется добротностью контура.
.
Величина обратная 
называется затуханием (
)
Параллельное соединение 
Условие резонанса: 
, т. е 
.
При равенстве реактивных проводимостей ветвей противоположные по фазе реактивные составляющие токов 
и 
равны по величине.
Такой режим работы цепи называют резонансом токов.
, 
, 
тогда 
или 
,
т. к. 
, то 
.
т. е. общий ток носит чисто активный характер (совпадает с 
) и может быть меньше 
и 
.
Символический метод анализа электрических цепей синусоидального тока.
В режиме синусоидального тока можно перейти от уравнений составленных для мгновенных значений (дифференциальных уравнений) к алгебраическим уравнениям, составленным относительно комплексов тока и ЭДС.
Например 
, 
Для схемы:
или
,
т. к. амплитуда действующего напряжения на 
, то знак 
говорит о том, что 
опережает 
на 90°.
Для емкости 
– напряжение отстает от тока на 90°.
Если 
– комплексная амплитуда действующей ЭДС, то
и 
,
т. о.умножение на равносильно повороту вектора на 90°, а на 
– на “-90°”.
Три формы записи комплексных чисел:
– алгебраическая форма,
– показательная форма,
– тригонометрическая.
Операции с комплексными числами
Сложение и вычитание комплексных чисел производится в алгебраической форме.
.
Деление и умножение производится в показательной форме:
;.
,
где 
, а 
.
-
Элементы цепи переменного тока
Резистор в цепи постоянного тока
По закону Ома, в замкнутой цепи
постоянного тока
напряжение на зажимах источника меньше
ЭДС
U =
IR; U = E – Ir
-
Резистор в цепи переменного тока
Р
ассмотрим
схему, состоящую из источника переменного
тока, резистора и идеальных проводов.
Предположим, что напряжение на резисторе
изменяется по гармоническому закону
U = U0
cos ω t .
Найдем силу тока, протекающего через
резистор.
По закону Ома для участка цепи
I=U/R ==> I = I0
cos ω t
Амплитуда силы тока I0
= U0/R
Ток и напряжение изменяются по
одинаковому гармоническому закону
(косинуса), то есть совпадают по фазе.
Это означает, что, например, в тот
момент времени, когда в цепи максимальна
сила тока, напряжение на резисторе также
максимально.
-
Конденсатор в цепи переменного тока
Включим конденсатор в цепь постоянного
тока.Некоторый заряд перетечет от
источника тока на обкладки конденсатора.В цепи возникает кратковременный
импульс зарядного тока. Конденсатор
заряжается до напряжения источника,
после чего ток прекращается. Через
конденсатор постоянный ток течь не
может!
Р
ассмотрим
процессы, происходящие при включении
конденсатора в цепь переменного тока
зарядный ток
.
Через диэлектрик, разделяющий обкладки
конденсатора, электрический ток
протекать, как и прежде, не может. Но в
результате периодически повторяющихся
процессов зарядки и разрядки конденсатора
в цепи появится переменный ток.
Если напряжение в цепи изменяется по
гармоническому закону,
U = U0cos ωt
то заряд на обкладках конденсатора
изменяется
также погармоническому закону
q=Cu = CU0cos
ωt
и силу тока в цепи можно найти как
производную заряда
i = q/
i= -CU0
ω sin ωt
= CU0ω
cos(ωt+π/2),
i= I0ω
cos(ωt+π/2)
Амплитуда силы тока I0
= CU0ω
Из полученной формулы видно, что в любой
момент времени
фаза тока больше фазы напряжения на
π/2.
В цепи переменного напряжение на
конденсаторе тока отстает по фазе от
тока на π/2, или
на четверть периода.
Емкостное сопротивление
Величину
называют емкостным сопротивлением.
Связь между амплитудными значениями
силы тока и напряжения формально
совпадает с законом Ома для участка
цепи
Такое же соотношение выполняется для
действующих значений силы тока и
напряжения.
Емкостное сопротивление конденсатора
зависит от частоты переменного
напряжения. С увеличением частоты
колебаний напряжения емкостное
сопротивление уменьшается, поэтому
амплитуда силы тока увеличивается прямо
пропорционально частоте I0
= CU0ω.
При уменьшении частоты амплитуда силы
тока уменьшается и при ω=0 обращается в
0. Отметим, что нулевая частота колебаний
означает, что в цепи протекает постоянный
ток.
-
Катушка индуктивности в цепи переменного тока
Мы предполагаем, что катушка индуктивности
обладает пренебрежимо малым активным
сопротивлением R. Такой
элемент включать в цепь постоянного
тока нельзя, потому что произойдет
короткое замыкание.
В цепи переменного тока мгновенному
нарастанию силы тока препятствует ЭДС
самоиндукции. При этом для сверхпроводника
ei+u=0.
Используя закон Фарадея для самоиндукции
ei= -Li/ ,
можно показать, что, если сила тока в
цепи изменяется по гармоническому
закону
i= I0cos(ωt),
то колебания напряжения на катушке
описываются
уравнением
U = – I0
Lωsin
ωt = I0
Lω cos(ωt+π/2),
то есть колебания напряжения опережают
по фазе колебания силы тока на π/2.Произведение U0
= I0 Lω
является амплитудой напряжения:
U = U0
cos(ωt+π/2)
Индуктивное
сопротивление
Величину 
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
13.02.201521.66 Mб28Bammes_Der_Nackte_Mensch.pdf
- #
- #
- #
- #
- #
- #
Рассмотрим цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки индуктивности.
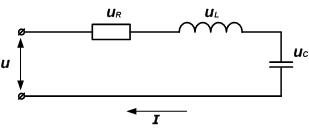
Напряжение на зажимах цепи
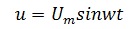
или
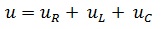
где
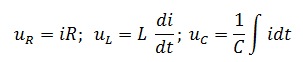
Выполнив подстановку, получим
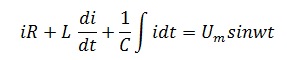
Подставим в последнее выражение ток в цепи, зная, что он равен
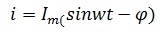
В итоге получим выражение
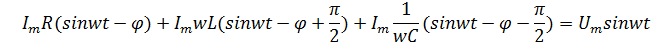
Из этого выражения можно увидеть сдвиг фаз каждого элемента. У резистора он отсутствует, то есть напряжение и ток совпадают по фазе, у катушки индуктивности напряжение опережает ток на угол π/2, а у конденсатора, напротив, отстает.
Сдвиг фаз RLС-цепи можно определить по формуле
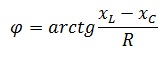
Полное сопротивление RLС-цепи
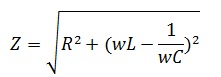
Амплитудное значение тока
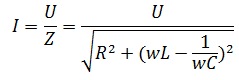
При построении векторной диаграммы RLC-цепи возможны три случая:
1 – Цепь носит активный характер, сдвиг фаз равен нулю, индуктивное и емкостное сопротивления равны. При этом в такой цепи наблюдается резонанс напряжений.
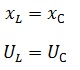
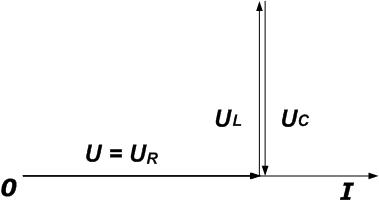
2 – Цепь носит индуктивный характер, в этом случае индуктивное сопротивление больше чем емкостное.
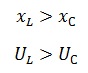
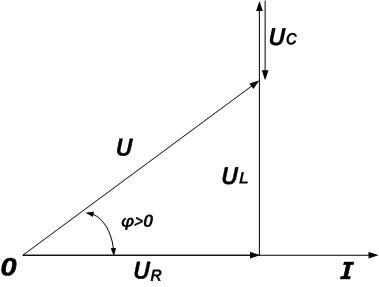
На векторной диаграмме, как правило, сначала откладывают вектор напряжения на катушке индуктивности, а затем из него вычетают напряжение на конденсаторе. После этого проводят вектор общего напряжения и определяют сдвиг фаз φ.
3 – Цепи носит емкостной характер, при этом емкостное сопротивление больше чем индуктивное.
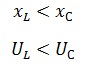
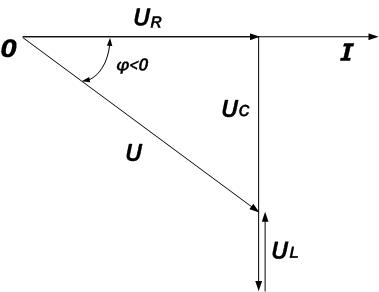
Построение векторной диаграммы выполняется аналогично цепи индуктивного характера, за тем исключением, что здесь сдвиг фаз отрицателен и вычитается индуктивное напряжение из напряжения на емкости.
Пример задачи
Цепь состоит из последовательно включенных резистора сопротивлением 25 Ом, конденсатора емкостью 200 мкФ и катушки индуктивности 30 мГн. Ток, протекающий в цепи, равен 0,75 А. Определите U,UR,UL,UC,φ. Постройте векторную диаграмму и определите характер цепи.
Найдем напряжение на каждом из элементов
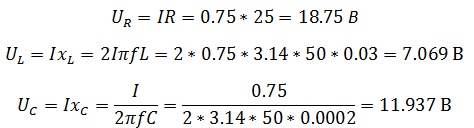
И общее в цепи
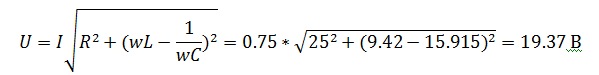
Сдвиг фаз равен
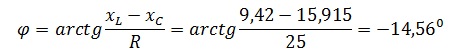
Векторная диаграмма
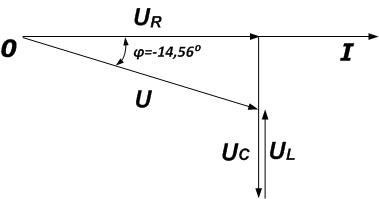
Из векторной диаграммы можно сделать вывод, что цепь носит емкостной характер.
«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно.
Кто из них шмара вавилонская?
– Ну, Света наверное.
– Вот! А мне, как кладовщику, видится немного другое: “поблядушка обыкновенная” – 2 штуки! »
«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным
да параллельным, от плюса к минусу со скоростью света в вакууме?
– С Божьей помощью, батюшка! С Божьей помощью…»
Ну да ладно, достаточно! Шутки – штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю – где надо…», а заодно
набросаю пару-тройку калькуляторов на заданную тему.
Итак.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи
равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для
всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.
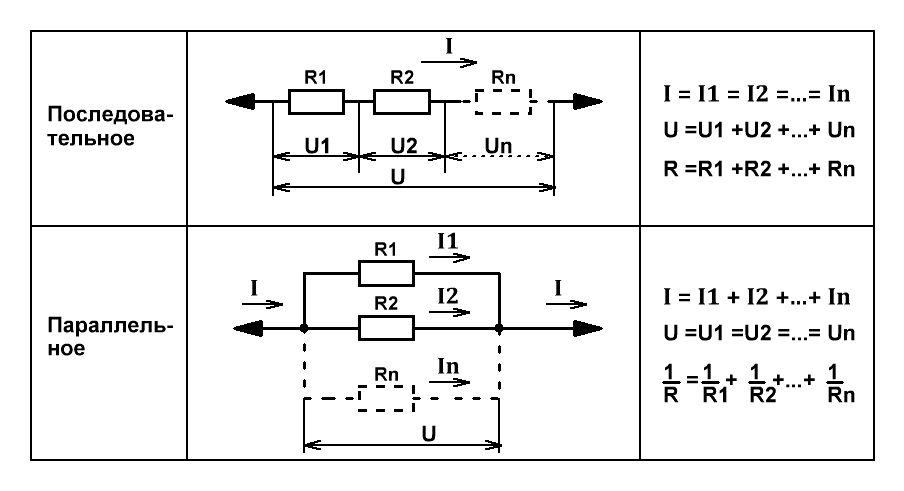
Рис.1
Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то
оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном
соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить…
Короче, все вводные, помеченные * – к заполнению не обязательны.
РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников
Тип соединения |
||
Сопротивление резистора R1 |
||
Сопротивление резистора R2 |
||
Сопротивление резистора R3* |
||
Сопротивление резистора R4* |
||
Общее напряжение в цепи (В)* |
||
Общее сопротивление цепи R |
||
Общий ток в цепи I |
||
Напряжение на резисторе R1 (U1) |
||
Ток через резистор R1 (I1) |
||
Напряжение на резисторе R2 (U2) |
||
Ток через резистор R2 (I2) |
||
Напряжение на резисторе R3 (U3) |
||
Ток через резистор R3 (I3) |
||
Напряжение на резисторе R4 (U4) |
||
Ток через резистор R4 (I4) |
Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение
напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин – сопротивление конденсаторов составляет в первом приближении бесконечность,
а катушек – ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную
зависимость от частоты.
Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и
катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения
реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников
и резисторов.
А в качестве общего напряжения в цепи – подставлять действующее значение амплитуды переменного тока.
Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и
параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:
С = С1+ С2+….+ Сn
и
1/L = 1/L1+ 1/L2 +…+ 1/Ln
для параллельных цепей и
L = L1 + L2 +….+ Ln
и
1/С = 1/С1+ 1/С2+…+ 1/Сn
для последовательных.
Как и в предыдущей таблице вводные, помеченные * – к заполнению не обязательны.
РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов
Тип соединения |
||
Ёмкость конденсатора С1 |
||
Ёмкость конденсатора С2 |
||
Ёмкость конденсатора С3* |
||
Ёмкость конденсатора С4* |
||
Общая ёмкость цепи С |
Ну и в завершении ещё одна таблица.
РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек
Тип соединения |
||
Индуктивность катушки L1 |
||
Индуктивность катушки L2 |
||
Индуктивность катушки L3 |
||
Индуктивность катушки L4 |
||
Общая индуктивность цепи L |
Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек,
то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание,
пересечения взаимных магнитных полей.
