Как найти напряженность через градиент потенциала

Работа сил электростатического поля. Потенциал

Электрическое
поле, подобно гравитационному, является
потенциальным. Т.е. работа, выполняемая
электростатическими силами, не зависит
от того, по какому маршруту заряд q
перемещен в электрическом поле из точки
1 в точку 2. Эта работа равна разности
потенциальных энергий, которыми обладает
перемещаемый заряд в начальной и конечной
точках поля:

А_1,2
= W₁
– W₂
. (7)

Можно показать,
что потенциальная энергия заряда q
прямо
пропорциональна величине этого заряда.
Поэтому в качестве энергетической
характеристики электростатического
поля используется отношение потенциальной
энергии пробного заряда q₀,
помещенного
в какую-либо точку поля, к величине этого
заряда:

.
(8)

Эта величина
представляет собой количество
потенциальной энергии на единицу
положительного заряда и называется
потенциалом
поля в
заданной точке. [φ] = Дж / Кл = В (Вольт).

Если принять, что
при удалении заряда q₀
в бесконечность
(r→
∞) его потенциальная энергия в поле
заряда q
обращается в нуль, то потенциал поля
точечного заряда q
на расстоянии r
от него:

. (9)

Если поле создаётся
системой точечных зарядов, то потенциал
результирующего поля равен алгебраической
(с учётом знаков) сумме потенциалов
каждого из них:

. (10)

Из определения
потенциала (8) и выражения (7) работа,
совершаемая силами электростатического
поля по перемещению заряда из

точки 1 в точку 2,
может быть представлена как:

(11)

Напряжённость как градиент потенциала

Найдем взаимосвязь
между напряженностью Е электростатического
поля, являющейся его силовой характеристикой,
и потенциалом φ – энергетической
характеристикой поля.

Работа по перемещению
точечного, положительного заряда q
вдоль произвольного направления х
из точки 1 в бесконечно близкую к ней
точку 2, х₂
– х₁
= dх,
будет равна: А_1,2
= q·
Е_х∙dх
или через потенциал: А_1,2
= q(φ₁
– φ₂)
= – q
·dφ.
Откуда:

, (12)

т.е. напряженность
поля равна градиенту потенциала, взятому
со знаком минус. Это означает, что
направлен в сторону убывания потенциала.

Для графического
изображения распределения потенциала
электростатического поля пользуются
эквипотенциальными
поверхностями
– поверхность, во всех точках которой
потенциал φ имеет одно и то же значение.
Для точечных зарядов в однородной среде,
например, эти поверхности представляют
собой сферы (рис.133а Трофимова, стр139).

Для любой точки
поля линии напряженности всегда
направлены по нормали к эквипотенциальным
поверхностям. (рис.133б Трофимова, стр139).

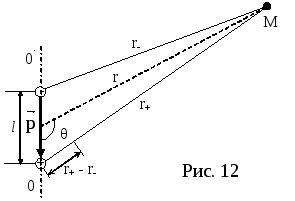
Э л е к т р и ч е с к и й д и п о л ь

Электрический
диполь –
система двух равных по величине
разноименных точечных зарядов +q
и -q,
расстояние

между которыми значительно меньше
расстояния до рассматриваемых точек
поля. Прямая, проходящая через оба
заряда, называется осью
диполя.
Вектор
,
направленный от отрицательного заряда
к положительному и равный по модулю
расстоянию между ними, называетсяплечом
диполя.
Вектор
,

,
(13)

называется
электрическим
моментом диполя
или дипольным
моментом.

Определим потенциал
и напряженность поля диполя в произвольной
точке M
на расстоянии r
от середины диполя. Потенциал поля в
точке М:

(14)

Учитывая, что l
‹‹ r,
r₊
≈ r_–
= r
и r_–
– r₊
≈ l
cos(π-θ),
окончательно для φ получим:

.
(15)

В соответствии с
принципом суперпозиции напряженность
поля диполя
.
Вывод формулы для модуля напряженности
поля диполя более сложен. Запишем эту
формулу без вывода:

(16)

Соседние файлы в папке Физика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Определение напряженности электрического поля с помощью потенциала

Публикации по материалам Д. Джанколи. “Физика в двух томах” 1984 г. Том 2.

Формулу можно использовать для определения разности потенциалов между двумя точками электрического поля, если напряженность поля в области между этими точками известна. Обращая эту формулу мы можем выразить напряженность электрического поля через его потенциал, т. е., зная V, мы сможем определить Е.

Посмотрим, как это делается.

Уравнение можно переписать в дифференциальной форме:

dV = -E·dl = -E_ldl,

где dV – бесконечно малая разность потенциалов между точками на расстоянии dl друг от друга, а E_l – составляющая напряженности электрического поля в направлении этого бесконечно малого перемещения dl.
Тогда:

Таким образом, составляющая напряженности электрического поля по любому направлению равна градиенту потенциала в этом направлении, взятому с обратным знаком. Градиентом величины V называется ее производная по определенному направлению dV/dl. Если направление не указывается, то градиент соответствует направлению наиболее быстрого изменения V; это соответствует направлению вектора Е в данной точке, поскольку именно в таком направлении составляющая вектора Е совпадает с полной величиной напряженности поля:

Если расписать составляющие вектора Е по координатам х, у, z и в качестве l взять направления вдоль осей х у, z,
то уравнение (24.8) можно записать в виде:

Здесь dV/dx – частная производная V по направлению х при условии, что у и z фиксированы.

В последнем примере мы вычислили напряженность электрического поля Е диполя в произвольной точке пространства. Складывая векторы напряженностей, создаваемых каждым зарядом в отдельности, получить этот результат было бы гораздо сложнее. Вообще
говоря, для многих распределений зарядов гораздо проще рассчитать потенциал, а затем по формуле (24.9) – напряженность электрического поля Е, чем вычислять по закону Кулона по отдельности Е для каждого заряда: скалярные величины складывать намного проще, чем
векторы.

Электростатическая потенциальная энергия

Предположим, что точечный заряд q перемещают в пространстве из точки а в точку b, электрические потенциалы
в которых, обусловленные другими зарядами, равны соответственно V_a и V_b. Изменение электростатической
потенциальной энергии заряда q в поле других зарядов составляет:

ΔU = U_b – U_a = q(V_b – V_a) = qV_ba

Пусть теперь имеется система нескольких точечных зарядов. Чему равна электростатическая потенциальная энергия системы?

Удобнее всего выбрать за нуль потенциальную энергию зарядов на очень больших (в идеале бесконечно больших) расстояниях друг от друга.
Потенциальная энергия уединенного точечного заряда Q₁ равна нулю, поскольку в отсутствие других зарядов на него не действует никакая сила. Если к нему поднести второй точечный заряд, Q₂, потенциал в точке, где находится второй заряд, будет равен:

Здесь r_{1 2} – расстояние между зарядами. Потенциальная энергия двух зарядов равна:

Она характеризует работу, необходимую для перемещения заряда Q₂ из бесконечности (V = 0) на расстояние r_{1 2} до
заряда Q_i (или со знаком минус работу, необходимую для разнесения зарядов на бесконечно большое расстояние).

Если система состоит из трех зарядов, то ее полная потенциальная энергия будет равна работе по перемещению всех трех зарядов из бесконечности в место их расположения. Работа по сближению зарядов Q₂ и Q₁ определяется выражением (24.10);

чтобы перенести заряд Q₃ из бесконечности в точку на расстоянии r_{1 3} от Q₁ и на расстоянии r_{2 3} от Q₂, требуется совершить работу:

В этом случае потенциальная энергия системы трех точечных зарядов будет равна:

Для системы четырех зарядов выражение для потенциальной энергии будет содержать шесть таких членов и т.п. (При составлении подобных сумм необходимо следить за тем, чтобы не учитывать одну и ту же пару дважды).
Часто нас интересует не полная электростатическая потенциальная энергия, а лишь часть ее. Например, может возникнуть необходимость найти потенциальную энергию одного диполя в присутствии другого диполя. Во взаимодействии участвуют четыре заряда: Q₁ и -Q₁ первого диполя и Q₂ и -Q₂ второго диполя.

Потенциальная энергия одного диполя и в присутствии другого (иногда ее называют энергией взаимодействия) представляет собой работу по сближению диполей с бесконечно большого расстояния. В этом случае нас не интересует взаимная потенциальная энергия зарядов Q₁ и -Q₁ или Q₂ и -Q₂; выражение для потенциальной энергии двух диполей будет содержать лишь четыре члена, соответствующие энергиям взаимодействия между зарядами: Q₁ и Q₂ ; Q₁ и -Q₂ ; -Q₁ и Q₂ ; -Q₁ и -Q₂.

Заключение

Электрический потенциал в любой точке пространства определяется как электростатическая потенциальная энергия единицы заряда. Разность потенциалов между двумя точками определяется взятой с обратным знаком работой, которая совершается полем при перемещении единичного электрического заряда между этими точками. Разность потенциалов измеряется в вольтах (1 В = 1 Дж/Кл) и иногда называется напряжением. Изменение
потенциальной энергии заряда q при прохождении им разности потенциалов V_bа равно ΔU = qV_ba.
Разность потенциалов V_bа между точками b и a в однородном электрическом поле напряженностью Е определяется формулой V = — Ed, где d – расстояние вдоль силовой линии поля между этими точками.
В неоднородном электрическом поле Е соответствующее выражение имеет вид .
Таким образом, зная Е, всегда можно определить V_bа. Если значение V известно, то составляющие
напряженности поля Е можно найти, обращая приведенное соотношение:

Е_x = -dV/dх , Е_y = -dV/dу , E_z = -dV/dz .

Эквипотенциальные линии или поверхности представляют собой геометрическое место точек одного потенциала; они всюду перпендикулярны силовым линиям поля. Электрический потенциал уединенного точечного заряда Q относительно нулевого потенциала (на бесконечности) равен:

Потенциал произвольного распределения зарядов можно определить, суммируя (интегрируя) потенциалы отдельных зарядов.

где r – расстояние от элемента заряда dq до точки, в которой определяется V.

Альтернативные статьи:
Постоянный ток, Переменный ток.

---

Уравнение Пуассона и распределение Больцмана (часть 1)

В продолжение предыдущей статьи «Есть ли плазма в космосе?» я хотел бы в познавательных целях рассказать об уравнениях, которые применялись при выводе уравнения Дебая-Хюккеля. Это уравнение Пуассона и распределение Больцмана.

Мы выяснили, что плазма квазинейтральна в равновесном состоянии и что под действием электрического поля от движущихся зарядов, заряженные частицы смещаются на дебаевскую длину и поле в пределах этой длины затухает. В электростатике взаимодействие заряженных частиц описывается кулоновским уравнением:

где – величины взаимодействующих точечных зарядов, – квадрат расстояния между зарядами. Коэффициент k является константой. Если мы используем систему в электростатических единицах СГС, обозначаемых СГСЭq, то k = 1. Если используется система СИ, то , где – диэлектрическая проницаемость среды, в которой расположены заряды, – электрическая постоянная, равная 8,86 ∙ .

В физике непосредственно силой не пользуются, а вводят понятие электростатического поля распределённых зарядов и измеряют поле величиной напряженности электрического поля. Для этого в каждую точку поля мысленно помещают единичный пробный заряд и измеряют силу, с которой поле зарядов действует на пробный заряд:

Отсюда, если подставить в это уравнение силу Кулона, то получим:

Но и этим физики не ограничиваются, для того чтобы описать полноценно электрическое поле. Рассмотрим единичный заряд, помещённый в электростатическое поле. Поле выполняет работу по перемещению этого заряда на элементарное расстояние ds из точки P1 в точку P2:

Величину называют разностью потенциалов или напряжением. Напряжение измеряется в Вольтах. Знак минус говорит нам о том, что само поле выполняет работу для переноса единицы положительного заряда. Силы, перемещающие заряды являются консервативными, так как работа по замкнутому пути равна всегда нулю, независимо от того, по какому пути перемещается заряд.

Отсюда следует глубокий смысл разности потенциалов. Если зафиксировать точку Р1 и перемещать заряд в переменную точку Р2, то работа зависит только от положения второй точки Р2. Таким образом мы можем ввести понятие потенциала. Потенциал – это силовая функция, показывающая какую необходимо выполнить работу полю, чтобы переместить заряд из бесконечности в данную точку P2, где условно принимают потенциал в бесконечности равным нулю.

Чтобы понять уравнение Пуассона, необходимо разбираться в «особой» векторной математике. Я вкратце расскажу про такие понятия как градиент поля и дивергенции (подразумевается, что читатель знаком с математическим анализом)
Пусть f(x,y,z) является некоторой непрерывной дифференцируемой функцией координат. Зная её частные производные в каждой точке пространства можно построить вектор, компоненты которого x, y, z равны соответствующим частным производным:

где – единичные векторы соответствующих осей x, y, z. Значок читается «набла» и является дифференциальным оператором

Этот оператор ввёл в математику Гамильтон. С набла можно выполнять обычные математические операции, такие как обычное произведение, скалярное произведение, векторное произведение и так далее.

Теперь вернёмся к электростатическому полю E. С одной стороны изменение потенциала при переходе из одной точки в другую имеет следующий вид:

С другой стороны, согласно формуле (*)

Применяя только что введённое понятие градиент, эта формула преобразуется в:

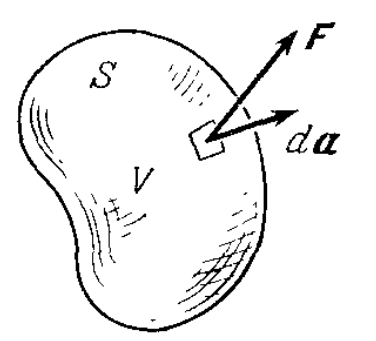
Теперь разберёмся с таким понятием, как дивергенция поля. Рассмотрим конечный замкнутый объем V произвольной формы (см. рис. ниже). Обозначим площадь этой поверхности S. Полный поток вектора F, выходящего из этого объема по определению равно

, где da является бесконечно малым вектором, величина которого равна площади малого элемента поверхности S, а направление совпадает с наружной нормалью к этому элементу.
Возьмём этот поток вектора F поделим на объём и найдём предел при стремящейся к нулю, т.е. будем стягивать объём в бесконечно малую точку.

Мы подошли к понятию дивергенции. Обозначается дивергенция символом div и является отношением потока вектора F к объёму V, при V стремящейся к нулю.

Прежде чем показать, как получается уравнение Пуассона, важно знать закон Гаусса и теорему Гаусса. Представим себе сферу, внутри которой находится заряд q. Заряд создаёт вокруг себя электрическое поле напряжённости E. Возьмём поток вектора E

где S площадь нашей сферы равная . Следовательно

Это и есть закон Гаусса, утверждающий, что поток электрического поля E через любую замкнутую поверхность равен произведению на полный заряд, охватываемый поверхностью:

где – плотность объёмного заряда, т.е. величина электрического заряда в единице объёма, и – элементарный объём, выделенный внутри нашего замкнутого объёма.

Теорема Гаусса (полное название теорема Гаусса-Остроградского) чисто математическая теорема о дивергенции. Перепишем полный поток вектора F следующим образом:

В пределе, когда N → ∞, →0 величина в скобках становится дивергенцией и сумма переходит в объёмный интеграл:

Это и есть теорема Гаусса, и является поистине самой важной формулой полевой теории. Применим эту теорему к электростатическому полю. С одной стороны, согласно закону Гаусса

А с другой стороны, согласно теореме Гаусса (только не путайте теорему с законом Гаусса):

Комбинируя два последних уравнения, получим:

Вспомним формулу (**) и подставим сюда вместо E потенциал поля

Дивергенция градиента это новый оператор, который в математике называют оператор Лапласа, или сокращённо лапласиан. Лапласиан обозначается значком набла следующим образом и равен

Перепишем предыдущую формулу в форме лапласиана:

Наконец мы получили уравнение Пуассона. В первой статье это уравнение было немного в другой форме, с учётом диэлектрической проницаемости среды. Вспомните силу Кулона в системе СИ, там константа . Соответственно в законе Гаусса будет не , а коэффициент . Таким образом получаем уравнение Пуассона в форме представленной в предыдущей статье

Таким образом по сути уравнение Пуассона – это закон Кулона (а точнее закон Гаусса) переписанный в другой форме, в обозначениях векторного дифференциального анализа.

В следующей статье мы разберём важное распределение из математической статистики — распределение Больцмана.

Уравнение Пуассона и Лапласа

В случае потенциального поля напряженность поля Е может быть выражена через градиент потенциала. При этом приходим к выражению

содержащему двойную дифференциальную операцию: дивергенцию от градиента. При использовании декартовой системы координат легко записать эту операцию через соответствующие производные. Действительно, представляя в формулу (1) составляющие grad φ как:

Операция div grad носит название лапласиана и обозначается знаком Δ. Используя оператор набла, рассматриваемую операцию можно представить как наблу квадрат, таким образом:

В случае декартовых координат и в применении к скалярной функции можно всегда считать операции ∇ 2 и Δ тождественными.

Уравнение (1) является основным уравнением потенциального электрического поля и носит название уравнения Пуассона.

В области поля, где заряды отсутствуют (где ρ = 0), уравнение (1) упрощается, так как в его правой части оказывается нуль. В последнем случае уравнение называют уравнением Лапласа.

и было названо дифференциальным уравнением электрического потенциального поля.

Рассмотрим несколько примеров.

Пример 1

В некоторой области поля потенциал изменяется по закону:

Содержится ли в этой области объемный заряд и чему он равен?

Решение

Путем прямого дифференцирования найдем:

Уравнение Лапласа удовлетворяется (объемный заряд равен нулю).

Пример 2

То же, что и в предыдущем примере, но описанное следующим уравнением:

Решение

Очевидно, что правая часть данного равенства в общем случае не равна нулю.

Примечание к примерам 1 и 2. Из рассмотрения встретившихся видов произведений можно сделать более общий вывод:

всегда удовлетворяет уравнению Лапласа (первый множитель в формуле (5) cos или sin, а второй ch или sh).

Уравнение пуассона и математическая постановка задач электростатики — справочник студента

Если имеется или конфигурация зарядов, или заряженное тело, то напряженность поля и потенциал поля могут быть найдены с помощью нормировки из формул (6.12) и (6.14).

Но имеется еще один путь, когда выводится дифференциальное уравнение для потенциала, решается это уравнение, находится , а затем с помощью (6.7) можно найти и этот путь чаще гораздо проще. Будем исходить из (6.

7) и дифференциальной формулировки закона Кулона (5.11). Чтобы его получить подставим в Выражение .

Таким образом, при заданном распределении зарядов (Задано) можно решить (7.1), найти , а затем из (6.7) найти . При решении задачи используются граничные условия и решение при корректной постановке единственно. При этом отпадает необходимость в нормировке потенциала, т. к. граничные условия заменяют эту процедуру.

Бесконечный равномерно заряженный круглый цилиндр.

Найдем с помощью уравнения Пуассона потенциал, создаваемый бесконечным цилиндром радиусом aС объемной плотностью Const.

Направим ось Z по оси цилиндра. Вследствие аксиальной симметрии распределения заряда потенциал также аксиально симметричен, т. е. . Поэтому удобно использовать цилиндрическую систему координат, аксиальный угол которой обозначим .

В цилиндрической системе координат уравнение Лапласа имеет вид:

1. Для решения введем две области:
2. 1.
3. 2.
4. При этом зададим граничное условие в виде: .
5. Тогда

Общие решения легко находятся интегрированием:

Где — постоянные интегрирования. Поскольку потенциал всюду должен быть конечен, а при , поэтому в последнем решении необходимо положить . Если учесть граничное условие ,то . Таким образом,

Поскольку поверхностные заряды отсутствуют, напряженность электрического поля на поверхности цилиндра непрерывна, т. е. непрерывна производная от потенциала. Условие непрерывности потенциала и его производной при R=A имеет вид:

• ,
• Откуда следует система алгебраических уравнений для A2 и B2:
• ,
• ,
• .
• Подставим это соотношение в , получим
• (7.3)
• (7.4)

Как и следовало ожидать, при R=A решения совпадают, т. е. .

Чтобы найти напряженность электрического поля, воспользуемся (6.7), которое запишем в виде . Тогда

В принципе, для нахождения E можно было воспользоваться электростатической теоремой Гаусса. Выделяя мысленно цилиндр с радиусом r

Решение уравнения пуассона для потенциала. Уравнение пуассона и математическая постановка задач электростатики

• К исследованию уравнений Лапласа и Пуассона приводит рассмотрение задач о стационарном процессе: это задачи гидродинамики, диффузии, распределения температуры, электростатики и др.
• Эти уравнения относятся к уравнениям эллиптического типа.
• Те задачи, которые приводят к уравнениям, содержащим время, называются нестационарными или динамическими задачами математической физики; задачи, приводящие к уравнениям, не содержащим время, называются стационарными или статическими.

Как было показано, уравнения математической физики имеют бесчисленное множество решений, зависящие от двух произвольных функций (речь идет об уравнениях второго порядка для функции двух переменных).

Для того, чтобы из множества решений выделить определенное, характеризующее процесс, необходимо на искомую функцию наложить дополнительные условия, которые диктуются физическими соображениями. Таковыми условиями для уравнений в частных производных являются, чаще всего, начальные и граничные условия.

Граничные условия — это условия заданные на границе рассматриваемой среды; начальные условия — это условия, относящиеся к какому-нибудь моменту времени, с которого начинается изучение данного физического явления. Дополнительные условия, так же как и само дифференциальное уравнение, выводятся на основе физических соображений, связанных с самим процессом.

Вместе с тем дополнительные условия должны быть такими, чтобы обеспечить выделение единственного решения из всего множества решений. Число граничных и начальных условий определяются типом уравнения, а их вид — заданным исходным состоянием на границе объекта и внешней среды. Для рассматриваемых нами уравнений число начальных условий равно порядку старшей производной по времени, входящей в уравнение, а число граничных условий — порядку старшей производной по координате.

1. Совокупность дифференциального уравнения и дополнительных условий представляют собой математическую формулировку физической задачи, и называется задачей математической физики.
2. Итак, задача математической физики состоит в отыскании решений уравнений в частных производных, удовлетворяющих некоторым дополнительным условиям, скажем, граничным и начальным.
3. Задача математической физики считается поставленной корректно, если решение задачи, удовлетворяющее всем ее условиям, существует, единственно и устойчиво.

Колебания струны. Граничные и начальные условия. Постановка краевых задач

Пусть струна находится под действием сильного начального натяжения. Если вывести струну из положения равновесия и подвергнуть действию какой-либо силы, то струна начнет колебаться.

Процесс колебания можно описать одной функцией, характеризующей вертикальное перемещение струны (отклонение от положения равновесия (рис. 2.2)).

При каждом фиксированном значении график функции на плоскости дает форму струны в момент времени.

Функция удовлетворяет уравнению

описывает свободные колебания струны без воздействия внешних усилий.

Уравнение (2.69) является простейшим уравнением гиперболического типа и в то же время одним из важнейших уравнений матфизики.

Одного уравнения движения (2.69) или (2.70) при математическом описании физического процесса недостаточно. При рассмотрении задачи о колебании струны дополнительные условия могут быть двух видов: начальные и граничные (краевые).

• Так как процесс колебаний струны зависит от ее начальной формы и распределения скоростей, то следует задать начальные условия:
• Будем говорить о трех типах граничных условий:
• где известные функции,

и известные постоянные.

Приведенные условия называют соответственно граничными условиями первого, второго, третьего рода. Условия I имеют место в том случае, когда концы объекта (струна, стержень и т.д.) перемещаются по заданному закону; условия II — в случае, когда к концам приложены заданные силы; условия III — в случае упругого закрепления концов.

Если функции, заданные в правой части равенства, равны нулю, то граничные условия называются однородными. Так, граничные условия (2.72) — однородные. Комбинируя различные перечисленные типы граничных условий, получим шесть типов простейших краевых задач.

В том случае, когда режим на концах не будет оказывать существенного влияния на ту часть струны, которая достаточно удалена от них, струну считают бесконечной. В силу этого вместо полной краевой задачи ставят предельную задачу — з а д а ч у К о ш и: найти решение уравнения (2.69) для при, удовлетворяющее начальным условиям

Если изучается процесс вблизи одной границы и влияние граничного режима на второй границе не имеет существенного значения на протяжении интересующего нас промежутка времени, то приходим к постановке задачи на полуограниченной прямой. В этом случае задаются начальные условия и одно из граничных условий I — III при.

Примеры решения задач

ПРИМЕР 2.42. Однородная струна длины совершает малые поперечные колебания. Поставить задача об определении отклонений точек струны от прямолинейного положения покоя, если в момент струна имела форму () и скорость каждой ее точки задается функцией. Рассмотреть случаи:

• а) концы струны закреплены;
• б) концы струны свободны;

в) к концам струны и, начиная с момента, приложены поперечные силы и соответственно;

г) концы струны закреплены упруго, т.е. каждый из концов испытывает сопротивление, пропорциональное отклонению конца.

Решение. Как известно, отклонения точек струны от положения равновесия удовлетворяют в отсутствии действующей внешней силы уравнению свободных колебаний (2.70)

Здесь, натяжение, линейная плотность, т.к. струна однородная.

Начальные условия имеют вид:

Займемся выводом граничных условий.

Случай а). Так как концы струны закреплены, то их отклонения в точках и должны быть равными нулю при любом, т.е.

Итак, физическая задача о колебаниях закрепленной на концах струны свелась к следующей математической задаче: найти функцию, определенную при и, являющуюся решением уравнения

и удовлетворяющую граничным условиям

и начальным условиям

Я хотел бы в познавательных целях рассказать об уравнениях, которые применялись при выводе уравнения Дебая-Хюккеля. Это уравнение Пуассона и распределение Больцмана.

Мы выяснили, что плазма квазинейтральна в равновесном состоянии и что под действием электрического поля от движущихся зарядов, заряженные частицы смещаются на дебаевскую длину и поле в пределах этой длины затухает. В электростатике взаимодействие заряженных частиц описывается кулоновским уравнением:

Где – величины взаимодействующих точечных зарядов, – квадрат расстояния между зарядами. Коэффициент k является константой. Если мы используем систему в электростатических единицах СГС, обозначаемых СГСЭq, то k = 1. Если используется система СИ, то , где – диэлектрическая проницаемость среды, в которой расположены заряды, – электрическая постоянная, равная 8,86 ∙ .

В физике непосредственно силой не пользуются, а вводят понятие электростатического поля распределённых зарядов и измеряют поле величиной напряженности электрического поля
. Для этого в каждую точку поля мысленно помещают единичный пробный заряд и измеряют силу, с которой поле зарядов действует на пробный заряд:

Отсюда, если подставить в это уравнение силу Кулона, то получим:
Но и этим физики не ограничиваются, для того чтобы описать полноценно электрическое поле. Рассмотрим единичный заряд, помещённый в электростатическое поле. Поле выполняет работу по перемещению этого заряда на элементарное расстояние ds из точки P1 в точку P2:

Величину называют разностью потенциалов или напряжением. Напряжение измеряется в Вольтах. Знак минус говорит нам о том, что само поле выполняет работу для переноса единицы положительного заряда. Силы, перемещающие заряды являются консервативными, так как работа по замкнутому пути равна всегда нулю, независимо от того, по какому пути перемещается заряд.

Отсюда следует глубокий смысл разности потенциалов. Если зафиксировать точку Р1 и перемещать заряд в переменную точку Р2, то работа зависит только от положения второй точки Р2.

Таким образом мы можем ввести понятие потенциала.

Потенциал – это силовая функция, показывающая какую необходимо выполнить работу полю, чтобы переместить заряд из бесконечности в данную точку P2, где условно принимают потенциал в бесконечности равным нулю.

Чтобы понять уравнение Пуассона, необходимо разбираться в «особой» векторной математике.

Я вкратце расскажу про такие понятия как градиент поля и дивергенции (подразумевается, что читатель знаком с математическим анализом)
Пусть f(x,y,z) является некоторой непрерывной дифференцируемой функцией координат.

Зная её частные производные в каждой точке пространства можно построить вектор, компоненты которого x, y, z равны соответствующим частным производным:

где – единичные векторы соответствующих осей x, y, z. Значок читается «набла» и является дифференциальным оператором

Этот оператор ввёл в математику Гамильтон. С набла можно выполнять обычные математические операции, такие как обычное произведение, скалярное произведение, векторное произведение и так далее.

Теперь вернёмся к электростатическому полю E. С одной стороны изменение потенциала при переходе из одной точки в другую имеет следующий вид:

С другой стороны, согласно формуле (*)
Применяя только что введённое понятие градиент, эта формула преобразуется в:
Теперь разберёмся с таким понятием, как дивергенция поля. Рассмотрим конечный замкнутый объем V произвольной формы (см. рис. ниже). Обозначим площадь этой поверхности S. Полный поток вектора F, выходящего из этого объема по определению равно
, где da является бесконечно малым вектором, величина которого равна площади малого элемента поверхности S, а направление совпадает с наружной нормалью к этому элементу.
Возьмём этот поток вектора F поделим на объём и найдём предел при стремящейся к нулю, т.е. будем стягивать объём в бесконечно малую точку.
Мы подошли к понятию дивергенции. Обозначается дивергенция символом div и является отношением потока вектора F к объёму V, при V стремящейся к нулю.

Прежде чем показать, как получается уравнение Пуассона, важно знать закон Гаусса и теорему Гаусса. Представим себе сферу, внутри которой находится заряд q. Заряд создаёт вокруг себя электрическое поле напряжённости E. Возьмём поток вектора E

где S площадь нашей сферы равная . Следовательно
Это и есть закон Гаусса, утверждающий, что поток электрического поля E через любую замкнутую поверхность равен произведению на полный заряд, охватываемый поверхностью:

где – плотность объёмного заряда, т.е. величина электрического заряда в единице объёма, и – элементарный объём, выделенный внутри нашего замкнутого объёма.

1. Теорема Гаусса (полное название теорема Гаусса-Остроградского) чисто математическая теорема о дивергенции. Перепишем полный поток вектора F следующим образом:
2. Таким образом по сути уравнение Пуассона – это закон Кулона (а точнее закон Гаусса) переписанный в другой форме, в обозначениях векторного дифференциального анализа.
3. В мы разберём важное распределение из математической статистики — распределение Больцмана.

1.15. Расчет одномерных электростатических полей по уравнениям Пуассона и Лапласа

Электростатическое поле в однородной среде с постоянной диэлектрической проницаемостью полностью характеризуется уравнением Пуассона (1.11) или (если в рассматриваемой области отсутствуют объемные связанные заряды) уравнением Лапласа (1.12).

Наиболее просто уравнения Пуассона и Лапласа решаются в случае одномерных полей, потенциалы которых зависят только от одной координаты. При этом дифференциальные уравнения в частных производных переходят в обыкновенные дифференциальные уравнения второго порядка, решение которых при известных граничных условиях является несложной задачей.

• Так, в прямоугольной системе координат уравнения Пуассона и Лапласа для одномерного поля будут иметь следующий вид:
• (1.22)
• (1.23)

Решение уравнения (1.22), очевидно, может быть получено лишь тогда, когда объемная плотность заряда r и абсолютное значение диэлектрической проницаемости e заданы как функции координат во всем пространстве. Например, если объемная плотность r изменяется вдоль оси ОХ по закону

1. (где коэффициент а и показатель степени n являются постоянными), то, в случае, когда e=const, частное решение уравнения Пуассона будет иметь следующий вид:
2. 
3. (1.24)
4. где С1 и С2 – постоянныеинтегрирования, которые определяются из граничных условий.
5. В случае, когда объемная плотность заряда r также является постоянной величиной, решение имеет вид
6. 
7. Частное решение уравнения Лапласа (1.29) можно представить следующим образом:
8. (1.25)

В цилиндрической системе координат для одномерного поля вид уравнения Пуассона или Лапласа и их решение зависят от того, функцией какой координаты является искомый потенциал U. Например, если потенциал U зависит только от радиальной координаты r (U=U(r)), то уравнения (1.11) и (1.12) будут иметь вид

(1.26)

(1.27)

Решение уравнения (1.26) определяется видом функции r. Если, например, объемная плотность заряда r изменяется вдоль радиуса r по закону

• 
• то искомое решение будет иметь вид:
• 
• (1.28)
• Для случая, когда объемная плотность заряда r не зависит от координаты r, решение уравнения (1.26) можно представить следующим образом:
• 
• (1.29)
• Решение уравнения Лапласа (1.27) имеет вид:
• 
• (1.30)
• Если искомый потенциал является функцией только одной угловой координаты j, то уравнения Пуассона и Лапласа приобретают следующий вид:
• (1.31)
• (1.32)
• При постоянном значении r уравнение (1.31) имеет частное решение
• .
• (1.33)
• Решение уравнение Лапласа (1.32) можно записать следующим образом:
• (1.34)
• В сферической системе координат для одномерного поля вид уравнения Пуассона или Лапласа и их решение зависят также от того, функцией какой координаты является искомый потенциал U.
• Так, если потенциал U зависит только от радиальной координаты r, то уравнения Пуассона и Лапласа будут иметь вид:
• (1.35)
• (1.36)
• При изменении объемной плотности заряда r по закону
• ,
• решение уравнения (1.35) можно представить следующим образом:
• (1.37)
• Если r является постоянной величиной, решение будет иметь вид
• (1.38)
• Уравнение Лапласа (1.36) имеет следующее решение:
• (1.39)
• В случае, если потенциал U зависит только от одной координаты q, уравнение Лапласа (1.12) будет иметь вид
• (1.40)
• Решение этого уравнения можно представить следующим образом:
• (1.41)
• Если потенциал U является функцией только одной координаты j, то уравнение (1.12) будет иметь вид
• а его решение является линейной функцией этой координаты

Пример 1. Плоский конденсатор с двумя слоями диэлектрика подключен к источнику постоянного напряжения U0=100В (рис. 1.25). Относительные значения диэлектрической проницаемости слоев er1=3, er2=6. Толщина слоев – d1=d2=1мм.

1. Один из слоев заряжен с объемной плотностью r, которая изменяется по толщине по закону r=10-4х Кл/м3.
2. Пренебрегая краевым эффектом, найти распределение потенциала и напряженности поля в слоях диэлектрика.
3. Построить графики изменения потенциала и напряженности электрического поля вдоль оси ОХ.
4. Решение.

Данная задача по расчету электрического поля является одномерной. В первом слое электрический потенциал отвечает уравнению Лапласа (1.23), а во втором – уравнению Пуассона (1.22). Решение этих уравнений можно представить с помощью выражений (1.24) и (1.25) , соответственно, при n=1 и а=1.

• Для определения постоянных интегрирования используем граничные условия на внешних границах области и на границе раздела двух диэлектриков (внутренней границе).
• Будем при этом считать, что правая пластина имеет нулевой потенциал.
• Здесь D1 и D2 – нормальные составляющие вектора электрического смещения.
• Из первого равенства следует, что С2=U0.
• Перепишем три следующих граничных условия, подставляя в них соответствующие выражения для потенциалов и вектора электрического смещения:
• Решая последнюю систему из трех уравнений относительно неизвестных С1, С3, и С4, получим С1=-66670,

Таким образом, окончательно выражения для напряженности поля и потенциалов можно записать в виде:

Графики изменения потенциала и напряженности поля представлены на рис. 1.26

На графике все значения представлены в относительных единицах, причем за базисные значения приняты значения потенциала и напряженности поля на поверхности левой пластины (Ub=100 В, Eb=66670 В/м).

Пример 2. Бесконечно длинный диэлектрический (er=4) полый цилиндр заряжен и находится в воздухе. Радиус внутренней поверхности цилиндра R1=2мм, наружной – R2=6мм (рис.1.27). Объемная плотность заряда r является функцией расстояния от оси цилиндра r=0.1r.

Найти законы изменения потенциала и напряженности поля в функции расстояния от оси цилиндра. Построить графики изменения указанных функций вдоль радиуса.

Решение. Поле в данном случае является одномерным, поскольку напряженность поля и потенциал зависят только от одной радиальной координаты.

При решении задачи по расчету электрического поля в заданной области, эту область необходимо разбить на три подобласти. В первой из них (0?r?R1) поле отсутствует (Е=0). Во второй подобласти (R1?r?R2) электрический потенциал отвечает уравнению Пуассона (1.26), а в третьей (R2? r??) – уравнению Лапласа (1.27), которые имеют решения (1.28) (при n=1,a=0.1) и (1.30).

1. Перепишем эти решения в следующем виде:
2. Здесь индексы у потенциалов обозначают их принадлежность ко второй и третьей подобластям.

Постоянные интегрирования определим из граничных условий, которые можно поставить как из классических граничных условий, так и из следующих соображений. Поскольку поле внутри цилиндра отсутствует, то при r=R1, можно принять Е2=0.

Отсюда сразу определяем постоянную С1=7.533. Примем потенциал равным нулю на наружной поверхности цилиндра (U2=0 при r=R2), тогда

и, таким образом, С2=106.335.

• Потенциал U3 со стороны третьей подобласти на этой же поверхности (r=R2) также будет равен нулю.
• Здесь же на границе раздела двух диэлектриков равны между собой нормальные составляющие векторов электрического смещения, а с учетом того, что в нашем случае вектор электрического смещения имеет одну составляющую, которая направлена по радиусу, то это означает, что на границе раздела равны между собой и сами векторы электрического смещения.
• Перепишем последнее уравнение в следующем виде:
• (1.43)

Решая совместно уравнения (1.42) и (1.43), находим постоянные интегрирования С3=-783.427, С4=-4008.

1. Таким образом, выражения для напряженности электрического поля и потенциала принимают вид
2. Потенциал в первой подобласти (внутри цилиндра) является величиной постоянной, равной значению потенциала со стороны второй подобласти на внутренней поверхности цилиндра.

График изменения потенциала и напряженности электрического поля представлен на рис. 1.28. Все значения на графике даны в относительных единицах. За базисное значение напряженности поля принято ее значение на наружной поверхности цилиндра Eb=130.6кВ/м.

В качестве базисного значения потенциала принято абсолютное значение потенциала на расстоянии 0.01м от оси цилиндра Ub=400.2В.

Это же расстояние r=0.01м принято за базисное значение радиальной координаты.

Пример 3. Цилиндрический бесконечно длинный конденсатор заполнен двухслойным диэлектриком, относительные значения диэлектрической проницаемости слоев которого равны соответственно er1=2 и er2=4.

Радиус внутренней жилы равен R1=1мм, внутренний радиус наружной обкладки – R3=4мм, радиус поверхности раздела слоев диэлектрика – R2=2мм (рис. 1.29). К обкладкам конденсатора приложено постоянное напряжение Uо = 100 В. Один из диэлектриков заряжен (внутренний).

• Объемная плотность заряда является функцией расстояния r от оси конденсатора r=аr2 (а=10).
• Определить закон изменения потенциала и напряженности электрического поля в каждом слое.
• Построить графики изменения напряженности поля и потенциала вдоль радиуса.

Решение. В данной задаче поле так же является одномерным. Поэтому электрический потенциал в первом слое диэлектрика (R1?r?R2) удовлетворяет уравнению (1.26), а во втором слое (R2?r?R3) – уравнению (1.27). Эти уравнения имеют решения (1.28) и (1.30), соответственно. Перепишем их (при n=2) в следующем виде:

1. Для определения постоянных интегрирования С1, С2, С3, С4 поставим граничные условия.
2. Так, если принять потенциал наружного электрода равным нулю, то потенциал внутреннего электрода будет равен U0.
3. ; (1.44)
4. .
5. (1.45)
6. На границе раздела слоев диэлектриков (r=R2) равны между собой потенциалы и векторы электрического смещения (вектор электрического смещения имеет одну составляющую, направленную вдоль радиуса).

Решая систему уравнений, составленную из последних двух уравнений и уравнений (1.44) и (1.45) относительно постоянных интегрирования, получаем С1=-94.917, С2=-555.628, С3=-48.588, С4=-268.279.

• Таким образом, выражения для напряженности электрического поля и потенциала принимают вид

Графики изменения данных функций вдоль радиуса представлены на рис. 1.30.

Все значения на графике даны в относительных единицах. За базисное значение напряженности поля и потенциала приняты их значения на поверхности внутреннего электрода Eb=95.06кВ/м,

Ub=100В. За базисное значение радиальной координаты принят внутренний радиус наружного электрода R2.

Пример 4. Две протяженные проводящие пластины расположены в воздухе под углом a0=p/4 друг к другу и не соприкасаются (рис. 1.31). Напряжение между пластинами U0=100В.

Пренебрегая краевым эффектом, определить закон распределения потенциала и напряженности электрического поля между пластинами.

Поле между пластинами является одномерным (все величины зависят только от одной угловой координаты a цилиндрической системы координат). Потенциал, в этом случае, удовлетворяет уравнению (1.32) с решением (1.34).

1. Постоянные интегрирования определяются из граничных условий
2. или
3. Из данной системы уравнений определяем постоянные интегрирования С2=0, С1=U0/a0.
4. Таким образом, закон изменения искомых функций вдоль угловой координаты a цилиндрической системы координат можно окончательно представить следующим образом:
5. Как видно из последних выражений, эквипотенциальными поверхностями являются полуплоскости, проходящие через ось OZ и изолированными драг от друга, а линиями поля являются дуги окружностей с центром в начале координат.

Пример 5. Шар из диэлектрика (er = 4) заряжен и расположен в воздухе. Объемная плотность заряда является функцией расстояния r от центра шара: r = k*r (k = 0,05p). Радиус шара R = 2см.

Рассчитать потенциал и напряженность электрического поля внутри и вне шара.

Данная задача была решена в примере 3 раздела 1.14 с помощью теоремы Гаусса.

Покажем, что этой же цели можно добиться и путем решения уравнений Пуассона (1.35) и Лапласа (1.36), которым удовлетворяет потенциал поля внутри и вне шара, соответственно.

Выражения, определяющие этот потенциал внутри (1.37) и вне шара (1.39), можно для данного случая представить в следующем виде:

Постоянные интегрирования определяются из известных граничных условий и с помощью некоторых физических соображений. Так, потенциал в центре шара (r=0) имеет конечное значение, поэтому постоянную С1 необходимо принимать равной нулю (С1=0). Далее, принимая потенциал равный нулю в точке, лежащей в бесконечности (r=?), получаем С4=0.

• Оставшиеся две постоянные С2 и С3 определяем исходя из того, что на поверхности шара (r=R) равны между собой потенциалы и нормальные составляющие вектора электрического смещения
• Перепишем данные граничные условия в следующем виде:

Решая совместно последние уравнения, находим постоянные интегрирования. C2=38460, С3=-709,964.

1. Подставляя значения этих постоянных в формулы для потенциалов, получаем
2. Отсюда видно, что данные выражения полностью аналогичны тем, которые были получены в примере 3 предыдущего раздела.

Пример 6. Две тонкие проводящие поверхности в виде коаксиальных конусов с изолированными вершинами расположены в воздухе. Потенциал первой поверхности U1=0, второй – U2=100В (рис. 1.32), q1=p/6, q2=2p/3.

Найти закон распределения потенциалов и напряженности электрического поля в пространстве между конусами.

Данная задача является одномерной, поскольку, в силу симметрии, решение для потенциала U зависит только от угла q. Поле в данном случае характеризуется уравнением (1.40) и имеет решение (1.41).

Исходя из заданных граничных условий составим уравнения для нахождения постоянных интегрирования С1 и С2

Решая данную систему, получим С1=53.583, С2=70.567.

• Таким образом, выражение для определения потенциала будет иметь вид
• Напряженность электрического поля имеет одну составляющую

Эквипотенциальными поверхностями являются поверхности конусов с изолированными вершинами. При q=p/2 один из конусов переходит в плоскость. Линии поля лежат на меридианах.

Вывод уравнения Пуассона в электростатике

Уравнение Пуассона для потенциала электростатического поля.

и связью напряженности с потенциалом электростатического поля (2)

Если второе из рассматриваемых соотношений подставить в первое, можно получить уравнение Пуассона, связывающее потенциал электростатического поля с величиной объёмной плотности электрического заряда:

Левую часть уравнения Пуассона обычно записывают с помощью специального оператора «лапласиана скалярной функции»

Если ввести в рассмотрение оператор Гамильтона (другое его название – «оператор набла»)

• где — орты декартовой системы координат, то формально дивергенцию вектора можно рассматривать как результат скалярного произведения «вектора» набла на вектор , а градиент скалярной функции как произведение «вектора» набла на скаляр, только при этом надо помнить, что оператор набла – дифференциальный оператор — при записи операции должен стоять перед функцией, на которую он действует:
• (6)
• Лапласиан, таким образом, можно рассматривать как последовательное применение оператора Гамильтона (оператора набла):
• . (7)
• Итак, уравнение Пуассона для потенциала электростатического поля в вакууме имеет вид:
• (8)

В частном случае, когда объёмная плотность электрического заряда равна нулю, т.е. в рассматриваемой области отсутствуют распределенные по объёму электрические заряды, уравнение Пуассона переходит в уравнение Лапласа

Уравнение Лапласа в электростатике описывает изменение потенциала в пространстве, свободном от электрических зарядов.

Значение уравнений Пуассона и Лапласа для изучения электростатических явлений чрезвычайно велико: в отличие от дифференциальной формы теоремы Гаусса эти уравнения — уравнения для единственной неизвестной функции, решение этих уравнений можно получить при самых общих предположениях о характере распределения в пространстве неподвижных и неизменных по величине электрических зарядов. Конкретные результаты получаются с обязательным учетом «граничных условий», т.е. условий, налагаемых на общее решение уравнения Пуассона спецификой рассматриваемой области пространства, свойств замыкающей область поверхности и особенностей распределения электрических зарядов по этой поверхности.

1. Выражение для лапласиана скалярной функции (4) записано в декартовой системе координат. В цилиндрической системе координат ( ) уравнение Пуассона принимает вид
2. , (10)
3. а в сферической системе координат( ) –
4. . (11)
5. В произвольной системе координат можно воспользоваться известными определениями дивергенции вектора и градиента скалярной функции (символическая форма записи).

Дата добавления: 2017-09-01; просмотров: 4004;

Уравнения Пуассона и Лапласа

• Основная задача электростатики.
• Основная задача электростатики состоит в определении напряженности электрического поля по заданному распределению источников поля — неподвижных электрических зарядов. В общем случае решение такой задачи упрощается, если его проводить в два этапа:
• 1) сведение задачи к решению дифференциального уравнения для потенциала;
• 2) нахождение напряженности поля по уже найденному потенциалу.

Учтем . Скалярное произведение двух векторных операторов Гамильтона порождает скалярный дифференциальный оператор второго порядка – оператор Лапласа:

В декартовых координатах оператор Лапласа записывается как

С учетом (1.62) из (1.61) следует уравнение Пуассона

После решения уравнения Пуассона (1.64) относительно потенциала по заданному распределению плотности заряда можно найти напряженность поля по формуле .

При переходе от дискретного к непрерывному распределению зарядов формула

для потенциала поля системы зарядов заменяется формулой

Решение основной задачи электростатики оказывается однозначным. Это следует из однозначности решения прямой задачи электромагнетизма о нахождении электромагнитного поля по заданным источникам поля, граничным и начальным условиям для поля.

Решение обратной задачи электростатики (нахождение распределения источников поля — зарядов по электрическому полю, заданному в конечном объеме) в общем случае неоднозначно.

Пример.Однородно заряженный шар создает вне своего объема такое же электрическое поле, как и точечный заряд, равный заряду шара и помещенный в точку центра шара.

Для решения уравнения Лапласа, как и уравнения Пуассона, должны быть заданы граничные условия для потенциала. Эти условия задаются на поверхности, ограничивающей область, где надо найти потенциал.

Не нашли то, что искали? Воспользуйтесь поиском:

[spoiler title=”источники:”]

http://elenergi.ru/uravneniya-puassona-i-laplasa-dlya-potencialnogo-polya.html

http://school16rostov.ru/estestvennye/uravnenie-puassona-i-matematicheskaya-postanovka-zadach-elektrostatiki-spravochnik-studenta.html

[/spoiler]