Как найти напряженность электрического поля формулы - Сайт, где вы сможете решить свои вопросы

Что такое электрическое поле

Долгое время ученые не могли толком объяснить, как именно заряженные тела взаимодействуют друг с другом, не соприкасаясь. Майкл Фарадей первым выяснил, что между ними есть некое промежуточное звено. Его выводы подтвердил Джеймс Максвелл, который установил, что для воздействия одного такого объекта на другой нужно время, а значит, они взаимодействуют через «посредника».

В современной физике электрическое поле — это некая материя, которая возникает вокруг заряженных тел и обусловливает их взаимодействие. Если речь идет о неподвижных объектах, поле называют электростатическим.

Тела, имеющие одноименные заряды, будут отталкиваться, а разноименные — притягиваться.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Определение напряженности электрического поля

Для исследования электрического поля используются точечные заряды. Давайте выясним, что это такое.

Точечным зарядом называют такой наэлектризованный объект, размерами которого можно пренебречь, поскольку он слишком мал в сравнении с расстоянием, отделяющим этот объект от других заряженных тел.

Теперь поговорим непосредственно о напряженности, которая является одной из главных характеристик электрического поля. Это векторная физическая величина. В отличие от скалярных она имеет не только значение, но и направление.

Для того, чтобы исследовать электрическую напряженность, нужно в поле заряженного тела q₁ поместить еще один точечный заряд q₂ (допустим, они оба будут положительными). Со стороны q₁ на q₂ будет действовать некая сила. Очевидно, что для расчетов нужно иметь в виду как значение данной силы, так и ее направление.

Напряженность электрического поля — это показатель, равный отношению силы, действующей на заряд в электрическом поле, к величине этого заряда.

Напряженность является силовой характеристикой поля. Она говорит о том, как сильно влияние поля в данной точке не только на другой заряд, но также на живые и неживые заряженные объекты.

Важно!

Иногда можно услышать оборот «напряжение электрического поля», но это ошибка — правильно говорить «напряженность».

Единицы измерения и формулы

Из указанного выше определения понятно, как найти напряженность электрического поля в некой точке:

E = F / q, где F — действующая на заряд сила, а q — величина заряда, расположенного в данной точке.

Если нужно выразить силу через напряженность, мы получим следующую формулу:

Направление напряженности электрического поля всегда совпадает с направлением действующей силы. Если взять отрицательный точечный заряд, формулы будут работать аналогично.

Поскольку сила измеряется в ньютонах, а величина заряда — в кулонах, единицей измерения напряженности электрического поля является Н/Кл (ньютон на кулон).

Принцип суперпозиции

Допустим, у нас есть несколько зарядов, которые взаимодействуют. Вокруг каждого существует свое электрическое поле. Тогда существует некая точка или область, в которой одновременно существует электрическое поле нескольких зарядов. Чему равна общая напряженность электрического поля, создаваемого этими зарядами?

Было установлено, что общая сила воздействия на конкретный заряд, расположенный в поле, является суммой сил, действующих на данный заряд со стороны каждого тела. Из этого следует, что и напряженность поля в любой взятой точке можно вычислить, просуммировав векторно напряженности, создаваемые каждым зарядом в отдельности в той же точке. Это и есть принцип суперпозиции.

Это правило корректно для любых полей, за некоторыми исключениями. Принцип суперпозиции не соблюдается в следующих случаях:

расстояние между зарядами очень мало — порядка 10^-15м;
речь идет о сверхсильных полях с напряженностью более 10²⁰в/м.

Но задачи с такими данными выходят за пределы школьного курса физики.

Напряженность поля точечного заряда

У электрического поля, создаваемого точечным зарядом, есть одна особенность — ввиду малой величины самого заряда оно очень слабо влияет на другие наэлектризованные тела. Именно поэтому такие «точки» используют для исследований.

Но прежде чем рассказать, от чего зависит напряженность электрического поля точечного заряда, рассмотрим подробнее, как взаимодействуют эти заряды.

Закон Кулона

Предположим, в вакууме есть два точечных заряда, которые статично расположены на некотором расстоянии друг от друга. В зависимости от одноименности или разноименности они могут притягиваться либо отталкиваться. В любом случае на них действуют силы, направленные вдоль соединяющей их прямой.

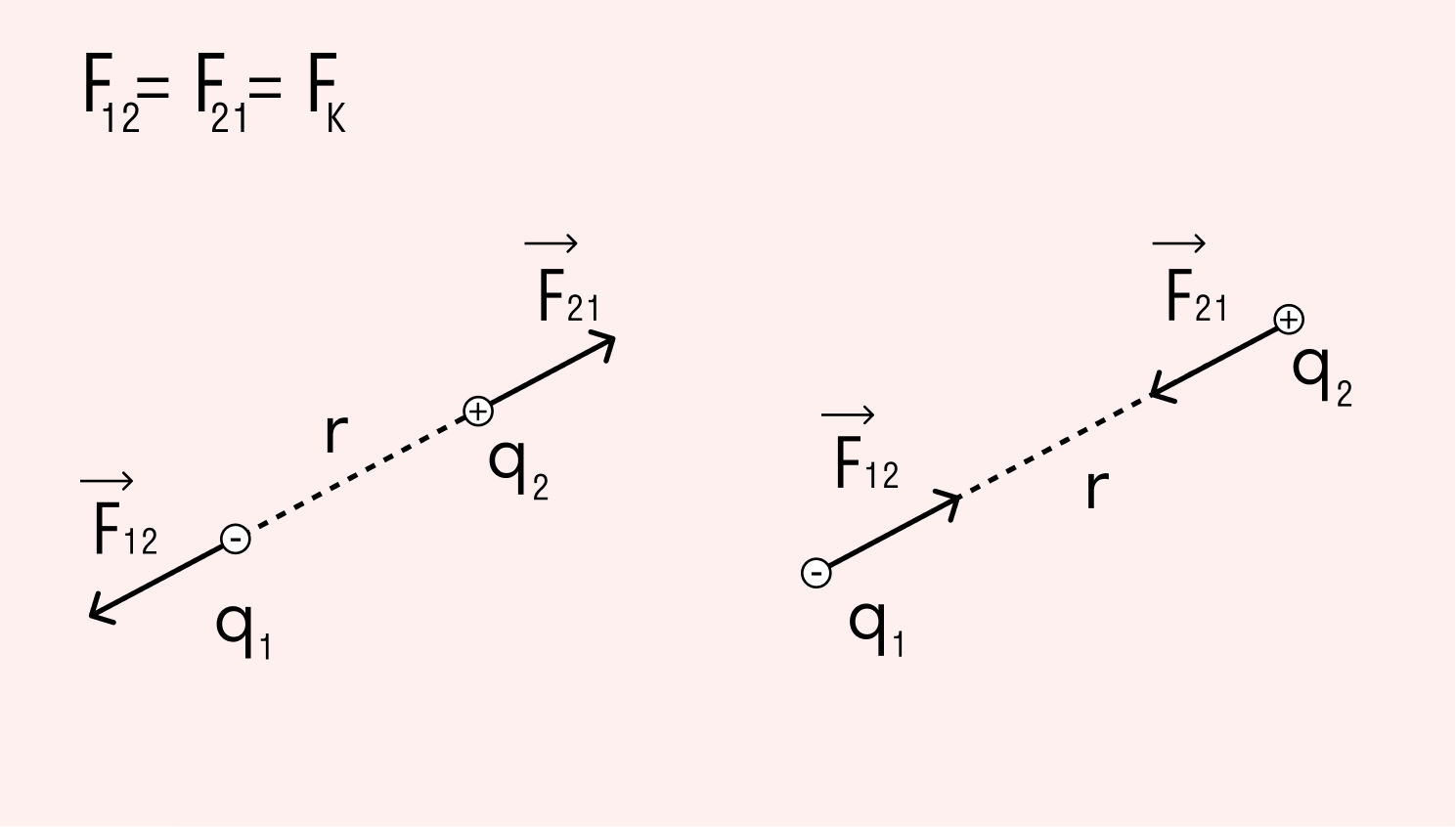
Закон Кулона

Модули сил, действующих на точечные заряды в вакууме, пропорциональны произведению данных зарядов и обратно пропорциональны квадрату расстояния между ними.

Силу электрического поля в конкретной точке можно найти по формуле: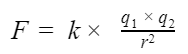 где q₁ и q₂ — модули точечных зарядов, r — расстояние между ними.

В формуле участвует коэффициент пропорциональности k, который был определен опытным путем и представляет собой постоянную величину. Он обозначает, с какой силой взаимодействуют два тела с зарядом 1 Кл, расположенные на расстоянии 1 м.

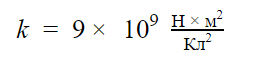
Важно!

Сила взаимодействия двух точечных зарядов остается прежней при появлении сколь угодно большого количества других зарядов в данном поле.

Учитывая все вышесказанное, напряжение электрического поля точечного заряда в некой точке, удаленной от заряда на расстояние r, можно вычислить по формуле:

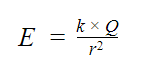
Итак, мы выяснили, что называется напряженностью электрического поля и от чего зависит эта величина. Теперь посмотрим, как она изображается графическим способом.

Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.

Линии напряженности

Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном.

Линии напряженности — это прямые, которые совпадают с силовыми линиями в системе из положительного и отрицательного зарядов. Касательные к ним в каждой точке электрического поля имеют то же направление, что и напряженность этого поля.

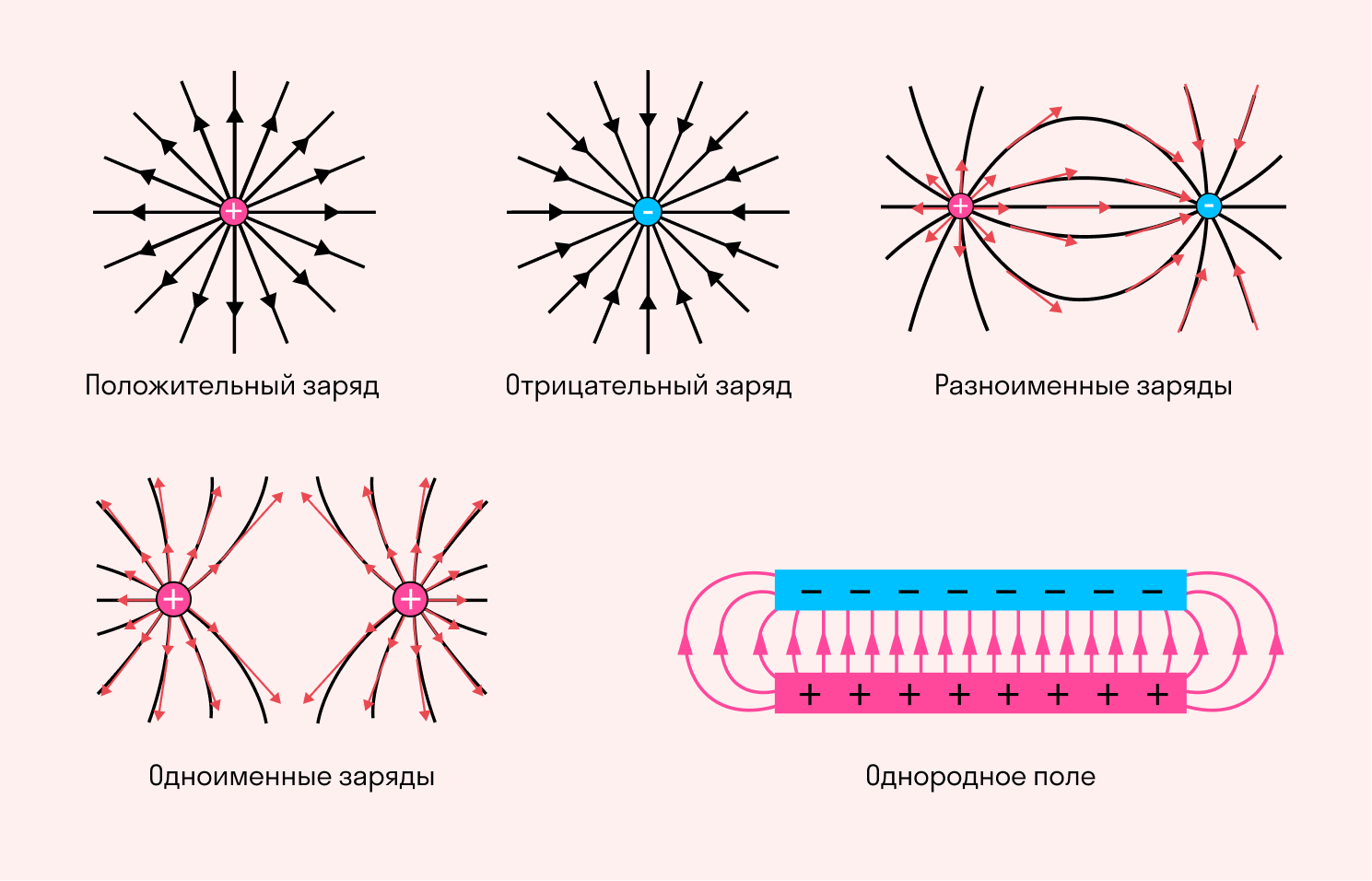
При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно). В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля.

Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними.

Источник

Напряжённость электрического поля

Размерность	LMT⁻³I⁻¹
Единицы измерения
СИ	В/м
Примечания
векторная величина

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и равная отношению силы , действующей на неподвижный малый по величине точечный заряд, помещённый в данную точку, к величине этого заряда ${displaystyle q^{*}}$ ^[1]:

${displaystyle {vec {E}}={frac {vec {F}}{q^{*}}}.}$

Напряжённость электрического поля иногда называют силовой характеристикой электрического поля, так как всё отличие от вектора силы, действующей на заряженную частицу, состоит в постоянном^[2] множителе.

В каждой точке в данный момент времени существует своё значение вектора vec E (вообще говоря — разное^[3]
в разных точках пространства), таким образом, vec E — это векторное поле. Формально это отражается в записи

представляющей напряжённость электрического поля как функцию пространственных координат (и времени, так как vec E может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле^[4], и законы, которым оно подчиняется, суть предмет электродинамики.

Напряжённость электрического поля в Международной системе единиц (СИ) измеряется в вольтах на метр [В/м] или в ньютонах на кулон [Н/Кл].

Напряжённость электрического поля в классической электродинамике[править | править код]

Напряжённость электрического поля — одна из основных фундаментальных величин классической электродинамики. В этой области физики сопоставимыми с ней по значимости являются только вектор магнитной индукции (совместно с вектором напряжённости электрического поля образующий тензор электромагнитного поля) и электрический заряд. С некоторой точки зрения столь же важными представляются потенциалы электромагнитного поля (образующие вместе единый электромагнитный потенциал).

Остальные понятия и величины классической электродинамики, такие как электрический ток, плотность тока, плотность заряда, вектор поляризации, а также вспомогательные поле электрической индукции и напряженность магнитного поля — хотя безусловно важны и содержательны, по сути оказываются вторичными или производными.

Ниже выделены основные контексты классической электродинамики в отношении напряжённости электрического поля.

Сила воздействия электромагнитного поля на заряженные частицы[править | править код]

Полная сила, с которой электромагнитное поле (включающее электрическую и магнитную составляющие) действует на заряженную частицу, выражается формулой силы Лоренца:

${displaystyle {vec {F}}=q^{*}{vec {E}}+q^{*}[{vec {v}}times {vec {B}}]}$

где ${displaystyle q^{*}}$ — электрический заряд частицы, — её скорость,
— вектор магнитной индукции; косым крестом times обозначено векторное произведение. Формула приведена в единицах СИ.

Эта формула является более общей по сравнению с формулой, данной в определении напряжённости электрического поля, так как включает в себя также действие на заряженную частицу (если та движется) со стороны магнитного поля.

Частица предполагается точечной. Однако эта формула позволяет рассчитать и силы, действующие со стороны электромагнитного поля на тела любой формы с любым распределением зарядов и токов — если воспользоваться обычным для физики приёмом разбиения сложного тела на маленькие (математически — бесконечно малые) части, каждая из которых может считаться точечной и таким образом входящей в область применимости формулы Лоренца. Разумеется, для того, чтобы эта формула была применена (даже в простых случаях, таких, как расчёт силы взаимодействия двух точечных зарядов), необходимо уметь рассчитывать vec E и .

Остальные формулы, применяемые для расчёта электромагнитных сил (например, формулу для силы Ампера) можно считать следствиями^[5] фундаментальной формулы силы Лоренца или частными случаями её применения.

Уравнения Максвелла[править | править код]

Достаточным вместе с формулой силы Лоренца теоретическим фундаментом классической электродинамики являются уравнения электромагнитного поля, называемые уравнениями Максвелла. Их стандартная традиционная форма представляет собой четыре уравнения, в три из которых входит вектор напряжённости электрического поля:

${displaystyle {begin{aligned}operatorname {div} {vec {E}}&={frac {rho }{varepsilon _{0}}},&operatorname {rot} {vec {E}}&=-{frac {partial {vec {B}}}{partial t}},\operatorname {div} {vec {B}}&=0,&operatorname {rot} {vec {B}}&=mu _{0}{vec {j}}+{frac {1}{c^{2}}}{frac {partial {vec {E}}}{partial t}}.end{aligned}}}$

Здесь rho — плотность заряда, vec j — плотность тока, $varepsilon _{0}$ — электрическая постоянная, $mu _{0}$ — магнитная постоянная, — скорость света (уравнения записаны в системе СИ). В приведённом виде уравнения Максвелла являются «уравнениями для вакуума» (их более общий вариант, применимый и для описания поведения электромагнитного поля в среде, а также иные формы записи уравнений — см. в статье Уравнения Максвелла).

Этих четырёх уравнений вместе с пятым — уравнением силы Лоренца — в принципе достаточно, чтобы полностью описать классическую (не квантовую) электродинамику, то есть они представляют её полные законы. Для решения реальных задач с их помощью необходимы ещё уравнения движения «материальных частиц» (в классической механике это законы Ньютона), а также дополнительная информация о конкретных свойствах рассматриваемых физических тел и сред (их упругости, электропроводности, поляризуемости и др.) и о других силах, участвующих в задаче (например, о гравитации), однако вся эта информация уже не входит в рамки электродинамики как таковой, хотя и оказывается зачастую необходимой для построения замкнутой системы уравнений, позволяющих решить ту или иную конкретную задачу в целом.

«Материальные уравнения»[править | править код]

Дополнительными формулами (обычно не точными, а приближёнными или иногда даже эмпирическими), которые используются в классической электродинамике при решении практических задач и носят название «материальных уравнений», являются

закон Ома;
закон поляризации;
в разных случаях многие другие формулы и соотношения.

Связь с потенциалами[править | править код]

Связь напряжённости электрического поля с потенциалами в общем случае такова:

${displaystyle {vec {E}}=-nabla varphi -{frac {partial {vec {A}}}{partial t}},}$

где — скалярный и векторный потенциалы,

{displaystyle {vec {B}}=operatorname {rot} {vec {A}}.}

В частном случае стационарных (не меняющихся со временем) полей первое уравнение упрощается до

Это выражение связывает электростатическое поле с электростатическим потенциалом.

Электростатика[править | править код]

Теоретически и практически важным случаем является ситуация, когда заряженные тела неподвижны (например, исследуется состояние равновесия) или скорость их движения достаточно мала, чтобы можно было приближённо воспользоваться способами расчета, справедливыми для неподвижных тел. Этим случаем занимается раздел электродинамики, называемый электростатикой.

Как указано выше, напряжённость электрического поля в этом случае выражается через скалярный потенциал как

или, покомпонентно,

${displaystyle E_{x}=-{frac {partial varphi }{partial x}},quad E_{y}=-{frac {partial varphi }{partial y}},quad E_{z}=-{frac {partial varphi }{partial z}},}$

то есть электростатическое поле оказывается потенциальным полем.
( varphi в этом случае — случае электростатики — принято называть электростатическим потенциалом).

Правомерно и обратное соотношение:

{displaystyle varphi =-int {vec {E}}cdot {vec {dl}}.}

Уравнения Максвелла при этом также сильно упрощаются (уравнения с магнитным полем можно вообще исключить, а в уравнение с дивергенцией можно подставить ) и сводятся к уравнению Пуассона:

$Delta varphi =-{frac {rho }{varepsilon _{0}}},$

а в областях, свободных от заряженных частиц, — к уравнению Лапласа:

Учитывая линейность этих уравнений, а следовательно, применимость к ним принципа суперпозиции, достаточно найти поле одного точечного заряда, чтобы потом получать потенциал или напряжённость поля, создаваемого любым распределением зарядов (суммируя решения для точечных зарядов).

Теорема Гаусса[править | править код]

В электростатике широко используется теорема Гаусса, содержание которой сводится к интегральной форме единственного нетривиального для электростатики уравнения Максвелла:

$oint limits _{S}{vec E}cdot {vec {dS}}={frac {Q}{varepsilon _{0}}},$

где интегрирование проводится по любой замкнутой поверхности (вычисляется поток
vec E через эту поверхность), — полный (суммарный) заряд внутри этой поверхности.

Эта теорема даёт удобный способ расчета напряжённости электрического поля в случае, когда источники поля имеют высокую симметрию: сферическую, цилиндрическую или зеркальную + трансляционную. В частности, таким способом легко находится поле точечного заряда, сферы, цилиндра, плоскости.

Напряжённость электрического поля точечного заряда[править | править код]

Для точечного заряда в электростатике верен закон Кулона, который в системе СИ записывается:

$varphi ={frac {1}{4pi varepsilon _{0}}}cdot {frac {q}{r}},$

или

${displaystyle {vec {E}}={frac {1}{4pi varepsilon _{0}}}cdot {frac {q}{r^{2}}}cdot {frac {vec {r}}{r}}quad left(E={frac {1}{4pi varepsilon _{0}}}cdot {frac {q}{r^{2}}}right)}$

Исторически закон Кулона был открыт первым, хотя с теоретической точки зрения уравнения Максвелла более фундаментальны. С этой точки зрения он является их следствием. Получить этот результат проще всего, исходя из теоремы Гаусса, учитывая сферическую симметрию задачи: выбрать поверхность в виде сферы с центром в точечном заряде, учесть, что направление vec E будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса : $4pi r^{2}$ , имеем ${displaystyle 4pi r^{2}E=q/varepsilon _{0}}$ , откуда сразу получаем ответ для .

Ответ для varphi получается интегрированием :

{displaystyle varphi =-int {vec {E}}cdot {vec {dl}}=-int E,dr.}

Для системы СГС формулы и их вывод аналогичны, отличие от СИ лишь в константах:

$varphi ={frac {q}{r}},$

${displaystyle {vec {E}}={frac {q}{r^{2}}}{frac {vec {r}}{r}}quad left(E={frac {q}{r^{2}}}right)}$

Электрическое поле произвольного распределения зарядов[править | править код]

По принципу суперпозиции для напряжённости поля совокупности дискретных источников имеем:

${displaystyle {vec {E}}={vec {E}}_{1}+{vec {E}}_{2}+{vec {E}}_{3}+dots ,}$

где каждое

${displaystyle {vec {E}}_{i}={frac {1}{4pi varepsilon _{0}}}{frac {q_{i}}{(Delta {vec {r}}_{i})^{2}}}{frac {Delta {vec {r}}_{i}}{|Delta {vec {r}}_{i}|}}quad left(Delta {vec {r}}_{i}={vec {r}}-{vec {r}}_{i}right)}$

Подставив, получаем:

${vec E}({vec r})=sum limits _{i}{frac {1}{4pi varepsilon _{0}}}{frac {q_{i}}{(Delta {vec r}_{i})^{2}}}{frac {Delta {vec r}_{i}}{|Delta {vec r}_{i}|}},$

Для непрерывного распределения аналогично:

${displaystyle {vec {E}}({vec {r}})=int limits _{V}{frac {1}{4pi varepsilon _{0}}}{frac {rho ({vec {hat {r}}}),dV}{({vec {r}}-{vec {hat {r}}})^{2}}}{frac {{vec {r}}-{vec {hat {r}}}}{|{vec {r}}-{vec {hat {r}}}|}},}$

где — область пространства, где расположены заряды (ненулевая плотность заряда), или всё пространство,
— радиус-вектор точки, для которой считаем vec E ,
— радиус-вектор источника, пробегающий все точки области при интегрировании, — элемент объёма. Можно подставить вместо ;
вместо ;
вместо .

Системы единиц[править | править код]

В системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в ньютонах на кулон или в вольтах на метр (русское обозначение: В/м; международное: V/m).

Измерение напряженности электрического поля[править | править код]

Измерения напряженности электрического поля в электроустановках сверхвысокого напряжения производят приборами типа ПЗ-1, ПЗ-1 м и др.

Измеритель напряженности электрического поля работает следующим образом: в антенне прибора электрическое поле создает ЭДС которая усиливается с помощью транзисторного усилителя, выпрямляется полупроводниковыми диодами и измеряется стрелочным микро-амперметром. Антенна представляет собой симметричный диполь, выполненный в виде двух металлических пластин, размещенных одна над другой. Поскольку наведенная в симметричном диполе ЭДС. пропорциональна напряженности электрического поля, шкала мили-амперметра отградуирована в киловольтах на метр (кВ/м).

Измерение напряженности должно производиться во всей зоне, где может находиться человек в процессе выполнения работы. Наибольшее измеренное значение напряженности является определяющим. При размещении рабочего места на земле наибольшая напряженность обычно бывает на высоте роста человека.

Точки измерения выбираются по ГОСТ 12.1.002 зависимости от расположения рабочего места и от оснащения его средствами защиты согласно таблице:

Точки измерений напряженности электрического поля

Расположение рабочего места	Средства защиты	Точки измерений
Без поднятия на оборудование и конструкции	Без средств защиты	На высоте 1,8 м от поверхности земли
То же	Средства коллективной защиты	На высоте 0,5; 1,0 и 1,8 м от поверхности земли
С поднятием на оборудование и конструкции	Независимо от наличия средств защиты	На высоте 0,5; 1,0 и 1,8 м от площадки рабочего места и на расстоянии 0,5 м от заземленных токоведущих частей оборудования

Литература[править | править код]

Сивухин Д. В. Общий курс физики. — Изд. 4-е, стереотипное. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — 656 с. — ISBN 5-9221-0227-3; ISBN 5-89155-086-5..

Примечания[править | править код]

↑ Напряжённость электрического поля // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 246. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
↑ Для любой частицы её электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
↑ Иногда его значения могут оказываться и одинаковыми в разных точках пространства; если одинаков всюду в пространстве (или в какой-то области), говорят об однородном электрическом поле — это частный, наиболее простой, случай электрического поля; в реальности электрическое поле может быть однородным лишь приближённо, то есть различия в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
↑ Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (в которой вектор напряжённости электрического поля вместе с вектором магнитной индукции входит в тензор электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле — одна из основных составляющих электромагнитного поля, не утрачивает смысла.
↑ Хотя исторически многие из них были открыты раньше.

См. также[править | править код]

Электрическая индукция
Уравнения Максвелла
Закон Кулона

Источник

Электрическое поле

Электродинамика – раздел физики, изучающий свойства и взаимодействия электрических зарядов, осуществляемые посредством электромагнитного поля.

Электростатикой называется раздел электродинамики, в котором рассматриваются свойства и взаимодействия неподвижных электрически заряженных тел или частиц.

Электромагнитное взаимодействие – это взаимодействие между электрически заряженными частицами или макротелами.

Точечный заряд – заряженное тело, размер которого мал по сравнению с расстоянием, на котором оценивается его действие.

Содержание

Электризация тел
Взаимодействие зарядов. Два вида зарядов
Закон сохранения электрического заряда
Закон Кулона
Действие электрического поля на электрические заряды
Напряженность электрического поля
Принцип суперпозиции электрических полей
Потенциальность электростатического поля
Потенциал электрического поля. Разность потенциалов
Проводники в электрическом поле
Диэлектрики в электрическом поле
Электрическая емкость. Конденсатор
Энергия электрического поля конденсатора
Основные формулы раздела «Электрическое поле»

Электризация тел

Электризация – процесс сообщения телу электрического заряда, т. е. нарушение его электрической нейтральности. Процесс электризации представляет собой перенесение с одного тела на другое электронов или ионов. В результате электризации тело получает возможность участвовать в электромагнитном взаимодействии.

Способы электризации:

трением, – например, электризация эбонитовой палочки при трении о мех. При тесном соприкосновении двух тел часть электронов переходит с одного тела на другое; в результате этого на поверхности у одного из тел создается недостаток электронов и тело получает положительный заряд, а у другого – избыток, и тело заряжается отрицательно. Величины зарядов тел одинаковы;
через влияние (электростатическая индукция) – тело остается электрически нейтральным, электрические заряды внутри него перераспределяются так, что разные части тела приобретают разные по знаку заряды;
при соприкосновении заряженного и незаряженного тела – заряд при этом распределяется между этими телами пропорционально их размерам. Если размеры тел одинаковы, то заряд распределяется между ними поровну;
при ударе;
под действием излучения – под действием света с поверхности проводника могут вырываться электроны, при этом проводник приобретает положительный заряд.

Взаимодействие зарядов. Два вида зарядов

Электрический заряд – скалярная физическая величина, характеризующая способность тела участвовать в электромагнитных взаимодействиях.

Обозначение – ( q ), единица измерения в СИ – кулон (Кл).

Существуют два вида электрических зарядов: положительный и отрицательный. Наименьший отрицательный заряд имеет электрон (–1,6·10^-19 Кл), наименьший положительный заряд (1,6·10^-19 Кл) – протон. Минимальный заряд, который может быть сообщен телу, равен заряду электрона (элементарный заряд). Если тело имеет избыточные (лишние) электроны, то тело заряжено отрицательно, если у тела недостаток электронов, то тело заряжено положительно.

Величина заряда тела будет равна

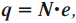
где ( N ) — число избыточных или недостающих электронов;
( e ) — элементарный заряд, равный 1,6·10^-19 Кл.

Важно!
Частица может не иметь заряда, но заряд без частицы не существует.

Электрические заряды взаимодействуют:

заряды одного знака отталкиваются:

заряды противоположных знаков притягиваются:

Прибор для обнаружения электрического заряда называется электроскоп. Основная часть прибора – металлический стержень, на котором закреплены два листочка металлической фольги, помещенные в стеклянный сосуд. При соприкосновении заряженного тела со стержнем электроскопа заряды распределяются между листочками фольги. Так как заряд листочков одинаков по знаку, они отталкиваются.

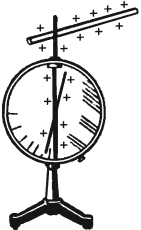
Для измерения зарядов можно использовать и электрометр. Основные части его – металлический стержень и стрелка, которая может вращаться вокруг горизонтальной оси. Стержень со стрелкой закреплен в пластмассовой втулке и помещен в металлический корпус, закрытый стеклянными крышками. При соприкосновении заряженного тела со стержнем стержень и стрелка получают электрические заряды одного знака. Стрелка поворачивается на некоторый угол.

Закон сохранения электрического заряда

Систему называют замкнутой (электрически изолированной), если в ней не происходит обмена зарядами с окружающей средой.

В любой замкнутой (электрически изолированной) системе сумма электрических зарядов остается постоянной при любых взаимодействиях внутри нее.

Полный электрический заряд ( (q) ) системы равен алгебраической сумме ее положительных и отрицательных зарядов ( (q_1, q_2 … q_N) ):

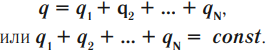
Важно!
В природе не возникают и не исчезают заряды одного знака: положительный и отрицательный заряды могут взаимно нейтрализовать друг друга, если они равны по модулю.

Закон Кулона

Закон Кулона был открыт экспериментально: в опытах с использованием крутильных весов измерялись силы взаимодействия заряженных шаров.

Закон Кулона формулируется так:
сила взаимодействия ( F ) двух точечных неподвижных электрических зарядов в вакууме прямо пропорциональна их модулям ( q_1 ) и ( q_2 ) и обратно пропорциональна квадрату расстояния между ними ( r ):

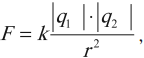
где ( k=frac{1}{4pivarepsilon_0}=9cdot10^9 ) (Н·м²)/Кл² – коэффициент пропорциональности,
( varepsilon_0=8.85cdot10^{-12} ) Кл²/(Н·м²) – электрическая постоянная.

Коэффициент ( k ) численно равен силе, с которой два точечных заряда величиной 1 Кл каждый взаимодействуют в вакууме на расстоянии 1 м.

Сила Кулона направлена вдоль прямой, соединяющей взаимодействующие заряды. Заряды взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению.

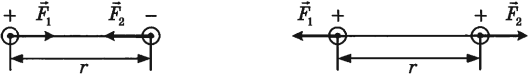
Значение силы Кулона зависит от среды, в которой они находятся. В этом случае формула закона:

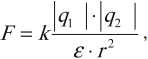
где ( varepsilon ) – диэлектрическая проницаемость среды.

Закон Кулона применим к взаимодействию

неподвижных точечных зарядов;
равномерно заряженных тел сферической формы.

В этом случае ( r ) – расстояние между центрами сферических поверхностей.

Важно!
Если заряженное тело протяженное, то его необходимо разбить на точечные заряды, рассчитать силы их попарного взаимодействия и найти равнодействующую этих сил (принцип суперпозиции).

Действие электрического поля на электрические заряды

Электрическое поле – это особая форма материи, существующая вокруг электрически заряженных тел.

Впервые понятие электрического поля было введено Фарадеем. Он объяснял взаимодействие зарядов следующим образом: каждый заряд создает вокруг себя электрическое поле, которое с некоторой силой действует на другой заряд.

Свойства электрического поля заключаются в том, что оно:

материально;
создается зарядом;
обнаруживается по действию на заряд;
непрерывно распределено в пространстве;
ослабевает с увеличением расстояния от заряда.

Действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать и перемещать эти тела по отношению к заряженному телу.

Силу, с которой электрическое поле действует на заряд, можно рассчитать по формуле:

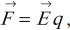
где ( vec{E} ) – напряженность электрического поля, ( q ) – заряд.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.

Алгоритм решения задач о точечных зарядах и системах, сводящихся к ним:

сделать рисунок; указать силы, действующие на точечный заряд, помещенный в электрическое поле;
записать для заряда условие равновесия или основное уравнение динамики материальной точки;
выразить силы электрического взаимодействия через заряды и поля и подставить эти выражения в исходное уравнение;
если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению добавить уравнение закона сохранения зарядов;
записать математически все вспомогательные условия;
решить полученную систему уравнений относительно неизвестной величины;
проверить решение

Напряженность электрического поля

Напряженность электрического поля ( vec{E} ) – векторная физическая величина, равная отношению силы ( F ), действующей на пробный точечный заряд, к величине этого заряда ( q ):

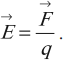
Обозначение – ( vec{E} ), единица измерения в СИ – Н/Кл или В/м.

Напряженность поля точечного заряда в вакууме вычисляется по формуле:

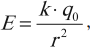
где ( k=frac{1}{4pivarepsilon_0}=9cdot10^9 ) (Н·м²)/Кл²,
( q_0 ) – заряд, создающий поле,
( r ) – расстояние от заряда, создающего поле, до данной точки.

Напряженность поля точечного заряда в среде вычисляется по формуле:

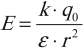
где ( varepsilon ) – диэлектрическая проницаемость среды.

Важно!
Напряженность электрического поля не зависит от величины пробного заряда, она определяется величиной заряда, создающего поле.

Направление вектора напряженности в данной точке совпадает с направлением силы, с которой поле действует на положительный пробный заряд, помещенный в эту точку.

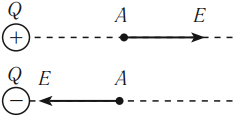
Линией напряженности электрического поля называется линия, касательная к которой в каждой точке направлена вдоль вектора напряженности ( vec{E} ).

Линии напряженности электростатического поля начинаются на положительных электрических зарядах и заканчиваются на отрицательных электрических зарядах или уходят в бесконечность от положительного заряда и приходят из бесконечности к отрицательному заряду.

Распределение линий напряженности вокруг положительного и отрицательного точечных зарядов показано на рисунке.

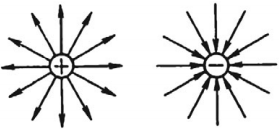
Определяя направление вектора ( vec{E} ) в различных точках пространства, можно представить картину распределения линий напряженности электрического поля.

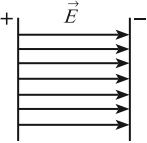
Поле, в котором напряженность одинакова по модулю и направлению в любой точке, называется однородным электрическим полем. Однородным можно считать электрическое поле между двумя разноименно заряженными металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу.

Принцип суперпозиции электрических полей

Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов.

Принцип суперпозиции электрических полей: напряженность электрического поля системы ( N ) зарядов равна векторной сумме напряженностей полей, создаваемых каждым из них в отдельности:

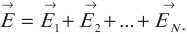
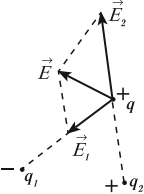
Электрические поля от разных источников существуют в одной точке пространства и действуют на заряд независимо друг от друга.

Потенциальность электростатического поля

Электрическое поле с напряженностью ( vec{E} ) при перемещении заряда ( q ) совершает работу. Работа ( A ) электростатического поля вычисляется по формуле:

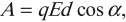
где ( d ) – расстояние, на которое перемещается заряд,
( alpha ) – угол между векторами напряженности электрического поля и перемещения заряда.

Важно!
Эта формула применима для нахождения работы только в однородном электростатическом поле.

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.

Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.

Важно!
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным.

Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой ( W ), так как буквой ( E ) обозначают напряженность поля:

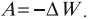
Потенциальная энергия заряда ( q ), помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – ( varphi ), единица измерения в СИ – вольт (В).

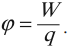
Потенциал ( varphi ) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

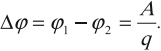
Обозначение – ( Deltavarphi ), единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой ( U ) и называют напряжением.

Важно!
Разность потенциалов ( Deltavarphi=varphi_1-varphi_2 ), а не изменение потенциала ( Deltavarphi=varphi_2-varphi_1 ). Тогда работа электростатического поля равна:

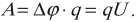
Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле.

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда ( q ) в точке, удаленной от него на расстояние ( r ), вычисляется по формуле:

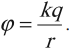
Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (( r =R ), где ( R ) – радиус шара). Напряженность поля внутри шара равна нулю.

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

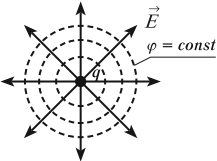
Разность потенциалов и напряженность связаны формулой:

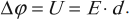
Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

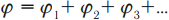
Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

установить характер и особенности электростатических взаимодействий объектов системы;
ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
записать законы сохранения и движения для объектов;
выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
составить систему уравнений и решить ее относительно искомой величины;
проверить решение.

Проводники в электрическом поле

Проводниками называют вещества, в которых может происходить упорядоченное перемещение электрических зарядов, т. е. протекать электрический ток.

Проводниками являются металлы, водные растворы солей, кислот, ионизованные газы. В проводниках есть свободные электрические заряды. В металлах валентные электроны взаимодействующих друг с другом атомов становятся свободными.

Если металлический проводник поместить в электрическое поле, то под его действием свободные электроны проводника начнут перемещаться в направлении, противоположном направлению напряженности поля. В результате на одной поверхности проводника появится избыточный отрицательный заряд, а на противоположной – избыточный положительный заряд.

Эти заряды создают внутри проводника внутреннее электрическое поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Под действием внешнего электростатического поля электроны проводимости в металлическом проводнике перераспределяются так, что напряженность результирующего поля в любой точке внутри проводника равна нулю. Электрические заряды расположены на поверхности проводника.

Важно!
Если внутри проводника есть полость, то напряженность в ней будет равна нулю независимо от того, какое поле имеется вне проводника и как заряжен проводник. Внутренняя полость в проводнике экранирована (защищена) от внешних электростатических полей. На этом основана электростатическая защита.

Явление перераспределения зарядов во внешнем электростатическом поле называется электростатической индукцией.

Заряды, разделенные электростатическим полем, взаимно компенсируют друг друга, если проводник удалить из поля. Если такой проводник разрезать, не вынося из поля, то его части будут иметь заряды разных знаков.

Важно!
Во всех точках поверхности проводника вектор напряженности направлен перпендикулярно к его поверхности. Поверхность проводника является эквипотенциальной (потенциалы всех точек поверхности проводника равны).

Диэлектрики в электрическом поле

Диэлектриками называют вещества, не проводящие электрический ток. Диэлектриками являются стекло, фарфор, резина, дистиллированная вода, газы.

В диэлектриках нет свободных зарядов, все заряды связаны. В молекуле диэлектрика суммарный отрицательный заряд электронов равен положительному заряду ядра. Различают полярные и неполярные диэлектрики.

В молекулах полярных диэлектриков ядра и электроны расположены так, что центры масс положительных и отрицательных зарядов не совпадают и находятся на некотором расстоянии друг от друга. То есть молекулы представляют собой диполи независимо от наличия внешнего электрического поля. В отсутствие внешнего электрического поля из-за теплового движения молекул диполи расположены хаотично, поэтому суммарная напряженность поля всех диполей диэлектрика равна нулю.

Если в отсутствие внешнего электрического поля центры масс положительных и отрицательных зарядов в молекуле диэлектрика совпадают, то он называется неполярным. Пример такого диэлектрика – молекула водорода. Если такой диэлектрик поместить во внешнее электрическое поле, то направления векторов сил, действующих на положительные и отрицательные заряды, будут противоположными. В результате молекула деформируется и превращается в диполь. При внесении диэлектрика в электрическое поле происходит его поляризация.

Поляризация диэлектрика – процесс смещения в противоположные стороны разноименных связанных зарядов, входящих в состав атомов и молекул вещества в электрическом поле.

Если диэлектрик неполярный, то в его молекулах происходит смещение положительных и отрицательных зарядов. На поверхности диэлектрика появятся поверхностные связанные заряды. Связанными эти заряды называют потому, что они не могут свободно перемещаться отдельно друг от друга.

Внутри диэлектрика суммарный заряд равен нулю, а на поверхностях заряды не скомпенсированы и создают внутри диэлектрика поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Это значит, что внутри диэлектрика поле имеет меньшую напряженность, чем в вакууме.

Физическая величина, равная отношению модуля напряженности электрического поля в вакууме к модулю напряженности электрического поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества:

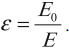
В полярном диэлектрике во внешнем электрическом поле происходит поворот диполей, и они выстраиваются вдоль линий напряженности.

Если внесенный в электрическое поле диэлектрик разрезать, то его части будут электрически нейтральны.

Электрическая емкость. Конденсатор

Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд.

Обозначение – ( C ), единица измерения в СИ – фарад (Ф).

Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел.

Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:

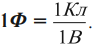
Формула для вычисления электроемкости:

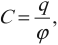
где ( q ) – заряд проводника, ( varphi ) – его потенциал.

Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится.

Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов.

Электроемкость конденсатора рассчитывается по формуле:

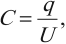
где ( q ) – модуль заряда одной из обкладок,
( U ) – разность потенциалов между обкладками.

Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками.

Плоский конденсатор представляет две параллельные пластины площадью ( S ), находящиеся на расстоянии ( d ) друг от друга.

Электроемкость плоского конденсатора:

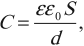
где ( varepsilon ) – диэлектрическая проницаемость вещества между обкладками,
( varepsilon_0 ) – электрическая постоянная.

На электрической схеме конденсатор обозначается:

Виды конденсаторов:

по типу диэлектрика – воздушный, бумажный и т. д.;
по форме – плоский, цилиндрический, сферический;
по электроемкости – постоянной и переменной емкости.

Конденсаторы можно соединять между собой.

Параллельное соединение конденсаторов

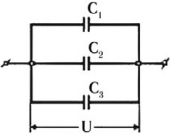
При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:

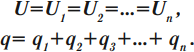
Общая емкость:

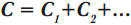
Последовательное соединение конденсаторов

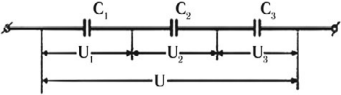
При последовательном соединении конденсаторов соединяют их разноименно заряженные обкладки.

Заряды конденсаторов при таком соединении равны:

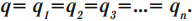
Общее напряжение:

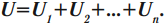
Величина, обратная общей емкости:

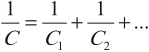
При таком соединении общая емкость всегда меньше емкостей отдельных конденсаторов.

Важно!
Если конденсатор подключен к источнику тока, то разность потенциалов между его обкладками не изменяется при изменении электроемкости и равна напряжению источника. Если конденсатор заряжен до некоторой разности потенциалов и отключен от источника тока, то его заряд не изменяется при изменении электроемкости.

Применение конденсаторов
Конденсаторы используются в радиоэлектронных приборах как накопители заряда, для сглаживания пульсаций в выпрямителях переменного тока.

Энергия электрического поля конденсатора

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Электрическая энергия конденсатора сосредоточена в пространстве между обкладками конденсатора, то есть в электрическом поле, поэтому ее называют энергией электрического поля. Формулы для вычисления энергии электрического поля:

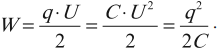
Так как напряженность электрического поля прямо пропорциональна напряжению, то энергия электрического поля конденсатора пропорциональна квадрату напряженности.

Плотность энергии электрического поля:

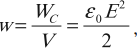
где ( V ) – объем пространства между обкладками конденсатора.

Плотность энергии не зависит от параметров конденсатора, а определяется только напряженностью электрического поля.

Основные формулы раздела «Электрическое поле»

Электрическое поле

2.9 (58.62%) 130 votes

Источник

Напряженность электрического поля

Напряженность электрического поля в данной точке пространства — это физическая величина равная отношению силы действующей на пробный заряд, помещённый в данную точку поля, к величине этого заряда. Напряжённость поля является векторной величиной.

E = F/Q
Где:
E — Напряжённость электрического поля
F — Сила, действующая на положительный точечный заряд
Q — Величина пробного заряда

Сила (F) измеряется в ньютонах (Н), заряд (Q) измеряется в кулонах (Кл), а напряжённость электрического поля (E) измеряется:

либо в ньютонах на кулон (Н/Кл),
либо в вольтах на метр (В/м).

Пример:

Какую силу (F) оказывает электрическое поле (E) равное 7,2 × 10^5 Н/Кл на точечный заряд −0,250 мкКл (микрокулонов)?

Формула: E = F/Q или F = Q × E

Q = −0,250 мкКл = − 0,250 ×10^(−6) Кл (отрицательное)

E = 7,2 × 10^5 Н/Кл

F = (0,250 ×10^(−6) Кл) × (7,2 × 10^5 Н/Кл) = 0,180 Н

Сила направлена противоположно направлению поля, т.к. Q является отрицательным.

Что такое электрическое поле?

Электрический заряд создаёт вокруг себя электрическое поле, оно действует с некой силой и на другие находящиеся вокруг него заряды. Электрическое поле может возникнуть и в веществе, и в вакууме, т.е. ему не нужна какая-либо специфическая среда.

Электростатическое поле можно изобразить в виде силовых линий (или линий напряжённости). Силовая линия — это воображаемая линия, проведённая таким образом, что касательная к ней в каждой точке поля указывает направление вектора напряжённости электрического поля в этой точке.

Изображение силовых линий

Что такое напряженность поля точечного заряда?

Напряженность поля точечного заряда определяется формулой:

E = (k × |Q|)/r²

Где:

k = 9×(10^9) (в единицах Н.м²/Кл²)

Q – заряд, создающий поле,

r – расстояние точки А от заряда Q

Пример:

Вычислите силу и направление электрического поля (E) от точечного заряда 2,00 нКл (нанокулонов) на расстоянии 5 мм от заряда.

Формула: E = (k × |Q|)/r²

Решение:

Q = 2 × 10^(−9) Кл

r = 5 × 10^(−3) м

Помним, что k = 9×(10^9) (в единицах Н.м²/ Кл²)

Значит:

E = (9×(10^9) Н.м²/ Кл²) × (2 × 10^(−9) Кл) / ((5 × 10^(−3) м)²) ≈ 7,19 × 10^5 Н/Кл

Вектор напряжённости

Векторы напряженности поля точечного заряда можно изобразить таким образом.

Вектор напряжённости в данной точке направлен вдоль прямой, соединяющей точку с зарядом, и важно учитывать, что:

направление зависит от q: от заряда при q > 0 и к заряду при q < 0;
удаляясь от заряда, модуль напряжённости поля убывает прямо пропорционально квадрату расстояния от точки до заряда.

Узнайте также про:

Магнитное поле Земли
Магнитную индукцию
Уравнения Максвелла
Закон сохранения энергии
Модуль Юнга
Резонанс
Энтропию

Источник

Содержание:

Определение и формула напряженности электрического поля
Принцип суперпозиции напряженностей электрических полей
Напряженность поля в диэлектрике
Напряженность поля точечного заряда
Связь напряженности и потенциала
Единицы измерения напряженности электрического поля
Примеры решения задач

Определение и формула напряженности электрического поля

Определение

Вектор напряженности $bar{E}$ – это силовая характеристика электрического поля. В некоторой точке поля, напряженность равна
силе, с которой поле действует на единичный положительный заряд, размещенный в указанной точке, при этом направление силы и напряженности
совпадают. Математическое определение напряженности записывается так:

$$bar{E}=frac{bar{F}}{q}$$

где $bar{F}$ – сила, с которой электрическое поле действует на
неподвижный, «пробный», точечный заряд q, который размещают в рассматриваемой точке поля. При этом считают, что «пробный» заряд
мал на столько, что не искажает исследуемого поля.

Если поле является электростатическим, то его напряженность от времени не зависит.

Если электрическое поле является однородным, то его напряженность во всех точках поля одинакова.

Графически электрические поля можно изображать при помощи силовых линий. Силовыми линиями (линиями напряженности) называют
линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности в этой точке поля.

Принцип суперпозиции напряженностей электрических полей

Если поле создано несколькими электрическими полями, то напряженность результирующего поля равна векторной сумме напряженностей отдельных полей:

$$bar{E}=sum_{i=1}^{n} bar{E}_{i}(2)$$

Допустим, что поле создается системой точечных зарядов и их распределение непрерывно, тогда результирующая напряженность находится как:

$$bar{E}=int d bar{E}(3)$$

интегрирование в выражении (3) проводят по всей области распределения заряда.

Напряженность поля в диэлектрике

Напряженность поля $bar{E}$ в диэлектрике равна векторной сумме
напряженностей полей, создаваемых свободными зарядами $bar{E}_0$ и
связанными (поляризационными зарядами) $bar{E}_p$:

$$bar{E}=bar{E}_{0}+bar{E}_{p}(4)$$

В том случае, если вещество, которое окружает свободные заряды однородный и изотропный диэлектрик, то напряженность
$bar{E}$ равна:

$$bar{E}=frac{bar{E}_{0}}{varepsilon}(5)$$

где $varepsilon$ – относительная диэлектрическая проницаемость вещества в исследуемой точке
поля. Выражение (5) обозначает то, что при заданном распределении зарядов напряженность электростатического поля в однородном изотропном
диэлектрике меньше, чем в вакууме в $varepsilon$ раз.

Напряженность поля точечного заряда

Напряженность поля точечного заряда q равна:

$$bar{E}=frac{1}{4 pi varepsilon varepsilon_{0}} frac{q}{r^{3}} bar{r}(6)$$

где $varepsilon_{0}=8,85 cdot 10^{-12}$ Ф/м (система СИ) – электрическая постоянная.

Связь напряженности и потенциала

В общем случае напряженность электрического поля связана с потенциалом как:

$$bar{E}=-operatorname{grad} varphi-frac{partial bar{A}}{partial t}(7)$$

где $varphi$ – скалярный потенциал,
$bar{a}$ – векторный потенциал.

Для стационарных полей выражение (7) трансформируется в формулу:

$$bar{E}=-operatorname{grad} varphi(8)$$

Единицы измерения напряженности электрического поля

Основной единицей измерения напряженности электрического поля в системе СИ является: [E]=В/м(Н/Кл)

Примеры решения задач

Пример

Задание. Каков модуль вектора напряженности электрического поля
$bar{E}$ в точке, которая определена радиус- вектором
$bar{r}_{2}=7 bar{i}+3 bar{j}$ (в метрах), если электрическое поле создает положительный точечный
заряд (q=1Кл), который лежит в плоскости XOY и его положение задает радиус вектор
$bar{r}_{1}=bar{i}-5 bar{j}$, (в метрах)?

Решение. Модуль напряжения электростатического поля, которое создает точечный заряд, определяется формулой:

$$E=frac{1}{4 pi varepsilon varepsilon_{0}} frac{q}{r^{2}}(1.1)$$

r- расстояние от заряда, создающего поле до точки в которой ищем поле.

$$bar{r}=bar{r}_{2}-bar{r}_{1}=6 bar{i}-8 bar{j}(1.2)$$

Из формулы (1.2) следует, что модуль $bar{r}$ равен:

$$r=|bar{r}|=sqrt{36+64}=10(mathrm{~m})$$

Подставим в (1.1) исходные данные и полученное расстояние r, имеем:

$$E=9 cdot 10^{9} frac{1}{100}=9 cdot 10^{7}left(frac{B}{m}right)$$

Ответ. $E=9 cdot 10^{7}left(frac{B}{m}right)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Запишите выражение для напряженности поля в точке, которая определена радиус – вектором
$bar{r}$, если поле создается зарядом, который распределен по объему V с плотностью
$rho=rho(r)$ .

Решение. Сделаем рисунок.

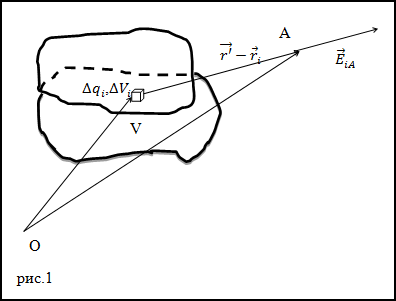
Проведем разбиение объема V на малые области с объемами
$Delta V_{i}$ заряды этих объемов
$Delta q_{i}$, тогда напряженность поля точечного заряда в точке А (рис.1) будет равна:

$$bar{E}_{i A}=frac{1}{4 pi varepsilon_{0}} frac{Delta q_{i}}{left|bar{r}^{prime}-bar{r}_{i}right|^{3}}left(bar{r}^{prime}-bar{r}_{i}right)(2.1)$$

Для того чтобы найти поле, которое создает все тело в точке А, используем принцип суперпозиции:

$$bar{E}_{A}=sum_{i=1}^{N} bar{E}_{i A}=frac{1}{4 pi varepsilon_{0}} sum_{i=1}^{N} frac{Delta q_{i}}{left|bar{r}^{prime}-bar{r}_{i}right|^{3}}left(bar{r}^{prime}-bar{r}_{i}right)(2.2)$$

где N – число элементарных объемов, на которые разбивается объем V.

Плотность распределения заряда можно выразить как:

$rholeft(bar{r}_{i}right)=frac{Delta q_{i}}{Delta V_{i}}(2.3)$

Из выражения (2.3) получим:

$Delta q_{i}=rholeft(bar{r}_{i}right) Delta V_{i}(2.4)$

Подставим выражение для элементарного заряда в формулу (2.2), имеем:

$$bar{E}_{A}=frac{1}{4 pi varepsilon_{0}} sum_{i=1}^{N} frac{rholeft(bar{r}_{i}right) Delta V_{i}}{left|bar{r}^{prime}-bar{r}_{i}right|^{3}}left(bar{r}^{prime}-bar{r}_{i}right)(2.5)$$

Так ка распределение зарядов задано непрерывное, то если устремить
$Delta V_i$ к нулю, то можно перейти от суммирования к интегрированию, тогда:

$$bar{E}_{A}=frac{1}{4 pi varepsilon_{0}} int_{V} frac{rho(bar{r})}{left|bar{r}^{prime}-bar{r}right|^{3}}left(bar{r}^{prime}-bar{r}right) d V$$

Ответ. $bar{E}_{A}=frac{1}{4 pi varepsilon_{0}} int_{V} frac{rho(bar{r})}{left|bar{r}^{prime}-bar{r}right|^{3}}left(bar{r}^{prime}-bar{r}right) d V$

Читать дальше: Формула пути.

Источник

Что такое электрическое поле

Определение напряженности электрического поля

Единицы измерения и формулы

Принцип суперпозиции

Напряженность поля точечного заряда

Закон Кулона

Линии напряженности

Напряжённость электрического поля в классической электродинамике[править | править код]

Сила воздействия электромагнитного поля на заряженные частицы[править | править код]

Уравнения Максвелла[править | править код]

«Материальные уравнения»[править | править код]

Связь с потенциалами[править | править код]

Электростатика[править | править код]

Теорема Гаусса[править | править код]

Напряжённость электрического поля точечного заряда[править | править код]

Электрическое поле произвольного распределения зарядов[править | править код]

Системы единиц[править | править код]

Измерение напряженности электрического поля[править | править код]

Литература[править | править код]

Примечания[править | править код]

См. также[править | править код]

Электрическое поле

Электризация тел

Взаимодействие зарядов. Два вида зарядов

Закон сохранения электрического заряда

Закон Кулона

Действие электрического поля на электрические заряды

Напряженность электрического поля

Принцип суперпозиции электрических полей

Потенциальность электростатического поля

Потенциал электрического поля. Разность потенциалов

Проводники в электрическом поле

Диэлектрики в электрическом поле

Электрическая емкость. Конденсатор

Энергия электрического поля конденсатора

Основные формулы раздела «Электрическое поле»

Что такое электрическое поле?

Что такое напряженность поля точечного заряда?

E = (k × |Q|)/r²

Вектор напряжённости

Определение и формула напряженности электрического поля

Принцип суперпозиции напряженностей электрических полей

Напряженность поля в диэлектрике

Напряженность поля точечного заряда

Связь напряженности и потенциала

Единицы измерения напряженности электрического поля

Примеры решения задач

Вам также может понравиться

Как найти серьги по артикулу 585 золотой

Сталкер тень чернобыля как найти секретную дверь

Как найти количество моль меди

Добавить комментарий Отменить ответ