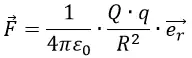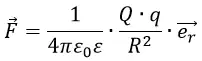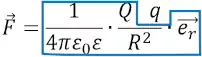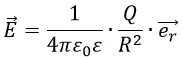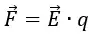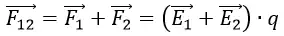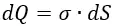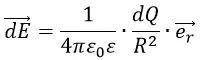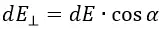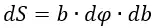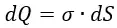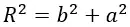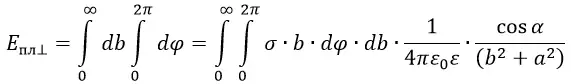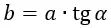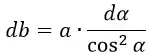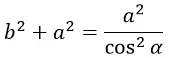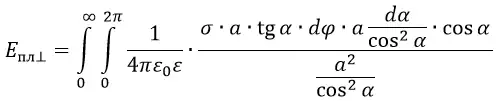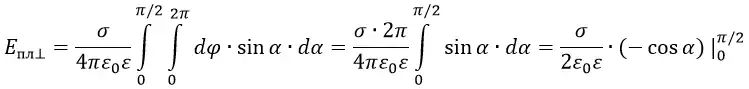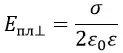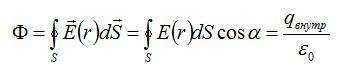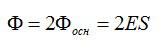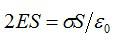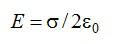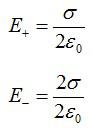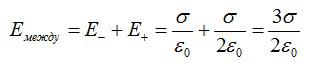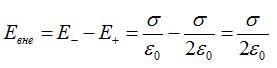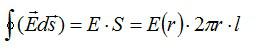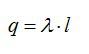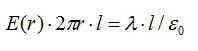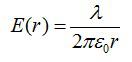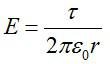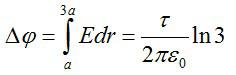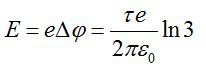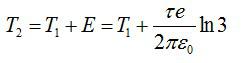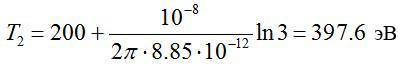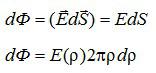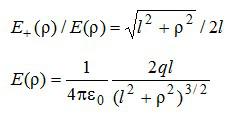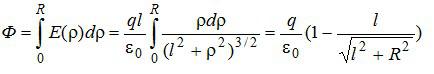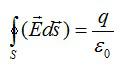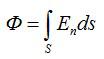Где ε0 – диэлектрическая проницаемость вакуума;
R – расстояние между двумя зарядами Q и q;
Q и q – величины электрических зарядов;
er – единичный вектор, направленный по линии зарядов.
Если два электрических заряда Q и q помещены не в вакуум, в пространство с веществом, то к формуле добавляется относительная диэлектрическая проницаемость ε, которая отличает проводящие свойства какого-либо вещества от вакуума. ε является безразмерной константой.
В данной формуле можно выделить часть, которая не зависит от пробного заряда q:
Обозначим её буквой E:
Она носит название «напряжённость электрического поля». Из определения следует, что напряжённость поля не зависит от величины пробного заряда q, помещённого в точку. Напряжённость электрического поля определяется однозначно исходным зарядом Q, а также расстоянием R до точки, то есть геометрией пространства.
В таком случае сила кулона F будет равна:
Эта формула применима для любого точечного заряда.
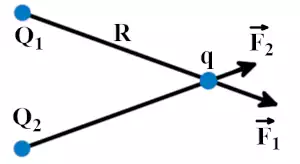
Электрическое поле обладает свойством суперпозиции. Если есть несколько электрических зарядов Q1 и Q2, то каждый заряд взаимодействует с точечными силами F1 и F2, и общая сила складывается по правилу сложения векторов.
В такой ситуации можно написать:
F12 – суммарная сила.
Из формулы можно увидеть, что напряжённость электрического поля складывается. Этот факт называется принципом суперпозиции электрического поля, и он будет использован для расчёта сложной системы электрических зарядов, то есть зарядов, распределённых по плоскости.
Расчёт напряжённости электрического поля плоской пластины
Постановка задачи: имеется бесконечная плоская пластина с определённой плотностью заряда σ. Выделим на ней площадку dS. Заряд dQ площадки dS будет равен:
Будем считать, что плоская пластина равномерно заряжена и σ не зависит от координат.
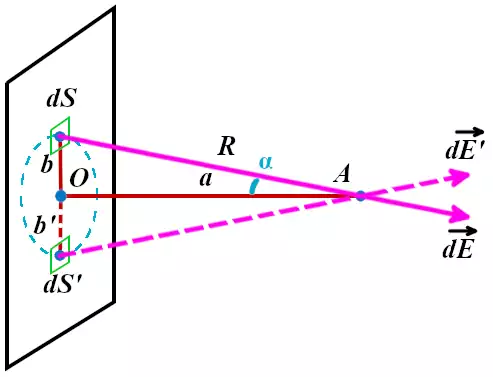
Посчитаем напряжённость электрического поля всей плоской пластины в точке A, находящейся на удалении a от этой пластины: E(A)=?
Для примера возьмём на плоской пластине небольшую площадку площадью dS на удалении b от центра. Обладая электрическим зарядом dQ, эта площадка создаёт электрическое поле с напряжённостью dE в точке A по закону Кулона.
На расстоянии b‘, равному расстоянию b, будет находится площадка dS‘, которая будет создавать электрическое поле с напряжённостью dE‘, равное по величине напряжённости поля dE, но направленное под другим углом. При сложении двух этих полей сумма расположенных параллельно пластине составляющих их векторов будет равны нулю. В связи с этим нам нужно учитывать только составляющую, расположенную перпендикулярно поверхности плоской пластины.
Обозначим угол между напряжённостью поля dE и перпендикуляром к пластине через α. Тогда интересующая нас составляющая dE⊥ будет равна:
Точно такую же составляющую будут создавать все точки на плоской пластине, находящиеся на удалении b от точки O. Это связано с тем, что расстояния от них до точки A, а также углы между перпендикуляром и напряжённостями электрического поля будут такими же.
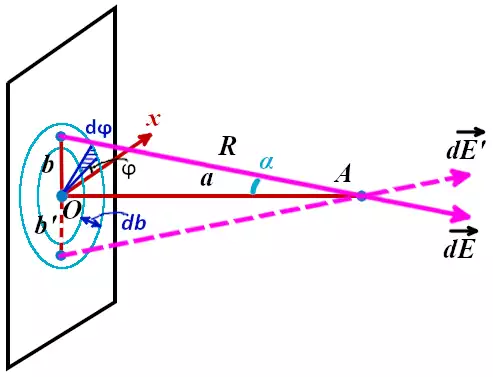
Выделим окружность радиусом b и толщиной db на плоской пластине. В полученном кольце рассмотрим элемент, расположенный под углом ϕ к оси x. Элемент вырезается из кольца в виде сегмента с размером dϕ. При малости dϕ и при малости db этот участок плоской пластины можно считать квадратом. В таком случае площадь dS будет равна:
Заряд dQ равен:
Полную напряжённость электрического поля кольца можно посчитать путём интегрирования по ϕ. А полное поле всей пластины можно посчитать путём интегрирования всех колец по b от 0 до ∞.
Для вычисления интеграла сделаем замену переменных и выразим всё через угол α. В этом случае получим:
В данной формуле сокращаем cos2α и a. Интеграл от 0 до ∞ выразится в интеграл от 0 до π/2.
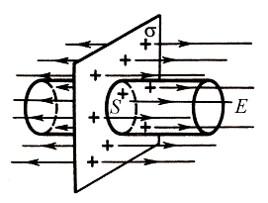
Физический смысл этой формулы состоит в том, что напряжённость электрического поля около равномерно заряженной плоской пластины не зависит от расстояния до этой пластины.
Для школьников.
Получена формула для напряжённости электрического поля плоского конденсатора, широко применяемого в электрических цепях. Для этого надо применить теорему Гаусса и найти сначала формулу напряжённости для одной заряженной пластины, а затем для параллельных заряженных пластин.
Итак, рассмотрена теорема Гаусса и её применение для получения формул нахождения напряжённости электростатических полей, создаваемых протяжёнными заряженными телами. По ходу найдено выражения для напряжённости электрического поля плоского конденсатора.
Подумайте над решением следующих задач:
1. К вертикальной равномерно заряженной пластине с плотностью заряда 4 10 -7 Кл/м2 прикреплена нить. На нити подвешен заряженный шарик массой 1 г. Знаки заряда пластины и шарика одинаковы. Найти заряд шарика, если нить образует с вертикалью угол 30 градусов. Ответ: 2,5 10 -7 Кл
2. Электрон влетает в плоский горизонтально расположенный конденсатор длиной 5 см. При вылете из конденсатора электрон отклоняется от своего первоначального направления на 2 мм. Напряжённость электрического поля внутри конденсатора 20 кВ/м. Какую скорость и кинетическую энергию имел электрон перед влётом в конденсатор? Ответ: 4,7 10 7 м/с; 10 -15 Дж.
Отвечаю на вопрос о напряжённости электрического поля, создаваемого заряженной пластинкой конечных размеров:
На рисунке ниже показана тонкая заряженная пластинка конечных размеров и силовые линии электрического поля, создаваемого ею.
В этом случае полученная формула для напряжённости поля, создаваемого бесконечной заряженной плоскостью, справедлива только для точек, расположенных внутри области, ограниченной пунктирной линией.
В других точках, расположенных всё дальше от пластинки и всё ближе к её краям, будет всё более отличаться от поля, создаваемого бесконечной заряженной плоскостью.
На расстояниях значительно больших размера пластинки электрическое поле можно рассматривать как поле точечного заряда (заряд пластинки принимается за точечный заряд).
Занятие 6. Дифференцирование. Интегрирование.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: решение задач к занятию 47.
Следующая запись: Как поведёт себя электрон, влетевший в электрическое поле плоского конденсатора?
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия, начиная с электростатики, даны в Занятии 45.
В этой статье мы будем использовать закон Гаусса для расчета электрического поля между двумя пластинами и электрического поля конденсатора.
Электрическое поле между двумя пластинами:
Компания электрическое поле электрическое свойство, связанное с любым зарядом в космосе. Таким образом, электрическое поле – это любая физическая величина, которая принимает разные значения электрической силы в разных точках данного пространства.
Электрическое поле – это область или область, в каждой точке которой действует электрическая сила.
В общих чертах электрические поля можно описать как электрическую силу на единицу заряда.
Если мы рассмотрим бесконечную плоскость, имеющую однородный заряд на единицу площади, т. Е., То для бесконечной плоскости электрическое поле может быть задано как:
Давайте посмотрим на электрическое поле, когда задействованы две заряженные пластины.
Между двумя заряженными пластинами существует однородное электрическое поле:
Согласно закону Кулона электрическое поле вокруг точечного заряда уменьшается по мере удаления от него. Однако однородное электрическое поле может быть создано путем выравнивания двух бесконечно больших проводящих пластин параллельно друг другу.
«Если в каждой точке данного пространства напряженность электрического поля остается неизменной, то электрическое поле называется однородным электрическим полем».
Силовые линии однородного электрического поля стремятся быть параллельны друг другу, и расстояние между ними также равно.
Параллельные силовые линии и однородное электрическое поле между двумя параллельными пластинами обеспечивают одинаковую силу притяжения и отталкивания испытательного заряда независимо от того, где он находится в поле.
Линии поля всегда проходят от областей с высоким потенциалом к областям с низким потенциалом.
Направление электрического поля между двумя пластинами:
Электрическое поле распространяется от положительно заряженной пластины к отрицательно заряженной.
Например, предположим, что верхняя пластина положительна, а нижняя пластина отрицательна, тогда направление электрического поля задается, как показано на рисунке ниже.

Положительные и отрицательные заряды ощущают силу под действием электрического поля, но ее направление зависит от тип заряда, положительный или отрицательный. Положительные заряды воспринимают силы в направлении электрического поля, тогда как отрицательные заряды ощущают силы в противоположном направлении..
Электрическое поле между двумя параллельными пластинами одного заряда:
Предположим, у нас есть две бесконечные пластины, которые параллельны друг другу и имеют положительную плотность заряда. Теперь мы вычисляем чистое электрическое поле, создаваемое этими двумя заряженными параллельными пластинами.

Оба электрических поля противостоят друг другу в центре двух пластин. В результате они нейтрализуют друг друга, что приводит к нулевому электрическому полю внутри.
∴Ein = 0
Оба электрических поля направлены в одном направлении вне пластин, то есть слева и справа. Таким образом, его векторная сумма будет? /? 0.
Eout = E1 + E2
Электрическое поле между двумя параллельными пластинами противоположного заряда:
Предположим, у нас есть две пластины с плотностями заряда + ර и -ර. Расстояние d разделяет эти две пластины.
Пластина с положительной плотностью заряда создает электрическое поле E = ර / 2 ε0. И направление его – наружу или от пластины, в то время как пластина с отрицательной плотностью заряда имеет противоположное направление, то есть направление внутрь.
Итак, когда мы используем принцип суперпозиции с обеих сторон пластин, снаружи и внутри пластин, то мы можем видеть, что вне пластины оба вектора электрического поля имеют одинаковую величину и противоположное направление, и, таким образом, оба электрических поля компенсируют друг друга. . Так, вне пластин не будет электрического поля.
∴Eвых=0
Поскольку они поддерживают друг друга в одном направлении, чистое электрическое поле между двумя пластинами составляет E = ර / ε0.
Eв = E1 + E2
Это тот факт, что мы используем для формирования конденсатора с параллельными пластинами.
Электрическое поле между двумя пластинами задано напряжением:
В физике для описания любого распределения заряда используется либо разность потенциалов ΔV, либо электрическое поле E. Разность потенциалов ΔV тесно связана с энергией, а электрическое поле E связано с силой.
E – векторная величина, подразумевая, что она имеет как величину, так и направление, тогда как ΔV – это скалярная переменная без направления.
Когда между двумя проводящими пластинами, параллельными друг другу, подается напряжение, создается однородное электрическое поле.
Сила электрического поля прямо пропорциональна приложенному напряжению и обратно пропорциональна расстоянию между двумя пластинами.
Электрическое поле между двумя параллельными пластинчатыми конденсаторами:
Параллельный пластинчатый конденсатор:
Конденсатор с параллельными пластинами состоит из двух проводящих металлических пластин, которые соединены параллельно и разнесены на определенное расстояние. Диэлектрическая среда заполняет зазор между двумя пластинами.
Диэлектрическая среда представляет собой изолирующий материал, и это может быть воздух, вакуум или некоторые непроводящие материалы, такие как слюда, стекло, электролитический гель, бумажная вата и т. Д. Диэлектрический материал препятствует прохождению тока через него из-за своего непроводящего свойства.
Однако при приложении напряжения к параллельным пластинам атомы диэлектрической среды поляризуются под действием электрического поля. В процессе поляризации образуются диполи, и эти положительные и отрицательные заряды будут накапливаться на пластинах конденсатора с параллельными пластинами. По мере накопления зарядов через конденсатор течет ток, пока разность потенциалов между двумя параллельными пластинами не уравняется с потенциалом источника.
Напряженность электрического поля конденсатора не должна превышать напряженность поля пробоя диэлектрического материала в конденсаторах с параллельными пластинами. Если рабочее напряжение конденсатора превышает его предел, пробой диэлектрика вызывает короткое замыкание между пластинами, немедленно разрушая конденсатор.
Таким образом, чтобы защитить конденсатор от такой ситуации, не следует превышать предел приложенного напряжения и выбирать диапазон напряжения конденсаторов.
Электрическое поле между параллельными пластинами конденсатора:
На следующем рисунке показан конденсатор с параллельными пластинами.
В этом случае мы возьмем две большие проводящие пластины, параллельные друг другу, и разделим их на d. Зазор заполнен диэлектрической средой, как показано на рисунке. Расстояние d между двумя пластинами значительно меньше площади каждой пластины. Поэтому мы можем написать d <
Здесь плотность заряда 1-й пластины составляет +, а плотность заряда 2-й пластины -ර. Пластина 1 имеет общий заряд Q, а пластина 2 имеет общий заряд -Q.
Как мы видели ранее, когда взяты две параллельные пластины с противоположным распределением заряда, электрическое поле во внешней области будет равно нулю.
В результате чистое электрическое поле в центре конденсатора с параллельными пластинами можно рассчитать следующим образом:
E = E1 + E2
= ර / 2 ε + ර / 2 ε
= ර / ε
Где ර – поверхностная плотность заряда пластины
ε – диэлектрическая проницаемость диэлектрического материала, используемого для формирования конденсаторов.
Из приведенного выше уравнения мы можем сказать, что диэлектрическая среда вызывает уменьшение напряженности электрического поля, но она используется для увеличения емкости и поддержания контакта проводящих пластин.
Величина электрического поля между двумя заряженными пластинами:
Если принять во внимание две бесконечно большие пластины, напряжение не подается, то величина электрического поля согласно закону Гаусса должна быть постоянной. Но электрическое поле между двумя пластинами, как мы заявляли ранее, зависит от плотности заряда пластин.
Следовательно, если две пластины имеют одинаковые плотности заряда, то электрическое поле между ними равно нулю, а в случае противоположных плотностей заряда электрическое поле между двумя пластинами задается постоянным значением.
Когда заряженным пластинам подается напряжение, величина электрического поля определяется разностью потенциалов между ними. Более высокая разность потенциалов создает сильное электрическое поле, а большее расстояние между пластинами приводит к слабому электрическому полю.
Таким образом, расстояние между пластинами и разность потенциалов являются важными факторами напряженности электрического поля.
Часто задаваемые вопросы:
Q. Чем электрическое поле между параллельными пластинами отличается от электрического поля вокруг заряженной сферы?
Ответ Электрические поля между параллельными пластинами и вокруг заряженной сферы неодинаковы. Посмотрим, как они различаются.
Электрическое поле между параллельными пластинами зависит от плотности заряда пластин. Если они заряжены противоположно, то поле между пластинами / ε0, а если у них есть заряды, то поле между ними будет равно нулю.
Вне заряженной сферы электрическое поле определяется выражением тогда как поле внутри сферы равно нулю. В этом случае r представляет собой расстояние между точкой и центром.
В. Что произойдет с электрическим полем и напряжением, если расстояние между пластинами конденсатора увеличится вдвое?
Ответ E = ර / ε0 определяет электрическое поле между конденсаторами с параллельными пластинами по закону Гаусса.
Согласно закону Гаусса электрическое поле остается постоянным, поскольку оно не зависит от расстояния между двумя пластинами конденсатора. Если говорить о разности потенциалов, она прямо пропорциональна расстоянию между двумя пластинами конденсатора и определяется выражением
Таким образом, если расстояние увеличивается вдвое, то увеличивается и разность потенциалов.
В. Как рассчитать электрическое поле в конденсаторе с параллельными пластинами?
Ответ В конденсаторах с параллельными пластинами обе пластины заряжены противоположно. Таким образом, электрическое поле вне пластин будет нейтрализовано.
Обе пластины заряжены противоположно, поэтому поле между пластинами будет поддерживать друг друга. Кроме того, между двумя пластинами присутствует диэлектрическая среда, поэтому диэлектрическая проницаемость диэлектрика также будет важным фактором.
Закон Гаусса и концепция суперпозиции используются для расчета электрического поля между двумя пластинами.
Е = Е1 + Е2
=
=
Где ර – поверхностная плотность заряда
ε – диэлектрическая проницаемость диэлектрического материала.
Q. Почему электрическое поле между пластинами конденсаторов уменьшается при введении диэлектрической пластины? Объясните с помощью схемы.
Ответ Когда диэлектрический материал помещается между параллельными пластинами конденсатора под действием внешнего электрического поля, атомы диэлектрического материала поляризуются.
Накопление заряда на обкладках конденсатора вызвано индуцированным зарядом в диэлектрическом материале. Как показано на рисунке ниже, это накопление заряда вызывает электрическое поле между двумя пластинами, которое сопротивляется внешнему электрическому полю.
На приведенном выше рисунке показана диэлектрическая пластина между двумя пластинами конденсатора, поскольку диэлектрическая пластина индуцирует противоположное электрическое поле; следовательно, чистое электрическое поле между пластинами конденсатора уменьшается.
Q. Две идентичные металлические пластины получают положительный заряд Q1 и Q2 соответственно. Если их соединить вместе, чтобы сформировать конденсатор с параллельными пластинами с емкостью C, разность потенциалов между ними составит …… ..
Ответ Емкость конденсатора с параллельными пластинами, который состоит из двух одинаковых металлических пластин, рассчитывается следующим образом:
Где C – емкость конденсатора с параллельными пластинами.
A – площадь каждой пластины
d – расстояние между параллельными пластинами
Скажем, плотность поверхностного заряда равна
Теперь чистое электрическое поле можно определить как
Возможная разница представлена,
Таким образом, подставляя указанные выше значения в это уравнение, мы получаем разность потенциалов
В. Что происходит, когда между параллельными пластинами конденсатора вводится диэлектрический материал?
Ответ Электрическое поле, напряжение и емкость изменяются, когда мы вводим диэлектрический материал между параллельными пластинами конденсатора.
Электрическое поле падает, когда диэлектрический материал вводится между параллельными пластинами конденсатора из-за накопления заряда на параллельных пластинах, что создает электрическое поле в направлении, противоположном внешнему полю.
Электрическое поле определяется выражением
Электрическое поле и напряжение пропорциональны друг другу; таким образом, напряжение также уменьшается.
С другой стороны, емкость конденсатора увеличивается, поскольку она пропорциональна диэлектрической проницаемости диэлектрического материала.
В. Существует ли магнитное поле между пластинами конденсатора?
Ответ Магнитные поля существуют между двумя пластинами только тогда, когда электрическое поле между двумя пластинами изменяется.
Таким образом, когда конденсатор заряжается или разряжается, электрическое поле между двумя пластинами изменяется, и только в это время существует магнитное поле.
В. Что происходит, когда сильное электрическое поле сохраняется в очень маленькой области пространства? Есть ли предел емкости?
Ответ Конденсаторы – это электрические устройства, которые используют постоянное электрическое поле для хранения электрических зарядов в виде электроэнергия. Между пластинами конденсатора лежит диэлектрический материал.
Если приложенное внешнее электрическое поле превышает напряженность поля пробоя диэлектрического материала, то изолирующий диэлектрический материал становится проводящим. Электрический пробой приводит к возникновению искры между двумя пластинами, которая разрушает конденсатор.
Каждый конденсатор имеет разную емкость в зависимости от используемого диэлектрического материала, площади пластин и расстояния между ними.
Допуск конденсатора находится где-то между в
рекламируемой стоимости.
В. Каковы применения закона Гаусса?
Ответ Закон Гаусса имеет различные приложения.
В некоторых случаях расчет электрических полей требует жесткого интегрирования и становится довольно сложным. Мы используем закон Гаусса, чтобы упростить оценку электрических полей без сложного интегрирования.
- Электрическое поле на расстоянии r в случае бесконечно длинной проволоки E =? / 2? Ε0
Где ? – линейная плотность заряда проволоки.
- Напряженность электрического поля почти бесконечного плоского листа E = ර / 2 ε0
- Напряженность электрического поля на внешней поверхности сферической оболочки равна
и E = 0 внутри оболочки.
- Напряженность электрического поля между двумя параллельными пластинами E = / ε0, когда диэлектрическая среда находится между двумя пластинами, тогда E = / ε.
В. Формула для емкости с параллельными пластинами:
Ответ Поддерживая электрическое поле, конденсаторы используются для хранения электрических зарядов в электрической энергии.
Когда пластины разделены воздухом или пространством, формула конденсатора с параллельными пластинами выглядит так:
, Где C – емкость конденсатора.
Электрическое поле заряженной пластины
Пример 2.9.
Область
пространства, ограниченная двумя
параллельными друг другу бесконечными
плоскостями, расположенными на расстоянии
2а
друг от друга, заряжена однородно по
объему с плотностью .
Используя формулировку электростатической
теоремы Гаусса, покажите, что
Ось Х
перпендикулярна упомянутым бесконечным
плоскостям, а точка х
= 0 выбрана в центре
слоя. Зависимость Ex(x)
представьте графически.
Решение.
В силу симметрии
распределения заряда, линии напряженности
перпендикулярны рассматриваемому слою
и направлены от центральной плоскости
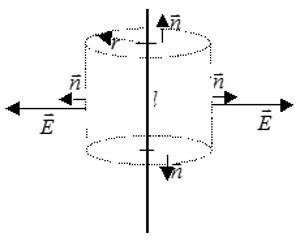
слоя в обе стороны. Поэтому в качестве
замкнутой гауссовой поверхности
построим цилиндр, основания которого
параллельны и симметричны плоскости,
соответствующей положению x=0
заряженного слоя, а ось перпендикулярна
ему. Согласно теореме Гаусса:
.
Так как образующие
цилиндра параллельны линиям напряженности
,
то поток вектора напряженности сквозь
боковую поверхность цилиндра равен
нулю. А полный поток через гауссову
поверхность равен сумме потоков через
его основания, то есть равен
.
Используя теорему Гаусса, найдем
напряженность электрического поля вне
и внутри заряженного слоя.
При
заряд, заключенный внутри цилиндрической
поверхности, равен,
поэтому напряженность электрического
поля внутри слоя равна.
При
заряд, заключенный внутри цилиндрической
поверхности, равен,
поэтому напряженность электрического
поля снаружи слоя равна.
График
напряженности проекциипоказан на Рис.8.
|
|
|
Рис.8 |
Электрическое поле заряженной нити
Пример 2.10.
Вычислить напряженность электрического
поля бесконечно тонкой и бесконечно
длинной прямолинейной нити, однородно
заряженной электричеством с линейной
плотностью l.
Решение.
Найдем напряженность электрического
поляс
помощью теоремы Гаусса. Наличие осевой
симметрии в распределении заряда,
позволяет сделать вывод о том, что векторнаправлен радиально к линии заряда или
от нее, в зависимости от знака заряда.
Ввиду той же симметрии величинаЕможет зависеть только от расстояния до
заряженной нити
Е =Е( r ).
Для определения этой зависимости выберем
гауссову поверхность следующим образом.
Построим цилиндр с боковой поверхностью
удаленной от нити на расстояние rи
основаниями, перпендикулярными к нити
(Рис.9а). Поток векторачерез оба основания цилиндра равен
нулю, т.к..
Поток через боковую поверхность равенЕ× S, т.к.,S– площадь боковой поверхности.
Поэтому полный поток через выбранную
Гауссову поверхность равен.
Заряд нити внутри рассматриваемой
поверхности равен заряду отрезка нити
длиной l:
Применяя теорему Гаусса, получим
соотношение:
,
откуда найдем
.
График зависимости представлен на
Рис.9б.
|
|
|
|
Рис.9а |
Рис.9б |
Электрическое поле заряженного цилиндра
Пример 2.11.
Поверхность бесконечного длинного
кругового цилиндра заряжена однородно
с линейной плотностью λ. Определите
напряженность электрического поля
внутри и вне цилиндра. Полученный
результат представьте на графике,
где–
проекция вектора напряженности на осьr, перпендикулярную
поверхности цилиндра, с началом отсчета
на его оси симметрии.
Решение.
Наличие осевой симметрии в распределении
заряда, позволяет сделать вывод о том,
что вектор
направлен радиально – к линии оси цилиндра
или от нее, в зависимости от знака заряда.
Ввиду той же симметрии величина
напряженности может зависеть только
от расстояния до оси цилиндра:
Е = Е ( r ).
Для определения этой зависимости выберем
гауссову поверхность следующим образом.
Построим цилиндр с боковой поверхностью
удаленной от оси на расстояние
и
основаниями, перпендикулярными к оси
цилиндра. Поток векторачерез оба основания цилиндра равен
нулю, т.к..
Поток через боковую поверхность равенЕ× S, т.к.,
S- площадь боковой поверхности. Из теоремы
Гаусса следует:
Для величины проекции
получим:
,
еслиr<R,
,
если>R.
График этой зависимости, представленный
на Рис.10, характеризуется скачком
величины напряженности при
,
что отражает идеализацию распределения
заряда на геометрической поверхности.
|
|
|
Рис.10 |
Пример 2.12.
Область внутри бесконечного длинного
кругового прямого цилиндра радиуса Rзаряжена однородно с объемной плотностьюρ. Определите напряженность
электрического поля внутри и вне
цилиндра. Полученный результат представьте
на графике,
где–
проекция вектора напряженности на осьr, перпендикулярную
поверхности цилиндра, с началом отсчета
на его оси симметрии.
Решение.
Наличие осевой симметрии в распределении
заряда, позволяет сделать вывод о том,
что вектор
направлен радиально – к линии оси
распределения заряда или от нее, в
зависимости от знака заряда. Ввиду той
же симметрии величина Е может зависеть
только от расстояния до оси:
Е = Е ( r )
Для определения этой зависимости выберем
гауссову поверхность следующим образом
. Построим цилиндр с боковой поверхностью
удаленной от нити на расстояние r
и основаниями, перпендикулярными к
нити. Высота цилиндра.
Поток векторачерез оба основания цилиндра равен
нулю, т.к..
Поток через боковую поверхность равенЕ× S, т.к.,
S- площадь боковой поверхности. Из теоремы
Гаусса следует:
Для величины проекции
получим:
при
при
.
График, представленный на Рис.11
характеризуется отсутствием скачка
величины напряженности поля при r=Rв отличие от случая распределения заряда
на поверхности цилиндра.
|
|
|
Рис.11 |
|
Дифференциальная форма теоремы
Пример
В некоторой Решение.
Плотность |
Пример 2.14
Вычислите
дивергенцию напряженности
электрического поля точечного заряда
в произвольной точке пространства в
декартовой системе координат.
Решение.
Локальная форма
теоремы Гаусса позволяет выразить
дивергенцию напряженности электрического
поля через локальную плотность
распределения заряда по соотношению
.
Плотность объемного распределения
точечного заряда равна нулю в любой
точке вне заряда. Следовательно,,
при.
Конечно же, этот результат можно получить
и прямым расчетом:
так
как=
,
=
,
=
39
Соседние файлы в папке Книга Калашникова
- #
- #
- #
- #
- #
- #
- #
- #
Теорема Гаусса выражает связь между потоком вектора напряженности электрического поля через замкнутую поверхность и алгебраической суммой зарядов, заключенных в объеме, ограниченном этой поверхностью. О примерах использования теоремы Гаусса на практике поговорим в этой статье.
Присоединяйтесь к нам в телеграме, чтобы не только решать задачи, но и быть в курсе актуальных новостей для студентов всех специальностей.
Задачи на теорему Гаусса с решением
Если вам нужно сначала освежить теоретические знания, читайте подробную теорию по теореме Гаусса в нашем справочнике. Ну а перед решением задач не забудьте повторить памятку и на всякий случай держите под рукой полезные формулы.
Кстати, при решении задач на теорему Гаусса придется довольно часто брать интегралы. Хотите научиться делать это по-быстрому? У нас уже есть отдельная статья и видео на эту тему.
Задача на теорему Гаусса №1: напряженность поля плоскости
Условие
Определите напряженность поля бесконечной заряженной плоскости. Поверхностная плотность заряда сигма.
Решение
Линии напряженности перпендикулярны рассматриваемой плоскости и направлены в обе стороны от неё. Выберем в качестве гауссовой поверхности цилиндр с основанием, параллельным плоскости:
По теореме Гаусса:
Поток сквозь цилиндр равен сумме потоков сквозь боковую поверхность цилиндра и потокам сквозь оба его основания. Поток сквозь боковую поверхность равен нулю, так как линии напряженности параллельны ей:
Согласно теореме Гаусса:
Отсюда:
Ответ: см. выше.
Задача на теорему Гаусса №2: напряженность поля двух пластин
Условие
Электрическое поле создано двумя параллельными заряженными тонкими пластинами с поверхностными плотностями заряда + сигма и -2 сигма. Площадь каждой пластины S, расстояние между пластинами d можно считать значительно меньшим их продольных размеров. Какова напряженность электрического поля, созданного этими пластинами?
Решение
Для электрического поля действует принцип суперпозиции: результирующее поле равно векторной сумме отдельных полей каждой пластины. Из предыдущей задачи мы знаем формулу, по которой вычисляется напряженность поля тонкой заряженной пластины, запишем для каждой из них:
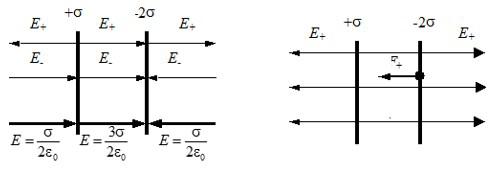
Векторы напряженности между пластинами совпадают по направлению, результирующая напряженность равна:
Справа и слева от пластин, во внешней области, векторы направлены в разные стороны:
Для наглядности приведем рисунок:
Ответ: см. выше.
Задача на теорему Гаусса №3: напряженность электрического поля бесконечной нити
Условие
Определить напряженность электрического поля, создаваемую бесконечной тонкой нитью, равномерно заряженной с линейной плотностью заряда лямбда.
Решение
Напряженность будем искать при помощи теоремы Гаусса. Наша задача – определить зависимость напряженности от расстояния от нити. В качестве поверхности выберем цилиндр с боковыми стенками, параллельными нити. Будем учитывать только поток вектора напряженности через боковую поверхность, так как поток через основания цилиндра равен нулю:
Заряд нити внутри рассматриваемой поверхности равен заряду отрезка нити длиной l:
По теореме Гаусса:
Отсюда:
Ответ: см. выше.
Задача с применением теоремы Гаусса №4
Условие
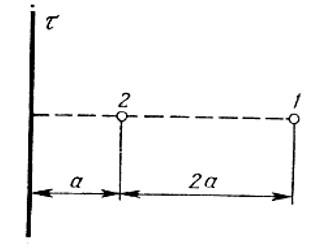
Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределённым зарядом (τ = 10 нКл/м). Определить кинетическую энергию Т2 электрона в точке 2, если в точке 1 его кинетическая энергия Т1 = 200 эВ. Расстояние точки 2 от линии равно а = 0,5 см, точки 1 – b=1,5 см.
Решение
Ранее рассмотренные задачи были примерами вычисления полей с помощью теоремы Гаусса. Теперь рассмотрим задачу, которая решается сиспользованием этой информации. Из предыдущей задачи возьмем выражение для напряженности поля заряженной нити:
Разность потенциалов поля в двух точках будет равна:
При прохождении этой разницы потенциалов электрон приобретёт кинетическую энергию:
Конечная энергия частицы будет равна:
Получим:
Ответ: 397.6 эВ.
Задача на теорему Гаусса №5: поток электрического поля
Условие
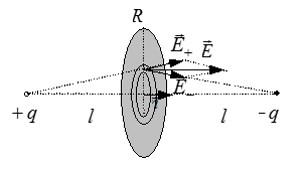
Два точечных заряда q и –q расположены на расстоянии 2l друг от друга. Найти поток вектора напряженности через круг радиуса R. Плоскость круга проходит через его середину и перпендикулярна отрезку прямой, соединяющей заряды.
Решение
Рассмотрим элементарный поток результирующего электрического поля через бесконечно малую кольцевую зону круга:
В записи потока учтено, что вектор напряженности перпендикулярен поверхности круга. Выразим напряженность электрического поля через «ро», используя подобие треугольников, показанных на рисунке:
Вычисление потока сводится к взятию интеграла:
Ответ: см. выше.
Примеры применения теоремы Гаусса можно найти не только в электростатике, но и в других областях физики.
Вопросы на теорему Гаусса
Вопрос 1. Сформулируйте теорему Гаусса.
Ответ. Теорема Гаусса гласит:
Поток вектора напряженности электростатического поля через замкнутую поверхность равен алгебраической сумме зарядов внутри поверхности, деленной на эпсилон нулевое (электрическую постоянную).
Вопрос 2. Что такое поток вектора напряженности?
Ответ. Поток вектора напряженности – скалярная физическая величина, определяемая как число линий вектора напряженности, пронизывающих некоторую поверхность S. Поток напряженности электрического поля через поверхность S конечного размера определяется как алгебраическая сумма элементарных потоков:
Вопрос 3. Что такое силовые линии напряженности?
Ответ. Это линии, с помощью которых используются для графического представления поля:
- касательная к силовой линии в каждой точке пространства направлена вдоль вектора поля;
- густота силовых линий пропорциональна напряженности поля в данной точке;
- поток вектора напряженности пропорционален числу силовых линий, пронизывающих поверхность.
Вопрос 4. Где начинаются и где заканчиваются силовые линии?
Ответ. Силовые линии начинаются и заканчиваются на зарядах, оставаясь непрерывными в пустом пространстве.
Вопрос 5. Верно ли утвержление: теорема Гаусса справедлива только для неподвижных зарядов.
Ответ. Нет, так как заряд частицы не зависит от ее скорости.
Нужна помощь в решении задач и других студенческих заданий? Обратитесь в профессиональный студенческий сервис за качественным решением проблем.