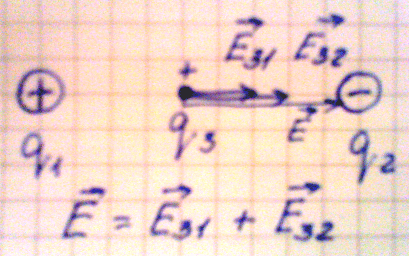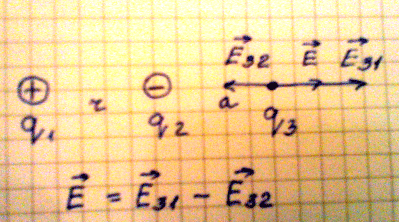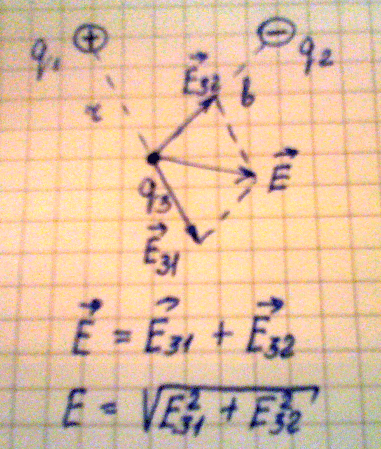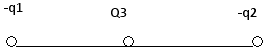Как найти напряженность электрического поля по рисунку

Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.

Задачи урока:

• формирование понятия напряжённости электрического поля; дать понятие о
  линиях напряжённости и графическое представление электрического поля;
• научить учащихся применять формулу E=kq/r² в решении
  несложных задач на расчёт напряжённости.

Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.

Графически изображая поле, следует помнить, что линии напряженности
электрического поля:

1. нигде не пересекаются друг с другом;
2. имеют начало на положительном заряде (или в бесконечности) и конец на
   отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
3. между зарядами нигде не прерываются.

Рис.1

Силовые линии положительного заряда:

Рис.2

Силовые линии отрицательного заряда:

Рис.3

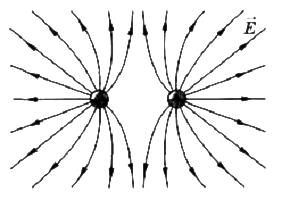
Силовые линии одноименных взаимодействующих зарядов:

Рис.4

Силовые линии разноименных взаимодействующих зарядов:

Рис.5

Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
или
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда

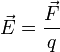
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда

где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.

В системе СИ
Н·м²/Кл²,

где ε₀ – электрическая
постоянная, равная 8,85·10^-12 Кл²/Н·м²;

q – электрический заряд (Кл);

r – расстояние от заряда до точки в которой определяется напряженность.

Направление вектора напряженности совпадает с направлением силы Кулона.

Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.

Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:

Рассмотрим несколько случаев определения напряженности.

1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:

Е₃₁ – напряженность точечного заряда 3 со стороны заряда 1;

Е₃₂ – напряженность точечного заряда 3 со стороны заряда 2.

Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е₃₁ и Е₃₂.

Напряженность в данной точке определяется по формуле:

Е = kq₁/x² + kq₂/(r – x)²

где: r – расстояние между первым и вторым зарядом;

х – расстояние между первым и точечным зарядом.

Рис.6

2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е₃₁ и Е₃₂.

Формула напряженности в данной точке равна:

Е = kq1/(r + a)² – kq₂/a²

Где: r – расстояние между взаимодействующими зарядами;

а – расстояние между вторым и точечным зарядом.

Рис.7

3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:

Е = (Е₃₁² +Е₃₂²)^1/2

Следовательно:

Е = ((kq₁/r² )² + (kq₂/b²)²)^1/2

Рис.8

Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.

4. Закрепление темы.

Проверочная работа.

Вариант № 1.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: электрическое поле – это ….

3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Вариант № 2.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: напряженностью называется …

3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Задачи на дом:

Для школьников.

Приведём решение трёх задач на применение принципа суперпозиции (наложения) электростатических полей.

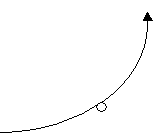
Задача 1. Два точечных одинаковых положительных заряда по 20 нКл каждый расположены в двух вершинах равностороннего треугольника со стороной 2 м в вакууме. Найти напряжённость поля в третьей вершине треугольника.

В точке А вектора напряженности электрических полей каждого заряда направлены вдоль их силовых линий (от зарядов).

Применим принцип суперпозиции для проекций указанных векторов на оси х и у:

Таким образом, вектор напряжённости результирующего электрического поля в точке А направлен вертикально вверх, а модуль напряжённости равен 77 В/м.

Задача 2. Электрическое поле образовано двумя одинаковыми разноимёнными точечными зарядами по 5 нКл. Расстояние между зарядами 10 см. Определить напряжённость поля: 1) в точке, лежащей посередине между зарядами; 2) в точке, лежащей на продолжении линии, соединяющей центры зарядов, на расстоянии 10 см от отрицательного заряда; 3) в точке, лежащей на расстоянии 10 см от положительного и отрицательного зарядов.

В точке А оба вектора напряжённости, создаваемых положительным и отрицательным зарядами, направлены вправо (на рисунке не показаны). Тогда результирующее поле находится через сумму полей, создаваемых первым и вторым зарядами:

В точке В результирующее поле направлено влево и равно:

В точке С вектор напряжённости результирующего электрического поля направлен вправо. Его модуль найдём из треугольника:

Ответ: 36000 В/м; 3400 В/м; 4500 В/м.

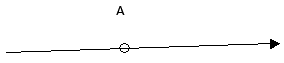
Задача 3. Электрическое поле создано двумя точечными зарядами 30 нКл и -10 нКл. Расстояние между зарядами 20 см. Определить напряжённость электрического поля в точке, находящейся на расстоянии 15 см от первого и на расстоянии второго (отрицательного) зарядов.

Покажем направления векторов напряжённости, создаваемых в искомой точке первым и вторым зарядами. Их модули найдём из формул:

Складывая вектора находим вектор результирующего поля. Модуль напряжённости результирующего поля находим по теореме косинусов:

Косинус угла найдём отдельно из треугольника образованного расстояниями:

Косинус угла оказался равным 0,25. Подставив все численные значения в формулу, получим результирующую напряжённость равную 16, 7 кВ/м.

Итак, приведено решение трёх задач на применение принципа суперпозиции (наложения) полей. Сначала в интересующей точке поля рисуем вектора напряжённости электрического поля, создаваемого каждым зарядом в отдельности. Затем, складывая их, находим напряжённость суммарного поля. В первой задаче проще просуммировать проекции векторов напряжённости на оси. Там, где угол между векторами напряжённости, создаваемыми отдельными зарядами, отличен от нуля, пользуются теоремой косинусов (задачи 2 и 3).

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Нахождение напряжённости электростатического поля.

Следующая запись:Как рассчитать напряжённость поля заряженной пластины. Поле конденсатора.

Ссылки на другие занятия (до электростатики) даны в Занятии 1.

Ссылки на занятия (начиная с электростатики) даны в Занятии 45.

Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей»

Подробности

Обновлено 13.08.2018 18:42

Просмотров: 1334

«Физика – 10 класс»

При решении задач с использованием понятия напряжённости электрического поля нужно прежде всего знать формулы (14.8) и (14.9), определяющие силу, действующую на заряд со стороны электрического поля, и напряжённость поля точечного заряда. Если поле создаётся несколькими зарядами, то для расчёта напряжённости в данной точке надо сделать рисунок и затем определить напряжённость как геометрическую сумму напряжённостей полей.

Задача 1.

Два одинаковых положительных точечных заряда расположены на расстоянии r друг от друга в вакууме. Определите напряжённость электрического поля в точке, расположенной на одинаковом расстоянии r от этих зарядов.

Р е ш е н и е.

Согласно принципу суперпозиции полей искомая напряжённость равна геометрической сумме напряжённостей полей, созданных каждым из зарядов (рис. 14.17): = ₁ + ₂.

Модули напряжённостей полей зарядов равны:

Диагональ параллелограмма, построенного на векторах ₁ и ₂, есть напряжённость результирующего поля, модуль которой равен:

Задача 2.

Проводящая сфера радиусом R = 0,2 м, несущая заряд q = 1,8 • 10^-4 Кл, находится в вакууме. Определите: 1) модуль напряжённости электрического поля на её поверхности; 2) модуль напряжённости ₁ электрического поля в точке, отстоящей на расстоянии r₁ = 10 м от центра сферы; 3) модуль напряжённости ₀ в центре сферы.

Р е ш е н и е.

Электрическое поле заряженной сферы вне её совпадает с полем точечного заряда. Поэтому

Следовательно,

3) напряжённость поля в любой точке внутри проводящей сферы равна
нулю: Е₀ = 0.

Задача 3.

В однородное электрическое поле напряжённостью Е₀ = 3 кН/Кл внесли точечный заряд q = 4 • 10^-10 Кл. Определите напряжённость электрического поля в точке А, находящейся на расстоянии r = 3 см от точечного заряда. Отрезок, соединяющий заряд и точку А, перпендикулярен силовым линиям однородного электрического поля.

Р е ш е н и е.

Согласно принципу суперпозиции напряжённость электрического поля в точке А равна векторной сумме напряжённостей однородного поля ₀ и поля ₁, созданного в этой точке внесённым электрическим зарядом. На рисунке 14.18 показаны эти два вектора и их сумма. По условию задачи векторы ₀ и ₁ взаимно перпендикулярны. Напряжённость поля точечного заряда

Тогда напряжённость электрического поля в точке А равна:

Задача 4.

В вершинах равностороннего треугольника со стороной а = 3 см находятся три точечных заряда q₁ = q₂ = 10^-9 Кл, q₃ = -2 • 10^-9 Кл. Определите напряжённость электрического поля в центре треугольника в точке О.

Р е ш е н и е.

Согласно принципу суперпозиции полей напряжённость поля в точке О равна векторной сумме напряжённостей полей, созданных каждым зарядом в отдельности: ₀ = ₁ + ₂ + ₃, причём где

На рисунке 14.19 показаны векторы напряжённостей ₁, ₂, ₃. Сначала сложим векторы ₁ и ₂. Как видно из рисунка, угол между этими векторами равен 120°. Следовательно, модуль суммарного вектора равен модулю l₁l и направлен в ту же сторону, что и вектор ₃.

Окончательно запишем:

Задача 5.

Расстояние между двумя неподвижными зарядами q₁ = -2 X 10^-9 Кл и q₂ = 10^-9 Кл равно 1 м. В какой точке напряжённость электрического поля равна нулю?

Р е ш е н и е.

Очевидно, что на отрезке между зарядами напряжённость не может быть равна нулю, так как напряжённости полей ₁ и ₂, созданных этими зарядами, направлены в одну сторону (рис. 14.20).

Следовательно, напряжённость поля может быть равна нулю или справа, или слева от зарядов на линии, проходящей через эти заряды.

Так как модуль первого заряда больше, чем модуль второго, то эта точка должна находиться ближе ко второму заряду, т. е. в нашем случае справа от зарядов. Расстояние от второго заряда до точки А обозначим через х. Тогда из условия, что |‘₁| = ‘₂, можно записать:

Решая это уравнение, получаем

Окончательно

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Электростатика – Физика, учебник для 10 класса – Класс!ная физика

Что такое электродинамика —
Электрический заряд и элементарные частицы. Закон сохранения заряд —
Закон Кулона. Единица электрического заряда —
Примеры решения задач по теме «Закон Кулона» —
Близкодействие и действие на расстоянии —
Электрическое поле —
Напряжённость электрического поля. Силовые линии —
Поле точечного заряда и заряженного шара. Принцип суперпозиции полей —
Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» —
Проводники в электростатическом поле —
Диэлектрики в электростатическом поле —
Потенциальная энергия заряженного тела в однородном электростатическом поле —
Потенциал электростатического поля и разность потенциалов —
Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности —
Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» —
Электроёмкость. Единицы электроёмкости. Конденсатор —
Энергия заряженного конденсатора. Применение конденсаторов —
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»

Если снять шерстяной свитер в сухую погоду, мы услышим треск. А если снимать свитер в темноте, иногда можно даже заметить искорки электрических разрядов.

Если расчесывать в сухую погоду сухие волосы пластмассовой расческой, то происходит ее электризация трением. Наэлектризованная расческа получит заряд и сможет притягивать небольшие кусочки бумаги.

Проделывая опыт с расческой и сухими волосами, можно убедиться, что наэлектризованные волосы и расческа буду притягиваться. Мы наблюдаем притяжение, значит, волосы и расческа обладают противоположными зарядами. Приближая расческу к волосам, обнаружим, что притяжение между ними возрастает.

Этот опыт позволил убедиться, что заряды действуют друг на друга на расстоянии. Чем ближе заряды находятся, тем сильнее их взаимное действие друг на друга.

Из механики известно, что существует ударное взаимодействие тел, когда, например, один бильярдный шар ударяется о другой такой же шар. В школьной физике рассматривают два вида ударного взаимодействия – абсолютно упругий и абсолютно неупругий удар.

Существует, так же, безударное взаимное действие тел – их притяжение, или отталкивание. К примеру, в механике, силу притяжения между телами, имеющими массу, вычисляют с помощью закона всемирного тяготения.

А силу взаимодействия электрических зарядов описывает закон Кулона.

Взаимодействие зарядов передается без участия вещества

Заряды будут притягиваться и отталкиваться не только в воздухе, но, даже в безвоздушном пространстве. В этом легко убедиться, если поместить заряженный электроскоп под колокол и откачать из-под колокола воздух. Полоски бумаги, имеющие одинаковые заряды, все так же, продолжат отталкиваться, независимо от того, в воздухе ли они находятся, либо в безвоздушном пространстве.

Это значит, что передача взаимодействия зарядов происходит не через вещество.

Ученые из Англии – Майкл Фарадей и Джеймс Максвелл, долгое время изучали электрические заряды. Они выяснили, что заряды окружены особым видом материи, которую они назвали электрическим полем.

Любой заряд окружен электрическим полем — особым видом материи.

Теории дальнодействия и близкодействия

Физики выдвигали различные теории, пытаясь объяснить взаимодействие зарядов. Наибольшее распространение получили две – их называют теориями близкодействия и дальнодействия.

Дальнодействие

Теория дальнодействия сообщает, что один заряд действует на другой заряд непосредственно. То есть, чтобы передать действие одного заряда на другой, посредники не нужны.

Кроме того, взаимодействие происходит мгновенно на любых расстояниях. Это значит, что если убрать один из взаимодействующих зарядов, то его действие на оставшийся заряд прекратится мгновенно.

Близкодействие

В противоположность этой теории Майкл Фарадей предложил свою теорию близкодействия.

Эта теория заявляет о том, что непосредственно действовать друг на друга заряды не могут. То есть, для передачи своего воздействия заряду нужна некоторый помощник. И каждый заряд создает в пространстве вокруг себя этого помощника. Фарадей назвал его электрическим полем.

На другие заряды будет действовать не сам заряд, а поле, созданное этим зарядом. Такое поле распространяется в пространстве не мгновенно, а с конечной скоростью.

Примечание: Как выяснилось позже, это очень большая скорость – триста тысяч километров в секунду. Ее называют скоростью света.

Поэтому, если один из взаимодействующих зарядов быстро убрать, то второй заряд узнает о его исчезновении не мгновенно, а через некоторое, пусть небольшое, время.

Получается, что взаимодействие зарядов протекает не непосредственно, а в виде цепочки. Каждый заряд создает вокруг себя поле, именно поле действует на другой заряд, помещенный в него.

А сила, действующая на заряд, расположенный в какой-либо точке пространства, зависит от характеристик поля в этой точке.

В настоящее время общепринятой теорией, объясняющей взаимодействие зарядов, является теория близкодействия Фарадея. Так как эта теория полностью подтвердилась экспериментально.

Примечание: Кроме электрических существуют, так же, магнитные поля. В отличие от электростатического, магнитное поле не имеет своих магнитных источников. Оно возникает в пространстве вокруг движущихся зарядов. То есть, магнитное поле – это поле электрических зарядов, находящихся в движении.

Джеймс Клерк Максвелл в середине 19-го века показал, что электрическое и магнитное поля связаны и это электромагнитное поле распространяется в пространстве с очень большой, но конечной скоростью.

Поле и вещество – это два вида материи

Мир, окружающий нас, материален. Значит, материя – это то, что существует реально, независимо от того, наблюдаем ли мы за ней, или нет.

Она может проявлять себя в виде двух частей — вещества и поля. Нас окружает вещество, а атомы и молекулы — это мельчайшие единицы вещества.

Поле – это еще один вид материи. Поле веществом не является, однако, оно существует реально.

Как обнаружить электрическое поле

Мы не чувствуем электрическое поле, так как у нас нет органов чувств, способных его обнаружить.

Но, используя нечто, что обладает чувствительностью к электрическому полю, можно убедиться, что поле, окружающее заряды, существует.

В качестве чувствительного элемента можно использовать любой электрический заряд. Потому, что любой заряд окружен своим собственным электрическим полем и, благодаря ему может чувствовать подобные поля, создаваемые другими зарядами. Такой заряд, используемый для обнаружения поля, физики называют пробным.

Примечания:

1. Некоторые живые существа могут чувствовать электрические поля, например, некоторые виды рыб.
2. Электрическое поле можно обнаружить по его действию на заряды, а, так же, с помощью различных приборов.
3. Поле заряда действует с некоторой силой на расположенный рядом другой заряд. То есть, заряды действуют друг на друга благодаря своим электрическим полям.

Мы можем обнаружить электрическое поле благодаря его действию на другие заряды. Электрическая сила — это сила, с которой поле действует на внесенный в него пробный заряд.

Примечание: Не следует путать пробный и элементарный заряд.

Две характеристики электростатического поля

Поле, окружающее неподвижные заряды, называют электростатическим полем.

Электрическое поле можно описать двумя величинами – векторной величиной — напряженностью (large vec{E}) и скалярной величиной – потенциалом (large varphi ).

Примечание: Применяют, так же, еще одну характеристику электрического поля — вектор электрической индукции (large vec{D}).

Описываем электрическое поле с помощью вектора

Рассмотрим два неподвижных точечных электрических заряда. Один заряд обозначим большой буквой Q:

(large Q left( text{Кл}right) ) – этот заряд создает вокруг себя электрическое поле.

Чтобы обнаружить это поле, на некотором расстоянии от заряда Q поместим еще один заряд.

(large r left( text{м}right) ) — расстояние между зарядами.

(large q left( text{Кл}right) ) — второй заряд, будем называть его пробным.

Примечания:

1. Заряд точечный, если его размерами можно пренебречь;
2. Обычно знак такого пробного заряда выбирают положительным. Пробный заряд имеет небольшую величину, такую, что поле, создаваемое им, на другие заряды почти не влияет.

Свойство 1: Поле, создаваемое зарядом, влияет только на другие заряды. Это поле не влияет на заряд, породивший его.

Благодаря своим электрическим полям заряды q и Q действуют друг на друга. Силу их взаимодействия можно рассчитать по закону Кулона:

[large |vec{F}| = k cdot frac {|q| cdot |Q|}{r^{2}} ]

(large F left( H right) ) – сила, с которой два точечных заряда притягиваются, или отталкиваются;

Для нас важным сейчас является само наличие взаимодействия. Чтобы не выяснять, будет ли сила воздействия силой притяжения, или отталкивания, каждый заряд поместим внутрь модуля.

Свойство 2: Электрическое поле, принадлежащее заряду Q в какой-либо точке пространства, не зависит от того, есть ли в этой точке какой-то другой заряд.

Что такое напряженность поля

Введем физическую величину, которая описывает поле заряда Q и не зависит от пробного q заряда. Для этого разделим обе части уравнения на пробный q заряд:

[large frac {|vec{F}|}{|q|} = k cdot frac {|Q|}{r^{2}} ]

Обратите внимание, что правая часть полученного уравнения не зависит от пробного заряда. Потому, что пробный заряд, обозначенный малой буквой q, не входит в правую часть. Правая часть зависит только от заряда, создавшего поле и обозначенного большой буквой Q.

Введем обозначение для дроби, расположенной в левой части полученного уравнения:

[large boxed { vec{E} = frac {vec{F}}{q} } ]

( large vec{E} left( frac {B}{text{м}} right) ) – напряженность электрического поля, измеряется в Вольтах, деленных на метр, или в Ньютонах, деленных на Кулон;

Напряженность электростатического поля в выбранной точке пространства – это векторная величина. Она равна отношению силы, действующей на пробный заряд, находящийся в выбранной точке поля к величине этого заряда. В различных точках поля силы могут быть разными, значит, будут различаться и напряженности в этих точках.

Чтобы найти (длину) модуль вектора E напряженности поля, создаваемого точечным зарядом, приравняем к величине E правую часть полученного выше выражения:

[large boxed {|vec{E}| = k cdot frac {|Q|}{r^{2}} } ]

(large k = 9cdot 10^{9}  left( H cdot frac{text{м}^{2}}{text{Кл}^{2}}right)) – постоянная величина;

(large |Q| left( text{Кл}right) ) — заряд, создающий в пространстве вокруг себя электрическое поле;

(large r left( text{м}right) ) – расстояние от заряда Q до точки, в которую мы поместили пробный заряд.

Примечание: Поле мы измеряем в той точке, в которую помещаем пробный заряд.

Напряженность – это вектор. Две главные характеристики вектора – его длина и направление.

Величина ( large vec{E} ) является силовой характеристикой электрического поля. Чем больше напряженность E, тем больше сила F, действующая на пробный заряд, помещенный в это поле.

[large boxed { frac {1 Н}{ 1 text{Кл}} = frac {1 B}{ 1 text{м}} } ]

Если на заряд 1 Кулон, помещенный в электростатическое поле, действует сила 1 Ньютон, то напряженность этого поля равна единице.

По третьему закону Ньютона, силы, с которыми взаимодействуют два заряда, будут равными.

Каждый неподвижный заряд создает свое собственное электростатическое поле. Если заряды имеют различные величины, то напряженности их полей различаются.

Куда направлен вектор Е

Обратим в очередной раз внимание на формулу:

[large vec{E} = frac {vec{F}}{q} ]

Заряд q – скалярная величина. А сила F – векторная.

Воспользуемся математическими свойствами векторов: разделив вектор F на скаляр q, мы получим новый вектор E:

1. его длина отличается от вектора F.
2. направления векторов F и E совпадают (либо векторы F и E направлены в противоположные стороны).

Вектор E сонаправлен с вектором силы, действующей на помещенный в поле пробный заряд. Для положительного заряда его вектор E направлен от этого заряда. А для отрицательного заряда его вектор E направлен к этому заряду.

Примечание: Однонаправленные или противоположно направленные, то есть, параллельные векторы, называют коллинеарными. У них может отличаться длина.

Как изменяется длина вектора Е с расстоянием

Длина вектора напряженности с расстоянием быстро убывает. Об этом можно судить с помощью формулы, описывающей модуль данного вектора:

[large E = k cdot frac {Q}{r^{2}} ]

Расстояние r возводится в квадрат и расположено в знаменателе. Это значит, что если расстояние увеличится в 2 раза, то напряженность уменьшится в 4 раза.

А если, например, расстояние увеличится в 3 раза, то напряженность уменьшится в 9 раз.

На рисунке 9 отражено изменение длины вектора напряженности. Обратите внимание на направление этого вектора и знак заряда:

Мы можем выразить зависимость напряженности от расстояния с помощью знака пропорции:

[large E sim frac {1}{r^{2}} ]

Подобную зависимость на графике можно отразить такой кривой:

Как видно из рисунка 10, увеличение расстояния до заряда в четыре раза вызывает ослабление напряженности его поля в шестнадцать раз.

Как по известной напряженности вычислить силу, с которой поле действует на заряд

Если известна напряженность поля, то силу, которая действует на заряд, помещенный в это поле, можно вычислить по формуле:

[large boxed{ vec{E} cdot q = vec{F} } ]

(large q left( text{Кл}right) ) – заряд, положительный, или отрицательный, помещенный в выбранную точку пространства, в которой существует электрическое поле;

Формула записана в векторном виде. Это значит, что она позволяет найти обе характеристики силы, действующей на заряд — направление вектора силы и его модуль.

Умножив заряд на напряженность в выбранной точке поля, можно вычислить силу, действующую на заряд со стороны поля.

Так как напряженность входит в формулу для вычисления силы, ее называют силовой характеристикой электрического поля.

Зная силу, мы можем по второму закону Ньютона вычислить ускорение заряда. А с помощью формул кинематики для равнопеременного движения, зная ускорение, можно определить перемещение заряда или траекторию его движения.

Как изобразить электрическое поле единичного заряда

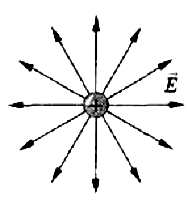
Пусть неподвижный положительный точечный заряд создает в пространстве, окружающем его, электрическое поле. Нарисуем несколько векторов напряженности этого поля.

Красной точкой на рисунке обозначен заряд. А черным цветом обозначены точки, в которые помещали пробный заряд и измеряли поле.

По длине векторов можно сделать вывод, чем ближе к заряженному телу расположен пробный заряд, тем сильнее на него действует поле. Увеличив же расстояние между заряженным телом и пробным зарядом, заметим, что действие поля уменьшится.

Поля, действие которых будет различаться в разных точка пространства, называют неоднородными. Значит, электрическое поле вокруг точечных зарядов, неоднородное.

Изображаем неоднородное электрическое поле силовыми линиями

Как видно, мы можем изобразить поле с помощью нарисованных в различных точках векторов напряженности. Однако, есть более удобный способ.

Присмотревшись к рисунку, можно заметить, что векторы напряженности, окружающие заряд, располагаются на некоторых прямых. Эти прямые обозначены пунктирными линиями на рисунке. Из называют линиями электрического поля, или линиями напряженности.

Примечание: Изображать электростатическое поле удобнее не с помощью векторов, а с помощью линий напряженности.

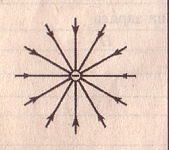
Если заряд единственный, а поблизости от него других зарядов нет, то его поле изображают радиально расходящимися во все стороны линиями.

Линии положительных зарядов направлены от них, а линии отрицательных зарядов – к этим зарядам, так же, как векторы напряженности.

Мы помним, что вектор напряженности описывает силу, с которой поле, созданное зарядом может действовать на другие заряды. Поэтому, линии напряженности, так же, часто называют силовыми линиями поля.

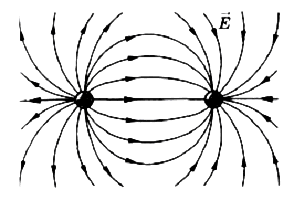
Как выглядит поле двух взаимодействующих зарядов

Рассмотрим теперь поле взаимодействующих зарядов — положительного и отрицательного.

Как видно, линии взаимодействующих зарядов искривляются и, их конфигурация искажается.

Мы знаем, что поле одного точечного заряда неоднородное. Поле двух взаимодействующих зарядов, так же, неоднородное.

Теперь проведем обобщение, на рисунке неоднородное поле изображают:

• либо прямыми линиями, радиально расходящимися во все стороны от одиночного заряда, либо
• кривыми линиями, для взаимодействующих зарядов.

По мере удаления от зарядов расстояние между линиями будет увеличиваться. Чем дальше линии располагаются одна от другой в некоторой области пространства, тем слабее поле в этой области.

Будет ли поле действовать на заряд, расположенный между силовыми линиями

У начинающих изучать электростатику часто возникает вопрос, а будет ли на заряд, находящийся на рисунке между силовыми линиями, действовать сила с стороны электрического поля? Конечно, будет.

Не имеет значения, находится ли заряд на силовой линии на рисунке, или в пространстве между силовыми линиями. Поле существует во всех точках рассматриваемой области, поэтому на заряд будет действовать сила в любой точке поля, независимо, находится ли эта точка на силовой линии, или нет.

Примечание: Силовые линии – это всего лишь способ графического обозначения поля в некоторой области пространства. Поле существует во всех точках пространства, а не только на силовых линиях.

Свойства силовых линий электростатического поля

Можно выделить два свойства силовых линий поля, создаваемого неподвижными зарядами:

1. Силовые линии имеют начало и конец – они начинаются на положительных и заканчиваются на отрицательных зарядах.
2. Напряженность поля больше в той области, в которой линии располагаются гуще.

Примечание: Существует, так же, вихревое электрическое поле. Это поле не связано с неподвижными зарядами. Его линии замкнуты сами на себя. Картина такого поля представляет собой нечто похожее на вихрь, отсюда и появилось его название. Подробнее о вихревом электрическом поле написано в статье, посвященной электромагнитным волнам.

Поле сильней там, где его линии располагаются ближе одна к другой, а так же там, где длиннее вектор Е.

Где заканчиваются линии единственного заряда

Линии электростатического поля, начавшись на положительном заряде, должны закончиться на каком-либо отрицательном заряде.

Если поблизости от какого-либо заряда не располагается второй заряд, имеющий противоположный знак, то линии поля такого одинокого заряда уходят в бесконечность.

Там, далеко, на бесконечности, всегда найдется заряд, имеющий противоположный знак, на котором будут заканчиваться линии рассматриваемого одиночного заряда.

Почему заряды называют источниками электрического поля

Электростатическое поле имеет свои электрические источники.

Нам известно, что линии электростатического поля имеют начало и конец. Они начинаются на положительных зарядах, а на отрицательных зарядах заканчиваются.

Поэтому, положительные заряды называют источниками поля, а отрицательные – стоками.

Как изобразить однородное электрическое поле

Если равномерно распределить заряды по двум плоским поверхностям, расположив эти поверхности на некотором расстоянии параллельно, то в пространстве между этими поверхностями электрическое поле будет однородным.

Примечание: Система из двух параллельных проводящих поверхностей, расположенных на некотором расстоянии одна от другой, называют электрическим конденсатором.

Однородное поле на рисунке изображают параллельными прямыми линиями, расстояние между которыми не изменяется.

Такие поля можно создать только в некоторой ограниченной области пространства. Их удобно изучать, потому, что в любой точке такого поля вектор напряженности будет иметь одно и то же направление и длину.

Если во всех точках пространства, в которых существует электрическое поле, вектор напряженности имеет одинаковое направление и длину, то это поле называют однородным.

Примечание: Если говорить начистоту, то у концов плоских поверхностей линии поля будут искривляться. Это значит, что у краев поле не будет однородным.

Поэтому, для создания однородного электрического поля в учебной литературе рассматривают абстрактные бесконечно протяженные плоскости.

Читайте отдельную статью том, как обозначают распределенные заряды (откроется в новой вкладке).

Связь между векторами E неоднородного поля и линиями напряженности

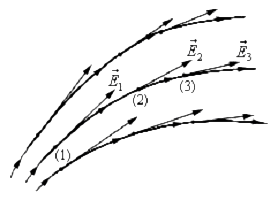
Рассмотрим еще раз рисунок, на котором изображено поле двух взаимодействующих зарядов. Выберем на нем одну силовую линию. Вычислим длины нескольких векторов E и нарисуем их в выбранных точках, расположенных на этой линии.

Если через каждый вектор напряженности провести прямую линию, можно заметить, что эти линии образуют семейство касательных. Такие касательные прямые линии ограничивают собой кривую. Эта кривая и будет являться силовой линией.

Теперь можно дать определение силовых линий:

Силовая линия электростатического поля – это линия, касательная к которой в любой выбранной точке будет сонаправлена с вектором напряженности электрического поля в этой же точке.

В отдельной статье будет рассказано о работе электрического поля и еще одной его характеристике — потенциале.

Принцип суперпозиции

(примеры решения задач)

Закон Кулона.
Электростатическое поле системы точечных
зарядов

Пример 1.1

В однородном электрическом поле
напряженностью
закреплен точечный отрицательный заряд.
В точкеA, положение
которой определяется расстояниеми углом(см.
рис.), модуль вектора напряженности
результирующего электрического поля.
Определите угол.

Решениe.

Напряженность результирующего поля
согласно принципу суперпозиции равна

,

гденапряженность
поля, создаваемого точечным зарядомqв точкеА(рис.)

.

По теореме косинусов

.

Учитывая, что по условию задачи,
получим для искомого угла:

.

Пример 1.2

Два
одинаковых небольших металлических
шарика с зарядами и,
находящихся на расстоянии l = 0,2 м
друг от друга притягиваются с силой
H.
После того как шарики привели в
соприкосновение и опять развели на то
же расстояниеl,
они стали отталкиваться с силой
Н.
Найдитеи.

Решение.

Так как в начале
шарики притягивались, то их заряды
противоположны по знаку и по закону
Кулона

(1)

После
того, как шарики были приведены в
соприкосновение, заряды перераспределяются,
и на каждом из шариков заряд, согласно
закону сохранения заряда, становится
равным
Поэтому они стали взаимодействовать с
силой

(2)

Уравнения
(1) и (2), дают систему уравнений для
неизвестных и

решив которую,
находим искомые заряды

Кл,

Кл.

Заметим,
что в соответствии с симметрией задачи
возможны и
такие значения зарядов:
Кл,
 Кл.

Пример 1.3

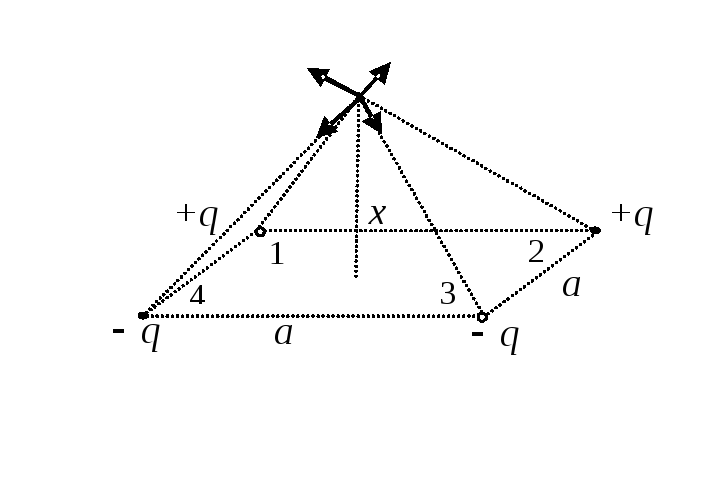
В вершинах квадрата, со стороной а,помещены четыре зарядаq(см. рис.).

Найдите напряженность электрического
поля на перпендикуляре, восстановленном
из центра квадрата, как функцию его
длины x.

Решение.

Из принципа суперпозиции полей,
результирующее поле, создаваемое
зарядами, равно:

=,
где.

Задача сводится к суммированию четырех
равных по величине, но разных по
направлению векторов
.Найдем векторную сумму полей положительного
и отрицательного зарядов 1 и 3. Из подобия
треугольников на рисунке получим:

,
т.е..

Аналогично, складывая поля 2-го и 4-го
зарядов найдем
.
Для сложения векторовиучтем
их равенство по величине и взаимную
перпендикулярность. По теореме Пифагора,
получим

.

Пример 1.4

На рисунке изображена одна из линий
напряженности электрического поля двух
неподвижных точечных зарядов
и.
Известно, что нКл.
Определите.

Решение.

Введем систему координат, выбрав ее,
как показано на рисунке, т.е. ось xпроходит через заряды, а осьyпроходит через «вершину» линии поля.
Так как вектор поля направлен по
касательной к линии поля, то в точке
«вершины»Е_y= 0. По принципу суперпозиции для поля
в этой точке имеем:

,
где

,

.

После подстановки и преобразований,
найдем, взяв значения геометрических
параметров из рисунка в условии задачи
a₁ =2, a₂
= 8, b = 4:

нКл.

Электростатическое
поле заряженных тел (непрерывное
распределение зарядов)

Пример 1.5

На единицу длины
тонкого однородно заряженного стержня
АВ,имеющего форму дуги окружностирадиуса R
с центром в точке О,
приходится заряд
.
Найдите модуль напряженности электрического
поля в точкеО,
если угол АОВ
равен
.

Решение.

Выберем оси координат так, чтобы начало
координат совпадало с точкой О, а
осьубыла симметрично расположена
относительно концов дугиАВ(рис.).

Разобьем стержень на элементарные
участки длины dl с зарядом,
который можно рассматривать как точечный.

Найдем напряженность поля, создаваемого
зарядом этого элементарного участка
стержня в точке 0:

,

где
–
радиус вектор, направленный от элементаdlк точке, напряженность
которой вычисляется. Напряженность
результирующего поля найдем,
воспользовавшись принципом суперпозиции.
В силу симметрии результирующее поле
будет направлено вдоль осиу(рис.).
Запишем выражение для проекции:

.

Приведем правую часть последнего
уравнения к одной переменной интегрирования
– углу
(учитывая, что)

.

Проинтегрировав левую часть полученного
уравнения от
доE, а правую отдо,
найдем модуль напряженности электрического
поля, создаваемого в точкеОдугойАВ:

.

Рассмотрим специальные случаи
использования формулы для
расчета поля, создаваемого частью дуги
окружности в ее центре
:

а) Модуль напряженности электрического
поля, создаваемого 1/4 части дуги окружности
радиуса Rв ее центре:

.

б) Модуль напряженности электрического
поля, создаваемого тонким полукольцом
радиуса Rв его центре:

.

в) Модуль напряженности электрического
поля, создаваемого тонким кольцом
радиуса Rв его центре:

.

г) Модуль напряженности электрического
поля в центре тонкого кольца радиуса
R, если половины этого
кольца заряжены разноименными зарядами
с линейными плотностями зарядаи.

Напряженность электрического поля,
создаваемого каждой из половинок равна:

,

.

Согласно
принципу суперпозиции найдем результирующее
поле в центре

.

Из рисунка видно, что направления
векторов
исовпадают,
поэтому результирующее поле в центре
такого кольца равно

.

Соседние файлы в папке Примеры решений

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #