Как найти напряженность электрического поля точечного заряда

Напряженность электрического поля точечного заряда

4.5

Средняя оценка: 4.5

Всего получено оценок: 124.

4.5

Средняя оценка: 4.5

Всего получено оценок: 124.

Для характеристики электрического поля применяется такая величина, как напряженность. Любой электрический заряд создает поле, и, следовательно, всегда можно указать его напряженность. Найдем напряженность электрического поля точечного заряда.

Напряженность электрического поля

Электрические поля проявляются в силовом взаимодействии между зарядами. Сила взаимодействия между зарядами $q$ и $q_1$ находится с помощью закона Кулона:

$$F=k{qq_1over r^2}$$

Рис. 1. Закон Кулона.

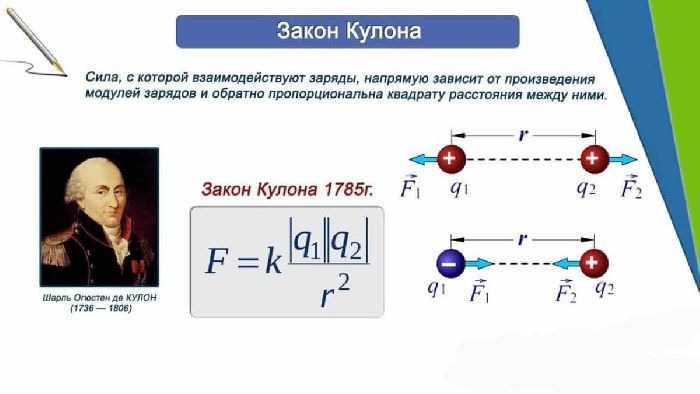
Если рассмотреть поле, порождаемое зарядом $q$, то при фиксированном заряде $q_1$ и расстоянии $r$, сила взаимодействия между зарядами будет прямо пропорциональна величине заряда $q$. А значит, отношение этой силы к заряду $q$ не зависит от $q$, и может быть принято, как силовая характеристика поля.

Напряженность электрического поля — это отношение силы, действующей на пробный заряд, помещаемый в поле, к величине этого заряда.

$$overrightarrow E={overrightarrow F over q}$$

Напряженность поля — векторная величина, имеющая то же направление, что и направление силы, действующей на положительный заряд.

Если в каждой точке поля изобразить вектор напряженности, то эти векторы сольются в линии, которые называются линиями напряженности. Они полностью характеризуют распределение поля в пространстве. На пробный положительный заряд, помещенный в поле, будет действовать сила, касательная к линии напряженности, проходящей через эту точку.

Например, так выглядит поле двух разноименных зарядов, находящихся рядом:

Рис. 2. Лини напряженности диполя.

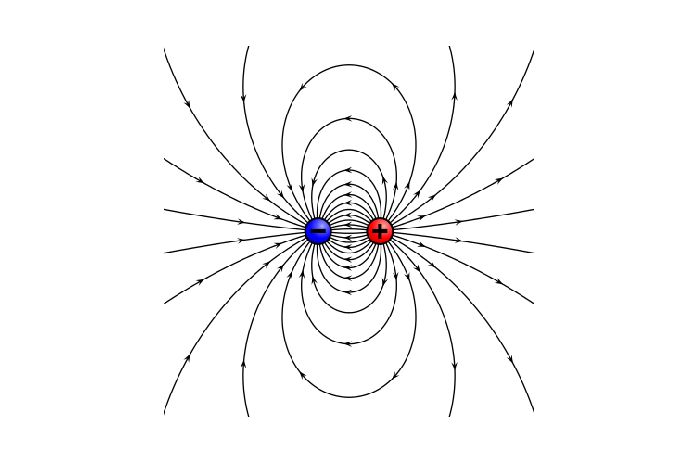
Напряженность поля точечного заряда

Наиболее просто выглядит поле точечного заряда. Поскольку закон Кулона описывает взаимодействие между двумя точечными зарядами, то его можно непосредственно подставить в выражение для напряженности. В результате, мы получим формулу напряженности электрического поля точечного заряда:

$$E={F over q}=k{qover r^2}$$

Вектор напряженности лежит на линии, соединяющей точечный заряд с точкой, в которой находится напряженность. При этом вектор направлен в сторону заряда, если он отрицателен, и в противоположную, если он положителен.

Построив много таких векторов, можно получить картину линий напряженности поля точечного заряда. Линии будут начинаться на положительном заряде и радиальными лучами уходить в бесконечность. Если заряд отрицателен, то линии будут приходить в заряд радиальными лучами из бесконечности.

Чем ближе к заряду, тем линии будут располагаться гуще. Это иллюстрирует тот факт, что чем ближе к заряду, тем напряженность выше.

Рис. 3. Линии напряженности точечного заряда.

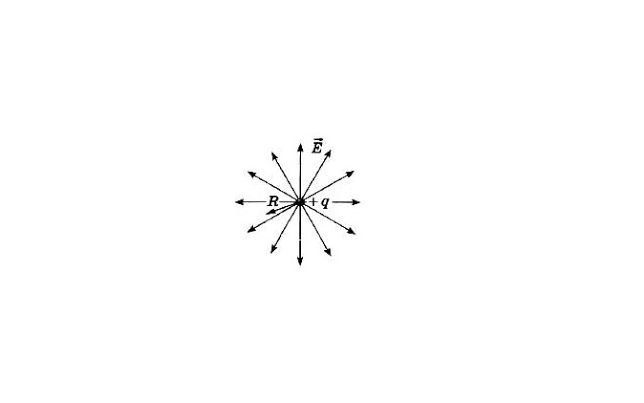
Что мы узнали?

Напряженность электрического поля — это отношение силы, действующей на пробный заряд, помещенный в поле, к величине этого пробного заряда. Поле можно изобразить в виде множества векторов напряженности, которые сливаются в линии. Линии напряженности поля точечного заряда являются радиальными лучами, уходящими в бесконечность.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.5

Средняя оценка: 4.5

Всего получено оценок: 124.

А какая ваша оценка?

Источник

Напряжённость электрического поля

Размерность	LMT⁻³I⁻¹
Единицы измерения
СИ	В/м
Примечания
векторная величина

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и равная отношению силы , действующей на неподвижный малый по величине точечный заряд, помещённый в данную точку, к величине этого заряда ${displaystyle q^{*}}$ ^[1]:

${displaystyle {vec {E}}={frac {vec {F}}{q^{*}}}.}$

Напряжённость электрического поля иногда называют силовой характеристикой электрического поля, так как всё отличие от вектора силы, действующей на заряженную частицу, состоит в постоянном^[2] множителе.

В каждой точке в данный момент времени существует своё значение вектора vec E (вообще говоря — разное^[3]
в разных точках пространства), таким образом, vec E — это векторное поле. Формально это отражается в записи

представляющей напряжённость электрического поля как функцию пространственных координат (и времени, так как vec E может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле^[4], и законы, которым оно подчиняется, суть предмет электродинамики.

Напряжённость электрического поля в Международной системе единиц (СИ) измеряется в вольтах на метр [В/м] или в ньютонах на кулон [Н/Кл].

Напряжённость электрического поля в классической электродинамике[править | править код]

Напряжённость электрического поля — одна из основных фундаментальных величин классической электродинамики. В этой области физики сопоставимыми с ней по значимости являются только вектор магнитной индукции (совместно с вектором напряжённости электрического поля образующий тензор электромагнитного поля) и электрический заряд. С некоторой точки зрения столь же важными представляются потенциалы электромагнитного поля (образующие вместе единый электромагнитный потенциал).

Остальные понятия и величины классической электродинамики, такие как электрический ток, плотность тока, плотность заряда, вектор поляризации, а также вспомогательные поле электрической индукции и напряженность магнитного поля — хотя безусловно важны и содержательны, по сути оказываются вторичными или производными.

Ниже выделены основные контексты классической электродинамики в отношении напряжённости электрического поля.

Сила воздействия электромагнитного поля на заряженные частицы[править | править код]

Полная сила, с которой электромагнитное поле (включающее электрическую и магнитную составляющие) действует на заряженную частицу, выражается формулой силы Лоренца:

${displaystyle {vec {F}}=q^{*}{vec {E}}+q^{*}[{vec {v}}times {vec {B}}]}$

где ${displaystyle q^{*}}$ — электрический заряд частицы, — её скорость,
— вектор магнитной индукции; косым крестом times обозначено векторное произведение. Формула приведена в единицах СИ.

Эта формула является более общей по сравнению с формулой, данной в определении напряжённости электрического поля, так как включает в себя также действие на заряженную частицу (если та движется) со стороны магнитного поля.

Частица предполагается точечной. Однако эта формула позволяет рассчитать и силы, действующие со стороны электромагнитного поля на тела любой формы с любым распределением зарядов и токов — если воспользоваться обычным для физики приёмом разбиения сложного тела на маленькие (математически — бесконечно малые) части, каждая из которых может считаться точечной и таким образом входящей в область применимости формулы Лоренца. Разумеется, для того, чтобы эта формула была применена (даже в простых случаях, таких, как расчёт силы взаимодействия двух точечных зарядов), необходимо уметь рассчитывать vec E и .

Остальные формулы, применяемые для расчёта электромагнитных сил (например, формулу для силы Ампера) можно считать следствиями^[5] фундаментальной формулы силы Лоренца или частными случаями её применения.

Уравнения Максвелла[править | править код]

Достаточным вместе с формулой силы Лоренца теоретическим фундаментом классической электродинамики являются уравнения электромагнитного поля, называемые уравнениями Максвелла. Их стандартная традиционная форма представляет собой четыре уравнения, в три из которых входит вектор напряжённости электрического поля:

${displaystyle {begin{aligned}operatorname {div} {vec {E}}&={frac {rho }{varepsilon _{0}}},&operatorname {rot} {vec {E}}&=-{frac {partial {vec {B}}}{partial t}},\operatorname {div} {vec {B}}&=0,&operatorname {rot} {vec {B}}&=mu _{0}{vec {j}}+{frac {1}{c^{2}}}{frac {partial {vec {E}}}{partial t}}.end{aligned}}}$

Здесь rho — плотность заряда, vec j — плотность тока, $varepsilon _{0}$ — электрическая постоянная, $mu _{0}$ — магнитная постоянная, — скорость света (уравнения записаны в системе СИ). В приведённом виде уравнения Максвелла являются «уравнениями для вакуума» (их более общий вариант, применимый и для описания поведения электромагнитного поля в среде, а также иные формы записи уравнений — см. в статье Уравнения Максвелла).

Этих четырёх уравнений вместе с пятым — уравнением силы Лоренца — в принципе достаточно, чтобы полностью описать классическую (не квантовую) электродинамику, то есть они представляют её полные законы. Для решения реальных задач с их помощью необходимы ещё уравнения движения «материальных частиц» (в классической механике это законы Ньютона), а также дополнительная информация о конкретных свойствах рассматриваемых физических тел и сред (их упругости, электропроводности, поляризуемости и др.) и о других силах, участвующих в задаче (например, о гравитации), однако вся эта информация уже не входит в рамки электродинамики как таковой, хотя и оказывается зачастую необходимой для построения замкнутой системы уравнений, позволяющих решить ту или иную конкретную задачу в целом.

«Материальные уравнения»[править | править код]

Дополнительными формулами (обычно не точными, а приближёнными или иногда даже эмпирическими), которые используются в классической электродинамике при решении практических задач и носят название «материальных уравнений», являются

закон Ома;
закон поляризации;
в разных случаях многие другие формулы и соотношения.

Связь с потенциалами[править | править код]

Связь напряжённости электрического поля с потенциалами в общем случае такова:

${displaystyle {vec {E}}=-nabla varphi -{frac {partial {vec {A}}}{partial t}},}$

где — скалярный и векторный потенциалы,

{displaystyle {vec {B}}=operatorname {rot} {vec {A}}.}

В частном случае стационарных (не меняющихся со временем) полей первое уравнение упрощается до

Это выражение связывает электростатическое поле с электростатическим потенциалом.

Электростатика[править | править код]

Теоретически и практически важным случаем является ситуация, когда заряженные тела неподвижны (например, исследуется состояние равновесия) или скорость их движения достаточно мала, чтобы можно было приближённо воспользоваться способами расчета, справедливыми для неподвижных тел. Этим случаем занимается раздел электродинамики, называемый электростатикой.

Как указано выше, напряжённость электрического поля в этом случае выражается через скалярный потенциал как

или, покомпонентно,

${displaystyle E_{x}=-{frac {partial varphi }{partial x}},quad E_{y}=-{frac {partial varphi }{partial y}},quad E_{z}=-{frac {partial varphi }{partial z}},}$

то есть электростатическое поле оказывается потенциальным полем.
( varphi в этом случае — случае электростатики — принято называть электростатическим потенциалом).

Правомерно и обратное соотношение:

{displaystyle varphi =-int {vec {E}}cdot {vec {dl}}.}

Уравнения Максвелла при этом также сильно упрощаются (уравнения с магнитным полем можно вообще исключить, а в уравнение с дивергенцией можно подставить ) и сводятся к уравнению Пуассона:

$Delta varphi =-{frac {rho }{varepsilon _{0}}},$

а в областях, свободных от заряженных частиц, — к уравнению Лапласа:

Учитывая линейность этих уравнений, а следовательно, применимость к ним принципа суперпозиции, достаточно найти поле одного точечного заряда, чтобы потом получать потенциал или напряжённость поля, создаваемого любым распределением зарядов (суммируя решения для точечных зарядов).

Теорема Гаусса[править | править код]

В электростатике широко используется теорема Гаусса, содержание которой сводится к интегральной форме единственного нетривиального для электростатики уравнения Максвелла:

$oint limits _{S}{vec E}cdot {vec {dS}}={frac {Q}{varepsilon _{0}}},$

где интегрирование проводится по любой замкнутой поверхности (вычисляется поток
vec E через эту поверхность), — полный (суммарный) заряд внутри этой поверхности.

Эта теорема даёт удобный способ расчета напряжённости электрического поля в случае, когда источники поля имеют высокую симметрию: сферическую, цилиндрическую или зеркальную + трансляционную. В частности, таким способом легко находится поле точечного заряда, сферы, цилиндра, плоскости.

Напряжённость электрического поля точечного заряда[править | править код]

Для точечного заряда в электростатике верен закон Кулона, который в системе СИ записывается:

$varphi ={frac {1}{4pi varepsilon _{0}}}cdot {frac {q}{r}},$

или

${displaystyle {vec {E}}={frac {1}{4pi varepsilon _{0}}}cdot {frac {q}{r^{2}}}cdot {frac {vec {r}}{r}}quad left(E={frac {1}{4pi varepsilon _{0}}}cdot {frac {q}{r^{2}}}right)}$

Исторически закон Кулона был открыт первым, хотя с теоретической точки зрения уравнения Максвелла более фундаментальны. С этой точки зрения он является их следствием. Получить этот результат проще всего, исходя из теоремы Гаусса, учитывая сферическую симметрию задачи: выбрать поверхность в виде сферы с центром в точечном заряде, учесть, что направление vec E будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса : $4pi r^{2}$ , имеем ${displaystyle 4pi r^{2}E=q/varepsilon _{0}}$ , откуда сразу получаем ответ для .

Ответ для varphi получается интегрированием :

{displaystyle varphi =-int {vec {E}}cdot {vec {dl}}=-int E,dr.}

Для системы СГС формулы и их вывод аналогичны, отличие от СИ лишь в константах:

$varphi ={frac {q}{r}},$

${displaystyle {vec {E}}={frac {q}{r^{2}}}{frac {vec {r}}{r}}quad left(E={frac {q}{r^{2}}}right)}$

Электрическое поле произвольного распределения зарядов[править | править код]

По принципу суперпозиции для напряжённости поля совокупности дискретных источников имеем:

${displaystyle {vec {E}}={vec {E}}_{1}+{vec {E}}_{2}+{vec {E}}_{3}+dots ,}$

где каждое

${displaystyle {vec {E}}_{i}={frac {1}{4pi varepsilon _{0}}}{frac {q_{i}}{(Delta {vec {r}}_{i})^{2}}}{frac {Delta {vec {r}}_{i}}{|Delta {vec {r}}_{i}|}}quad left(Delta {vec {r}}_{i}={vec {r}}-{vec {r}}_{i}right)}$

Подставив, получаем:

${vec E}({vec r})=sum limits _{i}{frac {1}{4pi varepsilon _{0}}}{frac {q_{i}}{(Delta {vec r}_{i})^{2}}}{frac {Delta {vec r}_{i}}{|Delta {vec r}_{i}|}},$

Для непрерывного распределения аналогично:

${displaystyle {vec {E}}({vec {r}})=int limits _{V}{frac {1}{4pi varepsilon _{0}}}{frac {rho ({vec {hat {r}}}),dV}{({vec {r}}-{vec {hat {r}}})^{2}}}{frac {{vec {r}}-{vec {hat {r}}}}{|{vec {r}}-{vec {hat {r}}}|}},}$

где — область пространства, где расположены заряды (ненулевая плотность заряда), или всё пространство,
— радиус-вектор точки, для которой считаем vec E ,
— радиус-вектор источника, пробегающий все точки области при интегрировании, — элемент объёма. Можно подставить вместо ;
вместо ;
вместо .

Системы единиц[править | править код]

В системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в ньютонах на кулон или в вольтах на метр (русское обозначение: В/м; международное: V/m).

Измерение напряженности электрического поля[править | править код]

Измерения напряженности электрического поля в электроустановках сверхвысокого напряжения производят приборами типа ПЗ-1, ПЗ-1 м и др.

Измеритель напряженности электрического поля работает следующим образом: в антенне прибора электрическое поле создает ЭДС которая усиливается с помощью транзисторного усилителя, выпрямляется полупроводниковыми диодами и измеряется стрелочным микро-амперметром. Антенна представляет собой симметричный диполь, выполненный в виде двух металлических пластин, размещенных одна над другой. Поскольку наведенная в симметричном диполе ЭДС. пропорциональна напряженности электрического поля, шкала мили-амперметра отградуирована в киловольтах на метр (кВ/м).

Измерение напряженности должно производиться во всей зоне, где может находиться человек в процессе выполнения работы. Наибольшее измеренное значение напряженности является определяющим. При размещении рабочего места на земле наибольшая напряженность обычно бывает на высоте роста человека.

Точки измерения выбираются по ГОСТ 12.1.002 зависимости от расположения рабочего места и от оснащения его средствами защиты согласно таблице:

Точки измерений напряженности электрического поля

Расположение рабочего места	Средства защиты	Точки измерений
Без поднятия на оборудование и конструкции	Без средств защиты	На высоте 1,8 м от поверхности земли
То же	Средства коллективной защиты	На высоте 0,5; 1,0 и 1,8 м от поверхности земли
С поднятием на оборудование и конструкции	Независимо от наличия средств защиты	На высоте 0,5; 1,0 и 1,8 м от площадки рабочего места и на расстоянии 0,5 м от заземленных токоведущих частей оборудования

Литература[править | править код]

Сивухин Д. В. Общий курс физики. — Изд. 4-е, стереотипное. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — 656 с. — ISBN 5-9221-0227-3; ISBN 5-89155-086-5..

Примечания[править | править код]

↑ Напряжённость электрического поля // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 246. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
↑ Для любой частицы её электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
↑ Иногда его значения могут оказываться и одинаковыми в разных точках пространства; если одинаков всюду в пространстве (или в какой-то области), говорят об однородном электрическом поле — это частный, наиболее простой, случай электрического поля; в реальности электрическое поле может быть однородным лишь приближённо, то есть различия в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
↑ Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (в которой вектор напряжённости электрического поля вместе с вектором магнитной индукции входит в тензор электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле — одна из основных составляющих электромагнитного поля, не утрачивает смысла.
↑ Хотя исторически многие из них были открыты раньше.

См. также[править | править код]

Электрическая индукция
Уравнения Максвелла
Закон Кулона

Источник

Электростатика – раздел электродинамики,
изучающий взаимодействие неподвижных
электрических зарядов.

Электрический заряд – физическая
величина, определяющая силу электромагнитного
взаимодействия. Заряд обозначается
буквой q, измеряется
в кулонах (Кл).

В природе существует два вида
электрических зарядов, которые условно
назвали «положительный» и «отрицательный».
Заряды одного знака отталкиваются,
разных знаков – притягиваются.

Электрический заряд всегда связан с
частицей. Существуют частицы без заряда,
но не существует заряда без частицы.
Величина электрического заряда не
зависит от скорости движения частицы.

Минимальный заряд, встречающийся в
природе, называется элементарным.
Величина элементарного заряда е =
1,610^-19
Кл. Заряды электрона, протона, позитрона
(античастица для электрона) равны по
модулю элементарному. Заряд любого
макроскопического тела кратен
элементарному, т. е. электрический заряд
– дискретная величина.

Все вещества состоят из атомов или
молекул. Атом состоит из положительно
заряженного ядра и отрицательно
заряженных электронов, движущихся
вокруг ядра. Поэтому любое макроскопическое
тело содержит электрически заряженные
частицы. Если суммарный заряд тела равен
нулю, то говорят что тело электрически
нейтральное или незаряженное. Электрический
заряд любой системы равен алгебраической
сумме зарядов тел, входящих в систему.
Заряды могут перераспределятся между
телами системы. Если система тел
электрически изолирована (через границу
системы не проникают другие заряды), то
в ней выполняется закон сохранения
заряда:

алгебраическая сумма зарядов электрически
изолированной системы постоянна:

q₁
+ q₂
+ … + q_n
= const.

Электризация – это процесс получения
электрически заряженных тел из
нейтральных.

При электризации трением одни вещества
отдают электроны, а другие их присоединяют.
Причина этого явления – в различии
энергии связи электронов с атомами в
этих веществах. Атом, потерявший электрон
называется положительным ионом,
присоединивший к себе электрон –
отрицательным ионом.

Точечный заряд – это заряженное
тело, размер которого много меньше
расстояния его возможного действия на
другие тела.

Закон Кулона (1875 г.): Сила взаимодействия
между двумя неподвижными точечными
зарядами, находящимися в вакууме, прямо
пропорциональна произведению модулей
зарядов, обратно пропорциональна
квадрату расстояния между ними и
направлена по прямой, соединяющей
заряды:
.

Коэффициент k, входящий
в закон Кулона, зависит от выбора системы
единиц. В системе СИ
.
Здесь

– электрическая постоянная.

Закон Кулона был получен экспериментально.
Он справедлив только для точечных
зарядов или равномерно заряженных
шаров. Электростатические взаимодействия
осуществляются посредством
электростатического поля.

Электростатическое поле это вид
материи который образуется неподвижными
электрическими зарядами и его можно
обнаружить по его действию на неподвижные
электрические заряды.

Силовой характеристикой электростатического
поля является напряженность –
векторная физическая величина, численно
равная силе с которой поле действует
на единичный пробный положительный
заряд, помещенный в заданной точке поля.
.
Направление вектора напряженности
совпадает с направлением вектора силы,
действующей на положительный заряд,
помещенный в данной точке поля. Из закона
Кулона на основании определения
напряженности поля получаем формулу
для напряженности поля точечного заряда
на расстоянии r от него:

Для наглядности электростатическое
поле представляют непрерывными линиями
напряженности – касательные к которым
в каждой точке совпадают по направлению
с направлением вектора напряженности
электростатического поля в данной
точке.

Линии напряженности не пересекаются
(в противном поле напряженность поля в
точке пересечения не имела бы определенного
значения); начинаются на положительных
зарядах (источники поля) и стекаются к
отрицательным зарядам (стоки). Модуль
вектора напряженности пропорционален
числу линий напряженности на густоте
линий напряженности можно судить о
модуле вектора напряженности на единицу
поверхности (густоте линий напряженности).

Электростатическое поле, векторы
напряженности которого одинаковы во
всех точках пространства, называется
однородным.

Принцип суперпозиции электрических
полей: напряженность поля системы
зарядов в данной точке равна векторной
сумме напряженностей полей, созданным
в этой точке каждым зарядом в отдельности:
.

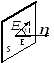
Теорема Гаусса.

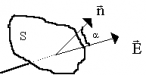
Потоком вектора напряженности через
замкнутый контур площадью S
называется произведение проекции
вектора напряженности на нормаль к
контуру на площадь контура:
.

Поток вектора напряженности через
произвольную замкнутую поверхность
равен алгебраической сумме зарядов,
расположенных внутри этой поверхности,
деленной на электрическую постоянную:
.

Напряженность поля точечного заряда.

Для
определения напряженности проведем
сферическую поверхность S
радиусом r с центром
совпадающим с зарядом и воспользуемся
теоремой Гаусса. Так как внутри указанной
области находится только один заряд q,
то согласно указанной теореме получим
равенство:

(1), где E_n
– нормальная составляющая напряженности
электрического поля. Из соображений
симметрии нормальная составляющая
должна быть равна самой напряженности
и постоянна для всех точек сферической
поверхности, поэтому E=E_n=const.
Поэтому ее можно вынести за знак суммы.
Тогда равенство (1) примет вид
,
что и было получено из закона Кулона и
определения напряженности электрического
поля.

Электрическое поле заряженной сферы

Если
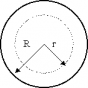
сфера проводящая, то весь заряд находится
на поверхности. Рассмотрим две области
I – внутри сферы радиуса
R с зарядом q
и вне сферы область II.

Для определения напряженности в области
I проведем сферическую
поверхность S₁
радиусом r₁ (0<r₁<R)
и воспользуемся теоремой Гаусса. Так
как внутри указанной области зарядов
нет, то согласно указанной теореме
получим равенство:

(1), где E_n
– нормальная составляющая напряженности
электрического поля. Из соображений
симметрии нормальная составляющая
должна быть равна самой напряженности
и постоянна для всех точек сферической
поверхности, поэтому E₁=E_n=const.
Поэтому ее можно вынести за знак суммы.
Тогда равенство (1) примет вид
.
Т. к. площадь сферы не равна нулю, то Е₁=0
(во всех точках области I)
– внутри проводника зарядов нет и
напряженность поля равна нулю.

В области II Rr₂
проведем сферическую поверхность S₂
радиусом r₂ и
воспользуемся теоремой Гаусса:

(2), 

– напряженность поля вне сферы
рассчитывается по той же формуле, что
и напряженность поля точечного заряда.

Электрическое поле заряженного шара

Заряд равномерно распределен по всему
объему шара, поэтому введем понятие
объемной плотности заряда:
.
Рассмотрим две области I
– внутри сферы радиуса R
с зарядом q и вне сферы
область II.

Для определения напряженности в области
I проведем сферическую
поверхность S₁
радиусом r₁ (0<r₁<R)
и воспользуемся теоремой Гаусса:

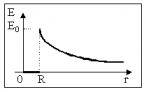
– напряженность поля внутри шара
увеличивается прямо пропорционально
расстоянию до центра шара.

В области II R
 r₂
проведем сферическую поверхность S₂
радиусом r₂ и
воспользуемся теоремой Гаусса:

(2), 

– напряженность поля вне шара рассчитывается
по той же формуле, что и напряженность
поля точечного заряда.

Электрическое поле заряженной нити

Для
равномерно заряженной нити введем
понятие линейной плотности заряда.
Для определения напряженности окружим
участок проволоки длиной ℓ
цилиндрической поверхностью S
радиусом r с осью совпадающей
с проволокой и воспользуемся теоремой
Гаусса. При этом весь поток вектора
напряженности будет проходить только
через боковую поверхность цилиндра,
площадь которой
,
т.к. поток через оба основания цилиндра
равен нулю. Тогда

– напряженность поля нити убывает обратно
пропорционально расстоянию.

Напряженность поля заряженной плоскости

Если
плоскость бесконечна и заряжена
равномерно, т. е. поверхностная плотность
заряда  = q/S
одинакова в любом ее месте, то линии
напряженности электрического поля в
любой точке перпендикулярны этой
плоскости. Такое же направление они
сохраняют и на любом расстоянии от
плоскости, т.е. поле заряженной плоскости
однородное.

Для нахождения напряженности электрического
поля заряженной плоскости мысленно
выделим в пространстве цилиндр, ось
которого перпендикулярна заряженной
плоскости, а основания параллельны ей
и одно из оснований проходит через
интересующую нас точку поля. Цилиндр
вырезает из заряженной плоскости участок
площадью S, и такую же
площадь имеют основания цилиндра,
расположенные по разные стороны от
плоскости (рис.). Согласно теореме Гаусса
поток Ф вектора напряженности
электрического поля через поверхность
цилиндра связан с электрическим зарядом
внутри цилиндра выражением
.
С другой стороны, так как линии
напряженности пересекают лишь основания
цилиндра, поток вектора напряженности
можно выразить через напряженность
электрического поля у обоих оснований
цилиндра:
.
В самом деле, поток через боковую
поверхность цилиндра (см. рис.), равен
нулю, поскольку линии напряженности
параллельны боковой поверхности
цилиндра.

Из двух выражений для потока вектора
напряженности получим:
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Законом Кулона описывается взаимодействие заряженных частиц. Однако большинство сил, с которыми мы работали, возникает при взаимодействии тел посредством контакта (т.е. тела касаются друг друга). В случае электромагнитного взаимодействия контакта нет, тогда взаимодействие происходит посредством неких невидимых элементов. Тогда взаимодействия между частицами вещества и удалёнными друг от друга макроскопическими телами осуществляются через посредство физических полей, которые создаются этими частицами или телами в окружающем пространстве. В случае с заряженными частицами, эти поля назовём электромагнитными.

Тогда логика электромагнитного взаимодействия такова: заряд создаёт вокруг себя электромагнитное поле, которое, в свою очередь, действует на любой другой заряд displaystyle q , находящийся на любом расстоянии от источника.

Закон Кулона описывает взаимодействие между двумя зарядами:

$displaystyle left| {{F}_{k}} right|=kfrac{left| Q right|left| q right|}{{{r}^{2}}}$ (1)

где

Рис. 1. Закон Кулона. Пробный заряд

Сила (1) зависит от обоих зарядов, что не позволяет толком описать электрическое поле, создаваемое каждым из взаимодействующих частиц. Тогда придумаем немного другую систему: возьмём пробный заряд — некий малый заряд, который не будет искажать поле исследуемого нами заряда displaystyle left| Q right| . Поместим пробный заряд в различные точки пространства рядом с исследуемым нами зарядом и проиллюстрируем силы Кулона (рис. 1).

В принципе, значение силы Кулона можно найти в любой точке пространства, однако данные силы зависят как от заряда источника, так и от значения пробного заряда. Введём новую переменную, поделив значение силы Кулона на значение пробного заряда:

$displaystyle vec{E}=frac{{{{vec{F}}}_{k}}}{q}$ (2)

где
- — вектор напряжённости электрического поля.

Подставим силу Кулона в (1):

$displaystyle vec{E}=kfrac{Qq}{q{{r}^{3}}}vec{r}=kfrac{Q}{{{r}^{3}}}vec{r}$ (3)

Исходя из (3), можно заключить, что напряжённость электрического поля зависит от заряда источника поля и точки наблюдения, описываемой расстоянием от заряда (рис. 2).

Рис. 2. Напряжённость электрического поля

Т.е. напряжённость электрического поля — параметр, описывающий поле, создаваемое зарядом-источником. Значение напряжённости электрического поля позволяет оценить сильно или слабо будет действовать поле на заряд, помещённый в него. Размерность displaystyle vec{E} — В/м.

Исходя из (3), можно найти напряжённость поля точечного заряда. Напряжённость электрического поля — величина векторная, поэтому для её нахождения необходимо знать как модуль, так и направление вектора. Начнём с модуля:

$displaystyle left| {vec{E}} right|=kfrac{left| Q right|}{{{r}^{3}}}left| {vec{r}} right|=kfrac{left| Q right|}{{{r}^{2}}}$ (4)

Рис. 3. Напряжённость электрического поля (направление)

Чтобы выяснить направление вектора, воспользуемся уравнением (2). Исходя из (2), можно заключить, что направление напряжённости электрического поля совпадает с направлением силы Кулона, а направление силы Кулона зависит от знака взаимодействующих зарядов. Чтобы не заморачиваться с рассмотрением этих зарядов в каждой задаче, просто договоримся. Если источник поля (заряд) положителен, тогда напряжённость поля направлена от заряда, если источник поля (заряд) отрицателен, тогда напряжённость поля направлена к заряду (рис. 3).

Напряжённость системы зарядов. Принцип суперпозиции напряжённости.

В случае, если в задаче источниками поля являются несколько зарядов, тогда напряжённость в интересующей точке можно найти как векторную сумму напряжённостей от каждого из зарядов:

$displaystyle {{vec{E}}_{o}}=sumlimits_{i}{{{{vec{E}}}_{i}}}$ (5)

Важно: поиск векторной суммы чаще всего сопряжён с реализацией теоремы Пифагора, теоремы косинусов или синусов, иногда с проецированиием векторов напряжённости на оси с последующим суммированием.

Рис. 4. Принцип суперпозиции напряжённости

Проиллюстрируем: пусть в системе присутствует 3 заряда ( $displaystyle {{q}_{2}}$ , $displaystyle {{q}_{3}}$ , $displaystyle {{vec{r}}_{1}}$ ), найти напряжённость в точке А, находящейся на заданном расстоянии от каждого из них ( $displaystyle {{vec{r}}_{2}}$ , $displaystyle {{vec{r}}_{3}}$ , $displaystyle {{vec{r}}_{3}}$ ) (рис. 4).

Пользуясь знаниями о зарядах, расставляем направления напряжённостей от каждого из зарядов, значение модуля каждой из них можем найти из (4). А далее геометрически складываем, получая искомый $displaystyle {{vec{E}}_{o}}$ .

Напряжённость поля бесконечной заряженной плоскости.

Отдельно в школьной физике рассматривается бесконечная (осень большая) заряженная равномерно плоскость (рис. 5).

Рис. 5. Напряжённость бесконечной плоскости

Напряжённость такой плоскости вблизи её:

$displaystyle E=frac{sigma }{2varepsilon {{varepsilon }_{0}}}$ (6)

В (6) использовалось определение поверхностной плотности заряда:

$displaystyle sigma =frac{Q}{S}$ (7)

Важно: напряжённость бесконечной плоскости не зависит от расстояния от плоскости.

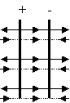
Напряжённость поля двух бесконечных заряженных плоскостей (конденсатор).

Рис. 6. Напряжённость двух бесконечных плоскостей

Если составить систему из двух бесконечных плоскостей, заряженных одинаковым по модулю и различным по знаку зарядом (при этом площади плоскостей одинаковы), то общая напряжённость между ними:

$displaystyle {{E}_{0}}=frac{sigma }{2varepsilon {{varepsilon }_{0}}}+frac{sigma }{2varepsilon {{varepsilon }_{0}}}=frac{sigma }{varepsilon {{varepsilon }_{0}}}=frac{q}{varepsilon {{varepsilon }_{0}}S}$ (8)

Уравнение (8) характеризует напряжённость внутри конденсатора (рис. 6).

Вывод: в случае, если в задаче требуется найти напряжённость, она дана, достаточно рассмотреть систему. Различных систем, а соответственно, и формул, немного: точечный заряд, шар, система точечных зарядов и бесконечные плоскости. Для каждой системы — своё решение.

Источник

Напряженность поля точечного заряда.
Обозначим: q – заряд, создающий поле, q₀ – заряд, помещенный в поле (внешний заряд). Закон Кулона: . Напряженность поля: . Тогда напряженность поля точечного заряда:
Теорема Гаусса. Потоком вектора напряженности наз. величина Ф, равная произведению модуля вектора напряженности на площадь контура S, ограничивающую некоторую площадь, и на косинус угла между вектором напряженности и нормалью (перпендикуляром) к площадке.
Если считать, что напряженность пропорциональна числу силовых линий, приходящихся на единицу площади поверхности (т.е. густоте), то поток напряженности пропорционален полному числу силовых линий, пересекающих данный контур.
Поток линий напряженности электростатического поля через произвольную замкнутую поверхность прямо пропорционален величине заряда, находящегося в области пространства, ограниченного данной поверхностью.
*Применения теоремы Гаусса.*
1. Напряженность поля заряженной проводящей сферы радиуса R. Сфера заряжена по поверхности. А) Внутри сферы заряда нет . Е=0
Б) Снаружи сферы.
На поверхности сферы:
2. Напряженность поля шара заряженного по объему.
Введем понятие объемной плотности заряда: Объемная плотность заряда показывает, какой заряд содержится в единице объема заряженного по всему объему тела. Объем шара произвольного радиуса . Обозначим q – заряд шара, q₀ – заряд, находящийся внутри объема произвольного радиуса.
Тогда заряд сферы радиуса r , будет: Следовательно: . – напряженность поля внутри шара, равномерно заряженного по объему. Снаружи – см. 1.
3. Напряженность поля бесконечной заряженной плоскости.
Введем понятие поверхностной плотности заряда: . Тогда . Коэффициент 2 появляется, т.к. плоскость окружена двумя поверхностями площадью S. Поле бесконечной заряженной плоскости не зависит от расстояния от плоскости! Можно пользоваться, когда расстояние много меньше размеров плоскости. 4. Напряженность поля плоского воздушного конденсатора. Из рисунка видим, что снаружи конденсатора поля пластин взаимно скомпенсированы, и общее поле равно нулю. Внутри конденсатора поля складываются. Используя вывод п.3 получаем: . Формула справедлива при условии, что расстояние между пластинами много меньше размеров самих пластин и вдали от краев пластин.