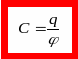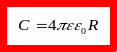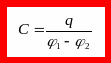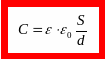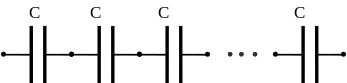Как найти напряженность электрического поля в конденсаторе – Сайт, где вы сможете решить свои вопросы

Конденсатор. Энергия электрического поля

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Ёмкость уединённого проводника
Ёмкость плоского конденсатора
Энергия заряженного конденсатора
Энергия электрического поля

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.

Но прежде введём понятие электрической ёмкости.

к оглавлению ▴

Ёмкость уединённого проводника

Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение $varphi$ , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать $1/C$ , так что

$varphi = frac{displaystyle q}{displaystyle C vphantom{1^a}}.$

Величина $C$ называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

$C = frac{displaystyle q}{displaystyle varphi }.$ (1)

Например, потенциал уединённого шара в вакууме равен:

$varphi = frac{displaystyle kq}{displaystyle R vphantom{1^a}}=frac{displaystyle q}{displaystyle 4 pi varepsilon_0R vphantom{1^a}},$

где $q$ — заряд шара, $R$ — его радиус. Отсюда ёмкость шара:

$C=4 pi varepsilon_0R.$ (2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью $varepsilon$ , то его потенциал уменьшается в $varepsilon$ раз:

$varphi = frac{displaystyle q}{displaystyle 4 pi varepsilon_0 varepsilon R vphantom{1^a}}.$

Соответственно, ёмкость шара в $varepsilon$ раз увеличивается:

$C=4 pi varepsilon_0 varepsilon R.$ (3)

Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.

Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на $1$ В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным $6400$ км.

$C = 4 pi varepsilon_0 R approx 4 cdot 3,14 cdot 8,85 cdot 10^{-12} cdot 6400 cdot 10^3 approx 712$ мкФ.

Как видите, $1$ Ф — это очень большая ёмкость.

Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной $varepsilon_0$ . В самом деле, выразим $varepsilon_0$ из формулы (2):

$varepsilon_0 = frac{displaystyle C} {displaystyle 4 pi R vphantom{1^a}}.$

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

$varepsilon_0 = 8,85 cdot 10^{-12}$ Ф.

Так легче запомнить, не правда ли?

к оглавлению ▴

Ёмкость плоского конденсатора

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух $left ( varepsilon =1 right ).$

Пусть заряды обкладок равны $+q$ и $-q$ . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина $q$ — заряд положительной обкладки — называется зарядом конденсатора.

Пусть $S$ — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

$E_+ = E_-=frac{displaystyle sigma }{displaystyle 2 varepsilon_0 vphantom{1^a}}.$

Здесь $E_+$ — напряжённость поля положительной обкладки, $E_-$ — напряженность поля отрицательной обкладки, $sigma$ — поверхностная плотность зарядов на обкладке:

$sigma =frac{displaystyle q}{displaystyle S vphantom{1^a}}.$

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля $vec{E}$ имеем:

$vec{E} = vec{E}_+ + vec{E}_-$

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

$E = E_+ - E_-=0.$

Внутри конденсатора поле удваивается:

$E = E_+ + E_-= frac{displaystyle sigma }{displaystyle varepsilon_0},$

или

$E = frac{displaystyle q}{displaystyle varepsilon_0 S vphantom{1^a}}.$ (4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно $d$ . Поскольку поле внутри конденсатора является однородным, разность потенциалов $U$ между обкладками равна произведению $E$ на $d$ (вспомните связь напряжения и напряжённости в однородном поле!):

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 S vphantom{1^a}}.$ (5)

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

$C=frac{displaystyle q}{displaystyle U vphantom{1^a}}.$ (6)

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на $1$ В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:

$C=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}}.$ (7)

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью $varepsilon$ . Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в $varepsilon$ раз, так что вместо формулы (4) теперь имеем:

$E=frac{displaystyle q}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$ (8)

Соответственно, напряжение на конденсаторе:

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$ (9)

Отсюда ёмкость плоского конденсатора с диэлектриком:

$C=frac{displaystyle varepsilon_0 varepsilon S}{displaystyle d vphantom{1^a}}.$ (10)

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.

к оглавлению ▴

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора $q$ , площадь обкладок $S$ .

Возьмём на второй обкладке настолько маленькую площадку, что заряд $q_0$ этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

$F_0 = q_0E_1,$

где $E_1$ — напряжённость поля первой обкладки:

$E_1=frac{displaystyle sigma }{displaystyle 2 varepsilon _0 vphantom{1^a}}=frac{displaystyle q}{displaystyle 2varepsilon_0 S vphantom{1^a}}.$

Следовательно,

$F_0=frac{displaystyle q_0q}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила $F$ притяжения второй обкладки к первой складывается из всех этих сил $F_0$ , с которыми притягиваются к первой обкладке всевозможные маленькие заряды $q_0$ второй обкладки. При этом суммировании постоянный множитель $q/(2 varepsilon_0 S)$ вынесется за скобку, а в скобке просуммируются все $q_0$ и дадут $q$ . В результате получим:

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$ (11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины $d_1$ до конечной величины $d_2$ . Сила притяжения пластин совершает при этом работу:

$A = F(d_1 - d_2).$

Знак правильный: если пластины сближаются $(d_2 < d_1)$ , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины $(d_2 > d_1)$ , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

$A=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}left ( d_1-d_2 right )=frac{displaystyle q^2d_1}{displaystyle 2varepsilon_0 S vphantom{1^a}}-frac{displaystyle q^2d_2}{displaystyle 2varepsilon_0 S vphantom{1^a}}=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}}-frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}=W_1-W_2,$

где
$W_1=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}},$
$W_2=frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}$

Это можно переписать следующим образом:

$A = -(W_2 - W_1) = - Delta W,$

где

$W=frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}}.$ (12)

Работа потенциальной силы $F$ притяжения обкладок оказалась равна изменению со знаком минус величины $W$ . Это как раз и означает, что $W$ — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.

Используя соотношение $q = CU$ , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

$W=frac{displaystyle qU}{displaystyle 2 vphantom{1^a}},$ (13)

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}.$ (14)

Особенно полезными являются формулы (12) и (14).

Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью $varepsilon$ . Сила притяжения обкладок уменьшится в $varepsilon$ раз, и вместо (11) получим:

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 varepsilon S vphantom{1^a}}.$

При вычислении работы силы $F$ , как нетрудно видеть, величина $varepsilon$ войдёт в ёмкость $C$ , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).

Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

к оглавлению ▴

Энергия электрического поля

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}} cdot frac{displaystyle (Ed)^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}Sd.$

Но $Sd = V$ — объём конденсатора. Получаем:

$W=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}V.$ (15)

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля $E$ , сосредоточенного в некотором объёме $V$ .

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина $omega = W/V$ — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:

$omega =frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}.$ (16)

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в $varepsilon$ раз, и вместо формул (15) и (16) будем иметь:

$W =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}V.$ (17)

$omega =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}.$ (18)

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Конденсатор. Энергия электрического поля» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Напряженность электрического поля в конденсаторе. Калькулятор онлайн.

Онлайн калькулятор вычисления напряженности электрического поля в конденсаторе, позволит найти напряженность E плоского, цилиндрического и сферического конденсаторов и даст подробное решение.
Единицы измерения, могут включать любые приставки Си. Калькулятор автоматически переведет одни единицы в другие.

Калькулятор вычислит:
Напряженность электрического поля в плоском конденсаторе.
Напряженность электрического поля в цилиндрическом конденсаторе.
Напряженность электрического поля в сферическом конденсаторе.

Напряженность электрического поля в плоском конденсаторе

Напряженность электрического поля в плоском конденсаторе 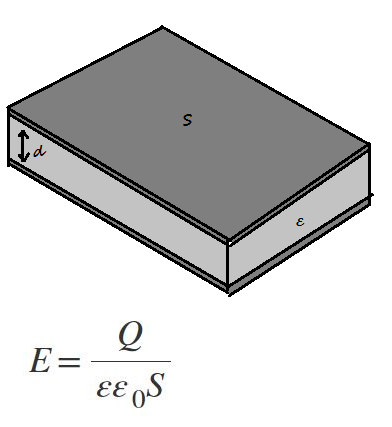Плоский конденсатор представляет собой две параллельные проводящие пластины, разделенные диэлектриком, расположенные на малом расстоянии друг от друга.

В плоском конденсаторе электрическое поле E однородно и не зависит от расстояния d между пластинами, так как расстояние d мало по сравнению с размерами пластин.

Напряженность электрического поля в плоском конденсаторе определяется формулой, где
Q – заряд на пластине
ε₀ – электрическая постоянная, ε₀ = 8.85418781762039 × 10^-12
ε – диэлектрическая проницаемость диэлектрика
S – площадь пластины

Единицей измерения напряженности электрического поля является – Вольт (В, V).

Диэлектрическая проницаемость ε =
Заряд Q =
Площадь пластины S =
Единица измерения напряженности поля E

Напряженность электрического поля в цилиндрическом конденсаторе

Напряженность электрического поля в цилиндрическом конденсаторе 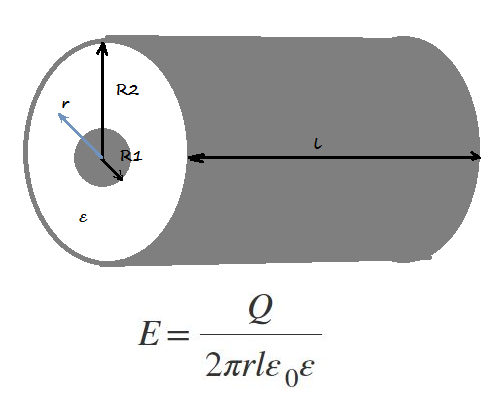Цилиндрический конденсатор представляет собой конденсатор, обкладками, которого являются два цилиндра, внутренний с радиусом R₁ и внешний с радиусом R₂. Между обкладками находится диэлектрик с диэлектрической проницаемостью ε.

Напряженность электрического поля в цилиндрическом конденсаторе определяется формулой, где
Q – заряд
π – число Пи (3.14)
ε₀ – электрическая постоянная, ε₀ = 8.85418781762039 × 10^-12
ε – диэлектрическая проницаемость диэлектрика
l – длина цилиндра
r – расстояние от оси симметрии цилиндров до точки, в которой необходимо найти напряженность электрического поля. Важно R1 < r < R2, так как в области от центра конденсатора и до R1, а так же в области превышающей R2 зарядов нет и поле равно нулю.

Единицей измерения напряженности электрического поля является – Вольт (В, V).

Диэлектрическая проницаемость ε =
Заряд Q =
Радиус r =
Длина l =
Единица измерения напряженности поля E

Напряженность электрического поля в сферическом конденсаторе

Напряженность электрического поля в сферическом конденсаторе 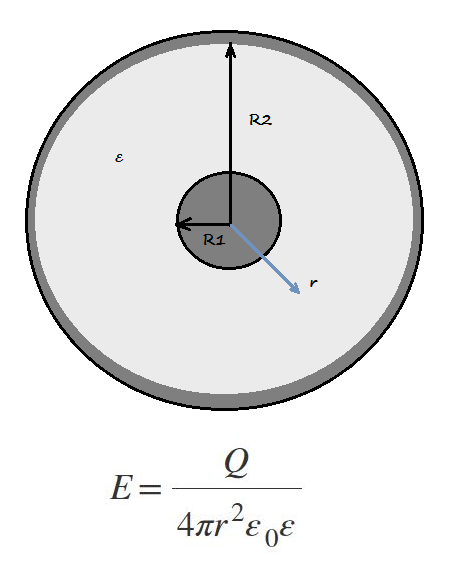Сферический конденсатор представляет собой конденсатор, обкладками которого являются две концентрические сферы, радиусами R1 и R2, между которыми расположен диэлектрик, с диэлектрической проницаемостью ε.

Напряженность электрического поля в сферическом конденсаторе определяется формулой, где
Q – заряд
π – число Пи (3.14)
ε₀ – электрическая постоянная, ε₀ = 8.85418781762039 × 10^-12
ε – диэлектрическая проницаемость диэлектрика
r – расстояние от оси симметрии цилиндров до точки, в которой необходимо найти напряженность электрического поля. Важно R1 < r < R2, так как в области от центра конденсатора и до R1, а так же в области превышающей R2 зарядов нет и поле равно нулю.

Единицей измерения напряженности электрического поля является – Вольт (В, V).

Диэлектрическая проницаемость ε =
Заряд Q =
Радиус r =
Единица измерения напряженности поля E

Вам могут также быть полезны следующие сервисы

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажер по математике

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Источник

Для школьников.

Получена формула для напряжённости электрического поля плоского конденсатора, широко применяемого в электрических цепях. Для этого надо применить теорему Гаусса и найти сначала формулу напряжённости для одной заряженной пластины, а затем для параллельных заряженных пластин.

Итак, рассмотрена теорема Гаусса и её применение для получения формул нахождения напряжённости электростатических полей, создаваемых протяжёнными заряженными телами. По ходу найдено выражения для напряжённости электрического поля плоского конденсатора.

Подумайте над решением следующих задач:

1. К вертикальной равномерно заряженной пластине с плотностью заряда 4 10 -7 Кл/м2 прикреплена нить. На нити подвешен заряженный шарик массой 1 г. Знаки заряда пластины и шарика одинаковы. Найти заряд шарика, если нить образует с вертикалью угол 30 градусов. Ответ: 2,5 10 -7 Кл

2. Электрон влетает в плоский горизонтально расположенный конденсатор длиной 5 см. При вылете из конденсатора электрон отклоняется от своего первоначального направления на 2 мм. Напряжённость электрического поля внутри конденсатора 20 кВ/м. Какую скорость и кинетическую энергию имел электрон перед влётом в конденсатор? Ответ: 4,7 10 7 м/с; 10 -15 Дж.

Отвечаю на вопрос о напряжённости электрического поля, создаваемого заряженной пластинкой конечных размеров:

На рисунке ниже показана тонкая заряженная пластинка конечных размеров и силовые линии электрического поля, создаваемого ею.

В этом случае полученная формула для напряжённости поля, создаваемого бесконечной заряженной плоскостью, справедлива только для точек, расположенных внутри области, ограниченной пунктирной линией.

В других точках, расположенных всё дальше от пластинки и всё ближе к её краям, будет всё более отличаться от поля, создаваемого бесконечной заряженной плоскостью.

На расстояниях значительно больших размера пластинки электрическое поле можно рассматривать как поле точечного заряда (заряд пластинки принимается за точечный заряд).

Занятие 6. Дифференцирование. Интегрирование.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: решение задач к занятию 47.

Следующая запись: Как поведёт себя электрон, влетевший в электрическое поле плоского конденсатора?

Ссылки на занятия до электростатики даны в Занятии 1.

Ссылки на занятия, начиная с электростатики, даны в Занятии 45.

Источник

Конденсатор представляет собой устройство, которое накапливает электрический заряд в виде разности потенциалов между двумя пластинами и электрического поля в конденсаторе при приложении источника напряжения.

Разность потенциалов создается переносом электронов от положительной клеммы к отрицательной клемме конденсатора и созданием электрического поля в конденсаторе. Эта разность зарядов хранит электрическую энергию в виде потенциала заряда и пропорциональна плотности заряда на каждой пластине.

Электрическое поле в формуле конденсатора

Подобно положительным и отрицательным зарядам, пластина конденсатора также ведет себя как акцепторная и донорная пластина, когда источник проходит через пластины конденсатора. Положительный вывод конденсатора будет отдавать электрон, и эти свободные электроны будут приняты отрицательным выводом конденсатора.

Различные типы конденсаторов; Кредит изображения: Pixabay

Из-за подвижности свободных зарядов внутри конденсатора будет введен электрический поток и полное электрическое поле в конденсаторе будет

Е=δ/∈₀

Плотность заряда каждой пластины конденсатора называется поверхностной плотностью, которая определяется как заряд, присутствующий на поверхности пластины на единицу площади, и выражается как σ =В/О.

Следовательно,

$E=\frac{Q}{\varepsilon _0A}$

Это уравнение дает электрическое поле, создаваемое между двумя пластинами конденсатора.

Электрическое поле внутри конденсатора

Конденсатор состоит из двух обкладок с разной плотностью заряда. электрический поток проходит через обе поверхности каждой пластины, следовательно, площадь = 2A.

Рассмотрим две пластины, имеющие положительную плотность поверхностного заряда и отрицательную плотность поверхностного заряда, разделенные расстоянием d. Пусть А – площадь пластин. Линия электрического потока проходит от положительно заряженной пластины к пластине с большинством отрицательных носителей, как показано на рисунке ниже.

электрическое поле в конденсаторе

Параллельный пластинчатый конденсатор

Пусть P будет любой точкой посередине двух заряженных пластин конденсатора.

Применяя закон Гаусса,

φ =ЭА

Электрическое поле, создаваемое одной заряженной пластиной конденсатора, равно

E.2A= q/ε₀

Мы знаем, что σ = Q/A

$\Rightarrow q=\sigma A$

Используя это в приведенном выше уравнении

$E.2A=\frac{\sigma A}{\varepsilon _0}$ $2E=\frac{\sigma }{\varepsilon _0}$ $E=\frac{\sigma }{2\varepsilon _0}$

Следовательно, результирующее электрическое поле в любой точке между пластинами конденсатора будет складываться.

$E=\frac{\sigma }{2\varepsilon _0}+\frac{\sigma }{2\varepsilon _0}$ $E=\frac{\sigma }{\varepsilon _0}$

Подставляя значение для σ, мы получаем

$E=\frac{q}{\varepsilon _0 A}$

Это полное электрическое поле внутри конденсатора из-за двух параллельных пластин.

Какое электрическое поле создает плоский конденсатор с площадью поверхности 0.3 м?² и несущий заряд 1.8С?

Данный: д=1.8°С

А= 0.3 м²

У нас есть

$E=\frac{q}{\varepsilon _0 A}$ $=\frac{1.8}{8.85\times 10^{-12}\times 0.3}$

= 0.68 х 10¹² В / м

Электрическое поле, создаваемое параллельным конденсатором с зарядом 1.8 Кл, составляет 0.68 х 10¹² В / м.

Электрическое поле вне конденсатора

Теперь, если точка P лежит вне конденсатора, то электрическое поле в точке P из-за пластины, имеющей положительно заряженную поверхностную плотность, равно

$E_1=\frac{\sigma }{2\varepsilon _0 }$

Принимая во внимание, что электрическое поле в точке P из-за отрицательного заряда пластины поверхностной плотности конденсатора равно

$E_2=\frac{-\sigma }{2\varepsilon _0 }$

Следовательно, суммарное электрическое поле, создаваемое обеими пластинами конденсатора, равно

Э=Э₁+E₂

$E=\frac{\sigma }{2\varepsilon _0 }-\frac{\sigma }{2\varepsilon _0 }$

Е = 0

В любой точке вне конденсатора электрическое поле всегда равно нулю. Потому что при подаче электрического тока через конденсатор один вывод конденсатора будет иметь положительную поверхностную плотность заряда, а другой – отрицательную.

Электрическое поле в конденсаторе с диэлектриком

Теперь мы знать, что в присутствии вакуума, электрическое поле внутри конденсатора равно E=σ/ε₀ , разность потенциалов между двумя пластинами равна V=Ed, где d — расстояние, разделяющее две пластины, и, следовательно, емкость в этом случае равна

С= Q/V = ε₀Объявление

Теперь, если мы поместим диэлектрик между двумя пластинами конденсатора с поляризацией, занимающий все пространство между двумя пластинами, поверхностные плотности заряда двух пластин равны +σ_p и –σ_n. Таким образом, суммарная плотность поверхностного заряда обеих пластин равна

$\pm \left ( \sigma_p -\sigma _n \right )$

Следовательно, электрическое поле через конденсатор равно

$E=\frac{\left ( \sigma_p -\sigma _n \right )}{\varepsilon _0}$

Таким образом, разность потенциалов становится

$V=Ed=\frac{\left ( \sigma_p -\sigma _n \right )}{\varepsilon _0}d$

Для линейных диэлектриков

$\left ( \sigma_p -\sigma _n \right )\propto \sigma$

Итак,

$\left ( \sigma_p -\sigma _n \right )=\frac{\sigma }{k}$

Где k является диэлектрической проницаемостью и больше 1, т.е. k>1.

Следовательно, разность потенциалов теперь становится

$V=\frac{\sigma d}{\varepsilon _0 k}$

Вставка значения поверхностной плотности заряда

V= Qd/Aε₀k

Следовательно, емкость конденсатора равна

С= Q/V = ε₀кА/д

ε₀k — диэлектрическая проницаемость среды и обозначается как ε

Поэтому уравнение теперь становится

C= εA/d

Чему равны электрическое поле и разность потенциалов конденсатора в присутствии диэлектрической среды с проницаемостью 6×10?^-12 C²N^-1m^-2 шириной 3 см при плотности поверхностного заряда 6 Кл/м² и -5.8 Кл/м²?

Данный: σ_p=6 Кл/м²

σ_n=-5.8 Кл/м²

ε₀= 6 x 10^-12 C²N^-1m^-2

г=3 см=0.03 м

Электрическое поле конденсатора равно

$E=\frac{\left ( \sigma_p -\sigma _n \right )}{\varepsilon _0}$ $=\frac{\left (6-5.8 \right )}{6\times 10^{-12}}$ $=\frac{0.2}{6\times 10^{-12}}$ $=3.3\times 10^{10}V/m$

Электрическое поле конденсатора равно 3.3 х 10¹⁰ В/м, поэтому разность потенциалов между обкладками конденсатора равна

В=Эд

= 3.3 х 10¹⁰ х 0.03

= 0.099 х 10¹⁰ V

= 0.1 х 10¹⁰ V

Разность потенциалов между двумя пластинами конденсатора составляет 0.1 х 10¹⁰V.

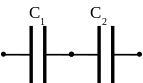
Последовательный конденсатор электрического поля

При последовательном соединении конденсаторов разность потенциалов между обкладками складывается. Если у нас есть два конденсатора C₁ и C₂ соединены последовательно, а разность потенциалов на пластинах равна V₁ и V₂ соответственно, тогда чистая разность потенциалов становится

В=В₁+V₂

Емкость C= Q/V

Следовательно, V=Q/C

Используя это в приведенном выше уравнении, мы получаем

В=К/К₁ + вопрос/ответ₂

Решение этого дальше

$V=Q\left ( \frac{1}{C_1}+\frac{1}{C_2} \right )$ $V=Q\left ( \frac{C_1+C_2}{C_1C_2} \right )$

Разность потенциалов также равна V=Ed

Следовательно, электрическое поле из-за последовательно соединенных конденсаторов можно рассчитать как

Е= В/д

$E=\frac{Q}{d}\ \left ( \frac{C_1+C_2}{C_1C_2} \right )$

Если есть n конденсаторов, соединенных последовательно, то электрическое поле на n конденсаторах будет равно

$E=\frac{Q}{d}\ \frac{\sum_{1}^{n}C_n}{\prod_{1}^{n}C_n}$

Электрическое поле в цилиндрическом конденсаторе

Цилиндрический конденсатор состоит из двух цилиндрических пластин. Внутренний цилиндр имеет положительную плотность поверхностного заряда +σ радиуса «r», а внешний цилиндр имеет отрицательную плотность поверхностного заряда –σ радиуса «R».

Электрическое поле в цилиндрическом конденсаторе

Электрический поток проходит от поверхности внутреннего цилиндра к внешнему цилиндру, как показано на рисунке выше. На рис. (б) показано поперечное сечение цилиндрического конденсатора. Пусть ds — поверхность Гаусса в середине двух заряженных цилиндров.

Электрическое поле внутри внутреннего цилиндра равно нулю, так как через эту область нет электрического потока, а также снаружи цилиндра радиуса R также равно нулю. Электрический поток течет между двумя цилиндрами на расстоянии s от центра.

Электрический поток через гауссову поверхность ds определяется выражением

$\oint E.ds=\frac{q}{\varepsilon _0}$ $E\oint ds=\frac{q}{\varepsilon _0}$ $ES=\frac{q}{\varepsilon _0}$ $S=2\pi sh$

Следовательно,

$E\times 2\pi sh=\frac{q}{\varepsilon _0}$ $E=\frac{q}{2\pi \varepsilon _0 sh}$

Это уравнение дает электрическое поле, создаваемое цилиндрическим конденсатором.

Чему равно электрическое поле в точке, удаленной на 0.6 см от центра цилиндрического конденсатора высотой 2 см, имеющего внешний радиус 0.8 см и внутренний радиус 0.35 см, несущего заряд 5 Кл?

Данный: г = 0.35 см = 0.0035 м

Р = 0.8 см = 0.08 м

S = 0.6 см = 0.06 м

ч = 2 см = 0.02 м

Q=5С

У нас есть,

$E=\frac{Q}{2\pi \varepsilon _0 sh}$ $=\frac{5}{2\pi \times 8.85\times 10^{-12}\times 0.06\times 0.02}$ $=\frac{5}{0.067\times 10^{-12}}$

= 74.62 х 10¹² В / м

Электрическое поле конденсатора на расстоянии 0.6 см от центра цилиндрического конденсатора равно 74.62 х 10¹² В / м.

Напряженность электрического поля в конденсаторе

Напряженность электрического поля вне области заряженного конденсатора всегда равна нулю, так как носители заряда присутствуют на поверхности конденсатора.

Во внутренней области конденсатора напряженность электрического поля равна отношению плотности поверхностных носителей заряда, а проницаемость среды в этой области одинакова во всех точках внутри конденсатора.

$E=\frac{\sigma }{\varepsilon _0 }$

Где σ – поверхностная плотность заряда носителей заряда, присутствующих на пластине конденсатора, а

ε₀проницаемость среды

Кроме того, электрическое поле можно рассчитать, измерив разность потенциалов между двумя пластинами и найдя расстояние между пластинами как

Э=В/д

Где V — разность потенциалов между обкладками конденсатора и

d – расстояние между двумя пластинами

Электрическое поле в сферическом конденсаторе

Подобно цилиндрическому конденсатору, сферический конденсатор также состоит из двух сфер, имеющих противоположные носители заряда на поверхности каждой сферы.

Рассмотрим сферу радиуса ‘R₂‘ с плотностью поверхностного заряда как +σ и другой сферой радиуса ‘R₁‘ плотности поверхностного заряда –σ, покрывающего малую сферическую оболочку.

Схема сферического конденсатора

Электрический поток течет от сферы, состоящей из положительной поверхностной плотности заряда, к внешней сфере. Рассмотрим гауссову поверхность «ds» в середине двух сферических поверхностей на расстоянии «r» от центра сфер. Пусть заряд равен q на поверхности Гаусса. Применяя закон Гаусса

$\oint E.ds=\frac{q}{\varepsilon _0}$ $E\oint ds=\frac{q}{\varepsilon _0}$ $ES=\frac{q}{\varepsilon _0}$

S — площадь поверхности, равная 4πr², следовательно, мы получаем

Е х 4πr² = д/е₀

Электрическое поле в сферическом конденсаторе равно

E= q/4πε₀r²

Разность потенциалов между двумя заряженными сферами равна

$V=\int_{R_2}^{R_1}E.dr$

Мы нашли электрическое поле сферического конденсатора, поэтому подставим его в это уравнение.

$V=\int_{R_2}^{R_1}\frac{q}{4\pi \varepsilon _0 r^2}.dr$ $V=\frac{q}{4\pi \varepsilon _0 }\int_{R_2}^{R_1}\frac{1}{r^2}.dr$ $V=\frac{q}{4\pi \varepsilon _0 }\left [ \frac{1}{R_2}-\frac{1}{R_1} \right ]$ $V=\frac{q}{4\pi \varepsilon _0 }\left [ \frac{R_1-R_2}{R_1R_2} \right ]$

Следовательно, емкость сферического конденсатора равна

C= кв/В

Подставив значение разности потенциалов, получим

$C=4\pi \varepsilon _0 \ \frac{R_1R_2}{R_1-R_2}$

Это уравнение дает емкость сферического конденсатора.

Часто задаваемые вопросы

Чему равно электрическое поле заряженного шара радиусом 3 см, несущего заряд 4 Кл?

Данный: г=3 см=0.03 м

Q=4С

Электрическое поле внутри сферы E=0.

Площадь поверхности шара равна

А = 4πr²

=4π х (0.03)²

= 0.01 м²

Следовательно, поверхностная плотность заряда шара равна

σ = Q/А

= 4С/0.01 м²

=400 Кл/м²

Поэтому электрическое поле заряженного шара равно

$E=\frac{\sigma }{\varepsilon _0}$ $=\frac{400}{8.85\times 10^{-12}}$

= 45.2 х 10¹² В / м

Компания электрическое поле на поверхности и в точке вне сферы 45.2 х 10¹² В / м.

Чему равно электрическое поле сферического конденсатора на расстоянии 4 см от центра, имеющего внутренний радиус 3 см и внешнюю сферу 5 см, несущую заряд 2 мКл?

Данный: R₁=3 см=0.03 м

R₂=5 см=0.05 м

г = 4 см = 0.04 м

q= 2 мКл

Электрическое поле на гауссовой поверхности на расстоянии 0.04 м от центра сферического конденсатора равно

$E=\frac{q}{4\pi \varepsilon _0 r^2}$ $=\frac{2\times 10^{-6}}{4\pi \times 8.85\times 10^{-12}\times 0.04^2}$ $=\frac{2\times 10^{-6}}{0.178\times 10^{-12}}$ $=\frac{2\times 10^{6}}{0.178}$

= 11.23 х 10⁶ В / м

Емкость сферического конденсатора равна

$C=4\pi \varepsilon _0 \ \frac{R_1R_2}{R_1-R_2}$ $=4\pi \times 8.85\times 10^{-12}\times \frac{0.03\times 0.05}{0.05-0.03}$ $=\frac{0.167\times 10^{-12}}{0.02}$

= 8.3 х 10^-12F

Источник

Уединенный
проводник.

Это проводник,
расположенный относительно других тел
на расстоянии во много раз большем, чем
его размеры.

Электрическая
емкость (электроемкость) уединенного
проводника. (С)

Это физическая величина, равная отношению заряда проводника к потенциалу этого проводника.
В Си электроемкость измеряется в Фарадах:	.
Электроемкость не зависит от величины заряда на проводнике, а зависит от геометрических размеров проводника, его формы и диэлектрической проницаемости среды, в которую он помещен.

Основная задача
для электрической ёмкости проводника.

Вычисление потенциала проводника по известной величине заряда на нем,
или наоборот, вычисление заряда на проводнике по известной величине его потенциала.

Емкость уединенного проводящего шара.

Так как потенциал
шара можно вычислить по формуле

то ёмкость
уединенного проводящего шара может
быть вычислена по формуле:

Frame2

Конденсатор.

Конденсатор – это
система двух близко расположенных
проводников, расстояние
между которыми мало по сравнению с их
размерами. При
этом проводники разделены диэлектриком,
который не дает возможности разноимённым
зарядам соединиться и нейтрализовать
друг друга.

Обкладки конденсатора.

Образующие
конденсатор проводники называют
обкладками
конденсатора.

Обкладки
конденсатора берутся такой формы и
располагаются на таком расстоянии
друг от друга, чтобы создаваемое
зарядами конденсатора электрическое
поле было сосредоточено между обкладками
и не рассеивалось в окружающее
пространство. В этом случае окружающие
тела не оказывают влияние на ёмкость
конденсатора.

В
зависимости от формы обкладок
конденсаторы бывают сферические,
цилиндрические и плоские.

Заряд конденсатора.

Под зарядом
конденсатора понимают модуль заряда
одной из обкладок. При сообщении заряда
конденсатору его обкладки приобретают
одинаковые по модулю, но противоположные
по знаку заряды. Так как разноимённые
заряды притягиваются, они располагаются
на внутренних поверхностях обкладок с
большей плотностью.

Электроемкость
конденсатора

это физическая
величина, численно равная величине
заряда, который необходимо перенести
с одной электрически нейтральной
обкладки конденсатора на другую для
того, чтобы между ними образовалось
электрическое поле с разностью
потенциалов между обкладками

1
Вольт

.

Frame3

Электроемкость
конденсатора не зависит от величины
его заряда, а зависит от геометрических
размеров и формы его обкладок, а также
диэлектрической проницаемости среды
между обкладками, так как диэлектрик
поляризуется в поле конденсатора, и
его связанные заряды уменьшают разность
потенциалов между его обкладками.

Плоский конденсатор

это система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Электрическое поле плоского конденсатора в основном локализовано между пластинами.
	Вблизи краев пластин и в окружающем пространстве также возникает
сравнительно слабое электрическое поле, которое называют полем рассеяния.
В целом ряде задач можно приближенно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками

Напряженность электростатического поля плоского конденсатора.

Каждая из заряженных пластин плоского конденсатора создает вблизи поверхности электрическое поле, модуль напряженности которого выражается соотношением:	;
Согласно принципу суперпозиции напряженность поля, создаваемого обеими пластинами, равна сумме напряженностей и полей каждой из пластин:
Учитывая направление векторов напряженностей каждой пластины, избавимся от векторов.
Внутри конденсатора, между пластинами, поля имеют одинаковое направление напряженностей:
, тогда
Снаружи конденсатора вектора напряженностей направлены противоположно друг другу: ,
поэтому

Напряженность электростатического поля плоского конденсатора.
Внутри конденсатора	Снаружи конденсатора

Электроемкость плоского конденсатора.

По
определению поверхностная плотность
заряда пластин равна:

где
q
– заряд,

S
– площадь каждой пластины.

Разность
потенциалов между пластинами в однородном
электрическом поле равна:

где d
– расстояние между пластинами,

Е-напряженность
поля конденсатора.

Из
определения электроемкости конденсатора
можно получить формулу для расчета
электроемкости плоского конденсатора.

Электроемкость
плоского конденсатора прямо
пропорциональна площади пластин
(обкладок) и обратно пропорциональна
расстоянию между ними, а если пространство
между обкладками заполнено диэлектриком,
электроемкость конденсатора
увеличивается в ε раз.

Frame4

Сферический конденсатор
это система из двух концентрических проводящих сфер радиусами R₁ и R₂, с диэлектрической средой между этими сферами.
Электроемкость сферического конденсатора можно вычислить по формуле:

Цилиндрический
конденсатор

это
система из двух соосных проводящих
цилиндров радиусами R₁
и R₂
и длины L
с диэлектрической средой между
цилиндрами.

Электроемкость
цилиндрического конденсатора можно
вычислить по формуле:

Конденсаторы
переменной ёмкости.

Конденсаторы,
устройство которых позволяет изменять
один из параметров, от которого зависит
электроёмкость конденсатора.

Например, у
плоского конденсатора емкость можно
увеличить, если увеличить площадь его
пластин, так как

.

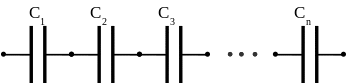
Последовательное
соединение конденсаторов

Соединение, при
котором первая обкладка каждого
следующего конденсатора соединяется
со второй обкладкой предыдущего.

При последовательном
соединении конденсаторы имеют одинаковый
заряд, так как в результате явления
электростатической индукции на обкладках
соседних конденсаторов происходит
разделение заряда.

Общая разность
потенциалов равна сумме разностей
потенциалов на каждом конденсаторе.

₀–
_n₌(₀–
₁)+(
₁–
₂)+(
₂–
₃)+…+(
_n-1–
_n)

Поделив обе части
выражения на величину заряда конденсатора,
получим:

Учитывая, что
ёмкость конденсатора

,
запишем получившееся выражение в новой
форме.

При последовательном
соединении всегда выполняется условие:

(электроемкость
батареи конденсаторов меньше, чем
минимальная емкость одного из
конденсаторов).

Последовательное
соединение n
конденсаторов различной емкости.

Разность
потенциалов

Заряд

Эквивалентная
электроемкость батареи

₀–_n=(₀–
₁)+(₁–
₂)+

+(
₂–
₃)+…+(
_n-1–
_n)

q₁=
q₂=
q₃=…=
q_n

Последовательное
соединение двух конденсаторов различной
емкости.

Разность
потенциалов

Заряд

Эквивалентная
электроемкость батареи

₀–
₂
=(₀–
₁)+(₁–
₂)

q₁=
q₂



Последовательное
соединение n
конденсаторов

одинаковой ёмкости.

Разность
потенциалов

Заряд

Эквивалентная
электроемкость батареи

₀–
_n=n(₀–
₁)

q₁=
q₂=
q₃=…=
q_n

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
21.04.2015625.62 Кб361.docx
#
#
#
#
#
#
#

Источник

Конденсатор. Энергия электрического поля

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Ёмкость уединённого проводника

Ёмкость плоского конденсатора

Энергия заряженного конденсатора

Энергия электрического поля

Напряженность электрического поля в конденсаторе. Калькулятор онлайн.

Электрическое поле в формуле конденсатора

Электрическое поле внутри конденсатора

Какое электрическое поле создает плоский конденсатор с площадью поверхности 0.3 м?2 и несущий заряд 1.8С?

Электрическое поле вне конденсатора

Электрическое поле в конденсаторе с диэлектриком

Последовательный конденсатор электрического поля

Электрическое поле в цилиндрическом конденсаторе

Напряженность электрического поля в конденсаторе

Электрическое поле в сферическом конденсаторе

Часто задаваемые вопросы

Чему равно электрическое поле заряженного шара радиусом 3 см, несущего заряд 4 Кл?

Чему равно электрическое поле сферического конденсатора на расстоянии 4 см от центра, имеющего внутренний радиус 3 см и внешнюю сферу 5 см, несущую заряд 2 мКл?

Плоский конденсатор

Напряженность электростатического поля плоского конденсатора.

Электроемкость плоского конденсатора.

Вам также может понравиться

Как составить исковое заявление в суд невыплата зарплаты

Код 8007000е произошла неизвестная ошибка windows update как исправить

Как найти собаку по клейму на зоопортале

Добавить комментарий Отменить ответ

Какое электрическое поле создает плоский конденсатор с площадью поверхности 0.3 м?² и несущий заряд 1.8С?