Как найти напряженность электрического поля в треугольнике

Для школьников.

Приведём решение трёх задач на применение принципа суперпозиции (наложения) электростатических полей.

Задача 1. Два точечных одинаковых положительных заряда по 20 нКл каждый расположены в двух вершинах равностороннего треугольника со стороной 2 м в вакууме. Найти напряжённость поля в третьей вершине треугольника.

В точке А вектора напряженности электрических полей каждого заряда направлены вдоль их силовых линий (от зарядов).

Применим принцип суперпозиции для проекций указанных векторов на оси х и у:

Таким образом, вектор напряжённости результирующего электрического поля в точке А направлен вертикально вверх, а модуль напряжённости равен 77 В/м.

Задача 2. Электрическое поле образовано двумя одинаковыми разноимёнными точечными зарядами по 5 нКл. Расстояние между зарядами 10 см. Определить напряжённость поля: 1) в точке, лежащей посередине между зарядами; 2) в точке, лежащей на продолжении линии, соединяющей центры зарядов, на расстоянии 10 см от отрицательного заряда; 3) в точке, лежащей на расстоянии 10 см от положительного и отрицательного зарядов.

В точке А оба вектора напряжённости, создаваемых положительным и отрицательным зарядами, направлены вправо (на рисунке не показаны). Тогда результирующее поле находится через сумму полей, создаваемых первым и вторым зарядами:

В точке В результирующее поле направлено влево и равно:

В точке С вектор напряжённости результирующего электрического поля направлен вправо. Его модуль найдём из треугольника:

Ответ: 36000 В/м; 3400 В/м; 4500 В/м.

Задача 3. Электрическое поле создано двумя точечными зарядами 30 нКл и -10 нКл. Расстояние между зарядами 20 см. Определить напряжённость электрического поля в точке, находящейся на расстоянии 15 см от первого и на расстоянии второго (отрицательного) зарядов.

Покажем направления векторов напряжённости, создаваемых в искомой точке первым и вторым зарядами. Их модули найдём из формул:

Складывая вектора находим вектор результирующего поля. Модуль напряжённости результирующего поля находим по теореме косинусов:

Косинус угла найдём отдельно из треугольника образованного расстояниями:

Косинус угла оказался равным 0,25. Подставив все численные значения в формулу, получим результирующую напряжённость равную 16, 7 кВ/м.

Итак, приведено решение трёх задач на применение принципа суперпозиции (наложения) полей. Сначала в интересующей точке поля рисуем вектора напряжённости электрического поля, создаваемого каждым зарядом в отдельности. Затем, складывая их, находим напряжённость суммарного поля. В первой задаче проще просуммировать проекции векторов напряжённости на оси. Там, где угол между векторами напряжённости, создаваемыми отдельными зарядами, отличен от нуля, пользуются теоремой косинусов (задачи 2 и 3).

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Нахождение напряжённости электростатического поля.

Следующая запись:Как рассчитать напряжённость поля заряженной пластины. Поле конденсатора.

Ссылки на другие занятия (до электростатики) даны в Занятии 1.

Ссылки на занятия (начиная с электростатики) даны в Занятии 45.

Определение напряженности в любой точке электрического поля

Разделы: Физика

Цель урока: дать понятие напряжённости электрического поля и ее определения в любой точке поля.

• формирование понятия напряжённости электрического поля; дать понятие о линиях напряжённости и графическое представление электрического поля;
• научить учащихся применять формулу E=kq/r 2 в решении несложных задач на расчёт напряжённости.

Электрическое поле – это особая форма материи, о существовании которой можно судить только по ее действию. Экспериментально доказано, что существуют два рода зарядов, вокруг которых существуют электрические поля, характеризующиеся силовыми линиями.

Графически изображая поле, следует помнить, что линии напряженности электрического поля:

1. нигде не пересекаются друг с другом;
2. имеют начало на положительном заряде (или в бесконечности) и конец на отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
3. между зарядами нигде не прерываются.

Рис.1

Силовые линии положительного заряда:

Рис.2

Силовые линии отрицательного заряда:

Рис.3

Силовые линии одноименных взаимодействующих зарядов:

Рис.4

Силовые линии разноименных взаимодействующих зарядов:

Рис.5

Силовой характеристикой электрического поля является напряженность, которая обозначается буквой Е и имеет единицы измерения или . Напряженность является векторной величиной, так как определяется отношением силы Кулона к величине единичного положительного заряда

В результате преобразования формулы закона Кулона и формулы напряженности имеем зависимость напряженности поля от расстояния, на котором она определяется относительно данного заряда

где: k – коэффициент пропорциональности, значение которого зависит от выбора единиц электрического заряда.

В системе СИ Н·м 2 /Кл 2 ,

где ε ₀ – электрическая постоянная, равная 8,85·10 -12 Кл 2 /Н·м 2 ;

q – электрический заряд (Кл);

r – расстояние от заряда до точки в которой определяется напряженность.

Направление вектора напряженности совпадает с направлением силы Кулона.

Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным. В ограниченной области пространства электрическое поле можно считать приблизительно однородным, если напряженность поля внутри этой области меняется незначительно.

Общая напряженность поля нескольких взаимодействующих зарядов будет равна геометрической сумме векторов напряженности, в чем и заключается принцип суперпозиции полей:

Рассмотрим несколько случаев определения напряженности.

1. Пусть взаимодействуют два разноименных заряда. Поместим точечный положительный заряд между ними, тогда в данной точке будут действовать два вектора напряженности, направленные в одну сторону:

Е₃₁ – напряженность точечного заряда 3 со стороны заряда 1;

Е₃₂ – напряженность точечного заряда 3 со стороны заряда 2.

Согласно принципу суперпозиции полей общая напряженность поля в данной точке равна геометрической сумме векторов напряженности Е₃₁ и Е₃₂.

Напряженность в данной точке определяется по формуле:

где: r – расстояние между первым и вторым зарядом;

х – расстояние между первым и точечным зарядом.

Рис.6

2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной на расстояние а от второго заряда. Если учесть, что поле первого заряда больше, чем поле второго заряда, то напряженность в данной точке поля равна геометрической разности напряженности Е₃₁ и Е₃₂.

Формула напряженности в данной точке равна:

Е = kq1/(r + a) 2 – kq₂/a 2

Где: r – расстояние между взаимодействующими зарядами;

а – расстояние между вторым и точечным зарядом.

Рис.7

3. Рассмотрим пример, когда необходимо определить напряженность поля в некоторой удаленности и от первого и от второго заряда, в данном случае на расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные заряды отталкиваются , а разноименные притягиваются, имеем два вектора напряженности исходящие из одной точки, то для их сложения можно применить метод противоположному углу параллелограмма будет являться суммарным вектором напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:

Рис.8

Исходя из данной работы, следует, что напряженность в любой точке поля можно определить, зная величины взаимодействующих зарядов, расстояние от каждого заряда до данной точки и электрическую постоянную.

4. Закрепление темы.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: электрическое поле – это ….

3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы

Оценка работы другим учеником

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: напряженностью называется …

3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы

Оценка работы другим учеником

1. Два заряда q₁ = +3·10 -7 Кл и q₂ = −2·10 -7 Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите напряженность поля в точке С, расположенной на линии, соединяющей заряды, на расстоянии 0,05 м вправо от заряда q₂.

2. В некоторой точке поля на заряд 5·10 -9 Кл действует сила 3·10 -4 Н. Найти напряженность поля в этой точке и определите величину заряда, создающего поле, если точка удалена от него на 0,1 м.

ВУЗ. Найти напряженность поля и потенциал (30.10.2011)

Чертов А. Г., Воробьев А. А. Задачник по физике: Учебное пособие для вузов. 7 изд., 2001 г.

• версия для печати
• Войдите или зарегистрируйтесь, чтобы отправлять комментарии

Комментарии

В центре треугольника напряженность равна геометрической сумме напряженностей, создаваемых зарядами 1, 2 и 3.

Заряды по модулю равны, поэтому:

E₁ = E₂ = E₃ = 3k|q| / a 2 , так как a(√3) / 3 — расстояние от вершины треугольника до центра треугольника О.

Напряженность поля в точке О: E = E₃ + E₁ cos 60° + E₂ cos 60° = 2E₁ = 6k|q| / a 2 .

Потенциал в точке O равен алгебраической сумме потенциалов, создаваемых зарядами 1, 2 и 3:

В вершинах равностороннего треугольника со стороной а находятся заряды +q, +q и -q. Найти напряженность поля Е в центре треугольника

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,284
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,093
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

[spoiler title=”источники:”]

http://www.afportal.ru/university/112

http://www.soloby.ru/310113/%D1%80%D0%B0%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D0%BE%D1%80%D0%BE%D0%BD%D0%BD%D0%B5%D0%B3%D0%BE-%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0-%D0%BD%D0%B0%D0%BF%D1%80%D1%8F%D0%B6%D0%B5%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D1%8C-%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0

[/spoiler]

Условие задачи:

В серединах всех сторон равностороннего треугольника расположены одинаковые точечные заряды 1 нКл. В двух вершинах этого треугольника помещены точечные заряды -4 нКл каждый. Длина стороны треугольника 2 м. Определить напряженность электрического поля в третьей вершине треугольника.

Задача №6.2.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(q_1=1) нКл, (q_2=-4) нКл, (l=frac{r}{2}), (r=2) м, (E-?)

Решение задачи:

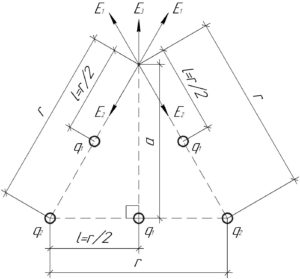Для начала найдём суммарный вектор напряженности электрического поля (E_0), создаваемого зарядами (q_1) и (q_2), лежащими на одной стороне треугольника, в третьей вершине равностороннего треугольника. Каждый из этих зарядов будет создавать электрическое поле напряженностью (E_1) и (E_2) соответственно, модуль которых можно определить по формулам:

[left{ begin{gathered}
{E_1} = frac{{k{q_1}}}{{{l^2}}} hfill \
{E_2} = frac{{kleft| {{q_2}} right|}}{{{r^2}}} hfill \
end{gathered} right.]

Коэффициент пропорциональности (k) равна 9·10⁹ Н·м²/Кл².

По условию заряды (q_1) расположены в серединах сторон треугольника, то есть (l=frac{r}{2}). Учитывая это и раскрывая модуль во второй формуле (так как ({q_2} < 0), то (left| {{q_2}} right| = – {q_2})), то получим:

[left{ begin{gathered}
{E_1} = frac{{4k{q_1}}}{{{r^2}}} hfill \
{E_2} = frac{{ – k{q_2}}}{{{r^2}}} hfill \
end{gathered} right.]

Поскольку вектора (overrightarrow {{E_1}}) и (overrightarrow {{E_2}}) противонаправлены (так как заряды (q_1) и (q_2) имеют разные знаки), то модуль суммарного вектора напряженности электрического поля (E_0), создаваемого зарядами (q_1) и (q_2) в третьей вершине равностороннего треугольника, равен:

[{E_0} = {E_1} – {E_2}]

[{E_0} = frac{{4k{q_1}}}{{{r^2}}} – left( {frac{{ – k{q_2}}}{{{r^2}}}} right)]

[{E_0} = frac{k}{{{r^2}}}left( {4{q_1} + {q_2}} right)]

Любопытства ради посчитаем численное значение:

[{E_0} = frac{{9 cdot {{10}^9}}}{{{2^2}}}left( {4 cdot 1 cdot {{10}^{ – 9}} + left( { – 4 cdot {{10}^{ – 9}}} right)} right) = 0;В/м]

Значит суммарное электрическое поле в третьей вершине треугольника, создаваемое четырьмя зарядами (q_1) и (q_2), лежащими на боковых сторонах треугольника, равно нулю. Поэтому искомая напряженность поля (E) равна напряженности поля (E_3), создаваемого зарядом (q_1), лежащим в середине основания треугольника (смотрите схему).

[E = {E_3}]

[{E_3} = frac{{k{q_1}}}{{{a^2}}}]

Здесь (a) – длина высоты равностороннего треугольника. Высота в равностороннем треугольнике является ещё и медианой (так как равносторонний треугольник – частный случай равнобедренного). Поэтому из теоремы Пифагора имеем:

[{a^2} = {r^2} – frac{{{r^2}}}{4}]

[{a^2} = frac{{3{r^2}}}{4}]

Тогда:

[{E_3} = frac{{4k{q_1}}}{{3{r^2}}}]

В итоге имеем:

[E = frac{{4k{q_1}}}{{3{r^2}}}]

Произведем вычисления:

[E = frac{{4 cdot 9 cdot {{10}^9} cdot 1 cdot {{10}^{ – 9}}}}{{3 cdot {2^2}}} = 3;В/м = 0,03;В/см]

Ответ: 0,03 В/см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.2.24 Одинаковые по модулю, но разные по знаку заряды 40 нКл расположены
6.2.26 В двух противоположных вершинах квадрата со стороной 30 см находятся заряды
6.2.27 В трёх вершинах квадрата со стороной 30 см находятся точечные заряды

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

---

Закон Кулона 

Закон сохранения электрического заряда

Напряженность

Принцип суперпозиции

Электрическое поле

Потенциал электростатического поля

Разность потенциалов

---

Теория

Совсем чуть−чуть. 

Закон Кулона — сила, с которой два точечных заряда действуют друг на друга. Она обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их зарядов.

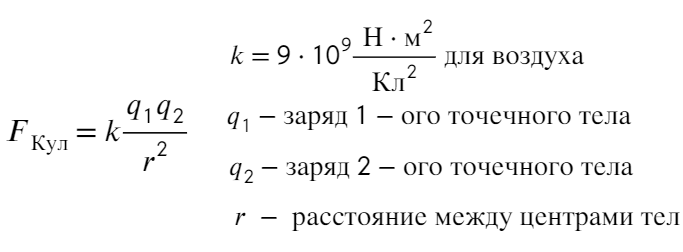
Заряды с одинаковым знаком отталкиваются, с разными — притягиваются. По III з. Ньютона сила действия одного заряда равна силе действия другого:

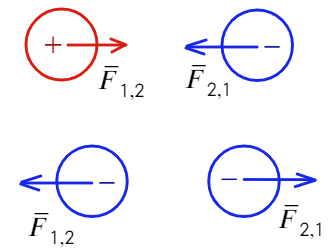
Наглядно рассказывается об этом в видео.
А напряженность — силовая характеристика электрического поля. По-простому: электрическое поле действует на заряд, и вот сила, с которой поле действует на заряд, и есть напряженность. 

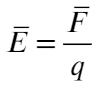
Напряженность НЕ зависит от величины заряда, помещенного в поле!

Задачи

Задача 1 Два одинаковых маленьких положительно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 5 раз. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₂ к F₁.

Скажем, что заряд одного шарика q, другого 5q. Тогда сила Кулона между ними:

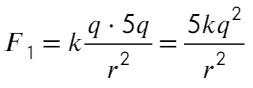
А если теперь соединить два шарика, то общий заряд разделится пополам (на каждый шарик). Общий заряд 5q + q = 6q, тогда на каждом шарике окажется по 3q. Тогда сила Кулона:

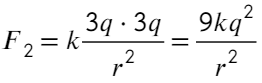
Отношение получится таким:

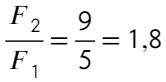
Ответ: 1,8

Задача 2 Два одинаковых маленьких разноименно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 4 раза. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₁ к F₂.

Та же самая задача? А вот и нет, одно слово другое: разноименно вместо положительных. Это значит, что один шарик будет заряжен положительно, другой отрицательно. По сравнению с первым случаем сила Кулона никак не изменится по модулю (только по нарпавлению).

А вот после соприкосновения изменится. Общий заряд: 5q − q = 4q или q − 5q = − 4q, тогда на каждый шар пойдет по 2q:

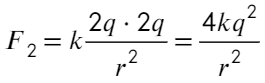
Отношение:

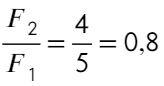
Ответ: 0,8

Задача 3 На нерастяжимой нити висит шарик массой 100 г, имеющий заряд 20 мкКл. Как необходимо зарядить второй шарик, который подносят снизу к первому шарику на расстояние 30 см, чтобы сила натяжения: а) увеличилась в 4 раза; б) рассмотреть случай невесомости?

В начальный момент времени на шарик действуют две силы:

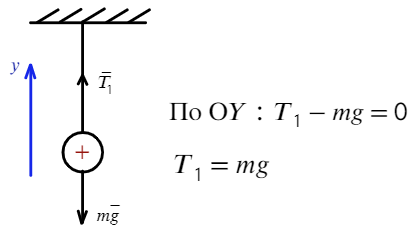а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:

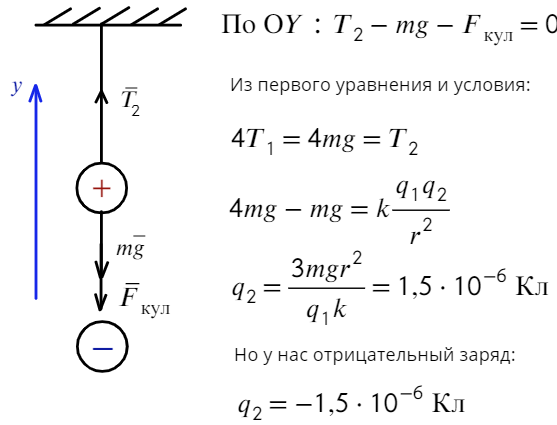б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:

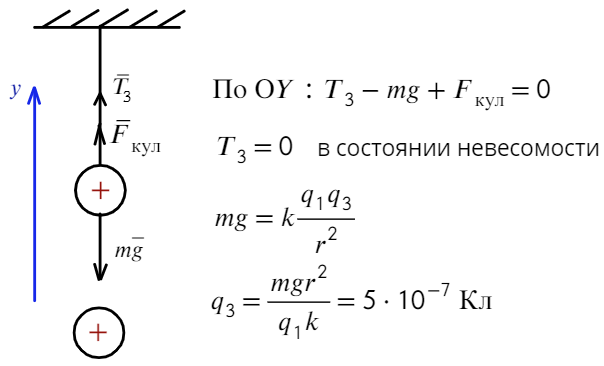Ответ: −1,5 мкКл, 500 нКл.

Задача 3 Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает с поверхности пластинки электрон, который попадает в электрическое поле с напряженностью 125 В/м. Найти расстояние, которое он пролетит прежде, чем разгонится до скорости, равной 1% от скорости света. 

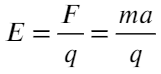
В задаче говорится про электрон, значит, его массу m = 9,1×10⁻³¹ кг и заряд q = 1,6 × 10⁻¹⁹ Кл можно посмотреть в справочных данных.

Найдем ускорение электрона в электрическом поле:

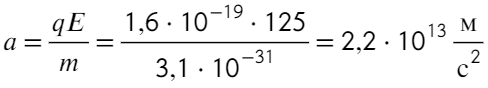
Остается найти пройденный путь в равноускоренном движении при нулевой начальной скорости: 

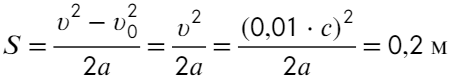
Ответ: 0,2 м

Задача 4 Полый заряженный шарик массой m = 0,4 г. движется в однородном горизонтальном электрическом поле из состояния покоя. Модуль напряженности электрического поля E = 500 кВ/м. Траектория шарика образует с вертикалью угол α = 45°. Чему равен заряд шарика? 

Для начала разберемся, какие силы действуют на заряд:

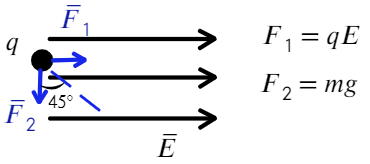
Заряд движется под углом 45 градусов, значит, отношением сил будет тангенс 45°:

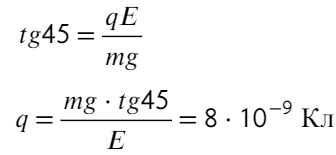
Ответ: 8×10⁻⁹ Кл

Задача 5 При нормальных условиях электрический «пробой» сухого воздуха наступает при напряжённости электрического поля 30 кВ/см. В результате «пробоя» молекулы газа, входящие в состав воздуха, ионизируются и появляются свободные электроны. Какую кинетическую энергию приобретёт такой электрон, пройдя в электрическом поле расстояние 10⁻⁵ см? Ответ выразите в электронвольтах. (ЕГЭ)

Задача кажется весьма тяжелой, но это обманчиво. Воспользуемся знакомой формулой напряженности: 

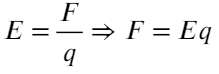
Домножим на длину обе части, тогда слева получится работа, а работа — это изменение энергии:

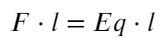
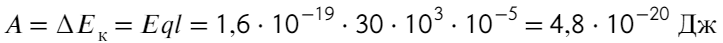
Переводить сантиметры не обязательно, они сократятся. Чтобы перевести джоули в электронвольты, нужно разделить на 1,6 × 10⁻¹⁹

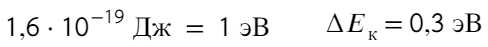
Ответ: 0,3 эВ

Задача 6 В вершинах равностороннего треугольника со стороной «а» находятся заряды +q, +q и -q. Найти напряженность поля Е в центре треугольника.

Покажем, как направлена напряженность: для двух положительных зарядов — от них (красные стрелочки), для отрицательного заряда — к нему (синяя стрелочка).

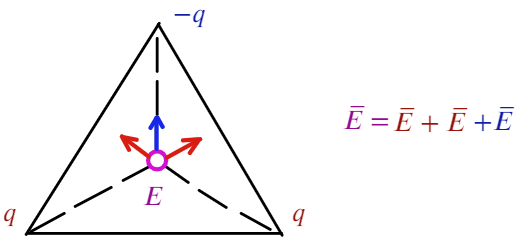
Угол между синим вектором и красным составляет 60°. Если продлить красный вектор до стороны, получится прямоугольный треугольник. Тогда, чтобы посчитать результирующую напряженность, спроецируем красные векторы на синий: 

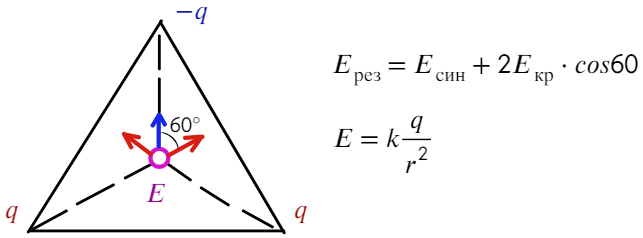
Остается разобрать на каком расстоянии находятся заряды от центра треугольника. Высоту треугольника можно найти по т. Пифагора, равна она а√3/2. А расстояние тогда составит 2/3 от высоты:

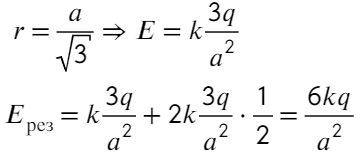
Ответ: 6kq/a²

Задача 6 Два шарика с зарядами Q = –1 нКл и q = 5 нКл соответственно, находятся в однородном электрическом поле с напряженностью Е = 18 В/м, на расстоянии r = 1 м друг от друга. Масса первого шарика равна M = 5 г. Определите, какую массу должен иметь второй шарик, чтобы они двигались с прежним между ними расстоянием и с постоянным по модулю ускорением. (ЕГЭ – 2016)

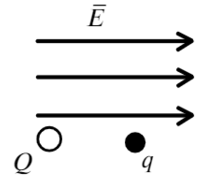
Направим ось X вправо и покажем, какие силы действуют на каждый заряд.

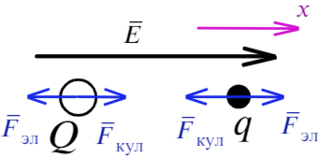
На положительный заряд электрическая сила действует по линиям напряженности, для отрицательного заряда все наоборот. Силы кулона направлены к зарядам, они разноименные. Составим уравнение для каждого заряда:

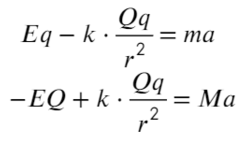
Сумма всех сила равна ma, потому что в условии сказано, что шарики двигаются с постоянным ускорением, а чтобы расстояние не менялось, двигаться они должны в одном направлении.

Разделим одно уравнение на другое и выразим массу:

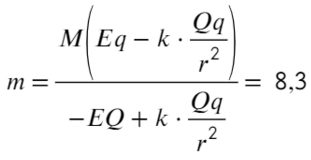
Ответ: 8,3 гр.

Задача 7 Четыре маленьких одинаковых шарика, связанных нерастяжимыми нитями одинаковой длины, заряженызарядами q, q, q и 2q. Сила натяжения нити, связывающей первый и второй шарики, равна T. Найти силу натяжения нити, связывающейвторой и третий шарики. (Росатом)

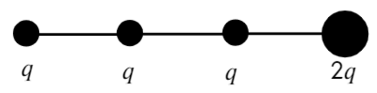
Покажем, каким силам противодействует сила натяжения Т. Воспользуемся принципом суперпозиции и законом Кулона:

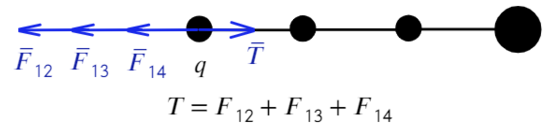
Сила натяжения Т удерживает первый шарик, других сил для него нет, значит, больше ничего для первого случая не требуется. 

Как проще это запомнить: проводим линию перпендикулярно той нити, о которой говорим (красная черточка), после записываем только те силы между шариками, которые появляются по разные стороны от проведенной линии:

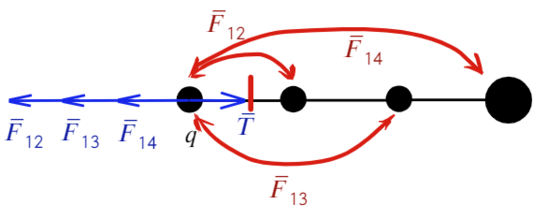
Теперь также составим уравнения для силы натяжения между вторым и третьим шариком:

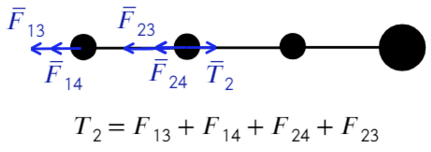
Распишим каждое уравнение по закону кулона, скажем, что расстояние между соседними шариками равно «а»:

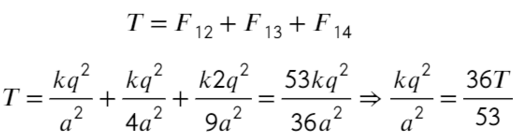
Второе уравнение с подстановкой выражения из первого:

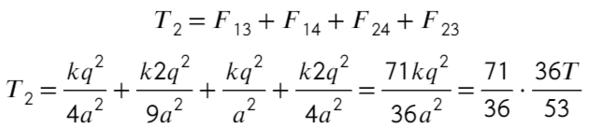
Ответ: 71T/53

Задача 8 Точечный заряд, расположенный в точке C, создаёт в точках A и B поле с напряжённостью Ea и Eb соответственно (см. рисунок; угол ACB — прямой). Найти напряжённость электрическогополя, создаваемого этим зарядом в точке M, являющейся основанием перпендикуляра, опущенного из точки C на прямую AB. (Росатом)

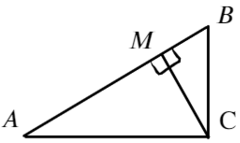
Запишем, чему равна напряженность в каждой из этих точек, взяв длины отрезков за a; b; h:

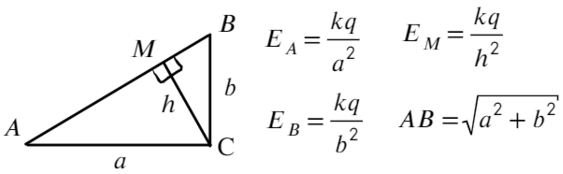
Площадь прямоугольного треугольника можно найти как полупроизведение катетов или как полупроизведение высоты и основания:

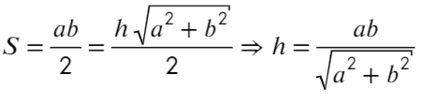
Возведем в квадрат получившиеся уравнение, а дальше смертельный номер: возводим в −1 степень и домножаем обе части на kq:

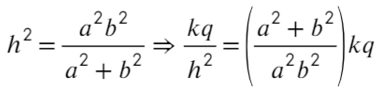
Выразим a² и b² через напряженность:

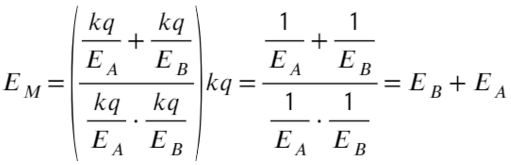
Ответ: Ea+Eb

Задача 9 Частицы с массами M и m, и зарядами q и −q соответственно вращаются с угловой скоростью ω по окружностям вокруг оси, направленной по внешнемуоднородному электрическому полю с напряжённостью E (рис.). Найдите расстояние L между частицами и расстояние H между плоскостями их орбит. (Всеросс. 2008)

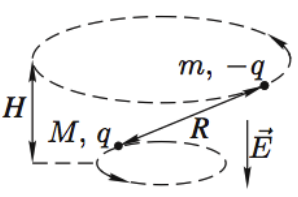Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:

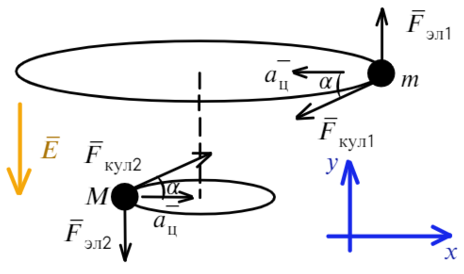
Запишем уравнения по осям на верхнюю частицу:

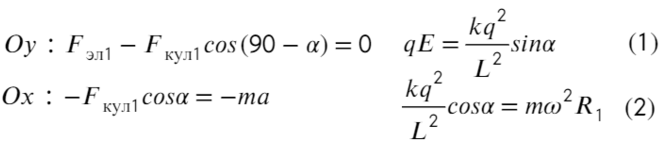
На нижнюю частицу:

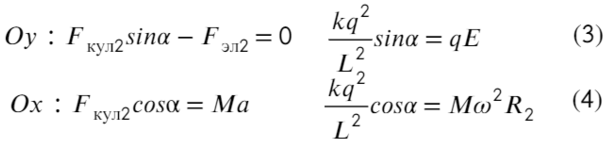
Построим два треугольника, которые показывают расстояние между частицами и высоту между ними. 

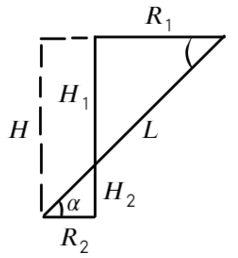
Разделим уравнения друг на друга, а также выразим тангенс угла из этих треугольников:

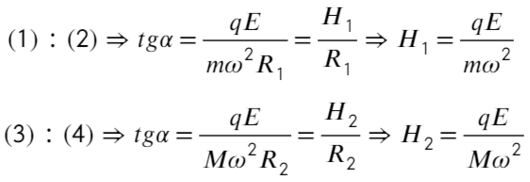
Сложим два уравнения, чтобы найти расстояние между плоскостями:

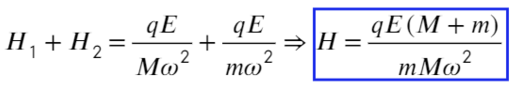
Пункт «а» решили, теперь с расстоянием разберемся: выразим из ур-ия (1) длину, а дальше из треугольника выразим синус угла альфа:

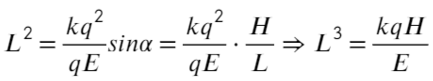
Вместо Н подставим то, что мы нашли:

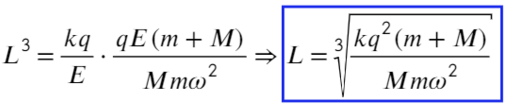
Задача 10 В точке O к стержню привязана непроводящая нить длиной R c зарядом q на конце. Известный эталонный заряд Q₂ и измеряемый заряд Q₁ установлены на расстояниях L₂ и L₁ от точки O. Все заряды одногознака и могут считаться точечными. Найдите величину заряда Q₁, если в состоянии равновесия нить отклонена на угол β от отрезка, соединяющегозаряды Q₂ и Q₁. (Всеросс. 2018)

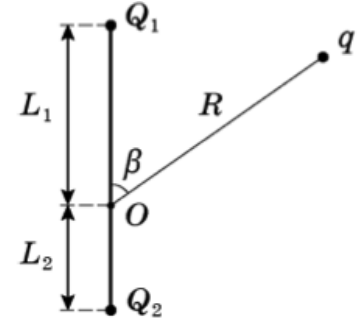
Проведем оси, подпишем расстояние от Q₁ до q и от Q₂ до q. Запишем ур-ия сил на каждую ось:

Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:

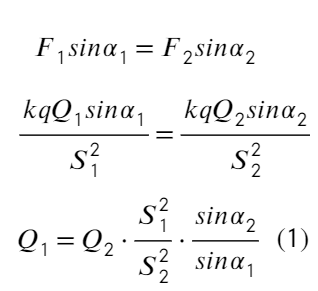
Из прямоугольных треугольников можно получить такие соотношения, а также из теоремы косинусов выразить S₁ и S₂:

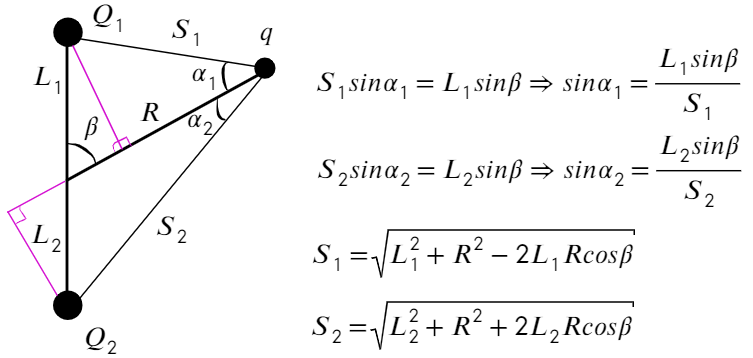
Подставим в ур-ие (1):

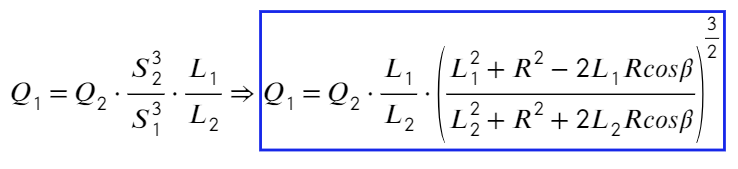
В качестве закрепления материала решите несколько похожих задач с ответами. 

Будь в курсе новых статеек, видео и легкого технического юмора.