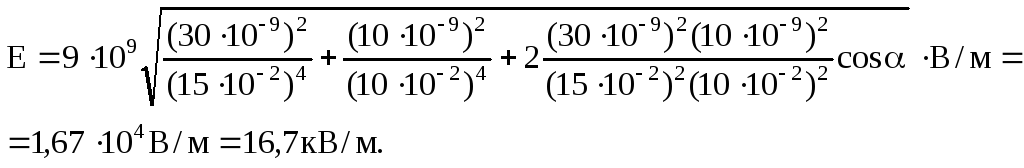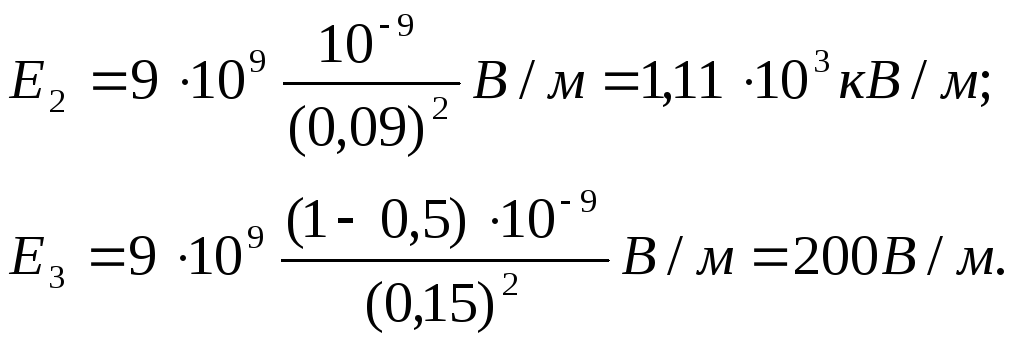Как найти напряженность поля двух точечных зарядов

Для школьников.

Приведём решение трёх задач на применение принципа суперпозиции (наложения) электростатических полей.

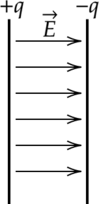
Задача 1. Два точечных одинаковых положительных заряда по 20 нКл каждый расположены в двух вершинах равностороннего треугольника со стороной 2 м в вакууме. Найти напряжённость поля в третьей вершине треугольника.

В точке А вектора напряженности электрических полей каждого заряда направлены вдоль их силовых линий (от зарядов).

Применим принцип суперпозиции для проекций указанных векторов на оси х и у:

Таким образом, вектор напряжённости результирующего электрического поля в точке А направлен вертикально вверх, а модуль напряжённости равен 77 В/м.

Задача 2. Электрическое поле образовано двумя одинаковыми разноимёнными точечными зарядами по 5 нКл. Расстояние между зарядами 10 см. Определить напряжённость поля: 1) в точке, лежащей посередине между зарядами; 2) в точке, лежащей на продолжении линии, соединяющей центры зарядов, на расстоянии 10 см от отрицательного заряда; 3) в точке, лежащей на расстоянии 10 см от положительного и отрицательного зарядов.

В точке А оба вектора напряжённости, создаваемых положительным и отрицательным зарядами, направлены вправо (на рисунке не показаны). Тогда результирующее поле находится через сумму полей, создаваемых первым и вторым зарядами:

В точке В результирующее поле направлено влево и равно:

В точке С вектор напряжённости результирующего электрического поля направлен вправо. Его модуль найдём из треугольника:

Ответ: 36000 В/м; 3400 В/м; 4500 В/м.

Задача 3. Электрическое поле создано двумя точечными зарядами 30 нКл и -10 нКл. Расстояние между зарядами 20 см. Определить напряжённость электрического поля в точке, находящейся на расстоянии 15 см от первого и на расстоянии второго (отрицательного) зарядов.

Покажем направления векторов напряжённости, создаваемых в искомой точке первым и вторым зарядами. Их модули найдём из формул:

Складывая вектора находим вектор результирующего поля. Модуль напряжённости результирующего поля находим по теореме косинусов:

Косинус угла найдём отдельно из треугольника образованного расстояниями:

Косинус угла оказался равным 0,25. Подставив все численные значения в формулу, получим результирующую напряжённость равную 16, 7 кВ/м.

Итак, приведено решение трёх задач на применение принципа суперпозиции (наложения) полей. Сначала в интересующей точке поля рисуем вектора напряжённости электрического поля, создаваемого каждым зарядом в отдельности. Затем, складывая их, находим напряжённость суммарного поля. В первой задаче проще просуммировать проекции векторов напряжённости на оси. Там, где угол между векторами напряжённости, создаваемыми отдельными зарядами, отличен от нуля, пользуются теоремой косинусов (задачи 2 и 3).

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Нахождение напряжённости электростатического поля.

Следующая запись:Как рассчитать напряжённость поля заряженной пластины. Поле конденсатора.

Ссылки на другие занятия (до электростатики) даны в Занятии 1.

Ссылки на занятия (начиная с электростатики) даны в Занятии 45.

Электрическое поле представляет собой векторное поле, существующее вокруг тел или частиц, обладающее электрическим зарядом, а также возникающее при изменении магнитного поля.

Напряженность электрического поля — это отношение вектора силы (vec{F}), с которой поле действует на пробный заряд (q), к самому пробному заряду с учетом его знака.

[vec{E}=dfrac{vec{F}}{q}]

Единицы измерения: (displaystyle [text{В}/text{м}]) (вольт на метр).

всегда начинаются на положительных зарядах и заканчиваются на отрицательных.

— такое поле в данной области пространства. если вектор напряженности поля одинаков в каждой точке области.

При равномерном распределении электрического заряда (q) по поверхности площади (S) поверхностная плотность заряда (displaystyle sigma) постоянна и равна

[sigma =dfrac{q}{S}]

Напряженность электростатического поля точечного заряда Q в точке A, удаленной на расстояние (r) от заряда (Q), определяется формулой:

[E=dfrac{kcdot |Q|}{r^2}]

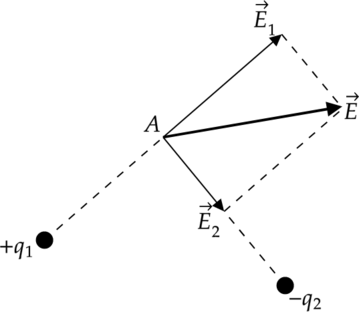
Принцип суперпозиции полей

Пусть заряды (displaystyle q_1, q_2, q_3,… , q_n) по отдельности создают в данной точке поля (vec{E}_1), (vec{E}_2),…,(vec{E}_n). Тогда система этих зарядов создает в данной точке поле (vec{E}), равное векторной сумме напряженностей полей отдельных зарядов.

[vec{E}=vec{E}_1+vec{E}_2+…+vec{E}_n]

Разберемся, что такое принцип суперпозиции на примере электрического поля. Благодаря ему, можно найти напряженность двух точечных зарядов, в каждой точке поля (А). Рассмотрим рисунок:

здесь видно, что для нахождения направления результирующего вектора (vec{E}), нужно сложить вектора (vec{E}_1) и (vec{E}_2) по правилу параллелограмма. Это и есть принцип суперпозиции.

Теорема Гаусса

Поток вектора напряженности электростатического поля (vec{E}) через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную (varepsilon_0).

Заряженная плоскость

Её электрическое поле однородно, то есть его напряжённость одинакова на любом расстоянии от плоскости, линии напряжённости параллельны. По теореме Гаусса:

[E=dfrac{|sigma|}{2varepsilon_0varepsilon}]

Заряженная сфера

Рассмотрим электрическое поле равномерно заряженной сферы. Поток напряжённости через любую замкнутую поверхность внутри сферы равен нуля, так как внутри этой поверхности нет заряда. Отсюда следует, что внутри сферы напряжённость равна нулю.

(E=0) при (r<R).

Проведём сферическую поверхность радиусом (r>R). Пусть её заряд равен (q). По теореме Гаусса:

[E=kdfrac{|q|}{r^2varepsilon}]

Заряженный шар

Рассмотрим электрическое поле равномерно заряженного шара. Напомним, что объём шара равен (V=dfrac{4}{3}pi R^3). Тогда его заряд (q=dfrac{4}{3}pi R^3rho). Напряжённость поля вне шара (r>R) можно найти так же, как и вне сферы:

[E=kdfrac{4pi R^3 rho}{3r^2varepsilon}]

Для нахождения напряжённости внутри шара применим теорему Гаусса для сферической поверхности радиусом (r<R). По теореме Гаусса:

[E=kdfrac{4pi rho r}{3varepsilon}]

2017-11-29 23:05

Если электрическое поле создано одним точечным зарядом

, то напряженность этого поля в какой-либо точке, отстоящей на расстоянии

 от заряда, равна, согласно закону Кулона,

(15.1)

и направлена вдоль прямой, соединяющей заряд с этой точкой. Таким образом, напряженность поля точечного заряда изменяется по мере удаления от заряда обратно пропорционально квадрату расстояния. При положительном заряде

 поле направлено вдоль радиуса от заряда, при отрицательном

 – вдоль радиуса по направлению к заряду (рис. 29).

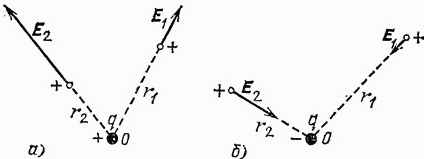
Рис.29. Напряженность поля точечного заряда в разных точках пространства: а) напряженность ноля положительного заряда; б) напряженность поля отрицательного заряда

Посмотрим теперь, чему равна напряженность поля, вызванного двумя точечными зарядами

 и

. Пусть

 – напряженность поля в некоторой точке

 (рис. 30), вызванная зарядом

 (когда заряд

 удален), а

 – напряженность в той же точке, вызванная зарядом

 (когда удален заряд

). Эти величины определяются формулой (15.1). Опыт показывает, что при совместном действии обоих зарядов напряженность поля в точке

 может быть найдена по правилу параллелограмма: если из точки

 отложить отрезки, изображающие по модулю и по направлению напряженности

 и

, и на этих отрезках, как на сторонах, построить параллелограмм, то напряженность

 результирующего поля по модулю и направлению представится диагональю этого параллелограмма. Правило сложения напряженностей полей аналогично правилу сложения сил в механике. Так же как и в механике, применимость правила параллелограмма означает независимость действия электрических полей (о принципе независимости действия сил см. в томе I).

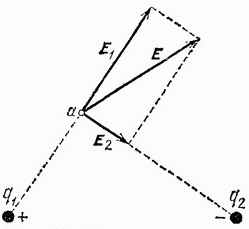
Рис. 30. Напряженность поля двух точечных зарядов

Последовательно применяя правило параллелограмма, можно вычислить напряженность поля не только двух, но и какого угодно числа точечных зарядов.

Подобным же образом можно вычислить и напряженность поля, созданного большим протяженным заряженным телом. Для этого нужно мысленно разбить это тело на малые части и каждую часть принять за точечный заряд, а затем сложить по правилу параллелограмма созданные этими частями заряда напряженности. При этом, однако, вычисления могут оказаться очень сложными.

Напомним, что с направленными величинами, складывающимися по правилу параллелограмма, мы уже встречались в томе I (сила, скорость, ускорение и т. д.). Мы назвали их векторами. Мы видим, что напряженность электрического поля есть вектор.

15.1.
Какая сила действует на положительный заряд 30 нКл, находящийся на расстоянии 15 см от отрицательного заряда – 40 нКл и на расстоянии 10 см от положительного заряда 20 нКл? Расстояние между вторым и третьим зарядами равно 20 см. При решении задачи воспользуйтесь циркулем и линейкой.

Условие задачи:

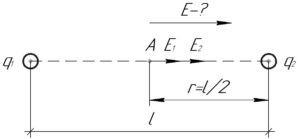
Найти напряженность поля, создаваемого двумя точечными зарядами 2 и -4 нКл в точке, лежащей посередине прямой, соединяющей заряды, если напряженность поля, создаваемого только первым зарядом в этой точке, равна 2 мВ/м.

Задача №6.2.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(q_1=2) нКл, (q_2=-4) нКл, (r=frac{l}{2}), (E_1=2) мВ/м, (E-?)

Решение задачи:

Модули напряженностей электрических полей (E_1) и (E_2), создаваемых зарядами (q_1) и (q_2), в точке A, находящейся посередине между зарядами, определим по таким формулам:

[left{ begin{gathered}
{E_1} = frac{{k{q_1}}}{{{r^2}}} hfill \
{E_2} = frac{{kleft| {{q_2}} right|}}{{{r^2}}} hfill \
end{gathered} right.]

Так как ({q_2} < 0), значит модуль в нижней формуле раскроем таким образом:

[left| {{q_2}} right| = – {q_2}]

Тогда:

[left{ begin{gathered}
{E_1} = frac{{k{q_1}}}{{{r^2}}} hfill \
{E_2} = frac{{ – k{q_2}}}{{{r^2}}} hfill \
end{gathered} right.]

Поделим нижнее равенство на верхнее:

[frac{{{E_2}}}{{{E_1}}} = frac{{ – {q_2}}}{{{q_1}}}]

[{E_2} = frac{{ – {q_2}}}{{{q_1}}}{E_1};;;;(1)]

Так как напряженность поля положительного заряда (E_1) направлено от заряда (q_1), а напряженность поля отрицательного заряда (E_2) направлено к заряду (q_2), то получается, что напряженности (E_1) и (E_2) будут сонаправлены (смотри схему). Тогда искомую напряженность поля (E) найдём по формуле:

[E = {E_1} + {E_2}]

Учитывая формулу (1), имеем:

[E = {E_1} – frac{{{q_2}}}{{{q_1}}}{E_1}]

[E = {E_1}left( {1 – frac{{{q_2}}}{{{q_1}}}} right)]

Численный ответ задачи равен:

[E = 2 cdot {10^{ – 3}} cdot left( {1 – frac{{left( { – 4} right) cdot {{10}^{ – 9}}}}{{2 cdot {{10}^{ – 9}}}}} right) = 6 cdot {10^{ – 3}};В/м = 0,06;мВ/см]

Ответ: 0,06 мВ/см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.2.19 Два точечных заряда 4 и -2 нКл находятся друг от друга на расстоянии 60 см. Определить
6.2.21 Определить расстояние между двумя точечными зарядами 16 и -6 нКл, если
6.2.22 В однородном электрическом поле напряженностью 40 кВ/м, направленным

§ 14. НАПРЯЖЕННОСТЬ
ЭЛЕКТРИЧЕСКОГО ПОЛЯ.

ЭЛЕКТРИЧЕСКОЕ
СМЕЩЕНИЕ

Основные
формулы

 Напряженность
электрического поля

E=F/Q,

где F — сила,
действующая на точечный положительный
заряд Q, помещенный в данную точку
поля.

 Сила, действующая
на точечный заряд Q, помещенный в
электрическое поле,

F=QE.

 Поток вектора
напряженности Е электрического
поля:

а) через произвольную
поверхность S,
помещенную в неоднородное поле,

или
,

где 
— угол между вектором напряженности Е
и нормалью n к элементу поверхности;
dS — площадь элемента поверхности;
E_n — проекция вектора
напряженности на нормаль;

б) через плоскую
поверхность, помещенную в однородное
электрическое поле,

Ф_E=ЕScos.

 Поток вектора
напряженности Е через замкнутую
поверхность

,

где
интегрирование ведется по всей
поверхности.


Теорема Остроградского
— Гаусса. Поток вектора напряженности
Е
через любую замкнутую поверхность,
охватывающую заряды
Q_l,
Q₂,
. . .,
Q_n,

,

где

— алгебраическая
сумма зарядов, заключенных внутри
замкнутой поверхности; п — число
зарядов.

 Напряженность
электрического поля, создаваемого
точечным зарядом Q
на расстоянии r от
заряда,

.

Напряженность
электрического поля, создаваемого
металлической сферой радиусом
R, несущей заряд
Q,
на расстоянии r от
центра сферы:

а) внутри сферы
(r<.R)

E=0;

б) на поверхности
сферы (r=R)

;

в) вне сферы
(r>R)

.

 Принцип
суперпозиции (наложения) электрических
полей, согласно которому напряженность
Е результирующего поля, созданного
двумя (и более) точечными зарядами, равна
векторной (геометрической) сумме
напряженностей складываемых полей:

Е=E₁+Е₂+…+Е_n.

В
случае двух электрических полей с
напряженностями Е₁
и Е₂
модуль вектора напряженности

,

где 
— угол между векторами E₁
и E₂.

 Напряженность
поля, создаваемого бесконечно длинной
равномерно заряженной нитью (или
цилиндром) на расстоянии r
от ее оси,

,
где  — линейная
плотность заряда.

Линейная плотность
заряда есть величина, равная отношению
заряда, распределенного по нити, к длине
нити (цилиндра):

 Напряженность
поля, создаваемого бесконечной равномерно
заряженной плоскостью,

где 
— поверхностная плотность заряда.

Поверхностная
плотность заряда есть величина, равная
отношению заряда, распределенного по
поверхности, к площади этой поверхности:

.

 Напряженность
поля, создаваемого двумя параллельными
бесконечными равномерно и разноименно
заряженными плоскостями, с одинаковой
по модулю поверхностной плотностью о
заряда (поле плоского конденсатора)

.

Приведенная формула
справедлива для вычисления напряженности
поля между пластинами плоского
конденсатора (в средней части его)
только в том случае, если расстояние
между пластинами много меньше линейных
размеров пластин конденсатора.

 Электрическое
смещение D
связано с напряженностью E
электрического поля соотношением

D=₀E.

Это соотношение
справедливо только для изотропных
диэлектриков.

 Поток вектора
электрического смещения выражается
аналогично потоку вектора напряженности
электрического поля:

а) в случае
однородного поля поток сквозь плоскую
поверхность

;

б) в случае
неоднородного поля и произвольной
поверхности

,

где D_n
— проекция вектора D на направление
нормали к элементу поверхности, площадь
которой равна dS.

 Теорема
Остроградского — Гаусса. Поток вектора
электрического смещения сквозь любую
замкнутую поверхность, охватывающую
заряды Q₁,Q₂,
…,Q_n,

,

где п—число
зарядов (со своим знаком), заключенных
внутри замкнутой поверхности.

 Циркуляция
вектора напряженности электрического
поля есть величина, численно равная
работе по перемещению единичного
точечного положительного заряда вдоль
замкнутого контура. Циркуляция выражается
интегралом по замкнутому контуру
,
где E_l—проекция
вектора напряженности Е в данной точке
контура на направление касательной к
контуру в той же точке.

В случае
электростатического поля циркуляция
вектора напряженности равна нулю:

.

Примеры
решения задач

П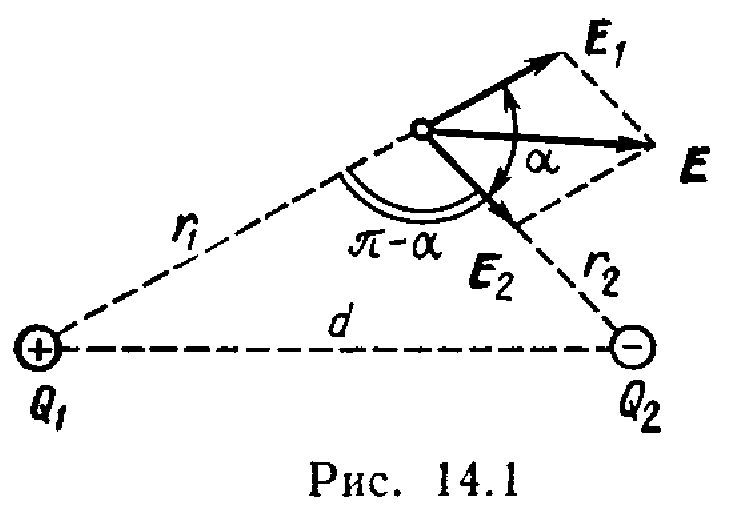ример
1. Электрическое поле создано двумя
точечными зарядами: Q₁=30
нКл и Q₂=
–10 нКл. Расстояние d
между зарядами равно 20 см. Определить
напряженность электрического поля в
точке, находящейся на расстоянии r₁=15
см от первого и на расстоянии r₂=10
см от второго зарядов.

Решение.
Согласно принципу суперпозиции
электрических полей, каждый заряд
создает поле независимо от присутствия
в пространстве других зарядов. Поэтому
напряженность Е электрического
поля в искомой точке может быть найдена
как векторная сумма
напряженностей E₁ и Е₂
полей, создаваемых каждым зарядом в
отдельности: E=E₁+E₂.

Напряженности
электрического поля, создаваемого в
вакууме первым и вторым зарядами,
соответственно равны

(1)

Вектор E₁
(рис. 14.1) направлен по силовой линии от
заряда Q₁,
так как заряд Q₁>0;
вектор Е₂ направлен также
по силовой линии, но к заряду
Q₂,
так как Q₂<0.

Модуль вектора Е
найдем по теореме косинусов:

, (2)

где угол 
может быть найден из треугольника со
сторонами r₁,
r₂
и d:

.

В данном случае
во избежание громоздких записей вычислим
отдельно значение cos.
По этой формуле найдем

cos
=0,25.

Подставляя выражения
E₁
и E₂
а по формулам (1) в равенство (2) и вынося
общий множитель 1/(4₀)
за знак корня, получаем

.

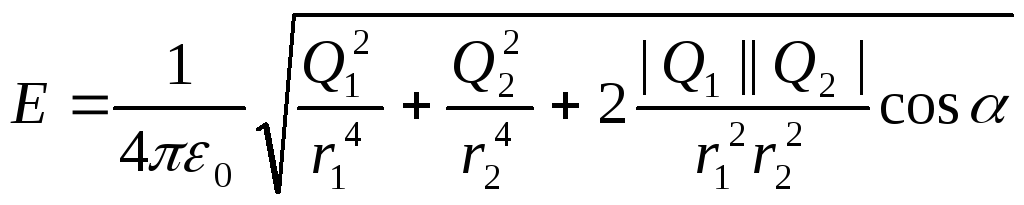
Подставив значения
величин ,
₀,
Q₁,
Q₂,
r₁-,
r₂
и  в последнюю
формулу и произведя вычисления, найдем

Пример 2.
Электрическое поле создано двумя
параллельными бесконечными заряженными
плоскостями с поверхностными плотностями
заряда ₁=0,4
мкКл/м² и ₂=0,1
мкКл/м². Определить напряженность
электрического поля, созданного этими
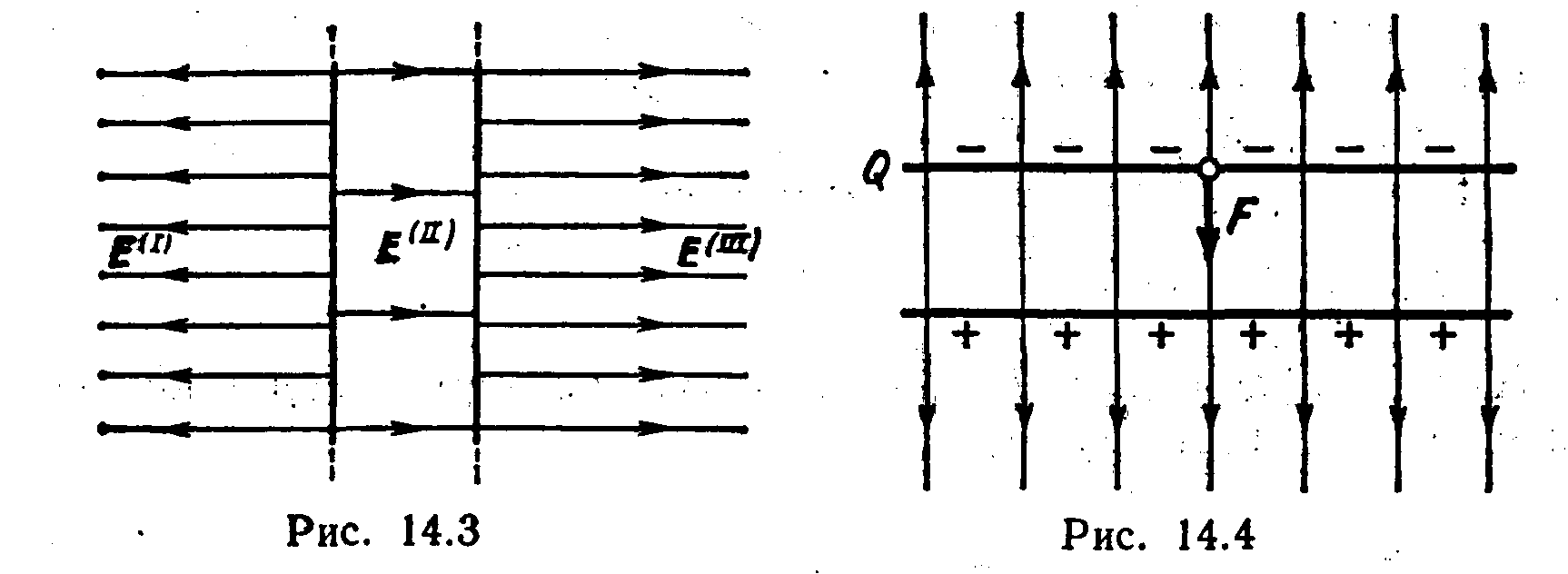
заряженными плоскостями.

Р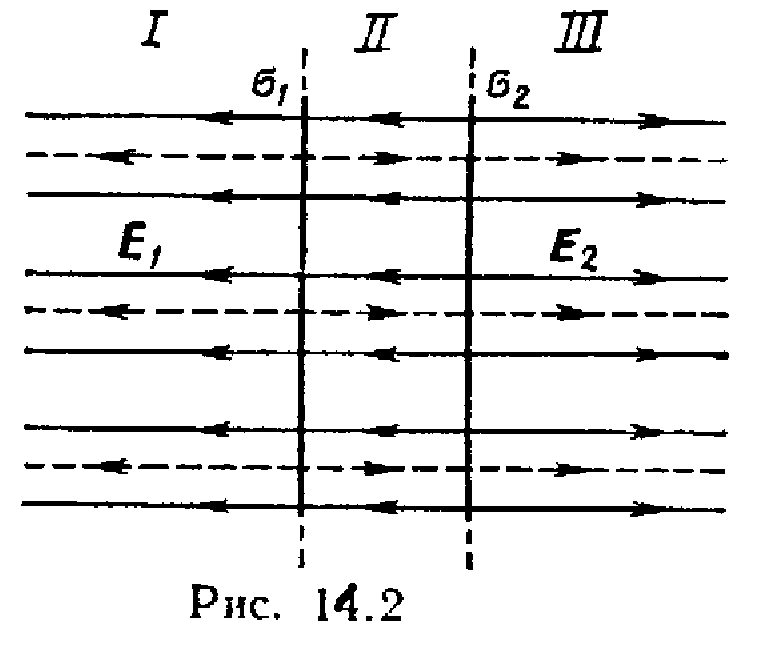ешение.
Согласно принципу суперпозиции, поля,
создаваемые каждой заряженной плоскостью
в отдельности, накладываются друг на
друга, причем каждая заряженная плоскость
создает электрическое поле независимо
от присутствия другой заряженной
плоскости (рис. 14.2).

Напряженности
однородных электрических полей,
создаваемых первой и второй плоскостями,
соответственно равны:

;

.

Плоскости делят
все пространство на три области: I,
II и III.
Как вид но из рисунка, в первой и
третьей областях электрические силовые
линии обоих полей направлены в одну
сторону и, следовательно, напряженности
суммарных полей Е^(I)
и E^(III)
в первой и третьей областях равны между
собой и равны сумме напряженностей
полей, создаваемых первой и второй
плоскостями: Е^(I)=
E^(III)=E₁+E₂,
или

Е^(I)=
E^(III)=.

Во второй области
(между плоскостями) электрические
силовые линии полей направлены в
противоположные стороны и, следовательно,
напряженность поля E^(II)
равна разности напряженностей полей,
создаваемых первой и второй плоскостями:
E^(II)=|E₁-E₂|,
или

.

Подставив данные
и произведя вычисления, получим

E^(I)=E^(III)=28,3кВ/м=17
кВ/м.

Картина
распределения силовых линий суммарного
поля представлена на рис. 14.3.

Пример 3. На
пластинах плоского воздушного конденсатора
находится заряд Q=10
нКл. Площадь S
каждой пластины конденсатора равна 100
см² Определить силу F,
с которой притягиваются пластины. Поле
между пластинами считать однородным.

Решение. Заряд
Q одной пластины
находится в поле, созданном зарядом
другой пластины конденсатора.
Следовательно, на первый заряд действует
сила (рис. 14.4)

F=E₁Q,, (1)

где E₁
— напряженность поля, создаваемого
зарядом одной пластины. Но
где
 – поверхностная
плотность заряда пластины.

Формула (1) с учетом
выражения для E₁
примет вид

F=Q²/(2₀S).

Подставив значения
величин Q, ₀
и S в эту формулу и
произведя вычисления, получим

F=565
мкН.

Пример 4.
Электрическое поле создано, бесконечной
плоскостью, заряженной с поверхностной
плотностью =400
нКл/м², и бесконечной прямой
нитью, заряженной с линейной плотностью
=100 нКл/м. На расстоянии
r=10 см от нити находится
точечный заряд Q=10
нКл. Определить силу, действующую на
заряд, ее направление, если заряд и нить
лежат в одной плоскости, параллельной
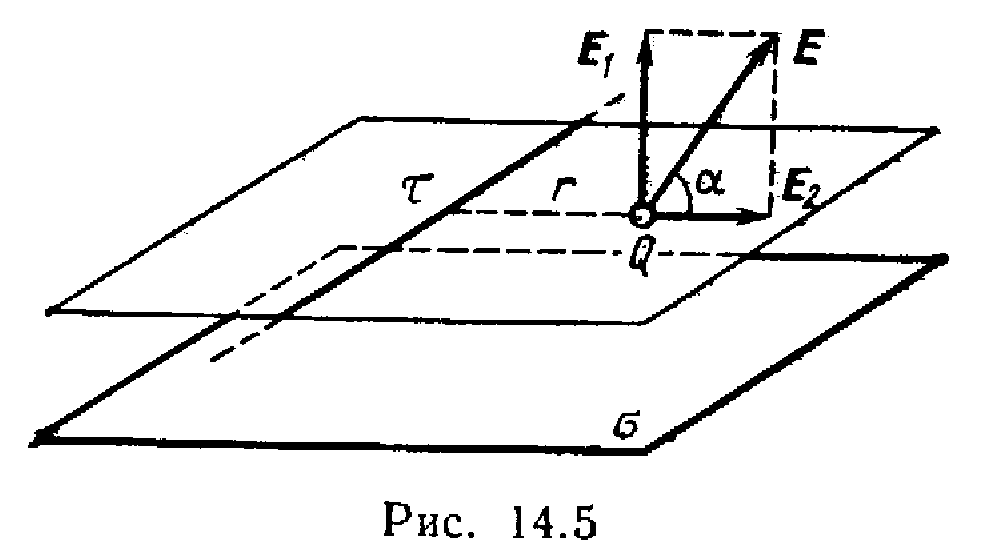
заряженной плоскости.

Решение. Сила,
действующая на заряд, помещённый в поле,

F=EQ, (1)

где Е —
напряженность поля в точке, в которой
находится заряд Q.

Определим
напряженность Е поля, создаваемого,
по условию задачи, бесконечной заряженной
плоскостью и бесконечной заряженной
нитью. Поле, создаваемое бесконечной
заряженной плоскостью, однородно, и его
напряженность в любой точке

. (2)

Поле, создаваемое
бесконечной заряженной линией,
неоднородно. Его напряженность зависит
от расстояния и определяется по формуле

. (3)

Согласно принципу
суперпозиции электрических полей,
напряженность поля в точке, где находится
заряд Q,
равна векторной сумме напряженностей
E₁
и Е₂ (рис. 14.5):
E=E₁+E₂.
Так как векторы E₁
и Е₂ взаимно
перпендикулярны, то

.

Подставляя выражения
E₁
и E₂ по
формулам (2) и (3) в это
равенство, получим

,

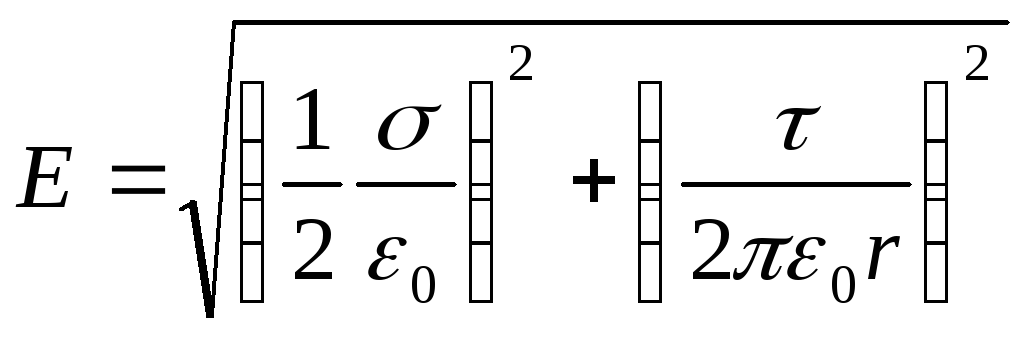
или
.

Теперь найдем силу
F, действующую на
заряд, подставив выражение Е в
формулу (1):

. (4)

Подставив значения
величин Q, ₀,
, ,
 и r
в формулу (4) и сделав вычисления, найдем

F=289
мкН.

Направление силы
F, действующей на положительный
заряд Q, совпадает с направлением
вектора напряженности Е поля.
Направление же вектора Е задается
углом  к заряженной
плоскости. Из рис. 14.5 следует, что

,
откуда
.

Подставив значения
величин , r,
 и 
в это выражение и вычислив, получим

=51°3

Пример 5.
Точечный заряд Q=25
нКл находится в ноле, созданном прямым
бесконечным цилиндром радиусом
R=1
см, равномерно заряженным с поверхностной
плотностью =2 мкКл/м².
Определить силу, действующую на заряд,
помещенный от оси цилиндра на расстоянии
r=10 см.

Решение. Сила,
действующая на заряд Q, находящийся
в поле,

F=QE, (1)

где Е —
напряженность поля в точке, в которой
находится заряд Q.

Как известно,
напряженность поля бесконечно длинного
равномерно заряженного цилиндра

E=/(2₀r), (2)

где 
— линейная плотность
заряда.

Выразим линейную
плотность  через
поверхностную плотность .
Для этого выделим элемент цилиндра
длиной l и выразим
находящийся на нем заряд Q₁
двумя, способами:

Q₁=S=2Rl
и Q₁=l.

Приравняв правые
части этих равенств, получим l=2Rl.
После сокращения на l
найдем =2R.
С учетом этого формула (2) примет вид
E=R/(₀r).
Подставив это выражение Е в формулу
(1), найдем искомую силу:

F=QR/(₀r). (3)

Так как
R и r
входят в формулу в виде отношения, то
они могут быть выражены в любых, но
только одинаковых единицах.

Выполнив вычисления
по формуле (3), найдем

F=2510^-9210^-610^-2/(8,8510^-121010^-2)H==56510^-6H=565мкH.

Направление силы
F совпадает с
направлением вектора напряженности
Е, а последний в силу симметрии (цилиндр
бесконечно длинный) направлен
перпендикулярно цилиндру.

Пример 6.
Электрическое поле создано тонкой
бесконечно длинной нитью, равномерно
заряженной с линейной плотностью =30
нКл/м. На расстоянии а=20 см от нити
находится плоская круглая площадка
радиусом r=1 см.
Определить поток вектора напряженности
через эту площадку, если плоскость ее
составляет угол =30°
с линией напряженности, проходящей
через середину площадки.

Решение. Поле,
создаваемое бесконечно равномерно,
заряженной нитью, является неоднородным.
Поток вектора напряженности в этом
случае выражается интегралом

, (1)

где E_n
— проекция вектора Е на нормаль
n к поверхности площадки
dS. Интегрирование
выполняется по всей поверхности площадки,
которую пронизывают линии напряженности.

П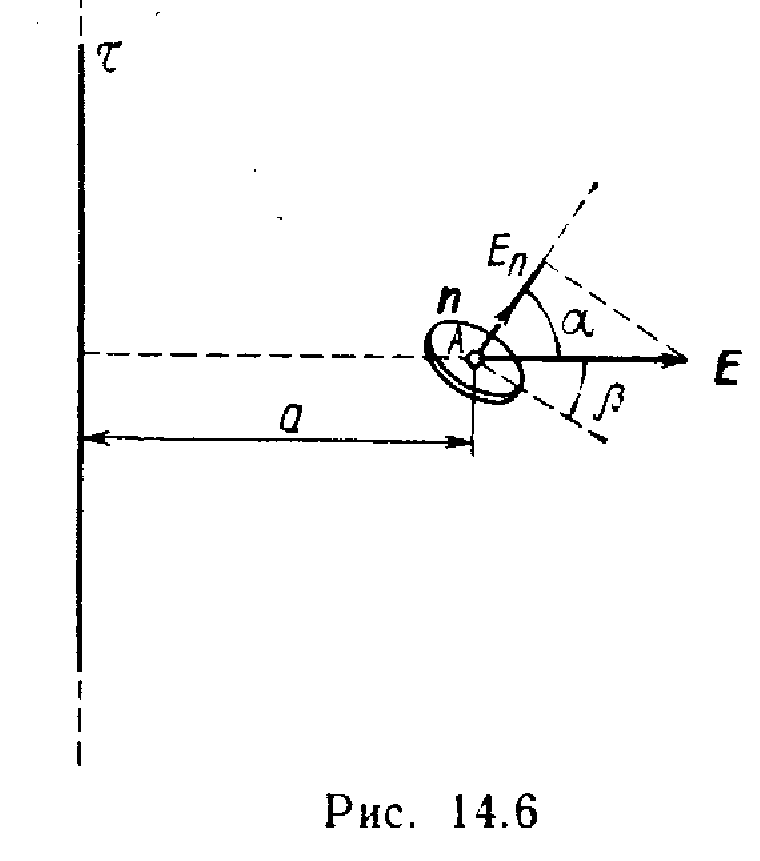роекция
Е_п вектора напряженности
равна, как видно из рис. 14.6,

Е_п=Еcos,

где 
— угол между направлением вектора и
нормалью n. С учетом этого формула
(1) примет вид

.

Так как размеры
поверхности площадки малы по сравнению
с расстоянием до нити (r<<a),
то электрическое поле в пределах площадки
можно считать практически однородными.
Следовательно, вектор напряженности Е
очень мало. меняется по модулю и
направлению в пределах площадки, что
позволяет заменить под знаком интеграла
значения Е и cos
их средними значениями <E>
и <cos>
и вынести их за знак интеграла:

Выполняя
интегрирование и заменяя <E>
и <cos>
их приближенными значениями Е_A
и cos_A,
вычисленными для средней точки площадки,
получим

Ф_E=Е_Acos_AS=r²Е_Acos_A. (2)

Напряженность Е_A
вычисляется по формуле E_A=/(2₀a).
Из

рис. 14.6 следует
cos_A=cos(/2—)=sin.

С учетом выражения
Е_A и
cos_A
равенство (2.) примет вид

.

Подставив в
последнюю формулу данные и произведя
вычисления, найдем

Ф_E=424
мВ.м.

Пример 7.
Две концентрические проводящие сферы
радиусами R₁=6
см и R₂=10
см несут соответственно заряды
Q₁=l
нКл и Q₂=
–0,5 нКл. Найти напряженность
Е поля в точках, отстоящих от центра
сфер на расстояниях r₁=5
см, r₂=9
см r₃=15см.
Построить график Е(r).

Решение.
Заметим, что точки, в которых требуется
найти напряженности электрического
поля, лежат в трех областях (рис. 14.7):
область I (r<R₁),
область II (R₁<r₂<R₂),
область III (r₃>R₂).

1. Для определения
напряженности E₁
в области I проведем
сферическую поверхность
S₁
радиусом r₁
и воспользуемся теоремой Остроградского—Гаусса.
Так как внутри области I
зарядов нет, то согласно указанной
теореме получим равенство

, (1)

где E_n
— нормальная составляющая напряженности
электрического поля.

Из соображений
симметрии нормальная составляющая E_n
должна быть равна самой напряженности
и постоянна для всех точек сферы, т. е.
En=E₁=const.
Поэтому ее можно вынести за знак
интеграла. Равенство (1) примет вид

.

Так как площадь
сферы не равна нулю, то

E₁=0,

т. е. напряженность
поля во всех точках, удовлетворяющих
условию r₁<.R₁,
будет равна нулю.

2. В области II
сферическую поверхность проведем
радиусом r₂.
Так как внутри этой поверхности находится,
заряд Q₁,
то для нее, согласно теореме
Остроградского—Гаусса, можно
записать равенство

. (2)

Так как
E_n=E₂=const,
то из условий симметрии следует

,
или ES₂=Q₁/₀,

откуда

E₂=Q₁/(₀S₂).

Подставив сюда
выражение площади сферы, получим

E₂=Q/(4). (3)

3. В области III
сферическую поверхность проведем
радиусом r₃.
Эта поверхность охватывает
суммарный заряд Q₁+Q₂.
Следовательно, для нее уравнение,
записанное на основе теоремы
Остроградского — Гаусса, будет иметь
вид

.

Отсюда, использовав
положения, примененные в первых двух
случаях, найдем

. (4)

Убедимся в том,
что правые части равенств (3) и (4) дают
единицу напряженности электрического
поля;

Выразим все величины
в единицах СИ (Q₁=10^-9
Кл, Q₂=
–0,510^-9
Кл, r₁=0,09
м, r₂=15
м, l/(4₀)=910⁹
м/Ф) и произведем вычисления:

4. Построим график
E(r).В
области I (r₁<R₁)
напряженность E=0. В
области II (R₁r<.R₂)
напряженность E₂(r)
изменяется по закону l/r².
В точке r=R₁
напряженность E₂(R₁)=Q₁/(4₀R)=2500
В/м.В точке r=R₁
(r стремится к
R₁
слева) E₂(R₂)=Q₁/(4₀R)=900В/м.
В области III (r>R₂)E₃(r)
изменяется по закону 1/r²,
причем в точке r=R₂
(r стремится к R₂
справа) Е₃(R₂)=(Q₁–|Q₂|)/(4₀R)=450
В/м. Таким образом, функция Е(r)
в точках r=R₁
и r=R₂
терпит разрыв. График зависимости Е(r)
представлен на рис. 14.8.

Задачи

Напряженность
поля точечных зарядов

14.1. Определить
напряженность Е электрического
поля, создаваемого точечным зарядом
Q=10
нКл на расстоянии r=10
см от него. Диэлектрик —
масло.

14.2. Расстояние
d между двумя
точечными зарядами Q₁=+8
нКл и Q₂=
–5,3 нКл равно 40 см. Вычислить
напряженность Е поля в точке, лежащей
посередине между зарядами. Чему равна
напряженность, если второй заряд будет
положительным?

14.3. Электрическое
поле создано двумя точечными зарядами
Q₁=10
нКл и Q₂=
–20 нКл, находящимися на расстоянии
d=20
см друг от друга. Определить напряженность
E поля в точке, удаленной
от первого заряда на r₁=30
см и от второго на r₂=50
см.

14.4. Расстояние
d между двумя точечными положительными
зарядами Q₁=9Q
и Q₂=Q
равно 8 см. На каком расстоянии г от
первого заряда находится точка, в которой
напряженность Е поля зарядов равна
нулю? Где находилась бы эта точка, если
бы второй заряд был отрицательным?

14.5. Два точечных
заряда Q₁=2Q
и Q₂=
–Q находятся на
расстоянии d друг от друга. Найти
положение точки на прямой, проходящей
через эти заряды, напряженность Е
поля в которой равна нулю,

14.6. Электрическое
поле создано двумя точечными зарядами
Q₁=40
нКл и Q₂=
–10 нКл, находящимися на расстоянии
d=10 см друг от друга.
Определить напряженность Е поля в
точке, удаленной от первого заряда на
r₁=12
см и от второго на r₂=6
см.

Напряженность
поля заряда, распределенного по кольцу
и сфере

14.7. Тонкое
кольцо радиусом R=8 см
несет заряд, равномерно распределенный
с линейной плотностью =10
нКл/м. Какова напряженность Е
электрического поля в точке, равноудаленной
от всех точек кольца на расстояние r=10
см?

14.8. Полусфера
несет заряд, равномерно распределенный
с поверхностной плотностью =1,нКл/м².
Найти напряженность Е электрического
поля в геометрическом центре полусферы.

14.9. На
металлической сфере радиусом R=10
см находится заряд Q=l
нКл. Определить напряженность Е
электрического поля в
следующих точках: 1) на расстоянии r₁=8
см от центра сферы; 2) на
ее поверхности; 3) на расстоянии r₂=15
см от центра сферы. Построить график
зависимости E от r.

14.10. Две
концентрические металлические заряженные
сферы радиусами R₁=6cм
и R₂=10
см несут соответственно заряды
Q₁=1
нКл и Q₂=
–0,5 нКл. Найти
напряженности Е поля в точках.
отстоящих от центра сфер на расстояниях
r₁=5 см, r₂=9
см, r₃=15
см. Построить график зависимости Е(r).

Напряженность
поля заряженной линии

14.11. Очень
длинная тонкая прямая проволока несет
заряд, равномерно распределенный по
всей ее длине. Вычислить линейную
плотность  заряда,
если напряженность E
поля на расстоянии а=0,5 м от проволоки
против ее середины равна 200 В/м.

14.12. Расстояние
d между двумя длинными
тонкими проволоками, расположенными
параллельно друг другу, равно 16 см.
Проволоки равномерно заряжены
разноименными зарядами с линейной
плотностью ||=^150.
мкКл/м. Какова напряженность Е поля
в точке, удаленной на r=10
см как от первой, так и от второй проволоки?

14.13. Прямой
металлический стержень диаметром d=5
см и длиной l=4 м несет
равномерно распределенный по его
поверхности заряд Q=500
нКл. Определить напряженность Е
поля в точке, находящейся против середины
стержня на расстоянии а=1 см от его
поверхности.

14.14. Бесконечно
длинная тонкостенная металлическая
трубка радиусом R=2
см несет равномерно распределенный по
поверхности заряд (=1
нКл/м²). Определить напряженность
Е поля в точках, отстоящих от оси
трубки на расстояниях r₁=l
см, r₂=3
см. Построить график зависимости Е(r).