Как найти напряженность поля электрона

Электрическое поле. ЗАДАЧИ с решениями

Формулы, используемые на уроках по теме «Электрическое поле. ЗАДАЧИ» в 10-11 классах при подготовке к ЕГЭ.

---

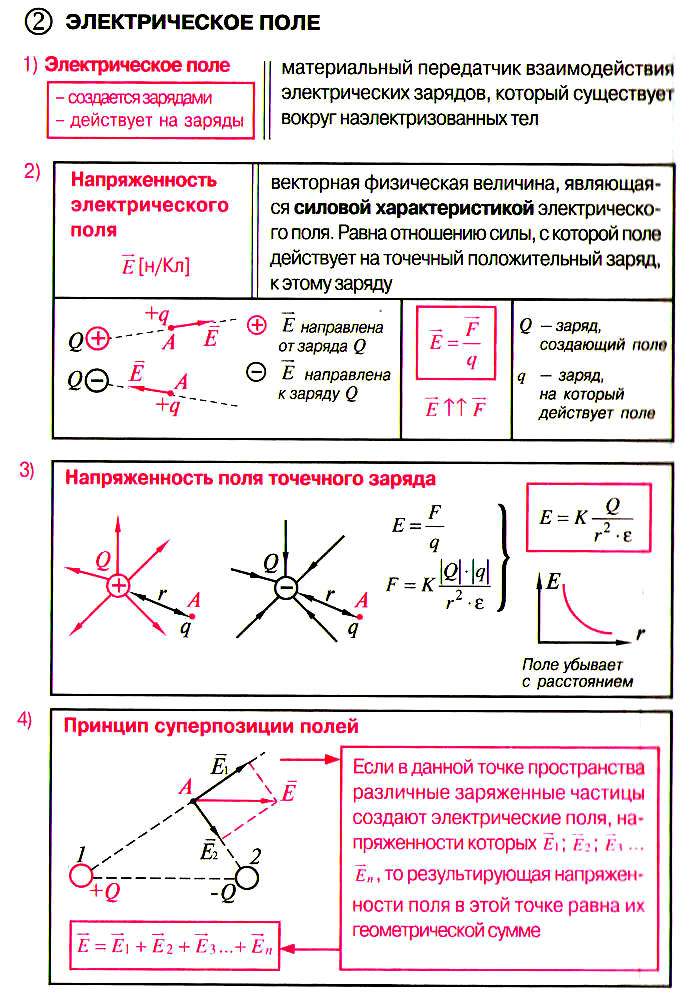
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

---

Задача № 1.
 Электрон движется без начальной скорости вдоль силовой линии однородного электрического поля напряженностью Е = 2 • 10⁴ Н/Кл. Какой путь S он пролетит прежде, чем его скорость станет v = 100 км/с ? Среда — воздух. Модуль заряда электрона е = 1,6 • 10^–19 Кл, его масса m_e = 9,1 • 10^–31 кг.

---

Задача № 2.
 Пылинка с зарядом q = 1 нКл неподвижно висит в однородном электрическом поле напряженностью Е = 2 • 10⁴ Н/Кл, вектор напряженности которого направлен вверх (рис. 2-9). Найти массу пылинки т. Сколько избыточных электронов N содержит пылинка? 

---

Задача № 3.
 Заряженный шар диаметром D находится в равновесии в жидком диэлектрике плотностью р₁ с диэлектрической проницаемостью ε (рис. 2-10). Найти поверхностную плотность зарядов на шаре σ, если плотность вещества шара р₂. Напряженность электрического поля в диэлектрике Е, вектор напряженности направлен вверх. 

---

Задача № 4.
 На каком расстоянии г₂ от точечного заряда напряженность электрического поля этого заряда в жидком диэлектрике с диэлектрической проницаемостью ε₂ = 81 (вода) такая же, как на расстоянии r₁ = 9 см от этого заряда в воздухе?

---

Задача № 5.
 Электрон влетает в однородное электрическое поле со скоростью v₀, направленной перпендикулярно вектору напряженности Е (рис. 2-11). Под каким углом φ к линиям вектора напряженности будет направлен вектор его скорости через время t полета в поле? Чему будет равна работа сил поля А за это время? Чему будет равна кинетическая энергия электрона W_к через время t ? Напряженность поля Е. Масса электрона т_е и его заряд е известны. 

---

Задача № 6.
 Тонкая металлическая пластинка массой m падает вертикально вниз равноускоренно так, что ее плоскость остается горизонтальной. Падению пластинки противодействует сила сопротивления среды F_соnp. Найти напряженность электрического поля Е, возникающего внутри пластинки вследствие инерции свободных электронов. Масса электрона m_e, его заряд е.

---

Задача № 7.
 К бесконечной, вертикальной, равномерно заряженной плоскости прикреплена одним кондом невесомая нить, на другом конце которой находится одноименно с нитью заряженный шарик радиусом R = 0,5 см, несущий заряд q = 1 • 10^–10 Кл. Плотность вещества шарика р = 2 • 10³ кг/м³. Натяжение нити F_н = 4,9 • 10^–2 Н. Какой угол а образует с плоскостью нить, на которой висит шарик (рис. 2-12)? Среда – воздух. Чему равна поверхностная плотность σ зарядов на плоскости? 

---

Задача № 8.
 Сфера радиусом R = 1 см равномерно заряжена. Поверхностная плотность зарядов на сфере σ = 10 нКл/см². Найти напряженность Е₁ электрического поля на расстоянии r₁ = 10 см от центра сферы (рис. 2-13). Построить график зависимости напряженности Е от расстояния r в пределах от r₀ = 0 до r₁ = 10 см. Среда — воздух. 

---

Задача № 9.
 Заряды q₁ = 20 нКл и q₂ = 10 нКл расположены на расстоянии r = 10 см друг от друга. Найти напряженность электрического поля Е₁, созданного этими зарядами в точке 1, расположенной на расстоянии r₁ = 4 см от заряда q₁ и напряженность Е₂ в точке 2, расположенной на расстоянии г₂ = 2 см от заряда q₂ (рис. 2-15). Среда — вакуум. 

---

Задача № 10.
 Два одноименных точечных заряда q и 4q расположены на расстоянии r друг от друга. На каком расстоянии r₁ от заряда q находится точка М, в которой напряженность поля этих зарядов Е = 0? На каком расстоянии r₂ от заряда q находится такая точка, если эти заряды разноименные?

---

Задача № 11.
 На расстоянии г = 3 см от поверхности шара радиусом R = 2 см находится точечный отрицательный заряд q = –2 нКл. Шар заряжен положительно с поверхностной плотностью зарядов σ = 2 нКл/м². Найти напряженность поля Е, созданного заряженным шаром и точечным зарядом, в точке, расположенной на расстоянии r₁ = 4 см от центра шара, и г₂ = 3 см от заряда q. Среда — воздух.

---

Задача № 12.
 В вершинах равностороннего треугольника со стороной а находятся заряды q, –q и q. Найти напряженность поля Е, созданного этими зарядами в центре треугольника. Среда — воздух.

(с) В учебных целях использованы цитаты из учебного пособия «Новый репетитор по физике для подготовки к ЕГЭ : задачи и методы их решения / И.Л. Касаткина; под ред. Т.В. Шкиль. — Ростов н /Д : Феникс».

---

Это конспект по теме «Электрическое поле. ЗАДАЧИ с решениями». Выберите дальнейшие действия:

• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

4

Электронная
микроскопия

Лекция
№7

Из уравнения (8)
следует, что скорость электрона выражается
через ускоряющее напряжение как

(9)

Известно, что длина
волны частицы
связана с его массой
и скоростью
уравнением Де-Бройля. (Де Бройль перенес
корпускулярно-волновой дуализм в
отношении излучения
на частицы, обладающие массой покоя,
каковыми и являются электроны)

(10)

Если в это уравнение
подставить найденное нами выражение
скорости электрона, находящегося в поле
ускоряющего напряжения U,
то получим

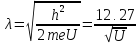(11)

где λ
получится в ангстремах, если напряжение
подставить в вольтах. Длина волны,
вычисленная таким образом называется
дебройлевской.

Если ускоряющее
напряжение более 50 кВ, то нужно учитывать
релятивистскую поправку, и вместо U
использовать выражение для U^*

(12)

Как электрон
движется в электростатическом поле

Электростатическое
поле характеризуется двумя величинами:

• скалярным
  потенциалом φ
  и

• вектором
  напряженности
  .

Потенциал
поля в некоторой точке определяется
работой,
которую необходимо затратить на
перемещение единичного положительного
заряда из бесконечности (или другой
точки пространства с
условно
принятым нулевым потенциалом) в данную
точку.

Разность
потенциалов
между двумя точками, или приложенное к
этим точкам напряжение, очевидно, равна
работе,
затрачиваемой на перемещение заряда
из одной точки в другую.

Напряженность
поля Ε
равна
силе,
с которой поле действует на единичный
положительный заряд.

Для электрона,
имеющего отрицательный заряд —е,
эта сила

(13)

Для определения
направления вектора напряженности
удобно электростатическое поле
представить с помощью эквипотенциальных
поверхностей,
т.е. геометрических
мест точек с одинаковым потенциалом: φ
= const.

Тогда вектор
напряженности

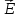
• будет направлен
  перпендикулярно
  к поверхности равного потенциала

• в сторону уменьшения
  потенциалов.

Очевидно, что чем
гуще будут расположены эквипотенциальные
поверхности, тем большую энергию
приобретает электрон за единицу длины
своего пути.

Напряженность
поля и
характеризует эту «густоту»
эквипотенциальных поверхностей, или
скорость
изменения потенциала,
выражаемую так называемым градиентом
потенциала. Таким образом,

(14)

и уравнение (4)
приобретает вид

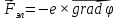
(15)

Следовательно, в
электростатическом поле электрон будет
двигаться вдоль градиента потенциала
в сторону увеличения последнего.

Точное совпадение
траектории движения электрона с силовой
линией (т. е. линией, перпендикулярной
к эквипотенциальным поверхностям) может
и не иметь места, так как при переходе
из одной области поля в другую электрон,
изменяя свою скорость, будет частично
сохранять направление движения, которое
он имел ранее. Тем не менее, при переходе
через эквипотенциальные поверхности
траектория электрона будет изменяться,
т. е. электрон будет испытывать преломление.

Преломление
электронов в электрическом поле.

Физической основой
формирования светооптического изображения
является преломление светового луча
на границе раздела двух сред (например,
воздуха и стекла линзы).

Учитывая, что и
траектория электрона испытывает
преломление при переходе через области
с разными потенциалами, рассмотрим по
аналогии со световой оптикой закон
преломления электронов в электрическом
поле.

Рассмотрим
пространство, разделенное двумя
близлежащими металлическими сетками
с потенциалами φ_χ
и φ₂

Рис. Преломление
траектории электрона при скачкообразном
изменении потенциала

Приближенно можно
считать, что потенциал в каждой области
постоянен и равен соответственно φ₁
и φ₂.

Пусть υ₁
—
скорость, с которой электрон из области
I подходит к двойному разделяющему
слою—преломляющей границе, а υ₂
—скорость,
с которой он выходит из этого слоя в
область II.

Углы α₁
и α₂
назовем углами падения и преломления.
Разложим вектор скорости на две
составляющие: υ’
и υ”.

Из определения
напряженности электрического поля
очевидно, что на электрон, пересекающий
двойной слой, будет действовать сила,
перпендикулярная
поверхности сетки — поверхности равного
потенциала.

Отсюда следует,
что составляющая скорости электрона,
направленная параллельно слою, останется
неизменной, т. е.

υ’₁
= υ’₂

или

υ₁sin
α₁
= υ₂sin
α₂

Но как следует из
формулы (16)

(16)

(17)

что после подстановки
в выражение (22) дает

(18)

Сравнивая это
выражение с законом преломления в
световой оптике, мы видим, что получается
полная аналогия, если для электроннооптического
показателя преломления принять (с
точностью до постоянного множителя)
величину n

.
(19)

Модель такого
двойного электрического слоя может
быть осуществлена при помощи двух
параллельных сеток.

Если электрон
ускоряется, то, пройдя двойной слой, он
приближается в большей или меньшей
степени к нормали. Если электрон
тормозится, то его траектория отходит
от нормали.

Двойной слой
действует как отражающий, если внутри
его начальная нормальная компонента
v_xcos
обращается
в нуль.

Полученный закон
преломления остается справедливым и в
том случае, если двойной преломляющий
слой образован не плоскими, а криволинейными
поверхностями и если изменение потенциала
в переходной области сколь угодно мало.

Поэтому
эквипотенциальные
поверхности электростатического поля
также можно рассматривать как поверхности
изменения потенциала, на которых электрон
претерпевает преломление.

Таким образом, на
основании аналогии между законами
преломления световых и электронных
лучей, лежащей в основе всей электронной
геометрической оптики, можно утверждать,
что эквипотенциальные поверхности
электрического поля являются аналогами
преломляющих поверхностей линз в
световой оптике.

Следовательно,
создавая с помощью заряженных электродов
определенной конфигурации требуемую
форму эквипотенциальных поверхностей,
можно получить электрическое поле,
обладающее необходимыми оптическими
свойствами для получения электроннооптических
изображений.

Наряду с указанной
аналогией между световой и электронной
оптикой имеется и существенное различие.

• В световой оптике
  для получения изображений используются
  однородные
  среды
  (воздух, стекло, иммерсионные жидкости),
  где показатель преломления изменяется
  дискретно, скачкообразно переходя на
  границе раздела от одного значения к
  другому.

• В электростатическом
  поле показатель
  преломления меняется непрерывно
  и является функцией координат
  рассматриваемой точки пространства.
  Следовательно, электрическое поле
  действует как оптически неоднородная
  среда.

/var/www/studfiles2/data/www/download/2706/299/26VLaKENRD.mZO5

Соседние файлы в папке Новая папка

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #