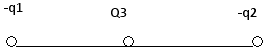Как найти напряженность поля между двумя точками

Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.

Задачи урока:

• формирование понятия напряжённости электрического поля; дать понятие о
  линиях напряжённости и графическое представление электрического поля;
• научить учащихся применять формулу E=kq/r² в решении
  несложных задач на расчёт напряжённости.

Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.

Графически изображая поле, следует помнить, что линии напряженности
электрического поля:

1. нигде не пересекаются друг с другом;
2. имеют начало на положительном заряде (или в бесконечности) и конец на
   отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
3. между зарядами нигде не прерываются.

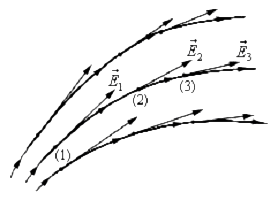
Рис.1

Силовые линии положительного заряда:

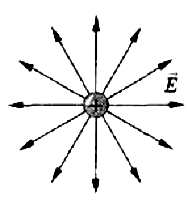
Рис.2

Силовые линии отрицательного заряда:

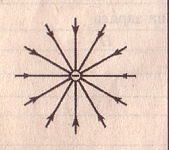
Рис.3

Силовые линии одноименных взаимодействующих зарядов:

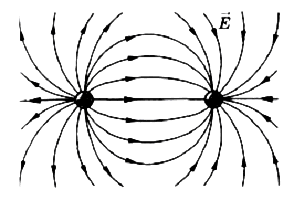
Рис.4

Силовые линии разноименных взаимодействующих зарядов:

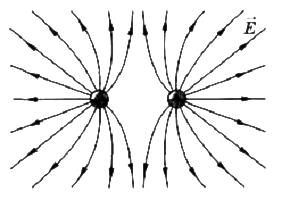
Рис.5

Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
или
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда

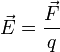
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда

где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.

В системе СИ
Н·м²/Кл²,

где ε₀ – электрическая
постоянная, равная 8,85·10^-12 Кл²/Н·м²;

q – электрический заряд (Кл);

r – расстояние от заряда до точки в которой определяется напряженность.

Направление вектора напряженности совпадает с направлением силы Кулона.

Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.

Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:

Рассмотрим несколько случаев определения напряженности.

1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:

Е₃₁ – напряженность точечного заряда 3 со стороны заряда 1;

Е₃₂ – напряженность точечного заряда 3 со стороны заряда 2.

Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е₃₁ и Е₃₂.

Напряженность в данной точке определяется по формуле:

Е = kq₁/x² + kq₂/(r – x)²

где: r – расстояние между первым и вторым зарядом;

х – расстояние между первым и точечным зарядом.

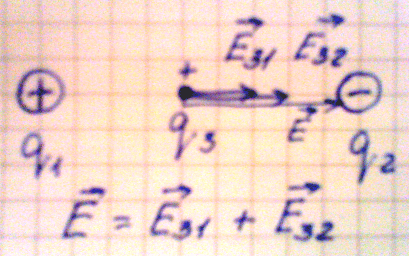
Рис.6

2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е₃₁ и Е₃₂.

Формула напряженности в данной точке равна:

Е = kq1/(r + a)² – kq₂/a²

Где: r – расстояние между взаимодействующими зарядами;

а – расстояние между вторым и точечным зарядом.

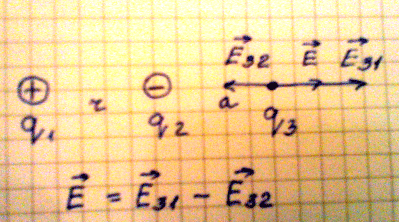
Рис.7

3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:

Е = (Е₃₁² +Е₃₂²)^1/2

Следовательно:

Е = ((kq₁/r² )² + (kq₂/b²)²)^1/2

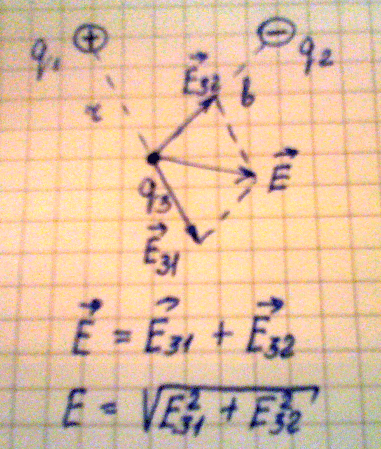
Рис.8

Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.

4. Закрепление темы.

Проверочная работа.

Вариант № 1.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: электрическое поле – это ….

3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Вариант № 2.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: напряженностью называется …

3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Задачи на дом:

Для школьников.

Приведём решение трёх задач на применение принципа суперпозиции (наложения) электростатических полей.

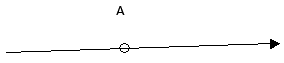
Задача 1. Два точечных одинаковых положительных заряда по 20 нКл каждый расположены в двух вершинах равностороннего треугольника со стороной 2 м в вакууме. Найти напряжённость поля в третьей вершине треугольника.

В точке А вектора напряженности электрических полей каждого заряда направлены вдоль их силовых линий (от зарядов).

Применим принцип суперпозиции для проекций указанных векторов на оси х и у:

Таким образом, вектор напряжённости результирующего электрического поля в точке А направлен вертикально вверх, а модуль напряжённости равен 77 В/м.

Задача 2. Электрическое поле образовано двумя одинаковыми разноимёнными точечными зарядами по 5 нКл. Расстояние между зарядами 10 см. Определить напряжённость поля: 1) в точке, лежащей посередине между зарядами; 2) в точке, лежащей на продолжении линии, соединяющей центры зарядов, на расстоянии 10 см от отрицательного заряда; 3) в точке, лежащей на расстоянии 10 см от положительного и отрицательного зарядов.

В точке А оба вектора напряжённости, создаваемых положительным и отрицательным зарядами, направлены вправо (на рисунке не показаны). Тогда результирующее поле находится через сумму полей, создаваемых первым и вторым зарядами:

В точке В результирующее поле направлено влево и равно:

В точке С вектор напряжённости результирующего электрического поля направлен вправо. Его модуль найдём из треугольника:

Ответ: 36000 В/м; 3400 В/м; 4500 В/м.

Задача 3. Электрическое поле создано двумя точечными зарядами 30 нКл и -10 нКл. Расстояние между зарядами 20 см. Определить напряжённость электрического поля в точке, находящейся на расстоянии 15 см от первого и на расстоянии второго (отрицательного) зарядов.

Покажем направления векторов напряжённости, создаваемых в искомой точке первым и вторым зарядами. Их модули найдём из формул:

Складывая вектора находим вектор результирующего поля. Модуль напряжённости результирующего поля находим по теореме косинусов:

Косинус угла найдём отдельно из треугольника образованного расстояниями:

Косинус угла оказался равным 0,25. Подставив все численные значения в формулу, получим результирующую напряжённость равную 16, 7 кВ/м.

Итак, приведено решение трёх задач на применение принципа суперпозиции (наложения) полей. Сначала в интересующей точке поля рисуем вектора напряжённости электрического поля, создаваемого каждым зарядом в отдельности. Затем, складывая их, находим напряжённость суммарного поля. В первой задаче проще просуммировать проекции векторов напряжённости на оси. Там, где угол между векторами напряжённости, создаваемыми отдельными зарядами, отличен от нуля, пользуются теоремой косинусов (задачи 2 и 3).

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Нахождение напряжённости электростатического поля.

Следующая запись:Как рассчитать напряжённость поля заряженной пластины. Поле конденсатора.

Ссылки на другие занятия (до электростатики) даны в Занятии 1.

Ссылки на занятия (начиная с электростатики) даны в Занятии 45.

№
37. Связь между напряженностью и разностью потенциалов электрического поля.

 Напряженность
электрического поля – величина, численно равная силе, действующей на заряд.

Потенциал φ – величина, численно равная
потенциальной  энергии  заряда.

 Каждой точке
электрического поля соответствуют определенные значения потенциала и напряженности.
Найдем связь напряженности электрического поля с потенциалом.
   Пусть заряд q перемещается
в направлении вектора напряженности однородного электрического поля  из точки 1 в точку 2,
находящуюся на расстоянии  от точки 1 (рис.93, стр. 119).
Электрическое поле совершает работу: A=qEΔd

 Эту работу согласно формуле можно выразить через
разность потенциалов в точках 1 и 2:  A=qU

   Приравнивая выражения для работы, найдем модуль
вектора напряженности поля: 

qEΔd=qU

E=  =

   Где U –
разность потенциалов между точками 1 и 2, которые
связаны вектором перемещения , совпадающим по направлению с вектором напряженности  .
   Формула E=

показывает: чем меньше меняется потенциал на
расстоянии , тем меньше напряженность электростатического
поля. Если потенциал не меняется совсем, то напряженность поля равна нулю.
   Так как при
перемещении положительного заряда в направлении вектора напряженности  электростатическое поле совершает
положительную работу , то потенциал  больше потенциала .
   Следовательно, напряженность
электрического поля направлена в сторону убывания потенциала.
   Любое
электростатическое поле в достаточно малой области пространства можно считать
однородным. Поэтому формула E=    справедлива
для произвольного электростатического поля, если только расстояние  настолько мало, что изменением
напряженности поля на этом расстоянии можно пренебречь.

  Единица напряженности
электрического поля. Единицу напряженности электрического поля в СИ
устанавливают, используя последнюю формулу . Напряженность
электрического поля численно равна единице, если разность потенциалов между
двумя точками на расстоянии 1 м в однородном поле равна 1
В. Наименование этой единицы – вольт на метр (В/м).
   Напряженность можно
также выражать в ньютонах на кулон. Действительно,

Эквипотенциальные поверхности.

Потенциал 
электростатического  поля  представляет  собой  функцию, меняющуюся от точки к
точке. Однако, во всяком реальном случае можно выделить совокупность точек,
потенциалы которых одинаковы.

Геометрическое
место точек постоянного потенциала называется поверхностью равногопотенциала
или эквипотенциальной поверхностью.

Возьмем
равномерно заряженную бесконечную плоскость. Поле, создаваемое та

кой 
плоскостью  однородно,  а  линии напряженности  нормальны  к плоскости.

Отсюда
следует, что работа перемещения заряда  из  некоторой  точки В1
в любую другую точку В2,
находящуюся на таком же  расстоянии  от  заряженной поверхности, что и точка В1равна
нулю. Действительно, при перемещении некоторого заряда q по  прямой В1
В2 сила,  действующая на заряд со стороны поля, будет все время 
перпендикулярна  к перемещению,  а,  следовательно,  ее  работа  равна нулю. Но
эта работа может быть представлена, с другой стороны, в виде:

A
= q(φ₁– φ₂)= 0

где
φ₁ и φ₂ – соответственно
потенциалы точек В1 и В2. Отсюда, так как

А
= 0, то φ₁= φ₂, т.е., потенциалы
точек, равноудаленных от заряженной

плоскости,
одинаковы. Таким образом, поверхности равного потенциала (эквипотенциальные
поверхности) являются плоскостями, параллельными заряженной плоскости. Если
плоскость заряжена положительно, то значение потенциала убывает по мере
удаления от заряженной плоскости. Очевидно, что поверхности равного потенциала
расположены симметрично по обе стороны от заряженной плоскости.

Эквипотенциальные
поверхности поля точечного заряда это сферы с радиусом

r,
центр которых находится в центре точечного заряда, т.е. φ=.

На 
рисунке 95  вектор  напряженности E перпендикулярен эквипотенциальным
поверхностям.

Покажем, 
что  вектор  напряженности перпендикулярен  эквипотенциальной  поверхности.
Рассмотрим работу по перемещению заряда  по  поверхности  равного  потенциала 
на малом  участке  пути  ∆d. При  этом,  работа электрической 
силы F=qE на данном пути будет:

A=F∆dcos
α= qE∆dcos
α, где α – угол между направлением силы f

и
перемещением ∆d. С другой стороны, эта работа  может 
быть  выражена  как  произведение величины перемещающегося заряда на разность
потенциалов в начальном и конечном положениях заряда, т.е. A
= q(φ₁– φ₂)

Так
как перемещение идет по эквипотенциальной поверхности, то разность потенциалов (φ₁–
φ₂)=0   и   qE∆dcos
α=0, или cosα= 0,
значит α = 90⁰  т.е.

угол
между направлением силы F и
перемещением ∆d равен 90⁰.
Но F и Е совпадают,  поэтому  угол 
между E и  ∆d,  α=90⁰, т.е.
направление вектора напряженности электростатического поля всегда
перпендикулярно к эквипотенциальной поверхности.

Значит, если провести поверхность,
перпендикулярную в каждой ее точке силовым линиям, то при перемещении заряда
вдоль этой поверхности работа не совершается. А это означает, что все точки
поверхности, перпендикулярной силовым линиям, имеют один и тот же потенциал.
   Поверхности равного потенциала называют эквипотенциальными.
   Эквипотенциальные
поверхности однородного
поля представляют собой плоскости (рис.94, стр. 120), а поля точечного
заряда – концентрические сферы (рис. 95, стр. 120).

   Подобно силовым линиям, эквипотенциальные
поверхности качественно характеризуют распределение поля в пространстве. Вектор напряженности перпендикулярен
эквипотенциальным поверхностям и направлен в сторону уменьшения потенциала.
   Эквипотенциальные
поверхности строятся обычно так, что разность потенциалов между двумя соседними
поверхностями постоянна. Поэтому согласно формуле расстояния между соседними
эквипотенциальными поверхностями увеличиваются по мере удаления от точечного
заряда, так как напряженность поля уменьшается.
   Эквипотенциальные
поверхности однородного поля расположены на равных расстояниях друг от друга.
   Эквипотенциальной является
поверхность любого проводника в электростатическом поле. Ведь силовые
линии перпендикулярны поверхности проводника. Причем не только поверхность, но
и все точки внутри проводника имеют один и тот же потенциал. Напряженность поля
внутри проводника равна нулю, значит, равна нулю и разность потенциалов между
любыми точками проводника.
  

Модуль напряженности электростатического поля
численно равен разности потенциалов между двумя близкими точками в этом поле,
деленной на расстояние между этими точками.

В однородном электрическом
поле напряженностью Е = 2*10⁵ В/м
переместили заряд q = –20 нКл в направлении
силовой линии поля на расстояние d = 10 см. Найти работу
поля А, изменение потенциальной
энергии поля ΔW_п и напряжение (разность
потенциалов) U между начальной и конечной
точками перемещения.

Домашнее
задание

§ 45-46,
вопросы.

Задачи по электростатике можно разделить на две группы: задачи о точечных зарядах и задачи о заряженных телах, размеры которых нельзя не учитывать [1—5].

Решение задач по расчёту электрических полей и взаимодействий точечных зарядов основано на применении закона Кулона и не вызывает особых затруднений. Более сложным является определение напряжённости поля и взаимодействия заряженных тел конечных размеров: сферы, цилиндра, плоскости. При вычислении напряжённости электростатических полей различной конфигурации следует подчеркнуть важность принципа суперпозиции и использовать его при рассмотрении полей, созданных не только точечными зарядами, но и зарядами, распределёнными по поверхности и объёму. При рассмотрении действия поля на заряд формула F=qE в общем случае справедлива для точечных заряженных тел и только в однородном поле применима для тел любых размеров и формы, несущих заряд q.

Электрическое поле конденсатора получается в результате наложения двух полей, созданных каждой пластиной.

В плоском конденсаторе можно рассматривать одну пластину как тело с зарядом q₁ помещённое в электрическое поле напряжённостью Е₂, созданное другой пластиной.

Рассмотрим несколько задач.

1. Бесконечная плоскость заряжена с поверхностной плотностью σ>0. Найдите напряжённость поля Е и потенциал ϕ по обе стороны плоскости, считая потенциал плоскости равным нулю. Постройте графики зависимостей Е(х), ϕ(х). Ось х перпендикулярна плоскости, точка х=0 лежит на плоскости.

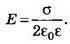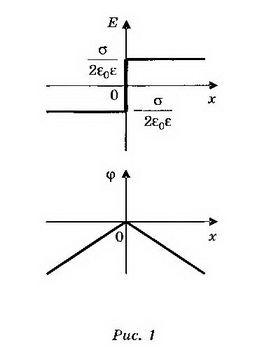
Решение. Электрическое поле бесконечной плоскости является однородным и симметричным относительно плоскости. Его напряжённостьСвязь между напряжённостью и разностью потенциалов между двумя точками однородного электростатического поля выражается формулой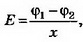где х — расстояние между точками, измеренное вдоль силовой линии. Тогда  ϕ₂=ϕ₁-Eх. При х<0 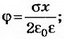при х>0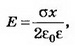 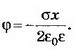 Зависимости Е(х) и ϕ(х) представлены на рисунке 1.

2. Две плоскопараллельные тонкие пластины, расположенные на малом расстоянии d друг от друга, равномерно заряжены зарядом поверхностной плотностью σ₁ и σ₂. Найдите напряжённости поля в точках, лежащих между пластинами и с внешней стороны. Постройте график зависимости напряжённости Е(х) и потенциала ϕ(х), считая ϕ(0)=0. Рассмотрите случаи, когда: a) σ₁=-σ₂; б) σ₁= σ₂; в) σ₁=3σ₂–

Решение. Так как расстояние между пластинами мало, то их можно рассматривать как бесконечные плоскости.

Напряжённость поля положительно заряженной плоскости равна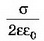и направлена от неё; напряжённость поля отрицательно заряженной плоскости направлена к ней.

Согласно принципу суперпозиции поле в любой рассматриваемой точке будет создаваться каждым из зарядов в отдельности.

а) Поля двух плоскостей, заряженных равными и противоположными по знаку зарядами (плоский конденсатор), складываются в области между плоскостями и взаимно уничтожаются во внешних областях (рис. 2, а).

При х<0 Е=0, ϕ=0; при 0<x<d 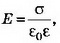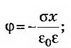при x>d Е=0,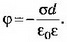Графики зависимости напряжённости и потенциала от расстояния х приведены на рисунке 2, б, в.

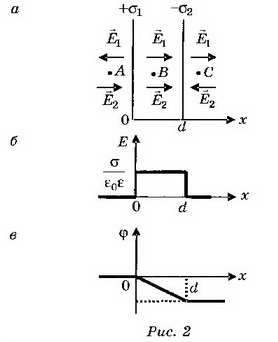
Если плоскости конечных размеров, то поле между плоскостями не будет строго однородным, а поле вне плоскостей не будет точно равно нулю.

б) Поля плоскостей, заряженных равными по величине и знаку зарядами (σ₁=σ₂), компенсируют друг друга в пространстве между плоскостями и складываются во внешних областях (рис. 3, а). При х<0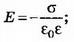при 0<x<d E=0; при х>d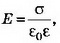 

Воспользовавшись графиком Е(х) (рис. 3, б), построим качественно график зависимости ϕ(х) (рис. 3, в).

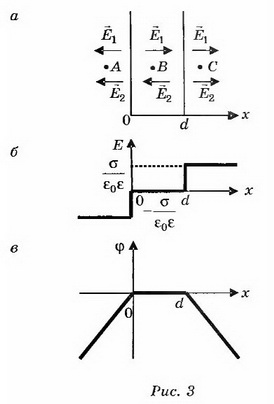
в) Если σ₁= σ₂, то, учитывая направления полей и выбирая направление направо за положительное, находим:

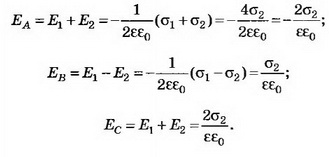
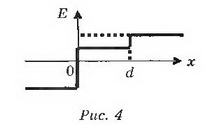
Зависимость напряжённости Е от расстояния показана на рисунке 4.

3. На одной из пластин плоского конденсатора ёмкостью С находится заряд q₁=+3q, а на другой q₂=+q. Определите разность потенциалов между пластинами конденсатора.

Решение. 1-й способ. Пусть площадь пластины конденсатора S, а расстояние между ними d. Поле внутри конденсатора однородное, поэтому разность потенциалов (напряжение) на конденсаторе можно определить по формуле U=E*d, где Е — напряжённость поля внутри конденсатора.

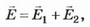
где Е₁, Е₂ — напряжённости поля, создаваемого пластинами конденсатора.

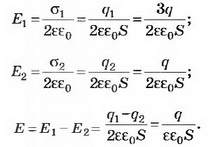
Тогда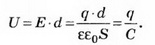

2-й способ. Добавим на каждую пластину заряд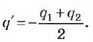Тогда пластины конденсатора будут иметь заряды +q и -q. Поля одинаковых зарядов пластин внутри конденсатора компенсируют друг друга. Добавленные заряды не изменили поле между пластинами, а значит, и разность потенциалов на конденсаторе. U=q/C.

4. В пространство между обкладками незаряженного плоского конденсатора вносят тонкую металлическую пластину, имеющую заряд +q. Определите разность потенциалов между обкладками конденсатора.

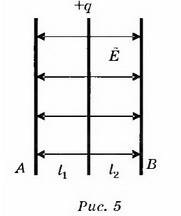
Решение. Так как конденсатор не заряжен, то электрическое поле создаётся только пластиной, имеющей заряд q (рис. 5). Это поле однородное, симметричное относительно пластины, и его напряжённость 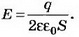Пусть потенциал металлической пластины равен  ϕ. Тогда потенциалы обкладок А и В конденсатора будут равны ϕ-ϕ_А=ϕEl₁; ϕ_А=ϕ-El₁; ϕ-ϕ_B=ϕ-El₂; ϕ_B=ϕ-El₂.

Разность потенциалов между обкладками конденсатора 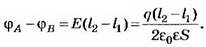Если пластина находится на одинаковом расстоянии от обкладок конденсатора, то разность потенциалов между обкладками равна нулю.

5. В однородное электрическое поле напряжённостью Е₀ перпендикулярно силовым линиям помещают заряженную металлическую пластину с плотностью заряда на поверхности каждой стороны пластины σ (рис. 6). Определите напряжённость поля Е’ внутри и снаружи пластины и поверхностную плотность зарядов σ₁и σ₂, которая возникнет на левой и правой сторонах пластины.

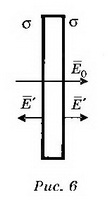
Решение. Поле внутри пластины равно нулю и является суперпозицией трёх полей: внешнего поля Е₀, поля, создаваемого зарядами левой стороны пластины, и поля, создаваемого зарядами правой стороны пластины. Следовательно,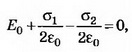где σ₁ и σ₂ — поверхностная плотность заряда на левой и правой сторонах пластины, которая возникает после внесения пластины в поле Е₀. Суммарный заряд пластины не изменится, поэтому σ₁+σ₂=2σ, откуда σ₁=σ-ε₀E₀, σ₂=σ+ε₀E₀. Поле снаружи пластины является суперпозицией поля Е₀ и поля заряженной пластины Е. Слева от пластины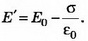Справа от пластины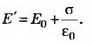 

6. В плоском воздушном конденсаторе напряжённость поля Е= 10⁴ В/м. Расстояние между обкладками d=2 см. Чему будет равна разность потенциалов, если между пластинами параллельно им поместить металлический лист толщиной d₀=0,5 см (рис. 7)?

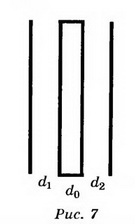
Решение. Поскольку электрическое поле между пластинами однородное, то U=Ed, U=200 В.

Если между пластинами пометить металлический лист, то получается система из двух последовательно соединённых конденсаторов с расстоянием между пластинами d₁ и d₂. Ёмкости этих конденсаторов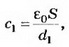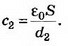Их общая ёмкость

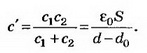
Так как конденсатор отключён от источника тока, то заряд конденсатора при внесении металлического листа не меняется: q’=CU=С’U₁;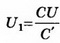где 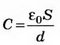 емкость конденсатора до внесения в него металлического листа. Получаем:

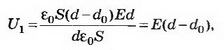
U₁=150 В.

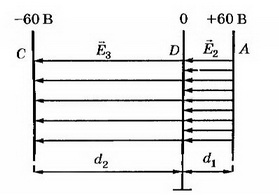
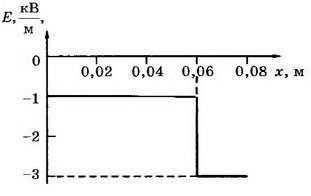
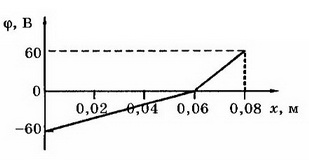
7. На пластинах А и С, расположенных параллельно на расстоянии d=8 см друг от друга, поддерживаются потенциалы ϕ₁= 60 В и ϕ₂=-60 В соответственно. Между ними поместили заземлённую пластину D на расстоянии d₁=2 см от пластины А. На сколько изменилась напряжённость поля на участках AD и CD? Постройте графики зависимостей ϕ(x) и Е(х).

Решение. Первоначальная напряжённость поля между пластинами А и С:

E₁=1,5 кВ/м.

Напряжённость поля на участке AD: Е₂= ϕ₁/d₁, Е₂=3 кВ/м, т. е. увеличилась на 1,5 кВ/м. Напряжённость поля на участке CD  Е₃= ϕ₂/d₂, т.е. уменьшилась на Е₃=0,5 кВ/м.  Поскольку векторы 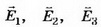направлены противоположно положительному направлению оси Ох, то Е_г, Е₂, Е₃<0 (рис. 8).

8. Точечный заряд q=5*10^-9 Кл находится на расстоянии 3 см от проводящей заземлённой стенки. Найдите поверхностную плотность заряда, индуцированного на стенке в точке А, ближайшей к заряду, и в точке В, находящейся на расстоянии 5 см от заряда.

Решение. В точках А, В, расположенных в непосредственной близости к поверхности проводника (рис. 9), поле создаётся точечным зарядом q и зарядом q’, индуцированным на стенке: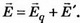

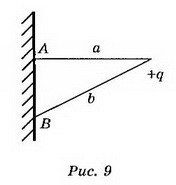
В точке А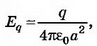где а — расстояние от заряда до стенки,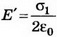. Но поле внутри проводника равно нулю; следовательно,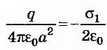. Отсюда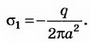  

В точке В величина нормальной составляющей напряжённости поля точечного заряда

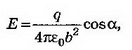
где b — расстояние от заряда до точки, cosα=a/b,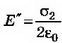— напряжённость поля плоскости.

Следовательно,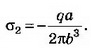

Список использованной литературы

1. Балаш, В. А. Задачи по физике и методы их решения / В. А. Балаш. — 4-е изд. — М. : Просвещение, 1983. — 432 с.

2. Бутиков, Е. И. Физика в примерах и задачах / Е. И. Бутиков, А. А. Быков, А. С. Кондратьев. — 3-е изд. — М. : Наука, 1989. — 462 с.

3. Зилъберман, Г. Е. Электричество и магнетизм / Г. Е. Зильберман. — М. : Наука, 1990. — 384 с.

4. Меледин, Г. В. Физика в задачах / Г. В. Меледин. — 2-е изд. — М. : Наука, 1990. — 270 с.

5. Сборник задач по физике / Л. П. Баканина [и др.]; под ред. С. М. Козела. — М. : Наука, 1990. — 347 с.