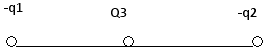Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.
Задачи урока:
- формирование понятия напряжённости электрического поля; дать понятие о
линиях напряжённости и графическое представление электрического поля; - научить учащихся применять формулу E=kq/r2 в решении
несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.
Графически изображая поле, следует помнить, что линии напряженности
электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на
отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями; - между зарядами нигде не прерываются.
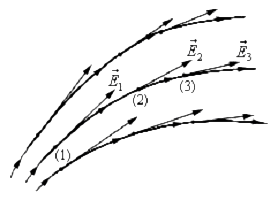
Рис.1
Силовые линии положительного заряда:
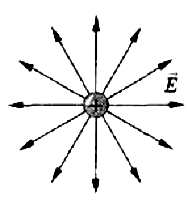
Рис.2
Силовые линии отрицательного заряда:
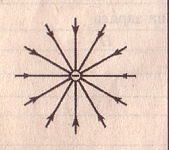
Рис.3
Силовые линии одноименных взаимодействующих зарядов:
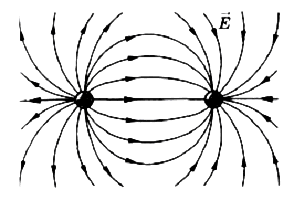
Рис.4
Силовые линии разноименных взаимодействующих зарядов:
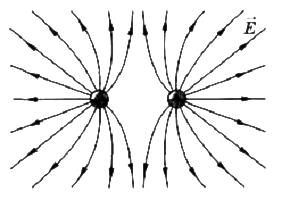
Рис.5
Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
![]() или
или
![]() .
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда
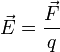
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда
![]()
где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.
В системе СИ
![]() Н·м2/Кл2,
Н·м2/Кл2,
где ε0 – электрическая
постоянная, равная 8,85·10-12 Кл2/Н·м2;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:
![]()
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
Е = kq1/x2 + kq2/(r – x)2
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
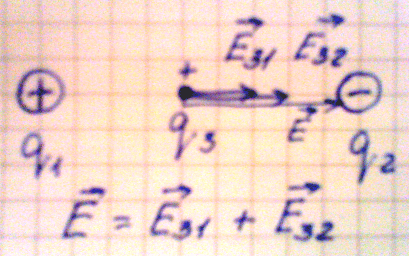
Рис.6
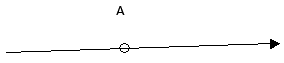
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a)2 – kq2/a2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
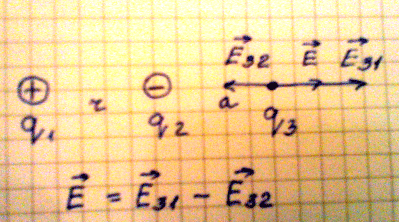
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
Е = (Е312 +Е322)1/2
Следовательно:
Е = ((kq1/r2 )2 + (kq2/b2)2)1/2
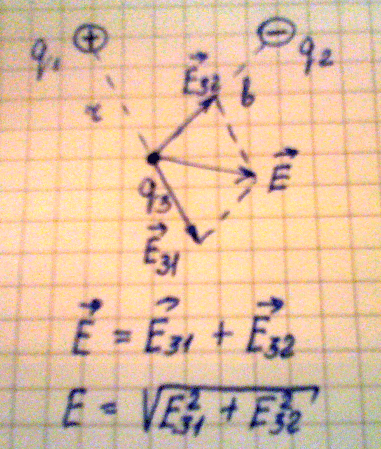
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
Проверочная работа.
Вариант № 1.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Вариант № 2.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Задачи на дом:
1. Два заряда q1 = +3·10-7 Кл и q2 = −2·10-7
Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите
напряженность поля в точке С, расположенной на линии, соединяющей заряды, на
расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10-9 Кл действует сила 3·10-4
Н. Найти напряженность поля в этой точке и определите величину заряда,
создающего поле, если точка удалена от него на 0,1 м.
Для школьников.
Приведём решение трёх задач на применение принципа суперпозиции (наложения) электростатических полей.
Задача 1. Два точечных одинаковых положительных заряда по 20 нКл каждый расположены в двух вершинах равностороннего треугольника со стороной 2 м в вакууме. Найти напряжённость поля в третьей вершине треугольника.
В точке А вектора напряженности электрических полей каждого заряда направлены вдоль их силовых линий (от зарядов).
Применим принцип суперпозиции для проекций указанных векторов на оси х и у:
Таким образом, вектор напряжённости результирующего электрического поля в точке А направлен вертикально вверх, а модуль напряжённости равен 77 В/м.
Задача 2. Электрическое поле образовано двумя одинаковыми разноимёнными точечными зарядами по 5 нКл. Расстояние между зарядами 10 см. Определить напряжённость поля: 1) в точке, лежащей посередине между зарядами; 2) в точке, лежащей на продолжении линии, соединяющей центры зарядов, на расстоянии 10 см от отрицательного заряда; 3) в точке, лежащей на расстоянии 10 см от положительного и отрицательного зарядов.
В точке А оба вектора напряжённости, создаваемых положительным и отрицательным зарядами, направлены вправо (на рисунке не показаны). Тогда результирующее поле находится через сумму полей, создаваемых первым и вторым зарядами:
В точке В результирующее поле направлено влево и равно:
В точке С вектор напряжённости результирующего электрического поля направлен вправо. Его модуль найдём из треугольника:
Ответ: 36000 В/м; 3400 В/м; 4500 В/м.
Задача 3. Электрическое поле создано двумя точечными зарядами 30 нКл и -10 нКл. Расстояние между зарядами 20 см. Определить напряжённость электрического поля в точке, находящейся на расстоянии 15 см от первого и на расстоянии второго (отрицательного) зарядов.
Покажем направления векторов напряжённости, создаваемых в искомой точке первым и вторым зарядами. Их модули найдём из формул:
Складывая вектора находим вектор результирующего поля. Модуль напряжённости результирующего поля находим по теореме косинусов:
Косинус угла найдём отдельно из треугольника образованного расстояниями:
Косинус угла оказался равным 0,25. Подставив все численные значения в формулу, получим результирующую напряжённость равную 16, 7 кВ/м.
Итак, приведено решение трёх задач на применение принципа суперпозиции (наложения) полей. Сначала в интересующей точке поля рисуем вектора напряжённости электрического поля, создаваемого каждым зарядом в отдельности. Затем, складывая их, находим напряжённость суммарного поля. В первой задаче проще просуммировать проекции векторов напряжённости на оси. Там, где угол между векторами напряжённости, создаваемыми отдельными зарядами, отличен от нуля, пользуются теоремой косинусов (задачи 2 и 3).
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Нахождение напряжённости электростатического поля.
Следующая запись:Как рассчитать напряжённость поля заряженной пластины. Поле конденсатора.
Ссылки на другие занятия (до электростатики) даны в Занятии 1.
Ссылки на занятия (начиная с электростатики) даны в Занятии 45.
Законом Кулона описывается взаимодействие заряженных частиц. Однако большинство сил, с которыми мы работали, возникает при взаимодействии тел посредством контакта (т.е. тела касаются друг друга). В случае электромагнитного взаимодействия контакта нет, тогда взаимодействие происходит посредством неких невидимых элементов. Тогда взаимодействия между частицами вещества и удалёнными друг от друга макроскопическими телами осуществляются через посредство физических полей, которые создаются этими частицами или телами в окружающем пространстве. В случае с заряженными частицами, эти поля назовём электромагнитными.
Тогда логика электромагнитного взаимодействия такова: заряд создаёт вокруг себя электромагнитное поле, которое, в свою очередь, действует на любой другой заряд
, находящийся на любом расстоянии от источника.
Закон Кулона описывает взаимодействие между двумя зарядами:
(1)
- где

Рис. 1. Закон Кулона. Пробный заряд
Сила (1) зависит от обоих зарядов, что не позволяет толком описать электрическое поле, создаваемое каждым из взаимодействующих частиц. Тогда придумаем немного другую систему: возьмём пробный заряд — некий малый заряд, который не будет искажать поле исследуемого нами заряда
. Поместим пробный заряд в различные точки пространства рядом с исследуемым нами зарядом и проиллюстрируем силы Кулона (рис. 1).
В принципе, значение силы Кулона можно найти в любой точке пространства, однако данные силы зависят как от заряда источника, так и от значения пробного заряда. Введём новую переменную, поделив значение силы Кулона на значение пробного заряда:
(2)
- где
— вектор напряжённости электрического поля.
Подставим силу Кулона в (1):
(3)
Исходя из (3), можно заключить, что напряжённость электрического поля зависит от заряда источника поля и точки наблюдения, описываемой расстоянием от заряда (рис. 2).

Рис. 2. Напряжённость электрического поля
Т.е. напряжённость электрического поля — параметр, описывающий поле, создаваемое зарядом-источником. Значение напряжённости электрического поля позволяет оценить сильно или слабо будет действовать поле на заряд, помещённый в него. Размерность — В/м.
Исходя из (3), можно найти напряжённость поля точечного заряда. Напряжённость электрического поля — величина векторная, поэтому для её нахождения необходимо знать как модуль, так и направление вектора. Начнём с модуля:
(4)

Рис. 3. Напряжённость электрического поля (направление)
Чтобы выяснить направление вектора, воспользуемся уравнением (2). Исходя из (2), можно заключить, что направление напряжённости электрического поля совпадает с направлением силы Кулона, а направление силы Кулона зависит от знака взаимодействующих зарядов. Чтобы не заморачиваться с рассмотрением этих зарядов в каждой задаче, просто договоримся. Если источник поля (заряд) положителен, тогда напряжённость поля направлена от заряда, если источник поля (заряд) отрицателен, тогда напряжённость поля направлена к заряду (рис. 3).
Напряжённость системы зарядов. Принцип суперпозиции напряжённости.
В случае, если в задаче источниками поля являются несколько зарядов, тогда напряжённость в интересующей точке можно найти как векторную сумму напряжённостей от каждого из зарядов:
(5)
Важно: поиск векторной суммы чаще всего сопряжён с реализацией теоремы Пифагора, теоремы косинусов или синусов, иногда с проецированиием векторов напряжённости на оси с последующим суммированием.

Рис. 4. Принцип суперпозиции напряжённости
Проиллюстрируем: пусть в системе присутствует 3 заряда (,
,
), найти напряжённость в точке А, находящейся на заданном расстоянии от каждого из них (
,
,
) (рис. 4).
Пользуясь знаниями о зарядах, расставляем направления напряжённостей от каждого из зарядов, значение модуля каждой из них можем найти из (4). А далее геометрически складываем, получая искомый .
Напряжённость поля бесконечной заряженной плоскости.
Отдельно в школьной физике рассматривается бесконечная (осень большая) заряженная равномерно плоскость (рис. 5).

Рис. 5. Напряжённость бесконечной плоскости
Напряжённость такой плоскости вблизи её:
(6)
В (6) использовалось определение поверхностной плотности заряда:
(7)
Важно: напряжённость бесконечной плоскости не зависит от расстояния от плоскости.
Напряжённость поля двух бесконечных заряженных плоскостей (конденсатор).

Рис. 6. Напряжённость двух бесконечных плоскостей
Если составить систему из двух бесконечных плоскостей, заряженных одинаковым по модулю и различным по знаку зарядом (при этом площади плоскостей одинаковы), то общая напряжённость между ними:
(8)
Уравнение (8) характеризует напряжённость внутри конденсатора (рис. 6).
Вывод: в случае, если в задаче требуется найти напряжённость, она дана, достаточно рассмотреть систему. Различных систем, а соответственно, и формул, немного: точечный заряд, шар, система точечных зарядов и бесконечные плоскости. Для каждой системы — своё решение.
1. Определение напряженности
Как вы уже знаете из курса физики основной школы, электрическое взаимодействие заряженных тел осуществляется посредством электрического поля: каждое заряженное тело создает вокруг себя электрическое поле, которое действует на другие заряженные тела. Представление об электрическом поле ввел английский ученый Майкл Фарадей в первой половине 19-го века.
Электрическое поле в данной точке пространства можно охарактеризовать с помощью силы, действующей со стороны этого поля на точечный заряд, помещенный в данную точку. (Этот заряд должен быть достаточно мал, чтобы создаваемое им поле не изменяло распределения зарядов, которые создают данное поле.)
Как показывает опыт, сила 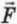 , действующая на заряд q, пропорциональна величине этого заряда. Следовательно, отношение силы к заряду не зависит от величины заряда и характеризует само электрическое поле.
, действующая на заряд q, пропорциональна величине этого заряда. Следовательно, отношение силы к заряду не зависит от величины заряда и характеризует само электрическое поле.
Напряженностью 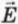 электрического поля в данной точке называют физическую величину, равную отношению силы
электрического поля в данной точке называют физическую величину, равную отношению силы 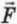 , действующей со стороны поля на заряд q, помещенный в данную точку поля, к величине этого заряда:
, действующей со стороны поля на заряд q, помещенный в данную точку поля, к величине этого заряда:

Напряженность поля – векторная величина. Ее направление в каждой точке совпадает с направлением силы, действующей на положительный заряд, помещенный в эту точку.
Единицей напряженности поля является 1 Н/Кл. 1 Н/Кл – небольшая напряженность. Например, напряженность электрического поля вблизи поверхности Земли, обусловленная электрическим зарядом Земли, составляет примерно 130 Н/Кл.
Если известна напряженность поля 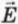 в данной точке, то можно найти силу
в данной точке, то можно найти силу 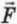 , действующую на заряд q, помещенный в эту точку, по формуле
, действующую на заряд q, помещенный в эту точку, по формуле

Из формул (1) и (2) следует, что направление напряженности поля в данной точке совпадает с направлением силы, действующей на положительный заряд, помещенный в эту точку.
Напряженность поля точечного заряда
Если внести в поле положительного точечного заряда Q другой положительный заряд, он будет отталкиваться от заряда Q.
Следовательно, напряженность поля положительного точечного заряда во всех точках пространства направлена от этого заряда. На рисунке 51.1 изображены векторы напряженности поля точечного заряда в некоторых точках. Видно, что при удалении от заряда модуль напряженности поля уменьшается.
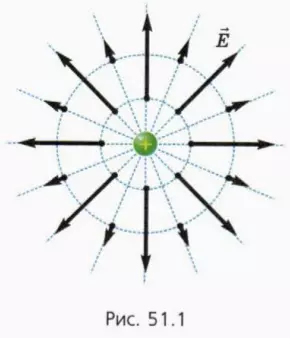
? 1. Объясните, почему модуль напряженности поля точечного заряда Q на расстоянии r от заряда выражается формулой

Подсказка. Воспользуйтесь законом Кулона и определением напряженности поля.
? 2. Чему равна напряженность поля точечного заряда 2 нКл на расстоянии 2 м от него?
? 3. Модуль напряженности поля точечного заряда на расстоянии 0,5 м от него равен 90 Н/Кл. Чему может быть равен этот заряд?
Принцип суперпозиции полей
Если заряд находится в поле, созданном несколькими зарядами, то каждый из этих зарядов действует на данный заряд независимо от других.
Отсюда следует, что равнодействующая сил, действующих на данный заряд со стороны других зарядов, равна векторной сумме сил, действующих на данный заряд со стороны каждого из остальных зарядов.
Это означает, что справедлив принцип суперпозиции полей:
напряженность поля, созданного несколькими зарядами, равна векторной сумме напряженностей полей, созданных каждым из зарядов:
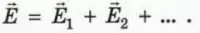
Используя принцип суперпозиции, можно найти напряженность поля, создаваемого несколькими зарядами.
? 4. Два точечных заряда расположены на расстоянии 60 см друг от друга. Модуль каждого заряда равен 8 нКл. Чему равен модуль напряженности поля, создаваемого этими зарядами:
а) в точке, расположенной на середине отрезка, соединяющего заряды, если заряды одноименные? разноименные?
б) в точке, находящейся на расстоянии 60 см от каждого заряда, если заряды одноименные? разноименные?
Для каждого из этих случаев сделайте в тетради чертеж, поясняющий решение.
2. Линии напряженности
На примере поля точечного заряда (рис. 51.1) можно заметить, что векторы напряженности электрического поля в разных точках пространства выстраиваются вдоль некоторых линий.
В случае точечного заряда эти линии представляют собой прямые лучи, проведенные из точки, в которой находится заряд. В поле, созданном несколькими зарядами, зти линии будут некоторыми кривыми, причем напряженность поля в каждой точке будет направлена по касательной к одной из таких линий.
Воображаемые линии, касательные к которым в каждой точке совпадают с направлением напряженности электрического поля, называют линиями напряженности электрического поля.
Линии напряженности начинаются на положительных зарядах и заканчиваются на отрицательных. Густота линий напряженности пропорциональна модулю напряженности.
? 5. Объясните, почему линии напряженности электрического поля не могут пересекаться.
Поля точечных зарядов
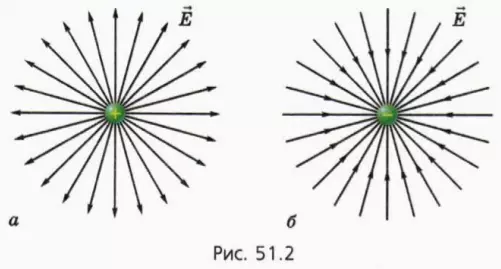
? 6. Объясните, почему линии напряженности электрического поля положительного и отрицательного точечных зарядов имеют вид, изображенный на рисунках 51.2, а и 51.2, б.
? 7. На рисунке 51.3 изображены линии напряженности поля, созданного одинаковыми по модулю зарядами (разноименными и одноименными). В некоторых точках для наглядности изображены векторы напряженности поля.
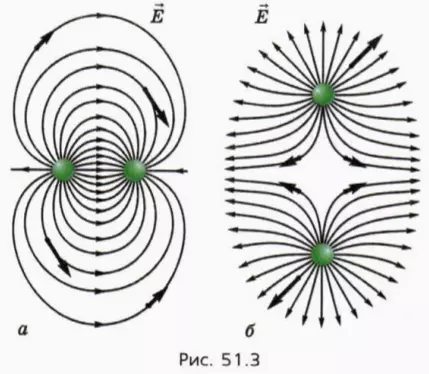
а) Перенесите рисунки в тетрадь и обозначьте на них знаки зарядов.
б) Изобразите в тетради линии напряженности поля, созданного двумя одноименными зарядами, которое не совпадает ни с одним из приведенных рисунков.
в) Чему равна напряженность поля в центральной точке рисунка 51.3, б (в середине отрезка, соединяющего заряды? Поясните ваш ответ с помощью закона Кулона.
Поле равномерно заряженной сферы
На рисунке 51.4 изображены линии напряженности электрического поля равномерно заряженной сферы.
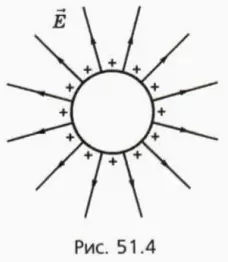
Мы видим, что вне сферы зто поле совпадает с полем точечного заряда, ровного суммарному заряду сферы и расположенного в центре сферы.
Можно доказать, что внутри заряженной сферы напряженность поля ровна нулю. (Доказательство этого факта выходит за рамки нашего круга.)
? 8. На сфере радиусом 5 см находится заряд 6 нКл. Чему равна напряженность поля этого заряда:
а) в центре сферы?
б) на расстоянии 4 см от центра сферы?
в) на расстоянии 10 см от центра сферы?
г) вне сферы на расстоянии 1 см от ближайшей к этой точке поверхности сферы?
Однако напряженность электрического поля внутри заряженной сферы не обязательно равна нулю! Если внутри этой сферы находится заряженное тело, то согласно принципу суперпозиции напряженность электрического поля равна векторной сумме напряженности поля, создаваемого зарядом этого тела, и напряженности поля, создаваемого зарядом сферы.
Внутри сферы поле создается только заряженным телом, находящимся внутри сферы, потому что напряженность поля, созданного заряженной сферой, внутри сферы равна нулю. А в любой точке вне сферы напряженность поля можно найти, складывая векторы напряженности поля, создаваемого телом, расположенным внутри сферы, и поля, создаваемого зарядом сферы.
? 9. Имеются две концентрические (имеющие общий центр) сферы радиусом 5 см и 10 см. Заряд внутренней сферы равен 6 нКл, а заряд внешней сферы равен –9 нКл. Чему равен модуль напряженности поля в точке, находящейся от общего центра сфер на расстоянии, равном:
а) 3 см; б) 6 см; в) 8 см; г) 12 см; д) 20 см?
Поле равномерно заряженной плоскости
На рисунке 51.5 изображены линии напряженности электрического поля вблизи равномерно заряженной плоской пластины.
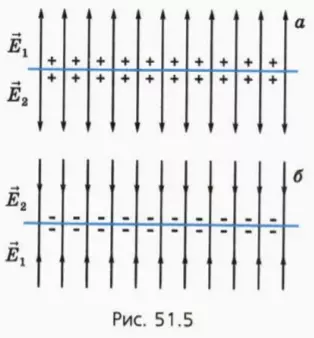
Будем считать, что размеры пластины намного больше расстояний от нее до тех точек пространства, в которых мы рассматриваем напряженность поля. В таких случаях говорят о поле равномерно заряженной плоскости.
Напряженность поля равномерно заряженной плоскости практически одинакова (по модулю и по направлению) во всех точках пространства по одну сторону от плоскости. Линии напряженности этого поля представляют собой параллельные прямые, перпендикулярные плоскости и расположенные на равных расстояниях друг от друга. Такое электрическое поле называют однородным.
По другую сторону плоскости изменяется только направление напряженности поля, а ее модуль остается таким же.
? 10. Напряженность электрического поля, создаваемого большой однородно заряженной пластиной, равна 900 Н/Кл. На расстоянии 40 см от пластины находится точечный заряд, равный по модулю 1 нКл.
а) На каком расстоянии от точечного заряда модуль напряженности его поля равен модулю напряженности поля пластины?
б) На каком расстоянии от плоскости результирующая напряженность поля плоскости и точечного заряда равна нулю, если знак точечного заряда совпадает со знаком заряда плоскости? Если знак точечного заряда противоположен знаку заряда плоскости?
Поле двух разноименно заряженных плоских пластин
Возьмем две одинаковые равномерно заряженные пластины, заряды которых равны по модулю, но противоположны по знаку. Расположим пластины параллельно друг друту на малом расстоянии друг от друга (рис. 51.6).
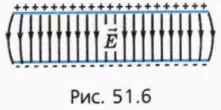
? 11. Объясните, почему в пространстве между пластинами напряженность поля в 2 раза больше, чем напряженность поля, создаваемого каждой из пластин, а вне пластин практически равна нулю.
Подсказка. Воспользуйтесь принципом суперпозиции электрических полей.
Как увидеть линии напряженности?
Поставим опыт
Поместим в электрическое поле состоящие из диэлектрика мелкие тела продолговатой формы – кристаллики, частицы манной крупы, мелко настриженные волосы и т. п. В электрическом поле они поворачиваются так, чтобы их более длинная сторона была направлена вдоль вектора напряженности поля. В результате эти тела выстраиваются вдоль линий напряженности, делая их форму видимой. На рисунке 51.7 приведены полученные таким образом «картины» электрических полей, создаваемых заряженным шариком (рис. 51.7, а) и двумя разноименно заряженными шариками (рис. 51.7, б).
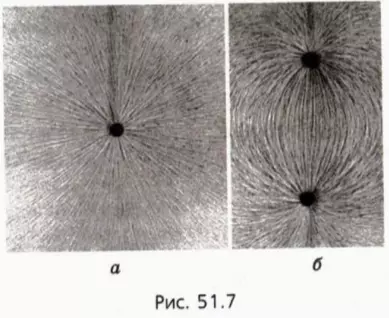
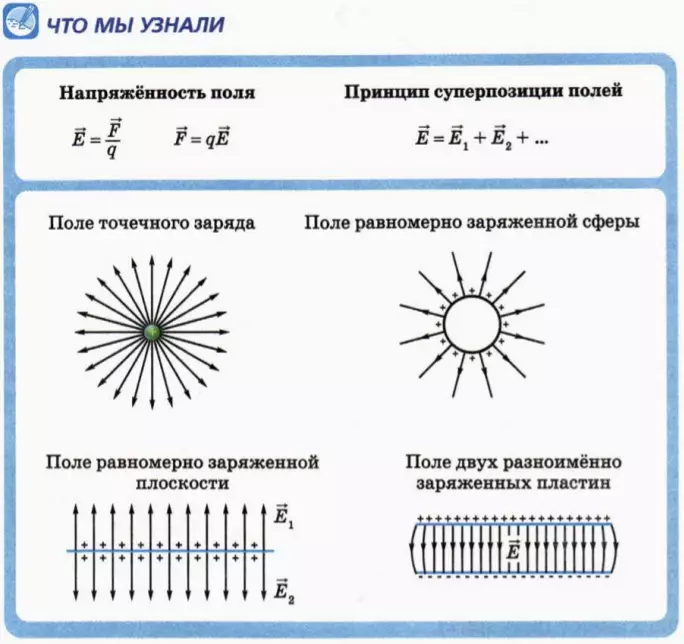
Дополнительные вопросы и задания
12. Небольшой заряженный шарик массой 0,2 г подвешен на нити в однородном электрическом поле, напряженность которого направлена горизонтально и равна по модулю 50 кН/Кл.
а) Изобразите на чертеже положение равновесия шарика и силы, действующие на него.
б) Чему равен заряд шарика, если нить отклонена от вертикали на угол 30º?
13. Какова должна быть напряженность поля, чтобы капелька воды радиусом 0,01 мм находилась в этом поле в равновесии, потеряв 103 электронов? Как должна быть направлена напряженность поля?
Методика
решения задач на нахождение напряжённости
результирующего поля аналогична методике
нахождения результирующей силы,
действующей на точечный заряд со стороны
других точечных зарядов (см. раздел
1.1), только вместо закона Кулона
используется формула напряженности
точечного заряда (2.2).
 .
.
Задача
2.1. Два
точечных заряда q1
и q2
находятся на расстоянии d
друг от друга. Найти напряжённость в
точках А, В, С и D
(рис. 13). Считаем расстояния от зарядов
q1
и q2
до заданных точек известными и во всех
случаях обозначаем r1
и r2
соответственно.
Р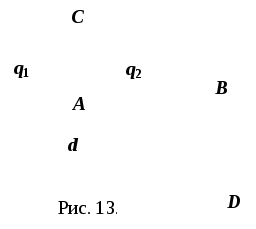 ешение.
ешение.
Сделаем рисунок для каждого случая
отдельно. Так как заряды оба отрицательные,
то векторы напряжённостей
![]() и
и![]() направлены в каждом случае к зарядамq1
направлены в каждом случае к зарядамq1
и q2
вдоль линии, соединяющей заряд и заданную
точку, и берут начало в заданной точке.
Направление
результирующего вектора
![]() определяетсяпо
определяетсяпо
принципу суперпозиции
путём векторного сложения. Поэтому
векторная запись для всех случаев
одинакова:
![]() .
.
Модуль
(длина) каждого из векторов рассчитывается
по формуле напряженности точечного
заряда (2.2). Модуль результирующего
вектора определяется из геометрических
построений.
-
В
точке А (рис. 14, а) векторы
 и
и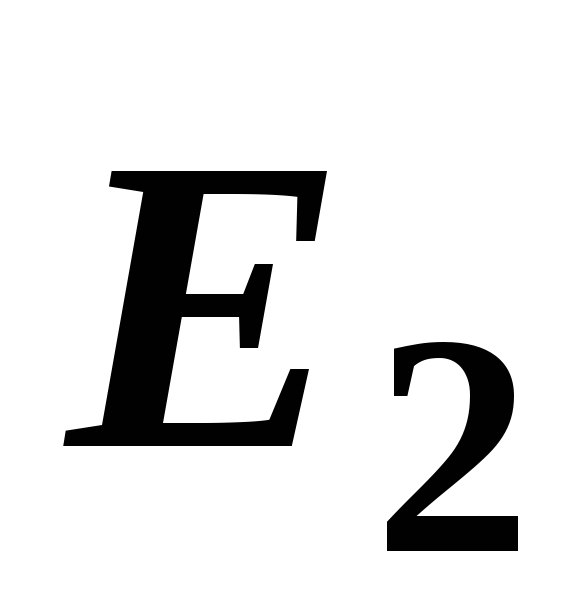 направлены в противоположные стороны,
направлены в противоположные стороны,
поэтому модуль результирующего вектора определяется как разность модулей
определяется как разность модулей
векторов и
и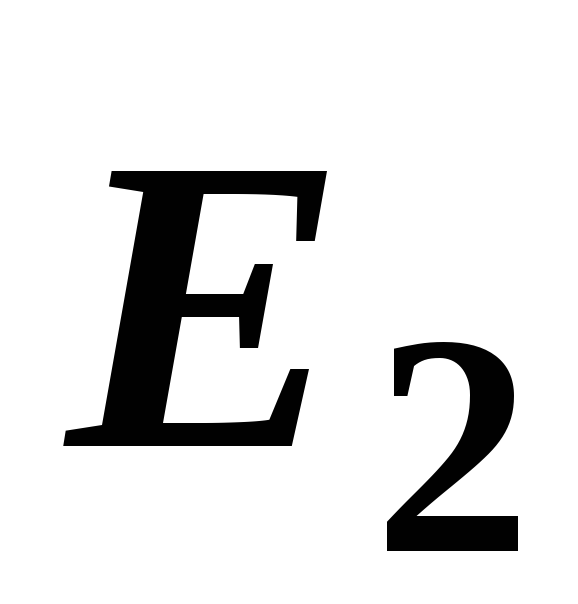 и направлен в сторону большего вектора:
и направлен в сторону большего вектора:
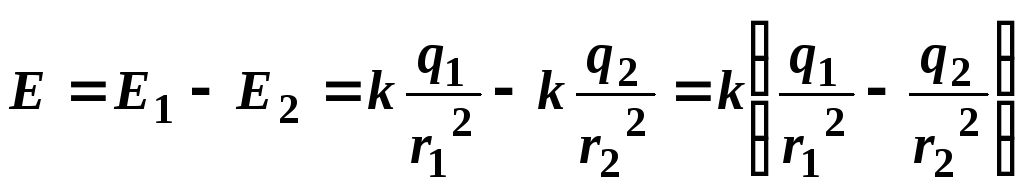 .
.
-
В
точке В (рис. 14, б) векторы
 и
и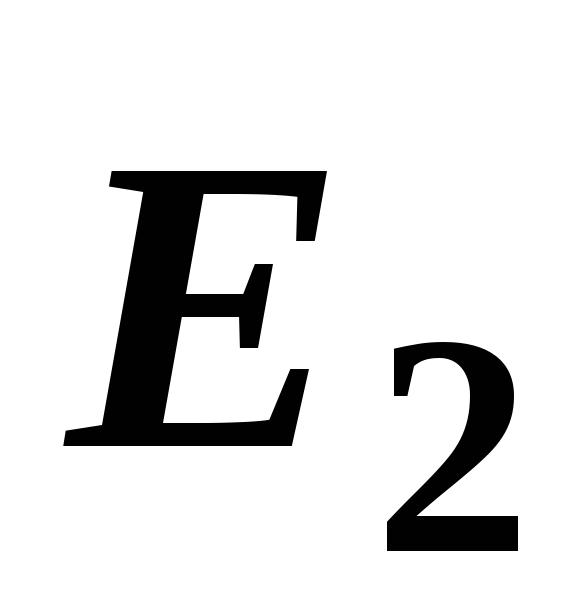 направлены в одну сторону, поэтому
направлены в одну сторону, поэтому
модуль результирующего вектора определяется
определяется
как сумма модулей векторов и
и и направлен в эту же сторону:
и направлен в эту же сторону:
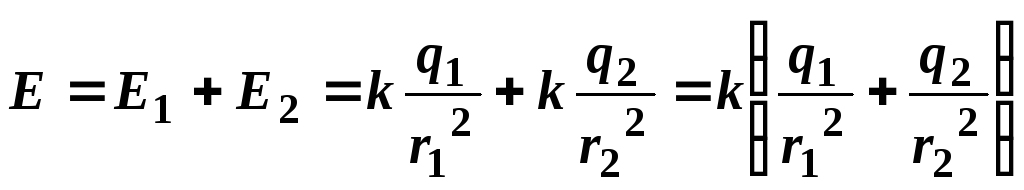 .
.
-
В
 точке С (рис. 14, в) векторы
точке С (рис. 14, в) векторы и
и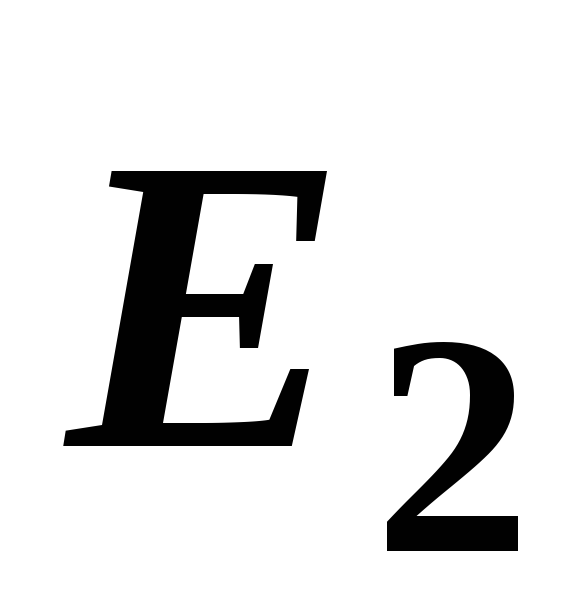 взаимно перпендикулярны, поэтому модуль
взаимно перпендикулярны, поэтому модуль
результирующего вектора является гипотенузой прямоугольного
является гипотенузой прямоугольного
треугольника и определяется по теореме
Пифагора:
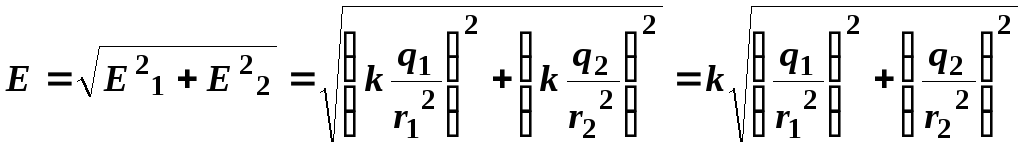 .
.
-
В
точке D
(рис. 14, г) векторы
 и
и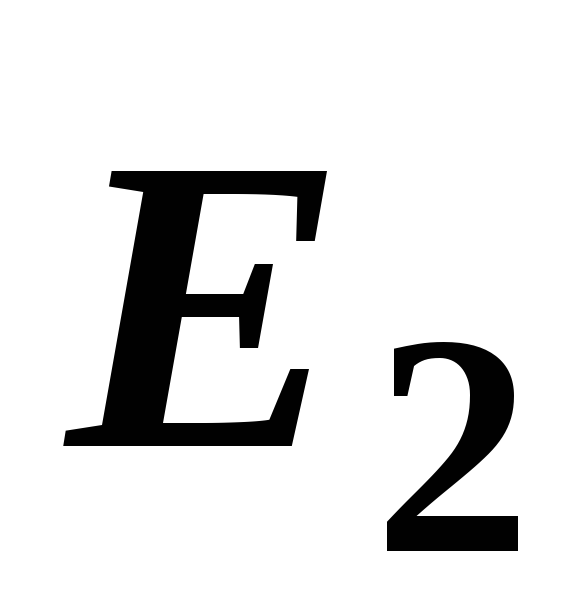 образуют треугольник, поэтому модуль
образуют треугольник, поэтому модуль
результирующего вектора определяется
определяется
по теореме косинусов:
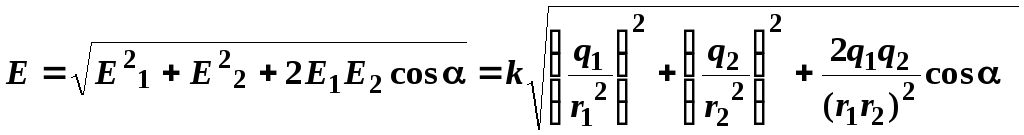 .
.
Если
угол α
неизвестен, то его определяют, используя
теорему косинусов для треугольника со
сторонами r1,
r2,
d:
![]() .
.
Задача
2.2. Поле
создано тремя одинаковыми точечными
зарядами q,
расположенными в вершинах равностороннего
треугольника со стороной а.
Вычислить напряжённость электростатического
поля в точке, находящейся на пересечении
высот этого треугольника.
Решение.
Так как напряжённость электростатического
поля
![]() – величина
– величина
векторная, то необходимо определить
направление этого вектора и его модуль
(длину).
Направление
вектора напряжённости результирующего
поля определяем с помощью принципа
суперпозиции:
![]() ,
,
где
![]() ,
,![]() и
и![]() – напряжённость электростатического
– напряжённость электростатического
поля, созданного каждым зарядом в
отдельности.
-
С
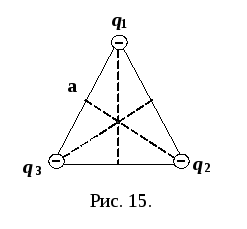 начала
начала
строим векторы ,
,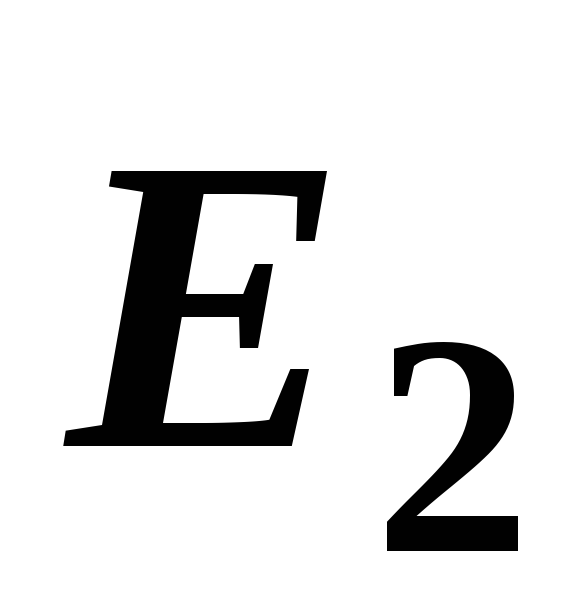 и
и ,
,
берущиеначало
в заданной точке. Так как все заряды
одинаковые, а заданная точка равноудалена
от них, то длины этих векторов будут
равны. Поскольку знак зарядов
отрицательный, то векторы
 ,
,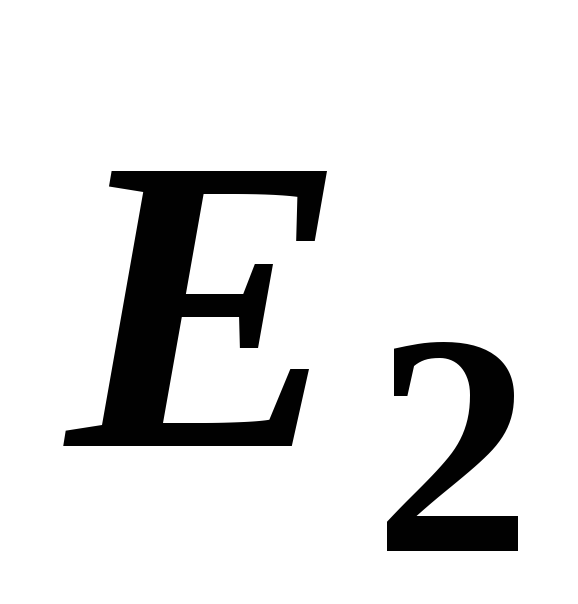 и
и будут направлены к зарядам (рис. 15).
будут направлены к зарядам (рис. 15). -
Складываем
геометрически векторы
 и
и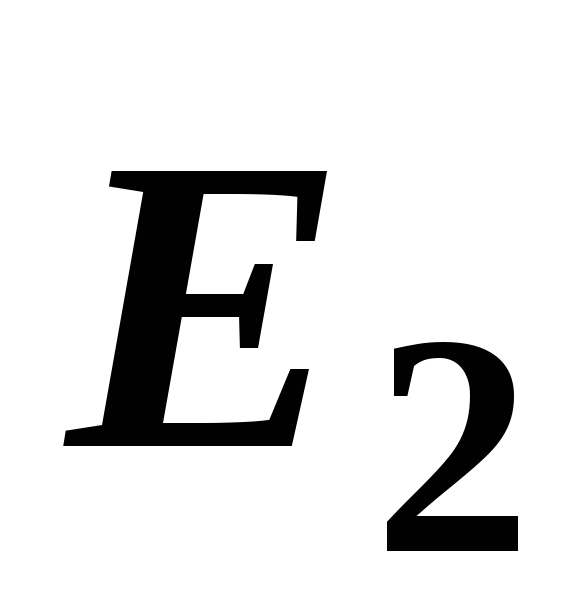 .
.
Результирующий вектор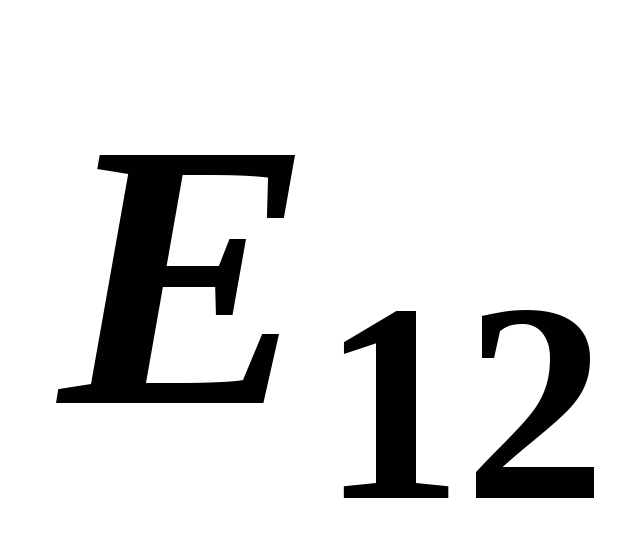 будет лежать на той же прямой, что и
будет лежать на той же прямой, что и
вектор .
. -
Находим
длину вектора
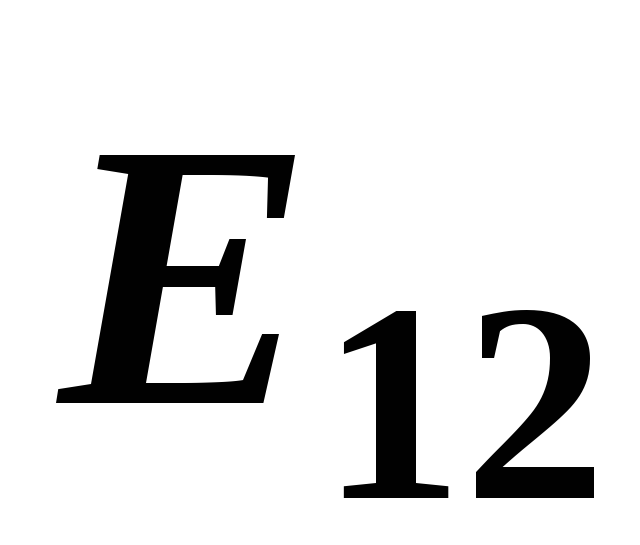 по теореме косинусов:
по теореме косинусов:
![]() ,
,
где
α
– угол между векторами
![]() и
и![]() .
.
С
учётом того, что Е1
= Е2,
α = 120º, cos 120º
= – 0,5, получим:
![]() .
.
-
Складываем
геометрически векторы
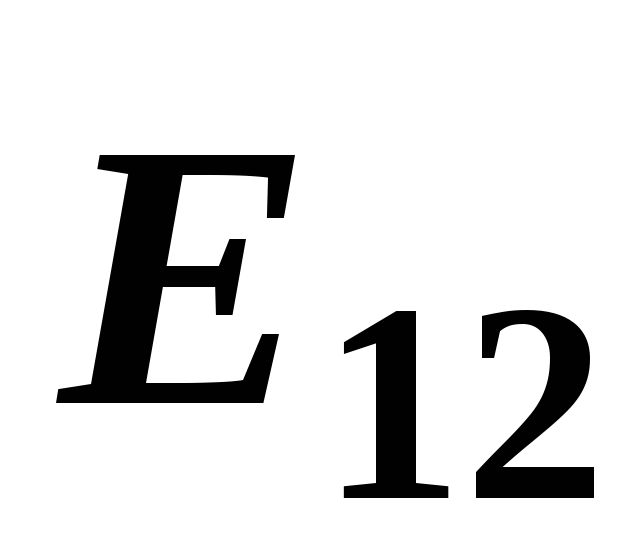 и
и .Так
.Так
как эти векторы равны по длине и
противоположны по направлению, то их
векторная сумма равна нулю:
![]() .
.
Методика
расчета не меняется, если образующие
систему заряды имеют другие знаки и
расположения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #