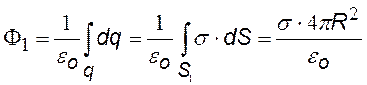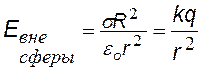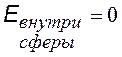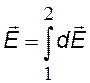
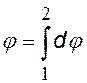
при непрерывном
распределении зарядов
В качестве примера получения выражения для напряженности поля с помощью принципа суперпозиции найдем напряженность поля тонкого стержня конечной длины, равномерно заряженного с линейной плотностью заряда t
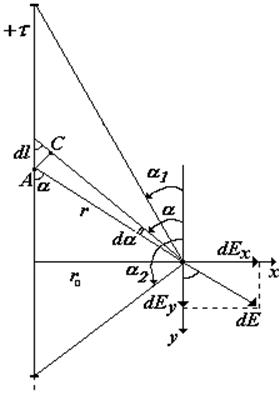
Выберем бесконечно малый элемент dl стержня с зарядом dq. Поскольку напряженности от различных элементов направлены по-разному, введем оси проекций х и у. Итегрируя, найдем результирующие напряженности Ех и Еу.
|
|
dE— напряженность от элемента стержня dl с зарядом dq = t×dl, dEх и dEy – проекции dE на направления х и у. |
|
|
|
Чтобы проинтегрировать, сведем к одной переменной a |
|
|
|
длина дуги АС при малых углах, она же из треугольника (А, С, dl) |
|
|
|
||
|
|
|
модуль напряженности |
|
|
Для бесконечно длинной нити a1 ® 0, a2 ® 180о, следовательно, Еу = 0 и Е = Ех (cos180o = -1), r – расстояние от точки, в которой определяется напряженность, до нити. |
Этот пример показывает, что вычисление напряженности полей представляет собой достаточно сложную задачу даже в нашем случае, когда мы не учитывали поле вблизи концов стержня.
Основной задачей электростатики является вычисление полей заряженных тел. Найти напряженность поля заряженного тела можно с помощью:
1) принципа суперпозиции — это сложная математическая задача, решаемая только в некоторых простых случаях или
2) теоремы Гаусса, которая упрощает расчеты, но только в случае бесконечной плоскости, бесконечной нити (цилиндра) или сфер и шаров (см. ниже).
Теорема Гаусса.
Сначала введем понятие «поток вектора» — это скалярная величина
|
(Н×м2/Кл = В×м) |
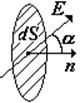
элементарный поток вектора напряженности Е, n – нормаль к площадке, dS – элементарная площадка – это такая малая площадка, в пределах которой Е = const; Еn – проекция вектора Е на направление нормали n |
|
|
|
поток вектора напряженности через конечную площадку S |
|
|
|
-²- -²- -²-через замкнутую поверхность S |
|
|
|
при дискретном распределении зарядов |
Теорема Гаусса: «Поток вектора напряженности через любую замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на eо» (eо – электрическая постоянная) |
|
|
при непрерывном распределении зарядов |
Применение теоремы Гаусса.
Чтобы найти напряженность с помощью теорем Гаусса, нужно взять интеграл. А как его взять, если мы Е еще только пытаемся найти? Кроме того, под интегралом «мешает» cosa. Надо суметь выбрать такую замкнутую поверхность (ее удобно называть гауссовой), в каждой точке которой было бы Е = const, и cosa = const. Тогда в левой части теоремы Е и cosa можно будет вынести из-под знака интеграла. Поэтому практически теорему Гаусса можно применить только в следующих случаях: сфера, шар, длинная нить, длинный цилиндр, бесконечная плоскость.
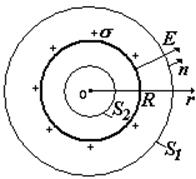
1) Сфера, заряженная с поверхностной плотностью заряда s (Кл/м2)
Рассмотрим области : 1) вне сферы (![]() ) и внутри ее (
) и внутри ее (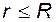 ). Выберем поверхности: 1) S1 и 2) S2 – обе поверхности – сферы, концентрические с заряженной сферой. Сначала найдем потоки вектора Е через выбранные поверхности, а затем воспользуемся теоремой.
). Выберем поверхности: 1) S1 и 2) S2 – обе поверхности – сферы, концентрические с заряженной сферой. Сначала найдем потоки вектора Е через выбранные поверхности, а затем воспользуемся теоремой.
|
|
Потоки вектора Е через S1 ( E^n, a = 0, cosa = 1. |
|
|
|
по теореме Гаусса; F2 = 0, т. к. S2 не охватывает никаких зарядов. Приравнивая потоки из (¨) и (¨¨), найдем E(r). |
|
|
|
||
|
q = s×2pR2 – полный заряд сферы |
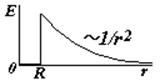
Вне сферы поле такое же, как поле точечного заряда. На границе сферы происходит скачок напряженности. |
2)Тонкая длинная нить, заряженная с линейной плотностью заряда t (Кл/м)
В этом случае «гауссова» поверхность – соосный с нитью цилиндр длиной l.
Сначала найдем поток, потом воспользуемся теоремой Гаусса.
Принцип
суперпозиции позволяет рассчитать
электростатические поля любой системы
неподвижных зарядов, поскольку если
заряды не точечные, то их всегда можно
свести к совокупности точечных зарядов.
Методика
расчета напряженности состоит из двух
частей:
-
Первая
(дифференцирование) заключается в
разбиении заряженных тел на малые
области, каждая из которых может
считаться точечным зарядом, и применении
к ним формулы напряжённости
электростатического поля точечного
заряда. -
Вторая
(интегрирование) заключается в векторном
суммировании напряжённостей
электростатических полей.
 .
.
Задача
2.8. Вычислить
напряжённость поля, создаваемого тонким
стержнем длиной ℓ,
несущим равномерно распределённый по
длине заряд с линейной плотностью +
τ в точке,
равноудалённой от концов стержня,
находящейся на расстоянии r0
от его середины.
Решение.
Выделим на стержне бесконечно малый
участок
![]() ,
,
заряд которого можно считать точечным
(рис. 27, а):
![]()
(1)
Воспользуемся
формулой напряжённости поля точечного
заряда в дифференциальном виде:
![]()
 (2)
(2)
Сделаем
геометрические преобразования. Из ![]()
(см. рис. 27, а):
![]() (3)
(3)
Из
![]()
(рис. 27, б):
![]() (4)
(4)
Так
как угол
![]() мал, то
мал, то![]()
Из
![]()
(см. рис. 27, а):
![]() .
.
(5)
Подставив
в формулу (4) а
и r
из (5) и (3), получим:
![]() (6)
(6)
Подставив
r
из (3) и
![]() из (6) в формулу (2), получим:
из (6) в формулу (2), получим:
 . (7)
. (7)
Так
как
![]() вектор, то
вектор, то![]() .
.
Из
рис. 27, а:
![]() .
.
Чтобы
найти полную напряжённость, нужно
проинтегрировать её составляющие:
![]() .
.
Модуль напряжённости
![]() .
.
Для
половины стержня угол φ
изменяется от 0 до α,
а для всего стержня – от α
до – α
![]() Так
Так
как
![]() ,
,
то![]() .
.
![]() Так
Так
как
![]() ,
,
то![]() .
.
Из
![]()
на рис. 27, а выразим ![]() :
:
![]() .
.
Окончательно
получим:
![]() .
.
Задача 2.9.
На тонком кольце равномерно распределен
заряд с линейной плотностью заряда+
τ.Определить напряженность
электростатического поля в точке,
расположенной на оси кольца и удаленной
на расстояниеа от плоскости
кольца.
Р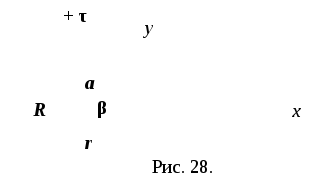 ешение.
ешение.
Выделим на кольце элемент длины
![]() (рис. 28). ЗарядdQ=τ
(рис. 28). ЗарядdQ=τ![]() ,находящийся на выделенном участке,
,находящийся на выделенном участке,
можно считать точечным. Напряженность
электростатического поля![]() ,
,
создаваемого точечным зарядомdQ:
![]() ,
,
где
![]() – расстояние от элемента
– расстояние от элемента
![]() до заданной точки.
до заданной точки.
Выразим вектор
![]() через проекции
через проекции![]() и
и![]() на оси координат:
на оси координат:
![]() .
.
Напряженность
![]() найдем интегрированием вдоль длины
найдем интегрированием вдоль длины
окружностиℓ:
![]() .
.
Так как кольцо
симметрично относительно заданной
точки, то все проекции на ось х
скомпенсируют друг друга, то есть
интеграл
![]() .
.
Тогда
![]() ,
,
где
![]() .
.
Из
рис. 28:
![]() ;
;
![]() .
.
С
учетом того, что длина окружности ℓ
= 2πR, а коэффициент![]() ,
,
окончательно получим:
![]() .
.
2.3. Потенциал. Эквипотенциальные поверхности
Электростатическое
поле обладает потенциальной энергией,
поэтому наряду с напряженностью поля
![]() для описания полей используется такая
для описания полей используется такая
характеристика поля, какпотенциал.
Потенциал
электростатического поля φ
– СФВ, являющаяся энергетической
характеристикой поля и численно равная
потенциальной энергии, которой обладал
бы в данной точке поля единичный
положительный точечный заряда:
![]() (2.10)
(2.10)
За
единицу измерения потенциала в СИ
принимают 1 Вольт
[φ] = 1В = ![]() .
.
Потенциал
не зависит ни от потенциальной энергии
WП
ни от заряда q
+,
а является характеристикой поля.
Подчеркнем,
что, в отличие от напряженности, потенциал
– не векторная, а скалярная
величина. Он может быть как положительным,
так и отрицательным. Потенциал поля,
созданного положительным зарядом,
положителен,
а потенциал поля, созданного отрицательным
зарядом, отрицателен.
Для потенциала
справедлив принцип
суперпозиции:
потенциал поля, созданного в данной
точке системой положительных и
отрицательных зарядов, равен алгебраической
сумме потенциалов полей, созданных
каждым зарядом в отдельности с учетом
их знаков:
![]() . (2.11)
. (2.11)
Численное значение
потенциала зависит от выбора нулевого
уровня φ.
Нулевой уровень
потенциала
– геометрическое место точек поля,
потенциал которых принимается равным
нулю и выбирается произвольно: в
бесконечности, на поверхности Земли и
т. д.
Потенциал поля,
созданного точечным зарядом Q
на расстоянии r
от него:
![]() . (2.12)
. (2.12)
Д ля
ля
графического изображения распределения
потенциала пользуютсяэквипотенциальными
поверхностями
– поверхностями, во всех точках которых
потенциал φ
имеет одно и то же значение.
Форма эквипотенциальных
поверхностей может быть разная, например,
для точечного заряда эквипотенциальные
поверхности – концентрические
сферы
(рис. 29).
Эквипотенциальных
поверхностей вокруг каждого заряда
можно провести бесчисленное множество.
Однако их обычно проводят так, чтобы
разности потенциалов между соседними
эквипотенциальными поверхностями были
одинаковы. Тогда густота эквипотенциальных
поверхностей характеризует напряженность
поля в разных точках. Чем гуще
эквипотенциальные поверхности, тем
больше напряженность поля.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Пример решения задачи на расчет нормальных напряжений в сечениях прямого ступенчатого стержня при продольном нагружении.
Задача
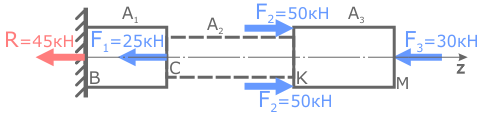
Рассчитать величину напряжений в стержне заданной формы, нагруженном продольными силами и построить их эпюру.
Другие примеры решений >
Помощь с решением задач >
Поперечное сечение стержня — квадрат со сторонами a=22мм.
Допустимые напряжения [σ]=160МПа
Пример решения
Предыдущие пункты решения задачи:
- Расчет опорной реакции стержня,
- Построение эпюры внутренних продольных сил,
- Подбор размеров квадратного сечения стержня по условию прочности.
Как известно, расчет нормальных напряжений при растяжении-сжатии производится по формуле:
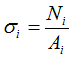
т.е. напряжения определяются отношением соответствующей величины внутренней силы к площади поперечного сечения на рассматриваемом участке стержня.
Площади поперечного сечения стержня:
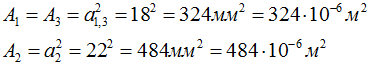
В пределах участка стержня, где внутренняя сила и площадь постоянны, напряжения тоже будут одинаковы, при этом положительные (растягивающие) внутренние силы в сечениях вызывают действие положительных напряжений, и наоборот.
Величину и знаки внутренних сил примем с построенной эпюры N.
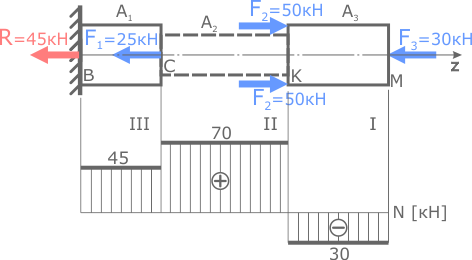
Расчет напряжений
Напряжения на I силовом участке (KM)
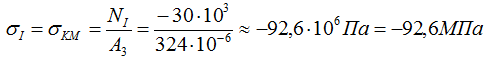
На II участке (CK)
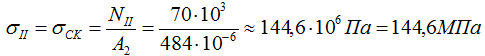
На III участке (BC)
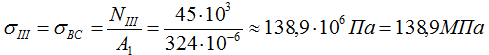
По этим данным строим эпюру нормальных напряжений σ.
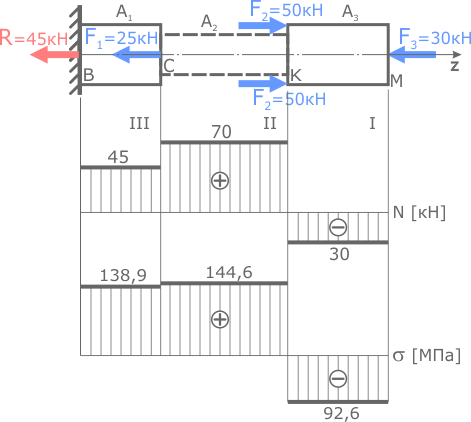
По эпюре видно, что все напряжения лежат в пределах допустимых значений, следовательно, поперечные размеры стержня были рассчитаны правильно и необходимая прочность обеспечена.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Тема: Определить напряжённость (Прочитано 4780 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Определить напряжённость E поля, создаваемого тонким, длинным стержнем, равномерно заряженным с линейной плотностью тау=20 мкКл/м в точке, находящейся на расстоянии A = 2 см от стержня вблизи его середины. Сделать рисунок.

Записан
Решение: для определения напряжённости поля, создаваемого бесконечно длинным стержнем, воспользуемся теоремой Остроградского-Гаусса: поток вектора напряженности электрического поля через замкну-тую поверхность пропорционален заряду, заключенному в ней:
[ ointlimits_{S}{vec{E}cdot dvec{S}}=frac{1}{{{varepsilon }_{0}}}cdot Q,text{ }Ecdot S=frac{Q}{{{varepsilon }_{0}}}cdot ]
Здесь ε0 = 8,85 ∙ 10-12 Ф/м – электрическая постоянная. Представим вокруг стержня коаксиальную замкнутую поверхность – цилиндр, радиуса r и длиной L (L = ∞). Для оснований E =0, для боковой поверхности зависит от расстояния r. Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра. Учтём, что r = a. В этом случае
[ begin{align}
& S=text{ }2pi cdot rcdot L,text{ }Q=tau cdot L,text{ } \
& Ecdot 2pi cdot rcdot L=frac{tau cdot L}{{{varepsilon }_{0}}},text{ }E=frac{tau }{2pi cdot {{varepsilon }_{0}}cdot r}, \
end{align} ]
[ E=frac{tau }{2pi cdot {{varepsilon }_{0}}cdot a}=frac{20cdot {{10}^{-6}}}{2cdot 3,14cdot 8,85cdot {{10}^{-12}}cdot 2cdot {{10}^{-2}}}=1,8cdot {{10}^{7}}. ]
Ответ: 1,8•107 В/м
« Последнее редактирование: 06 Февраля 2016, 07:29 от alsak »

Записан
Дан тонкий стержень длиной l = 10 см, по которому равномерно распределен заряд Q = 8 × 10−8 Кл. Найти напряженность поля в точке, лежащей на продолжении стержня, на расстоянии хo = 10 см от его ближайшего конца.
Источник: сборник задач МЭИ 1992 “Электричество”.
Мое решение.

Итак, Е (А) = Q / (4πeor2),
где r — расстояние между точкой и зарядом.
Пусть k = 1 / (4πeor2).
Т. к. у нас не точка, а тонкий стержень, то мы его можем разбить на маленькие заряды dq и dE (A) = k • dq / (l + xo − x),
где х — это расстояние от “0” до точки dq.
Теперь чтобы найти полную напряженность, нам надо просуммировать все dE, то есть проинтегрировать dE от 0 до l, и вот тут я теряюсь, потому что не могу найти dq, как его нужно выразить, я не знаю 🙁
В итоге должен получиться интеграл что-то вроде того:

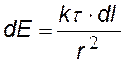
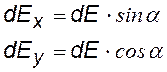
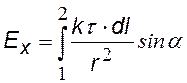
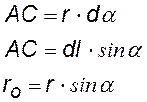
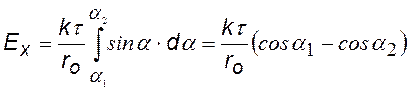
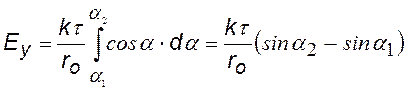
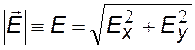
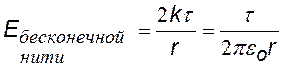
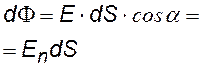
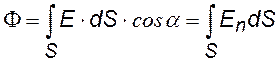
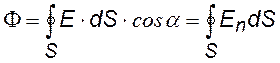
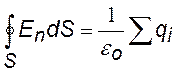
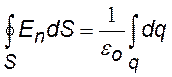
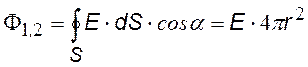 (¨)
(¨)