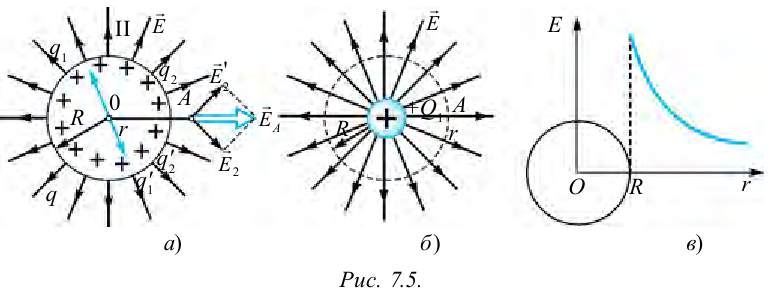
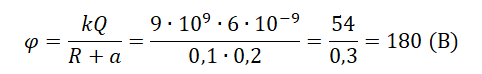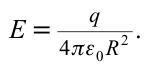Любые заряженные тела создают вокруг себя электростатическое поле. Рассмотрим особенности электростатического поля, создаваемого точечным зарядом и заряженной сферой.
Электростатическое поле точечного заряда
Направление силовых линий электростатического поля точечного заряда
Модуль напряженности не зависит от значения пробного заряда q0:
E=FKq0=kQq0r2q0=kQr2
Модуль напряженности точечного заряда в вакууме:
E=kQr2
Модуль напряженности точечного заряда в среде:
E=kQεr2
Сила Кулона:
−FKулона=q−E
Потенциал не зависит от значения пробного заряда q0:
φ=Wpqo=±kQq0rq0=±kQr
Потенциал точечного заряда в вакууме:
φ=±kQr
Потенциал точечного заряда в среде:
φ=±kQεr
Внимание! Знак потенциала зависит только от знака заряда, создающего поле.
Эквипотенциальные поверхности для данного случая — концентрические сферы, центр которых совпадает с положением заряда.
Работа электрического поля по перемещению точечного заряда:
A12=±q(φ1−φ2)
Пример №1. Во сколько раз увеличится модуль напряженности электрического поля, созданного точечным зарядом Q в некоторой точке, при увеличении значения этого заряда в 5 раз?
Модуль напряженности электрического поля, созданного точечным зарядом, определяется формулой:
E=kQεr2
Формула показывает, что модуль напряженности и электрический заряд — прямо пропорциональные величины. Следовательно, если заряд, который создает поле, увеличится в 5 раз, то модуль напряженности создаваемого поля тоже увеличится в 5 раз.
Электростатическое поле заряженной сферы
Направление силовых линий электростатического поля заряженной сферы:
Модуль напряженности электростатического поля заряженной сферы:
| Внутри проводника (расстояние меньше радиуса сферы, или r < R) |
E=0 |
| На поверхности проводника (расстояние равно радиусу сферы, или r = R) |
E=kQR2 |
| Вне проводника (расстояние больше радиуса сферы, или r > R) |
E=kQr2=kQ(R+a)2 a — расстояние от поверхности сферы до изучаемой точки. r — расстояние от центра сферы до изучаемой точки. |
Сила Кулона:
−FK=q−E
Потенциал:
| Внутри проводника и на его поверхности (r < R или r = R) |
φ=±kQR |
| Вне проводника (r > R) |
φ=±kQr=±φ=±kQR+a |
Пример №2. Определить потенциал электростатического поля, создаваемого заряженной сферой радиусом 0,1 м, в точке, находящейся на расстоянии 0,2 м от этой сферы. Сфера заряжена положительна и имеет заряд, равный 6 нКл.
6 нКл = 6∙10–9 Кл
Так как сфера заряжена положительно, то потенциал тоже положителен:
Задание EF18107
Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F. Чему станет равен модуль этих сил, если один заряд увеличить в n раз, другой заряд уменьшить в n раз, а расстояние между ними оставить прежним?
Ответ:
а) F
б) nF
в) Fn
г) n2F
Алгоритм решения
1.Записать исходные данные.
3.Применить закон Кулона к обоим зарядам для 1 и 2 случая.
4.Установить, как меняется сила, с которой заряды действуют друг на друга.
Решение
Запишем исходные данные:
• Первая пара зарядов: q1 и q2.
• Вторая пара зарядов: q1’ = nq1 и q2’=q2/n.
• Расстояние между зарядами: r1 = r2 = r.
Закон Кулона:
FK=k|q1||q2|r2
Применим закон Кулона к парам зарядов. Закон Кулона для первой пары:
FK1=k|q1||q2|r2
Закон Кулона для второй пары:
FK2=k|nq1|∣∣q2n∣∣r2=k|q1||q2|r2
Коэффициент n сократился. Следовательно, силы, с которыми заряды взаимодействуют друг с другом, не изменятся:
FK1=FK2
После изменения зарядов модуль силы взаимодействия между ними останется равным F.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18591
Ответ:
а) ↘
б) →
в) ↖
г) ↓
Алгоритм решения
1.Сделать чертеж. Обозначить все силы, действующие на центральный точечный заряд со стороны остальных точечных зарядов.
2.Найти равнодействующую сил геометрическим способом.
Решение
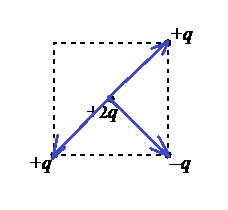
Сделаем чертеж. В центр помещен положительный заряд. Он будет отталкиваться от положительных зарядов и притягиваться к отрицательным:
Модули всех векторов сил, приложенных к центральному точечному заряду равны, так как модули точечных зарядов, расположенных в вершинах квадрата равны, и находятся они на одинаковом расстоянии от этого заряда.
Складывая векторы геометрически, мы увидим, что силы, с которыми заряд +2q отталкивается от точечных зарядов +q, компенсируют друг друга. Поэтому на заряд действует равнодействующая сила, равная силе, с которой он притягивается к отрицательному точечному заряду –q. Эта сила направлена в ту же сторону (к нижней правой вершине квадрата).
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22574
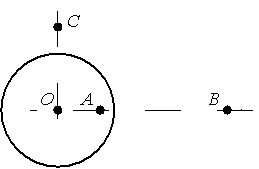
Установите соответствие между физическими величинами и их значениями.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать формулы для нахождения напряженности электростатического поля внутри и снаружи заряженной сферы.
2.Определить величину напряженности поля в указанных точках.
3.Установить соответствие между величинами и их значениями.
Решение
Внутри заряженной сферы напряженность электростатического поля равна 0. Поэтому напряженность в точке А равна 0.
EA=0
Снаружи заряженной сферы напряженность электростатического поля равна:
E=kQr2=kQ(R+a)2
Найдем напряженность электростатического поля в точке В, которая находится на расстоянии 3R от центра заряженной сферы:
EB=kQr2=kQ(3R)2=kQ9R2
Чтобы выразить EB через Eс, найдем напряженность электростатического поля в точке С, которая находится на расстоянии 3R/2 от центра заряженной сферы:
EС=kQr2=kQ(32R)2=4kQ9R2
Найдем отношение EB к Eс:
EBEС=kQ9R2÷4kQ9R2=kQ9R2·9R24kQ=14
Следовательно:
EB=EС4
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.5k
Электростатика – раздел электродинамики,
изучающий взаимодействие неподвижных
электрических зарядов.
Электрический заряд – физическая
величина, определяющая силу электромагнитного
взаимодействия. Заряд обозначается
буквой q, измеряется
в кулонах (Кл).
В природе существует два вида
электрических зарядов, которые условно
назвали «положительный» и «отрицательный».
Заряды одного знака отталкиваются,
разных знаков – притягиваются.
Электрический заряд всегда связан с
частицей. Существуют частицы без заряда,
но не существует заряда без частицы.
Величина электрического заряда не
зависит от скорости движения частицы.
Минимальный заряд, встречающийся в
природе, называется элементарным.
Величина элементарного заряда е =
1,610-19
Кл. Заряды электрона, протона, позитрона
(античастица для электрона) равны по
модулю элементарному. Заряд любого
макроскопического тела кратен
элементарному, т. е. электрический заряд
– дискретная величина.
Все вещества состоят из атомов или
молекул. Атом состоит из положительно
заряженного ядра и отрицательно
заряженных электронов, движущихся
вокруг ядра. Поэтому любое макроскопическое
тело содержит электрически заряженные
частицы. Если суммарный заряд тела равен
нулю, то говорят что тело электрически
нейтральное или незаряженное. Электрический
заряд любой системы равен алгебраической
сумме зарядов тел, входящих в систему.
Заряды могут перераспределятся между
телами системы. Если система тел
электрически изолирована (через границу
системы не проникают другие заряды), то
в ней выполняется закон сохранения
заряда:
алгебраическая сумма зарядов электрически
изолированной системы постоянна:
q1
+ q2
+ … + qn
= const.
Электризация – это процесс получения
электрически заряженных тел из
нейтральных.
При электризации трением одни вещества
отдают электроны, а другие их присоединяют.
Причина этого явления – в различии
энергии связи электронов с атомами в
этих веществах. Атом, потерявший электрон
называется положительным ионом,
присоединивший к себе электрон –
отрицательным ионом.
Точечный заряд – это заряженное
тело, размер которого много меньше
расстояния его возможного действия на
другие тела.
Закон Кулона (1875 г.): Сила взаимодействия
между двумя неподвижными точечными
зарядами, находящимися в вакууме, прямо
пропорциональна произведению модулей
зарядов, обратно пропорциональна
квадрату расстояния между ними и
направлена по прямой, соединяющей
заряды:
.
Коэффициент k, входящий
в закон Кулона, зависит от выбора системы
единиц. В системе СИ
.
Здесь
– электрическая постоянная.
Закон Кулона был получен экспериментально.
Он справедлив только для точечных
зарядов или равномерно заряженных
шаров. Электростатические взаимодействия
осуществляются посредством
электростатического поля.
Электростатическое поле это вид
материи который образуется неподвижными
электрическими зарядами и его можно
обнаружить по его действию на неподвижные
электрические заряды.
Силовой характеристикой электростатического
поля является напряженность –
векторная физическая величина, численно
равная силе с которой поле действует
на единичный пробный положительный
заряд, помещенный в заданной точке поля.
.
Направление вектора напряженности
совпадает с направлением вектора силы,
действующей на положительный заряд,
помещенный в данной точке поля. Из закона
Кулона на основании определения
напряженности поля получаем формулу
для напряженности поля точечного заряда
на расстоянии r от него:
.
Для наглядности электростатическое
поле представляют непрерывными линиями
напряженности – касательные к которым
в каждой точке совпадают по направлению
с направлением вектора напряженности
электростатического поля в данной
точке.
Линии напряженности не пересекаются
(в противном поле напряженность поля в
точке пересечения не имела бы определенного
значения); начинаются на положительных
зарядах (источники поля) и стекаются к
отрицательным зарядам (стоки). Модуль
вектора напряженности пропорционален
числу линий напряженности на густоте
линий напряженности можно судить о
модуле вектора напряженности на единицу
поверхности (густоте линий напряженности).
Электростатическое поле, векторы
напряженности которого одинаковы во
всех точках пространства, называется
однородным.
Принцип суперпозиции электрических
полей: напряженность поля системы
зарядов в данной точке равна векторной
сумме напряженностей полей, созданным
в этой точке каждым зарядом в отдельности:
.
Теорема Гаусса.
Потоком вектора напряженности через
замкнутый контур площадью S
называется произведение проекции
вектора напряженности на нормаль к
контуру на площадь контура:
.
Поток вектора напряженности через
произвольную замкнутую поверхность
равен алгебраической сумме зарядов,
расположенных внутри этой поверхности,
деленной на электрическую постоянную:
.
Напряженность поля точечного заряда.
Д
определения напряженности проведем
сферическую поверхность S
радиусом r с центром
совпадающим с зарядом и воспользуемся
теоремой Гаусса. Так как внутри указанной
области находится только один заряд q,
то согласно указанной теореме получим
равенство:
(1), где En
– нормальная составляющая напряженности
электрического поля. Из соображений
симметрии нормальная составляющая
должна быть равна самой напряженности
и постоянна для всех точек сферической
поверхности, поэтому E=En=const.
Поэтому ее можно вынести за знак суммы.
Тогда равенство (1) примет вид
,
что и было получено из закона Кулона и
определения напряженности электрического
поля.
Электрическое поле заряженной сферы
Е
сфера проводящая, то весь заряд находится
на поверхности. Рассмотрим две области
I – внутри сферы радиуса
R с зарядом q
и вне сферы область II.
Для определения напряженности в области
I проведем сферическую
поверхность S1
радиусом r1 (0<r1<R)
и воспользуемся теоремой Гаусса. Так
как внутри указанной области зарядов
нет, то согласно указанной теореме
получим равенство:
(1), где En
– нормальная составляющая напряженности
электрического поля. Из соображений
симметрии нормальная составляющая
должна быть равна самой напряженности
и постоянна для всех точек сферической
поверхности, поэтому E1=En=const.
Поэтому ее можно вынести за знак суммы.
Тогда равенство (1) примет вид
.
Т. к. площадь сферы не равна нулю, то Е1=0
(во всех точках области I)
– внутри проводника зарядов нет и
напряженность поля равна нулю.
В области II Rr2
проведем сферическую поверхность S2
радиусом r2 и
воспользуемся теоремой Гаусса:
(2),
– напряженность поля вне сферы
рассчитывается по той же формуле, что
и напряженность поля точечного заряда.
Электрическое поле заряженного шара
Заряд равномерно распределен по всему
объему шара, поэтому введем понятие
объемной плотности заряда:
.
Рассмотрим две области I
– внутри сферы радиуса R
с зарядом q и вне сферы
область II.
Для определения напряженности в области
I проведем сферическую
поверхность S1
радиусом r1 (0<r1<R)
и воспользуемся теоремой Гаусса:
– напряженность поля внутри шара
увеличивается прямо пропорционально
расстоянию до центра шара.
В области II R
r2
проведем сферическую поверхность S2
радиусом r2 и
воспользуемся теоремой Гаусса:
(2),
– напряженность поля вне шара рассчитывается
по той же формуле, что и напряженность
поля точечного заряда.
Электрическое поле заряженной нити
Д
равномерно заряженной нити введем
понятие линейной плотности заряда.
Для определения напряженности окружим
участок проволоки длиной ℓ
цилиндрической поверхностью S
радиусом r с осью совпадающей
с проволокой и воспользуемся теоремой
Гаусса. При этом весь поток вектора
напряженности будет проходить только
через боковую поверхность цилиндра,
площадь которой
,
т.к. поток через оба основания цилиндра
равен нулю. Тогда
– напряженность поля нити убывает обратно
пропорционально расстоянию.
Напряженность поля заряженной плоскости
Е
плоскость бесконечна и заряжена
равномерно, т. е. поверхностная плотность
заряда = q/S
одинакова в любом ее месте, то линии
напряженности электрического поля в
любой точке перпендикулярны этой
плоскости. Такое же направление они
сохраняют и на любом расстоянии от
плоскости, т.е. поле заряженной плоскости
однородное.
Для нахождения напряженности электрического
поля заряженной плоскости мысленно
выделим в пространстве цилиндр, ось
которого перпендикулярна заряженной
плоскости, а основания параллельны ей
и одно из оснований проходит через
интересующую нас точку поля. Цилиндр
вырезает из заряженной плоскости участок
площадью S, и такую же
площадь имеют основания цилиндра,
расположенные по разные стороны от
плоскости (рис.). Согласно теореме Гаусса
поток Ф вектора напряженности
электрического поля через поверхность
цилиндра связан с электрическим зарядом
внутри цилиндра выражением
.
С другой стороны, так как линии
напряженности пересекают лишь основания
цилиндра, поток вектора напряженности
можно выразить через напряженность
электрического поля у обоих оснований
цилиндра:
.
В самом деле, поток через боковую
поверхность цилиндра (см. рис.), равен
нулю, поскольку линии напряженности
параллельны боковой поверхности
цилиндра.
Из двух выражений для потока вектора
напряженности получим:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
Преподаватель который помогает студентам и школьникам в учёбе.
Электрическое поле заряженного шара в физике – формулы и определение с примерами
Электрическое поле заряженного шара:
Пусть электропроводящий шар радиусом
Определим напряженность поля, создаваемого заряженным шаром (сферой) в его центре, на поверхности и за его пределами. Для этого мы сначала разделим заряд 
Итоговая напряженность поля 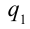
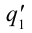
Найдем напряженность поля в произвольной точке 
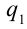
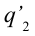
Напряженность электрического поля на поверхности заряженного шара определяется следующей формулой:
Из-за того, что напряженность поля, созданного в точке за пределами заряженного шара, одинаковы с полем, созданным точечным зарядом, напряженность поля, созданного в точке за пределами шара, определяется по формуле:
Это означает, что напряженность поля уменьшается обратно пропорционально квадрату расстояния (рис. 7.5 в).
Напряженность электрического поля зависит от свойств среды, в которой расположен заряд, создающий поле. Рассмотрим случай, когда между двумя противоположно заряженными пластинами помещен диэлектрик (рис. 7.6).
В диэлектрике свободных электронов очень мало. Основные электроны расположены в электронной оболочке атома. Под воздействием поля электрических зарядов пластин электронная оболочка деформируется. В результате центры положительных и отрицательных зарядов атома не накладываются друг на друга. Это явление называется поляризацией диэлектрика.
Напряженность поля 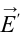
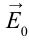
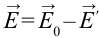
В таком случае напряженность поля в точке, расположенной на расстоянии 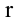
Также сила взаимодействия точечных зарядов, расположенных в однородном диэлектрике, будет в 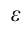
Диэлектрическая восприимчивость – это безразмерная величина.
- Электрические явления в физике
- Потенциал поля точечного заряда в физике
- Работа электрического поля при перемещении заряда в физике
- Энергия электрического поля
- Изменение агрегатного состояния вещества
- Электродинамика
- Электростатика
- Закон сохранения заряда в физике
Подготовка к олимпиаде. Применение теоремы Гаусса для вычисления напряженности электрического поля заряженных тел
Опубликовано ср, 08/14/2019 – 10:50 пользователем fizportal.ru
Применение теоремы Гаусса для вычисления напряженности электрического поля заряженных тел
Рассмотрим применение теоремы Гаусса для вычисления напряженности электрического поля заряженных тел простой формы: плоскости, сферы, шара, нити, цилиндра
1. Поле равномерно заряженной бесконечной плоскости
Когда заряд распределен по какой-либо поверхности, то для расчета полей удобно ввести поверхностную плотность заряда $sigma$. Выделим на плоской поверхности маленький участок площадью $Delta S$. Пусть заряд этого участка равен $Delta q$. Поверхностной плотностью заряда называют отношение заряда $Delta q$ к площади поверхности, по которой он распределен
$sigma = frac{Delta q}{Delta S}$.
Эта плотность может непрерывно изменяться вдоль поверхности. Конечно, электрический заряд имеет дискретную (прерывную) структуру, так как сосредоточен в элементарных частицах. Но если на поверхности площадью $Delta S$ содержится огромное число элементарных зарядов, то дискретную структуру заряда можно не принимать во внимание. Мы ведь пользуемся понятием плотности, считая, что масса непрерывно распределена в пространстве. А на самом деле все тела состоят из дискретных образований – атомов.
В случае равномерного распределения заряда $q$ по поверхности площадью $S$ поверхностная плотность заряда постоянна и равна $sigma = frac{q}{S} = const$.
Задача 1. Найдите напряженность электрического поля, создаваемого равномерно заряженной бесконечной плоскостью. Поверхностная плотность заряда $sigma$.
Решение
Для использования этой теоремы для определения напряженности поля, необходимо рассмотреть симметрию поля, которая, очевидно связана с симметрией зарядов. Распределение зарядов не изменится, если плоскость сместить на любой вектор $vec{a}$, лежащий в самой плоскости. Поэтому при таком смещении не изменится и напряженность поля (рис.).
Следовательно, напряженность поля может зависеть только от расстояния до плоскости $h$. Любая прямая, перпендикулярная плоскости является осью симметрии, то есть при повороте плоскости на любой угол относительно любой оси, перпендикулярной плоскости, распределение зарядов не изменяется – следовательно, и вектор напряженности при таком повороте не изменится, поэтому этот вектор должен быть перпендикулярен плоскости. Наконец, заряженная плоскость является плоскостью симметрии для поля. Поэтому в симметричных точках векторы напряженности также симметричны. Выявленные свойства симметрии электрического поля позволяют выбрать поверхность, для которой можно выразить поток вектора напряженности в простой форме. Итак, в качестве такой поверхности выберем поверхность прямого цилиндра, образующие которого перпендикулярны плоскости, а основания площадью $S$ параллельны ей и находятся на равных расстояниях от плоскости.
Прежде всего, заметим, что поток вектора напряженности через боковую поверхность цилиндра равен нулю, так как во всех точках боковой поверхности векторы напряженности $vec{E}$ и нормали $vec{n}$ взаимно перпендикулярны (поэтому $cosalpha = 0$) (рис.).
Поток через верхнее основание цилиндра может быть записан в виде
$Ф_1 = E_1 cdot S$,
так модуль напряженности поля на основании цилиндра постоянен, а по направлению совпадает с вектором нормали. Такое же значение имеет поток через нижнее основание.
Таким образом, суммарный поток вектора напряженности электрического поля через поверхность цилиндра равен
$Ф = E_1 cdot S + E_2 cdot S = 2E cdot S$.
С другой стороны, по теореме Гаусса
$Ф = frac{q}{varepsilon_0}$,
где $q$ – заряд, заключенный внутри поверхности цилиндра:
$q = sigma cdot S$.
Следовательно, $E = frac{sigma}{2varepsilon_0}$.
Главная составляющая успеха – анализ симметрии поля, позволивший разумно выбрать поверхность, для использования теоремы Гаусса. Также обратите внимание, что напряженность данного поля одинакова во всех точках, следовательно, это поля является однородным. Подчеркнем, независимость напряженности поля от расстояния до плоскости $h$ никак не следует из симметрии поля, это результат нашего расчета.
Примечание.
Для плоскости, заряженной отрицательно, результат будет таким же, лишь направление вектора $vec{E}$ изменится на противоположное.
2. Поле равномерно заряженной сферы
Задача 2. Найдите напряженность электрического поля, создаваемого равномерно заряженной сферой радиуса $R$. Суммарный заряд сферы $q$.
Решение
Опять начнем с рассмотрения симметрии поля. Очевидно, что поле, также как распределение зарядов имеет сферическую симметрию. Это означает, что модуль вектора напряженности зависит только от расстояния до центра сферы (или во всех точках, находящихся от центра сферы на одном расстоянии, модуль напряженности постоянен), а направление – радиальное, от центра сферы к точке наблюдения. Выберем в качестве замкнутой поверхности, к которой применим теорему Гаусса, сферу, концентрическую с заряженной оболочкой (рис.).
Пусть радиус сферы $r$ больше радиуса оболочки $r > R$. Тогда во всех точках этой сферы вектор напряженности направлен вдоль нормали к поверхности, а его модуль постоянен. Поэтому поток вектора напряженности $vec{E}$ через сферу равен произведению модуля напряженности на площадь сферы
$Ф = E cdot S = E cdot 4pi r^2$.
По теореме Гаусса это поток равен $Ф = frac{q}{varepsilon_0}$. Следовательно,
$E cdot 4pi r^2 = frac{q}{varepsilon_0}$, $E = frac{1}{4pi varepsilon_0}frac{q}{r^2}$.
Полученная формула, соответствует формуле закона Кулона для точечного заряда, следовательно, вне сферы, поле равномерно заряженной сферы, совпадает с полем точечного заряда, помещенного в центре сферы.
Поле внутри заряженной сферической оболочки также должно обладать сферической симметрией. Поэтому, поток вектора напряженности электрического поля через сферу, концентрическую с заряженной оболочкой и расположенную внутри нее (рис.)
также выражается формулой
$Ф = E cdot 4pi r^2$.
Однако внутри этой сферы электрических зарядов нет, поэтому, из теоремы Гаусса следует, что напряженность поля внутри сферы равна нулю. Подчеркнем, если бы теорема Гаусса была не справедлива, то внутри равномерно заряженной оболочки существовало бы электрическое поле.
Таким образом, функция, описывающая напряженность поля равномерно заряженной сферы радиуса $R$, имеет вид:
$E(r) = 0$, при $r < R$;
$E(r) = frac{kq}{r^2}$, при $r > R$.
Примечание.
1) Очевидно, что для сферы, заряженной отрицательно, формулы остаются справедливыми, только векторы напряженности будут направлены в противоположные стороны (к центру сферы).
2) Если вместо заряда q задана поверхностная плотность заряда $sigma$, то заряд будет равен $q = sigma S = sigma cdot 4pi R^2$, а напряженность
$E = frac{1}{4pi varepsilon_0}frac{1}{r^2}sigma 4pi R^2 = frac{sigma R^2}{epsilon_0 r^2}$.
3. Поле равномерно заряженного шара
Для характеристики распределения заряда по объему используется понятие объемной плотности заряда. Объемной плотностью заряда называется отношение заряда $Delta q$ к объему $Delta V$, в котором он распределен:
$rho = frac{Delta q}{Delta V}$.
Эта плотность может непрерывно изменяться внутри заряженного тела. Если заряд $q$ равномерно распределен по объему $V$, то объемная плотность заряда постоянна и равна:
$rho = frac{q}{V} = const$.
Задача 3. Вычислить напряженность электрического поля, создаваемого равномерно заряженным шаром радиуса $R$. Объемная плотность заряда $rho$.
Решение
Поле, создаваемое таким шаром, будет центрально-симметричным. Легко понять, что вне шара для поля получится такой же результат, что и для поля вне сферы (см. задачу 2),
$E = frac{1}{4pi varepsilon_0}frac{q}{r^2}$.
Полный заряд шара
$q = rho V = rho frac{4}{3}pi R^3$.
Тогда
$E = frac{1}{4pi varepsilon_0}frac{q}{r^2} = frac{1}{4pi varepsilon_0}frac{4pi R^3 rho}{3r^2} = frac{rho R^3}{3varepsilon_0 r^2}$
(при условии, что $r > R$).
Для нахождения поля внутри шара нужно применить теорему Гаусса к потоку напряженности через сферическую поверхность радиусом $r < R$ (рис.).
Поток вектора напряженности поля через поверхность этой сферы
$Ф = E cdot 4pi r^2$.
С другой стороны, по теореме Гаусса
$Ф = frac{q^/}{varepsilon_0}$,
где $q^/ = rho frac{4}{3}pi r^3$
– заряд, заключенный в сфере радиуса $r$. Следовательно,
$E cdot 4pi r^2 = frac{q^/}{varepsilon_0}, E = frac{1}{4pi varepsilon_0}frac{q^/}{r^2} = frac{1}{4pi varepsilon_0}frac{1}{r^2}rho frac{4}{3}pi r^3 = frac{rho cdot r}{3varepsilon_0}$.
Таким образом, внутри равномерно заряженного шара напряженность поля растет линейно с расстоянием от его центра.
Функция, описывающая напряженность поля равномерно заряженного шара радиуса $R$, имеет вид:
$E(r) = frac{rho}{3varepsilon_0}r$, при $r leq R$,
$E(r) = frac{rho R^3}{3varepsilon_0}frac{1}{r^2}$, при $r > R$.
Примечание.
Если вместо объемной плотности заряда $rho$ задан заряд $q$, то объемной плотности заряда будет равна
$rho = frac{q}{V} = frac{q}{frac{4}{3}pi R^3}$,
а напряженность
$E(r) = frac{r}{3varepsilon_0}frac{q}{frac{4}{3}pi R^3} = frac{q}{4pi varepsilon_0 R^3}cdot r = kfrac{q}{R^3}cdot r$, при $r leq R$,
$E(r) = frac{R^3}{3varepsilon_0}frac{1}{r^2}frac{q}{frac{4}{3}pi R^3} = frac{q}{4pi varepsilon_0}cdot frac{1}{r^2} = kfrac{q}{r^2}$, при $r > R$,
4. Поле равномерно заряженной нити
Для характеристики распределения заряда по длине используется понятие линейная плотности заряда. Линейной плотностью заряда называется отношение заряда $Delta q$ к длине $Delta l$, в которой он распределен:
$tau = frac{Delta q}{Delta l}$.
Эта плотность может непрерывно изменяться внутри заряженного тела. Если заряд $q$ равномерно распределен по длине $l$, то линейная плотность заряда постоянна и равна:
$tau = frac{q}{l} = const$.
Задача 4. Найдите напряженность электрического поля, создаваемого в вакууме бесконечно длинной заряженной нитью с линейной плотностью заряда t.
Решение
Проще всего решить задачу с помощью теоремы Гаусса. Вычислим поток напряженности через цилиндр, ось которого совпадает с заряженной нитью (рис.).
Радиус цилиндра $r$, а его высота $l$.
Из соображений симметрии очевидно, что линии напряженности $vec{E}$ перпендикулярны боковой поверхности цилиндра. Поэтому поток напряженности через боковую поверхность цилиндра равен
$Ф = ES = Ecdot 2pi rl$,
поток через основания цилиндра равен нулю ($alpha = frac{pi}{2}$).
С другой стороны, по теореме Гаусса
$Ф = frac{q}{varepsilon_0}$,
где $q = tau cdot l$ – заряд, заключенный внутри цилиндра. Следовательно,
$E cdot 2pi rl = frac{ltau}{varepsilon_0}$,
$E = frac{tau}{2pi varepsilon_0 r} = frac{2kcdot tau}{r}$.
5. Поле равномерно заряженного бесконечного цилиндра
Задача 5. Бесконечно длинный круговой цилиндр радиусом $R$ равномерно заряжен по объему с плотностью $rho$. Найти напряженность электростатического поля в точке, удаленной на расстояние $r$ от оси цилиндра.
Решение
Используя симметрию распределения заряда и теорему Гаусса, найдем напряженность электрического поля внутри и вне цилиндра. В качестве поверхности, через которую будем определять поток вектора $vec{E}$, выберем цилиндр радиусом $r$ и высотой $h$, имеющий ту же ось симметрии, что и заданный цилиндр (рис.).
Во всех точках боковой поверхности цилиндра вектор $vec{E}$ совпадает с внешней нормалью к этой поверхности и имеет одинаковую величину. Поток вектора $vec{E}$ через боковую поверхность цилиндра
$Ф = E_1 cdot S = E_1 cdot 2pi rh$,
поток через основания цилиндра равен нулю ($alpha = frac{pi}{2}$).
Из теоремы Гаусса следует, что
$Ф = frac{q}{varepsilon_0}$,
где $q = rho V = rho pi r^2h$ – заряд, заключенный внутри цилиндра.
Следовательно,
$E_1 cdot 2pi rh = frac{rho pi r^2h}{varepsilon_0}$, и $E_1 = frac{rho r}{2varepsilon_0}$.
Чтобы найти $E_2$ для $r > R$, окружим заданный цилиндр цилиндрической поверхностью радиусом $r > R$ и высотой $h$, ось симметрии которой совпадает с осью цилиндра (см. рис.).
Во всех точках боковой поверхности цилиндра вектор $vec{E}$ совпадает с внешней нормалью к этой поверхности и имеет одинаковую величину. Поток вектора $vec{E}$ через боковую поверхность цилиндра
$Ф = E_2 cdot S = E_2 cdot 2pi rh$,
поток через основания цилиндра равен нулю ($alpha = frac{pi}{2}$).
Из теоремы Гаусса следует, что
$Ф = frac{q}{varepsilon_0}$,
где $q = rho V = rho pi R^2h$ – заряд, заключенный внутри цилиндра. Следовательно,
$E_2 cdot 2pi rh = frac{rho pi R^2h}{varepsilon_0}$, и $E_2 = frac{rho R^2}{2varepsilon_0 r}$.
6. Дополнительные задачи
Задача 6. Докажите, что система свободных зарядов не может находиться в состоянии устойчивого равновесия. (Теорема Иршноу.)
Решение
Предположим противное, то есть какой-либо из зарядов, для определенности положительный, находится в состоянии устойчивого равновесия. По определению устойчивого равновесия, при выведении заряда из этого положения в любом направлении на сколь угодно малую величину, возникает сила, направленная к положению равновесия.
Окружим заряд, замкнутой поверхностью, например, сферой, так, чтобы внутрь ее не попадали другие заряды (рис.).
Очевидно, что для устойчивости необходимо, чтобы поле, создаваемое всеми прочими зарядами кроме рассматриваемого, на поверхности сферы было направлено к положению равновесия (только в этом случае возникает сила, возвращающая заряд в положение равновесия). Отсюда находим, что поток вектора $vec{E}$ через замкнутую поверхность отрицателен.
Но это противоречит теореме Гаусса, согласно которой данный поток, создаваемый зарядами вне сферы, равен нулю. Таким образом, теорема доказана.
Задача 7. С какой силой расталкиваются равномерно заряженные грани куба? Поверхностная плотность заряда $sigma$, длина ребра куба $l$.
Решение
Для определенности рассмотрим силу, действующую на верхнюю грань куба. Разобьем эту грань на малые площадки $Delta S_i$ и представим силу, действующую на грань, как сумму $vec{F_i}$ сил, действующих на каждую площадку $Delta S_i$:
$vec{F} = sum vec{F_i}$.
Обозначим через $vec{E_i}$ напряженность электрического поля, создаваемого в области нахождения площадки $Delta S_i$ зарядами всех граней, кроме самой верхней грани (рис.).
Тогда сила
$vec{F_i} = q^/ cdot vec{E_i} = sigma cdot Delta S_i cdot vec{E_i}$,
ее проекция на нормаль к грани $vec{n}$ равна
$F_{in} = sigma cdot Delta S_i cdot E_i^/ cdot cosalpha_i$,
а суммарная сила, действующая на верхнюю грань вдоль нормали $vec{n}$:
$F_n = sum F_{in} = sigma cdot sum{E_i^/ Delta S_i cdot cosalpha_i} = sigma cdot Ф^/$, (1)
где $sum{E_i^/ Delta S_i cdot cosalpha_i} = Ф^/$ – поток вектора $vec{E}$ через верхнюю грань куба, создаваемый зарядами всех других граней.
В качестве замкнутой поверхности для применения теоремы Гаусса выберем куб, размеры которого на бесконечно малую величину превышают размеры рассматриваемого куба, то есть их грани практически совпадают. Тогда поток через верхнюю грань куба внешнего куба равен
$Ф = Ф^/ + Ф^{//}$,
где
$Ф^{//} = E^{//} cdot S_1 = frac{sigma}{2varepsilon_0} cdot S_1 = frac{sigma}{2varepsilon_0} cdot l^2$
поток, создаваемый заряженной верхней гранью куба.
Тогда
$Ф = Ф^/ + frac{sigma}{2varepsilon_0} cdot l^2$, (2)
Воспользуемся теоремой Гаусса для всего куба
$Ф_0 = 6Ф = frac{q}{varepsilon_0}$,
где $q = sigma cdot 6l^2$ – заряд куба.
Тогда
$6Ф = frac{6l^2 cdot sigma}{varepsilon_0}$. (3)
Выразим $Ф^/$ из (2), а $Ф$ из (3)
$Ф^/ = Ф – frac{sigma}{2varepsilon_0} cdot l^2 = frac{sigma}{varepsilon_0} cdot l^2 – frac{sigma}{2varepsilon_0} cdot l^2 = frac{sigma}{2varepsilon_0} cdot l^2$.
Учитывая уравнение (1), окончательно находим:
$F_n = frac{sigma^2 cdot l^2}{2varepsilon_0}$.
Задача 8. Грани куба с ребром $a$ однородно заряжены с поверхностной плотностью $sigma$. В центр куба помещен заряд $Q$. С какой силой этот заряд взаимодействует с каждой из граней?
Решение
По теореме Гаусса вычислим $Ф$ – поток вектора напряженности, создаваемой зарядом $Q$, через поверхность куба. Он равен $frac{Q}{varepsilon_0}$. С другой стороны
$Ф = 6 cdot displaystylesum_{Delta S} frac{Q}{r^2} cdot Delta S cdot cosalpha$.
В этом выражении $Delta S$ – площадь малого элемента поверхности куба, $r$ – длина вектора, соединяющего заряд $Q$ с этим элементом, $alpha$ – угол, который составляет этот вектор с нормалью к элементу $Delta S$. Суммирование идет по одной из граней куба. Заметим, что сила $F$, действующая на грань куба, задается выражением:
$F = sigma cdot displaystylesum_{Delta S} frac{Q}{r^2} cdot Delta S cdot cosalpha$
Следовательно,
$F = sigma cdot frac{Ф}{6} = frac{sigma Q}{6varepsilon_0}$.
Направление линий напряженности,
как мы уже говорили, позволяет определить направление вектора напряженности в
различных точках поля. Густота этих линий говорит нам о том, в каких областях
пространства напряженность больше. Поэтому, мы можем сказать, что линии
напряженности — это непрерывные линии, касательные к которым в каждой точке,
через которую они проходят, совпадают с направлением векторов напряженности.
Если мы отметим точки 1 и
2 так, как показано на рисунке, то можно с уверенностью сказать, что
напряженность в точке 1 будет больше, чем напряженность в точке 2.
Если мы рассмотрим теперь
линии напряженности одноименно заряженных шариков, то они будут выглядеть
несколько иначе:
Также мы можем
рассмотреть линии напряженности положительно и отрицательно заряженного шарика:
Как вы видите, вне шарика
они не отличаются от линий напряженности точечных зарядов.
Рассмотрим еще один
важный пример: электрическое поле, создаваемое параллельными заряженными
пластинами. Одна из пластин заряжена отрицательно, а другая — положительно.
Еще раз напомним, что
линии напряженности направлены от плюса к минусу. Обратите внимание на
центральную часть электрического поля между этими пластинами: линии
напряженности здесь параллельны и расположены с одинаковой густотой. Такое
электрическое поле называется однородным. То есть однородное
электрическое поле — это поле, линии напряженности которого, параллельны друг
другу и расположены с одинаковой густотой. Если в качестве примера мы опять
рассмотрим точки 1 и 2, то можем сказать, что поле в точке 1 однородное, а в
точке 2 — неоднородное.
Вернемся теперь к вопросу
об электрическом поле заряженной сферы.
Обозначим радиус сферы за
R, а заряд сферы за Q,
предполагая, что этот заряд равномерно распределен по всей поверхности сферы.
Очевидно, что если мы расположим множество пробных зарядов вблизи поверхности сферы,
то убедимся, что вне сферы линии напряженности расположены точно так же, как и
линии напряженности точечного заряда. Тем не менее, внутри проводящей сферы
напряженность поля равна нулю. Напряженность внутри заряженного шара линейно
растет с увеличением расстояния от центра шара. О том, почему так происходит,
мы поговорим немного позже. Обозначим произвольное расстояние от центра сферы
за r. Тогда функция
зависимости напряженности заряженной сферы от r
будет такова:
Примеры решения задач.
Задача 1. Пылинка
массой 6
×
10−6 кг
неподвижно висит в однородном поле между параллельными противоположно
заряженными пластинами. Если модуль напряженности электрического поля между
пластинами составляет 300 Н/Кл, то каков заряд пылинки?
Задача 2. Шар
обладает зарядом 0,4 мкКл, который равномерно распределен по всему объёму шара.
На точечный заряд, равный 800 нКл, действует кулоновская сила, модуль которой
равен 0,2 мН. Определите, находится ли данный заряд внутри шара или нет?
Расстояние между центром шара и точечным зарядом составляет 60 см.