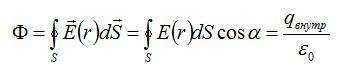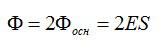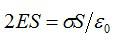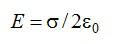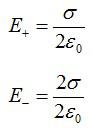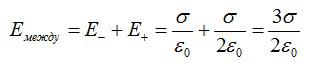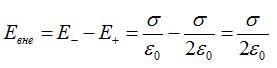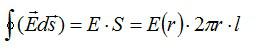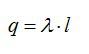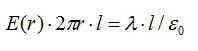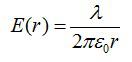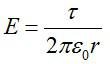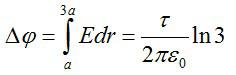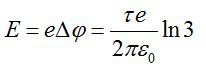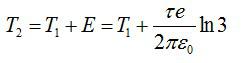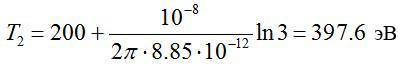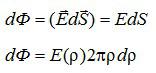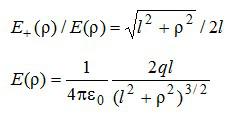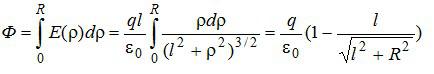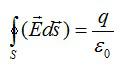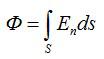Как найти напряженность заряженной нити

1. Применение теоремы Гаусса для расчёта электрических полей

   1. Поле бесконечной заряженной нити

Рассмотрим поле, созданное зарядом,
равномерно распределенным по бесконечной
нити. Эту задачу мы решили на прошлой
лекции, воспользовавшись принципом
суперпозиции электрических полей (см.
1.11).

Теперь покажем, несколько проще можно
рассчитать это поле с помощью теоремы
Гаусса.

Определим напряжённость поля на
расстоянии rот нити,
заряженной с постоянной линейной
плотностью:

,
[Кл/м] (2.10)

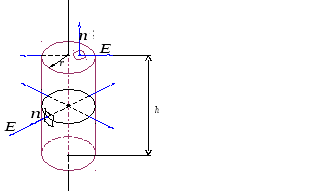
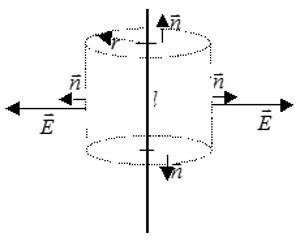
Окружим нить замкнутой цилиндрической
поверхностью (рис. 2.7.). Высота цилиндра
— h, а радиус его
основания —r.

Рис. 2.7.

Поле, созданное заряженной нитью,
обладает цилиндрической симметрией. В
связи с этим векторы напряжённости во
всех точках боковой поверхности цилиндра
будут одинаковы по модулю и направлены
радиально, то есть перпендикулярно к
боковой поверхности цилиндра. На
основаниях цилиндра векторы
,
направленные по-прежнему радиально,
«скользят» по основанию, образуя прямой
угол с нормалью.

Вычислим поток вектора
через поверхность выбранного цилиндра.
Полный поток через эту замкнутую
«гауссову» поверхность складывается
из потока через боковую поверхность
цилиндра и через два его основания:

Последние два интеграла равны нулю, так
как «скользящие» по основаниям цилиндра
векторы
не пронизывают их и не создают никакого
потока. Формально эти два интеграла
равны нулю, так как между векторамиипрямой угол и.
Таким образом

Во всех точках боковой поверхности
цилиндра E=Е_r=constи.

Поэтому поток через боковую поверхность
цилиндра равен

(2.11)

Это поток вектора напряжённости
электрического поля, вычисленный по
определению потока.

Теперь воспользуемся теоремой Гаусса,
отметив предварительно, что «заряд,
заключённый внутри гауссовой поверхности»
в данном случае сосредоточен на отрезке
нити h— на оси цилиндра:

Таким образом

(2.12)

Отсюда теперь легко получить знакомую
нам гиперболическую зависимость
напряжённости поля от расстояния до
нити — r(см. 1.11).

(2.13)

1. Поле бесконечной равномерно заряженной плоскости. Поле плоского конденсатора

Пусть электрическое поле создаётся
зарядом, равномерно распределённым по
поверхности безграничной плоскости, с
поверхностной плотностью (рис. 2.8.)

Рис. 2.8.

Из симметрии задачи следует, что поле
повсюду направлено перпендикулярно к
поверхности. Выясним, как меняется
напряжённость поля по мере удаления от
заряженной плоскости.

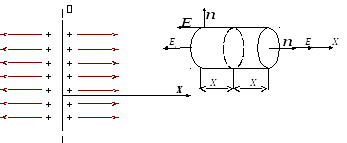
В качестве гауссовой поверхности удобно
выбрать цилиндр. Ось цилиндра направим
перпендикулярно плоскости, его основание
расположим на расстоянии Хсимметрично
по обе стороны от поверхности.

Вычислим поток вектора напряжённости
через боковую поверхность и основания
цилиндра. Как следует из рис. 2.8., поток
вектора напряжённости
через боковую поверхность цилиндра
равен нулю, так как здесь повсюду векторы
напряжённости «скользят» по поверхности
и.

Тогда полный поток через замкнутую
цилиндрическую поверхность можно
записать как поток через два основания
цилиндра.

(2.14)

Это величина, рассчитанная по определению
потока.

Теперь воспользуемся теоремой Гаусса,
заметив, что заряд q,
«находящийся внутри гауссовой
поверхности», в данном случае сосредоточен
на площадкеS=S_осн,
«вырезанной» цилиндром на бесконечной
плоскости

(2.15)

Объединим результаты(2.15) и (2.14) в уравнение
Гаусса:

Откуда следует

(2.16)

Вывод. Поле, созданное бесконечной
равномерно заряженной плоскостью,
однородно. Оно не меняется с расстоянием
от заряженной поверхности ни по величине,
ни по направлению.

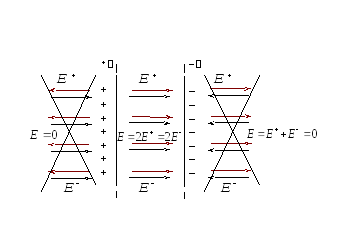
Теперь рассмотрим еще один важный
пример. Пусть поле создаётся двумя
бесконечными плоскостями, заряженными
разноименно, но с одинаковой по величине
поверхностной плотностью заряда (рис.
2.9.). Это важная идеализация электростатики
— плоский конденсатор. Каждая
обкладка этого конденсатора создаёт
однородное поле, напряжённость которого
мы только что установили (2.16):

.

Рис. 2.9.

Силовые линии поля положительно
заряженной плоскости направлены от
неё, а отрицательной — к плоскости. При
сложении этих полей, напряжённость
результирующего поля вне конденсатора
оказывается равной нулю, а внутри
конденсатора, где эти поля совпадают
по направлению, — поле удваивается:

. (2.17)

Соседние файлы в предмете Физика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Теорема Гаусса выражает связь между потоком вектора напряженности электрического поля через замкнутую поверхность и алгебраической суммой зарядов, заключенных в объеме, ограниченном этой поверхностью. О примерах использования теоремы Гаусса на практике поговорим в этой статье.

Присоединяйтесь к нам в телеграме, чтобы не только решать задачи, но и быть в курсе актуальных новостей для студентов всех специальностей.

Задачи на теорему Гаусса с решением

Если вам нужно сначала освежить теоретические знания, читайте подробную теорию по теореме Гаусса в нашем справочнике. Ну а перед решением задач не забудьте повторить памятку и на всякий случай держите под рукой полезные формулы.

Кстати, при решении задач на теорему Гаусса придется довольно часто брать интегралы. Хотите научиться делать это по-быстрому? У нас уже есть отдельная статья и видео на эту тему.

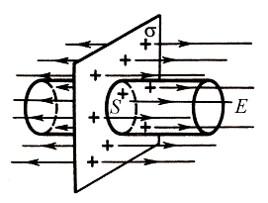
Задача на теорему Гаусса №1: напряженность поля плоскости

Условие

Определите напряженность поля бесконечной заряженной плоскости. Поверхностная плотность заряда сигма.

Решение

Линии напряженности перпендикулярны рассматриваемой плоскости и направлены в обе стороны от неё. Выберем в качестве гауссовой поверхности цилиндр с основанием, параллельным плоскости:

По теореме Гаусса:

Поток сквозь цилиндр равен сумме потоков сквозь боковую поверхность цилиндра и потокам сквозь оба его основания. Поток сквозь боковую поверхность равен нулю, так как линии напряженности параллельны ей:

Согласно теореме Гаусса:

Отсюда:

Ответ: см. выше.

Задача на теорему Гаусса №2: напряженность поля двух пластин

Условие

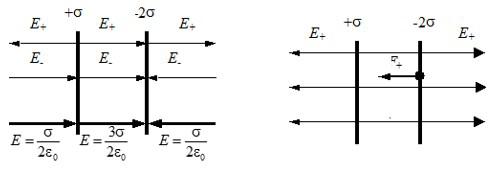
Электрическое поле создано двумя параллельными заряженными тонкими пластинами с поверхностными плотностями заряда + сигма  и -2 сигма. Площадь каждой пластины S, расстояние между пластинами d можно считать значительно меньшим их продольных размеров. Какова напряженность электрического поля, созданного этими пластинами?

Решение

Для электрического поля действует принцип суперпозиции: результирующее поле равно векторной сумме отдельных полей каждой пластины. Из предыдущей задачи мы знаем формулу, по которой вычисляется напряженность поля тонкой заряженной пластины, запишем для каждой из них:

Векторы напряженности между пластинами совпадают по направлению, результирующая напряженность равна:

Справа и слева от пластин, во внешней области, векторы направлены в разные стороны:

Для наглядности приведем рисунок:

Ответ: см. выше.

Задача на теорему Гаусса №3: напряженность электрического поля бесконечной нити

Условие

Определить напряженность электрического поля, создаваемую бесконечной тонкой нитью, равномерно заряженной с линейной плотностью заряда лямбда.

Решение

Напряженность будем искать при помощи теоремы Гаусса. Наша задача – определить зависимость напряженности от расстояния от нити. В качестве поверхности выберем цилиндр с боковыми стенками, параллельными нити. Будем учитывать только поток вектора напряженности через боковую поверхность, так как поток через основания цилиндра равен нулю:

Заряд нити внутри рассматриваемой поверхности равен заряду отрезка нити длиной l:

По теореме Гаусса:

Отсюда:

Ответ: см. выше.

Задача с применением теоремы Гаусса №4

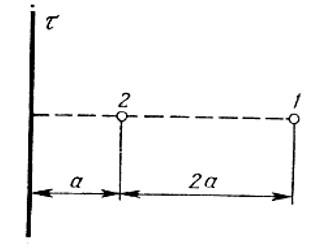
Условие

Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределённым зарядом (τ = 10 нКл/м). Определить кинетическую энергию Т2 электрона в точке 2, если в точке 1 его кинетическая энергия Т1 = 200 эВ. Расстояние точки 2 от линии равно а = 0,5 см, точки 1 – b=1,5 см.

Решение

Ранее рассмотренные задачи были примерами вычисления полей с помощью теоремы Гаусса. Теперь рассмотрим задачу, которая решается сиспользованием этой информации. Из предыдущей задачи возьмем выражение для напряженности поля заряженной нити:

Разность потенциалов поля в двух точках будет равна:

При прохождении этой разницы потенциалов электрон приобретёт кинетическую энергию:

Конечная энергия частицы будет равна:

Получим:

Ответ: 397.6 эВ.

Задача на теорему Гаусса №5: поток электрического поля

Условие

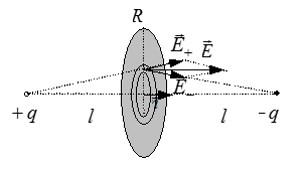
Два точечных заряда q и –q расположены на расстоянии 2l друг от друга. Найти поток вектора напряженности через круг радиуса R. Плоскость круга проходит через его середину и перпендикулярна отрезку прямой, соединяющей заряды.

Решение

Рассмотрим элементарный поток результирующего электрического поля через бесконечно малую кольцевую зону круга: 

В записи потока учтено, что вектор напряженности перпендикулярен поверхности круга. Выразим напряженность электрического поля через «ро», используя подобие треугольников, показанных на рисунке:

Вычисление потока сводится к взятию интеграла:

Ответ: см. выше.

Примеры применения теоремы Гаусса можно найти не только в электростатике, но и в других областях физики.

Вопросы на теорему Гаусса

Вопрос 1. Сформулируйте теорему Гаусса.

Ответ. Теорема Гаусса гласит:

Поток вектора напряженности электростатического поля через замкнутую поверхность равен алгебраической сумме зарядов внутри поверхности, деленной на эпсилон нулевое (электрическую постоянную).

Вопрос 2. Что такое поток вектора напряженности?

Ответ. Поток вектора напряженности – скалярная физическая величина, определяемая как число линий вектора напряженности, пронизывающих некоторую поверхность S. Поток напряженности электрического поля через поверхность S конечного размера определяется как алгебраическая сумма элементарных потоков:

Вопрос 3. Что такое силовые линии напряженности?

Ответ. Это линии, с помощью которых используются для графического представления поля:

• касательная к силовой линии в каждой точке пространства направлена вдоль вектора поля;
• густота силовых линий пропорциональна напряженности поля в данной точке;
• поток вектора напряженности пропорционален числу силовых линий, пронизывающих поверхность.

Вопрос 4. Где начинаются и где заканчиваются силовые линии?

Ответ. Силовые линии начинаются и заканчиваются на зарядах, оставаясь непрерывными в пустом пространстве.

Вопрос 5. Верно ли утвержление: теорема Гаусса справедлива только для неподвижных зарядов.

Ответ. Нет, так как заряд частицы не зависит от ее скорости.

Нужна помощь в решении задач и других студенческих заданий? Обратитесь в профессиональный студенческий сервис за качественным решением проблем.

Теорема Остроградского—Гаусса и ее применение для расчета электростатических полей

Пусть поле создается точечным электрическим зарядом q. Проведем замкнутую сферическую поверхность площадью S (рис. 2), окружающую этот заряд, центр которой совпадает с точкой нахождения заряда. Вычислим поток вектора напряженности через эту поверхность. За положительное направление нормали выберем направление внешней нормали (~vec n). В этом случае во всех точках сферической поверхности E = const и cos α = 1.

Модуль напряженности поля на расстоянии R от заряда (~E = frac{q}{4 pi varepsilon_0 varepsilon R^2}). Площадь поверхности сферы (~S = 4 pi R^2).

Следовательно, поток вектора напряженности через сферическую поверхность

(~N_S = frac{q 4 pi R^2}{4 pi varepsilon_0 varepsilon R^2} = frac{q}{varepsilon_0 varepsilon} .)

Полученный результат будет справедлив и для поверхности произвольной формы, а также при любом расположении заряда внутри этой поверхности. Действительно, если окружить сферу произвольной замкнутой поверхностью (рис. 2, а — поверхность изображена штрихами), то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

Если замкнутая поверхность произвольной формы охватывает заряд (рис. 2, б), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в поверхность, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линии, входящей в поверхность. Если же внутри поверхности площадью S₁ (см. рис. 2) заряды отсутствуют, то поток напряженности через эту поверхность равен нулю (N_S = 0).

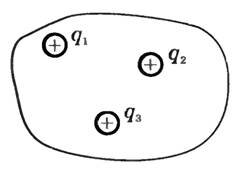
Если рассматриваемая поверхность охватывает не один, а несколько электрических зарядов, то под q следует понимать алгебраическую сумму этих зарядов (рис. 3) и

(~N_S = frac{q_1 + q_2 + q_3}{varepsilon_0 varepsilon} .)

Эта формула выражает теорему Остроградского—Гаусса: поток вектора напряженности через замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на произведение электрической постоянной и диэлектрической проницаемости среды.

Применим эту теорему для расчета электростатических полей некоторых проводников.

Равномерно заряженная бесконечная плоскость

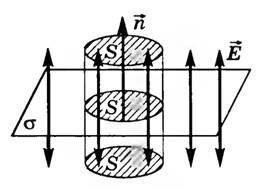
Пусть σ — поверхностная плотность заряда на плоскости (рис. 4).

В качестве поверхности площадью S выберем цилиндрическую поверхность, образующая которой перпендикулярна плоскости. Основания этого цилиндра расположены перпендикулярно линиям напряженности по обе стороны от плоскости. Так как образующие цилиндра параллельны линиям напряженности (α = 90°, cos α = 0), то поток через боковую поверхность цилиндра отсутствует, и полный поток через поверхность цилиндра равен сумме потоков через два основания: N = 2ES. Внутри цилиндра заключен заряд q = σS, поэтому, согласно теореме Остроградского-Гаусса, (~2ES = frac{sigma S}{varepsilon_0 varepsilon}), где ε = 1 (для вакуума), откуда следует, что напряженность поля равномерно заряженной бесконечной плоскости

(~E = frac{sigma}{2 varepsilon_0 varepsilon} .)

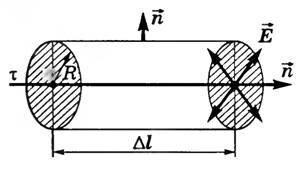
Бесконечная равномерно заряженная нить

Пусть τ — линейная плотность заряда нити. Выделим участок нити длиной Δl и окружим его цилиндрической поверхностью, расположенной так, что ось цилиндра совпадает с нитью (рис. 5).

Линии напряженности электростатического поля, создаваемого нитью в сечении, перпендикулярном самой нити, направлены перпендикулярно боковой поверхности цилиндра, поэтому поток напряженности сквозь боковую поверхность (~N = E cdot 2 pi R Delta l), где R — радиус цилиндра. Через оба основания цилиндра поток напряженности равен нулю (α = 90°, cos α = 0). Тогда полный поток напряженности через выделенный цилиндр

(~N = E cdot 2 pi R Delta l .)

Заряд, находящийся внутри этого цилиндра, q = τ · Δl.

Согласно теореме Остроградского—Гаусса, можно записать (~E cdot 2 pi R Delta l = frac{tau Delta l}{varepsilon_0 varepsilon}) . Следовательно, модуль напряженности поля, создаваемого равномерно заряженной бесконечно длинной нитью на расстоянии R от нее,

(~E = frac{tau}{2 pi varepsilon_0 varepsilon R} .)

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 220-222.