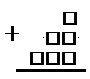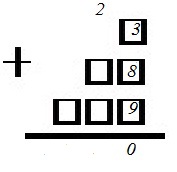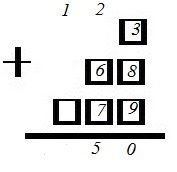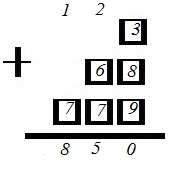Как найти натуральное число егэ - Сайт, где вы сможете решить свои вопросы

Свойства чисел

Задание №19 ЕГЭ по математике весьма необычно. Для его решения необходимо применить знания в области теории чисел. Тем не менее, задание является весьма решаемым, однако для школьников с оценкой хорошо и ниже я рекомендовал бы оставить это задание на последнюю очередь. Перейдем к рассмотрению типового варианта.

Разбор типовых вариантов заданий №19 ЕГЭ по математике базового уровня

Вариант 19МБ1

[su_note note_color=”#defae6″]

Найдите трехзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь оно такое число.

[/su_note]

Алгоритм выполнения:

Ввести условные обозначения.
Записать условия с помощью условных обозначений.
Преобразовать полученные выражения.
Логически рассуждая перебрать все возможные варианты, проверить их соответствие условиям.

Решение:

Обозначим первую цифру числа x, а вторую – y. Тогда третье число с учетом суммы цифр равной 20 будет равно 20 – (x + y). (x + y) обязательно меньше 10, иначе сумма равная 20 не получится.

По условию сумма квадратов цифр делится на 3, но не делится на 9. Запишем сумму квадратов цифр:

x ² + y² + (20 – (x + y))²

Преобразуем полученное выражение. Преобразуем квадрат разности с учетом формулы приведения.

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(20 – (x + y))² = 400 -40(x + y) + (x + y)²

Подставим получившееся выражение в начальное, получим:

x ² + y² + (20 – (x + y))² = x ² + y² + 400 – 40(x + y) + (x + y)²

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + y)²= x² + 2xy + y²

Подставим:

x ² + y² + (20 – (x + y))² = x ² + y² + 400 – 40(x + y) + (x + y)²= x ² + y² + 400 – 40(x + y) + x²+ 2xy + y²

Приведем подобные слагаемые(сложим x²с x² и y^{2 с}y²), получим:

x ² + y² + 400 – 40(x + y) + x²+ 2xy + y²= 2x ² + 2y² + 2 · 200 – 2 · 20(x + y) + 2xy

Вынесем множитель 2 за скобку:

2x ² + 2y² + 2 · 200 – 2 · 20(x + y) + 2xy = 2(x ² + y² + 200 – 20(x + y) + xy)

Для удобства объединим 200 и 20(x + y) и вынесем 20 за скобку, получим:

2(x ² + y² + 20(10 – (x + y)) + xy)

Множитель 2 – четный, поэтому он никак не влияет на делимость на 3 или 9. Можем его не брать в расчет и рассматривать выражение:

x ² + y² + 20(10 – (x + y)) + xy

Предположим, что и x, и y делятся на 3. Тогда x ² + y² + xy делится на 3, а 20(10 – (x + y)) – не делится. Следовательно, и вся сумма x ² + y² + 20(10 – (x + y)) + xy на 3 не делится.

Предположим, что на 3 делится только одна цифра. Тогда, учитывая, что (x + y) обязательно меньше 10, иначе сумма равная 20 не получится, подберем возможные пары.

(3;8), (6;5), (6;7), (6;8), (9;2), (9;4), (9;5), (9;7), (9;8).

Методом подстановки проверим, соответствуют эти пары условию.

x ² + y² + 20(10 – (x + y)) + xy = 3 ² + 8² + 20(10 – (3 + 8)) + 3 · 8 = 9 + 64 – 20 + 24 = 77

x ² + y² + 20(10 – (x + y)) + xy = 6 ² + 5² + 20(10 – (6 + 5)) + 6 · 5 = 36 + 25 – 20 + 30 = 71

x ² + y² + 20(10 – (x + y)) + xy = 6 ² + 7² + 20(10 – (6 + 7)) + 6 · 7 = 36 + 49 – 60 + 42 = 67

x ² + y² + 20(10 – (x + y)) + xy = 6 ² + 8² + 20(10 – (6 + 8)) + 6 · 8 = 36 + 64 – 80 + 48 = 68

x ² + y² + 20(10 – (x + y)) + xy = 9 ² + 2² + 20(10 – (9 + 2)) + 9 · 2 = 81 + 4 – 20 + 18 = 83

x ² + y² + 20(10 – (x + y)) + xy = 9 ² + 4² + 20(10 – (9 + 4)) + 9 · 4 = 81 + 16 – 60 + 36 = 73

Ни одна из полученных сумм не удовлетворяет условию «сумма квадратов цифр делится на 3, но не делится на 9».

Следующие пары можно не проверять, так как они дают уже имеющиеся тройки цифр.

Предположим, что ни одна из цифр числа не делится на 3.

Возможные пары:

(4;7), (5;7), (5;8), (7;8).

Проверим:

x ² + y² + 20(10 – (x + y)) + xy = 4 ² + 7² + 20(10 – (4 + 7)) + 4 · 7 = 16 + 49 – 20 + 28 = 73

x ² + y² + 20(10 – (x + y)) + xy = 5 ² + 7² + 20(10 – (5 + 7)) + 5 · 7 = 25 + 49 – 40 + 35 = 69

Сумма 69 удовлетворяет условию «сумма квадратов цифр делится на 3, но не делится на 9». Следовательно, подходят цифры 5,7,8 в любом порядке.

Ответ: 578

Вариант 19МБ2

[su_note note_color=”#defae6″]

На 6 карточках написаны цифры 1; 2; 3; 6; 9; 9 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 10. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения:

Вспомнить признак делимости на 10.
Разместить последние цифры каждого слагаемого таким образом, чтобы в сумме получилось 10.
Расположить оставшиеся карточки в произвольном порядке.

Решение:

1. Если сумма делится на 10 нацело, то последняя цифра должна быть 0, остальные цифры значения не имеют.

2. В первый квадрат поместим цифру 1, в следующем числе на последнем месте – цифру 3 (или 6), а в третьем – цифру 6 (или 3), получим (сумма 1+3+6=10):

3. Остальные цифры заполним произвольно, например, так:

и получится сумма

1+23+996 = 1020.

Ответ: 1020

Вариант 19МБ3

[su_note note_color=”#defae6″]

На 6 карточках написаны цифры 1; 2; 2; 3; 5; 7 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 20. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения:

Вспомнить признак делимости на 10 и сформулировать признак делимости на 20.
Разместить последние цифры каждого слагаемого таким образом, чтобы в сумме получилось 10.
Разместить предпоследние цифры каждого слагаемого таким образом, чтобы в сумме получилось четное число в результате с учетом суммы первых цифр.
Расположить оставшиеся карточки в произвольном порядке.

Решение:

1. Чтобы сумма делилась на 20, она должна заканчиваться на 0 и вторая цифра с конца должна быть четной (делиться на 2). Чтобы в конце суммы получить 0, первые три карточки следует выбрать так:

2. Чтобы вторую цифру получить четной, можно взять карточки 2 и 7 (к ней будет добавляться еще 1 от первой суммы 10):

3. В последнее место помещаем оставшуюся цифру 1, в результате имеем:

и сумма равна:

2+23+175=200.

Ответ: 200

Вариант 19МБ4

[su_note note_color=”#defae6″]

Найдите четырехзначное число, кратное 15, произведение цифр которого больше 0, но меньше 25. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

Если произведение >0, то, значит, оно не равно нулю. Следовательно, ни один из множителей не может быть равным 0.
Если произведение кратно 15, следовательно, оно кратно 5 и кратно 3.
Если произведение кратно 5, то результат его должен оканчиваться 0 или 5. В данном случае берем 5, т.к. 0 не может быть одним из множителей (см.п.1).
Итак, последняя цифра числа равна 5. Тогда произведение первых трех равно 25:5=5. Это означает, что нужно подобать 3 цифры так, чтобы их произведение было менее 5.
Из всех полученных наборов цифр выбираем такой, чтобы сумма этих цифр плюс 5 (последняя, 4-я цифра) была кратной 3.

Решение:

Поскольку по условию произведение всех цифр кратно 15, то оно кратно 5 и 3.

Кратность 5 означает, что последней цифрой числа может быть только 0 или 5. Но 0 в виде последней цифры означал бы, что произведение всех 4-х цифр стало бы равным 0; а это противоречит условию. Тогда последняя цифра искомого числа равна 5.

Тогда получим: x·y·z·5<25 → x·y·z<5, где x, y, z – соответственно, 1-я, 2-я и 3-я цифры искомого числа.

Меньше 5 произведение таких цифр: 1 1 1, 1 1 3, 1 1 2, 1 2 2.

Согласно признаку делимости на 3, выбираем из этих наборов такой, чтобы сумма его цифр плюс 5 делилась на 3:

1+1+1+5=8 – не подходит;

1+1+3+5=10 – не подходит;

1+2+2+5=10 – не подходит

1+1+2+5=9 – подходит.

Тогда условию задачи соответствуют числа: 1125, 1215, 2115.

Ответ: 1125, 1215, 2115

Вариант 19МБ5

[su_note note_color=”#defae6″]

Вычеркните в числе 85417627 три цифры так, чтобы получившееся число делилось на 18. В ответе укажите какое-нибудь одно получившееся число.

[/su_note]

Алгоритм выполнения

Число делится на 18, если оно кратно 2 и 9.
Кратность 2 означает, что число должно быть четным. Поэтому сразу отбрасывают последнюю – нечетную – цифру 7.
Кратность 9 означает, что сумма его цифр делится на 9. Значит, находим сумму оставшихся цифр. Далее определяем подходящее для полученной суммы число, кратное 9. Число должно быть таким, чтобы: а) оно было меньшим суммы цифр; б) разница между этой суммой и найденным числом позволяла выделить в числе 2 цифры, сумма которых была бы равной этой разнице. Вычеркиваем эти цифры.

Решение:

Т.к. по условию число кратно 18, то оно кратно 2 и кратно 9.

Поскольку число кратно 2, то оно должно оканчиваться четной цифрой. 7 – нечетная цифра, поэтому вычеркиваем ее. Осталось: 8541762.

Т.к. полученное число кратно 9, то сумма его цифр должна делиться на 9. Находим общую сумму его цифр: 8+5+4+1+7+6+2=33. Ближайшее число, которое делится на 9, – это 27.

33–27=6 – это сумма двух цифр, которые нужно вычеркнуть. Пары цифр, которые при этом в сумме дают 6, – это 5 и 1 или 4 и 2. Вычеркнув их, получаем соответственно: 84762 или 85176.

Кроме этого, на 9 делится 18. Тогда 33–18=15. В этом случае вычеркнуть придется 8 и 7. Получаем: 54162.

На 9 делится еще и 9, однако 33–9=24, а пары цифр, которые дали бы в сумме 24, естественно, не существует.

Ответ: 84762, 85176, 54162

Вариант 19МБ6

[su_note note_color=”#defae6″]

На шести карточках написаны цифры 3; 6; 7; 7; 8; 9 (по одной цифре на каждой карточке). В выражении

Вместо каждого квадратика положили карточку из данного набора. Оказалось, что полученная сумма делится на 10, но не делится на 20.

В ответе укажите какую-нибудь одну такую сумму.

[/su_note]

Алгоритм выполнения

Во 2-м предложении текста задачи фактически представлено условие, при котором сумма делится на 10, однако не делится на 2.
Из п.1 следует, что результирующее число должно оканчиваться 0, а предпоследняя его цифра должна быть нечетной.

Решение:

Для удобства восприятия разместим карточки в столбик:

Если число делится на 10, но не делится на 20, значит, оно точно не делится на 2 без последнего нуля.

Поскольку число кратно 10, то оно должно оканчиваться нулем. Поэтому в последнем разряде (единиц) нужно расположить 3 карточки с такими цифрами, чтоб их сумма оканчивалась на 0. Подходят здесь карточки: 1) 6, 7, 7; 2) 3, 8, 9. Их суммы равны 20. Соответственно, 0 мы пишем под чертой, а 2 переносим на предыдущий разряд (десятков):

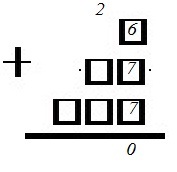
Чтобы число не делилось на 20, необходимо, чтобы перед нулем стояла нечетная цифра. Нечетная сумма здесь получится тогда, когда одно из слагаемых будет нечетным, а два других четными. Одно из этих (других) слагаемых – это перенесенная 2. Поэтому из оставшихся цифр следует взять: 1) 3 и 8; 2) 6 и 7. Получаем:

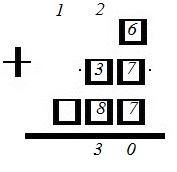
На место сотен ставим последнюю (оставшуюся) карточку с цифрой: 1) 9; 2) 7. Получаем, соответственно, числа 1030 и 850:

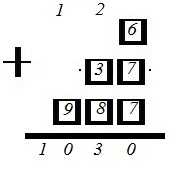
Ответ: 1030,850

Вариант 19МБ7

[su_note note_color=”#defae6″]

Найдите четное трехзначное натуральное число, сумма цифр которого на 1 меньше их произведения. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

Вводим буквенные обозначения для цифр искомого числа. Исходя из условия задачи, составляем уравнение.
Выражаем одну из цифр через 2 другие.
Подбираем для этих 2-х (других) цифр значения так, чтобы 3-я (выраженная) представляло бы собой натуральное число. Вычисляем 3-ю цифру.
Формируем искомое число так, чтобы оно было четным.

Решение:

Пусть цифры искомого числа – x, y, z. Тогда получаем:

xyz–(x+y+z)=1

xyz–x–y–z=1

zxy–z=x+y+1

z(xy–1)=x+y+1

z=(x+y+1)/(xy–1)

Знаменатель в этом выражении должен быть целым и положительным. Для простоты (а также для гарантии правильных расчетов) примем, что он должен быть равен 1. Тогда имеем: ху–1=1 → ху=2. Поскольку х и у это цифры, то их значения могут быть равными только 1 и 2 (т.к. только произведение этих однозначных натур.чисел дает в результате 2).

Отсюда z составляет: z=(1+2+1)/(1·2–1)=4/1=4.

Итак, имеем цифры: 1, 2, 4.

Т.к. по условию итоговое число должно быть четным, то оканчиваться оно может только 2 или 4. Тогда правильными вариантами чисел будут такие:

124, 142, 214, 412.

Ответ: 124, 142, 214, 412

Вариант 19МБ8

[su_note note_color=”#defae6″]

Найдите шестизначное число, которое записывается только цифрами 2 и 0 и делится на 24. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

Если число делится на 24, значит, оно делится на 8 и на 3.
Согласно признаку делимости на 8, 3 последних цифры его должны образовывать число, которое кратно 8.
Чтобы число делилось на 3, необходимо, чтобы сумма его цифр делилась на 3. Учитывая уже сформированную 2-ю часть числа (см.п.2), дополняем его первыми тремя цифрами соответственно.

Решение:

Чтобы искомое число было кратно 24, требуется, чтобы оно делилось на 8 и в то же время на 3.

Число делится на 8, если последние его 3 цифры образуют число, кратное 8. С использованием только двоек и нулей такое трехзначное число можно образовать так: 000, 002, 020, 022, 200, 202, 220, 222. Из этих чисел на 8 делится только 000 и 200.

Теперь нужно дополнить искомое число первыми 3-мя цифрами так, чтобы оно делилось еще и на 3.

В 1-м случае это будет единственный вариант: 222000.

Во 2-м случае вариантов два: 220200, 202200.

Ответ: 222000, 220200, 202200

Вариант 19МБ9

[su_note note_color=”#defae6″]

Найдите четырехзначное число, кратное 15, произведение цифр которого больше 35, но меньше 45. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

Если число кратно 15, значит, оно кратно 3 и 5.
Применяем признак делимости на 5 и условие задачи, согласно которому произведение цифр числа ≠0. Так получаем, что последняя цифра искомого числа – только 5.
Делим 35 на 5 и 45 на 5. Узнаем диапазон значений, которые может принимать произведение первых 3-х цифр числа. Узнаем, что оно может быть равно только 8.
Определяем последовательности цифр, которые дают при перемножении 8.
Проверяем полученные из найденных цифр числа на кратность трем.

Решение:

Кратность искомого числа 15 дает 2 условия: оно должно делиться на 5 и на 3.

Если число кратно 5, то оно должно оканчиваться цифрой 5 или 0. Однако 0 в данном случае использовать нельзя, поскольку при этом произведение цифр числа оказывается равным 0. По условию же это не так. Итак, последняя – 4-я – цифра числа равна 5.

По условию 35 < x·5 < 45, где х – произведение первых 3-х цифр числа. Тогда имеем: 7 < x < 9. Это неравенство верно только при х=8. Следовательно, для первых 3-х цифр должны выполняться равенства:

1·1·8=8, 1·2·4=8.

Отсюда получаем числа:

1185; 1245.

Проверяем их на кратность 3:

1+1+8+5=15;

1+2+4+5=12.

Вывод: оба найденные числа кратны 3. Плюс кратны их комбинации:

1815; 8115; 1425; 2145; 2415; 4125; 4215.

Ответ: 1815; 8115; 1425; 2145; 2415; 4125; 4215

Вариант 19МБ10

[su_note note_color=”#defae6″]

Найдите пятизначные число, кратное 25, любые две соседние цифры которого отличаются на 2. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

Принимаем во внимание, что на 25 делятся числа, которые придется последовательно делить на 5 дважды. Определяем, какой парой цифр они должны оканчиваться.
Учитывая, что 2-й частью условия является различие каждой соседней пары цифр исключительно на 2 единицы, выбираем подходящий вариант (или варианты) цифр.
Способом подбора находим остальные цифры и, соответственно, числа. Одно из них запишем в ответе.

Решение:

Если число делится на 25, то оно должно оканчиваться на: 00, 25, 50, 75. Т.к. соседние цифры должны отличаться строго на 2, то использовать для 4-й и 5-й цифр можем только 75. Получаем: ***75.

Далее ищем 3-ю цифру:

**975 или
**575.

Дальше получаем по аналогии:

1) *7975 → 97975 или 57975;

2) *3575 → 13575 или 53575, *7575 → 57575 или 97575.

Ответ: 97975, 57975, 13575, 53575, 57575, 97575

Вариант 19МБ11

[su_note note_color=”#defae6″]

Найдите трехзначное натуральное число, большее 600, которое при делении на 3, на 4 и на 5 дает в остатке 1 и цифры которого расположены в порядке убывания слева направо. В ответе укажите какое-нибудь такое число.

[/su_note]

Алгоритм выполнения

Определяем диапазон значений для 1-й цифры числа (сотен).
Определяем, какой может быть последняя цифра (единицы), приняв во внимание: 1) при делении на 5 дает в остатке 1; 2) на этом месте не может быть четная цифра, поскольку это одно из условий делимости на 4.
Способом подбора определяем набор чисел, которые при делении на 3 дают в остатке 1.
Из этого набора (см.п.3) отбрасываем числа, которые при делении на 4 дают остаток, отличный от 1.

Решение:

Т.к. искомое число >600 и при этом является трехзначным, то 1-й цифрой может быть только 6, 7, 8 или 9. Тогда получаем для искомого числа:

6***

7***

8***

9***

Если число при делении на 5 должно давать в остатке 1, значит, оно может оканчиваться только на 0+1=1 или на 5+1=6. Шестерку тут отбрасываем, поскольку в этом случае число четное и потенциально может делиться на 4. Поэтому имеем:

6**1

7**1

8**1

9**1

Если число при делении на 3 дает в остатке 1, значит, сумма его цифр должна быть кратной 3 плюс 1. Кроме того, учитываем, что цифры должны располагаться в числе в порядке убывания. Подбираем такие числа:

631

721

751

841

871

931

961

Из этой последовательности отбрасываем числа, для которых не выполняется условие о том, что число при делении на 4 должно давать в остатке 1.

Т.к. признак делимости на 4 заключается в том, что 2 последние цифры должны делиться на 4, то получаем:

для 631: 31=28+3, т.е. в остатке имеем 3; число не подходит

для 721: 21=20+1, т.е. в остатке – 1; число подходит

для 751: 51=48+3, т.е. в остатке – 3; число не подходит

для 841: 41=40+1, т.е. в остатке – 1; число подходит

для 871: 71=68+3, т.е. в остатке – 3; число не подходит

для 931: 31=28+3, т.е. в остатке – 3; число не подходит

для 961: 61=60+1, т.е. в остатке – 1; число подходит

Ответ: 721, 841, 961

Вариант 19МБ12

[su_note note_color=”#defae6″]

Найдите трехзначное натуральное число, большее 400, но меньшее 650, которое делится на каждую свою цифру и все цифры которого различны и не равны 0. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

Из условия следует, что числа могут начинаться только на 4,5 или 6.
При анализе чисел 4-й сотни отбрасываем числа: 1) 1-го десятка, т.к. в них содержится 0; 2) 4-го десятка, т.к. в этом случае первые две цифры совпадут; 3) числа 5-го десятка, т.к. они должны оканчиваться только на 5 или 0, что недопустимо. Кроме того, для всех четных десятков можно рассматривать только четные числа.
Числа 5-й сотни отбрасываем полностью, т.к. чтобы делиться на каждую свою цифру, они должны оканчиваться 5 или 0.
Для чисел 6-й сотни рассматривать можно только: 1) четные; 2) кратные 3; 3) не оканчивающиеся 0.

Решение:

Числа 40* и 4*0 отбрасываем, т.к. они содержат 0.

Числа 41* годятся только четные, т.к. это обязательное условия для кратности 4. Анализируем:

412 – подходит

414 – не подходит, т.к. в нем совпадают цифры

416 – не подходит, т.к. не делится на 6

418 – не подходит, т.к. не делится ни на 4, ни на 8

Из чисел 42* годятся только четные, поскольку должны делиться на 2:

422 и 424 – не подходят, т.к. в них совпадают цифры

426 – не подходит, т.к. не делится на 4

428 – не подходит, т.к. не делится на 8

Числа 43* годятся только четные и кратные 3. Поэтому тут подходит только 432.

Числа 44* не подходят полностью.

Числа 45* не подходят полностью, т.к. они должны оканчиваться только 5 (т.е. быть нечетными) или 0.

Числа 46*, 47*, 48*, 49* не подходят полностью, т.к. для каждого из них не выполняется 1 или несколько условий.

Числа 5-й сотни не годятся полностью. Они должны делиться на 5, а для этого оканчиваться либо 5, либо 0, что не допускается.

Числа 60* не годятся полностью.

Среди остальных можно рассматривать только четные, кратные 3, не оканчивающиеся 0. Опуская подробности перебора чисел, оговорим только, что из них годятся: 612, 624, 648. Для остальных не выполняется одно или несколько условий.

Ответ: 412, 432, 612, 624, 648

Вариант 19МБ13

[su_note note_color=”#defae6″]

Найдите четырехзначное число, кратное 45, все цифры которого различны и четны. В ответе укажите какое-нибудь одно такое число.

[/su_note]

Алгоритм выполнения

Если число кратно 45, значит, оно делится на 5 и на 9.
Рассматривать следует только числа четных сотен.
Оканчиваться числа могут только 0, т.к. 5 – нечетная цифра.
Сумма цифр числа должна быть равна 18. Только в этом случае можно составить его из всех четных цифр.

Решение:

Т.к. по условию цифры должны быть четными, то рассматривать можно только числа 2-й, 4-й, 6-й и 8-й тысяч. Это значит, что начинаться оно может с 2, 4, 6 или 8.

Если число кратно 45, то оно кратно 5 и кратно 9.

Если число кратно 5, то оно должно оканчиваться 5 или 0. Но поскольку все цифры должны быть четными, то подходит здесь только 0.

Т.о., получаем шаблоны чисел: 2**0, 4**0, 6**0, 8**0. Отсюда следует, что для проверки кратности 9 требуется, чтобы сумма первых 3-х цифр была равной 9, или 18, или 27 и т.д. Но подходит тут только 18. Основания: 1) для получения в сумме 9 нужно, чтобы одно из слагаемых было нечетным, а это противоречит условию; 2) 27 не подходит потому, что даже если взять самую большую 1-ю цифру 8, то сумма 2-й и 3-й цифр будет равна 27–8=19, что превышает допустимый предел. Еще большие суммы цифр, кратные 9, не подходят тем более.

Рассматриваем числа по тысячам.

Числа 2**0. Сумма средних цифр равна: 18–2=16. Получить 16 из четных чисел можно только так: 8+8. Однако цифры не должны повторяться. Поэтому подходящих условию чисел здесь нет.

Числа 4**0. Сумма средних цифр: 18–4=14. 14=8+6. Поэтому получаем: 4680 или 4860.

Числа 6**0. Сумма средних цифр: 18–6=12. 12=6+6, что не подходит, т.к. цифры повторяются. 12=4+8. Получаем: 6480 или 6840.

Числа 8**0. Сумма средних цифр: 18–8=10. 10=2+8, что не подходит, т.к. при этом будет повторяться 8. 10=4+6. Получаем: 8460 или 8640.

Ответ: 4680, 4860, 6480, 6840, 8460, 8640

Даниил Романович | Просмотров: 12.3k

Источник

было в ЕГЭ

в условии
в решении
в тексте к заданию
в атрибутах

Категория

Атрибут

Всего: 107 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Бесконечная десятичная дробь устроена следующим образом. Перед десятичной запятой стоит нуль. После запятой подряд выписаны все целые неотрицательные степени некоторого однозначного натурального числа В результате получается рациональное число. Найдите это число.

Сумма двух натуральных чисел равна 43, а их наименьшее общее кратное в 120 раз больше их наибольшего общего делителя. Найдите эти числа.

Длины сторон прямоугольника ― натуральные числа, а его периметр равен 4000. Известно, что длина одной стороны прямоугольника равна n% от длины другой стороны, где n ― также натуральное число.

а)  Какое наибольшее значение может принимать площадь прямоугольника?

б)  Какое наименьшее значение может принимать площадь прямоугольника?

в)  Найдите все возможные значения, которые может принимать площадь прямоугольника, если дополнительно известно, что n <100.

Длины сторон прямоугольника ― натуральные числа, а его периметр равен 200. Известно, что длина одной стороны прямоугольника равна n% от длины другой стороны, где n – также натуральное число.

а)  Какое наибольшее значение может принимать площадь прямоугольника?

б)  Какое наименьшее значение может принимать площадь прямоугольника?

в)  Найдите все возможные значения, которые может принимать площадь прямоугольника, если дополнительно известно, что n>100.

Даны n различных натуральных чисел, составляющих арифметическую прогрессию

а)  Может ли сумма всех данных чисел быть равной 14?

б)  Каково наибольшее значение n, если сумма всех данных чисел меньше 900?

в)  Найдите все возможные значения n, если сумма всех данных чисел равна 123.

Даны n различных натуральных чисел, составляющих арифметическую прогрессию

а)  Может ли сумма всех данных чисел быть равной 18?

б)  Каково наибольшее значение n, если сумма всех данных чисел меньше 800?

в)  Найдите все возможные значения n, если сумма всех данных чисел равна 111.

Семь экспертов оценивают кинофильм. Каждый из них выставляет оценку  — целое число баллов от 0 до 10 включительно. Известно, что все эксперты выставили различные оценки. По старой системе оценивания рейтинг кинофильма  — это среднее арифметическое всех оценок экспертов. По новой системе оценивания рейтинг кинофильма оценивают следующим образом: отбрасываются наименьшая и наибольшая оценки и подсчитывается среднее арифметическое оставшихся оценок.

а)  Может ли разность рейтингов, вычисленных по старой и новой системам оценивания равняться

б)  Может ли разность рейтингов, вычисленных по старой и новой системам оценивания равняться

в)  Найдите наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания.

Семь экспертов оценивают кинофильм. Каждый из них выставляет оценку  — целое число баллов от 0 до 12 включительно. Известно, что все эксперты выставили различные оценки. По старой системе оценивания рейтинг кинофильма  — это среднее арифметическое всех оценок экспертов. По новой системе оценивания рейтинг кинофильма оценивают следующим образом: отбрасываются наименьшая и наибольшая оценки и подсчитывается среднее арифметическое оставшихся оценок.

а)  Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться

б)  Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться

а)  Можно ли число 2014 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?

б)  Можно ли число 199 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр?

в)  Найдите наименьшее натуральное число, которое можно представить в виде суммы пяти различных натуральных чисел с одинаковой суммой цифр.

Дана бесконечная последовательность чисел в которой при каждом k член последовательности x_k является корнем уравнения

1.  Найдите наибольший порядковый номер k члена последовательности такой, что в десятичной записи числа x используется не более семи цифр.

2.  Укажите наименьшее натуральное число N, среди делителей которого содержится ровно 8 членов данной последовательности.

3.  Существует ли такое натуральное число n, что сумма n идущих подряд

членов этой последовательности равна некоторому члену этой последовательности.

4.  Существует ли набор из 2012 членов данной последовательности таких, что никакая сумма нескольких из этих чисел не является полным квадратом.

Даны натуральные числа a,b и такие, что Среднее арифметическое этих чисел делится на 13.

а)  Найдите наименьшую сумму такую, что она является квадратом натурального числа.

б)  Найдите наибольшее число c, если a=32, а сумма имеет наименьшее значение.

в)  Найдите наименьшее число b, если числа c, b и a в указанном порядке составляют арифметическую прогрессию с разностью n.

г)  Известно, что числа c, b и a в указанном порядке составляют возрастающую арифметическую прогрессию с разностью n. Найдите наименьшее n, при котором число c будет наименьшим, и все члены арифметической прогрессии будут являться квадратами натуральных чисел.

Дан набор натуральных чисел где Натуральное число A имеет вид где   — различные числа из набора p, k  — среднее арифметическое всех чисел p, а [k]  — целая часть числа k.

а)  Найти наименьшее возможное и наибольшее возможное число A, если

б)  Найдите наименьшее n, при котором число A больше 20.

в)   Найдите при каком минимальном n, выполняется равенство

На плоскости даны 8 отрезков. Длина каждого отрезка является натуральным числом, не превосходящим 20. Пусть n – число различных треугольников, которые можно составить из этих отрезков. Один и тот же отрезок может использоваться для разных треугольников, но не может использоваться дважды для одного треугольника.

а)  Может ли n = 60?

б)  Может ли n = 55?

в)  Найдите наименьшее возможное значение n, если среди данных отрезков нет трех равных.

Натуральные числа a,b,c образуют возрастающую арифметическую прогрессию, причём все они больше 500 и являются квадратами натуральных чисел. Найдите наименьшее возможное, при указанных условиях, значение

Про натуральное число N известно, что сумма его четырех наименьших натуральных делителей равна 12.

А)  Может ли сумма четырех наибольших натуральных делителей числа N равняться 195?

Б)  Может ли сумма четырех наибольших натуральных делителей числа N равняться 120?

В)  Найдите все возможные числа N, у которых сумма четырех наибольших натуральных делителей не превосходит 100.

А)  Найдите какое-либо натуральное число, у которого ровно 10 делителей (включая 1 и само число).

Б)  Найдите наименьшее натуральное число, у которого ровно 10 делителей.

В)  Найдите все трехзначные нечетные натуральные числа, у которых ровно 10 делителей.

Рассматриваются 10‐значные натуральные числа (все десять цифр в их записи различны). Среди таких чисел найдите:

а)  какое‐либо число, делящееся на 11;

б)  наибольшее число, делящееся на 11;

в)  наименьшее число, делящееся на 11.

(Натуральное число делится на 11, если знакочередующаяся сумма его цифр делится на 11. Например, число 61938085 делится на 11, так как 6 − 1 + 9 − 3 + 8 − 0 + 8 − 5  =  22.)

Рассматривается набор различных натуральных чисел, больших 1. Известно, что 1) каждое число набора является делителем 60, 2) произведение всех чисел набора равно

А)  Найдите наибольшее количество чисел в таком наборе.

Б)  Найдите наименьшее количество чисел в таком наборе.

В)  Сколько существует различных наборов, удовлетворяющих условиям (1) и (2)?

Имеется три пакета акций. Общее суммарное количество акций первых двух пакетов совпадает с общим количеством акций в третьем пакете. Первый пакет в 4 раза дешевле второго, а суммарная стоимость первого и второго пакетов совпадает со стоимостью третьего пакета. Одна акция из второго пакета дороже одной акции из первого пакета на величину, заключенную в пределах от 16 тыс. руб. до 20 тыс. руб., а цена акции из третьего пакета не меньше 42 тыс. руб. и не больше 60 тыс. руб. Определите, какой наименьший и наибольший процент от общего количества акций может содержаться в первом пакете.

Источники:

Варианты вступительных экзаменов в МГУ, экономический ф-т, 1997;

Всего: 107 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Цифры и числа – это не синонимы. Цифры – это символы, которыми записывают числа. Числа состоят из цифр, как слова состоят из букв. Пример: число (1806) состоит из цифр (1), (8), (0) и (6).
Однозначные числа – числа, состоящие из одной цифры, например (7). Двухзначные числа – состоящие из двух цифр, например (29). Трехзначные – из трёх, например (341). И так далее.
Простое число – число, имеющее только два делителя, – единицу и само себя (при этом число (1) простым не считается). Пример: (13) или (277).
Составное число – число, имеющее больше двух делителей. Например, (12) или (735).
Натуральное число – целое положительное число. Пример: (5), (34), (6908)…
(0) – не натуральное, (-7) – тоже.
Четное число – целое число делящиеся на (2). Нечетное число – целое число не делящиеся на (2). Пример: (12), (1000), (106) – четные; (3), (99), (9000001) – нечетные.
Если написано «попарно различные числа», это означает, что все числа в наборе разные. То есть, любые (2) числа не равны друг другу. (Для меня загадка, почему в задачах не пишут просто «все числа разные»).
Если цифры числа неизвестны, их можно записать буквами и провести сверху черточку. Пример: (overline{abc}) – число, состоящие из цифр (a), (b), (c).
Любое двухзначное число можно представить как: (overline{ab}=10a+b).
Трехзначное: (overline{abc}=100a+10b+c).
Четырехзначное: (overline{abcd}=1000a+100b+10c+d).
(n) – значное: (underbrace{overline{abcd…z}}_{n ;цифр} =10^{n-1}a+10^{n-2} b+…+z).
Признаки делимости
- На (2): последняя цифра числа делится на (2) (в том числе (0))
- На (3): сумма цифр числа делится на (3). Например, число (4635) делится на (3), т.к. (4+6+3+5=18) (а (18) делится на (3))
- На (4): две последние цифры либо нули, либо образуют число, делящееся на (4)
- На (5): последняя цифра (0) или (5)
- На (6): одновременно соблюдаются признаки делимости на (2) и (3)
- На (7): признаков делимости, увы, нет
- На (8): три последние цифры нули или образуют число, делящееся на (8)
- На (9): сумма цифр числа делится на (9)
- На (10): последняя цифра числа – ноль
- На (11): разность между суммой цифр, стоящих на нечетных местах, и суммой цифр, стоящих на четных местах, делится на (11).
  Например, число (281765) делится на (11), т.к. сумма цифр нечетных мест (2+1+6=9), сумма цифр на четных (8+7+5=20), т.е. разность между ними (11), а (11) делится на (11)
- На (25): две последнее цифры (00), (25), (50) или (75)
- На (100): две последнее цифры (00)
- На (125): три последнее цифры (000) или образуют число, делящееся на (125).

Делимость чисел:

Число (b) делится на число (a), если найдётся такое целое число (q), что (b=a cdot q).
Обозначается (b ,vdots , a). Например, (6) делится на (2), т.к. (6=2cdot 3).
Также в этом случае число (b) называют кратным числу (a).
Делитель – число, на которое делится другое число без остатка. Например: (a) – в предыдущем пункте делитель числа (b); (4) – делитель числа (8), (13) – делитель числа (39), (100) – делитель числа (10000).
Общим делителем чисел называют такое число, которое является делителем для каждого из них. Например, общим делителем чисел (12) и (30) будет число (4).
Два числа называются взаимно простыми, если их общим делителем является только (1). Например: (12) и (5); (25) и (14); (3) и (11).
Замечание: два любых простых числа автоматически являются взаимно простыми.
Если число делится на каждое из двух взаимно простых чисел, то оно делится и на их произведение.
Например, (5) и (3) – взаимно простые числа. Число (6825) делится и на (5) (последняя цифра числа пятерка), и на (3) (сумма цифр (6+8+2+5=21) – делится на (3)). Значит, (6825) делится на (15) (произведение (5) и (3)).
Если одно из двух чисел делится на некоторое число, то и их произведение делится на это число. Например, (9m, vdots , 3), так как (9) делится на (3) (здесь и далее (m), (k) и (n) – любые целые числа).
Если два числа делятся на некоторое число, то и их сумма, и их разность делятся на это число. Например, ((3k+9m), vdots , 3), так как (3k) – делится на (3) и (9m) – делится на (3). Еще пример: ((99-88+77), vdots , 11).
Если одно из чисел делится на некоторое число, а второе нет, то их сумма и их разность не делятся на это число. Например, если (k) целое, то: ((3k+17)) (3); ((930-174)) (10).
Если первое число делится на второе, а второе делится на третье, то и первое делится на третье. Или на языке математики – если (a, vdots , b) и (b, vdots , c), то (a, vdots , c).
Например, т.к. (1000, vdots , 100) и (100, vdots , 25), то и (1000, vdots , 25). Еще пример: если (63n, vdots , m) и (m) – четное, то (63n) – четное.
Если произведение нескольких чисел делится на некоторое простое число, то хотя бы одно из них делится на это простое число. Например, если (5k,⋮,3), то (k,⋮,3).

Основная теорема арифметики:

Каждое натуральное число, большее единицы, либо является простым, либо может быть разложено на простые множители.

Примеры:
число (20) может быть разложено в произведение (2cdot 2cdot 5)
число (105 =21 cdot 5=7cdot 3 cdot5)
число (17) – является простым числом и разложено быть не может.

Замечание: разложение (17) как (17cdot 1) – не подходит, т.к. единица не считается простым числом.

Любые два разложения одного и того же числа могут отличаться только порядком множителей.
Например, разложение числа (6) мы можем записать либо как (2cdot 3), либо как (3cdot 2) и более никак.
Замечание: вот именно поэтому (1) не считается простым числом, ведь иначе любое число имело бы бесконечно много разложений: (2cdot 3cdot 1); (2cdot 1cdot 3cdot 1); (2cdot 1cdot 3cdot 1cdot 1cdot 1)….

Арифметическая и геометрическая прогрессия

Источник

Анна Малкова

Задача №18 Профильного ЕГЭ по математике. Странная. Ни на что не похожая. В ней нет ни синусов, ни логарифмов, ни производных… но попробуй реши!

Мы разберем реальные задачи Профильного ЕГЭ на числа и их свойсва. Но не сразу. Сначала – подготовительные задачи. Они помогут понять основные принципы решения таинственной 18-й задачи.

1. Встретились как-то раз два математика. Когда-то они вместе учились в школе, много лет друг друга не видели, и им было о чем поговорить.
Один сказал, что у него трое сыновей. И что произведение возрастов этих детей равно 36.

Второй спросил: «А чему равна сумма их возрастов»

– А сумма возрастов, – сказал первый, – такая же, как и номер автобуса, который только что проехал мимо.

– Не хватает данных, – ответил второй.

– Хорошо, – согласился первый. – Старший сын рыжий.

Второй назвал возраст детей.

Как он это сделал?

Будем считать, что возрасты сыновей математика – целые положительные (то есть натуральные) числа. Произведение трех натуральных чисел равно 36. Запишем возможные варианты, а также сумму возрастов детей в каждом случае.

Возрасты детей	Сумма возрастов
1	1	36	38
1	2	18	21
1	3	12	16
1	4	9	14
1	6	6	13
2	2	9	13
2	3	6	11
3	3	4	10

Если бы номер проехавшего автобуса был равен 21, или 10, или 11, возрасты детей определялись бы однозначно. Но второй математик сказал, что ему не хватает данных. Значит, номер автобуса равен 13. Возможны варианты: 1, 6 и 6 лет или 2, 2 и 9 лет. Фраза «Старший сын рыжий» подразумевает, что среди мальчиков есть старший. В случае, когда возрасты детей равны 1, 6 и 6 лет, старших двое, и этот вариант не подходит. Значит, старшему 9 лет, а младшим по 2 года.

В задаче 18 Профильного ЕГЭ по математике тоже используется перебор вариантов. Но не хаотичный, а умный, то есть перебор вариантов по определенному правилу.

Вот еще одна задача, которая появилась задолго до ЕГЭ. Когда-то она была предложена на экзаменах в Финансовый университет и давно уже стала народной. В ней есть забавная ловушка, поэтому лучше решать ее большой компанией. Рекомендую учителям матклассов и ведущим курсов подготовки к ЕГЭ!

2.Два брата продали стадо овец, выручив за каждую овцу столько рублей, сколько было в стаде овец. Решив разделить выручку поровну, они поступили следующим образом: каждый брат, начиная со старшего, брал из общей суммы по 10 рублей. После того, как в очередной раз старший брат взял 10 рублей, остаток от выручки оказался меньше 10 рублей. Желая его компенсировать, старший брат отдал младшему свой нож. Во сколько рублей был оценен этот нож? (Все суммы денег выражаются натуральными числами).

Пусть в стаде овец, и за каждую выручили рублей.

Теперь у братьев есть $n^{2}$ рублей.

Пусть из кучки в $n^{2}$ рублей братья раз берут по 10 рублей. Старший, потом младший, опять старший, и опять младший… И вот старший брат взял десятку, и осталось
рублей. Теперь младший брат слегка обиженно смотрит на старшего, и старший отдает ему свой нож. Представили?

Пусть нож оценен в рублей.

Запишите систему условий. И проверьте, что у вас получилось.

Вот что у меня:

Первое уравнение вопросов не вызывает, правда? Со вторым – неравенством – тоже все понятно. Остаток от деления на 10 ненулевой и меньше 10, и мы записали эти условия в виде нестрогого неравенства. А вот третье уравнение…

Что же оно означает?
Каждый из братьев получил одинаковое количество десяток. И еще младший брат взял рублей и нож, оцененный в рублей (это левая часть уравнения). А старший брат взял на одну десятку больше, но зато лишился ножа – значит, он стал на рублей беднее.

Получаем: 2x=10-y , то есть y=10-2x .

Правая часть уравнения делится на 2. Значит, и левая его часть делится на 2, и тогда – четное число.

Тогда из первого уравнения следует, что $n^{2}$ – четная величина. Но если квадрат натурального числа является четной величиной, значит, и само число четно. И тогда
$n^{2}$ делится на 4.

Поскольку – четный остаток от деления на 10, то у может принимать значения: 2, 4, 6, 8.

Тогда запись $n^{2}=10k+y$ означает, что $n^{2}$ оканчивается на 2, 4, 6 или 8. Теперь 2 и 8 можно отбросить, поскольку ни один квадрат целого числа ни на 2, ни на 8 не заканчивается. Остаются варианты y=4 и y=6 . Что же из них является правильным ответом?

Вспомним еще одно условие: последним взял 10 рублей старший брат. Это значит, что , то есть количество десяток, – нечетно. Пусть k=2m+1 .

Если y=4 , то $n^{2}=10left ( 2m+1 right )=20m+14$ . Получим:

$n^{2}-20m=14$ .

Посмотрим внимательно на это уравнение в целых числах. Поскольку $n^{2}$ делится на 4, 20 делится на 4, то левая часть уравнения делится на 4. Но правая его часть, равная 14, на 4 не делится! Значит, у него нет решений, и y=4 не подходит.

Если y=6 , то $n^{2}=10left ( 2m+1 right )+6=20m+16$ , противоречий нет. В этом случае x=2.

Вот такие они – задачи на числа и их свойства. Иногда кажется, что условие и то, о чем спрашивается, никак не связаны. Научиться решать их – целое искусство.

Для того чтобы лучше освоить тему, читайте статью «Делимость чисел»

Интересно, что в Базовом ЕГЭ по математике тоже есть задание на числа и их свойства. И тоже под номером 19. Их вполне можно считать подготовительными.

Обратите внимание, что даже решая их подбором – мы не перебираем все числа подряд, а следуем определенному правилу.

3. Вычеркните в числе 24715905 три цифры так, чтобы получившееся число делилось на 30. В ответе укажите какое-нибудь одно получившееся число.

Чтобы число делилось на 30, оно должно делиться на 3 и на 10. Вычеркнем на конце исходного числа цифру 5. Получившееся число 2471590 делится на 10. Сумма его цифр равна 28. Вычеркнем цифры 7. Теперь сумма цифр равна 21, число 241590 делится на 3. Вычеркнем 9 – третью цифру. Число 24150 делится на 30, поскольку делится на 3 и на 10.

Ответ: 24150. Возможны и другие ответы.

4. Найдите четырехзначное число, кратное 66, все цифры которого различны и четны. В ответе укажите какое-нибудь такое число.

Если число кратно 66, то оно делится на 2, на 3 и на 11. Значит, оно четно, сумма его цифр делится на 3. Кроме того, выполняется признак деления на 11:

Число делится на 11 тогда и только тогда, когда суммы цифр на четных и нечетных позициях числа a равны или их разность кратна 11.

Четные цифры: 2, 4, 6, 8, 0.

Число 2640 четно, сумма цифр делится на 3, 2 + 4 = 6 + 0.

Ответ: 2640.

5. Найдите четырёхзначное число, большее 2000, но меньшее 4000, которое делится на 18 и каждая следующая цифра которого больше предыдущей. В ответе укажите какое-нибудь одно такое число.
Число делится на 18, если оно четно и сумма его цифр делится на 9.
Первая цифра нашего числа – либо 2, либо 3. Последняя 6 или 8 (четная).

Случай, когда первая цифра равна 2, а последняя цифра равна 6, не подходит: числа 2346 и 2456 не делятся на 9. Число 3456 – четно и делится на 9.

Ответ: 3456.

6. Приведите пример трёхзначного натурального числа, большего 600, которое при делении на 4, на 5 и на 6 даёт в остатке 3 и цифры которого расположены в порядке убывания слева направо. В ответе укажите ровно одно такое число.

Обозначим наше число А. Поскольку число А которое при делении на 4, на 5 и на 6 даёт в остатке 3, число В = А – 3 делится на 4, на 5 и на 6. Значит, В делится на их наименьшее общее кратное, то есть на 60.

Поскольку А ≥ 601, В ≥ 588. Возможные значения для В:
600, 660, 720, 780, 840, 900, 960.

Возьмем число 963. При делении на 4, на 5 и на 6 оно дает в остатке 3, и его цифры которого расположены в порядке убывания слева направо. Они даже образуют убывающую арифметическую прогрессию!

Ответ: 963.

7. Найдите натуральное число, большее 1340, но меньшее 1640, которое делится на каждую свою цифру и все цифры которого различны и не равны нулю. В ответе укажите какое-нибудь одно такое число.

Обозначим наше число А. Поскольку 1341 ≤ А ≤ 1639, первая цифра этого числа равна 1.

Возьмем число 1395. Оно делится на 1, на 3, на 9 и на 5. Просто подбор.

Ответ: 1395.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задачи ЕГЭ на числа и их свойства. Подготовительные задачи» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Единый государственный экзамен по математике базового уровня состоит из 20 заданий. В задании 19 проверяются навыки работы с цифровой записью числа. Школьник должен знать признаки делимости чисел на простые и составные числа и уметь применять их для решения различных задач. Здесь вы можете узнать, как решать задание 19 ЕГЭ по математике базового уровня, а также изучить примеры и способы решения на основе подробно разобранных заданий.

Приведите пример трёхзначного/четырехзначного натурального числа, кратного N, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число.