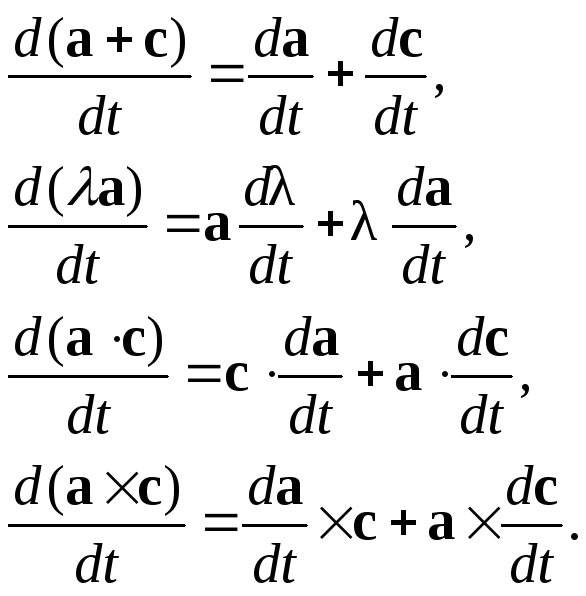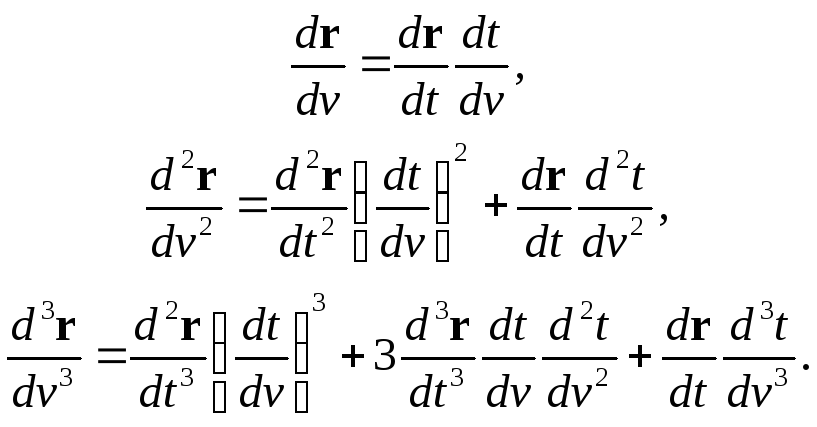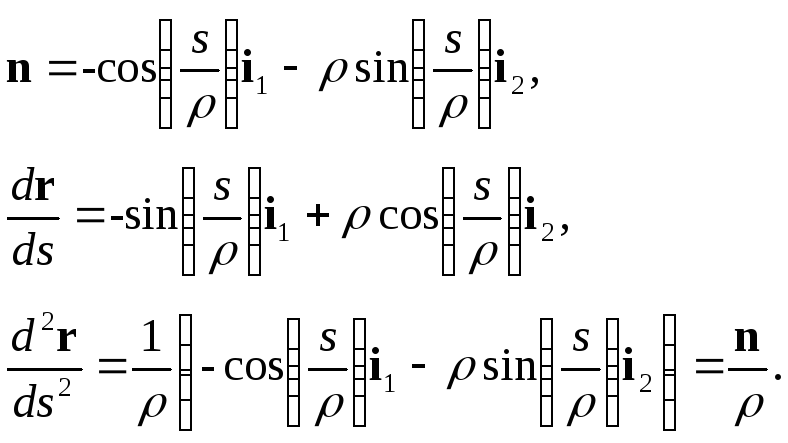Естественная параметризация (или натуральная параметризация) — параметризация кривой длиной её дуги. То есть параметром служит длина дуги кривой, отсчитываемая от некоторой фиксированной точки O, которая может быть выбрана произвольно. Такой параметр называется натуральным (часто обозначается s).
Тем самым, естественная параметризация кривой определена однозначно с точностью до выбора точки отсчета O (соответствующей нулевому значению натурального параметра) и ориентации, то есть выбора направления, в котором при удалении от O параметр возрастает.
Определение[править | править код]
Кривая 


![{displaystyle gamma |_{[a,b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3af66ac0c9df765665c7b18219b73f2a4e3a1772)

Свойства[править | править код]
- Первое из соотношений Френе очевидно вытекает из предыдущего свойства и определения кривизны
. Для доказательства второго соотношения воспользуемся тождествами
- где треугольные скобки обозначают скалярное произведение объемлющей евклидовой плоскости. Дифференцируя по
первое тождество, получаем
означающее, что вектор
параллелен вектору
то есть
с некоторым скалярным коэффициентом
. Дифференцируя второе тождество, получаем
Подставляя сюда
и
, получаем
Отсюда с учетом
, получаем
что и требовалось доказать.
См. также[править | править код]
- Дифференциальная геометрия кривых
- Длина кривой
Литература[править | править код]
- Бураго Д. Ю., Бураго Ю. Д., Иванов С. В. Курс метрической геометрии. — Москва-Ижевск, Институт компьютерных исследований, 2004.
- Мищенко А.С. Фоменко А.Т. Курс дифференциальной геометрии и топологии. — Физматлит, 2004. — ISBN 5-9221-0442-X.
- Топоногов В.А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 9785891552135.
Ссылки[править | править код]
- А. В .Чернавский. Лекции по классической дифференциальной геометрии (2 курс)
Кривой
линией или просто кривой будем называть
геометрическое место точек, координаты
которых описываются непрерывными и
однозначными функциями r1(t),
r2(t),
r3(t),
параметра
t,
принимающего
значения на отрезке tmin
≤ t
≤ tmax
. В
декартовой прямоугольной системе
координат Oe1e2e3
кривую
можно описать радиус-вектором
(37)
Представление
кривой в виде (37) называется параметрическим.
Далее будем предполагать, что координатные
функции ri(t)
имеют
непрерывные производные до любого
порядка, который нам потребуется. Точку
кривой r(t)
будем называть
обыкновенной,
если в этой точке не обращаться в нуль
длина вектора первой производной по
параметру r’
= dr/dt.
В противном
случае точку криво будем называть
особой.
Положение
точки кривой зависит от параметра t,
который
является её внутренней координатой.
Параметр t
своими
значениями однозначно определяет точки
кривой. Но так как он геометрически он
ничем не связан с кривой, то для нее
можно использовать другую параметризацию.
Для этого достаточно ввести новый
параметр v,
который связан с параметром t
функциональной
зависимостью
(38)
где
tmin
=
t(vmin),
tmax
=
t(vmax).
Будем
предполагать при этом, что функция t(v)
является
взаимно однозначной и монотонно
возрастающей. Когда параметр v
пробегает
свою область изменений от vmin
до vmax,
параметр t
пробегает
свою область изменения от tmin
до tmax.
Кривая (37),
выраженная через параметр v,
будет иметь вид
При
этом форма кривой останется прежней.
Как параметр t,
так и параметр
v
одинаково годятся, чтобы характеризовать
точки рассматриваемой кривой, и выбор
параметра зависит от нас. Мы будем
использовать эти свойства кривых, чтобы
согласовать параметрические длины
кривых. Пусть имеются две кривые: первая
a(t),
tmin
≤ t
≤ tmax,
вторая c(v),
vmin
≤ v
≤ vmax,
и нам нужно,
чтобы параметрические длины кривых
были одинаковыми. Изменим параметризацию
второй кривой так, чтобы пределы изменения
ее параметров совпадали с пределами
первой кривой. Для этого у второй кривой
введем параметр t,
связанный
параметром v
зависимостью
(39)
Вторая
кривая теперь будет иметь вид c
= c(t)
= c(v(t)),
tmin
≤ t
≤ tmax.
В частном
случае параметром кривой может служить
длинна ее дуги, отсчитываемой от начальной
точки. В общем случае параметром t,
как любая
координатная система, может бать
определен удобный для нас способом.
Для
векторной функции, как и для скалярной,
определяются производные. Производные
векторной функции также представляют
собой векторы. Для любых векторных
функции a(t)
и c(t)
и любой
скалярной функции λ(t)
справедливы
правила дифференцирования
В
декартовой прямоугольной системе
координат производные векторной функции
n
– го порядка
по ее параметру имеют простой вид
(40)
В криволинейной
системе координат базисные векторы
изменяют свою длину и направление при
переходе от одной точки к другой и
формулы для производных имеют более
сложный вид.
Если координатные
функции кривой в некоторой точке
достаточное число раз дифференцируемы,
то векторную функцию кривой в окрестности
этой точки можно разложить в ряд Тейлора
(41)
где
.
Производные
вычислены при некоторых значениях
параметра t
≤ ti
≤ t
+ ∆t.
Вектор qn
представляет
собой остаточный член ряда Тейлора. Из
свойств радов Тейлора координатной
функции ri(t)
следует, что
длина вектора qn
не
превосходит некоторое положительное
число, постоянное для всех t
из его области
изменения для кривой, и что предел длины
остаточного вектора стремится к нулю
при увеличении числа членов усеченного
ряда
При
изменении параметризации кривой r(t),
t(v)
производные
по новому параметру выражаются через
производные по старому параметру
следующим образом:
Исследуем
поведение кривой на бесконечно малом
участке в близи обыкновенной точки.
Если существуют производные по параметру
координатных функций, то кривая также
имеет производные по параметру
соответствующего порядка. Рассмотрим
геометрический смысл производной
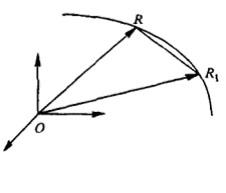
векторной функции. Пусть при каком-либо
значении параметра t
радиус-вектор
r(t)
указывает
на некоторую точку R.
Перейдем
к другому параметру t1
= t
+ ∆t,
при котором
векторная функция r(t
+ ∆t)
указывает
на некоторую другую точку R1.
Разность этих двух значений векторной
функции ∆r
= r(t
+ ∆t)
– r(t)
описывает
хорду RR1
(рис.
8).
Рис. 8
Вектор
(42)
параллелен
хорде RR1,
но в общем случае не равен ей по длине.
Устремим ∆t
к нулю, тогда
точка R1
будет
приближаться к точке R,
вектор (42) будет стремиться к касательной
к кривой в точке R.
Предел
отношения (42) при ∆t→0
является
первой производной векторной функции
(43)
Таким
образом, производная r’(t)
кривой r(t)
есть вектор,
направленный по касательной к кривой
в точке, определяемой параметром t.
Заметим, что
производная всегда направлена в сторону
возрастания параметра. Зная первую
производную радиус-вектора кривой,
можно вычислить длину кривой. Длина
кривой равна приделу, к которому стремится
длина ломанной, вписанной в кривую.
Таким образом, длин кривой равна интегралу
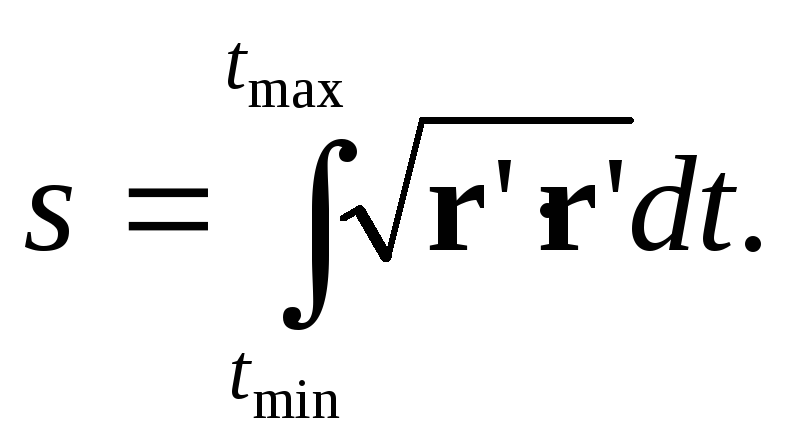
Натуральная
параметризация кривой. Длина
вектора производной зависит от способа
параметризации кривой. Существует
способ параметризации кривой, при
котором длина вектора производной равна
единице. Для этого используется
параметризация, геометрически связанная
с кривой, а именно: за параметр принимается
длина дуги кривой, отсчитываемая от
некоторой ее точки (например, начальной).
Действительно, в этом случае длина хорды
RR1
стремится к длине дуги ∆t,
а длина
вектора r’
стремится
к единице, когда ∆t
стремится
к нулю. Векторная зависимость
(45)
где
s
– длина
дуги, называется управление кривой с
натуральной параметризацией. Натуральная
параметризация удобна в теоретических
исследованиях, так как она упрощает
формулу. С практический точки зрения
она не всегда удобна, так как требует
знание длины дуги.
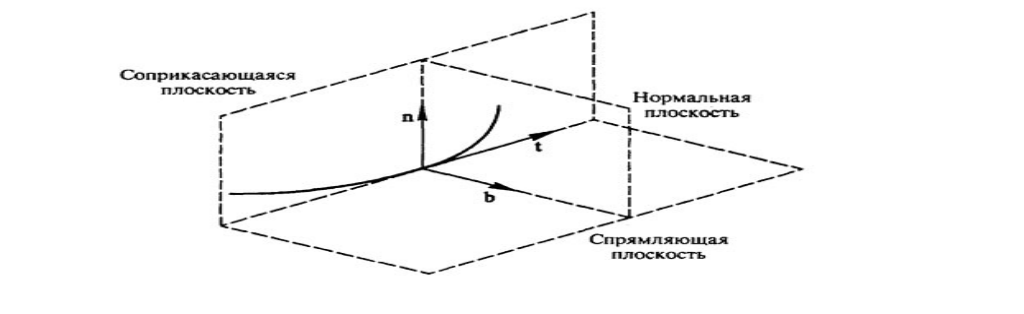
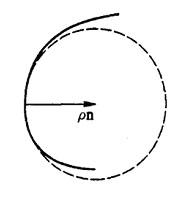
Сопровождающий
трехгранник. В
каждой точке кривой можно построить
плоскость, перпендикулярная ее первой
производной. Такая плоскость называется
нормальной
плоскостью кривой. Плоскость,
в которой лежит и первая производная
кривой и ее вторая производная, называется
соприкасающейся
плоскостью. Если
вторая производная кривой параллельна
первой производной или ее длина равна
нулю, то в качестве соприкасающейся
плоскости можно взять любую плоскость,
в которой лежит первая производная
кривой. Точка кривой, в которой вектор
первой и второй производных кривой
коллинеарны, называется точкой
распрямления. Точка распрямления не
зависит от способа параметризации
кривой. Название соприкасающихся
плоскостей обусловлено тем, что она
проходит через заданную точку кривой
с наивысшим порядком касания, и ее можно
определить как предельное положение
плоскости, построенной по трем бесконечно
близким точкам кривой. Плоскость,
перпендикулярная нормальной и
соприкасающейся плоскостям, называется
спрямляющей
плоскостью (рис.
9).
Рис.
9. Сопровождающий трехгранник кривой
Единичный
вектор, направленный вдоль первой
производной кривой, называется касательным
вектором кривой в
данной точке. Единичный вектор,
направленный вдоль линии пересечения
нормальной и соприкасающейся плоскостей
и направленный в сторону второй
производной (в сторону вогнутости
кривой), называется главной
нормалью кривой в
данной точке. Единичный вектор,
направленный вдоль линии пересечения
нормальной спрямляющей плоскости и
образующей с касательным и нормальным
вектором правую тройку векторов,
называется бинормалью
кривой в
данной точке.
Таким
образом, с каждой точкой кривой связаны
три взаимно перпендикулярные плоскости:
нормальная, соприкасающаяся и спрямляющая,
а также три взаимно ортогональных
вектора единичной длины: касательный
t,
нормаль n
и бинормаль
b
= t
× n.
Совокупность
трех перечисленных плоскостей и трех
векторов t,
n,
b
называется
сопровождающим
трехгранником кривой.
Тройка
векторов t,
n,
b
выражается
через производные векторной функции
кривой. Они помогут нам в исследовании
строения кривой в бесконечно малой
окрестности каждой ее точки. Тройка
единичных векторов связана соотношениями
(46)
Формула
Френе-Серре. Предположим,
что нам известно уравнение кривой с
натуральной параметризацией (45). В этом
случае
(47)
Из того, что длина
первой производной равна единице и не
меняется вдоль кривой, следует
(48)
т.е. векторы первой
и второй производной ортогональны.
Следовательно, вторая производная
кривой с натуральной параметризацией
направлена по главной нормали:
(49)
Коэффициент
k
называется
кривизной
кривой линии.
Ниже мы покажем, что обратная ее величина
равна радиусу окружности, соприкасающейся
с кривой в рассматриваемой точке.
Бинормаль по определению ортогональна
касательному вектору и главной нормали.
Из этого следует, что
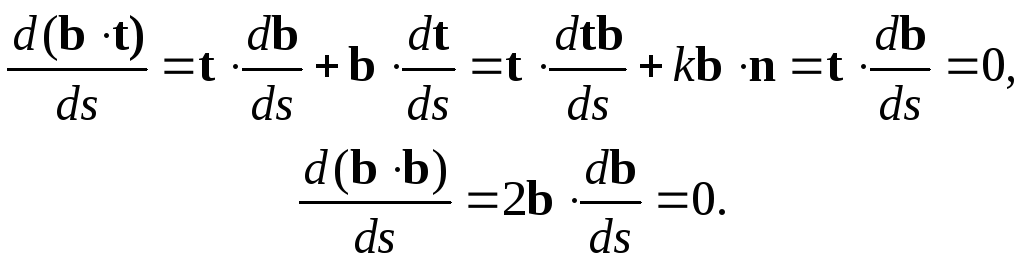
Таким
образом, вектор db/ds
ортогонален
векторам t
и b
и, следовательно,
он параллелен главной нормали. Это
принято записывать в виде
(51)
Коэффициент
χ
называется кручением
кривой линии.
Равенства (49) и (51) определяют производные
ортов t
и b
по длине
дуги. Найдем производную нормали по
длине дуги
(52)
Нами
получены дифференциальные зависимости
для векторов t,
n
и b:
которые
известны как формулы
Френе-Серре. Они
выражают производные векторов
сопровождающего трехгранника в виде
разложения по самим этим векторам.
Используя (46) и (47) и формулы Френе-Серре,
выразим векторы t,
n,
b,
кривизну и
кручение кривой через производные
радиус-вектора кривой по ее длине дуги
следующим образом:
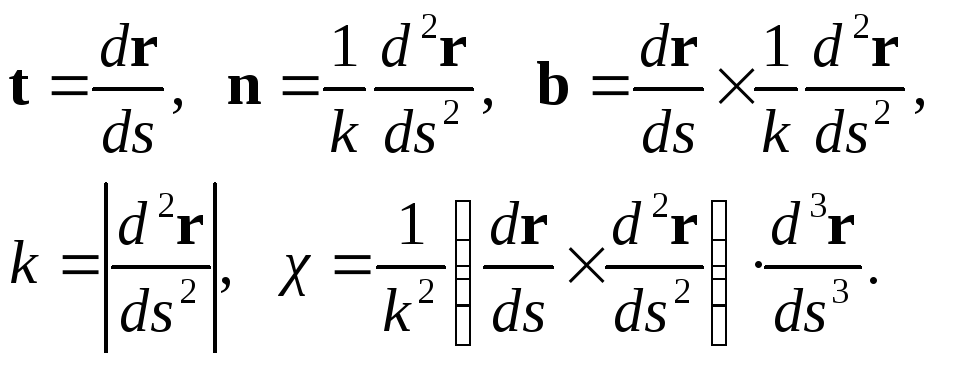
Соприкасающаяся
окружность. Поясним,
почему коэффициент k
называют
кривизной кривой. Построим окружность
радиусом равным некоторой величине ρ.
Ее уравнение
с натуральной параметризацией в некоторой
местной системе координат с ортами i1,
i2,
i3
имеет вид
Нормаль к окружности
и производные радиус-вектора окружности
равны
Очевидно,
что коэффициент пропорциональности k
для окружности
равен 1/ρ.
Таким образом,
если мы построим для кривой соприкасающуюся
с ней окружность (с
таким же d2r/ds2,
как у кривой),
то радиус этой окружности будет равен
ρ
(рис. 10).
Величина
ρ
= 1/k
называется
радиусом кривизны кривой. Для произвольной
кривой ее кривизна k
и кручение
χ
являются функциями параметра t.
Поясним,
почему коэффициент χ
называют кручением кривой. Построим в
некоторой точке кривой сопровождающий
трехгранник и посмотрим, как он будет
себя вести при движении вдоль кривой.
Получим, что при увеличении параметра
на небольшую величину Δt
касательный
вектор t
повернется
в сторону главной нормали n
на угол k,
а бинормаль
b
повернется
в сторону, противоположную главной
нормали n
на угол χ
(рис. 11).
Рис.
10. Соприкасающаяся с кривой окружность
Рис.
11. Вектор Дарбу
Если
наблюдать этот процесс, «сидя на кончике
вектора t»,
то мы увидим, что главная нормаль n
и соприкасающаяся
плоскость повернулись в сторону бинормали
b
на угол χ.
Теперь представим, что точка движется
по кривой, проходя единицу длины ее дуги
за единицу времени. В этом случае угловая
скорость вращения сопровождающего
трехгранника вокруг касательного
вектора будет равна кручению кривой χ.
Если кручение χ
= 0, то кривая является плоской. Справедливо
и обратное утверждение. Если кручение
кривой равно нулю, то соприкасающаяся
плоскость во всех точках кривой одна и
та же, все бинормали параллельны друг
другу, а кривая является плоской.
Полный
вектор угловой скорости вращения
сопровождающего трехгранника по
отношению к пути, проходимому по кривой,
называется вектором
Дарбу. Он
равен
(54)
Вектор
Дарбу придает механический смысл
формулам Френе-Серре (52), с использование
которого последние имеют вид
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
Кривизна и кручение. Натуральные уравнения кривой
Краткие теоретические сведения
Кривизна кривой
Кривизной $k$ кривой в данной точке называют модуль скорости вращения касательной по отношению к длине дуги.
Регулярная дважды дифференцируемая без особых точек кривая $gamma$, заданная векторной функцией $vec{r}=vec{r}(t)$, имеет в каждой точке определенную кривизну, причем
$$
|k(t)|=frac{|vec{r’}(t)times vec{r”}(t)|}{|vec{r'(t)}|^3}.
$$
Для кривой, заданной параметрически
$$ x=x(t), ,, y=y(t), ,, z=z(t), $$
кривизна в точке $P(t=t_0)$ находится по формуле:
$$
k^2(t_0)=frac{left| begin{array}{cc}
y’ & z’ \
y”& z” \
end{array}
right|^2+left| begin{array}{cc}
z’ & x’ \
z”& x” \
end{array}
right|^2+left| begin{array}{cc}
x’ & y’ \
x” & y” \
end{array}
right|^2}{Bigl((x’)^2+(y’)^2+(z’)^2Bigr)^3},
$$
где все производные вычисляются при $t=t_0$.
Если кривая задана естественной параметризацией $vec{r}=vec{r}(s)$, то векторы $vec{r’}(s)$ и $vec{r”}(s)$ перпендикулярны, причем $|vec{r’}(s)|=1$. Тогда выражение для кривизны принимает вид:
$$
k(s)= |vec{r”}(s)|.
$$
?
Что вы скажете о кривой, которая в каждой свой точке имеет нулевую кривизну?
Для плоской кривой, лежащей в плоскости $(xy)$, кривизну можно найти по формулам:
$$
begin{array}{rl}
x=x(t), y=y(t):& k = displaystylefrac{|x’y”-x”y’|}{left((x’)^2+(y’)^2right)^{3/2}}, \
y=y(x):& k = displaystylefrac{|y”|}{left(1+(y’)^2right)^{3/2}}, \
rho=rho(varphi):& k = displaystylefrac{|rho^2+2(rho’)^2-rhorho”|}{left(rho^2+(rho’)^2right)^{3/2}}.\
end{array}
$$
Кручение
Абсолютным кручением $varkappa$ кривой называют скорость вращения соприкасающейся плоскости вокруг касательной.
$$
|varkappa (t)|=frac{|(vec{r’}(t), vec{r”}(t), vec{r”’}(t))|}{|vec{r’}(t)times vec{r”}(t)|^2}.
$$
В случае естественной параметризации
$$
|varkappa(s)|=frac{|(vec{r’}(s), vec{r”}(s), vec{r”’}(s))|}{k^2(s)}
$$
Для плоской кривой кручение равно нулю: $varkappa=0$!
Натуральные уравнения кривой
Если кривая задана естественной параметризацией $vec{r}=vec{r}(s)$, то кривизна и кручение будут являться функциями длины дуги
$$
k=k(s), quad varkappa=varkappa(s).
$$
Система этих двух соотношений называется натуральными уравнениями кривой.
Натуральные уравнения полностью определяют форму кривой, ибо связывают инварианты, которые не меняются при преобразовании координат (при изменении положения указанной кривой в пространстве относительно системы координат).
Решение задач
Задача 1 (Феденко №351)
Найдите кривизну кривой:
$$
x=a,mbox{cos}^3t,,,y=a,mbox{sin}^3t.
$$
Задача 2 (Феденко №380)
Найдите параболу $y=ax^2+bx+c$, имеющую с синусоидой $y=mbox{sin}x$ в точке $A(pi/2,1)$ общие касательную и кривизну.
Задача 3 (Феденко №405)
Составьте натуральные уравнения кривой:
$$
x=a(mbox{cos},t+t,mbox{sin},t), ,, y=a(mbox{sin},t-t,mbox{cos},t).
$$
Краткое решение задачи 3
$$
s=frac{at^2}{2}.
$$
$$
k=frac{1}{at}.
$$
$$
t=frac{1}{ak} Rightarrow s= frac{1}{2ak^2}.
$$
Натуральные уравнения:
$$
k=frac{1}{at},,,s=frac{at^2}{2}
$$
или
$$
k^2=frac{1}{2as}.
$$
Феденко записывает ответы через радиус кривизны:
$R=frac{1}{k}$.
Задача 4 (Феденко №486, №514)
Найдите кривизну и кручение, составьте натуральные уравнения кривой:
$$
x=a,mbox{ch}t, , y=a,mbox{sh}t, , z=a, t.
$$
Решение задачи 4
Задачу можно решать двумя способами:
1 способ. Найти $k(t), varkappa(t), s(t)$.
2 способ. Сначала найти выразить $t$ через $s$ и записать естественную параметризацию кривой $vec{r}=vec{r}(s)$. А далее найти $k(s)$ и $varkappa(s)$.
Воспользуемся первым способом.
begin{gather*}
vec{r}(t_0)={a,mbox{ch}t, , a,mbox{sh}t, , at},\
vec{r’}(t_0)={a,mbox{sh}t, , a,mbox{ch}t, , a},\
vec{r”}(t_0)={a,mbox{ch}t, , a,mbox{sh}t, , 0}\
vec{r”’}(t_0)={a,mbox{sh}t, , a,mbox{ch}t, , 0}.
end{gather*}
$$
Rightarrow quad k^2(t) = frac{1}{4a^2mbox{ch}^4t}.
$$
$$
Rightarrow quad k(t) = frac{1}{2a,mbox{ch}^2t}.
$$
begin{equation*}
varkappa(t) = frac{ left|
begin{array}{ccc}
a,mbox{sh}t & a,mbox{ch}t & a \
a,mbox{ch}t & a,mbox{sh}t & 0 \
a,mbox{sh}t & a,mbox{ch}t & 0 \
end{array}
right|}{a^4cdot 2mbox{ch}^2t} = frac{1}{2a,mbox{ch}^2t}.
end{equation*}
В задаче №473 была та же кривая и мы получили, что
$$s=asqrt{2},mbox{sh},t.$$
Используя тождества для гиперболических функций, выразим $t$ через $s$ и подставим их в выражения для кривизны и кручения:
begin{equation*}
s=asqrt{2},mbox{sh}t=asqrt{2},sqrt{mbox{ch}^2t-1} ,, Rightarrow ,, mbox{ch}^2t=frac{s^2}{2a^2}+1 ,, Rightarrow
end{equation*}
begin{equation*}
k(s)=varkappa(s)=frac{1}{2a,mbox{ch}^2t} = frac{a}{s^2+2a^2}.
end{equation*}
Вычисления сделаны для $a>0$.
Задача 5 (Феденко №496)
Найдите функцию $f(t)$, для которой данная кривая — плоская:
$$
vec{r}(t)={a,mbox{cos}t, , a,mbox{sin}t, , f(t)}
$$
Решение задачи 5
$$
begin{array}{lll}
x=a,mbox{cos}t,, &y=a,mbox{sin}t, , &z=f(t),\
x’=-a,mbox{sin}t, , &y’=a,mbox{cos}t, , &z’=f'(t),\
x”=-a,mbox{cos}t, , &y”=-a,mbox{sin}t, , &z”=f”(t),\
x”’=a,mbox{sin}t, , &y”’=-a,mbox{cos}t, , &z”’=f”'(t).
end{array}
$$
Для плоской кривой кручение равно нулю:
begin{equation*}
varkappa(t) = left|
begin{array}{rrr}
-a,mbox{sin}t & a,mbox{cos}t & f'(t) \
-a,mbox{cos}t & -a,mbox{sin}t & f”(t) \
a,mbox{sin}t & -a,mbox{cos}t & f”'(t) \
end{array}
right| = left( f'(t) + f”'(t) right)cdot2a^2=0.
end{equation*}
begin{equation*}
f'(t)=-f”'(t) quad Rightarrow quad f(t)=c_1+c_2,mbox{sin}t+c_3,mbox{cos}t.
end{equation*}
?
Как найти уравнение плоскости, в которой лежит кривая?
Известно, что плоская кривая лежит в своей соприкасающейся плоскости!
Второй способ — составить уравнение плоскости по трем точкам.
Содержание:
- Определение 1 (неявный способ задания):
- Способы задания
По этой ссылке вы найдёте полный курс лекций по математике:
Наглядный геометрический объест — плоская кривая — приточных определениях приводит к нескольким различным, хотя и близким понятиям. Плоскую кривую можно понимать и как некоторое множество точек на плоскости и как множество точек плоскости вместе с очередностью их прохождения — ориентацией. Приведем два наиболее распространенных подхода к определению того, что представля ет собой плоская кривая. Пусть на плоскости введена прямоугольная декартова система координат Оху.
Определение 1 (неявный способ задания):
Плоской кривой называется множество 7 точек М плоскости, координаты х и у которых при подстановке в уравнение ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые. Способы задания. Естественная параметризация обращают его в тождество. Пример 1 Уравнение , задает окружность радиуса а с центром в точке 0(0,0) {рис. 1).
Другим распространенным способом задания плоской кривой является параметрический способ задания. Определение 2. Параметризованной плоской кривой называется множество 7 точек М плоскости, координаты г и у которых определяются соотношениями непрерывные на отрезке [а, 6] функции. Пример 2. — параметрические уравнения окружности радиуса а с центром в точке 0(0,0). При изменении параметра t от 0 до 2т соответствующая точка обегает окружность против часовой стрелки.
Данное определение допускает естественную физическую интерпретацию. Если воспринимать параметр t как время, то параметрически заданную кривую можно рассматривать как след движущейся точки М(х, у), координаты которой изменяются со временем по правилу (2). При этом вовсе не исключается случай, когда при своем движении переменная точка М в некоторый момент t* может вновь оказаться там, где ранее (в момент i, она уже находилась: (рис.2). Геометрически этоодна и та же точка.
Однако вследствие того, что в рассматриваемом процессе мы попадаем в нее дважды в разные моменты времени, это две разные точки кривой, задаваемой параметрическими уравнениями (2). Замечание. Строго говоря, определении I и 2 вводят в рассмотрение разные объекты. Поэтому для того, чтобы не впасть в заблуждение, нужно ясно представлять, в каком именно смысле рассматривается задаваемая кривая. Пусть кривая 7 задана параметрическими уравнениями называется начальной тонкой этой кривой, а точка ) — конечной тонкой кривой 7.
Кривая 7 называется замкнутой, если ее начальная и конечная точки совпадают (рис. 4).
– Рис. 4 Одно и то же м ножество точекн а плоскости можно задавать при помощи различных параметрических уравнений. Пример 3. Уравнения задают окружность радиуса а, обходимую в положительном направлении. Легко видеть, что, положив в формулах (3) 2хг3, мы приходим к соотношениям (4). Определение. Функция подчиненная условиям: а) Н{т) непрерывна на отрезке [а, /3]; h(r) строго возрастает на отрезке [се, >3]; в) область значения функции h(r) — отрезок [а, Ь], называется непрерывной заменой параметра кривой 7 (рис. 5). ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые.
Способы задания
Естественная параметризация Заменяя в формулах (2) параметр t на функцию Л(т), получаем уравнения — другую параметризацию кривой 7. Любую кривую можно параметризовать многими различными способами. Определение 3. Плоская кривая 7 называется п-гладкой относительно параметризации если функции ) принадлежит классу .
Если порядок п гладкости функций несуществен, то говорят просто о гладкой кривой. Пример 4. Кривая заданная уравнениями является 3-гладкой (рис. в а). Пример S. Кривая 7, заданная уравнениями является 2-гладкой. Однако множеств о точек на плоскости, описываемое этими уравнениями, имеет • точке О (при t ) особенность — излом (рис.вб). Это означает, что гладкость функций . задающих кривую, не обеспечивает плавного ее изменения.
Отметим, что производные этих функций при tодновременно обращаются а нуль. ТЪчка Мо гладкой кривой у, отвечающая значению t0 параметра, М0 в которой называется особой точкой этой кривой (относительно заданной параметризации). Точка Мо(*о) гладкой кривой 7, в которой называется обыкновенной, ншрегулярной, точкой этой кривой. Пример в. Все точки окружности (3) являются регулярными.
Пример 7. У кривой, задаваемой уравнениями (астроида) четыре особых точки (при t ж 0, | Последнее неравенство означает, что скорость кривой 7 относительно заданной параметризации не обращается в нуль ни в одной точке кривой. При изменении параметра t текущая точка M(t) перемещается порегулярной кривой 7, нигде не оста- навливаясь и не поворачивая вспять, поскольку скорость регулярной кривой ни при каких значениях параметра не обращается в нуль.
Возможно вам будут полезны данные страницы:
Пусть 7 — регулярная кривая, заданная параметрически. Обозначим через Мо точку кривой 7, отвечающую значению £о параметра, а через М — точку кривой 7, отвечающую значению t параметра из некоторой окрестности точки to (рис. 8, 9). Прямая М0Т называется касательной регулярной кривой 7 вточке Мо, если при (или, что то же, ) наименьший Д0 из углов между этой прямой и переменной прямой MqM стремится к нулю (рис. 9). Регулярная кривая имеет касательную в каждой своей точке.
Вектор скорости кривой в точке Мо коллинеарен ее ка- сательной в этой точке. Прямая, проходящая через точку Мо перпендикулярно касательной кривой 7 в этой точке, называется нормалью кривой вточке Мо. Замена параметра называется регулярной у если Л'(т во всех точках отрезка [а, /3]. В случае неявного задания (1) кривая 7 будет регулярной, если в каждой ее точке М(х, у) выполняется неравенство Точка Мо(жо> Уо) неявно заданной кривой 7 называется особой, если в этой точке Пример 8.
Кривая, заданная уравнением
(леммисюга Бернулт), имеет одну особую точку 0(0,0) — узел (рис.10). Различают несколько типов особых точек. Пусть М0(хо, уо) — особая точка кривой 7, Введем следующие обозначения возврата первого рода. Пример 12. (рис. 14). — точка возврата второго рода. Гладкая (тем более регулярная) кривая спрямляема. Длина кривой 7, заданной уравнениями (2), вычисляется по формуле Значение функции равно длине переменной дуги кривой7, заключенной между точками (рис. 15).
Функция на отрезке [а, 6) строго возрастает, Пример 11. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ Плоские кривые. Способы задания. Естественная параметризация и является гладкой на отрезке [а, 6]. Кроме того, область значений функции s(t) совпадает с отрезком [0, 5]. Тем самым, длину дуги можно взять за новый, естественный (натуральный) параметр кривой.
Параметризация кривой, где в качестве параметра взята длина дуги з, называется естественной параметризацией. Если естественная параметризация кривой, то Поэтому естественно параметризованную кривую часто называют кривой с единичной скоростью. Пример 13. Параметризация окружности радиусе а является естественной:
Лекции:
- Неопределенный интеграл
- График производной функции
- Перпендикулярность прямой и плоскости
- Выпуклость функции
- Сложение матриц: примеры решения
- Интегрирование рациональных дробей
- Модуль комплексного числа
- Пределы функций примеры решения
- Найти предел используя правило Лопиталя
- Решение неравенств