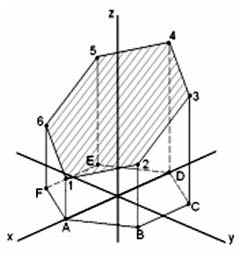
По принадлежности точек 1, 2 и 3 к соответствующим ребрам определяем их
Сечение многогранников плоскостями общего положения
ЗАДАЧА 1. Построить сечение призмы плоскостью общего положения и построить истинный вид сечения.
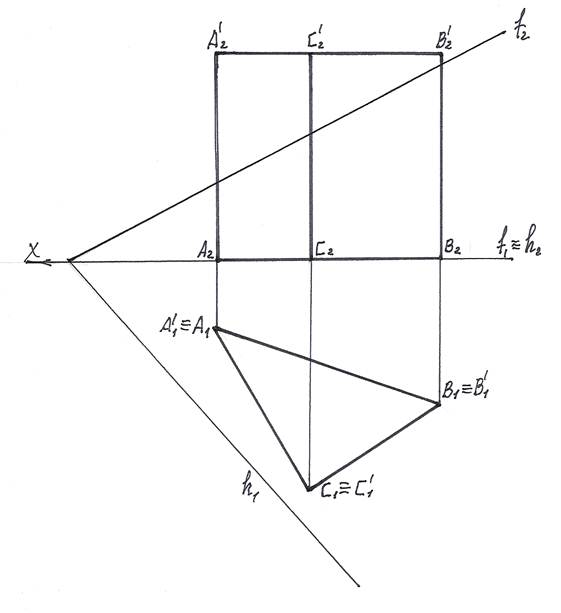
1). Для преобразования секущий пл. Г общего положения в плоскость прое-цирующую введем вместо пл. П2 новую пл. П4 так, чтобы она была перпендику-лярна плоскости П1 и проходила перпендикулярно горизонтали h секущей пл. Г.
На чертеже новую ось Х1,4 проводим перпендикулярно горизонтальной проекции горизонтали. Х1,4 ^ h1.
2). В плоскости П4 строим новую фронтальную проекцию призмы АВСА’В’С’.
Для этого проводим из А1, В1, С1, А’1, В’1, С’1 линии проекционных связей, перпендикулярные оси Х1,4, и на их продолжении от новой оси Х1,4 откладываем координаты Z точек А, В, С, А’, В’, С’.
Соединив полученные точки, получим новую фронтальную проекцию призмы.
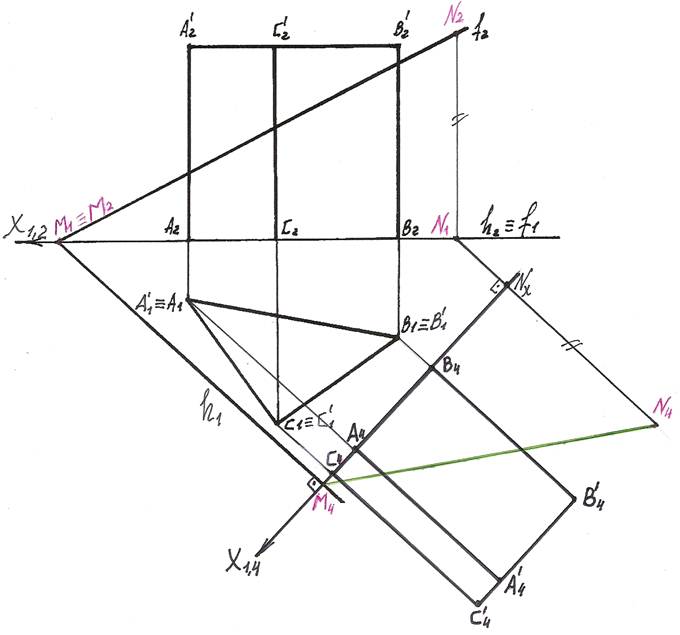
3). В новой системе плоскостей проекций П1/П4 секущая плоскость Г по построению фронтально — проецирующая, а значит, ее фронтальная проекция Г4 – прямая.
Для построения прямой достаточно иметь две точки, например М и N. Пусть точка М – точка пересечения фронтали и горизонтали плоскости Г.
М1 ≡ М2. Точку N возьмем произвольно на фронтали f. N2 Î f2.
По принадлежности к f построим горизонтальную N1 проекцию точки N. N1 Î f1.
Из М1 и N1 проводим линии проекционных связей, перпендикулярные оси Х1,4 и
на их продолжении от новой оси откладываем отрезки, равные координатам Z
Прямая М4N4 – новая фронтальная проекция секущей плоскости Г.
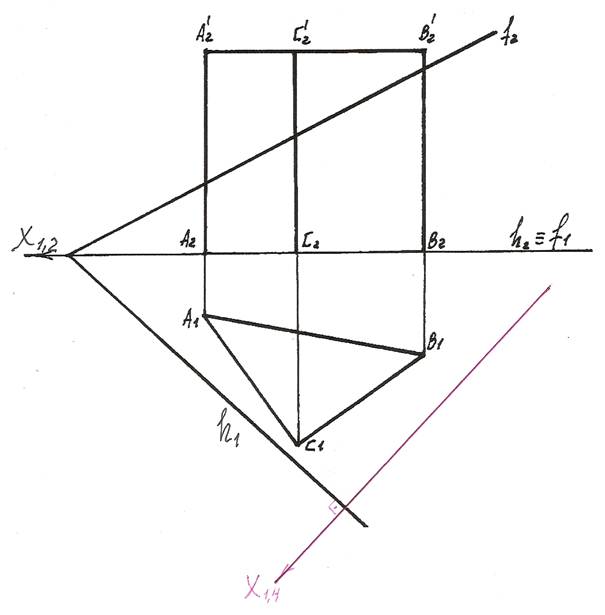
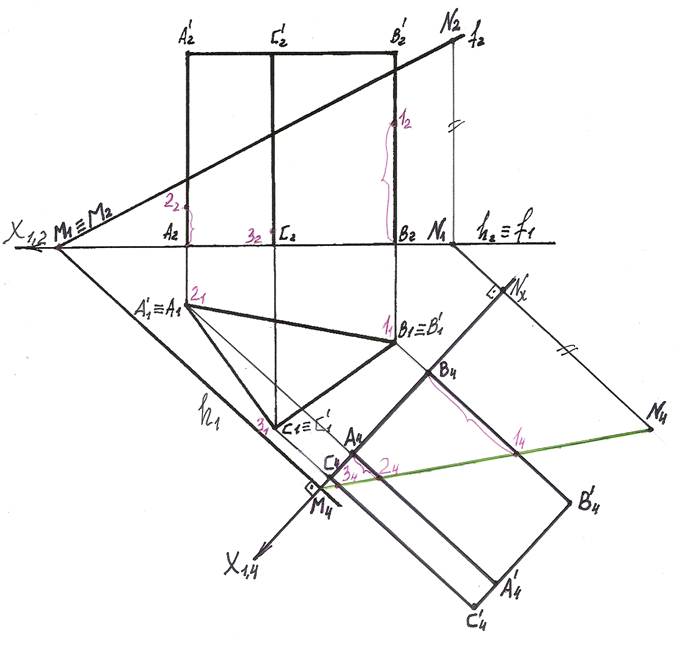4). На пересечении фронтальной проекции М4N4 секущей плоскости Г и ребер
призмы определяем вершины сечения 14, 24, 34.
По принадлежности точек 1, 2 и 3 к соответствующим ребрам определяем их
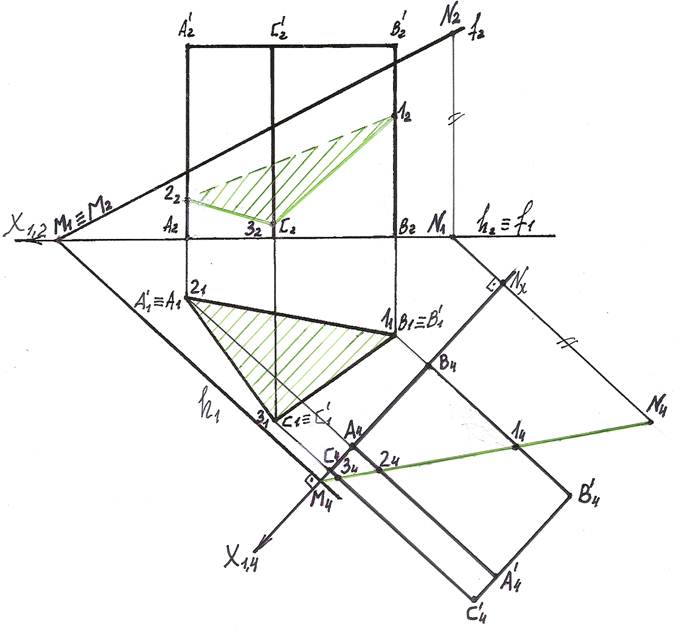
5). Соединяем полученные точки и получаем проекции сечения призмы плоскостью общего положения.
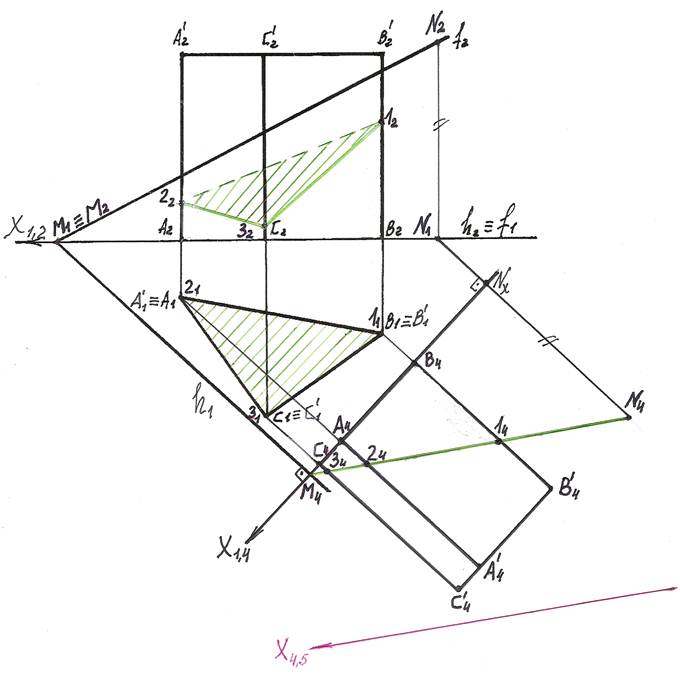
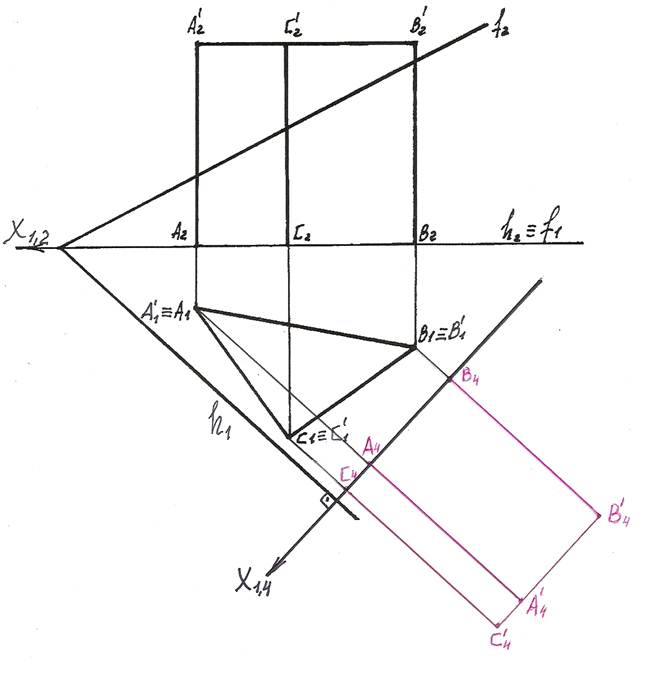
6). Для определения натуральной величины сечения введем еще одну вспомогатель-
На чертеже ось Х4,5 параллельна следу М4N4 секущей плоскости Г.
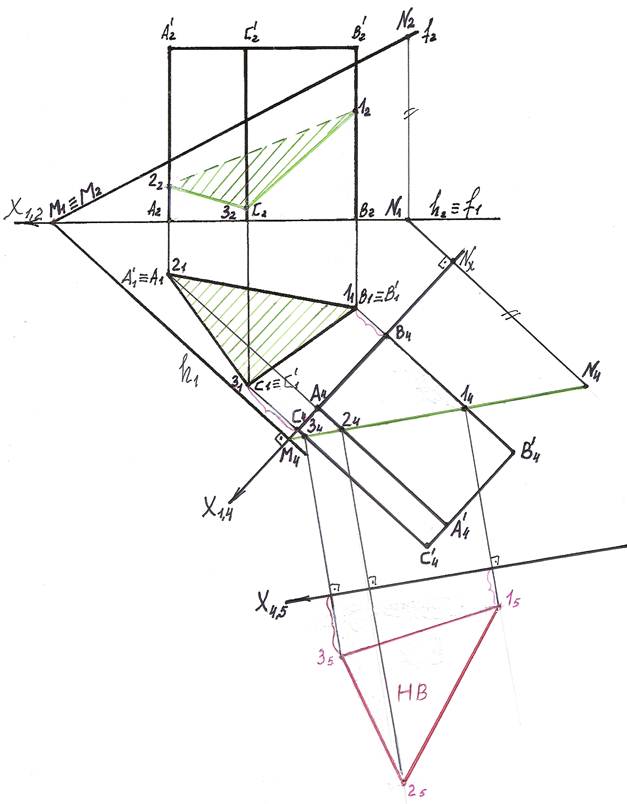
7). В новую плоскость П5 проецируем точки 1, 2 и 3. Для этого из 14, 24, 34 про-водим линии проекционных связей, перпендикулярные к оси Х4,5 и на их продолжении откладываем отрезки, равные расстояниям от оси Х1,4 до заме-няемых точек 11, 21, 31 (В411, А421, С431). Получаем точки 15, 25, 35.
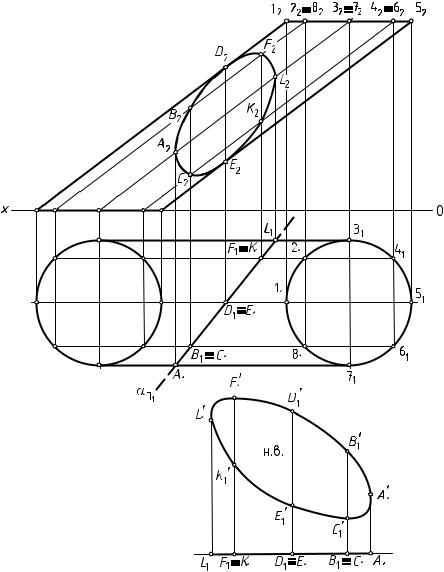
Задача 2. Построить сечение пирамиды SABС плоскостью общего положения
Т (h∩f) и найти его натуральную величину (рис.162).
Задача решается в следующей последовательности:
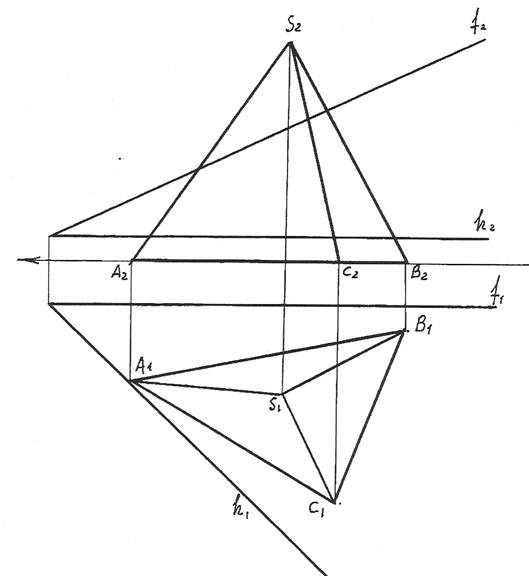
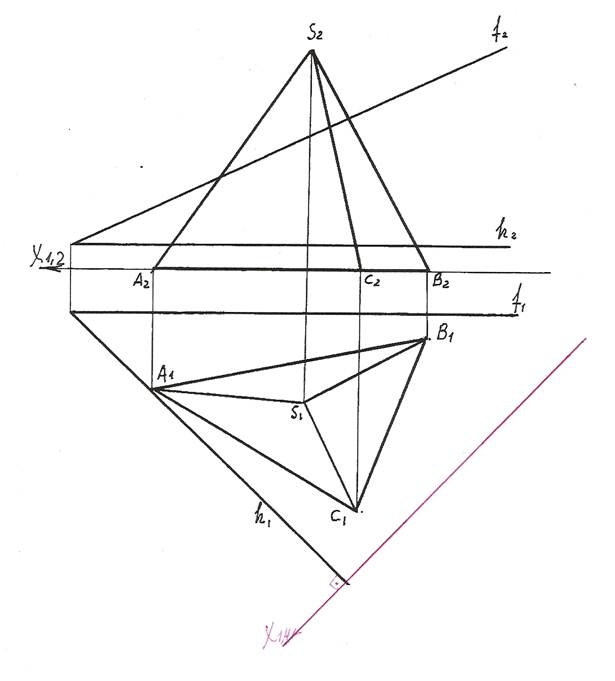
1). Для преобразования секущий пл. Т общего положения в плоскость прое-цирующую введем вместо пл. П2 новую пл. П4 так, чтобы она была перпен-дикулярна оставшейся плоскости П1 и проходила перпендикулярно горизонтали h секущей пл. Т. П2 ® П4, П4 ^ П1, П4 ^ h.
На чертеже новую ось Х1,4 проводим перпендикулярно горизонтальной проекции горизонтали. Х1,4 ^ h1.
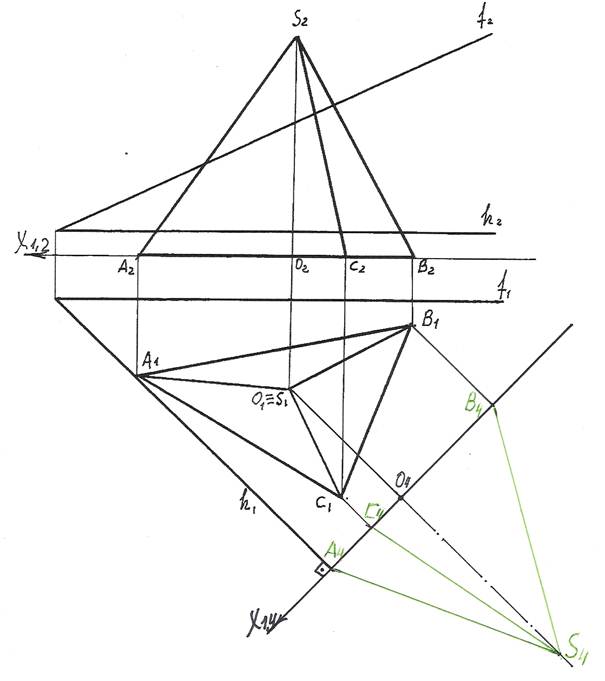
2). Теперь в плоскости П4 строим новую проекцию S4A4B4C4 пирамиды SABC. Для этого из горизонтальных проекций A1, B1, C1, S1 точек A, B, C, S проводим линии проекционных связей, перпендикулярные оси Х1,4 и на их продолжении от новой оси откладываем координаты Z этих точек. ZА = ZВ = ZС = 0; ZS = O2S2.
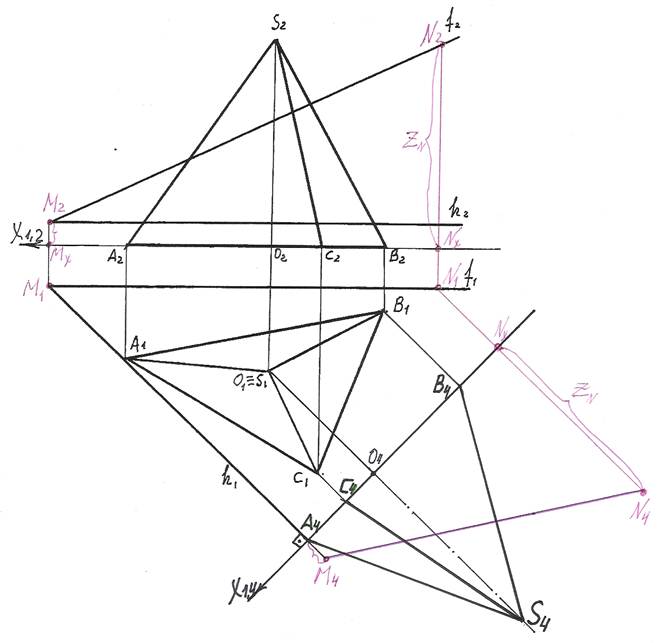
3). Затем строим новую проекцию секущей плоскости Т. Так как в новой системе плоскостей проекции П1/П4 секущая плоскость стала фронтально — проецирующей, то ее фронтальная проекция Т4 – прямая. Построить ее можно по двум точкам, положим, по точке М – точке пересечения фронтали и горизонтали и точке N, произвольно взятой на фронтали N2 Î f2.
По принадлежности к фронтали f построим горизонтальную N1 проекцию т.N.
N1 Î f1. Из М1 и N1 проводим линии проекционных связей, перпендикулярные оси Х1,4 и на их продолжении от новой оси откладываем отрезки, равные коорди-натам Z точек М и N. ZМ = МХМ2, ZN = NХN2. Получаем точки М4 и N4.
Прямая М4N4 – новая фронтальная проекция секущей плоскости Т.
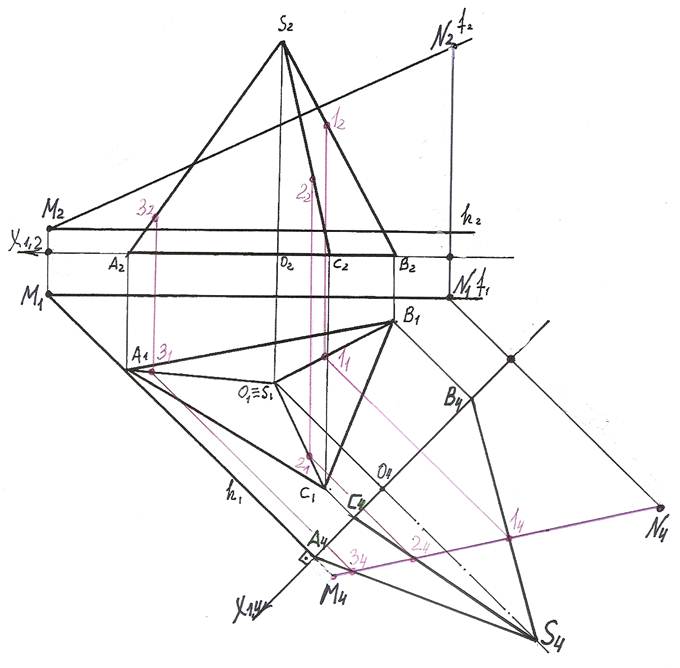
4). Вершины сечения лежат на пересечении фронтальной проекции M4N4 плоскости Т с новыми фронтальными проекциями ребер.
Горизонтальные проекции точек 1, 2, 3 получим по принадлежности их к соответствующим ребрам. 11 Î В1S1, 21 Î C1S1, 31 Î A1S1.
Фронтальные проекции 12, 22, 32 точек 1, 2, 3 также строим по принадлежности их к соответствующим ребрам. 12 Î В2S2, 22 Î C2S2, 32 Î A2S2.
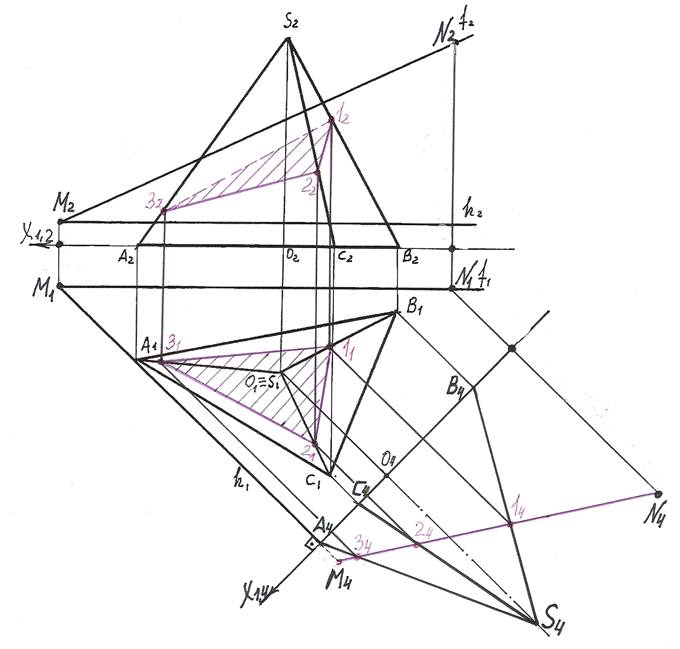
Соединяем точки 11, 21, 31 – получаем горизонтальную проекцию сечения.
Соединяем точки 12, 22, 32 – получаем фронтальную проекцию сечения.
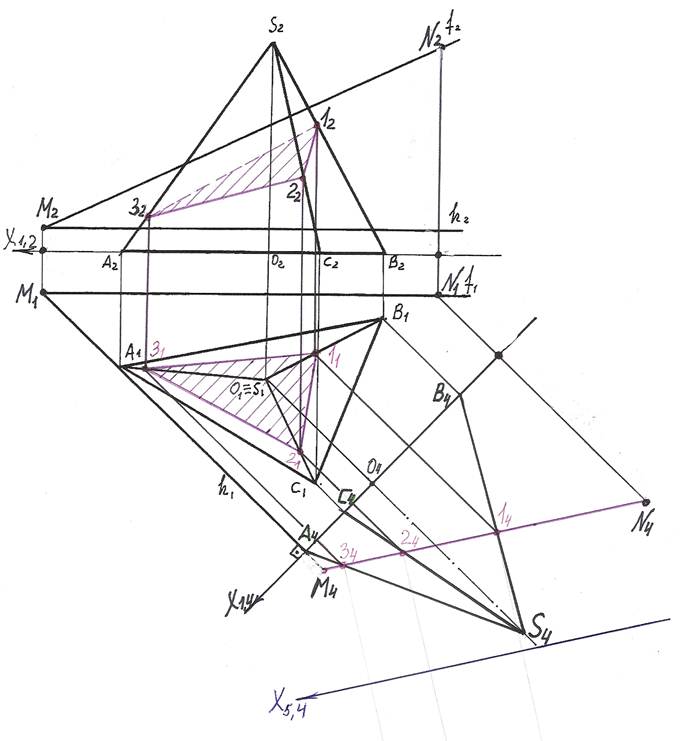
5). Далее, для определения натуральной величины сечения необходимо секущую плоскость преобразовать в плоскость уровня.
Для этого вместо плоскости П1 вводим новую плоскость П5, перпендикулярно оставшейся плоскости П4 так, чтобы она прошла параллельно секущей плоскости.
На чертеже новая ось Х4,5 пройдет параллельно следу M4N4 секущей плоскости Т.
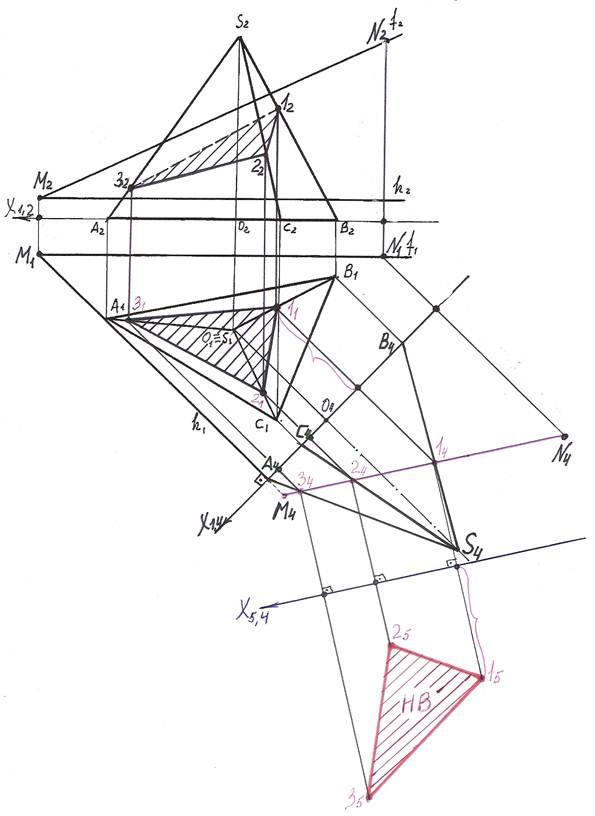
6). В новую плоскость П5 проецируем вершины сечения, точки 1, 2, 3. Для этого из точек 14, 24, 34 проводим линии проекционных связей, перпендикулярные оси Х4,5 и на их продолжении от новой оси Х4,5 откладываем отрезки, равные расстояниям
от оси Х1,4 до заменяемых точек 11, 21, 31 (координаты Y точек 1,2,3). Получаем точки 15, 25, 35; соединив эти точки получаем натуральную величину треугольника
∆ 1,2,3 – сечение пирамиды SABC плоскостью Т.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Студопедия рекомендует:
Формальная и неформальная коммуникация Можно выделить еще два вида организационной коммуникации: формальную.
Газовая хроматография Газовая хроматография представляет собой процесс разделения компонентов смеси.
Понятие о формах организации обучения. Соотношение между формами и методами обучения. Классификация основных и дополнительных форм обучения В педагогической литературе часто встречаются разные толкования таких понятий.
ПИЩЕВАРИТЕЛЬНАЯ СИСТЕМА Пищеварительная система представляет собой комплекс органов, функция которых заключается в механической и химической обработке.
Совместимость темпераментов и психологических портретов Для того чтобы лучше разобраться в принципах совместимости, хотелось бы обратить ваше внимание на некоторые теоретические моменты.
Источник
26 декабря, 2013 
Анна Веселова
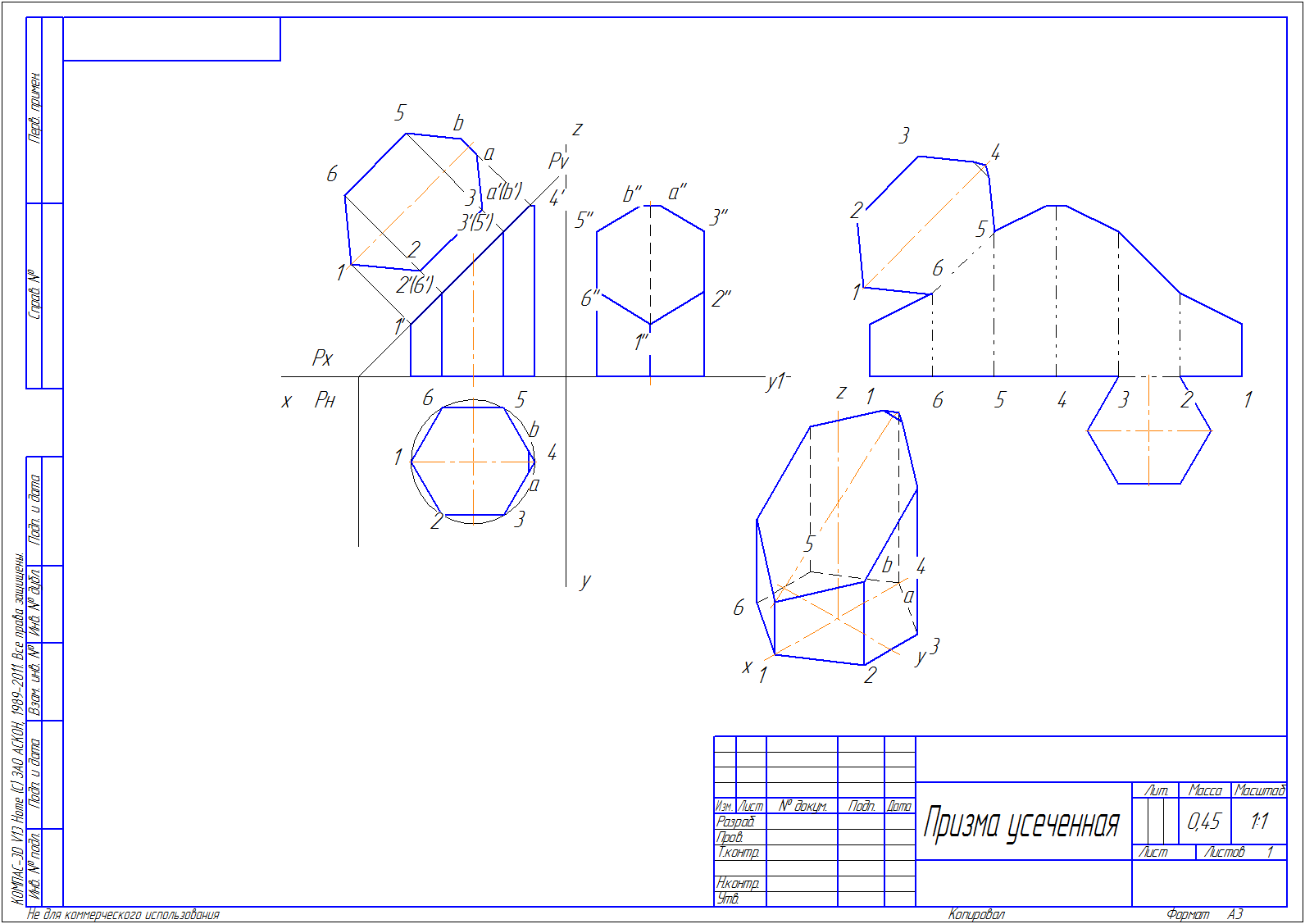
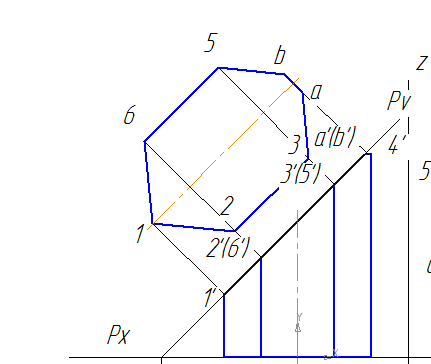
Здравствуйте! Сегодня мы коснемся такой темы, как сечение призмы плоскостью и построим развертку усеченной призмы в Компасе.
За основу возьмем 3d модель призмы из урока 2 по 3d моделированию.
Последовательность построения чертежа усеченной призмы
1. Создаем чертеж, меняем формат на А3.
2. На компактной панели активируем инструментальную панель «Виды», выбираем «Стандартные виды».
Находим файл с моделью призмы, создаем ассоциативный чертеж призмы.
4. Проводим осевые линии.
5. От центра симметрии призмы откладываем расстояние до следа секущей плоскости. В нашем примере это 37 мм. Из полученной точки проводим след секущей плоскости Pv под углом 45º
6. Обозначаем точки пересечения секущей плоскости с ребрами призмы на фронтальной проекции призмы и по линиям связи находим эти точки на оставшихся проекциях. Таким образом, получаем искаженные фигуры сечения призмы плоскостью в проекциях.
7. Но нам необходимо знать, как выглядит натуральный вид сечения призмы или действительная величина контура сечения. Строим его.
Построение натурального вида сечения призмы
8. Для построения из каждой точки фронтальной проекции поднимаем перпендикуляры.
9. Переносим соответствующие размеры с горизонтальной проекции призмы на новую горизонтальную проекцию (т. к. натуральный вид сечения мы строим способом перемены плоскостей проекций).
Развертка усеченной призмы
10. Развертку усеченной призмы будем строить на одной линии координатными осями проекций призмы. Так будет меньше вспомогательных построений.
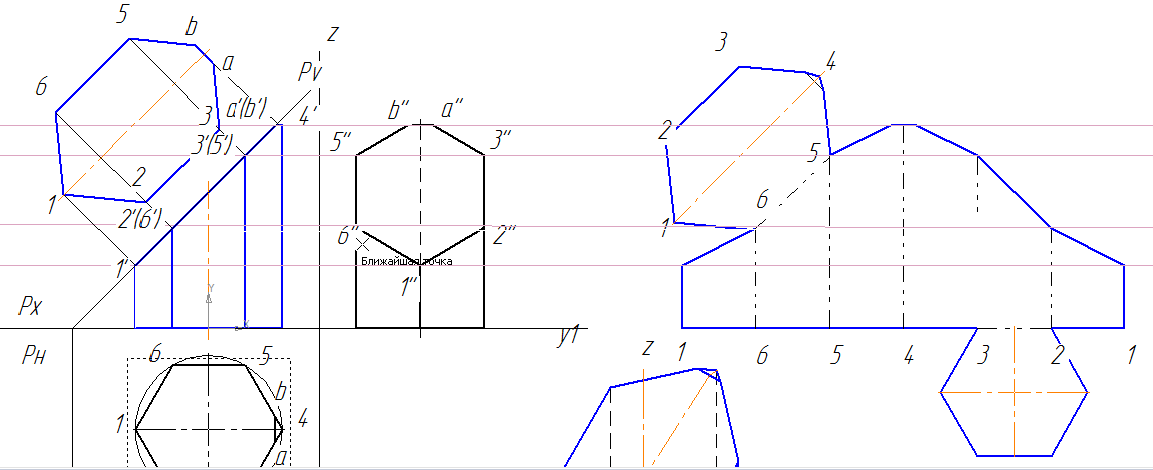
11. Сначала строим отрезок длиной, равной длине всех 6 ребер призмы, получается 120 мм.
12. Делим этот отрезок на 6 частей, нумеруем.
13. При помощи вспомогательных линий переносим высоты ребер усеченной призмы, соединяем вершины отрезков.
14. Действительную фигуру сечения переносим на развертку путем копирования (ctrl+выделяем левой кнопкой мыши), достраиваем нижнее основание призмы. Линии сгиба обозначаем специальной линией, она в Компасе называется – пунктир 2.
Строим изометрию усеченной призмы
15. Изометрию будем строить вручную, т. е. все операции построения в точности повторяют черчение аксонометрии на бумаге.
16. Проводим две вспомогательные линии под углами 30 и 150 градусов, строим изометрию нижнего основания – шестиугольник, нумеруем их.
17. Затем из каждой вершины шестиугольника поднимаем отрезки, высотой, равной высоте соответствующих отрезков на фронтальной проекции призмы. Соединяем точки. Изометрия готова.
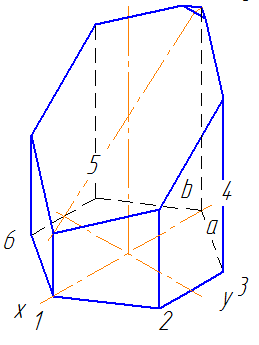
18. Теперь остается только оформить чертеж в соответствии с требованиями и заполнить основную надпись.
Весь процесс создания чертежа усеченной призмы подробно рассмотрен в небольшом видеоуроке.
Скачать чертеж бесплатно можно здесь
Теперь вы без труда построите сечение призмы плоскостью и развертку усеченной призмы.
The following two tabs change content below.
- Bio
- Latest Posts
Рада приветствовать Вас в своем блоге! Я создала его с целью помочь всем желающим освоить программу Компас 3d. Мы пройдем весь путь от азов черчения до создания серьезных сборок. Присоединяйтесь!
Понравился материал? Подпишись на обновления!
Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.
7.1. Общие понятия и определения. 7.2. Сечения многогранников и тел вращения плоскостями частного положения. Определение натуральной величины сечения. 7.3. Сечения многогранников и тел вращения плоскостями общего положения. Определение натуральной величины сечения
7.1. Общие понятия и определения
Сечением называется плоская фигура, полученная в результате пересечения геометрического тела секущей плоскостью и содержащая точки, принадлежащие поверхности тела и плоскости.
Сечение ограничивается замкнутой ломаной линией, если плоскостью пересекается гранная поверхность, и замкнутой кривой линией, если плоскостью пересекается кривая поверхность.
Построение линии сечения в общем случае сводится к определению точек пересечения ребер многогранника или образующих кривой поверхности с секущей плоскостью. Следовательно, построение линии сечения сводится к множественной задаче определения точек пересечения прямой с плоскостью.
7.2. Сечения многогранников и тел вращения плоскостями частного положения. Определение натуральной величины сечения
Сечение поверхностей гранных геометрических тел плоскостями частного положения. Сечением многогранника плоскостью является плоский многоугольник, вершины которого принадлежат ребрам, а стороны — граням многогранника. В зависимости от вида гранной поверхности и положения секущей плоскости сечение может принимать различные геометрические фигуры. Например, при пересечении поверхностей прямых правильных призмы и пирамиды плоскостями возможно образование геометрическихфигур, показанныхнарис. 88 и89.
Рис. 88. Сечение прямой призмы плоскостями частного положения
101
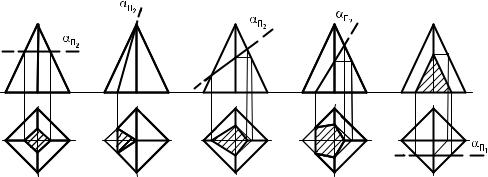
Рис. 89. Сечение прямой пирамиды плоскостями частного положения
Построение линии пересечения многогранника плоскостью сводится к многократному решению задачи на определение точек пересечения ребер многогранника с секущей плоскостью. Определение натуральной величины сечения гранной поверхности плоскостью определяют любым известным способом, например, способом совмещения секущей плоскости с плоскостью проекций, способом вращения, способом замены плоскостей проекций и т. д.
Рассмотрим некоторые примеры.
З а д а ч а 19
Дано: прямая шестигранная пирамида ABCDEFS с вершиной в точке S и фронтально-проецирующая плоскость α (рис. 90).
Выполнить: 1) построить линию пересечения пирамиды плоскостью; 2) определить натуральную величину сечения пирамиды плоскостью.
Порядок выполнения:
1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α
обладает собирательным свойством (любой геометрический элемент, принадлежащий фронтально-проецирующей плоскости, в т. ч. и линия пересечения пирамиды плоскостью, будет проецироваться в ее фронтальный след). Следовательно, пересечение фронтального следа αΠ2 с ребрами пирамиды образует фронтальную проекцию сечения
геометрического тела плоскостью 122232425262.
2.Горизонтальную проекцию сечения геометрического тела плос-
костью 112131415161 определяют из условия принадлежности точки прямой.
3.Натуральную величину сечения пирамиды плоскостью в данной задаче определяют способом вращения, совмещая секущую плоскость
сгоризонтальной плоскостью проекций, однако допустимо применение и любого другого способа.
102
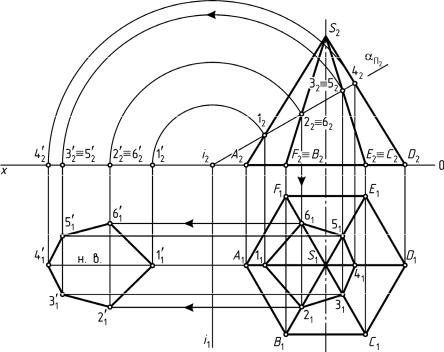
Рис. 90. Пересечение прямой пирамиды плоскостью частного положения
З а д а ч а 20 Дано: прямая шестигранная призма и фронтально-проецирующая
плоскость α (рис. 91).
Выполнить: 1) построить линию пересечения призмы плоскостью; 2) определить натуральную величину сечения призмы плоскостью.
Порядок выполнения:
1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α
обладает собирательным свойством (любой геометрический элемент, принадлежащий фронтально-проецирующей плоскости, будет проецироваться в ее фронтальный след). Следовательно, пересечение фронтального следа αΠ2 с ребрами призмы образует фронтальную проек-
цию сечения геометрического тела плоскостью 122232425262.
2.Призматическая поверхность является горизонтально-проеци- рующей, поэтому горизонтальную проекцию сечения геометрического
тела плоскостью 112131415161 определяют из этого условия и условия принадлежности точки прямой.
3.Натуральную величину сечения призмы плоскостью в данной задаче определяют способом вращения, совмещая секущую плоскость
сгоризонтальной плоскостью проекций, однако допустимо применение и любого другого способа.
103
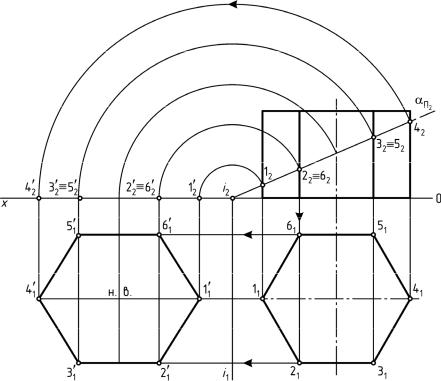
Рис. 91. Пересечение прямой призмы плоскостью частного положения
З а д а ч а 21
Дано: наклонная пирамида ABCDS с вершиной в точке S и горизон- тально-проецирующая плоскость α (рис. 92).
Выполнить: 1) построить линию пересечения пирамиды плоскостью; 2) определить натуральную величину сечения пирамиды плоскостью.
Порядок выполнения:
1. Горизонтальный след αΠ1 горизонтально-проецирующей плос-
кости α обладает собирательным свойством (любой геометрический элемент, принадлежащий горизонтально-проецирующей плоскости, в т. ч. и линия пересечения пирамиды плоскостью, будет проецироваться в ее горизонтальный след). Следовательно, пересечение следа αΠ1 с поверхностью наклонной пирамиды образует горизонтальную
проекциюсечениягеометрическоготелаплоскостью11213141.
2.Фронтальную проекцию сечения геометрического тела плоскостью 12223242 определяют из условия принадлежности точки прямой.
3.Натуральная величина сечения пирамиды плоскостью в данной задаче определена способом плоскопараллельного перемещения и вынесена за пределы графических построений.
104
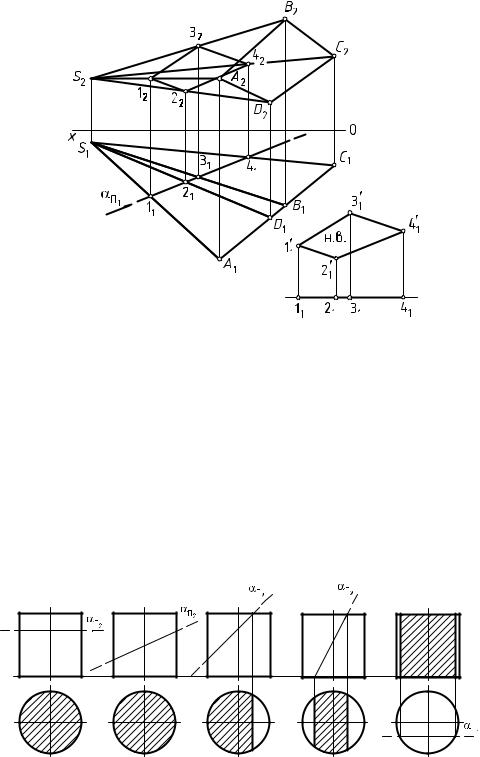
Рис. 92. Пересечение наклонной пирамиды плоскостью частного положения
Сечение поверхностей геометрических тел вращения плоско-
стями частного положения. Сечением тел вращения плоскостью является плоская кривая линия. В зависимости от вида поверхности вращения и положения секущей плоскости сечение может принимать различные геометрические фигуры. Так, при пересечении поверхности прямого кругового цилиндра плоскостью возможно образование следующих геометрических фигур:
окружности, если секущая плоскость перпендикулярна оси цилиндра, такое сечение называют нормальным (рис. 93, а);
эллипса, если секущая плоскость наклонена к оси цилиндра и пересекает все его образующие (рис. 93, б);
|
а |
б |
в |
г |
д |
|
Рис. 93. Пересечение прямого цилиндра плоскостями частного положения |
105
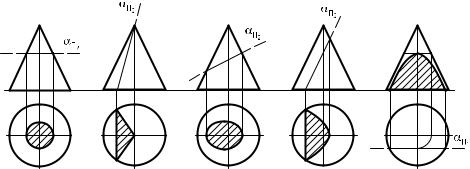
усеченного эллипса, если секущая плоскость наклонена к оси цилиндра и пересекает одно или оба его основания (рис. 93, в и г);
прямоугольника, если секущая плоскость параллельна оси цилинд-
ра (рис. 93, д).
При пересечении поверхности прямого кругового конуса плоскостью возможно образование следующих геометрических фигур:
окружности, если секущая плоскость перпендикулярна оси конуса
(рис. 94, а);
треугольника, если секущая плоскость пересекает конус через его вершину по двум образующим (рис. 94, б);
эллипса, если секущая плоскость наклонена к оси конуса и пересекает все его образующие (рис. 94, в).
параболы, если секущая плоскость параллельна одной из образующих конуса (рис. 94, г);
гиперболы, если секущая плоскость параллельна оси конуса или параллельна двум его образующим (рис. 94, д).
а б в г д
Рис. 94. Пересечение прямого конуса плоскостями частного положения
Построение линии пересечения тел вращения плоскостью сводится к многократному решению задачи на определение точек пересечения образующих кривой поверхности с секущей плоскостью.
Рассмотрим некоторые примеры. З а д а ч а 22
Дано: прямой круговой цилиндр и фронтально-проецирующая плоскость α (рис. 95, а).
Выполнить: 1) построить линию пересечения цилиндра плоскостью; 2) определить натуральную величину сечения цилиндра плоскостью.
Порядок выполнения:
1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α
обладает собирательным свойством. Следовательно, пересечение фронтального следа αΠ2 с поверхностью цилиндра образует фрон-
106
тальную проекцию сечения геометрического тела плоскостью
А21222D23242B25262C27282.
2.Цилиндрическая поверхность является горизонтально-проецирую- щей, поэтому горизонтальную проекцию сечения геометрического тела плоскостью А11121D13141B15161C17181 определяют из этого условия
иусловия принадлежности точки прямой.
3.Натуральную величину сечения цилиндра плоскостью в данной задаче определяют способом замены плоскостей проекций.
Рис. 95. Пересечение геометрических тел плоскостью частного положения
З а д а ч а 23 Дано: сфера и фронтально-проецирующая плоскость α (рис. 95, б).
Выполнить: 1) построить линию пересечения сферы плоскостью; 2) определить натуральную величину сечения сферы плоскостью.
Порядок выполнения:
1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α
обладает собирательным свойством. Следовательно, пересечение фронтального следа αΠ2 с поверхностью сферы образует фронтальную про-
екцию сечения геометрического тела плоскостью 1222426282725232.
107
2.Горизонтальную проекцию сечения геометрического тела
плоскостью 1121416181715131 определяют из условия принадлежности точки прямой.
3.Натуральную величину сечения сферы плоскостью в данной задаче определяют способом замены плоскостей проекций, однако допустимо применение и любого другого способа.
З а д а ч а 24 Дано: прямой круговой конус и фронтально-проецирующая плос-
костьα (рис. 96).
Выполнить: 1) построить линию пересечения конуса плоскостью; 2) определить натуральную величину сечения конуса плоскостью.
Рис. 96. Пересечение прямого конуса плоскостью частного положения
Порядок выполнения:
1. Фронтальный след αΠ2 фронтально-проецирующей плоскости α
обладает собирательным свойством. Следовательно, пересечение фронтального следа αΠ2 с поверхностью конуса образует фронталь-
ную проекцию сечения геометрического тела плоскостью
128242621022292523272.
2. Горизонтальную проекцию сечения геометрического тела плоскостью 118141611012191513171 определяют из условия принадлежности точки прямой.
108
3. Натуральную величину сечения конуса плоскостью в данной задаче определяют способом вращения, совмещая секущую плоскость с горизонтальной плоскостью проекций, однако допустимо применение и любого другого способа.
З а д а ч а 25 Дано: наклонный цилиндр и горизонтально-проецирующая плос-
кость α (рис. 97).
Рис. 97. Пересечение наклонного цилиндра плоскостью частного положения
Выполнить: 1) построить линию пересечения цилиндра плоскостью; 2) определить натуральную величину сечения цилиндра плоскостью.
109
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
10 дек2018
10 декабря 2018. Категория: #СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА/НАХОЖДЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ
Определение натуральной величины сечения
Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.
Дано: чертеж «Сечение комбинированной поверхности плоскостью».
Задание: Построить натуральную величину сечения, применив для этого любой способ преобразования чертежа.
Читать статью…
11 дек2018
11 декабря 2018. Автор статьи: Евгений Курицин. Категория: #СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА/НАХОЖДЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ
Натуральная величина сечения комбинированной поверхности
Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.
В предыдущем видеоуроке Пересечение поверхности плоскостью мы построили 3 проекции сечения. В этом видеоуроке мы построим натуральную величину сечения.
При использовании способа совмещения будет наложение изображений, поэтому фронталь плоскости сечения разместим на свободном поле чертежа. Радиус вращения каждой точки сечения возьмем с горизонтальной проекции и он будет соответствовать расстоянию от точки до продольной оси симметрии (оси вращения).
Читать статью…
10 дек2018
10 декабря 2018. Автор статьи: Евгений Курицин. Категория: #СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА/НАХОЖДЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ
Построение натуральной величины сечения
Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.
Дано: Пересечение многогранников (пирамиды и призмы)
Необходимо произвести построение натуральной величины сечения призмы, образованного гранью ACNM фронтально-проецирующей призмы.
Читать статью…
10 дек2018
10 декабря 2018. Автор статьи: Евгений Курицин. Категория: #СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА/НАХОЖДЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ
Натуральная величина треугольника
Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.
Задание: Определить натуральную величину треугольника ABC.
Дано: Таблица значения координат.
Читать статью…
10 дек2018
10 декабря 2018. Автор статьи: Евгений Курицин. Категория: #СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА/НАХОЖДЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ
Определение натуральной величины треугольника
Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.
Найти натуральную величину треугольника общего положения можно следующими действиями:
-
- Плоскопараллельным перемещением треугольник ABC приводится в положение проецирующией плоскости
- Вращением вокруг проецирующей прямой в пложение когда плоскость заданная треугольником будет параллельна плоскости проекций
В треугольнике ABC построим линию пересечения его с треугльником EDK.
Читать статью…
10 дек2018
10 декабря 2018. Автор статьи: Евгений Курицин. Категория: #СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА/НАХОЖДЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ
Способ совмещения как частный случай вращения
Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.
В предыдущем видеоуроке Автокад мы произвели сечение конуса плоскостью частного положения. В этом уроке мы найдем натуральную величину сечения конуса способом совмещения.
Дано: Сечение конуса плоскостью
Необходимо: Найти натуральную величину сечения конуса способом (методом) совмещения.
Способ совмещения в начертательной геометрии мы уже использовали в видеоуроке Автокад Построение натуральной величины сечения.
Читать статью…
10 дек2018
10 декабря 2018. Автор статьи: Евгений Курицин. Категория: #СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА/НАХОЖДЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ
Способ замены (перемены) плоскостей проекций
Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.
Чертеж Автокад Сечение цилиндра плоскостью содержит практически все данные для построения развертки усеченного цилиндра. Осталось только найти натуральную величину сечения цилиндра.
Натуральную величину сечения цилиндра найдем способом замены (перемены) плоскостей проекций.
Алгоритм решения задачи с использованием способа замены (перемены) плоскостей проекции.
Читать статью…
Цели и задачи уроки.
- Закрепление навыков и умений по построению
плоских и аксонометрических проекций 6-угольной
призмы, построение сечения призмы и определение
его натуральной величины, построение развертки. - Воспитание культуры труда, формирование
познавательного интереса к предмету,
инженерному делу. - Развитие пространственных представлений,
пространственного мышления.
Оборудование:
- модели геометрических тел,
- шаблоны для построения 6-и угольника в
изометрии, - развертка 6-и угольной призмы,
- чертежные инструменты и принадлежности.
План занятия.
- Повторение: положение прямых и плоскостей в
пространстве, способы преобразования чертежа. - Новый материал.
Лекционная часть.
2.1. Многогранники
2.2. Сечение многогранников
Практическая часть.
2.3. Построение 6-угольной призмы с сечением
фронтально-проецирующей плоскостью.
2.4. Построение развертки усеченной призмы.
Ход занятия
1. Вопросы для повторения:
Какие бывают прямые и плоскости?
– Общего и частного положения.
Как располагаются в пространстве проецирующие
прямые и проецирующие плоскости?
– Они перпендикулярны плоскостям проекций.
Назовите способы преобразования чертежа.
– Способ вращения, способ перемены плоскостей
проекций.
Когда применяется способ перемены плоскостей
проекций?
– Когда требуется определить натуральную
величину наклонного сечения для построения
развертки геометрического тела.
2. Записываем новую тему “Многогранники”.
Форма многих технических деталей представляет
собой сочетание простых геометрических тел.
Поэтому для выполнения чертежей изделий
необходимо знать, как правильно изображаются
различные геометрические тела. Рассмотрим
построение на комплексном чертеже основных
геометрических тел: призмы, пирамиды, цилиндра,
конуса, сферы, тора.
Призма.
Призмой называется многогранник, у которого 2
грани (основания) – равные многоугольники с
соответственно параллельными сторонами, а
боковые грани – прямоугольники (у прямой призмы)
или параллелограммы (у наклонной). Мы рассмотрим
прямую призму. Элементы призмы: вершины, ребра
(боковые и основания), грани (2 основания и
боковые).
Рассмотрим 3 проекции 6-угольной призмы. На
главном виде – это прямоугольники, боковые ребра
– это горизонтально проецирующие прямые,
6-угольник на виде сверху представляет собой
проекцию обоих оснований.
Сечение призмы выполнено
фронтально-проецирующей плоскостью.
Сечение поверхности геометрических тел
плоскостью называется плоская фигура, точки
которой принадлежат и поверхности тела, и
секущей плоскости. Сечение широко применяется в
техническом черчении для выявления формы и
внутреннего устройства предметов. В сечении
многогранника плоскостью образуется
многоугольник. Вершины многоугольника – это
точки пересечения ребер многогранника с секущей
плоскостью, стороны – это линии пересечения
секущей плоскости с гранями многогранника.
Задача на построение комплексного чертежа
усеченного многогранника состоит из решения
следующих вопросов:
- Построение проекций фигуры сечения.
- Определение натуральной величины сечения.
- Построение развертки отсеченной части.
- Построение аксонометрического изображения
отсеченной части.
Рассмотрим все поставленные задачи.
Задача 1. (см. Рис. 1).
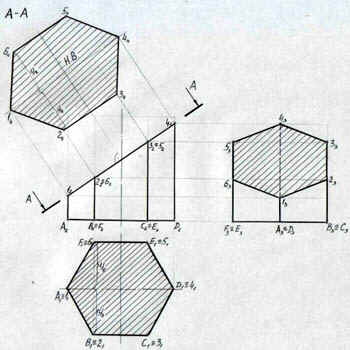
Для построения трех проекций усеченной призмы
выполняем следующие операции:
- Строим 3 проекции правильной 6-угольной призмы,
сторона основания а = 30, высота – произвольная. - Проводим фронтально-проецирующую секущую
плоскость А-А. - На горизонтальной проекции плоскость сечения
совпадает с проекцией основания ABCDEF, на
профильной проекции сечение строится путем
определения профильных проекций точек 1,2,3,4,5,6 и
их последовательного соединения.
Задача 2. (см. Рис. 1).
Решение задачи 2 проводится с использованием
чертежа, полученного при решении задачи 1. Для
определения натуральной величины сечения
используем метод вспомогательных секущих
плоскостей. Для решения задачи выполняем
следующие операции:
- На произвольном расстоянии и параллельно
секущей плоскости А-А проводим прямую. От
фронтальных проекций точек 1, 2, 3, 4, 5, 6 проводим
прямые, которые будут перпендикулярны плоскости
сечения. Прямые проводим до пересечения с новой
плоскостью проекций. - Новые проекции точек 1, 2, 3, 4, 5, 6 получаем
перенося горизонтальные проекции данных точек в
новую систему координат. - Полученный 6-и угольник в новой системе
плоскостей проекций и будет являться
натуральной величиной сечения 6-угольной призмы.
Задача 3. (см. Рис. 2).
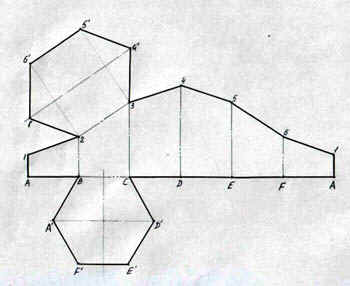
Разверткой (выкройкой) поверхности тела
называется плоская фигура, полученная путем
совмещения всех точек данной поверхности с
плоскостью без разрывов и складок.
Построение разверток выполняется обычно
графическими приемами, с применением способов,
предлагаемых начертательной геометрией.
Построение развертки поверхности многогранника
сводится к определению истинной величины каждой
его грани по чертежу многогранника (см. Рис. 1).
После этого грани многогранника стыкуются
(соединяются) по ребрам и вершинам.
Для решения задачи 3 выполняем следующие
операции:
Проводим горизонтальную прямую, на которой от
произвольно выбранной точки А, откладываем
отрезки AB, BC, CD, DE, EF, FA, равные длине стороны
основания а = 30.
Из точек A, B, C, D, E, F, A восстанавливаем
перпендикуляры и на них откладываем величины
ребер усеченной призмы. Величины данных отрезков
A1, B2, C3, D4, E5, F6, A1 берем с фронтальной проекции
усеченной призмы. Полученные точки соединяем и
получаем развертку боковой поверхности призмы.
К одному из отрезков основания, например к BC,
пристраиваем 6-угольник ABCDEF.
К одному из звеньев ломаной, например, к отрезку
2-3, пристраиваем 6-угольник 123456 (сечение призмы),
который переносим, используя метод засечек, с
рисунка 1.
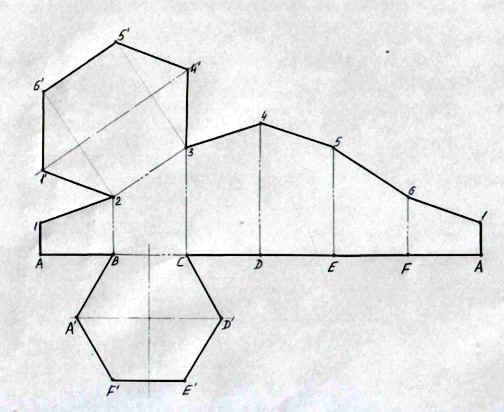
Рис |
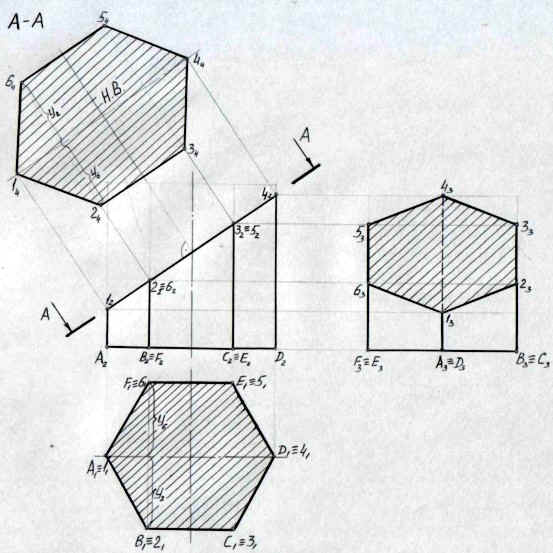
Рис |
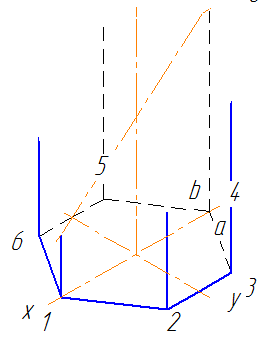
Задача 4. (см. рис. 3)
Строим усеченную 6-и угольную призму в
изометрии. Сторона основания призмы, а = 30. Для
выполнения задачи учащимся раздаются трафареты
6-и угольника в изометрии. Высоты A1, B2, C3, D4, E5, F6 –
берем с фронтальной проекции усеченной призмы.
