Как найти натуральный логарифм числа вручную - Сайт, где вы сможете решить свои вопросы

Как найти натуральный логарифм числа вручную? (Смысл я понимаю, но какой алгоритм нахождения?)

Егорка Сумкин

Знаток

(268),
закрыт

8 лет назад

Например ln(5);
Как же мне узнать какую надо степень у 2,718… чтобы получить 5.
Что-то не могу врубиться..

Илья

Высший разум

(360632)

8 лет назад

Ваш вопрос противоречит смыслу самого создания логарифмов. Они и предназначены были для того, чтоб использовать готовые таблицы. Один человек посчитал – и все могут пользоваться – заменять умножение сложением. Если каждый раз самому находить логарифмы, то это не упрощение расчетов, а существенное их усложнение.

Дивергент

Высший разум

(1538457)

8 лет назад

Это изучают в курсе высшей математики в ВУЗе, деточка. Есть разложение функции в ряд Маклорена, пример приведен тебе выше во втором ответе. Калькулятор, вычисляя ln(5), сначала решает уравнение
(1+x)/(1-x)=5
1+x=5-5*x
6*x=4
x=0,66666666666666666667
а затем подставляет это значение в ряд вместо х для вычисления логарифма с необходимой точностью, вот и все)) Можешь и сам это проделать, если время есть)) А вот КАК разложить ту или иную функцию в ряд Маклорена как раз и изучают в курсе высшей математики)))

Источник

Логарифмом положительного числа (c) по основанию (a) ((a>0, aneq1)) называется показатель степени (b), в которую надо возвести основание (a), чтобы получить число (c) ((c>0)), т.е.

(a^{b}=c) (Leftrightarrow) (log_{a}{c}=b)

Объясним проще. Например, (log_{2}{8}) равен степени, в которую надо возвести (2), чтоб получить (8). Отсюда понятно, что (log_{2}{8}=3).

Примеры:	(log_{5}{25}=2)	т.к. (5^{2}=25)
	(log_{3}{81}=4)	т.к. (3^{4}=81)
	(log_{2})(frac{1}{32})(=-5)	т.к. (2^{-5}=)(frac{1}{32})

Аргумент и основание логарифма

Любой логарифм имеет следующую «анатомию»:

Аргумент логарифма обычно пишется на его уровне, а основание – подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».

Как вычислить логарифм?

Чтобы вычислить логарифм – нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?

Например, вычислите логарифм: а) (log_{4}{16}) б) (log_{3})(frac{1}{3}) в) (log_{sqrt{5}}{1}) г) (log_{sqrt{7}}{sqrt{7}}) д) (log_{3}{sqrt{3}})

а) В какую степень надо возвести (4), чтобы получить (16)? Очевидно во вторую. Поэтому:

(log_{4}{16}=2)

б) В какую степень надо возвести (3), чтобы получить (frac{1}{3})? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени).

(log_{3})(frac{1}{3})(=-1)

в) В какую степень надо возвести (sqrt{5}), чтобы получить (1)? А какая степень делает любое число единицей? Ноль, конечно!

(log_{sqrt{5}}{1}=0)

г) В какую степень надо возвести (sqrt{7}), чтобы получить (sqrt{7})? В первую – любое число в первой степени равно самому себе.

(log_{sqrt{7}}{sqrt{7}}=1)

д) В какую степень надо возвести (3), чтобы получить (sqrt{3})? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень – это степень (frac{1}{2}).

(log_{3}{sqrt{3}}=)(frac{1}{2})

Пример: Вычислить логарифм (log_{4sqrt{2}}{8})

Решение:

(log_{4sqrt{2}}{8}=x)		Нам надо найти значение логарифма, обозначим его за икс. Теперь воспользуемся определением логарифма: (log_{a}{c}=b) (Leftrightarrow) (a^{b}=c)
((4sqrt{2})^{x}=8)		Что связывает (4sqrt{2}) и (8)? Двойка, потому что и то, и другое число можно представить степенью двойки: (4=2^{2}) (sqrt{2}=2^{frac{1}{2}}) (8=2^{3})
({(2^{2}cdot2^{frac{1}{2}})}^{x}=2^{3})		Слева воспользуемся свойствами степени: (a^{m}cdot a^{n}=a^{m+n}) и ((a^{m})^{n}=a^{mcdot n})
(2^{frac{5}{2}x}=2^{3})		Основания равны, переходим к равенству показателей
(frac{5x}{2})(=3)		Умножим обе части уравнения на (frac{2}{5})
(x=1,2)		Получившийся корень и есть значение логарифма

Ответ: (log_{4sqrt{2}}{8}=1,2)

Foxford

Зачем придумали логарифм?

Чтобы это понять, давайте решим уравнение: (3^{x}=9). Просто подберите (x), чтобы равенство сработало. Конечно, (x=2).

А теперь решите уравнение: (3^{x}=8).Чему равен икс? Вот в том-то и дело.

Самые догадливые скажут: «икс чуть меньше двух». А как точно записать это число? Для ответа на этот вопрос и придумали логарифм. Благодаря ему, ответ здесь можно записать как (x=log_{3}{8}).

Хочу подчеркнуть, что (log_{3}{8}), как и любой логарифм – это просто число. Да, выглядит непривычно, но зато коротко. Потому что, если бы мы захотели записать его в виде десятичной дроби, то оно выглядело бы вот так: (1,892789260714…..)

Пример: Решите уравнение (4^{5x-4}=10)

Решение:

(4^{5x-4}=10)		(4^{5x-4}) и (10) никак к одному основанию не привести. Значит тут не обойтись без логарифма. Воспользуемся определением логарифма: (a^{b}=c) (Leftrightarrow) (log_{a}{c}=b)
(log_{4}{10}=5x-4)		Зеркально перевернем уравнение, чтобы икс был слева
(5x-4=log_{4}{10})		Перед нами линейное уравнение. Перенесем (4) вправо. И не пугайтесь логарифма, относитесь к нему как к обычному числу.
(5x=log_{4}{10}+4)		Поделим уравнение на 5
(x=)(frac{log_{4}{10}+4}{5})		Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.

Ответ: (frac{log_{4}{10}+4}{5})

Десятичный и натуральный логарифмы

Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы ((a>0, aneq1)). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:

Натуральный логарифм: логарифм, у которого основание – число Эйлера (e) (равное примерно (2,7182818…)), и записывается такой логарифм как (ln{a}).

То есть, (ln{a}) это то же самое, что и (log_{e}{a}), где (a) – некоторое число.

Десятичный логарифм: логарифм, у которого основание равно 10, записывается (lg{a}).

То есть, (lg{a}) это то же самое, что и (log_{10}{a}), где (a) – некоторое число.

Основное логарифмическое тождество

У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:

Это свойство вытекает напрямую из определения. Посмотрим как именно эта формула появилась.

Вспомним краткую запись определения логарифма:

если (a^{b}=c), то (log_{a}{c}=b)

То есть, (b) – это тоже самое, что (log_{a}{c}). Тогда мы можем в формуле (a^{b}=c) написать (log_{a}{c}) вместо (b). Получилось (a^{log_{a}{c}}=c) – основное логарифмическое тождество.

Остальные свойства логарифмов вы можете найти здесь. С их помощью можно упрощать и вычислять значения выражений с логарифмами, которые «в лоб» посчитать сложно.

Пример: Найдите значение выражения (36^{log_{6}{5}})

Решение:

(36^{log_{6}{5}}=)		Сразу пользоваться свойством (a^{log_{a}{c}}=c) мы не можем, так как в основании степени и в основании логарифма – разные числа. Однако мы знаем, что (36=6^{2})
(=(6^{2})^{log_{6}{5}}=)		Зная формулу ((a^{m})^{n}=a^{mcdot n}), а так же то, что множители можно менять местами, преобразовываем выражение
(=6^{2cdotlog_{6}{5}}=6^{log_{6}{5}cdot2}=(6^{log_{6}{5}})^{2}=)		Вот теперь спокойно пользуемся основным логарифмическим тождеством.
(=5^{2}=25)		Ответ готов.

Ответ: (25)

Как число записать в виде логарифма?

Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что (log_{2}{4}) равен двум. Тогда можно вместо двойки писать (log_{2}{4}).

Но (log_{3}{9}) тоже равен (2), значит, также можно записать (2=log_{3}{9}) . Аналогично и с (log_{5}{25}), и с (log_{9}{81}), и т.д. То есть, получается

(2=log_{2}{4}=log_{3}{9}=log_{4}{16}=log_{5}{25}=log_{6}{36}=log_{7}{49}…)

Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.

Точно также и с тройкой – ее можно записать как (log_{2}{8}), или как (log_{3}{27}), или как (log_{4}{64})… Здесь мы как аргумент пишем основание в кубе:

(3=log_{2}{8}=log_{3}{27}=log_{4}{64}=log_{5}{125}=log_{6}{216}=log_{7}{343}…)

И с четверкой:

(4=log_{2}{16}=log_{3}{81}=log_{4}{256}=log_{5}{625}=log_{6}{1296}=log_{7}{2401}…)

И с минус единицей:

(-1=) (log_{2})(frac{1}{2})(=) (log_{3})(frac{1}{3})(=) (log_{4})(frac{1}{4})(=) (log_{5})(frac{1}{5})(=) (log_{6})(frac{1}{6})(=) (log_{7})(frac{1}{7})(…)

И с одной третьей:

(frac{1}{3})(=log_{2}{sqrt[3]{2}}=log_{3}{sqrt[3]{3}}=log_{4}{sqrt[3]{4}}=log_{5}{sqrt[3]{5}}=log_{6}{sqrt[3]{6}}=log_{7}{sqrt[3]{7}}…)

И так далее.

Любое число (a) может быть представлено как логарифм с основанием (b): (a=log_{b}{b^{a}})

Пример: Найдите значение выражения (frac{log_{2}{14}}{1+log_{2}{7}})

Решение:

(frac{log_{2}{14}}{1+log_{2}{7}})(=)		Превращаем единицу в логарифм с основанием (2): (1=log_{2}{2})
(=)(frac{log_{2}{14}}{log_{2}{2}+log_{2}{7}})(=)		Теперь пользуемся свойством логарифмов: (log_{a}{b}+log_{a}{c}=log_{a}{(bc)})
(=)(frac{log_{2}{14}}{log_{2}{(2cdot7)}})(=)(frac{log_{2}{14}}{log_{2}{14}})(=)		В числителе и знаменателе одинаковые числа – их можно сократить.
(=1)		Ответ готов.

Ответ: (1)

Смотрите также:
Логарифмические уравнения
Логарифмические неравенства

Источник

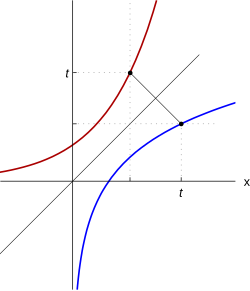
Функция натурального логарифма (синяя кривая) обратна к экспоненте (красная кривая)

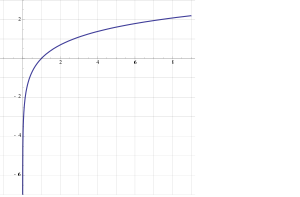
График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0

Натуральный логарифм — логарифм по основанию e, где — трансцендентная константа, равная приблизительно 2,72. Он обозначается как ln x , ${displaystyle log _{e}x}$ или иногда просто log x , если основание подразумевается^[1]. Обычно число под знаком логарифма вещественное, но можно расширить это понятие и на комплексные числа.

Из определения следует, что логарифмическая зависимость есть обратная функция для экспоненты ${displaystyle y=e^{x}}$ , поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (см. рисунок справа). Как и экспонента, логарифмическая функция относится к категории трансцендентных функций.

Натуральные логарифмы полезны для решения алгебраических уравнений, в которых неизвестная присутствует в качестве показателя степени, они незаменимы в математическом анализе. В приложениях натуральный логарифм участвует в математическом описании таких процессов, в которых скорость изменения некоторого количества в каждый момент обратно пропорциональна самому количеству. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада радиоактивного вещества: чем больше атомов распадается, тем меньше их становится и тем медленнее идет дальнейший процесс. Натуральные логарифмы играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения различных задач, (например, нахождение сложных процентов).

Определение[править | править код]

Натуральный логарифм числа — это показатель степени, в которую нужно возвести число e, чтобы получить . Другими словами, натуральный логарифм есть решение уравнения ${displaystyle e^{x}=a.}$

Примеры:

, потому что ${displaystyle e^{1}=e}$

;

, потому что ${displaystyle e^{0}=1}$

Вещественный натуральный логарифм[править | править код]

определяется как площадь под кривой ${displaystyle f(x)={frac {1}{x}}}$ от до .

Натуральный логарифм для вещественного числа определён и однозначен для любого положительного числа

Натуральный логарифм может быть также определён геометрически для любого положительного вещественного числа a как площадь под кривой ${displaystyle y={frac {1}{x}}}$ на промежутке . Простота этого определения, которое согласуется со многими другими формулами, в которых применяется данный логарифм, объясняет происхождение названия «натуральный».

Свойства[править | править код]

Из определения логарифма следует основное логарифмическое тождество^[2]:

${displaystyle e^{ln a}=a}$

Приведём сводку формул в предположении, что все значения положительны^[3]:

	Формула	Пример
Произведение
Частное	${displaystyle ln left({frac {x}{y}}right)=ln x-ln y}$	${displaystyle ln left({frac {1}{e^{2}}}right)=ln(1)-ln(e^{2})=0-2=-2}$
Степень	${displaystyle ln(x^{p})=pln x}$	${displaystyle ln(64)=ln(2^{6})=6ln 2}$
Корень	${displaystyle ln {sqrt[{p}]{x}}={frac {ln x}{p}}}$	${displaystyle ln {sqrt {10}}={frac {1}{2}}ln 10}$

Другие свойства:

Связь с логарифмами по другому основанию[править | править код]

Логарифм может быть определён для любого положительного основания, отличного от , а не только для , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем.

Логарифм $log _{a}b$ по основанию можно преобразовать^[4] в натуральный логарифм и обратно:

${displaystyle ln b={frac {log _{a}b}{log _{a}e}}=log _{a}bcdot ln a}$

${displaystyle log _{a}b={frac {ln b}{ln a}}}$

Связь десятичного ( lg x ) и натурального логарифмов^[5]:

ln xapprox 2{,}30259 lg x;quad lg xapprox 0{,}43429 ln x

Связь двоичного () и натурального логарифмов:

{displaystyle ln xapprox 0,693147operatorname {lb} x;quad operatorname {lb} xapprox 1{,}442695ln x}

Логарифмическая функция[править | править код]

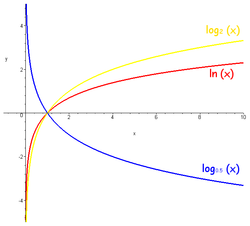
Графики логарифмических функций; красная кривая — натуральный логарифм

Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию y=ln x . Она определена при x>0 . Область значений: . Эта кривая часто называется логарифмикой^[6]. Из формулы замены основания логарифма видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси ; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.

Функция является строго возрастающей, она непрерывна и неограниченно дифференцируема всюду в своей области определения.

Ось ординат ( x=0 ) является вертикальной асимптотой, поскольку:

${displaystyle lim _{xto 0+}ln x=-infty }$

Производная натуральной логарифмической функции равна:

${frac {d}{dx}}ln x={frac {1}{x}}$

Простота этой формулы — одна из причин широкого использования именно натурального логарифма в анализе и при решении дифференциальных уравнений.

Проинтегрировав формулу для производной в интервале от x=1 до x=b , мы получаем:

$ln b=int limits _{1}^{b}{frac {dx}{x}}$

Другими словами, натуральный логарифм равен площади под гиперболой ${displaystyle y={frac {1}{x}}}$ для указанного интервала .

С точки зрения общей алгебры, логарифмическая функция осуществляет (единственно возможный) изоморфизм мультипликативной группы положительных вещественных чисел и аддитивной группы всех вещественных чисел. Другими словами, логарифмическая функция есть единственное (определённое для всех положительных значений аргумента) непрерывное решение функционального уравнения^[7]:

Аналитические свойства функции[править | править код]

Из формулы для производной натурального логарифма следует, что первообразная для гиперболы y=1/x имеет вид:

{displaystyle int {dx over x}=ln |x|+C,}

где — произвольная константа интегрирования. Поскольку функция y=1/x состоит из двух ветвей (одна для положительных, другая для отрицательных ), семейство первообразных для y=1/x тоже состоит из двух подсемейств, причём константы интегрирования у них независимы одна от другой.

Неопределённый интеграл от натурального логарифма легко найти интегрированием по частям:

В математическом анализе и теории дифференциальных уравнений большую роль играет понятие логарифмической производной функции f(x) :

${frac {d}{dx}}ln(f(x))={frac {f'(x)}{f(x)}}$

Методы вычисления логарифма[править | править код]

Разложим натуральный логарифм в ряд Тейлора вблизи единицы:

$ln(1+x)=x-{frac {x^{2}}{2}}+{frac {x^{3}}{3}}-{frac {x^{4}}{4}}+dots$

(Ряд 1)

Этот ряд, называемый «рядом Меркатора», сходится при . В частности:

$ln 2=1-{frac {1}{2}}+{frac {1}{3}}-{frac {1}{4}}+dots$

Формула ряда 1 непригодна для практического расчёта логарифмов из-за того, что ряд сходится очень медленно и только в узком интервале. Однако нетрудно получить из неё более удобную формулу:

$ln left({frac {1+x}{1-x}}right)=2left(x+{frac {x^{3}}{3}}+{frac {x^{5}}{5}}+{frac {x^{7}}{7}}+dots right)$

(Ряд 2)

Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа ${displaystyle z={frac {1+x}{1-x}}}$ , ибо тогда ${displaystyle x={frac {z-1}{z+1}}}$ по абсолютной величине меньше единицы. Данный алгоритм уже пригоден для реальных численных расчётов значений логарифмов, однако не является наилучшим с точки зрения трудоёмкости.

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула:^[8]^[9]:

$ln xapprox {frac {pi }{2M(1,4/s)}}-mln 2$

где обозначает арифметико-геометрическое среднее 1 и 4/s, и

$s=x,2^{m}>2^{{p/2}},$

m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.

Полезные пределы[править | править код]

Приведём несколько полезных пределов, связанных с логарифмами^[10]:

${displaystyle lim _{xto 0}{frac {ln(1+x)}{x}}=1}$

${displaystyle lim _{xto 0+}x^{b}ln x=0quad (b>0)}$

${displaystyle lim _{xto infty }{frac {ln x}{x^{b}}}=0quad (b>0)}$

$ln x=lim _{nto infty }nleft({sqrt[{n}]{x}}-1right)=lim _{nto infty }nleft(1-{frac {1}{sqrt[{n}]{x}}}right)$

$ln x=lim _{hto 0}{frac {x^{h}-1}{h}}$

Трансцендентность[править | править код]

Из теоремы Линдемана — Вейерштрасса (1885) вытекает следующее следствие: если аргумент есть алгебраическое число, отличное от единицы, то значение ln x есть не только иррациональное, но и трансцендентное число^[11].

Непрерывные дроби[править | править код]

Хотя для представления логарифма отсутствуют классические непрерывные дроби, но можно использовать несколько «обобщённых непрерывных дробей», в том числе:

${displaystyle ln(1+x)={frac {x^{1}}{1}}-{frac {x^{2}}{2}}+{frac {x^{3}}{3}}-{frac {x^{4}}{4}}+{frac {x^{5}}{5}}-dots ={cfrac {x}{1-0cdot x+{cfrac {1^{2}x}{2-1cdot x+{cfrac {2^{2}x}{3-2x+{cfrac {3^{2}x}{4-3x+{cfrac {4^{2}x}{5-4x+ddots }}}}}}}}}}}$

${displaystyle ln left(1+{frac {2x}{y}}right)={cfrac {2x}{y+{cfrac {x}{1+{cfrac {x}{3y+{cfrac {2x}{1+{cfrac {2x}{5y+{cfrac {3x}{1+ddots }}}}}}}}}}}}={cfrac {2x}{y+x-{cfrac {(1x)^{2}}{3(y+x)-{cfrac {(2x)^{2}}{5(y+x)-{cfrac {(3x)^{2}}{7(y+x)-ddots }}}}}}}}}$

История[править | править код]

Впервые натуральные логарифмы в современном понимании появились в 1619 году, когда лондонский учитель математики Джон Спейдель переиздал логарифмические таблицы Непера, исправленные и дополненные так, что они фактически стали таблицами натуральных логарифмов^[12]. В 1649 году бельгийский математик Грегуар де Сен-Венсан показал, что площадь под гиперболой ${displaystyle y={frac {1}{x}}}$ меняется по логарифмическому закону, и предложил называть этот вид логарифмов «гиперболическим»^[13].

Термин «натуральный логарифм» ввели в употребление Пьетро Менголи (1659 год) и Николас Меркатор в фундаментальном труде «Logarithmotechnia» (1668)^[14]^[15]. Там же Меркатор описал разложение натурального логарифма в «ряд Меркатора».

Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма^[16]. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Д’Аламбером и Эйлером. Бернулли и Д’Аламбер считали, что следует определить , в то время как Лейбниц доказывал, что логарифм отрицательного числа есть мнимое число^[16]. Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной^[17].

Комплексные логарифмы[править | править код]

Комплексный логарифм — аналитическая функция, получаемая распространением вещественного логарифма на всю комплексную плоскость (кроме нуля). В отличие от вещественного случая, функция комплексного логарифма многозначна.

Определение. Натуральный логарифм комплексного числа представляет собой^[6] решение уравнения $e^{w}=z.$

Ненулевое число можно представить в показательной форме:

$z=rcdot e^{{i(varphi +2pi k)}};;,$

где

— произвольное целое число

Тогда находится по формуле^[18]:

mathrm {Ln} ,z=ln r+ileft(varphi +2pi kright)

Здесь — вещественный логарифм. Отсюда вытекает:

Из формулы видно, что у одного и только одного из значений мнимая часть находится в интервале . Это значение называется главным значением комплексного натурального логарифма^[6]. Соответствующая (уже однозначная) функция называется главной ветвью логарифма и обозначается ln ,z . Если — вещественное число, то главное значение его логарифма совпадает с обычным вещественным логарифмом.

Логарифм отрицательного числа находится по формуле^[18]:

mathrm {Ln} (-x)=ln x+ipi (2k+1)qquad (x>0, k=0,pm 1,pm 2dots )

Примеры:

$ln(i)=i{frac {pi }{2}};;mathrm {Ln} (i)=i{frac {4k+1}{2}}pi$

Следует быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:

$ipi =ln(-1)=ln((-i)^{2})=2ln(-i)=2(-ipi /2)=-ipi$

— явная ошибка.

Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви ( k=-1 ). Причина ошибки — неосторожное использование свойства $log _{a}{(b^{p})}=p~log _{a}b$ , которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.

Функции натурального логарифма на комплексной плоскости (главная ветвь)
Суперпозиция трёх предыдущих графиков

Функция натурального логарифма комплексного числа может быть также определена как аналитическое продолжение вещественного логарифма на всю комплексную плоскость, кроме нуля. Пусть кривая Gamma начинается в единице, заканчивается в z, не проходит через нуль и не пересекает отрицательную часть вещественной оси. Тогда главное значение логарифма в конечной точке кривой Gamma можно определить по формуле^[19]:

$ln z=int limits _{Gamma }{du over u}$

Некоторые применения[править | править код]

Теория чисел[править | править код]

Распределение простых чисел асимптотически подчиняется простым законам^[20]:

Число простых чисел в интервале от 1 до приблизительно равно ${frac {n}{ln n}}$ .
k-е простое число приблизительно равно .

Математический анализ[править | править код]

Логарифмы нередко возникают при нахождении интегралов и при решении дифференциальных уравнений. Примеры:

${displaystyle int {operatorname {tg} x},dx=-ln |cos x|+C;quad int {frac {dx}{sqrt {x^{2}+a}}}=-ln left| x+{sqrt {x^{2}+a}} right|+C}$

Теория вероятностей и статистика[править | править код]

В статистике и теории вероятностей логарифм входит в ряд практически важных вероятностных распределений. Например, логарифмическое распределение^[21] используется в генетике и физике. Логнормальное распределение часто встречается в ситуациях, когда исследуемая величина есть произведение нескольких независимых положительных случайных переменных^[22].

Для оценки неизвестного параметра широко применяются метод максимального правдоподобия и связанная с ним логарифмическая функция правдоподобия^[23].

Флуктуации при случайном блуждании описывает закон Хинчина-Колмогорова.

Фракталы и размерность[править | править код]

Логарифмы помогают выразить размерность Хаусдорфа для фрактала^[24]. Например, рассмотрим треугольник Серпинского, который получается из равностороннего треугольника последовательным удалением аналогичных треугольников, линейный размер каждого из которых на каждом этапе уменьшается вдвое (см. рисунок). Размерность результата определяется по формуле:

${frac {ln 3}{ln 2}}approx 1{,}58$

Механика и физика[править | править код]

Принцип Больцмана в статистической термодинамике — одна из важнейших функций состояния термодинамической системы, характеризующая степень её хаотичности.

Формула Циолковского применяется для расчёта скорости ракеты.

Химия и физическая химия[править | править код]

Уравнение Нернста связывает окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, а также со стандартными электродными потенциалами окислительно-восстановительных пар.

Логарифм используется в определениях таких величин, как показатель константы автопротолиза (самоионизации молекулы) и водородный показатель (кислотности раствора).

Психология и физиология[править | править код]

Человеческое восприятие многих явлений хорошо описывается логарифмическим законом.

Закон Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности стимула^[25] — громкости звука^[26], яркости света.

Закон Фиттса: чем дальше или точнее выполняется движение организма, тем больше коррекции необходимо для его выполнения и тем дольше эта коррекция исполняется^[27].

Время на принятие решения при наличии выбора можно оценить по закону Хика^[en]^[28].

Примечания[править | править код]

↑ Mortimer, Robert G. Mathematics for physical chemistry (неопр.). — 3rd. — Academic Press, 2005. — С. 9. — ISBN 0-125-08347-5., Extract of page 9 Архивная копия от 24 июня 2016 на Wayback Machine
↑ Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 233.
↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187.
↑ Корн Г., Корн Т. Справочник по математике, 1973, с. 34.
↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189..
↑ ¹ ² ³ Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 159-160.
↑ Sasaki T., Kanada Y. Practically fast multiple-precision evaluation of log(x) (англ.) // Journal of Information Processing. — 1982. — Vol. 5, iss. 4. — P. 247—250.
↑ Ahrendt, Timm. Fast computations of the exponential function. Lecture notes in computer science (неопр.). — 1999. — Т. 1564. — С. 302—312. — doi:10.1007/3-540-49116-3_28.
↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 164.
↑ Рудио Ф. О квадратуре круга (Архимед, Гюйгенс, Ламберт, Лежандр). — Изд. 3-е. — М.—Л.: ОГИЗ, 1936. — С. 89. — 237 с. — (Классики естествознания).
↑ Cajori, Florian. A History of Mathematics, 5th ed (неопр.). — AMS Bookstore, 1991. — С. 152. — ISBN 0821821024.
↑ Flashman, Martin. Estimating Integrals using Polynomials. Дата обращения: 30 июня 2011. Архивировано 11 февраля 2012 года.
↑ Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II. — С. 63.
↑ J J O’Connor and E F Robertson. The number e. The MacTutor History of Mathematics archive (сентябрь 2001). Дата обращения: 30 июня 2011. Архивировано 11 февраля 2012 года.
↑ ¹ ² История математики, том III, 1972, с. 325-328..
↑ Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 27, 230—231..
↑ ¹ ² Корн Г., Корн Т. Справочник по математике, 1973, с. 623..
↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967, с. 45-46, 99-100..
↑ Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2.
↑ Weisstein, Eric W. Log-Series Distribution (англ.). MathWorld. Дата обращения: 26 апреля 2012. Архивировано 11 мая 2012 года.
↑ Логарифмически нормальное распределение // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
↑ Максимального правдоподобия метод // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
↑ Иванов М. Г. Размер и размерность // «Потенциал», август 2006.
↑ Головин С. Ю. ЗАКОН ВЕБЕРА-ФЕХНЕРА // Словарь практического психолога. Дата обращения: 17 апреля 2012. Архивировано 11 июня 2013 года.
↑ Ирина Алдошина. Основы психоакустики // Звукорежиссёр. — 1999. — Вып. 6. Архивировано 24 апреля 2012 года.
↑ Закон Фиттса // Психологическая энциклопедия (недоступная ссылка — история). Дата обращения: 17 апреля 2012. Архивировано 27 мая 2012 года.
↑ Welford, A. T. Fundamentals of skill. — London: Methuen, 1968. — P. 61. — ISBN 978-0-416-03000-6.

Литература[править | править код]

Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: АСТ, 2003, ISBN 5-17-009554-6.
Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.

Ссылки[править | править код]

“Разбираемся с натуральным логарифмом Архивная копия от 26 сентября 2013 на Wayback Machine” — перевод статьи Demystifying the Natural Logarithm (ln) | BetterExplained (англ.)

Источник

Если под руками нет таблиц, калькулятора или другой вычислительной техники, то для вычисления логарифма можно воспользоваться известной формулой разложения логарифма в ряд (ряд Тейлора)

Если же надо посчитать десятичный логарифм или логарифм с другим основанием, то надо воспользоваться свойством (формулой) логарифмов

и перейти от натуральных логарифмов к логарифмам с другим основанием.

система выбрала этот ответ лучшим

андреюшка
[114K]

10 лет назад

Я где-то читал, что посчитать логарифм можно и без таблицы, но для этого надо пройти очень длинную процедуру предварительных рассуждений. А в них очень легко запутаться. Следует идти более легким путем!

Приблизительно можно посчитать любой логарифм, и ошибка будет не такой же уж и большой.

Возьмем десятичный логарифм lg. Известно, что lg 10 = 1, а lg 1 = 0. Допустим вам надо найти логарифм числа, лежащего между 1 и 10. Например, 5. Любому человеку ясно, что это где-то посередине между 1 и 10. Значит и логарифм его будет приблизительно посередине. Берем складываем 0+1=1. Делим пополам, будет 0,5. Смотрим в таблицу десятичных логарифмов. Получаем 0,69897000433601880478626110527551 (эт я на калькуляторе вычислил в Виндовсе). Ну разница должен сказать небольшая. Всего-то 0,19. Для нормальной жизни пойдет. Нам же не ракету в космос запускать!

vdtest
[29.1K]

3 года назад

Вместо калькулятора можно пользоваться интернет браузером (действует даже на мобильнике и без связи с сетью интернет), можно выполнять вычисления формул и даже программы.

Чтобы посчитать натуральный логарифм числа надо просто написать в адресной строке браузера строчку:

javascript: alert( Math.log( число ))

например чтобы рассчитать натуральный логарифм 100 надо набрать

javascript: alert( Math.log(100) )

результат 4.605170185988092

десятичный логарифм 100 найдется по формуле

javascript: alert( Math.log(100)/ Math.log(10))

результат 2

gigabyte
[50K]

10 лет назад

Очень просто.

1) Взять таблицу. Например с авторством Брадис А.М. (точность 4 знака)

2) Воспользоваться логарифмической линейкой (точность до 3 знаков)

3) Воспользоваться небольшим набором формул для упрощения выражения (правда процесс может основательно затянуться)

а можно купить часы… например Breitling Navitimer, CITIZEN (модели BJ7010-59E, JQ8005-56E, JR3130-55E), Orient (модели OCEM58002DV, OCTD09001B, OCTD09003D) – их корпуса представляют собой ту же логарифмическую линейку.

Раньше этого чуда техники(а именно калькуляторов)не было и в помине,так ,если я не ошибаюсь мы в школе пользовались логарифмическими линейками.Правда если сейчас мне предложат сделать то же самое,то вряд ли смогу.Я и логарифм то с трудом сейчас представляю что такое,а не то чтоб его ещё и подсчитать)))

Знаете ответ?

Источник

Natural logarithm
Graph of part of the natural logarithm function. The function slowly grows to positive infinity as x increases, and slowly goes to negative infinity as x approaches 0 (“slowly” as compared to any power law of x).
General information
General definition	${displaystyle ln x=log _{e}x}$
Motivation of invention	Analytic proofs
Fields of application	Pure and applied mathematics
Domain, Codomain and Image
Domain	${displaystyle mathbb {R} _{>0}}$
Codomain
Image
Specific values
Value at +∞	+∞
Value at e	1
Specific features
Asymptote
Root	1
Inverse
Derivative	${displaystyle {dfrac {d}{dx}}ln x={dfrac {1}{x}},x>0}$
Antiderivative

The natural logarithm of a number is its logarithm to the base of the mathematical constant e, which is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, log_e x, or sometimes, if the base e is implicit, simply log x.^[1]^[2] Parentheses are sometimes added for clarity, giving ln(x), log_e(x), or log(x). This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity.

The natural logarithm of x is the power to which e would have to be raised to equal x. For example, ln 7.5 is 2.0149…, because e^2.0149… = 7.5. The natural logarithm of e itself, ln e, is 1, because e¹ = e, while the natural logarithm of 1 is 0, since e⁰ = 1.

The natural logarithm can be defined for any positive real number a as the area under the curve y = 1/x from 1 to a^[3] (with the area being negative when 0 < a < 1). The simplicity of this definition, which is matched in many other formulas involving the natural logarithm, leads to the term “natural”. The definition of the natural logarithm can then be extended to give logarithm values for negative numbers and for all non-zero complex numbers, although this leads to a multi-valued function: see Complex logarithm for more.

The natural logarithm function, if considered as a real-valued function of a positive real variable, is the inverse function of the exponential function, leading to the identities:

${displaystyle {begin{aligned}e^{ln x}&=xqquad {text{ if }}xin mathbb {R} _{+}\ln e^{x}&=xqquad {text{ if }}xin mathbb {R} end{aligned}}}$

Like all logarithms, the natural logarithm maps multiplication of positive numbers into addition:

^[4]

Logarithms can be defined for any positive base other than 1, not only e. However, logarithms in other bases differ only by a constant multiplier from the natural logarithm, and can be defined in terms of the latter, ${displaystyle log _{b}x=ln x/ln b=ln xcdot log _{b}e}$ .

Logarithms are useful for solving equations in which the unknown appears as the exponent of some other quantity. For example, logarithms are used to solve for the half-life, decay constant, or unknown time in exponential decay problems. They are important in many branches of mathematics and scientific disciplines, and are used to solve problems involving compound interest.

History[edit]

The concept of the natural logarithm was worked out by Gregoire de Saint-Vincent and Alphonse Antonio de Sarasa before 1649.^[5] Their work involved quadrature of the hyperbola with equation xy = 1, by determination of the area of hyperbolic sectors. Their solution generated the requisite “hyperbolic logarithm” function, which had the properties now associated with the natural logarithm.

An early mention of the natural logarithm was by Nicholas Mercator in his work Logarithmotechnia, published in 1668,^[6] although the mathematics teacher John Speidell had already compiled a table of what in fact were effectively natural logarithms in 1619.^[7] It has been said that Speidell’s logarithms were to the base e, but this is not entirely true due to complications with the values being expressed as integers.^[7]^: 152

Notational conventions[edit]

The notations ln x and log_e x both refer unambiguously to the natural logarithm of x, and log x without an explicit base may also refer to the natural logarithm. This usage is common in mathematics, along with some scientific contexts as well as in many programming languages.^{[nb 1]} In some other contexts such as chemistry, however, log x can be used to denote the common (base 10) logarithm. It may also refer to the binary (base 2) logarithm in the context of computer science, particularly in the context of time complexity.

Definitions[edit]

The natural logarithm can be defined in several equivalent ways.

Inverse of exponential[edit]

The most general definition is as the inverse function of $e^{x}$ , so that ${displaystyle e^{ln(x)}=x}$ . Because $e^{x}$ is positive and invertible for any real input , this definition of ln(x) is well defined for any positive x. For the complex numbers, $e^{z}$ is not invertible, so ln(z) is a multivalued function. In order to make ln(z) a proper, single-output function, we therefore need to restrict it to a particular principal branch, often denoted by . As the inverse function of $e^{z}$ , ln(z) can be defined by inverting the usual definition of $e^{z}$ :

${displaystyle e^{z}=lim _{nto infty }left(1+{frac {z}{n}}right)^{n}}$

Doing so yields:

${displaystyle ln(z)=lim _{nto infty }ncdot ({sqrt[{n}]{z}}-1)}$

This definition therefore derives its own principal branch from the principal branch of nth roots.

Integral definition[edit]

ln a as the area of the shaded region under the curve f(x) = 1/x from 1 to a. If a is less than 1, the area taken to be negative.

The area under the hyperbola satisfies the logarithm rule. Here A(s,t) denotes the area under the hyperbola between s and t.

The natural logarithm of a positive, real number a may be defined as the area under the graph of the hyperbola with equation y = 1/x between x = 1 and x = a. This is the integral^[3]

${displaystyle ln a=int _{1}^{a}{frac {1}{x}},dx.}$

If a is less than 1, then this area is considered to be negative.

This function is a logarithm because it satisfies the fundamental multiplicative property of a logarithm:^[4]

This can be demonstrated by splitting the integral that defines ln ab into two parts, and then making the variable substitution x = at (so dx = a dt) in the second part, as follows:

${displaystyle {begin{aligned}ln ab=int _{1}^{ab}{frac {1}{x}},dx&=int _{1}^{a}{frac {1}{x}},dx+int _{a}^{ab}{frac {1}{x}},dx\[5pt]&=int _{1}^{a}{frac {1}{x}},dx+int _{1}^{b}{frac {1}{at}}a,dt\[5pt]&=int _{1}^{a}{frac {1}{x}},dx+int _{1}^{b}{frac {1}{t}},dt\[5pt]&=ln a+ln b.end{aligned}}}$

In elementary terms, this is simply scaling by 1/a in the horizontal direction and by a in the vertical direction. Area does not change under this transformation, but the region between a and ab is reconfigured. Because the function a/(ax) is equal to the function 1/x, the resulting area is precisely ln b.

The number e can then be defined to be the unique real number a such that ln a = 1.

The natural logarithm also has an improper integral representation,^[8] which can be derived with Fubini’s theorem as follows:

${displaystyle ln left(xright)=int _{1}^{x}{frac {1}{u}}du=int _{1}^{x}int _{0}^{infty }e^{-tu} dt du=int _{0}^{infty }int _{1}^{x}e^{-tu} du dt=int _{0}^{infty }{frac {e^{-t}-e^{-tx}}{t}}dt}$

Properties[edit]

${displaystyle ln(x^{y})=yln xquad {text{for }};x>0}$
$lim _{{xto 0}}{frac {ln(1+x)}{x}}=1$
${displaystyle lim _{alpha to 0}{frac {x^{alpha }-1}{alpha }}=ln xquad {text{for }};x>0}$
${displaystyle {frac {x-1}{x}}leq ln xleq x-1quad {text{for}}quad x>0}$
${displaystyle ln {(1+x^{alpha })}leq alpha xquad {text{for}}quad xgeq 0;{text{and }};alpha geq 1}$

Derivative[edit]

The derivative of the natural logarithm as a real-valued function on the positive reals is given by^[3]

$frac{d}{dx} ln x = frac{1}{x}.$

How to establish this derivative of the natural logarithm depends on how it is defined firsthand. If the natural logarithm is defined as the integral

${displaystyle ln x=int _{1}^{x}{frac {1}{t}},dt,}$

then the derivative immediately follows from the first part of the fundamental theorem of calculus.

On the other hand, if the natural logarithm is defined as the inverse of the (natural) exponential function, then the derivative (for x > 0) can be found by using the properties of the logarithm and a definition of the exponential function. From the definition of the number ${displaystyle e=lim _{uto 0}(1+u)^{1/u},}$ the exponential function can be defined as ${displaystyle e^{x}=lim _{uto 0}(1+u)^{x/u}=lim _{hto 0}(1+hx)^{1/h}}$ , where The derivative can then be found from first principles.

${displaystyle {begin{aligned}{frac {d}{dx}}ln x&=lim _{hto 0}{frac {ln(x+h)-ln x}{h}}\&=lim _{hto 0}left[{frac {1}{h}}ln left({frac {x+h}{x}}right)right]\&=lim _{hto 0}left[ln left(left(1+{frac {h}{x}}right)^{frac {1}{h}}right)right]quad &&{text{all above for logarithmic properties}}\&=ln left[lim _{hto 0}left(1+{frac {h}{x}}right)^{frac {1}{h}}right]quad &&{text{for continuity of the logarithm}}\&=ln e^{1/x}quad &&{text{for the definition of }}e^{x}=lim _{hto 0}(1+hx)^{1/h}\&={frac {1}{x}}quad &&{text{for the definition of the ln as inverse function.}}end{aligned}}}$

Also, we have:

${displaystyle {frac {d}{dx}}ln ax={frac {d}{dx}}(ln a+ln x)={frac {d}{dx}}ln a+{frac {d}{dx}}ln x={frac {1}{x}}.}$

so, unlike its inverse function $e^{{ax}}$ , a constant in the function doesn’t alter the differential.

Series[edit]

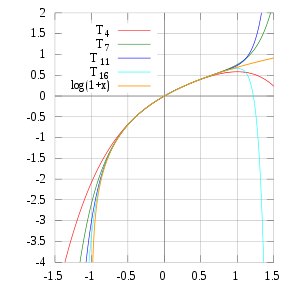
The Taylor polynomials for ln(1 + x) only provide accurate approximations in the range −1 < x ≤ 1. Beyond some x > 1, the Taylor polynomials of higher degree are increasingly worse approximations.

Since the natural logarithm is undefined at 0, ln(x) itself does not have a Maclaurin series, unlike many other elementary functions. Instead, one looks for Taylor expansions around other points. For example, if then^[9]

${displaystyle {begin{aligned}ln x&=int _{1}^{x}{frac {1}{t}},dt=int _{0}^{x-1}{frac {1}{1+u}},du\&=int _{0}^{x-1}(1-u+u^{2}-u^{3}+cdots ),du\&=(x-1)-{frac {(x-1)^{2}}{2}}+{frac {(x-1)^{3}}{3}}-{frac {(x-1)^{4}}{4}}+cdots \&=sum _{k=1}^{infty }{frac {(-1)^{k-1}(x-1)^{k}}{k}}.end{aligned}}}$

This is the Taylor series for ln x around 1. A change of variables yields the Mercator series:

${displaystyle ln(1+x)=sum _{k=1}^{infty }{frac {(-1)^{k-1}}{k}}x^{k}=x-{frac {x^{2}}{2}}+{frac {x^{3}}{3}}-cdots ,}$

valid for |x| ≤ 1 and x ≠ −1.

Leonhard Euler,^[10] disregarding , nevertheless applied this series to x = −1 to show that the harmonic series equals the natural logarithm of 1/(1 − 1), that is, the logarithm of infinity. Nowadays, more formally, one can prove that the harmonic series truncated at N is close to the logarithm of N, when N is large, with the difference converging to the Euler–Mascheroni constant.

The figure is a graph of ln(1 + x) and some of its Taylor polynomials around 0. These approximations converge to the function only in the region −1 < x ≤ 1; outside this region, the higher-degree Taylor polynomials devolve to worse approximations for the function.

A useful special case for positive integers n, taking ${displaystyle x={tfrac {1}{n}}}$ , is:

${displaystyle ln left({frac {n+1}{n}}right)=sum _{k=1}^{infty }{frac {(-1)^{k-1}}{kn^{k}}}={frac {1}{n}}-{frac {1}{2n^{2}}}+{frac {1}{3n^{3}}}-{frac {1}{4n^{4}}}+cdots }$

If then

${displaystyle {begin{aligned}ln(x)&=-ln left({frac {1}{x}}right)=-sum _{k=1}^{infty }{frac {(-1)^{k-1}({frac {1}{x}}-1)^{k}}{k}}=sum _{k=1}^{infty }{frac {(x-1)^{k}}{kx^{k}}}\&={frac {x-1}{x}}+{frac {(x-1)^{2}}{2x^{2}}}+{frac {(x-1)^{3}}{3x^{3}}}+{frac {(x-1)^{4}}{4x^{4}}}+cdots end{aligned}}}$

Now, taking ${displaystyle x={tfrac {n+1}{n}}}$ for positive integers n, we get:

${displaystyle ln left({frac {n+1}{n}}right)=sum _{k=1}^{infty }{frac {1}{k(n+1)^{k}}}={frac {1}{n+1}}+{frac {1}{2(n+1)^{2}}}+{frac {1}{3(n+1)^{3}}}+{frac {1}{4(n+1)^{4}}}+cdots }$

If then

${displaystyle ln(x)=ln left({frac {2x}{2}}right)=ln left({frac {1+{frac {x-1}{x+1}}}{1-{frac {x-1}{x+1}}}}right)=ln left(1+{frac {x-1}{x+1}}right)-ln left(1-{frac {x-1}{x+1}}right).}$

Since

${displaystyle {begin{aligned}ln(1+y)-ln(1-y)&=sum _{i=1}^{infty }{frac {1}{i}}left((-1)^{i-1}y^{i}-(-1)^{i-1}(-y)^{i}right)=sum _{i=1}^{infty }{frac {y^{i}}{i}}left((-1)^{i-1}+1right)\&=ysum _{i=1}^{infty }{frac {y^{i-1}}{i}}left((-1)^{i-1}+1right){overset {i-1to 2k}{=}};2ysum _{k=0}^{infty }{frac {y^{2k}}{2k+1}},end{aligned}}}$

we arrive at

${displaystyle {begin{aligned}ln(x)&={frac {2(x-1)}{x+1}}sum _{k=0}^{infty }{frac {1}{2k+1}}{left({frac {(x-1)^{2}}{(x+1)^{2}}}right)}^{k}\&={frac {2(x-1)}{x+1}}left({frac {1}{1}}+{frac {1}{3}}{frac {(x-1)^{2}}{(x+1)^{2}}}+{frac {1}{5}}{left({frac {(x-1)^{2}}{(x+1)^{2}}}right)}^{2}+cdots right).end{aligned}}}$

Using the substitution ${displaystyle x={tfrac {n+1}{n}}}$ again for positive integers n, we get:

${displaystyle {begin{aligned}ln left({frac {n+1}{n}}right)&={frac {2}{2n+1}}sum _{k=0}^{infty }{frac {1}{(2k+1)((2n+1)^{2})^{k}}}\&=2left({frac {1}{2n+1}}+{frac {1}{3(2n+1)^{3}}}+{frac {1}{5(2n+1)^{5}}}+cdots right).end{aligned}}}$

This is, by far, the fastest converging of the series described here.

The natural logarithm can also be expressed as an infinite product:^[11]

${displaystyle ln(x)=(x-1)prod _{k=1}^{infty }left({frac {2}{1+{sqrt[{2^{k}}]{x}}}}right)}$

Two examples might be:

${displaystyle ln(2)=left({frac {2}{1+{sqrt {2}}}}right)left({frac {2}{1+{sqrt[{4}]{2}}}}right)left({frac {2}{1+{sqrt[{8}]{2}}}}right)left({frac {2}{1+{sqrt[{16}]{2}}}}right)...}$

${displaystyle pi =(2i+2)left({frac {2}{1+{sqrt {i}}}}right)left({frac {2}{1+{sqrt[{4}]{i}}}}right)left({frac {2}{1+{sqrt[{8}]{i}}}}right)left({frac {2}{1+{sqrt[{16}]{i}}}}right)...}$

From this identity, we can easily get that:

${displaystyle {frac {1}{ln(x)}}={frac {x}{x-1}}-sum _{k=1}^{infty }{frac {2^{-k}x^{2^{-k}}}{1+x^{2^{-k}}}}}$

For example:

${displaystyle {frac {1}{ln(2)}}=2-{frac {sqrt {2}}{2+2{sqrt {2}}}}-{frac {sqrt[{4}]{2}}{4+4{sqrt[{4}]{2}}}}-{frac {sqrt[{8}]{2}}{8+8{sqrt[{8}]{2}}}}cdots }$

The natural logarithm in integration[edit]

The natural logarithm allows simple integration of functions of the form g(x) = f ‘(x)/f(x): an antiderivative of g(x) is given by ln(|f(x)|). This is the case because of the chain rule and the following fact:

${displaystyle {frac {d}{dx}}ln left|xright|={frac {1}{x}}, xneq 0}$

In other words, when integrating over an interval of the real line that does not include x=0 then

${displaystyle int {frac {1}{x}},dx=ln |x|+C}$

where C is an arbitrary constant of integration.^[12]
Likewise, when the integral is over an interval where ,

${displaystyle int {{frac {f'(x)}{f(x)}},dx}=ln |f(x)|+C.}$

For example, consider the integral of tan(x) over an interval that does not include points where tan(x) is infinite:

${displaystyle int tan x,dx=-int {frac {{frac {d}{dx}}cos x}{cos x}},dx=-ln left|cos xright|+C=ln left|sec xright|+C.}$

The natural logarithm can be integrated using integration by parts:

Let:

${displaystyle u=ln xRightarrow du={frac {dx}{x}}}$

then:

${displaystyle {begin{aligned}int ln x,dx&=xln x-int {frac {x}{x}},dx\&=xln x-int 1,dx\&=xln x-x+Cend{aligned}}}$

Efficient computation[edit]

For ln(x) where x > 1, the closer the value of x is to 1, the faster the rate of convergence of its Taylor series centered at 1. The identities associated with the logarithm can be leveraged to exploit this:

${displaystyle {begin{aligned}ln 123.456&=ln(1.23456cdot 10^{2})\&=ln 1.23456+ln(10^{2})\&=ln 1.23456+2ln 10\&approx ln 1.23456+2cdot 2.3025851.end{aligned}}}$

Such techniques were used before calculators, by referring to numerical tables and performing manipulations such as those above.

Natural logarithm of 10[edit]

The natural logarithm of 10, which has the decimal expansion 2.30258509…,^[13] plays a role for example in the computation of natural logarithms of numbers represented in scientific notation, as a mantissa multiplied by a power of 10:

${displaystyle ln(acdot 10^{n})=ln a+nln 10.}$

This means that one can effectively calculate the logarithms of numbers with very large or very small magnitude using the logarithms of a relatively small set of decimals in the range [1, 10).

High precision[edit]

To compute the natural logarithm with many digits of precision, the Taylor series approach is not efficient since the convergence is slow. Especially if x is near 1, a good alternative is to use Halley’s method or Newton’s method to invert the exponential function, because the series of the exponential function converges more quickly. For finding the value of y to give exp(y) − x = 0 using Halley’s method, or equivalently to give exp(y/2) − x exp(−y/2) = 0 using Newton’s method, the iteration simplifies to

${displaystyle y_{n+1}=y_{n}+2cdot {frac {x-exp(y_{n})}{x+exp(y_{n})}}}$

which has cubic convergence to ln(x).

Another alternative for extremely high precision calculation is the formula^[14]^[15]

$ln x approx frac{pi}{2 M(1,4/s)} - m ln 2,$

where M denotes the arithmetic-geometric mean of 1 and 4/s, and

${displaystyle s=x2^{m}>2^{p/2},}$

with m chosen so that p bits of precision is attained. (For most purposes, the value of 8 for m is sufficient.) In fact, if this method is used, Newton inversion of the natural logarithm may conversely be used to calculate the exponential function efficiently. (The constants ln 2 and π can be pre-computed to the desired precision using any of several known quickly converging series.) Or, the following formula can be used:

${displaystyle ln x={frac {pi }{Mleft(theta _{2}^{2}(1/x),theta _{3}^{2}(1/x)right)}},quad xin (1,infty )}$

where

${displaystyle theta _{2}(x)=sum _{nin mathbb {Z} }x^{(n+1/2)^{2}},quad theta _{3}(x)=sum _{nin mathbb {Z} }x^{n^{2}}}$

are the Jacobi theta functions.^[16]

Based on a proposal by William Kahan and first implemented in the Hewlett-Packard HP-41C calculator in 1979 (referred to under “LN1” in the display, only), some calculators, operating systems (for example Berkeley UNIX 4.3BSD^[17]), computer algebra systems and programming languages (for example C99^[18]) provide a special natural logarithm plus 1 function, alternatively named LNP1,^[19]^[20] or log1p^[18] to give more accurate results for logarithms close to zero by passing arguments x, also close to zero, to a function log1p(x), which returns the value ln(1+x), instead of passing a value y close to 1 to a function returning ln(y).^[18]^[19]^[20] The function log1p avoids in the floating point arithmetic a near cancelling of the absolute term 1 with the second term from the Taylor expansion of the ln. This keeps the argument, the result, and intermediate steps all close to zero where they can be most accurately represented as floating-point numbers.^[19]^[20]

In addition to base e the IEEE 754-2008 standard defines similar logarithmic functions near 1 for binary and decimal logarithms: log₂(1 + x) and log₁₀(1 + x).

Similar inverse functions named “expm1”,^[18] “expm”^[19]^[20] or “exp1m” exist as well, all with the meaning of expm1(x) = exp(x) − 1.^{[nb 2]}

An identity in terms of the inverse hyperbolic tangent,

${displaystyle mathrm {log1p} (x)=log(1+x)=2~mathrm {artanh} left({frac {x}{2+x}}right),,}$

gives a high precision value for small values of x on systems that do not implement log1p(x).

Computational complexity[edit]

The computational complexity of computing the natural logarithm using the arithmetic-geometric mean (for both of the above methods) is O(M(n) ln n). Here n is the number of digits of precision at which the natural logarithm is to be evaluated and M(n) is the computational complexity of multiplying two n-digit numbers.

Continued fractions[edit]

While no simple continued fractions are available, several generalized continued fractions are, including:

${displaystyle {begin{aligned}ln(1+x)&={frac {x^{1}}{1}}-{frac {x^{2}}{2}}+{frac {x^{3}}{3}}-{frac {x^{4}}{4}}+{frac {x^{5}}{5}}-cdots \[5pt]&={cfrac {x}{1-0x+{cfrac {1^{2}x}{2-1x+{cfrac {2^{2}x}{3-2x+{cfrac {3^{2}x}{4-3x+{cfrac {4^{2}x}{5-4x+ddots }}}}}}}}}}end{aligned}}}$

${displaystyle {begin{aligned}ln left(1+{frac {x}{y}}right)&={cfrac {x}{y+{cfrac {1x}{2+{cfrac {1x}{3y+{cfrac {2x}{2+{cfrac {2x}{5y+{cfrac {3x}{2+ddots }}}}}}}}}}}}\[5pt]&={cfrac {2x}{2y+x-{cfrac {(1x)^{2}}{3(2y+x)-{cfrac {(2x)^{2}}{5(2y+x)-{cfrac {(3x)^{2}}{7(2y+x)-ddots }}}}}}}}end{aligned}}}$

These continued fractions—particularly the last—converge rapidly for values close to 1. However, the natural logarithms of much larger numbers can easily be computed, by repeatedly adding those of smaller numbers, with similarly rapid convergence.

For example, since 2 = 1.25³ × 1.024, the natural logarithm of 2 can be computed as:

${displaystyle {begin{aligned}ln 2&=3ln left(1+{frac {1}{4}}right)+ln left(1+{frac {3}{125}}right)\[8pt]&={cfrac {6}{9-{cfrac {1^{2}}{27-{cfrac {2^{2}}{45-{cfrac {3^{2}}{63-ddots }}}}}}}}+{cfrac {6}{253-{cfrac {3^{2}}{759-{cfrac {6^{2}}{1265-{cfrac {9^{2}}{1771-ddots }}}}}}}}.end{aligned}}}$

Furthermore, since 10 = 1.25¹⁰ × 1.024³, even the natural logarithm of 10 can be computed similarly as:

${displaystyle {begin{aligned}ln 10&=10ln left(1+{frac {1}{4}}right)+3ln left(1+{frac {3}{125}}right)\[10pt]&={cfrac {20}{9-{cfrac {1^{2}}{27-{cfrac {2^{2}}{45-{cfrac {3^{2}}{63-ddots }}}}}}}}+{cfrac {18}{253-{cfrac {3^{2}}{759-{cfrac {6^{2}}{1265-{cfrac {9^{2}}{1771-ddots }}}}}}}}.end{aligned}}}$

The reciprocal of the natural logarithm can be also written in this way:

${displaystyle {frac {1}{ln(x)}}={frac {2x}{x^{2}-1}}{sqrt {{frac {1}{2}}+{frac {x^{2}+1}{4x}}}}{sqrt {{frac {1}{2}}+{frac {1}{2}}{sqrt {{frac {1}{2}}+{frac {x^{2}+1}{4x}}}}}}ldots }$

For example:

${displaystyle {frac {1}{ln(2)}}={frac {4}{3}}{sqrt {{frac {1}{2}}+{frac {5}{8}}}}{sqrt {{frac {1}{2}}+{frac {1}{2}}{sqrt {{frac {1}{2}}+{frac {5}{8}}}}}}ldots }$

Complex logarithms[edit]

The exponential function can be extended to a function which gives a complex number as e^z for any arbitrary complex number z; simply use the infinite series with x=z complex. This exponential function can be inverted to form a complex logarithm that exhibits most of the properties of the ordinary logarithm. There are two difficulties involved: no x has e^x = 0; and it turns out that e^2iπ = 1 = e⁰. Since the multiplicative property still works for the complex exponential function, e^z = e^z+2kiπ, for all complex z and integers k.

So the logarithm cannot be defined for the whole complex plane, and even then it is multi-valued—any complex logarithm can be changed into an “equivalent” logarithm by adding any integer multiple of 2iπ at will. The complex logarithm can only be single-valued on the cut plane. For example, ln i = iπ/2 or 5iπ/2 or –3iπ/2, etc.; and although i⁴ = 1, 4 ln i can be defined as 2iπ, or 10iπ or −6iπ, and so on.

Plots of the natural logarithm function on the complex plane (principal branch)
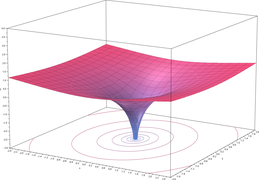
z = Re(ln(x + yi))
z = |(Im(ln(x + yi)))|
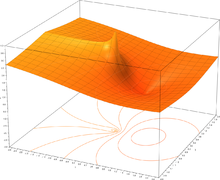
z = |(ln(x + yi))|
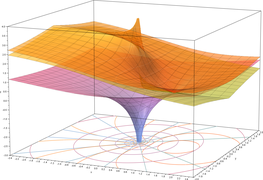
Superposition of the previous three graphs

Notes[edit]

^ Including C, C++, SAS, MATLAB, Mathematica, Fortran, and some BASIC dialects
^ For a similar approach to reduce round-off errors of calculations for certain input values see trigonometric functions like versine, vercosine, coversine, covercosine, haversine, havercosine, hacoversine, hacovercosine, exsecant and excosecant.

References[edit]

^ G.H. Hardy and E.M. Wright, An Introduction to the Theory of Numbers, 4th Ed., Oxford 1975, footnote to paragraph 1.7: “log x is, of course, the ‘Naperian’ logarithm of x, to base e. ‘Common’ logarithms have no mathematical interest“.
^ Mortimer, Robert G. (2005). Mathematics for physical chemistry (3rd ed.). Academic Press. p. 9. ISBN 0-12-508347-5. Extract of page 9
^ ^a ^b ^c Weisstein, Eric W. “Natural Logarithm”. mathworld.wolfram.com. Retrieved 2020-08-29.
^ ^a ^b “Rules, Examples, & Formulas”. Logarithm. Encyclopedia Britannica. Retrieved 2020-08-29.
^ Burn, R.P. (2001). Alphonse Antonio de Sarasa and Logarithms. Historia Mathematica. pp. 28:1–17.
^ O’Connor, J. J.; Robertson, E. F. (September 2001). “The number e”. The MacTutor History of Mathematics archive. Retrieved 2009-02-02.
^ ^a ^b Cajori, Florian (1991). A History of Mathematics (5th ed.). AMS Bookstore. p. 152. ISBN 0-8218-2102-4.
^ An improper integral representation of the natural logarithm., retrieved 2022-09-24
^ ““Logarithmic Expansions” at Math2.org”.
^ Leonhard Euler, Introductio in Analysin Infinitorum. Tomus Primus. Bousquet, Lausanne 1748. Exemplum 1, p. 228; quoque in: Opera Omnia, Series Prima, Opera Mathematica, Volumen Octavum, Teubner 1922
^ RUFFA, Anthony. “A PROCEDURE FOR GENERATING INFINITE SERIES IDENTITIES” (PDF). International Journal of Mathematics and Mathematical Sciences. International Journal of Mathematics and Mathematical Sciences. Retrieved 2022-02-27. (Page 3654, equation 2.6)
^ For a detailed proof see for instance: George B. Thomas, Jr and Ross L. Finney, Calculus and Analytic Geometry, 5th edition, Addison-Wesley 1979, Section 6-5 pages 305-306.
^ OEIS: A002392
^ Sasaki, T.; Kanada, Y. (1982). “Practically fast multiple-precision evaluation of log(x)”. Journal of Information Processing. 5 (4): 247–250. Retrieved 2011-03-30.
^ Ahrendt, Timm (1999). “Fast Computations of the Exponential Function”. Stacs 99. Lecture Notes in Computer Science. 1564: 302–312. doi:10.1007/3-540-49116-3_28. ISBN 978-3-540-65691-3.
^ Borwein, Jonathan M.; Borwein, Peter B. (1987). Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity (First ed.). Wiley-Interscience. ISBN 0-471-83138-7. page 225
^ Beebe, Nelson H. F. (2017-08-22). “Chapter 10.4. Logarithm near one”. The Mathematical-Function Computation Handbook – Programming Using the MathCW Portable Software Library (1 ed.). Salt Lake City, UT, USA: Springer International Publishing AG. pp. 290–292. doi:10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN 2017947446. S2CID 30244721. In 1987, Berkeley UNIX 4.3BSD introduced the log1p() function
^ ^a ^b ^c ^d Beebe, Nelson H. F. (2002-07-09). “Computation of expm1 = exp(x)−1” (PDF). 1.00. Salt Lake City, Utah, USA: Department of Mathematics, Center for Scientific Computing, University of Utah. Retrieved 2015-11-02.
^ ^a ^b ^c ^d HP 48G Series – Advanced User’s Reference Manual (AUR) (4 ed.). Hewlett-Packard. December 1994 [1993]. HP 00048-90136, 0-88698-01574-2. Retrieved 2015-09-06.
^ ^a ^b ^c ^d HP 50g / 49g+ / 48gII graphing calculator advanced user’s reference manual (AUR) (2 ed.). Hewlett-Packard. 2009-07-14 [2005]. HP F2228-90010. Retrieved 2015-10-10. Searchable PDF

Источник

Как найти натуральный логарифм числа вручную? (Смысл я понимаю, но какой алгоритм нахождения?)

Аргумент и основание логарифма

Как вычислить логарифм?

Чтобы вычислить логарифм – нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?

Зачем придумали логарифм?

Десятичный и натуральный логарифмы

Натуральный логарифм: логарифм, у которого основание – число Эйлера (e) (равное примерно (2,7182818…)), и записывается такой логарифм как (ln{a}).

Десятичный логарифм: логарифм, у которого основание равно 10, записывается (lg{a}).

Основное логарифмическое тождество

Как число записать в виде логарифма?

Любое число (a) может быть представлено как логарифм с основанием (b): (a=log_{b}{b^{a}})

Определение[править | править код]

Вещественный натуральный логарифм[править | править код]

Свойства[править | править код]

Связь с логарифмами по другому основанию[править | править код]

Логарифмическая функция[править | править код]

Аналитические свойства функции[править | править код]

Методы вычисления логарифма[править | править код]

Полезные пределы[править | править код]

Трансцендентность[править | править код]

Непрерывные дроби[править | править код]

История[править | править код]

Комплексные логарифмы[править | править код]

Некоторые применения[править | править код]

Теория чисел[править | править код]

Математический анализ[править | править код]

Теория вероятностей и статистика[править | править код]

Фракталы и размерность[править | править код]

Механика и физика[править | править код]

Химия и физическая химия[править | править код]

Психология и физиология[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

History[edit]

Notational conventions[edit]

Definitions[edit]

Inverse of exponential[edit]

Integral definition[edit]

Properties[edit]

Derivative[edit]

Series[edit]

The natural logarithm in integration[edit]

Efficient computation[edit]

Natural logarithm of 10[edit]

High precision[edit]

Computational complexity[edit]

Continued fractions[edit]

Complex logarithms[edit]

See also[edit]

Notes[edit]

References[edit]

Вам также может понравиться

Геометрия 8 класс как найти высоту трапеции

Как составить аналитику рисками

Как исправить биение патрона шуруповерта

Добавить комментарий Отменить ответ