Как найти натуральный логарифм двух

Как найти натуральный логарифм двух

Натуральный логарифм 2 в десятичной системе счисления (последовательность A002162 в OEIS) равен приблизительно

{displaystyle ln 2approx 0{,}693,147,180,559,945,309,417,232,121,458,176,568,075,500,134,360,255,254,120,680,009,493,393,621,969,694,715,605,863,326,996,418,687}

как показывает первая строка в таблице ниже. Логарифм числа 2 с другим основанием (b) можно вычислить из соотношения

{displaystyle log _{b}2={frac {ln 2}{ln b}}.}

Десятичный логарифм числа 2 (A007524) приблизительно равен

{displaystyle log _{10}2approx 0{,}301,029,995,663,981,195,213,738,894,724,493,026,768,189,881,462,108,541,310,427,461,127,108,189,274,424,509,486,927,252,118,186,172,040,684}

Обратное число к данному представляет собой двоичный логарифм 10:

{displaystyle log _{2}10={frac {1}{log _{10}2}}approx 3{,}32,192,809,488,736,234,787,031,942,948,939,017,586,483,139,302,458,061,205,475,639,581,593,477,660,862,521,585,013,974,335,937,015} (A020862).
Число Приближённое значение натурального логарифма OEIS
2 0,693147180559945309417232121458 последовательность A002162 в OEIS
3 1,09861228866810969139524523692 последовательность A002391 в OEIS
4 1,38629436111989061883446424292 последовательность A016627 в OEIS
5 1,60943791243410037460075933323 последовательность A016628 в OEIS
6 1,79175946922805500081247735838 последовательность A016629 в OEIS
7 1,94591014905531330510535274344 последовательность A016630 в OEIS
8 2,07944154167983592825169636437 последовательность A016631 в OEIS
9 2,19722457733621938279049047384 последовательность A016632 в OEIS
10 2,30258509299404568401799145468 последовательность A002392 в OEIS

По теореме Линдемана — Вейерштрасса натуральный логарифм любого натурального числа, отличного от 0 и 1 (в общем случае, для любого положительного алгебраического числа, кроме 1), является трансцендентным числом.

Неизвестно, является ли ln 2 нормальным числом.

Представление в виде рядов[править | править код]

{displaystyle sum _{n=1}^{infty }{frac {(-1)^{n+1}}{n}}=ln 2.} (Ряд Меркатора)
{displaystyle sum _{n=0}^{infty }{frac {1}{(2n+1)(2n+2)}}=ln 2.}
{displaystyle sum _{n=0}^{infty }{frac {(-1)^{n}}{(n+1)(n+2)}}=2ln 2-1.}
{displaystyle sum _{n=1}^{infty }{frac {1}{n(4n^{2}-1)}}=2ln 2-1.}
{displaystyle sum _{n=1}^{infty }{frac {(-1)^{n}}{n(4n^{2}-1)}}=ln 2-1.}
{displaystyle sum _{n=1}^{infty }{frac {(-1)^{n}}{n(9n^{2}-1)}}=2ln 2-{tfrac {3}{2}}.}
{displaystyle sum _{n=2}^{infty }{frac {1}{2^{n}}}[zeta (n)-1]=ln 2-{tfrac {1}{2}}.}
{displaystyle sum _{n=1}^{infty }{frac {1}{2n+1}}[zeta (n)-1]=1-gamma -{frac {ln 2}{2}}.}
{displaystyle sum _{n=1}^{infty }{frac {1}{2^{2n}(2n+1)}}zeta (2n)={frac {1-ln 2}{2}}.}
{displaystyle ln 2=sum _{n=1}^{infty }{frac {1}{2^{n}n}}=operatorname {Li} _{1}left({frac {1}{2}}right).} (Полилогарифм)
{displaystyle ln 2=sum _{n=1}^{infty }left({frac {1}{3^{n}}}+{frac {1}{4^{n}}}right){frac {1}{n}}.}
{displaystyle ln 2={frac {2}{3}}+{frac {1}{2}}sum _{kgeq 1}left({frac {1}{2k}}+{frac {1}{4k+1}}+{frac {1}{8k+4}}+{frac {1}{16k+12}}right){frac {1}{16^{k}}}.}
{displaystyle ln 2={frac {2}{3}}sum _{kgeq 0}{frac {1}{9^{k}(2k+1)}}.}
{displaystyle ln 2=sum _{kgeq 0}left({frac {14}{31^{2k+1}(2k+1)}}+{frac {6}{161^{2k+1}(2k+1)}}+{frac {10}{49^{2k+1}(2k+1)}}right).}
{displaystyle ln 2=sum _{n=1}^{infty }{frac {1}{4n^{2}-2n}}.}
{displaystyle ln 2=sum _{n=1}^{infty }{frac {2(-1)^{n+1}(2n-1)+1}{8n^{2}-4n}}.}

(здесь через γ обозначена постоянная Эйлера — Маскерони, ζ — дзета-функция Римана).

Иногда к данной категории формул относят формулу Бэйли — Боруэйна — Плаффа:

{displaystyle {begin{aligned}ln 2&={frac {1}{2}}+{frac {1}{2cdot 2^{2}}}+{frac {1}{3cdot 2^{3}}}+{frac {1}{4cdot 2^{4}}}+{frac {1}{5cdot 2^{5}}}+cdots \&=sum _{k=1}^{infty }{frac {1}{2^{k}cdot k}}={frac {1}{2}}sum _{k=0}^{infty }left[{frac {1}{2^{k}}}left({frac {1}{k+1}}right)right]\&={frac {1}{2}}P{big (}1,2,1,(1){big )}.end{aligned}}}

Представление в виде интегралов[править | править код]

{displaystyle int _{0}^{1}{frac {dx}{1+x}}=ln 2,{text{ или, равносильно, }}int _{1}^{2}{frac {dx}{x}}=ln 2.}
{displaystyle int _{1}^{infty }{frac {dx}{(1+x^{2})(1+x)^{2}}}={frac {1-ln 2}{4}}.}
{displaystyle int _{0}^{infty }{frac {dx}{1+e^{nx}}}={frac {ln 2}{n}};int _{0}^{infty }{frac {dx}{3+e^{nx}}}={frac {2ln 2}{3n}}.}
{displaystyle int _{0}^{infty }{frac {1}{e^{x}-1}}-{frac {2}{e^{2x}-1}},dx=ln 2.}
{displaystyle int _{0}^{infty }e^{-x}{frac {1-e^{-x}}{x}},dx=ln 2.}
{displaystyle int _{0}^{1}ln left({frac {x^{2}-1}{xln x}}right)dx=-1+ln 2+gamma .}
{displaystyle int _{0}^{frac {pi }{3}}operatorname {tg} x,dx=2int _{0}^{frac {pi }{4}}operatorname {tg} x,dx=ln 2.}
{displaystyle int _{-{frac {pi }{4}}}^{frac {pi }{4}}ln left(sin x+cos xright),dx=-{frac {pi ln 2}{4}}.}
{displaystyle int _{0}^{1}x^{2}ln(1+x),dx={frac {2ln 2}{3}}-{frac {5}{18}}.}
{displaystyle int _{0}^{1}xln(1+x)ln(1-x),dx={tfrac {1}{4}}-ln 2.}
{displaystyle int _{0}^{1}x^{3}ln(1+x)ln(1-x),dx={tfrac {13}{96}}-{frac {2ln 2}{3}}.}
{displaystyle int _{0}^{1}{frac {ln x}{(1+x)^{2}}},dx=-ln 2.}
{displaystyle int _{0}^{1}{frac {ln(1+x)-x}{x^{2}}},dx=1-2ln 2.}
{displaystyle int _{0}^{1}{frac {dx}{x(1-ln x)(1-2ln x)}}=ln 2.}
{displaystyle int _{1}^{infty }{frac {ln left(ln xright)}{x^{3}}},dx=-{frac {gamma +ln 2}{2}}.}

Другие формы представления числа[править | править код]

Разложение Пирса имеет вид (A091846)

{displaystyle ln 2=1-{frac {1}{1cdot 3}}+{frac {1}{1cdot 3cdot 12}}-cdots .}

Разложение Энгеля (A059180):

{displaystyle ln 2={frac {1}{2}}+{frac {1}{2cdot 3}}+{frac {1}{2cdot 3cdot 7}}+{frac {1}{2cdot 3cdot 7cdot 9}}+cdots .}

Разложение в виде котангенсов имеет вид A081785

{displaystyle ln 2=operatorname {ctg} ({operatorname {arcctg} 0-operatorname {arcctg} 1+operatorname {arcctg} 5-operatorname {arcctg} 55+operatorname {arcctg} 14187-cdots }).}

Представление в виде бесконечной суммы дробей[1] (знакопеременный гармонический ряд):

{displaystyle ln 2=1-{tfrac {1}{2}}+{tfrac {1}{3}}-{tfrac {1}{4}}+{tfrac {1}{5}}-cdots .}

Также можно представить натуральный логарифм 2 в виде разложения в ряд Тейлора:

{textstyle quad ln 2={tfrac {1}{2}}+{tfrac {1}{12}}+{tfrac {1}{30}}+{tfrac {1}{56}}+{tfrac {1}{90}}+cdots }

Представление в виде обобщённой непрерывной дроби:[2]

{displaystyle ln 2={cfrac {1}{1+{cfrac {1}{2+{cfrac {1}{3+{cfrac {2}{2+{cfrac {2}{5+{cfrac {3}{2+{cfrac {3}{7+{cfrac {4}{2+ddots }}}}}}}}}}}}}}}}={cfrac {2}{3-{cfrac {1^{2}}{9-{cfrac {2^{2}}{15-{cfrac {3^{2}}{21-ddots }}}}}}}}}

Вычисление других логарифмов[править | править код]

Если известно значение ln 2, то для вычисления логарифмов других натуральных чисел можно табулировать логарифмы простых чисел, а логарифмы смешанных чисел c затем определять исходя из разложения на простые множители:

{displaystyle c=2^{i}3^{j}5^{k}7^{l}cdots rightarrow ln c=iln 2+jln 3+kln 5+lln 7+cdots }

В таблице представлены логарифмы некоторых простых чисел.

Простое число Приблизительное значение натурального логарифма OEIS
11 2,39789527279837054406194357797 последовательность A016634 в OEIS
13 2,56494935746153673605348744157 последовательность A016636 в OEIS
17 2,83321334405621608024953461787 последовательность A016640 в OEIS
19 2,94443897916644046000902743189 последовательность A016642 в OEIS
23 3,13549421592914969080675283181 последовательность A016646 в OEIS
29 3,36729582998647402718327203236 последовательность A016652 в OEIS
31 3,43398720448514624592916432454 последовательность A016654 в OEIS
37 3,61091791264422444436809567103 последовательность A016660 в OEIS
41 3,71357206670430780386676337304 последовательность A016664 в OEIS
43 3,76120011569356242347284251335 последовательность A016666 в OEIS
47 3,85014760171005858682095066977 последовательность A016670 в OEIS
53 3,97029191355212183414446913903 последовательность A016676 в OEIS
59 4,07753744390571945061605037372 последовательность A016682 в OEIS
61 4,11087386417331124875138910343 последовательность A016684 в OEIS
67 4,20469261939096605967007199636 последовательность A016690 в OEIS
71 4,26267987704131542132945453251 последовательность A016694 в OEIS
73 4,29045944114839112909210885744 последовательность A016696 в OEIS
79 4,36944785246702149417294554148 последовательность A016702 в OEIS
83 4,41884060779659792347547222329 последовательность A016706 в OEIS
89 4,48863636973213983831781554067 последовательность A016712 в OEIS
97 4,57471097850338282211672162170 последовательность A016720 в OEIS

На третьем шаге логарифмы рациональных чисел r = a/b вычисляются как ln r = ln a − ln b, логарифмы корней: ln n√c = 1/n ln c.

Логарифм 2 полезен в том смысле, что степени 2 распределены достаточно плотно: определение степени 2i, близкой к степени bj другого числа b сравнительно несложно.

Известные значения[править | править код]

Это таблица последних записей по вычислению цифр {displaystyle ln(2)}. По состоянию на декабрь 2018 года в ней было вычислено больше цифр, чем в любом другом натуральном логарифме[3][4] натурального числа, кроме 1.

Дата Количество значащих цифр Авторы вычисления
7 января 2009 г. 15 500 000 000 A.Yee & R.Chan
4 февраля 2009 г. 31 026 000 000 A.Yee & R.Chan
21 февраля 2011 г. 50 000 000 050 Alexander Yee
14 мая 2011 г. 100 000 000 000 Shigeru Kondo
28 февраля 2014 г. 200 000 000 050 Shigeru Kondo
12 июля 2015 г. 250 000 000 000 Ron Watkins
30 января 2016 г. 350 000 000 000 Ron Watkins
18 апреля 2016 г. 500 000 000 000 Ron Watkins
10 декабря 2018 г. 600 000 000 000 Michael Kwok
26 апреля 2019 г., 1 000 000 000 000 Jacob Riffee
19 августа 2020 г. 1 200 000 000 100 Seungmin Kim[5][6]

Примечания[править | править код]

  1. ↑ Wells, David. The Penguin Dictionary of Curious and Interesting Numbers (англ.). — Penguin, 1997. — P. 29. — ISBN 0140261494.
  2. ↑ Borwein, J.; Crandall, R.; Free, G. On the Ramanujan AGM Fraction , I: The Real-Parameter Case (англ.) // Exper. Math.  (англ.) (рус. : journal. — 2004. — Vol. 13. — P. 278—280. — doi:10.1080/10586458.2004.10504540.
  3. ↑ y-cruncher – A Multi-Threaded Pi Program. www.numberworld.org. Дата обращения: 19 февраля 2021. Архивировано 16 апреля 2015 года.
  4. ↑ Natural Log of 2. www.numberworld.org. Дата обращения: 19 февраля 2021. Архивировано 9 июля 2021 года.
  5. ↑ y-cruncher – A Multi-Threaded Pi Program. web.archive.org (15 сентября 2020). Дата обращения: 19 февраля 2021.
  6. ↑ Natural Logarithm of 2 (Log(2)) (англ.). Polymath Collector (19 августа 2020). Дата обращения: 19 февраля 2021. Архивировано 17 октября 2020 года.

Литература[править | править код]

  • Brent, Richard P. Fast multiple-precision evaluation of elementary functions (англ.) // J. ACM : journal. — 1976. — Vol. 23, no. 2. — P. 242—251. — doi:10.1145/321941.321944.
  • Uhler, Horace S. Recalculation and extension of the modulus and of the logarithms of 2, 3, 5, 7 and 17 (англ.) // Proceedings of the National Academy of Sciences of the United States of America : journal. — 1940. — Vol. 26. — P. 205—212. — doi:10.1073/pnas.26.3.205.
  • Sweeney, Dura W. On the computation of Euler’s constant (англ.) // Mathematics of Computation  (англ.) (рус. : journal. — 1963. — Vol. 17. — P. 170—178. — doi:10.1090/S0025-5718-1963-0160308-X.
  • Chamberland, Marc. Binary BBP-formulae for logarithms and generalized Gaussian–Mersenne primes (англ.) // Journal of Integer Sequences : journal. — 2003. — Vol. 6. — P. 03.3.7. Архивировано 6 июня 2011 года.
  • Gourévitch, Boris; Guillera Goyanes, Jesús. Construction of binomial sums for π and polylogarithmic constants inspired by BBP formulas (англ.) // Applied Math. E-Notes : journal. — 2007. — Vol. 7. — P. 237—246.
  • Wu, Qiang. On the linear independence measure of logarithms of rational numbers (англ.) // Mathematics of Computation  (англ.) (рус. : journal. — 2003. — Vol. 72, no. 242. — P. 901—911. — doi:10.1090/S0025-5718-02-01442-4.

Ссылки[править | править код]

  • Weisstein, Eric W. Natural logarithm of 2 (англ.) на сайте Wolfram MathWorld.
  • Gourdon, Xavier; Sebah, Pascal The logarithm constant:log 2.
Источник

Калькулятор натуральных логарифмов поможет найти логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,72.

Обозначение натурального логарифма

Для обозначения натурального логарифма существует несколько способов:

  • ln
  • loge

Так же возможно написание прописными буквами.

Что такое натуральный логарифм

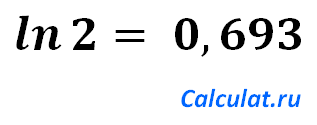
Натуральный логарифм калькулятор

Натуральный логарифм

Понятие натурального логарифма лучше проиллюстрировать примером. Например, натуральный логарифм числа 2 равен 0,693147180 потому, что

e0,693147180 = 2

Здесь e — основание натурального логарифма.

e =2,718281828

Таким образом натуральный логарифм — это степень, в которую нужно возвести число e для получения исходного числа, логарифм которого мы ищем. Вычисление натурального логарифма несложная задача и наш калькулятор поможет с расчетом.

Натуральный логарифм нуля не существует. Для чисел меньше единицы натуральный логарифм отрицательный.

Таблица натуральных логарифмов некоторых чисел

x ln x
1 0
2 0,693147
3 1,098612
4 1,386294
5 1,609438
6 1,791759
7 1,94591
8 2,079442
9 2,197225
10 2,302585
100 4,60517
1000 6,907755
10000 9,21034
100000 11,51293

Ваша оценка

[Оценок: 285 Средняя: 2.8]

Калькулятор натуральных логарифмов Автор admin средний рейтинг 2.8/5 – 285 рейтинги пользователей

Источник

Логарифмом положительного числа (c) по основанию (a) ((a>0, aneq1)) называется показатель степени (b), в которую надо возвести основание (a), чтобы получить число (c) ((c>0)), т.е.

(a^{b}=c)       (Leftrightarrow)       (log_{a}{c}=b)

Объясним проще. Например, (log_{2}{8}) равен степени, в которую надо возвести (2), чтоб получить (8). Отсюда понятно, что (log_{2}{8}=3).

Примеры:

                 

(log_{5}{25}=2)

         

т.к. (5^{2}=25)

(log_{3}{81}=4)

 

т.к. (3^{4}=81)

 

(log_{2})(frac{1}{32})(=-5)

 

т.к. (2^{-5}=)(frac{1}{32})

Аргумент и основание логарифма

Любой логарифм имеет следующую «анатомию»:

Аргумент и основание логарифма.png

Аргумент логарифма обычно пишется на его уровне, а основание – подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».

Как вычислить логарифм?

Чтобы вычислить логарифм – нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?

Например, вычислите логарифм:  а) (log_{4}{16})     б) (log_{3})(frac{1}{3})     в) (log_{sqrt{5}}{1})     г) (log_{sqrt{7}}{sqrt{7}})      д) (log_{3}{sqrt{3}})

а) В какую степень надо возвести (4), чтобы получить (16)? Очевидно во вторую. Поэтому: 

(log_{4}{16}=2)

б) В какую степень надо возвести (3), чтобы получить (frac{1}{3})? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени).

(log_{3})(frac{1}{3})(=-1)

в) В какую степень надо возвести (sqrt{5}), чтобы получить (1)? А какая степень делает любое число единицей? Ноль, конечно!

(log_{sqrt{5}}{1}=0)

г) В какую степень надо возвести (sqrt{7}), чтобы получить (sqrt{7})? В первую – любое число в первой степени равно самому себе.

(log_{sqrt{7}}{sqrt{7}}=1)

д) В какую степень надо возвести (3), чтобы получить (sqrt{3})? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень – это степень (frac{1}{2}).

(log_{3}{sqrt{3}}=)(frac{1}{2})

Пример: Вычислить логарифм (log_{4sqrt{2}}{8})

Решение:

(log_{4sqrt{2}}{8}=x)

                              

Нам надо найти значение логарифма, обозначим его за икс. Теперь воспользуемся определением логарифма:
(log_{a}{c}=b)       (Leftrightarrow)       (a^{b}=c)

((4sqrt{2})^{x}=8)

 

Что связывает (4sqrt{2}) и (8)? Двойка, потому что и то, и другое число можно представить степенью двойки:
(4=2^{2})         (sqrt{2}=2^{frac{1}{2}})         (8=2^{3})

({(2^{2}cdot2^{frac{1}{2}})}^{x}=2^{3})

 

Слева воспользуемся свойствами степени: (a^{m}cdot a^{n}=a^{m+n}) и ((a^{m})^{n}=a^{mcdot n})

(2^{frac{5}{2}x}=2^{3})

 

Основания равны, переходим к равенству показателей

(frac{5x}{2})(=3)

Умножим обе части уравнения на (frac{2}{5})

(x=1,2)

Получившийся корень и есть значение логарифма

Ответ: (log_{4sqrt{2}}{8}=1,2)

Foxford

Зачем придумали логарифм?

Чтобы это понять, давайте решим уравнение: (3^{x}=9). Просто подберите (x), чтобы равенство сработало. Конечно, (x=2).

А теперь решите уравнение: (3^{x}=8).Чему равен икс? Вот в том-то и дело.

Самые догадливые скажут: «икс чуть меньше двух». А как точно записать это число? Для ответа на этот вопрос и придумали логарифм. Благодаря ему, ответ здесь можно записать как (x=log_{3}{8}).

Хочу подчеркнуть, что (log_{3}{8}), как и любой логарифм – это просто число. Да, выглядит непривычно, но зато коротко. Потому что, если бы мы захотели записать его в виде десятичной дроби, то оно выглядело бы вот так: (1,892789260714…..)

Пример: Решите уравнение (4^{5x-4}=10)

Решение:

(4^{5x-4}=10)

                              

(4^{5x-4}) и (10) никак к одному основанию не привести. Значит тут не обойтись без логарифма.

Воспользуемся определением логарифма:
(a^{b}=c)       (Leftrightarrow)       (log_{a}{c}=b)

(log_{4}{10}=5x-4)

 

Зеркально перевернем уравнение, чтобы икс был слева

(5x-4=log_{4}{10})

 

Перед нами линейное уравнение. Перенесем (4) вправо.

И не пугайтесь логарифма, относитесь к нему как к обычному числу. 

(5x=log_{4}{10}+4)

 

Поделим уравнение на 5

(x=)(frac{log_{4}{10}+4}{5})

Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.

Ответ: (frac{log_{4}{10}+4}{5})

Десятичный и натуральный логарифмы

Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы ((a>0, aneq1)). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:

Натуральный логарифм: логарифм, у которого основание – число Эйлера (e) (равное примерно (2,7182818…)), и записывается такой логарифм как (ln{a}).

То есть, (ln{a}) это то же самое, что и (log_{e}{a}), где (a) – некоторое число.

Десятичный логарифм: логарифм, у которого основание равно 10, записывается (lg{a}).

То есть, (lg{a}) это то же самое, что и (log_{10}{a}), где (a) – некоторое число.

Основное логарифмическое тождество

У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:

Это свойство вытекает напрямую из определения. Посмотрим как именно эта формула появилась.

Вспомним краткую запись определения логарифма:

если     (a^{b}=c),    то   (log_{a}{c}=b)

То есть, (b) – это тоже самое, что (log_{a}{c}). Тогда мы можем в формуле (a^{b}=c) написать (log_{a}{c}) вместо (b). Получилось (a^{log_{a}{c}}=c) – основное логарифмическое тождество.

Остальные свойства логарифмов вы можете найти здесь. С их помощью можно упрощать и вычислять значения выражений с логарифмами, которые «в лоб» посчитать сложно.

Пример: Найдите значение выражения (36^{log_{6}{5}})

Решение:

(36^{log_{6}{5}}=)

                              

Сразу пользоваться свойством (a^{log_{a}{c}}=c) мы не можем, так как в основании степени и в основании логарифма – разные числа. Однако мы знаем, что (36=6^{2})

(=(6^{2})^{log_{6}{5}}=)

 

Зная формулу ((a^{m})^{n}=a^{mcdot n}), а так же то, что множители можно менять местами, преобразовываем выражение

(=6^{2cdotlog_{6}{5}}=6^{log_{6}{5}cdot2}=(6^{log_{6}{5}})^{2}=)

 

Вот теперь спокойно пользуемся основным логарифмическим тождеством.

(=5^{2}=25)

     

Ответ готов.

Ответ: (25)

Как число записать в виде логарифма?

Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что (log_{2}{4}) равен двум. Тогда можно вместо двойки писать (log_{2}{4}). 

Но (log_{3}{9}) тоже равен (2), значит, также можно записать (2=log_{3}{9})  . Аналогично и с (log_{5}{25}), и с (log_{9}{81}), и т.д. То есть, получается  

(2=log_{2}{4}=log_{3}{9}=log_{4}{16}=log_{5}{25}=log_{6}{36}=log_{7}{49}…)

Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.

Точно также и с тройкой – ее можно записать как (log_{2}{8}), или как (log_{3}{27}), или как (log_{4}{64})… Здесь мы как аргумент пишем основание в кубе:

(3=log_{2}{8}=log_{3}{27}=log_{4}{64}=log_{5}{125}=log_{6}{216}=log_{7}{343}…)

И с четверкой:

(4=log_{2}{16}=log_{3}{81}=log_{4}{256}=log_{5}{625}=log_{6}{1296}=log_{7}{2401}…)

И с минус единицей:

(-1=) (log_{2})(frac{1}{2})(=) (log_{3})(frac{1}{3})(=) (log_{4})(frac{1}{4})(=) (log_{5})(frac{1}{5})(=) (log_{6})(frac{1}{6})(=) (log_{7})(frac{1}{7})(…)

И с одной третьей:

(frac{1}{3})(=log_{2}{sqrt[3]{2}}=log_{3}{sqrt[3]{3}}=log_{4}{sqrt[3]{4}}=log_{5}{sqrt[3]{5}}=log_{6}{sqrt[3]{6}}=log_{7}{sqrt[3]{7}}…)

И так далее.

Любое число (a) может быть представлено как логарифм с основанием (b):       (a=log_{b}{b^{a}})

Пример: Найдите значение выражения (frac{log_{2}{14}}{1+log_{2}{7}})

Решение:

(frac{log_{2}{14}}{1+log_{2}{7}})(=)

          

Превращаем единицу в логарифм с основанием (2): (1=log_{2}{2})

(=)(frac{log_{2}{14}}{log_{2}{2}+log_{2}{7}})(=)

 

Теперь пользуемся свойством логарифмов:
(log_{a}{b}+log_{a}{c}=log_{a}{(bc)})

(=)(frac{log_{2}{14}}{log_{2}{(2cdot7)}})(=)(frac{log_{2}{14}}{log_{2}{14}})(=)

 

В числителе и знаменателе одинаковые числа – их можно сократить.

(=1)

 

Ответ готов.

Ответ: (1)

Смотрите также:
Логарифмические уравнения
Логарифмические неравенства

Источник
Автор статьи

Елена Борисовна Калюжная

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Прежде чем познакомится с понятием натурального логарифма, рассмотрим понятие постоянного числа $е$.

Число $e$

Определение 1

Число $e$ – это математическое постоянное, которое является трансцендентным числом и равно $e approx 2,718281828459045ldots$.

Определение 2

Трансцендентным называется число, которое не является корнем полинома с целыми коэффициентами.

Определение 3

Число $e$ является пределом выражения $(1+frac{1}{k})^k$ при $k$, которое стремится к бесконечности:

$e = lim_{k to infty} left(1 + frac{1}{k} right)^k$

Число е также носит название числа Эйлера, а иногда и числа Непера.

Замечание 2

Чтобы запомнить первые знаки числа $е$ зачастую пользуются следующим выражением: «$2$, $7$, дважды Лев Толстой». Конечно же, для того, чтобы можно было его использовать, необходимо помнить, что Лев Толстой родился в $1828$ г. Именно эти числа дважды повторяются в значении числа $е$ после целой части $2$ и десятичной $7$.

Рассмотрение понятия числа $е$ при изучении натурального логарифма мы начали именно потому, что оно стоит в основании логарифма $log_{e}⁡a$, который принято называть натуральным и записывать в виде $ln ⁡a$.

Натуральный логарифм

Часто при расчетах используют логарифмы, в основании которых стоит число $е$.

Определение 4

Логарифм с основанием $е$ называют натуральным.

«Натуральный логарифм и число е» 👇

Т.е. натуральный логарифм можно обозначить как $log_{e}⁡a$, но в математике принято использовать обозначение $ln ⁡a$.

Свойства натурального логарифма

  1. Т.к. логарифм по любому основанию от единицы равен $0$, то и натуральный логарифм единицы равен $0$:

    $ln ⁡1=0$.

  2. Натуральный логарифм от числа $е$ равен единице:

    $ln ⁡e=1$.

  3. Натуральный логарифм произведения двух чисел равен сумме натуральных логарифмов от этих чисел:

    $ln ⁡(ab)=ln ⁡a+ln ⁡b$.

  4. Натуральный логарифм частного двух чисел равен разнице натуральных логарифмов этих чисел:

    $ln⁡frac{a}{b}=ln ⁡a-ln⁡ b$.

  5. Натуральный логарифм степени числа может быть представлен в виде произведения показателя степени на натуральный логарифм подлогарифмического числа:

    $ln⁡ a^s=s cdot ln⁡ a$.

Пример 1

Упростить выражение $frac{2 ln ⁡4e-ln ⁡16}{ln ⁡5e-frac{1}{2} ln ⁡25}$.

Решение.

Применим к первому логарифму в числителе и в знаменателе свойство логарифма произведения, а ко второму логарифму числителя и знаменателя – свойство логарифма степени:

$frac{2 ln ⁡4e-ln⁡16}{ln ⁡5e-frac{1}{2} ln ⁡25}=frac{2(ln ⁡4+ln ⁡e )-ln⁡ 4^2}{ln ⁡5+ln ⁡e-frac{1}{2} ln⁡ 5^2}=$

откроем скобки и приведем подобные слагаемые, а также применим свойство $ln ⁡e=1$:

$=frac{2 ln ⁡4+2-2 ln ⁡4}{ln ⁡5+1-frac{1}{2} cdot 2 ln ⁡5}=frac{2}{ln ⁡5+1-ln ⁡5}=2$.

Ответ: $frac{2 ln ⁡4e-ln ⁡16}{ln ⁡5e-frac{1}{2} ln ⁡25}=2$.

Пример 2

Найти значение выражения $ln⁡ 2e^2+ln frac{1}{2e}$.

Решение.

Применим формулу суммы логарифмов:

$ln 2e^2+ln frac{1}{2e}=ln 2e^2 cdot frac{1}{2e}=ln ⁡e=1$.

Ответ: $ln 2e^2+ln frac{1}{2e}=1$.

Пример 3

Вычислить значение логарифмического выражения $2 lg ⁡0,1+3 ln⁡ e^5$.

Решение.

Применим свойство логарифма степени:

$2 lg ⁡0,1+3 ln e^5=2 lg 10^{-1}+3 cdot 5 ln ⁡e=-2 lg ⁡10+15 ln ⁡e=-2+15=13$.

Ответ: $2 lg ⁡0,1+3 ln e^5=13$.

Пример 4

Упростить логарифмическое выражение $ln frac{1}{8}-3 ln ⁡4$.

Решение.

Применим свойство логарифма степени:

$ln frac{1}{8}-3 ln ⁡4=ln 2^{-3}-3 ln 2^2=-3 ln⁡2-3 cdot 2 ln ⁡2=-9 ln ⁡2$.

Ответ: $ln frac{1}{8}-3 ln ⁡4=-9 ln ⁡2$.

Пример 5

Упростить логарифмическое выражение $ln frac{e^4}{25}$.

Решение.

Применим свойство логарифма частного:

$ln⁡ frac{e^4}{25}=ln e^4-ln ⁡25=$

во втором логарифме подлогарифмическое выражение запишем как число в степени:

$=ln e^4-ln 5^2=$

применим свойство логарифма степени к первому и второму логарифму:

$=4 ln ⁡e-2 ln ⁡5=$

применив свойство $ln ⁡e=1$, получим:

$=4-2 ln ⁡5$.

Ответ: $ln frac{e^4}{25}=4-2 ln ⁡5$.

Пример 6

Вычислить значение логарифмического выражения $3 ln frac{9}{e^2}-2 ln ⁡27$.

Решение.

Применим к обоим логарифмам свойство логарифма степени:

$3 ln frac{9}{e^2}-2 ln ⁡27=3 ln (frac{3}{e})^2-2 ln 3^3=3 cdot 2 ln frac{3}{e}-2 cdot 3 ln ⁡3=6 ln frac{3}{e}-6 ln ⁡3=$

применим к первому логарифму свойство логарифма частного:

$=6(ln ⁡3-ln ⁡e)-6 ln⁡ 3=$

откроем скобки и приведем подобные слагаемые:

$=6 ln ⁡3-6 ln ⁡e-6 ln ⁡3=-6$.

Ответ: $3 ln frac{9}{e^2}-2 ln ⁡27=-6$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Натуральные логарифмы чисел (Таблица)

I. Таблица натуральные логарифмы чисел 1)

1)Натуральный логарифм числа, не содержащегося среди аргументов таблицы, находится следующим образом. Пусть ищется ln 753. Имеем: ln 753 = ln (7,53 • 102) = ln 7,53 4- 2 ln 10. Первое слагаемое находим по таблице натуральных логарифмов, второе — по таблице III. Получаем: ln 753 = 2,0189 + 4,6052 = 6,6241. Таким же образом находим ln 0,00753 = ln (7,53 • 10″3) = 2,0189 – 6,9078 = -4,8889.

N 0 1 2 3 4 5 6 7 8 9
1,0 0,0000 0,0100 0,0198 0,0296 0,0392 0,0488 0,0583 0,0677 0,0770 0,0862
1,1 0,0953 0,1044 0,1133 0,1222 0,1310 0,1398 0,1484 0,1570 0,1655 0,1740
1,2 0,1823 0,1906 0,1989 0,2070 0,2151 0,2231 0,2311 0,2390 0,2469 0,2546
1,3 0,2624 0,2700 0,2776 0,2852 0,2927 0,3001 0,3075 0,3148 0,3221 0,3293
1,4 0,3365 0,3436 0,3507 0,3577 0,3646 0,3716 0,3784 0,3853 0,3920 0,3988
1,5 0,4055 0,4121 0,4187 0,4253 0,4318 0,4383 0,4447 0,4511 0,4574 0,4637
1,6 0,4700 0,4762 0,4824 0,4886 0,4947 0,5008 0,5068 0,5128 0,5188 0,5247
1,7 0,5306 0,5365 0,5423 0,5481 0,5539 0,5596 0,5653 0,5710 0,5766 0,5822
1,8 0,5878 0,5933 0,5988 0,6043 0,6098 0,6152 0,6206 0,6259 0,6313 0,6366
1,9 0,6419 0,6471 0,6523 0,6575 0,6627 0,6678 0,6729 0,6780 0,6831 0,6881
                     
2,0 0,6931 0,6981 0,7031 0,7080 0,7129 0,7178 0,7227 0,7275 0,7324 0,7372
2,1 0,7419 0,7467 0,7514 0,7561 0,7608 0,7655 0,7701 0,7747 0,7793 0,7839
2,2 0,7885 0,7930 0,7975 0,8020 0,8065 0,8109 0,8154 0,8198 0,8242 0,8286
2,3 0,8329 0,8372 0,8416 0,8459 0,8502 0,8544 0,8587 0,8629 0,8671 0,8713
2,4 0,8755 0,8796 0,8838 0,8879 0,8920 0,8961 0,9002 0,9042 0,9083 0,9123
2,5 0,9163 0,9203 0,9243 0,9282 0,9322 0,9361 0,9400 0,9439 0,9478 0,9517
2,6 0,9555 0,9594 0,9632 0,9670 0,9708 0,9746 0,9783 0,9821 0,9858 0,9895
2,7 0,9933 0,9969 1,0006 1,0043 1,0080 1,0116 1,0152 1,0188 1,0225 1,0260
2,8 1,0296 1,0332 1,0367 1,0403 1,0438 1,0473 1,0508 1,0543 1,0578 1,0613
2,9 1,0647 1,0682 1,0716 1,0750 1,0784 1,0818 1,0852 1,0886 1,0919 1,0953
                     
3,0 1,0986 1,1019 1,1053 1,1086 1,1119 1,1151 1,1184 1,1217 1,1249 1,1282
3,1 1,1314 1,1346 1,1378 1,1410 1,1442 1,1474 1,1506 1,1537 1,1569 1,1600
3,2 1,1632 1,1663 1,1694 1,1725 1,1756 1,1787 1,1817 1,1848 1,1878 1,1909
3,3 1,1939 1,1969 1,2000 1,2030 1,2060 1,2090 1,2119 1,2149 1,2179 1,2208
3,4 1,2238 1,2267 1,2296 1,2326 1,2355 1,2384 1,2413 1,2442 1,2470 1,2499
3,5 1,2528 1,2556 1,2585 1,2613 1,2641 1,2669 1,2698 1,2726 1,2754 1,2782
3,6 1,2809 1,2837 1,2865 1,2892 1,2920 1,2947 1,2975 1,3002 1,3029 1,3056
3,7 1,3083 1,3110 1,3137 1,3164 1,3191 1,3218 1,3244 1,3271 1,3297 1,3324
3,8 1,3350 1,3376 1,3403 1,3429 1,3455 1,3481 1,3507 1,3533 1,3558 1,3584
3,9 1,3610 1,3635 1,3661 1,3686 1,3712 1,3737 1,3762 1,3788 1,3813 1,3838
                     
4,0 1,3863 1,3888 1,3913 1,3938 1,3962 1,3987 1,4012 1,4036 1,4061 1,4085
4,1 1,4110 1,4134 1,4159 1,4183 1,4207 1,4231 1,4255 1,4279 1,4303 1,4327
4,2 1,4351 1,4375 1,4398 1,4422 1,4446 1,4469 1,4493 1,4516 1,4540 1,4563
4,3 1,4586 1,4609 1,4633 1,4656 1,4679 1,4702 1,4725 1,4748 1,4770 1,4793
4,4 1,4816 1,4839 1,4861 1,4884 1,4907 1,4929 1,4951 1,4974 1,4996 1,5019
4,5 1,5041 1,5063 1,5085 1,5107 1,5129 1,5151 1,5173 1,5195 1,5217 1,5239
4,6 1,5261 1,5282 1,5304 1,5326 1,5347 1,5369 1,5390 1,5412 1,5433 1,5454
4,7 1,5476 1,5497 1,5518 1,5539 1,5560 1,5581 1,5602 1,5623 1,5644 1,5665
4,8 1,5686 1,5707 1,5728 1,5748 1,5769 1,5790 1,5810 1,5831 1,5851 1,5872
4,9 1,5892 1,5913 1,5933 1,5953 1,5974 1,5994 1,6014 1,6034 1,6054 1,6074
                     
5,0 1,6094 1,6114 1,6134 1,6154 1,6174 1,6194 1,6214 1,6233 1,6253 1,6273
5,1 1,6292 1,6312 1,6332 1,6351 1,6371 1,6390 1,6409 1,6429 1,6448 1,6467
5,2 1,6487 1,6506 1,6525 1,6544 1,6563 1,6582 1,6601 1,6620 1,6639 1,6658
5,3 1,6677 1,6696 1,6715 1,6734 1,6752 1,6771 1,6790 1,6808 1,6827 1,6845
5,4 1,6864 1,6882 1,6901 1,6919 1,6938 1,6956 1,6974 1,6993 1,7011 1,7029
5,5 1,7047 1,7066 1,7084 1,7102 1,7120 1,7138 1,7156 1,7174 1,7192 1,7210
5,6 1,7228 1,7246 1,7263 1,7281 1,7299 1,7317 1,7334 1,7352 1,7370 1,7387
5,7 1,7405 1,7422 1,7440 1,7457 1,7475 1,7492 1,7509 1,7527 1,7544 1,7561
5,8 1,7579 1,7596 1,7613 1,7630 1,7647 1,7664 1,7681 1,7699 1,7716 1,7733
5,9 1,7750 1,7766 1,7783 1,7800 1,7817 1,7834 1,7851 1,7867 1,7884 1,7901
                     
6,0 1,7918 1,7934 1,7951 1,7967 1,7984 1,8001 1,8017 1,8034 1,8050 1,8066
6,1 1,8083 1,8099 1,8116 1,8132 1,8148 1,8165 1,8181 1,8197 1,8213 1,8229
6,2 1,8245 1,8262 1,8278 1,8294 1,8310 1,8326 1,8342 1,8358 1,8374 1,8390
6,3 1,8405 1,8421 1,8437 1,8453 1,8469 1,8485 1,8500 1,8516 1,8532 1,8547
6,4 1,8563 1,8579 1,8594 1,8610 1,8625 1,8641 1,8656 1,8672 1,8687 1,8703
6,5 1,8718 1,8733 1,8749 1,8764 1,8779 1,8795 1,8810 1,8825 1,8840 1,8856
6,6 1,8871 1,8886 1,8901 1,8916 1,8931 1,8946 1,8961 1,8976 1,8991 1,9006
6,7 1,9021 1,9036 1,9051 1,9066 1,9081 1,9095 1,9110 1,9125 1,9140 1,9155
6,8 1,9169 1,9184 1,9199 1,9213 1,9228 1,9242 1,9257 1,9272 1,9286 1,9301
6,9 1,9315 1,9330 1,9344 1,9359 1,9373 1,9387 1,9402 1,9416 1,9430 1,9445
                     
7,0 1,9459 1,9473 1,9488 1,9502 1,9516 1,9530 1,9544 1,9559 1,9573 1,9587
7,1 1,9601 1,9615 1,9629 1,9643 1,9657 1,9671 1,9685 1,9699 1,9713 1,9727
7,2 1,9741 1,9755 1,9769 1,9782 1,9796 1,9810 1,9824 1,9838 1,9851 1,9865
7,3 1,9879 1,9892 1,9906 1,9920 1,9933 1,9947 1,9961 1,9974 1,9988 2,0001
7,4 2,0015 2,0028 2,0042 2,0055 2,0069 2,0082 2,0096 2,0109 2,0122 2,0136
7,5 2,0149 2,0162 2,0176 2,0189 2,0202 2,0215 2,0229 2,0242 2,0255 2,0268
7,6 2,0281 2,0295 2,0308 2,0321 2,0334 2,0347 2,0360 2,0373 2,0386 2,0399
7,7 2,0412 2,0425 2,0438 2,0451 2,0464 2,0477 2,0490 2,0503 2,0516 2,0528
7,8 2,0541 2,0554 2,0567 2,0580 2,0592 2,0605 2,0618 2,0631 2,0643 2,0656
7,9 2,0669 2,0681 2,0694 2,0707 2,0719 2,0732 2,0744 2,0757 2,0769 2,0782
                     
8,0 2,0794 2,0807 2,0819 2,0832 2,0844 2,0857 2,0869 2,0882 2,0894 2,0906
8,1 2,0919 2,0931 2,0943 2,0956 2,0968 2,0980 2,0992 2,1005 2,1017 2,1029
8,2 2,1041 2,1054 2,1066 2,1078 2,1090 2,1102 2,1114 2,1126 2,1138 2,1150
8,3 2,1163 2,1175 2,1187 2,1199 2,1211 2,1223 2,1235 2,1247 2,1258 2,1270
8,4 2,1282 2,1294 2,1306 2,1318 2,1330 2,1342 2,1353 2,1365 2,1377 2,1389
8,5 2,1401 2,1412 2,1424 2,1436 2,1448 2,1459 2,1471 2,1483 2,1494 2,1506
8,6 2,1518 2,1529 2,1541 2,1552 2,1564 2,1576 2,1587 2,1599 2,1610 2,1622
8,7 2,1633 2,1645 2,1656 2,1668 2,1679 2,1691 2,1702 2,1713 2,1725 2,1736
8,8 2,1748 2,1759 2,1770 2,1782 2,1793 2,1804 2,1815 2,1827 2,1838 2,1849
8,9 2,1861 2,1872 2,1883 2,1894 2,1905 2,1917 2,1928 2,1939 2,1950 2,1961
                     
9,0 2,1972 2,1983 2,1994 2,2006 2,2017 2,2028 2,2039 2,2050 2,2061 2,2072
9,1 2,2083 2,2094 2,2105 2,2116 2,2127 2,2138 2,2148 2,2159 2,2170 2,2181
9,2 2,2192 2,2203 2,2214 2,2225 2,2235 2,2246 2,2257 2,2268 2,2279 2,2289
9,3 2,2300 2,2311 2,2322 2,2332 2,2343 2,2354 2,2364 2,2375 2,2386 2,2396
9,4 2,2407 2,2418 2,2428 2,2439 2,2450 2,2460 2,2471 2,2481 2,2492 2,2502
9,5 2,2513 2,2523 2,2534 2,2544 2,2555 2,2565 2,2576 2,2586 2,2597 2,2607
9,6 2,2618 2,2628 2,2638 2,2649 2,2659 2,2670 2,2680 2,2690 2,2701 2,2711
9,7 2,2721 2,2732 2,2742 2,2752 2,2762 2,2773 2,2783 2,2793 2,2803 2,2814
9,8 2,2824 2,2834 2,2844 2,2854 2,2865 2,2875 2,2885 2,2895 2,2905 2,2915
9,9 2,2925 2,2935 2,2946 2,2956 2,2966 2,2976 2,2986 2,2996 2,3006 2,3016

II. Таблица для перехода от натуральных логарифмов к десятичным 

(таблица умножения на М = log е = 0,4342945…)

  0 10 20 30 40 50 60 70 80 90
0 0,0000 4,3430 8,6859 13,0288 17,3718 21,7147 26,0577 30,4006 34,7436 39,0865
1 0,4343 4,7772 9,1202 13,4631 17,8061 22,1490 26,4920 30,8349 35,1779 39,5208
2 0,8686 5,2115 9,5545 13,8974 18,2404 22,5833 26,9263 31,2692 35,6122 39,9551
3 1,3029 5,6458 9,9888 14,3317 18,6747 23,0176 27,3606 31,7035 36,0464 40,3894
4 1,7372 6,0801 10,4231 14,7660 19,1090 23,4519 27,7948 32,1378 36,4807 40,8237
5 2,1715 6,5144 10,8574 15,2003 19,5433 23,8862 28,2291 32,5721 36,9150 41,2580
6 2,6058 6,9487 11,2917 15,6346 19,9775 24,3205 28,6634 33,0064 37,3493 41,6923
7 3,0401 7,3830 11,7260 16,0689 20,4118 24,7548 29,0977 33,4407 37,7836 42,1266
8 3,4744 7,8173 12,1602 16,5032 20,8461 25,1891 29,5320 33,8750 38,2179 42,5609
9 3,9086 8.2516 12,5945 16,9375 21,2804 25,6234 29,9663 34,3093 38,6522 42,9952

III. Таблица для перехода от десятичных логарифмов к натуральным

(таблица умножения на i = In 10 = 2,302585)

  0 10 20 30 40 50 60 70 80 90
0 0,0000 23,026 46,052 69,078 92,103 115,129 138,155 161,181 184,207 207,233
1 2,3026 25,328 48,354 71,380 94,406 117,431 140,458 163,484 186,509 209,535
2 4,6052 27,631 50,657 73,683 96,709 119,734 142,760 165,786 188,812 211,838
3 6,9078 29,934 52,959 75,985 99,011 122,037 145,062 166,089 191,115 214,140
4 9,2103 32,236 55,262 78,288 101,314 124,340 147,365 170,391 193,417 216,443
5 11,513 34,539 57,565 80,590 103,616 126,642 149,668 172,694 195,720 218,746
6 13,816 36,841 59,867 82,893 105,919 128,945 151,971 174,997 198,022 221,048
7 16,118 39,144 62,170 85,196 108,221 131,247 154,273 177,299 200,325 223,351
8 18,421 41,447 64,472 87,498 110,524 133,550 156,576 179,602 202,627 225,653
9 20,723 43,749 66,775 89,801 112,827 135,853 158,878 181,904 204,930 227,956

_______________

Источник информации: Справочник по высшей математике / М. Я. Выгодский. — М.: ACT: Астрель, 2006.

Поделитесь ссылкой с друзьями:

Похожие таблицы

Комментарии:

Источник

Добавить комментарий