В этой заметке речь пойдет о пределах. С ними сталкиваются в 10-11 классах на уроках физики, когда начинают выводить частоту колебаний математического или физического маятников. В математике с пределами сталкиваются, когда учащихся знакомят с производными и дифференцированием. Поэтому эта одно из самых базовых понятий математического анализа, в котором не должно быть пробелов.
Давайте начнем с простых (условно и относительно) пределов, которые вам могут попасться на первом курсе.
С некоторыми из них практически ничего не нужно делать, а только подставить значение…
А другие становятся легче, если разделить на общий одночлен, который представляет собой старшую степень переменной.
В пределах, имеющих радикалы частенько помогает домножение на “сопряженное” выражение. Также упростит понимание таких действий тот факт, если вы хорошо помните формулы сокращенного умножения, в частности разность квадратов.
Структурировать информацию лучше сразу
При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называют неопределенностями.
Перечислим все основные виды неопределенностей:
1) ноль делить на ноль
2) бесконечность делить на бесконечность
3) ноль умножить на бесконечность
4) бесконечность минус бесконечность
5) единица в степени бесконечность
6) ноль в степени ноль формула
7) бесконечность в степени ноль
ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.
Раскрывать неопределенности позволяет:
● упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);
● использование замечательных пределов;
● применение правила Лопиталя;
● использование замены бесконечно малого выражения ему эквивалентным (использование таблицы эквивалентных бесконечно малых).
Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только к первому и второму из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.
Правила Лопиталя – очень мощный метод, позволяющий быстро и эффективно устранить указанные неопределенности. Если числитель и знаменатель являются бесконечно малыми или бесконечно большими одновременно, то можно посчитать отношениях производных этих функций. При дифференцировании числителя и знаменателя значение предела не меняется.
Иногда приходится применять правило Лопиталя последовательно несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге.Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.
Для раскрытия неопределённостей видов 0^0, 1^∞, ∞^0 пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
Для раскрытия неопределённостей типа ∞/∞ используется следующий алгоритм:
● Выявление старшей степени переменной;
● Деление на эту переменную как числителя, так и знаменателя.Для раскрытия неопределённостей типа 0/0 существует следующий алгоритм:
● Разложение на множители числителя и знаменателя;
● Сокращение дроби.Для раскрытия неопределённостей типа ∞ – ∞ иногда удобно применить следующее преобразование:
● f(x) – g(x) = 1/ (1/f(x) ) – 1/(1/g(x)) = (1/g(x) – 1/f(x))/( (1/g(x)) * (1/f(x)) )
Данный вид неопределённостей может раскрываться с использованием асимптотических разложений уменьшаемого и вычитаемого, при этом бесконечно большие члены одного порядка должны уничтожаться.
При раскрытии неопределённостей также применяются замечательные пределы и их следствия.
Ещё немного примеров для закрепления материала
В пределах могут быть и суммы вместо функций. Подумайте какой подвох в следующем пределе ? Правильно ли получен ноль ?
Вы еще думаете, что пределы – это просто? А как насчет предела с параметром?
Интересная задачка по математике с параметрическим интегралом.
Чему равен предел lim[ I(a) ] при a → 0 если в качестве I(a) выступает интеграл: I(a) = Int( x⁵ ⋅ ( cos(a²x) + sin(5a²x) )^(x/a²) ) dx
в пределах от 2^a до 2^(a+1).
Так как предел считается от параметра, а параметр не зависит от переменной интегрирования, то вполне законно пронести предел внутрь выражения и применить его только к той части, которая представляет наибольшую сложность. Аппроксимация сводит выражение ко второму замечательному пределу. А дальше дело за аккуратными вычислениями интегралов по частям. Придумали другой способ? Напишите в комментариях.
Рассмотрим ещё один сложный предел, для которого вам не помогут табличные бесконечно малые функции в силу их небольшой точности
Интересный предел на базе второго замечательного предела.
Задача: вычислить предел lim(1/n + exp(-1/n))^(n²) при n → ∞
Пределы на базе второго замечательного могут быть очень запутанные. Приведу вам ещё один пример. Что может быть интереснее, чем посидеть зимним вечером за математическим анализом с чашечкой кофе? 🙂
Задание: найти предел
Естественно, интересно решить это аналитически. Потому что вбивать в математические пакеты сможет любой человек. Мы видим, что у нас одна зависящая от x функция возводится в степень другой зависимой от x функции. Уже это должно нам намекнуть “а не второй замечательный предел у нас тут спрятался?”
Конечно же он! Только нужно подойти к нему. Делаем искусственный прием, чтобы отсечь единичку от дроби, а оставшуюся часть заменить на некоторую переменную. Я назвал её t, но можно называть как угодно. Сразу же нужно посмотреть к чему будет стремиться данная переменная, при стремлении x —> 1. Видим, что стремление t происходит в бесконечность, а значит мы уже можем определиться с формой записи второго замечательного предела, под который будем подгонять наши преобразования.
Так как мы пытаемся перейти к t, в степени, в косинусе у нас находится голенькое x, то нам придется выразить его из предшествующей замены переменных. Получается квадратное уравнения, которое дает два корня. Эта неоднозначность не должна вас смущать, так как корень подходит только один, причем положительный для x, т.к. x —> 1 (значит x > 0)
Далее несколько преобразований приводят нас к тому, что у нас получается е в некоторой степени, лимит (предел) которой нам предстоит найти. Но степень оказывается тоже с неопределенностью в знаменателе 0 * infinity. Тогда мы искусственно перебрасываем лишнюю переменную в числитель. Применяем правило Лопиталя-Бернулли (предел отношений функций равен пределу отношения производных этих функций). И у нас получается что-то очень похожее на первый замечательный предел. Но на самом деле уже сюда достаточно подставить t = infinity и получить конечный ответ.
Решение полное будет выглядеть так:
Под вторым замечательным пределам также могут скрывать тригонометрические функции, которые также усложняют жизнь, потому что студенты часто пытаются разрешить их простейшими преобразованиями или разложением в ряд, что не всегда кончается успехом.
Например задание:
Интересный предел. Сложность в том, чтобы вспомнить универсальную тригонометрическую подстановку, затем не побояться её подставить и сделать правильную замену переменных, чтобы выделить второй замечательный предел.
Есть и задачи, где можно применить первый замечательный предел
Очередная интересная задача на нахождение предела. Не особо очевидное применение первого замечательного предела. Конечно же применение правила Бернулли — Лопиталя, возможно, упростило бы нахождение ответа, но разве ценителям математики интересны простые пути? 🙂
На сегодня закончим, ведь тут итак есть над чем задуматься. А с каким самым сложным пределом сталкивались вы на занятиях математикой? Расскажите об этом в комментариях!
Еще много полезного и интересного вы сможете найти на ресурсах:
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Physics.Math.Code в контакте (VK)
Physics.Math.Code в telegram
Physics.Math.Code в YouTube
Пределы с логарифмами: примеры решений
Часто в контрольных работах нужно вычислить пределы с логарифмами. Такие задачи можно решить двумя способами:
- С помощью следствия второго замечательного предела: $$ lim limits_{x to 0} frac{ln(1+f(x))}{f(x)} = 1 text{, если } f(x) to 0 $$
- С помощью свойства бесконечно малой эквивалентной функции: $$ ln(1+f(x)) sim f(x) text{, если } f(x) to 0 $$
Оба метода решения допустимы к сдаче преподавателю на проверку. Выберите для себя самый удобный, который будете легко понимать
| Пример 1 |
| Вычислить предел с логарифмом: $ limlimits_{x to 0} frac{ln(1+8x)}{2x} $ |
| Решение |
|
Метод 1: Воспользуемся следствием замечательного предела и приведем предел к виду похожему на него: $$ limlimits_{x to 0} frac{ln(1+8x)}{2x} = limlimits_{x to 0} frac{frac{ln(1+8x)}{8x}cdot small 8x}{2x} = $$ Замечаем, что $ lim limits_{x to 0} frac{ln(1+8x)}{8x} = 1 text{, так как } 8x to 0 $ Продолжаем решение с учетом замечания: $$ = lim limits_{x to 0} frac{8x}{2x} = frac{8}{2} = 4 $$ Метод 2: Используем свойство б.м.э. функции для преобразования натурального логарифма: $$ ln(1+8x) sim 8x text{, при } 8x to 0 $$ Решаем с учетом вышеприведенной эквивалентности: $$ lim limits_{x to 0} frac{ln(1+8x)}{2x} = limlimits_{x to 0} frac{8x}{2x} =frac{8}{2} = 4 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ limlimits_{x to 0} frac{ln(1+8x)}{2x} = 4 $$ |
| Пример 2 |
| Найти предел $ limlimits_{x to 2} frac{ln(x^2-7x+11)}{x-2} $ |
| Решение |
|
Метод 1: Выполняем преобразование под следствие замечательного предела: $$ limlimits_{x to 2} frac{ln(x^2-7x+11)}{x-2} = limlimits_{x to 2} frac{frac{ln(1 + x^2-7x+10)}{x^2-7x+10}cdot small (x^2-7x+10)}{x-2} = $$ Видно, что $ limlimits_{x to 2} frac{ln(1 + x^2-7x+10)}{x^2-7x+10} = 1 $ по след. замеч. предела. С учетом этого, продолжим вычислять интеграл: $$ = limlimits_{x to 2} frac{x^2-7x+10}{x-2} = $$ Логарифм пропал. Решим квадратное уравнение в числителе и распишем его на множители: $$ = limlimits_{x to 2} frac{(x-2)(x-5)}{x-2} = limlimits_{x to 2} (x-5) = 2-5=-3 $$ Метод 2: Решение начнем с преобразования предела: $$ limlimits_{x to 2} frac{ln(x^2-7x+11)}{x-2} = limlimits_{x to 2} frac{ln(1 + (x^2-7x+10))}{x-2} = $$ Так как $ x^2-7x+10 = 0 text{при} x = 2 $ , то имеем: $$ ln(1 + (x^2-7x+10)) sim x^2-7x+10 $$ С учетом эквивалентности продолжаем решать: $$ = limlimits_{x to 2} frac{x^2-7x+10}{x-2} = $$ Выполним разложение многочлена второй степени на множители: $$ = limlimits_{x to 2} frac{(x-2)(x-5)}{x-2} = $$ Далее, выполняем сокращение на $ x-2 $: $$ limlimits_{x to 2} frac{(x-2)(x-5)}{x-2} = limlimits_{x to 2} (x-5) = 2-5 = -3 $$ |
| Ответ |
| $$ limlimits_{x to 2} frac{ln(x^2-7x+11)}{x-2} = -3 $$ |
Содержание:
Замечательные пределы
Сравнение бесконечно малых функций
Признак существования предела (теорема о 2-х милиционерах)
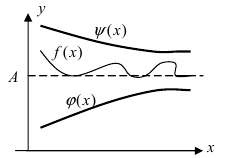
Теорема: Если значения функции
значениями функций
Рассмотрим геометрический смысл данной теоремы (Рис. 62). Из рисунка видно, что в случае, когда функции 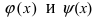
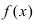
Рис. 62. Иллюстрация теоремы о “2-х милиционерах”.
Доказательство: Пусть 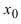
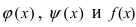
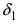
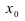
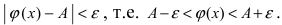
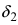
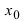
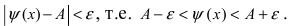
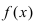
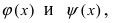
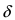
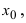
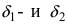
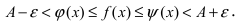
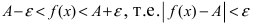
Первый замечательный предел
Определение: Предел отношения синуса какого-либо аргумента к этому аргументу при стремлении аргумента к нулю равен единице, т.е. 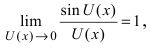
Пример:
Пределы являются первыми замечательными пределами 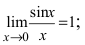
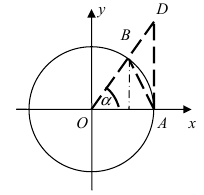
Доказательство: Для вывода этой формулы построим окружность с центром в точке О(0; 0) и радиусом R = 1. Выберем угол 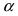
Рис. 63. Иллюстрация вывода формулы первого замечательного предела.
Из рисунка видно, что площади указанных фигу р связаны соотношением:
Вычислим эти площади
Следовательно, вышеприведенное неравенство приводится к виду 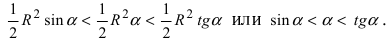
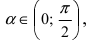
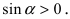
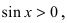
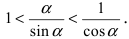
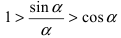
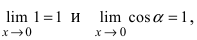
Аналогично проводится доказательство для любого значения угла
Таким образом, наличие в пределе, сводящемся к неопределенности 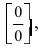
При вычислении первого замечательного предела используют следующие формулы:
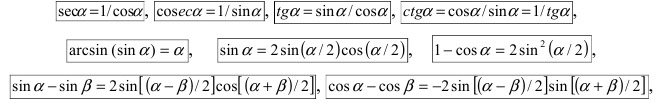
Табл. 1. Значения синуса и косинуса на интервале
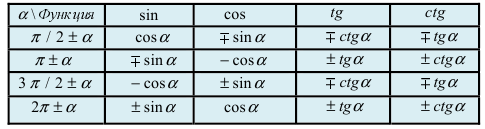
Табл. 2. Формулы приведения.
Пример:
Найти
Решение:
При подстановке предельной величины переменной х имеем неопределенность 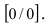
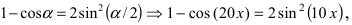
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 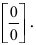
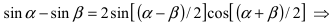
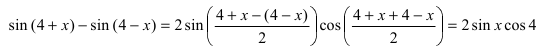
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 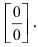
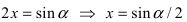
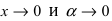
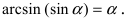
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 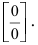
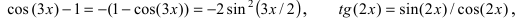
Число e и натуральные логарифмы. Второй замечательный предел
Рассмотрим логарифмическую функцию 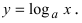
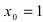
Определение: Натуральным логарифмом называется логарифм, для которого основание выбрано так, чтобы тангенс угла наклона касательной к положительному направлению оси абсцисс (Ох) был равен 1.
Основанием натурального логарифма является число 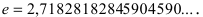
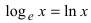
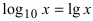
Определение: Вторым замечательным пределом называется предельное равенство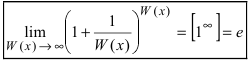
или
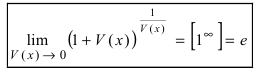
Замечание: Первая форма второго замечательного предела переходит во вторую с помощью замены 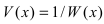
Замечание: Наличие неопределенности 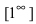
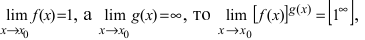
Пример:
Найти
Решение:
При подстановке предельного значения переменной х не имеем неопределенности
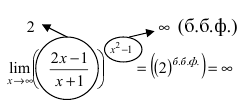
Пример:
Найти lim
Решение:
При подстановке предельного значения переменной х имеем неопределенность 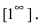
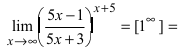
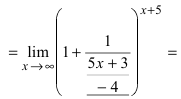
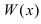
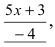
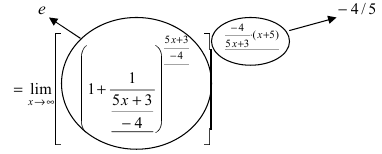
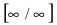
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределенность 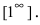
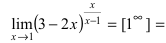
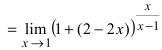
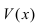
- Заказать решение задач по высшей математике
Сравнение бесконечно малых функций
Сравнить две бесконечно малые функции 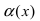
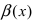
Определение: Если предел К не существует, то бесконечно малые функции 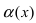
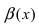
Пример:
Пусть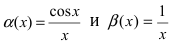
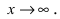
Решение:
Для доказательства вычислим предел 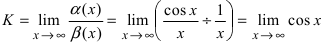
Определение: Если предел К равен нулю, то бесконечно малая функция 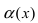
Пример:
Пусть 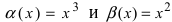
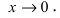
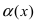
Решение:
Для доказательства вычислим предел 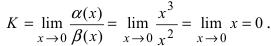
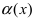
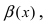
Определение: Если предел К равен 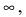
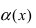
Пример:
Пусть 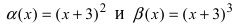
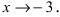
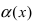
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малая функция 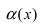
Определение: Если предел К равен конечному числу 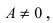
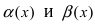
Пример:
Пусть 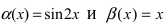
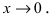
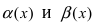
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малые функции 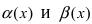
Определение: Если предел К равен 1, то бесконечно малые функции а(х) и Д(х) называются эквивалентными.
Пример:
Пусть 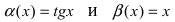
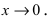
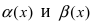
Решение:
Вычислим предел 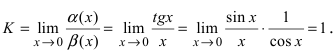

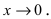
Теорема: Для того чтобы бесконечно малые функции 
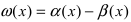

Доказательство:
1. Необходимость. Пусть бесконечно малая функция 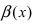
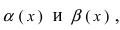
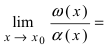
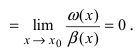
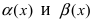
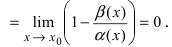
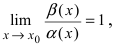
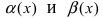
2. Достаточность. Пусть бесконечно малые функции 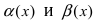
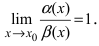
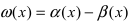
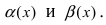
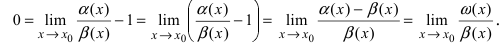
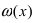
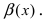
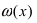
Замечание: При вычислениях одна бесконечно малая функция может быть заменена на эквивалентную бесконечно малую функцию. Например, функции 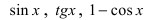
—вышмат
Замечательные пределы
Первый замечательный предел
Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:
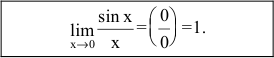
Пример №25
Найти
Решение:
Применим первый замечательный предел:
Второй замечательный предел
Числом е называется предел функции
(Для запоминания: 2<е<3; 1828 – год рождения Л.Н. Толстого) Следовательно,
Задача о непрерывном начислении процентов
Первоначальный вклад в банк составил 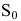
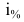
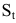
Решение:
Размер вклада будет увеличиваться ежегодно в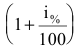
через t лет составит 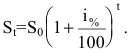
то будущая сумма составит 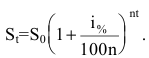
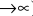
а за t лет:
Пример №26
Найти
Решение:
Т.к. 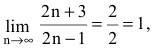
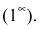
Пример №27
Найти
Решение:
Преобразуя выражение и используя непрерывность показательно-степенной функции, получим:
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
Содержание:
- Предел показательно-степенной функции
- Примеры с решением
Предел показательно-степенной функции
Показательно-степе иным и называют функции вида 

Функция 



Отсюда ясно, что показательно-степенная функция непрерывна при тех значениях х, при которых функции 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Если существуют пределы 





a) 


б) 
и потому 
Мы опускаем разбор остальных случаев и приводим следующую таблицу значений предела 
Возможно вам будут полезны данные страницы:
В случаях, соответствующих зачерненным клеткам, ответ неоднозначен и зависит от того, как именно стремятся
Примеры с решением
Пример 1.
Вычислим предел

Так как (см. п. 35)

Пример 2.
Вычислим предел:

а) Так как

б) Здесь 
Пример 3.
Вычислим предел:

а) Так как



66. Предел 



Последовательность с общим членом 











а из неравенств 
Итак, мы доказали, что
где, напомним, 

и 




Когда 


Если в этом равенстве положить 

Пример 4.
Вычислим
Решение:
Имеем:
Пример 5.
Вычислим
Решение:
Имеем:




и 

Если 




- Вычисление пределов, связанных с показательной и логарифмической функциями. Формулы (1) и (3) лежат в основе вычисления большинства пределов, связанных с показательной и логарифмической функциями.
Прологарифмировав обе части равенства (3) по основанию е, получаем 
Заметим теперь, что в силу непрерывности логарифмической функции для любого а > 0 имеем: 







Введем новую переменную z, положив 







Наконец докажем, что





Мы доказали в этом пункте следующие соотношения эквивалентности бесконечно малых (в дополнение к тем, что были получены выше в п. 53 и 58): если 
Пример 6.
Вычислим предел

Так как 




Пример 7.
Вычислим предел

Снова заменяем числитель и знаменатель эквива-лентными бесконечно малыми. Числитель запишем в виде 





а) 

б) 

в) 

Для вычисления таких пределов заменяют
, т. е. на e
и вычисляют предел
Тогда искомый предел равен 
Лекции:
- Исследовать сходимость ряда по признаку Даламбера
- Линейная комбинация векторов
- Площадь поверхности шара
- Производная сложной функции примеры решений
- Определение предела функции
- Криволинейный интеграл 2 рода
- Замечательные пределы, содержащие тригонометрические функции
- Уравнение в полных дифференциалах
- Действия со степенями
- Найти три первых отличных от нуля
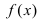
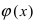
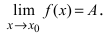
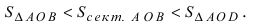
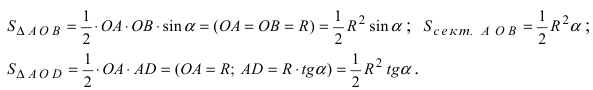
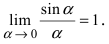
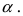
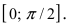

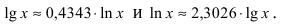
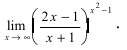
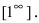
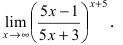
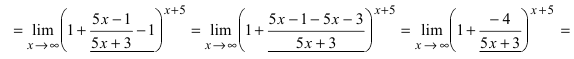
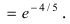
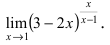
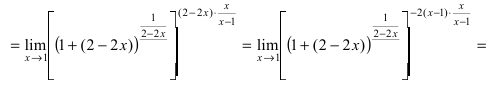
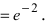
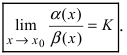
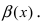
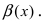
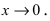
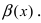
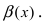
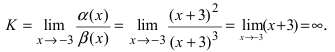
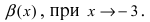
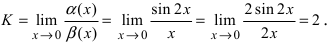
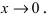
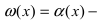
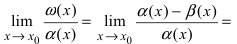
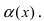
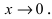
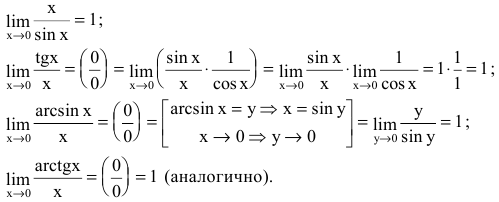
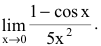
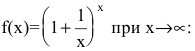
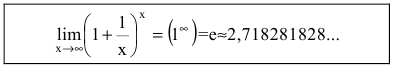
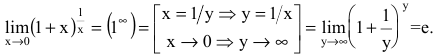
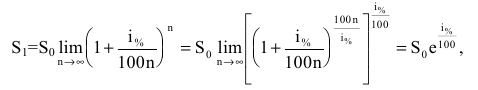
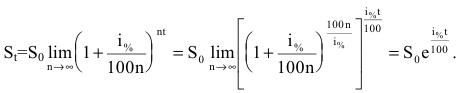
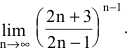
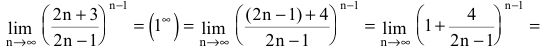
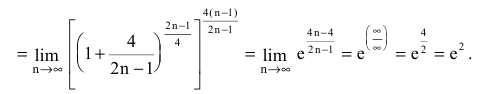
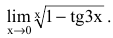
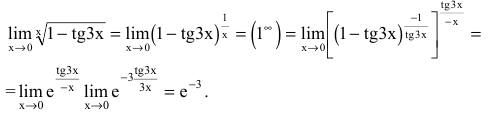






















 , т. е. на e
, т. е. на e и вычисляют предел
и вычисляют предел



