#статьи
- 6 окт 2022
-
0
Стыдные вопросы о логарифмах: всё, что нужно знать программисту
Объясняем, почему не стоит бояться логарифмов и как их считать в Python.
Иллюстрация: Оля Ежак для Skillbox Media

Журналист, изучает Python. Любит разбираться в мелочах, общаться с людьми и понимать их.
Прежде чем начать обсуждение, давайте немного освежим знания и решим несколько стандартных задачек:
- Чему равен log3 81?
- А lg 2 × lb 10?
- А сумма log216 2 + log216 3?
Если вы легко прорешали все три примера в уме, не пользуясь калькулятором, — можете сразу переходить к заключительной главе. Для тех же, кто слегка подзабыл школьные годы чудесные, — буквально пять минут ликбеза.
По большому счёту, логарифм — это просто перевёрнутая степень. Рассмотрим выражение 23 = 8. В нём:
- 2 — основание степени;
- 3 — показатель степени;
- 8 — результат возведения в степень.
У возведения в степень существует два обратных выражения. В одном мы ищем основание (это извлечение корня), в другом — показатель (это логарифмирование).
Таким образом, выражение 23 = 8 можно превратить в log2 8 = 3.
Закрепляем знания: логарифм — это число, в которое нужно возвести 2 (основание степени), чтобы получить 8 (результат возведения в степень).
Форма записи неинтуитивна, и поначалу можно легко спутать основание со степенью. Чтобы избежать этого, можно использовать следующее правило:
Основание у логарифма, как и у возведения в степень, находится внизу.
Чтобы лучше запомнить структуру записи, посмотрите на эти выражения и постарайтесь понять их смысл:
- log3 9 = 2
- log4 64 = 3
- log5 625 = 4
- log7 343 = 3
- log10 100 = 2
- log2 128 = 7
- log2 0,25 = −2
- log625 125 = 0,75
В общем виде запись logAB читается так: логарифм B по основанию A.
Главная часть любого логарифма — его основание. Именно наличие общего основания у нескольких логарифмических функций позволяет проводить с ними различные операции.
Основанием натурального логарифма является число Эйлера (e) — иррациональное число, приблизительно равное 2,71828.
На всякий случай напомним, что такое иррациональные числа. Так называют числа, которые нельзя записать в виде обыкновенной дроби с целыми числителем и знаменателем. При этом знаменатель не должен быть равен нулю.
Например, 0,333… — рациональное число, потому что его можно записать как 1/3. А вот число Пи или корень из 2 — иррациональны.
Так как натуральные логарифмы часто используются, для них ввели особый способ записи: ln x — это то же самое, что loge x.
Представим кристалл, который весит 1 кг и растёт со скоростью 100% в год. Можно ожидать, что через год он будет весить 2 кг, но это не так.
Каждая новая выращенная часть начнёт растить свою собственную. Когда в кристалле будет 1,1 кг, он будет расти со скоростью 1,1 кг в год, а когда в нём будет 1,5 кг — со скоростью 1,5 кг в год. Математики подсчитали, что через год масса кристалла составит e, или ≈ 2,71828 кг.
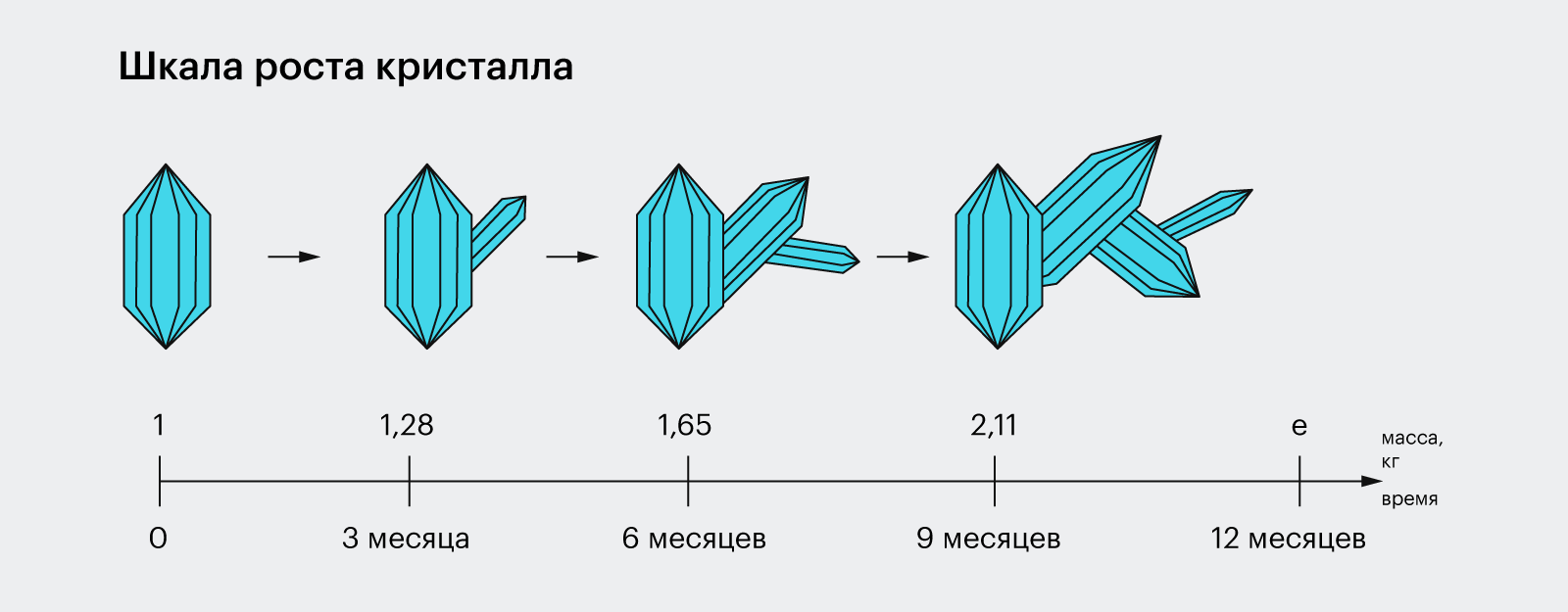
Такой рост называется экспоненциальным. По экспоненте размножаются бактерии, увеличиваются популяции, приумножаются доходы, растут снежные комья, распадается радиоактивное вещество и остывают напитки.
Чтобы узнать, какой массы достигнет кристалл через три, пять, десять лет, нужно возвести e в соответствующую степень.
e3 ≈ 20,0855 кг
e5 ≈ 148,4132 кг
e10 ≈ 22 026,4658 кг
Но как рассчитать, когда кристалл будет весить тонну? Составим уравнение:
ex = 1000
Нам известны основание степени и результат возведения в степень — осталось найти её показатель. Ничего не напоминает? Это ведь и есть логарифм x = loge 1000! Или, если использовать сокращённую запись, x = ln 1000.
Подставим в калькулятор и выясним, что x ≈ 6,9. Именно столько лет потребуется кристаллу, чтобы его масса достигла тонны.
Десятичный логарифм — логарифм, основание которого равно 10. Он обозначается lg x и очень удобен, потому что с ним легко вычислять круглые числа.

Двоичный логарифм — логарифм, основание которого равно 2. Он обозначается lb x и часто используется программистами, потому что компьютеры думают и считают в двоичной системе.

Список операций, которые можно совершать с логарифмами, ограничен. Если вы запомните все и научитесь их выполнять, то сможете щёлкать логарифмические задачки, как семечки.
У всех логарифмов есть ограничения. Их основание и аргумент должны быть больше нуля, при этом основание не может быть равно единице. На математическом языке это звучит так:

Перейдём к свойствам логарифмов. Они работают в обе стороны, и их применяют как слева направо, так и справа налево.
1. Логарифм единицы по любому основанию всегда равен нулю:
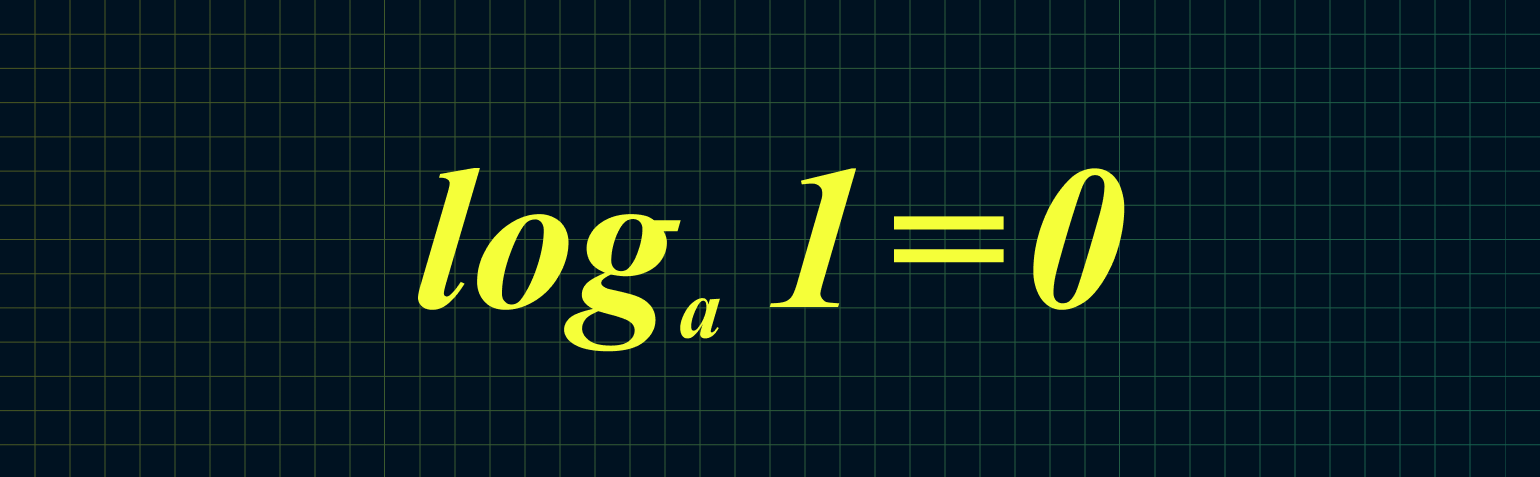
Например: log17 1 = 0
2. Логарифм, где число и основание совпадают, равен единице:
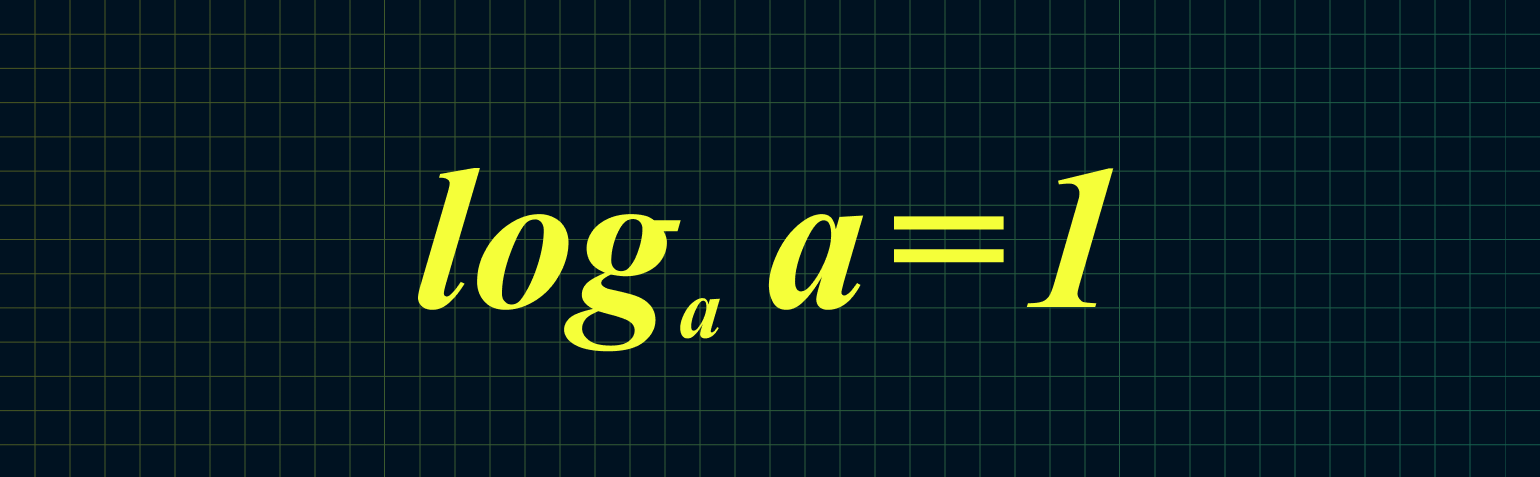
Например: log17 17 = 1
3. Основное логарифмическое тождество:
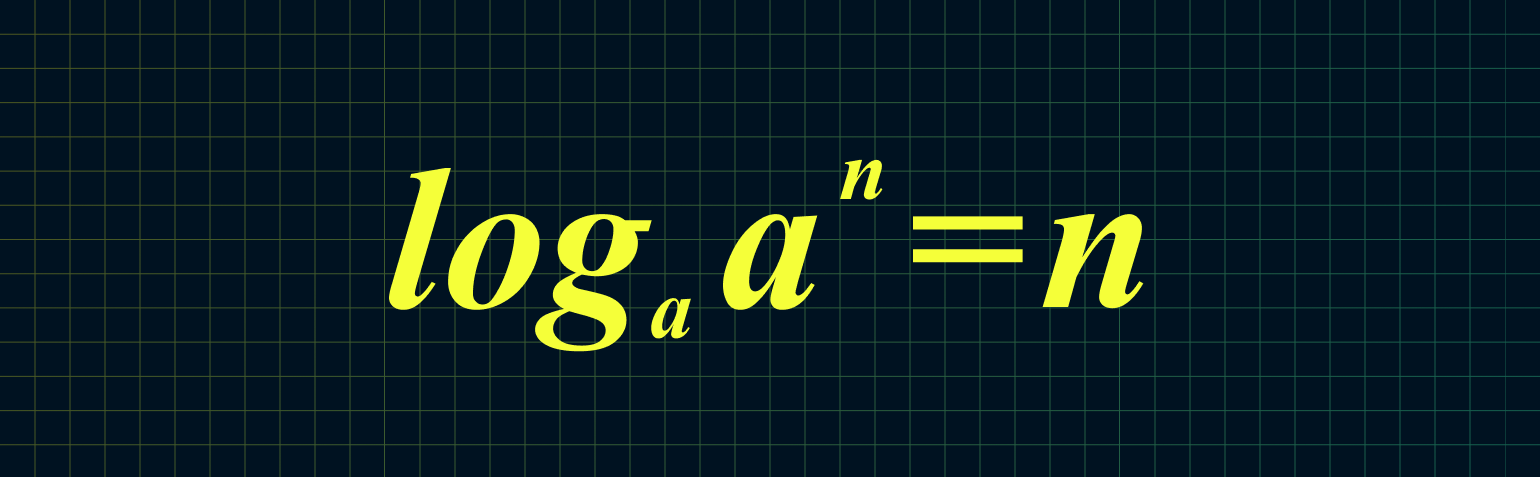
Например: log17 175 = 5
4. Логарифм произведения чисел равен сумме их логарифмов:
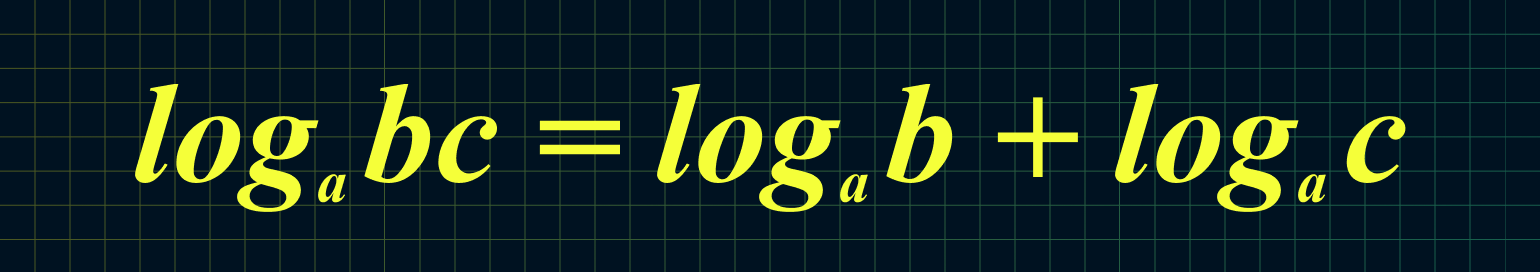
Например: log5 12,5 + log5 10 = log5 (12,5 × 10) = log5 125 = 3
5. Логарифм дроби равен разности логарифмов числителя и знаменателя:
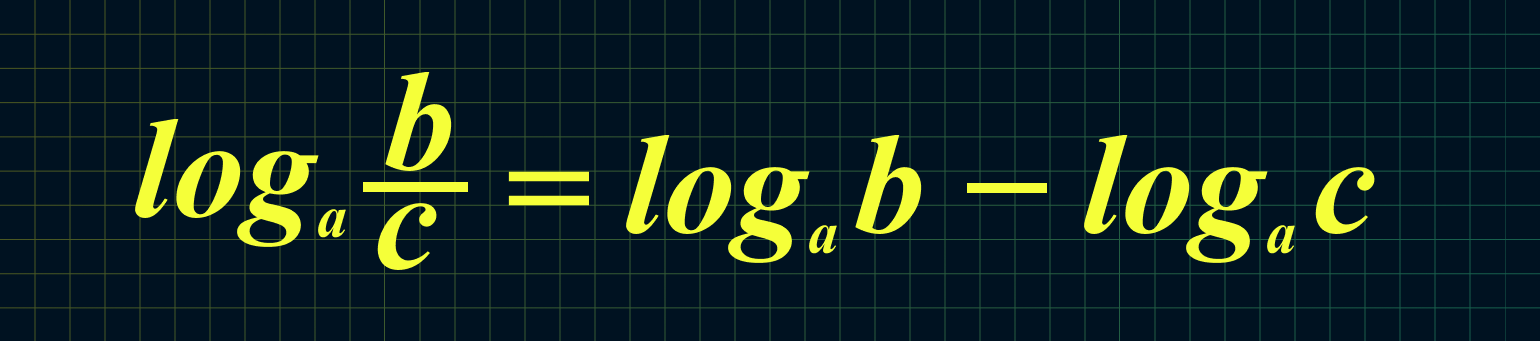
Например: log3 63 − log3 7 = log3 63/7 = log3 9 = 2
6. Если основание или аргумент возведены в степень, то их можно удобно выносить перед логарифмом:
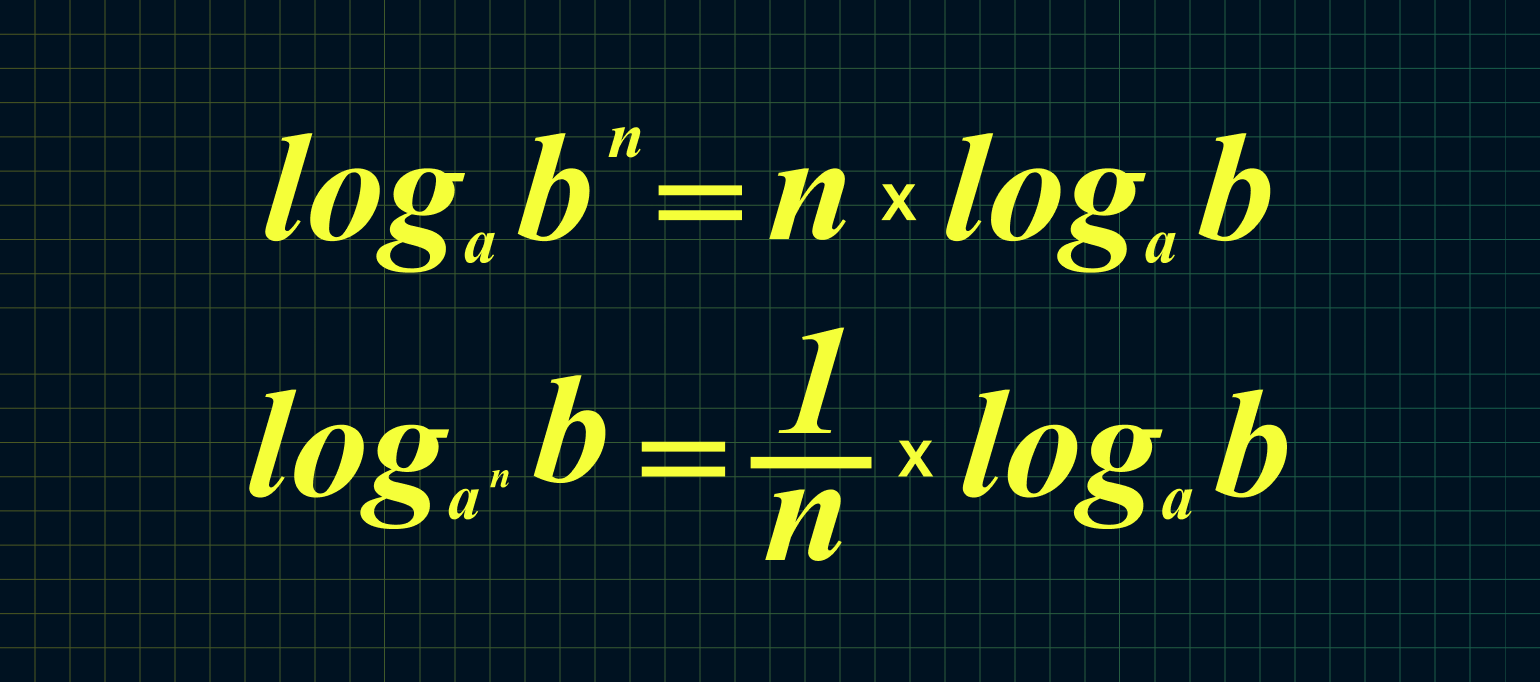
Из этих двух формул следует:
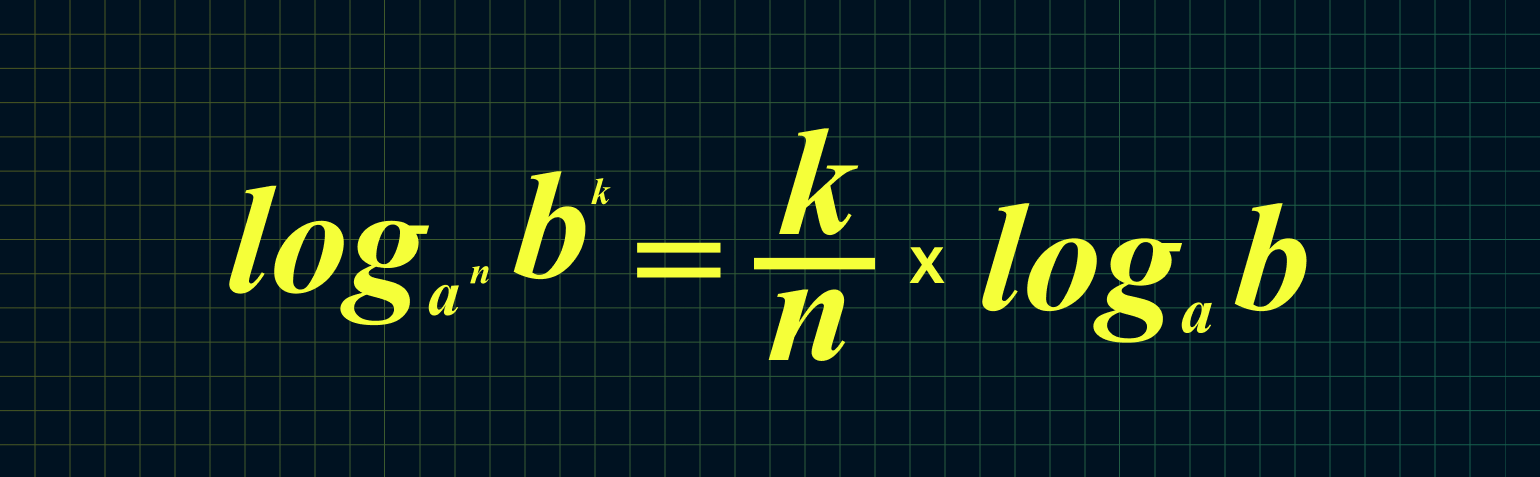
Например: log23 49 = 9/3 × log2 4 = 3 × 2 = 6
7. Если нам неудобно основание логарифма, то его можно изменить:
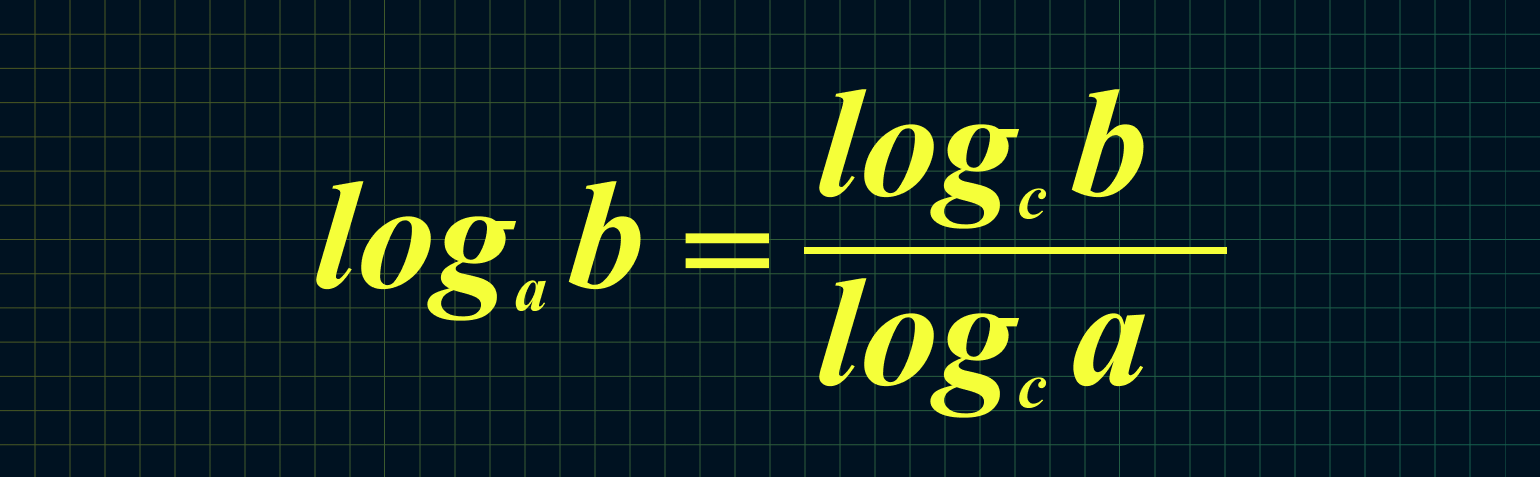
Например: log25 125 = log5 125/log5 25 = 3/2 = 1,5
Из этой формулы следует, что мы можем поменять местами основание и аргумент вот так:
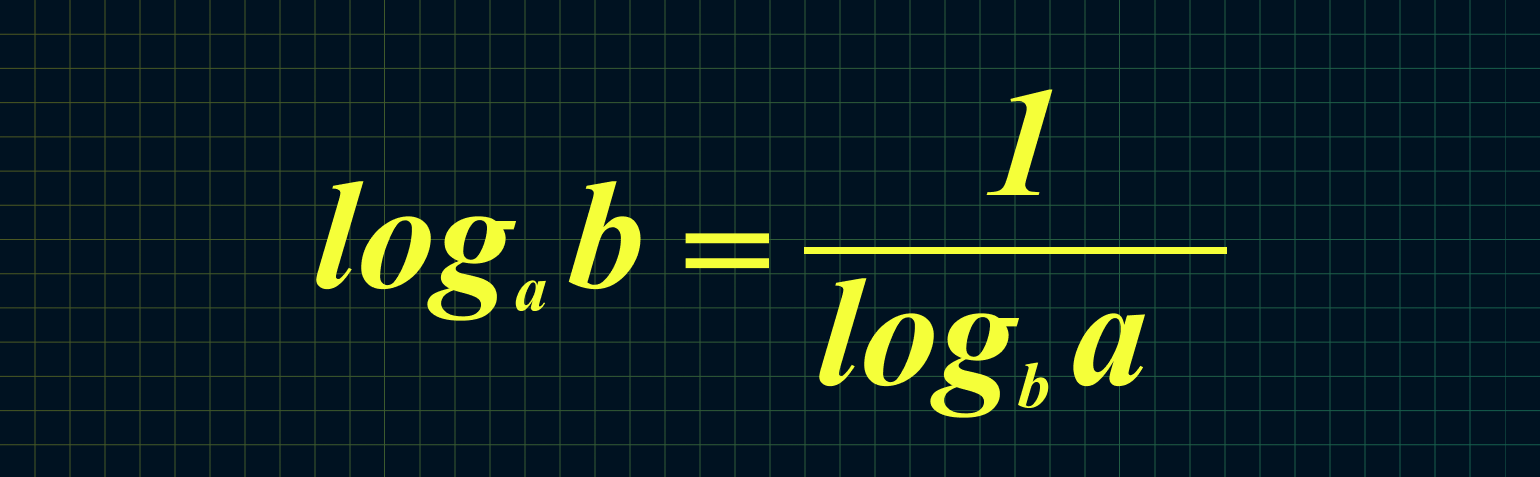
Например: log16 4 = 1/log4 16 = 1/2 = 0,5
А теперь возвращаемся к задачам, которые мы дали в начале статьи.
Пример 1
log3 81
Вспомните, что 81 — это 92. А 9 — это 32. Таким образом:
log3 81 = log3 92 = log3 32+2 = log3 34
Теперь логарифм не представляет для нас никаких сложностей. Воспользуемся свойством степени и вынесём четвёрку.
log3 34 = 4 × log3 3 = 4 × 1 =4
Ответ: 4.
Пример 2
lg 2 × lb 10
Переведём сокращённые записи в полный вид:
lg 2 × lb 10 = log10 2 × log2 10
Приведём оба логарифма к одному основанию.
log10 2 × log2 10 = 1/log2 10 × log2 10 = log2 10/log2 10 = 1
Ответ: 1.
Пример 3
log216 2 + log216 3
Воспользуемся свойством суммы.
log216 2 + log216 3 = log216 2 × 3 = log216 6
Представим 216 в виде степени числа 6 и вынесем с помощью свойства степени.
log216 6 = log63 6 = 1/3 × log6 6 = 1/3 × 1 = 1/3
Ответ: 1/3.
Чтобы работать с логарифмическими выражениями в Python, необходимо импортировать модуль math:
import math
И теперь посчитаем log2 8, используя метод math.log (b, a):
print (math.log (8, 2)) >>> 3.0
Обратите внимание на два момента. Во-первых, мы сначала передаём функции аргумент и только потом — основание. Во-вторых, функция всегда возвращает тип данных float, даже если результат целочисленный.
Если мы не передаём функции основание, то логарифм по умолчанию считается натуральным:
#math.e — метод для вызова числа Эйлера. print (math.log (math.e)) >>> 1.0
Для подсчёта десятичного и двоичного логарифма есть отдельные методы:
#Для десятичного. print (math.log10 (100)) >>> 2.0 #Для двоичного. print (math.log2 (512)) >>> 9.0
Ещё в Python есть специфичный метод, который прибавляет к аргументу единицу и считает натуральный логарифм от получившегося числа:
x = math.e print (math.log1p (x-1)) >>> 1.0
Когда х близок к нулю, этот метод даёт более точные результаты, чем math.log (1+x). Сравните:
x = 0.00001 print (math.log(x+1)) >>> 9.999950000398841e-06 print (math.log1p(x)) >>> 9.99995000033333e-06
Это все основные инструменты для работы с логарифмами в Python.

Научитесь: Профессия Python-разработчик
Узнать больше
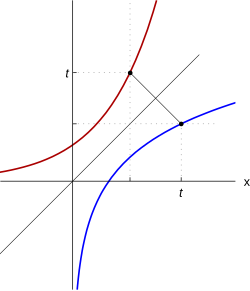
Функция натурального логарифма (синяя кривая) обратна к экспоненте (красная кривая)

График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0
Натуральный логарифм — логарифм по основанию e, где 





Из определения следует, что логарифмическая зависимость есть обратная функция для экспоненты 
Натуральные логарифмы полезны для решения алгебраических уравнений, в которых неизвестная присутствует в качестве показателя степени, они незаменимы в математическом анализе. В приложениях натуральный логарифм участвует в математическом описании таких процессов, в которых скорость изменения некоторого количества в каждый момент обратно пропорциональна самому количеству. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада радиоактивного вещества. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения различных задач, (например, нахождение сложных процентов).
Определение[править | править код]
Натуральный логарифм числа 




Примеры:
, потому что
;
, потому что
.
Вещественный натуральный логарифм[править | править код]





Натуральный логарифм 


Натуральный логарифм может быть также определён геометрически для любого положительного вещественного числа a как площадь под кривой 
![{displaystyle [1;a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91a5967cbecceb33e07a423d8275497d742a746e)
Свойства[править | править код]
Из определения логарифма следует основное логарифмическое тождество[2]:
Приведём сводку формул в предположении, что все значения положительны[3]:
| Формула | Пример | |
|---|---|---|
| Произведение |  |

|
| Частное |  |

|
| Степень |  |

|
| Корень | ![{displaystyle ln {sqrt[{p}]{x}}={frac {ln x}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5939f75f9d6f91d1efe70b5c2e4a6a6935d34de) |

|
Другие свойства:
Связь с логарифмами по другому основанию[править | править код]
Логарифм может быть определён для любого положительного основания, отличного от 

Логарифм 

Связь десятичного (
Связь двоичного (
Логарифмическая функция[править | править код]
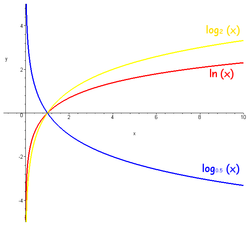
Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию 



Функция является строго возрастающей, она непрерывна и неограниченно дифференцируема всюду в своей области определения.
Ось ординат (
Производная натуральной логарифмической функции равна:
Простота этой формулы — одна из причин широкого использования именно натурального логарифма в анализе и при решении дифференциальных уравнений.

Проинтегрировав формулу для производной в интервале от 

Другими словами, натуральный логарифм 

![{displaystyle [1,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8771aaef108f3cf1381367f4874c74ae7b5e9aa5)
С точки зрения общей алгебры, логарифмическая функция осуществляет (единственно возможный) изоморфизм мультипликативной группы положительных вещественных чисел и аддитивной группы всех вещественных чисел. Другими словами, логарифмическая функция есть единственное (определённое для всех положительных значений аргумента) непрерывное решение функционального уравнения[7]:
Аналитические свойства функции[править | править код]
Из формулы для производной натурального логарифма следует, что первообразная для гиперболы 
где 



Неопределённый интеграл от натурального логарифма легко найти интегрированием по частям:
В математическом анализе и теории дифференциальных уравнений большую роль играет понятие логарифмической производной функции 
Методы вычисления логарифма[править | править код]
Разложим натуральный логарифм в ряд Тейлора вблизи единицы:

|
(Ряд 1) |
Этот ряд, называемый «рядом Меркатора», сходится при 

|
Формула ряда 1 непригодна для практического расчёта логарифмов из-за того, что ряд сходится очень медленно и только в узком интервале. Однако нетрудно получить из неё более удобную формулу:

|
(Ряд 2) |
Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа 

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула:[8][9]:
где 
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.
Полезные пределы[править | править код]
Приведём несколько полезных пределов, связанных с логарифмами[10]:
Трансцендентность[править | править код]
Из теоремы Линдемана — Вейерштрасса (1885) вытекает следующее следствие: если аргумент 

Непрерывные дроби[править | править код]
Хотя для представления логарифма отсутствуют классические непрерывные дроби, но можно использовать несколько «обобщённых непрерывных дробей», в том числе:
История[править | править код]
Впервые натуральные логарифмы в современном понимании появились в 1619 году, когда лондонский учитель математики Джон Спейдель переиздал логарифмические таблицы Непера, исправленные и дополненные так, что они фактически стали таблицами натуральных логарифмов[12]. В 1649 году бельгийский математик Грегуар де Сен-Венсан показал, что площадь под гиперболой 
Термин «натуральный логарифм» ввели в употребление Пьетро Менголи (1659 год) и Николас Меркатор в фундаментальном труде «Logarithmotechnia» (1668)[14][15]. Там же Меркатор описал разложение натурального логарифма в «ряд Меркатора».
Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма[16]. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Д’Аламбером и Эйлером. Бернулли и Д’Аламбер считали, что следует определить 
Комплексные логарифмы[править | править код]
Комплексный логарифм — аналитическая функция, получаемая распространением вещественного логарифма на всю комплексную плоскость (кроме нуля). В отличие от вещественного случая, функция комплексного логарифма многозначна.
Определение. Натуральный логарифм 



Ненулевое число 
где
— произвольное целое число
Тогда 
Здесь 
Из формулы видно, что у одного и только одного из значений мнимая часть находится в интервале ![{displaystyle (-pi ,pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)


Логарифм отрицательного числа находится по формуле[18]:
Примеры:
Следует быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:
— явная ошибка.
Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви (

- Функции натурального логарифма на комплексной плоскости (главная ветвь)
-

-

-

-

Суперпозиция трёх предыдущих графиков
Функция натурального логарифма комплексного числа может быть также определена как аналитическое продолжение вещественного логарифма на всю комплексную плоскость, кроме нуля. Пусть кривая 


Некоторые применения[править | править код]
Теория чисел[править | править код]
Распределение простых чисел асимптотически подчиняется простым законам[20]:
- Число простых чисел в интервале от 1 до
приблизительно равно
.
- k-е простое число приблизительно равно
.
Математический анализ[править | править код]
Логарифмы нередко возникают при нахождении интегралов и при решении дифференциальных уравнений. Примеры:
Теория вероятностей и статистика[править | править код]
В статистике и теории вероятностей логарифм входит в ряд практически важных вероятностных распределений. Например, логарифмическое распределение[21] используется в генетике и физике. Логнормальное распределение часто встречается в ситуациях, когда исследуемая величина есть произведение нескольких независимых положительных случайных переменных[22].
Для оценки неизвестного параметра широко применяются метод максимального правдоподобия и связанная с ним логарифмическая функция правдоподобия[23].
Флуктуации при случайном блуждании описывает закон Хинчина-Колмогорова.
Фракталы и размерность[править | править код]
![]()
Логарифмы помогают выразить размерность Хаусдорфа для фрактала[24]. Например, рассмотрим треугольник Серпинского, который получается из равностороннего треугольника последовательным удалением аналогичных треугольников, линейный размер каждого из которых на каждом этапе уменьшается вдвое (см. рисунок). Размерность результата определяется по формуле:
Механика и физика[править | править код]
Принцип Больцмана в статистической термодинамике — одна из важнейших функций состояния термодинамической системы, характеризующая степень её хаотичности.
Формула Циолковского применяется для расчёта скорости ракеты.
Химия и физическая химия[править | править код]
Уравнение Нернста связывает окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, а также со стандартными электродными потенциалами окислительно-восстановительных пар.
Логарифм используется в определениях таких величин, как показатель константы автопротолиза (самоионизации молекулы) и водородный показатель (кислотности раствора).
Психология и физиология[править | править код]
Человеческое восприятие многих явлений хорошо описывается логарифмическим законом.
Закон Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму интенсивности стимула[25] — громкости звука[26], яркости света.
Закон Фиттса: чем дальше или точнее выполняется движение организма, тем больше коррекции необходимо для его выполнения и тем дольше эта коррекция исполняется[27].
Время на принятие решения при наличии выбора можно оценить по закону Хика[en][28].
Примечания[править | править код]
- ↑ Mortimer, Robert G. Mathematics for physical chemistry (неопр.). — 3rd. — Academic Press, 2005. — С. 9. — ISBN 0-125-08347-5., Extract of page 9 Архивная копия от 24 июня 2016 на Wayback Machine
- ↑ Алгебра и начала анализа. Учебник для 10-11 классов. 12-е издание, М.: Просвещение, 2002. Стр. 233.
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187.
- ↑ Корн Г., Корн Т. Справочник по математике, 1973, с. 34.
- ↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 189..
- ↑ 1 2 3 Логарифмическая функция. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 159-160.
- ↑ Sasaki T., Kanada Y. Practically fast multiple-precision evaluation of log(x) (англ.) // Journal of Information Processing. — 1982. — Vol. 5, iss. 4. — P. 247—250.
- ↑ Ahrendt, Timm. Fast computations of the exponential function. Lecture notes in computer science (неопр.). — 1999. — Т. 1564. — С. 302—312. — doi:10.1007/3-540-49116-3_28.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, 1966, Том I, стр. 164.
- ↑ Рудио Ф. О квадратуре круга (Архимед, Гюйгенс, Ламберт, Лежандр). — Изд. 3-е. — М.—Л.: ОГИЗ, 1936. — С. 89. — 237 с. — (Классики естествознания).
- ↑ Cajori, Florian. A History of Mathematics, 5th ed (неопр.). — AMS Bookstore, 1991. — С. 152. — ISBN 0821821024.
- ↑ Flashman, Martin. Estimating Integrals using Polynomials. Дата обращения: 30 июня 2011. Архивировано 11 февраля 2012 года.
- ↑ Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II. — С. 63.
- ↑ J J O’Connor and E F Robertson. The number e. The MacTutor History of Mathematics archive (сентябрь 2001). Дата обращения: 30 июня 2011. Архивировано 11 февраля 2012 года.
- ↑ 1 2 История математики, том III, 1972, с. 325-328..
- ↑ Рыбников К. А. История математики. В двух томах. — М.: Изд. МГУ, 1963. — Т. II. — С. 27, 230—231..
- ↑ 1 2 Корн Г., Корн Т. Справочник по математике, 1973, с. 623..
- ↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной, 1967, с. 45-46, 99-100..
- ↑ Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2.
- ↑ Weisstein, Eric W. Log-Series Distribution (англ.). MathWorld. Дата обращения: 26 апреля 2012. Архивировано 11 мая 2012 года.
- ↑ Логарифмически нормальное распределение // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Максимального правдоподобия метод // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- ↑ Иванов М. Г. Размер и размерность // «Потенциал», август 2006.
- ↑ Головин С. Ю. ЗАКОН ВЕБЕРА-ФЕХНЕРА // Словарь практического психолога. Дата обращения: 17 апреля 2012. Архивировано 11 июня 2013 года.
- ↑ Ирина Алдошина. Основы психоакустики // Звукорежиссёр. — 1999. — Вып. 6. Архивировано 24 апреля 2012 года.
- ↑ Закон Фиттса // Психологическая энциклопедия (недоступная ссылка — история). Дата обращения: 17 апреля 2012. Архивировано 27 мая 2012 года.
- ↑ Welford, A. T. Fundamentals of skill. — London: Methuen, 1968. — P. 61. — ISBN 978-0-416-03000-6.
Литература[править | править код]
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: АСТ, 2003, ISBN 5-17-009554-6.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.
Ссылки[править | править код]
- “Разбираемся с натуральным логарифмом Архивная копия от 26 сентября 2013 на Wayback Machine” — перевод статьи Demystifying the Natural Logarithm (ln) | BetterExplained (англ.)
Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.
Теперь при помощи этой таблицы введем понятие логарифма.
Логарифм от числа 32 по основанию 2 ((log_{2}(32))) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:
$$ log_{2}(32)=5;$$
Аналогично, глядя в таблицу получим, что:
$$log_{2}(4)=2;$$
$$log_{2}(8)=3;$$
$$log_{2}(16)=4;$$
$$log_{2}(64)=6;$$
$$log_{2}(128)=7.$$
Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.
Теперь дадим определение логарифма в общем виде:
Логарифмом положительного числа (b) по основанию положительно числа (a) называется степень (c), в которую нужно возвести число (a), чтобы получить (b)
$$log_{a}(b)=c;$$
$$a^{c}=b.$$
Будьте внимательны! В первое время обычно путают, что такое основание и то, что стоит под логарифмом (аргумент). Логарифм – это всегда функция, зависящая от двух переменных. Чтобы их не путать, помните определение логарифма – это степень, в которую нужно возвести основание, чтобы получить аргумент.
Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:
$$log_{2}(5)=???$$
Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:
$$log_{2}(5)=2,32192809…$$
Или логарифм шести по основанию 4:
$$log_{4}(6)= 1.2924812…$$
На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!
Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм (log_{4}(6)). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6-ке:
$$ log_{4}(4) lt log_{4}(6) lt log_{4}(16);$$
$$ 1 lt log_{4}(6) lt 2. $$
Значит (log_{4}(6)) принадлежите промежутку от 1 до 2:
$$ log_{4}(6) in (1;2). $$
Как посчитать логарифм
Перед тем, как научиться считать логарифмы, нужно ввести несколько ограничений. Дело в том, что функция логарифма (log_{a}(b)) существует только при положительных значениях основания (a) и аргумента (b). И кроме этого на основание накладывается условие, что оно не должно быть равно (1).
$$ log_{a}(b) quad существует,;при quad a gt 0; ;b gt 0 ;a neq 1.$$
Почему так? Это следует из определения показательной функций. Показательная функция не может быть (0). А основание не равно (1), потому что тогда логарифм теряет смысл – ведь (1) в любой степени это будет (1).
При этих ограничениях логарифм существует.
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.
$$log_{3}(frac{1}{3})=-1;$$
Так как (вспоминайте определение отрицательной степени)
$$3^{-1}=frac{1}{3};$$
Теперь давайте разберем общий алгоритм вычисления логарифмов:
- Во-первых, постарайтесь представить основание и аргумент (то, что стоит под логарифмом) в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
- Разобраться в какую степень (x) нужно возвести основание, чтобы получить аргумент. Когда у вас там и там степени с одинаковым основанием, это сделать довольно просто.
- (x) и будет искомым значением логарифма.
Давайте разберем на примерах.
Пример 1. Посчитать логарифм (9) по основанию (3): (log_{3}(9))
- Сначала представим аргумент и основание в виде степени тройки:
$$ 3=3^1, qquad 9=3^2;$$ - Теперь надо разобраться в какую степень (x) нужно возвести (3^1), чтобы получить (3^2)
$$ (3^1)^x=3^2, $$
$$ 3^{1*x}=3^2, $$
$$ 1*x=2,$$
$$ x=2.$$ - Вот мы и решили:
$$log_{3}(9)=2.$$
Пример 2. Вычислить логарифм (frac{1}{125}) по основанию (5): (log_{5}(frac{1}{125}))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1, qquad frac{1}{125}=frac{1}{5^3}=5^{-3};$$ - В какую степень (x) надо возвести (5^1), чтобы получить (5^{-3}):
$$ (5^1)^x=5^{-3}, $$
$$ 5^{1*x}=5^{-3},$$
$$1*x=-3,$$
$$x=-3.$$ - Получили ответ:
$$ log_{5}(frac{1}{125})=-3.$$
Пример 3. Вычислить логарифм (4) по основанию (64): (log_{64}(4))
- Представим аргумент и основание в виде степени двойки:
$$ 64=2^6, qquad 4=2^2;$$ - В какую степень (x) надо возвести (2^6), чтобы получить (2^{2}):
$$ (2^6)^x=2^{2}, $$
$$ 2^{6*x}=2^{2},$$
$$6*x=2,$$
$$x=frac{2}{6}=frac{1}{3}.$$ - Получили ответ:
$$ log_{64}(4)=frac{1}{3}.$$
Пример 4. Вычислить логарифм (1) по основанию (8): (log_{8}(1))
- Представим аргумент и основание в виде степени двойки:
$$ 8=2^3 qquad 1=2^0;$$ - В какую степень (x) надо возвести (2^3), чтобы получить (2^{0}):
$$ (2^3)^x=2^{0}, $$
$$ 2^{3*x}=2^{0},$$
$$3*x=0,$$
$$x=frac{0}{3}=0.$$ - Получили ответ:
$$ log_{8}(1)=0.$$
Пример 5. Вычислить логарифм (15) по основанию (5): (log_{5}(15))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1 qquad 15= ???;$$
(15) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть:
$$ log_{5}(15).$$
Внимание!
Как понять, что некоторое число (a) не будет являться степенью другого числа (b). Это довольно просто – нужно разложить (a) на простые множители.
$$16=2*2*2*2=2^4,$$
(16) разложили, как произведение четырех двоек, значит (16) будет степенью двойки.
$$ 48=6*8=3*2*2*2*2,$$
Разложив (48) на простые множители, видно, что у нас есть два множителя (2) и (3), значит (48) не будет степенью.
Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.
Десятичный логарифм
На самом деле, все просто. Десятичный логарифм – это любой обыкновенный логарифм, но с основанием 10. Обозначается – (lg(a)).
Пример 6
$$ log_{10}(100)= lg(100)=2;$$
$$log_{10}(1000)=lg(1000)=3;$$
$$log_{10}(10)=lg(10)=1.$$
Натуральный логарифм
Натуральным логарифмом называется логарифм по основанию (e). Обозначение – (ln(x)). Что такое (e)? Так обозначают экспоненту, число-константу, равную, примерно, (2,718281828459…). Это число известно тем, что используется в многих математических законах. Просто запомните, что логарифмы с основанием (e) часто встречаются, и поэтому им придумали специальное название – натуральный логарифм.
Пример 7
$$ log_{e}(e^2)=ln(e^2)=2;$$
$$ log_{e}(e)=ln(e)=1;$$
$$ log_{e}(e^5)=ln(e^5)=5.$$
Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.
У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.
Свойства логарифмов
$$1. ; log_{a}(1)=0;$$
$$2. ; log_{a}(a)=1;$$
$$3. ; log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$4. ; log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$5. ; log_{a}(b^m)= m*log_{a}(b);$$
$$6. ; log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
$$ 7. ; log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0; ; c gt 0; ; c neq 1; $$
$$ 8. ; log_{a}(b)=frac{1}{log_{b}(a)};$$
$$ 9. ; a^{ log_{a}(b)}=b.$$
Давайте разберем несколько примеров на свойства логарифмов.
Пример 8. Воспользоваться формулой (3). Логарифм от произведения – это сумма логарифмов.
$$log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$ log_{3}(12)=log_{3}(3*4)=log_{3}(3)+log_{3}(4)=1+log_{3}(4);$$
$$ log_{3}(2.7)+log_{3}(10)=log_{3}(2.7*10)=log_{3}(27)=3;$$
Пример 9. Воспользоваться формулой (4). Логарифм от частного – это разность логарифмов.
$$ log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$ log_{7}(98)-log_{7}(2)=log_{7}(frac{98}{2})=log_{7}(49)=2;$$
Пример 10. Формула (5,6). Свойства степени.
$$log_{a}(b^m)= m*log_{a}(b);$$
$$log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
Логично, что будет выполняться и такое соотношение:
$$log_{a^m}(b^n)=frac{n}{m}* log_{a}(b);$$
И если (m=n), то:
$$log_{a^m}(b^m)=frac{m}{m}* log_{a}(b);=log_{a}(b)$$
$$log_{4}(9)=log_{2^2}(3^2)=log_{2}(3);$$
Пример 11. Формулы (7,8). Переход к другому основанию.
$$ log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0;c gt 0;c neq 1; $$
$$ log_{a}(b)=frac{1}{log_{b}(a)};$$
$$log_{4}(5)=frac{1}{log_{5}(4)};$$
$$log_{4}(5)=frac{log_{7}(5)}{log_{7}(4)};$$
Натуральный логарифм — это логарифм по основанию e (математическая константа, приблизительно равная числу 2.718281828459…).
- Определение натурального логарифма
- Связь с экспоненциальной функцией
- Свойства натурального логарифма
- Таблица натуральных логарифмов
- График натурального логарифма
Определение натурального логарифма
Когда e y = x, натуральный логарифм (ln) числа x выглядит следующим образом:
ln(x) = loge(x) = y
Связь с экспоненциальной функцией
Функция логарифма ln(x) является обратной к экспоненциальной функции ex.
Для х > 0,
f (f -1(x)) = eln(x) = x
или
f -1(f (x)) = ln(ex) = x
Свойства натурального логарифма
| Свойство | Формула | Пример |
| Логарифм умножения | ln (x ⋅ y) = ln (x) + ln (y) | ln (3 ⋅ 7) = ln (3) + ln (7) |
| Логарифм деления | ln (x / y) = ln (x) – ln (y) | ln (3 / 7) = ln (3) – ln (7) |
| Логарифм степени | ln (x y) = y ⋅ ln (x) | ln (28) = 8 ⋅ ln (2) |
| Логарифм корня |  |
 |
| Производная логарифма | f (x) = ln (x) ⇒ f ‘ (x) = 1 / x | |
| Интеграл логарифма | ∫ ln (x) dx = x ⋅ (ln (x) – 1) + C | |
| Логарифм отрицательного числа | ln (x) не определен, если x ≤ 0 | |
| Логарифм числа 0 | ln (0) не определен | |
| Логарифм числа 1 | ln (1) = 0 | |
| Логарифм комплексного числа | log z = ln (r) + i (θ + 2nπ) = ln (√(x 2 + y 2)) + i · arctan (y/x)), для комплексного числа z = re iθ = x + iy |
|
| Логарифм бесконечности | lim ln (x) = ∞, если x → ∞ | |
| Тождество Эйлера | ln (-1) = i ⋅ π |
microexcel.ru
Таблица натуральных логарифмов
| x | ln x |
| 0 | не определен |
| 0+ | – ∞ |
| 0.0001 | -9.210340 |
| 0.001 | -6.907755 |
| 0.01 | -4.605170 |
| 0.1 | -2.302585 |
| 1 | 0 |
| 2 | 0.693147 |
| e ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1.609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2.302585 |
| 20 | 2.995732 |
| 30 | 3.401197 |
| 40 | 3.688879 |
| 50 | 3.912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4.499810 |
| 100 | 4.605170 |
| 200 | 5.298317 |
| 300 | 5.703782 |
| 400 | 5.991465 |
| 500 | 6.214608 |
| 600 | 6.396930 |
| 700 | 6.551080 |
| 800 | 6.684612 |
| 900 | 6.802395 |
| 1000 | 6.907755 |
| 10000 | 9.210340 |
График натурального логарифма
Функция натурального логарифма задается как y = ln x. Существует только при неотрицательных значениях переменной x. График выглядит так:

Содержание:
- Свойства и основные формулы натурального логарифма
- Примеры решения задач
- Дополнительный материал
Для различного рода теоретических и практических исследований наиболее удобным
основанием логарифма
является иррациональное число $e$.
Определение
Логарифмом числа $b$
по основанию $a$
( $log _{a} b$ ) называется такое число
$c$, что
$b=a^{c}$.
Логарифм имеет смысл, если $a>0, a neq 1, b>0$.
Натуральным логарифмом называется логарифм по основанию $e$.
Такие логарифмы обозначаются символом ln. Запись $ln x$
означает тоже самое, что и $log _{e} x$.
Основание натурального логарифма – число е.
Свойства и основные формулы натурального логарифма
1 $ln 1=0$
Натуральный логарифм единицы равен нулю (Заметим, что логарифм по любому основанию от 1 равен 0).
2 $ln e=1$
3 $ln (x y)=ln x+ln y$
4 $ln frac{x}{y}=ln x-ln y$
5 $ln x^{n}=n cdot ln x$
6 График функции $y=ln x$ :
Примеры решения задач
Пример
Задание. Вычислить $frac{2 ln 3 e-ln 9}{3 ln 5 e-frac{3}{2} ln 25}$
Решение. Преобразуем данное выражение, применяя к первым логарифмам в числителе и
знаменателе свойство суммы логарифмов, а ко вторым свойство логарифма степени.
$frac{2 ln 3 e-ln 9}{3 ln 5 e-frac{3}{2} ln 25}=frac{2(ln 3+ln e)-ln 3^{2}}{3(ln 5+ln e)-frac{3}{2} ln 5^{2}}=$
$=frac{2 ln 3+2 ln e-2 ln 3}{3 ln 5+3 ln e-3 ln 5}=frac{2 ln e}{3 ln e}=frac{2 cdot 1}{3 cdot 1}=frac{2}{3}$
Ответ. $frac{2 ln 3 e-ln 9}{3 ln 5 e-frac{3}{2} ln 25}=frac{2}{3}$
Дополнительный материал
7 $(ln x)^{prime}=frac{1}{x}$
8 $int ln x mathrm{d} x=x ln x-x+C$
9 $lim _{x rightarrow 0+} ln x=-infty$
10 Ряд Маклорена для натурального логарифма:
$ln (1+x)=x-frac{x^{2}}{2}+frac{x^{3}}{3}-ldots+(-1)^{n+1} cdot frac{x^{n}}{n}+ldots,|x| lt 1$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Разложить в ряд Маклорена функцию $f(x)=ln left(1+x^{2}right)$
Решение. Сделаем замену $x^{2}=t$, тогда
$f(x)=ln (1+t)$. Используя приведенное выше разложение, получаем:
$f(x)=ln (1+t)=t-frac{t^{2}}{2}+frac{t^{3}}{3}-ldots+(-1)^{n+1} cdot frac{t^{n}}{n}+ldots,|t| lt 1$
Делаем обратную замену, получаем:
$f(x)=ln left(1+x^{2}right)=x^{2}-frac{left(x^{2}right)^{2}}{2}+frac{left(x^{2}right)^{3}}{3}-ldots+(-1)^{n+1} cdot frac{left(x^{2}right)^{n}}{n}+ldots,left|x^{2}right| lt 1$
или $f(x)=ln left(1+x^{2}right)=x^{2}-frac{x^{4}}{2}+frac{x^{6}}{3}-ldots+(-1)^{n+1} cdot frac{x^{2 n}}{n}+ldots, |x| lt 1$
Читать дальше: десятичный логарифм.

















![ln x=lim _{nto infty }nleft({sqrt[{n}]{x}}-1right)=lim _{nto infty }nleft(1-{frac {1}{sqrt[{n}]{x}}}right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7901ca277e9fe1a5be535f262d7d4a84fc51a3f)