По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
4.1. Краткие теоретические сведения
Многогранниками называются тела, ограниченные плоскими n-угольниками, которые называются гранями. Линии пересечения граней называются ребрами, точки пересечения ребер – вершинами. Для всех многогранников справедлива формула Эйлера: сумма граней и вершин за минусом числа ребер есть величина постоянная: Г + В – Р = 2.
Наиболее распространенными в технике многогранниками являются правильные и неправильные, прямые и наклонные призмы и пирамиды. Призмой называется многогранник, в основании которого находится плоский n-угольник, а остальные грани являются в общем случае параллелограммами. Пирамидой называется многогранник, в основании которого находится плоский n-угольник, а боковыми гранями являются треугольники с общей вершиной. На эпюре многогранники задаются проекциями ребер, так называемой сеткой ребер.
Типовой задачей для многогранников является задача о пересечении многогранников плоскостями частного и общего положения. Для построения фигуры сечения многогранника плоскостью используют следующие приемы:
-
- определение каждой вершины сечения, как точки пересечения ребер многогранника с секущей плоскостью (способ ребер);
- построение стороны сечения, как линии пересечения с секущей плоскостью граней многогранника (способ граней).
Чаще применяется первый из заданных приемов, второй же целесообразно применять в тех случаях, когда грани многогранника являются проецирующими плоскостями, линии пересечения которых с секущей плоскостью общего положения строятся очень просто.
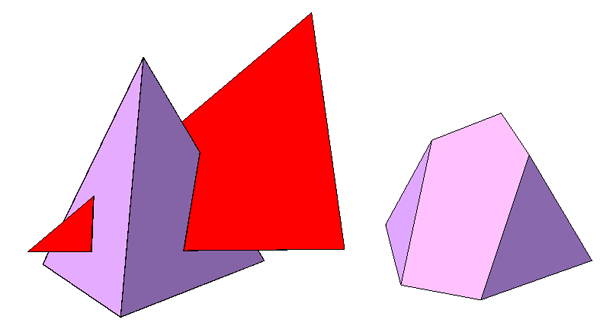
а б
Рисунок 4.1 – Пересечение пирамиды плоскостью (а — задание, б — результат)
В методе ребер несколько раз (по числу пересекаемых ребер) решается задача о пересечении прямой (ребра) с плоскостью (секущей плоскостью). В этом случае находятся точки 1, 2, 3 (рис. 4.1). Найденные точки являются вершинами сечения пирамиды плоскостью.
В методе граней несколько раз решается типовая задача о пересечении двух плоскостей (граней многогранника и секущей плоскости), в которой находят линии 1-2, 2-3, 3-1, являющиеся сторонами многоугольника (в данном примере, треугольника сечения). Если секущая плоскость является плоскостью частного положения, то задача решается упрощенно.
4.2. Способ перемены плоскостей проекций
Сущность способа перемены плоскостей проекций заключается в том, что положение геометрических элементов (точек, прямых, фигур, тел) в пространстве остается неизменным, а система плоскостей проекций заменяется новой, по отношению к которой эти элементы занимают положение, наиболее удобное для решения той или иной задачи.
В ряде случаев для решения задачи бывает достаточно заменить новой плоскостью одну из основных плоскостей проекций – фронтальную или горизонтальную. В других же случаях замена лишь одной плоскости проекций вопроса не разрешает и бывает необходимо последовательно заменить новыми плоскостями обе основные плоскости проекций.
При замене основной плоскости проекций новой плоскостью эта последняя должна располагаться по отношению к остающейся основной плоскости проекций перпендикулярно.
Рассмотрим способ перемены плоскостей проекций на примерах.
Для того чтобы данная прямая общего положения m=АВ оказалась линией уровня, следует ввести новую плоскость проекций π4, которая была бы ей параллельна (рис. 4.2 и 4.3).
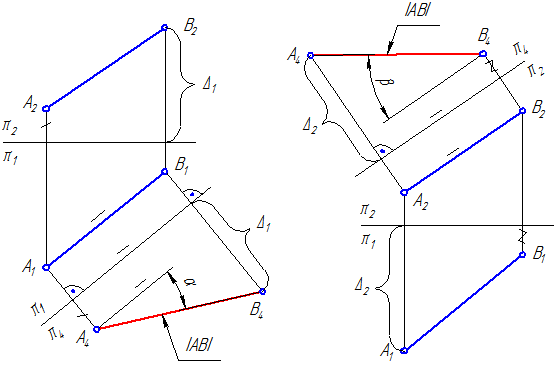
Рисунок 4.2 Рисунок 4.3
Н
На Рисунке 4.2 введена плоскость π4, параллельная прямой m и перпендикулярная к плоскости π1; по новым линиям связи от оси π1/π4 откладываем расстояния от точек А и В до плоскости π1 (отмеченное штрихом и D1). В новой системе плоскостей проекций π1/π4 прямая m является линией уровня.
На Рисунке 4.3 плоскость π4 параллельна прямой m=АВ и перпендикулярна к плоскости π2. Прямая m в системе π2/π4 является линией уровня.
Для того чтобы прямая линия была проецирующей прямой вводится плоскость проекций, перпендикулярная к ней. Для прямой общего положения требуется провести две замены плоскостей проекций. На Рисунке 4.4 прямая m=АВ спроецирована на параллельную ей плоскость π4. Затем вводится плоскость проекций π5, перпендикулярная m4. В системе плоскостей проекций π5/π4 прямая m проецируется в точку.
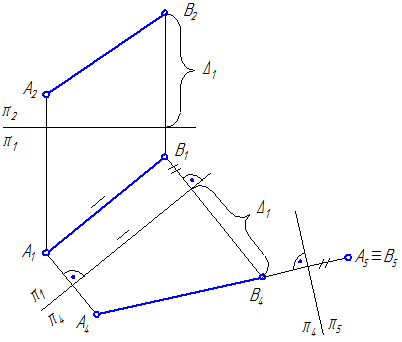
Рисунок 4.4 – Проецирование отрезка прямой в точку
Чтобы определить натуральную величину плоской фигуры общего положения (Рисунок 4.5), требуется сначала ввести такую плоскость проекций π4, чтобы образовалась система, в которой плоскость α, заданная треугольником АВС будет проецирующей. Данную подзадачу можно решить, введя дополнительную плоскость проекций π4 перпендикулярно либо горизонтальной проекции горизонтали, либо фронтальной проекции фронтали. Затем вводится дополнительная плоскость π5, перпендикулярная к плоскости π4 и параллельная плоскости α .
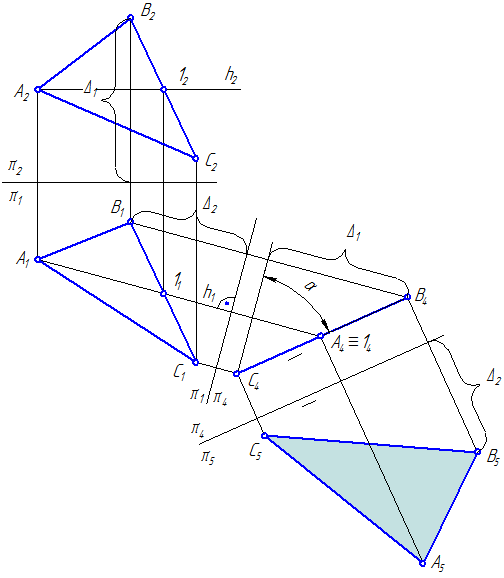
Рисунок 4.5 – Определение натуральной величины треугольника
4.3. Развертывание поверхностей
Разверткой называется плоская фигура, получаемая путем совмещения с плоскостью чертежа поверхности тела.
Построение разверток имеет большое значение в таких областях техники, как котлостроение, судостроение, кровельное и жестяночное дело, продукция которых изготовляется из листового материала.
Точные развертки могут быть построены лишь для линейчатых поверхностей, смежные положения образующих которых параллельны (цилиндрическая поверхность) или пересекаются (коническая поверхность).
Для нелинейчатых поверхностей, образующей которых является кривая линия (например, сферическая поверхность), можно построить развертки лишь приближенные. С этой целью такие поверхности разбиваются на небольшие элементы, и каждая такая часть кривой поверхности заменяется плоскостью. Это означает, что данная кривая поверхность заменяется вписанным в нее многогранником, развертка которого приближенно принимается за развертку кривой поверхности.
Развертка боковой поверхности пирамиды (Рисунок 4.7) состоит из трех треугольников, представляющих в истинном виде боковые грани пирамиды.
Для построения развертки необходимо предварительно определить истинные длины боковых ребер пирамиды. Повернув эти ребра вокруг высоты пирамиды до положения параллельного плоскости ?2, на фронтальной плоскости проекций получим их истинные длины в виде отрезков S2A2, S2B2, S2C2 (Рисунок 4.6).
Построив по трем сторонам S2A2, S2B2 и A1B1 грань пирамиды ASB (Рисунок 4.7), пристраиваем к ней смежную грань – треугольник BSC, а к последнему – грань CSA. Полученная фигура представит собою развертку боковой поверхности данной пирамиды.
Для получения полной развертки к одной из сторон основания пристраиваем основание пирамиды – треугольник АВС.
Для построения на развертке линии, по которой поверхность пирамиды пересечется плоскостью α (Рисунок 4.7), следует нанести на ребра SA, SB и SC, соответственно, точки 1, 2 и 3, в которых эта плоскость пересекает ребра, определив истинные длины отрезков S1, S2 и S3.
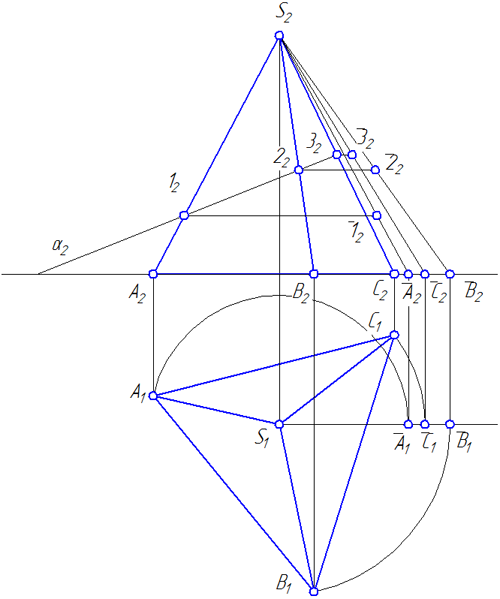
Рисунок 4.6 – Определение истинных длин ребер
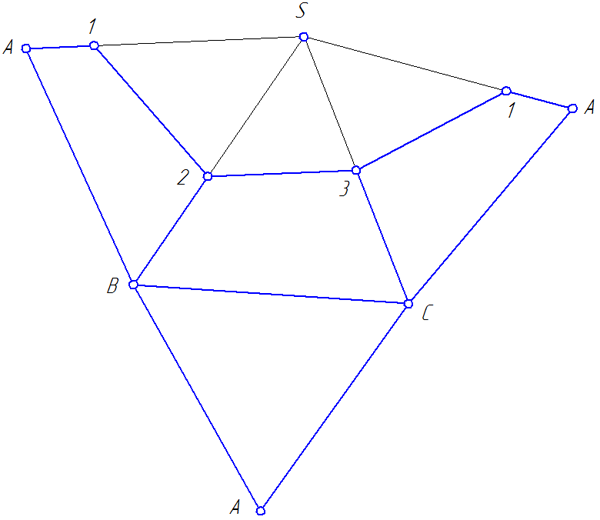
Рисунок 4.7 – Построение развертки
4.4. Задание 3. Построение натурального вида сечения пирамиды плоскостью
4.4.1. Условие задания
Задание следует выполнять в соответствии с алгоритмом:
-
- По координатам вершин (Таблицы 3.1- 3.3) построить: две проекции пирамиды 1234S;
-
- Выполнить две проекции сечения пирамиды плоскостью общего положения АВС (Таблица 3.4);
-
- Найти натуральный вид сечения способом перемены плоскостей проекций;
- Выполнить развертку верхней отсеченной части пирамиды.
4.4.2. Рекомендации по выполнению задания № 2
Порядок выполнения задачи следующий:
- Построить горизонтальные и фронтальные проекции пирамиды и 1234S и плоскости ∆АBC (Рисунок 4.8);
- Способом ребер или способом граней построить проекции сечения пирамиды 1234S плоскостью ∆АBC.
Способ ребер заключается в том, что ребро пирамиды (например, 1S) заключается во фронтально-проецирующую плоскость γ: γπ2≡12S2. Затем выполняется построение точки 8 пересечения ребра 1S с плоскостью γ:
Аналогично выполняется построение остальных точек искомого сечения.
Способом граней строятся линии пересечения с помощью плоскостей-посредников;
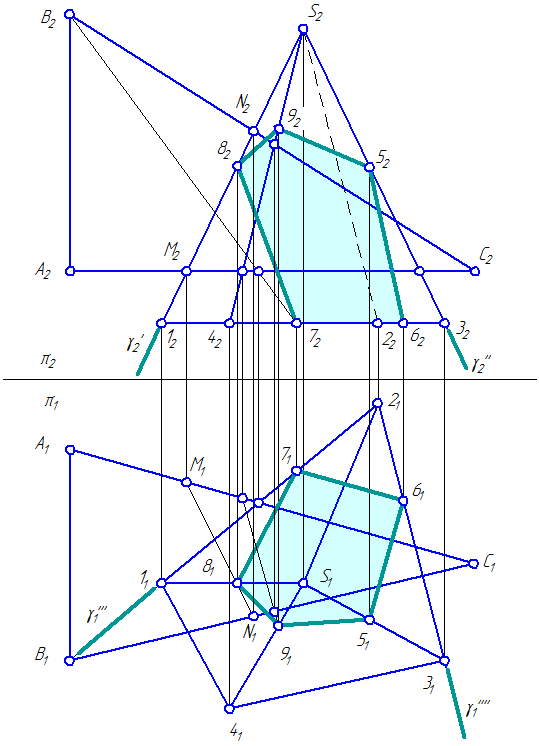
Рисунок 4.8 – Построение сечения
- Способом перемены плоскостей проекций найти натуральный вид сечения 56789.
Сущность способа перемены плоскостей проекций состоит в том, что положение геометрического образа (прямой, плоскости, поверхности) в пространстве остается неизменным, а система плоскостей проекций π1/π2 дополняется плоскостями, образующими с π1 или π2, либо между собой системы двух взаимно перпендикулярных плоскостей проекций. Расположение новой плоскости проекций по отношению к геометрическим образам выбирается в зависимости от условия задачи.
В данной задаче необходимо дважды ввести новые плоскости проекций: в системе плоскостей π1/π4 сечение 56789 станет проецирующей плоскостью, а в системе плоскостей проекций π4/π5 – плоскостью уровня;
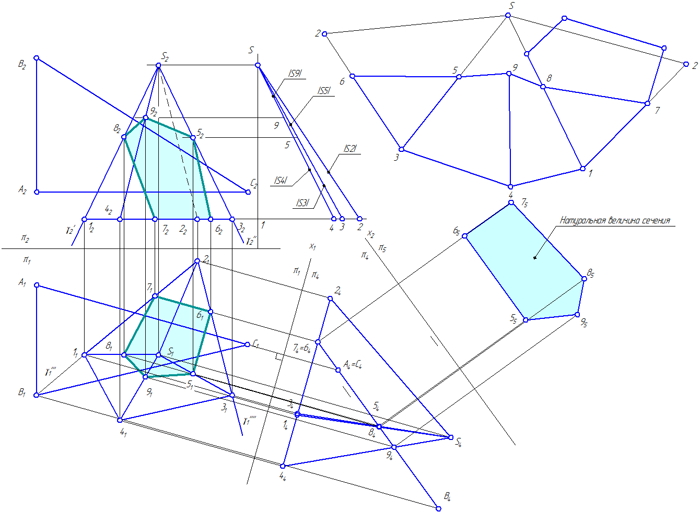
Рисунок 4.9 – Пересечение пирамиды плоскостью общего положения
- Выполнить развертку нижней отсеченной части пирамиды.
Видеопример выполнения задания №3
4.5. Варианты задания 3
| S | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| X | 50 | 90 | 30 | 10 | 70 |
| Y | 50 | 50 | 5 | 70 | 80 |
| Z | 90 | 10 | 10 | 10 | 10 |
| S | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| X | 50 | 90 | 30 | 10 | 70 |
| Y | 50 | 50 | 5 | 70 | 80 |
| Z | 90 | 0 | 0 | 0 | 0 |
| S | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| X | 50 | 100 | 25 | 5 | 80 |
| Y | 50 | 50 | 5 | 70 | 80 |
| Z | 100 | 10 | 10 | 10 | 10 |
| Вариант | Координаты (x, y, z) точек | Вариант | Координаты (x, y, z) точек | ||||
|---|---|---|---|---|---|---|---|
| А | В | С | А | В | С | ||
| 1 | 100;15;30 | 35; 85; 90 | 10; 45; 30 | 16 | 90; 0; 0 | 100; 50; 70 | 5; 55; 40 |
| 2 | 65; 10; 0 | 100; 50; 80 | 20; 80; 80 | 17 | 95; 35; 40 | 50; 35; 0 | 5; 65; 50 |
| 3 | 100; 25;40 | 15; 90; 90 | 50; 15; 0 | 18 | 50; 50; 45 | 0; 55; 0 | 100; 20; 5 |
| 4 | 30; 80; 90 | 20; 25; 0 | 100; 25; 40 | 19 | 30; 90; 60 | 90; 30; 20 | 0; 35; 0 |
| 5 | 100; 15; 20 | 100; 60; 90 | 10; 45; 20 | 20 | 95; 15; 0 | 5; 60; 20 | 70; 85; 80 |
| 6 | 90; 0; 0 | 100; 50; 80 | 5; 55; 40 | 21 | 100;15;30 | 35; 85; 90 | 10; 45; 30 |
| 7 | 95; 35; 50 | 50; 35; 0 | 5; 65; 50 | 22 | 65; 10; 0 | 100; 50; 80 | 20; 80; 80 |
| 8 | 50; 50; 55 | 0; 55; 5 | 100; 20; 5 | 23 | 100; 25;40 | 15; 90; 90 | 50; 15; 0 |
| 9 | 30; 90; 70 | 90; 30; 30 | 0; 35; 0 | 24 | 30; 80; 90 | 20; 25; 0 | 100; 25; 40 |
| 10 | 95; 15; 10 | 5; 60; 30 | 70; 85; 80 | 25 | 100; 15; 20 | 100; 60; 90 | 10; 45; 20 |
| 11 | 100;15;20 | 35; 85; 80 | 10; 45; 30 | 26 | 90; 0; 0 | 100; 50; 80 | 5; 55; 40 |
| 12 | 65; 10; 0 | 100; 50; 70 | 20; 80; 80 | 27 | 95; 35; 50 | 50; 35; 0 | 5; 65; 50 |
| 13 | 100; 25;30 | 15; 90; 80 | 50; 15; 0 | 28 | 50; 50; 55 | 0; 55; 5 | 100; 20; 5 |
| 14 | 30; 80; 80 | 20; 25; 0 | 100; 25; 40 | 29 | 30; 90; 70 | 90; 30; 30 | 0; 35; 0 |
| 15 | 100; 15; 10 | 100; 60; 80 | 10; 45; 20 | 30 | 95; 15; 10 | 5; 60; 30 | 70; 85; 80 |
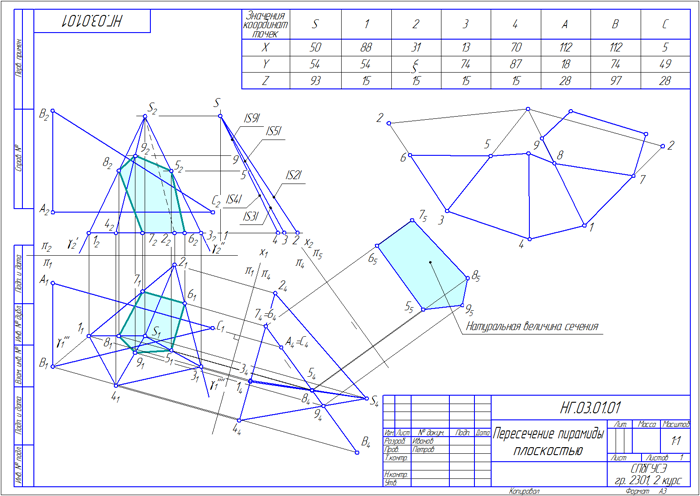
Рисунок 4.10 – Пример оформления задания 3
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
Определение натуральной величины сечения
Цель видеоурока Автокад/НГ: Обучение Автокад 2D на практике и закрепление пройденного материала раздела «Теоретические и практические видеоуроки Автокад». Закрепление знаний по решению задач на построение натуральной величины отрезка, треугольника, сечения и т.д. используя для этого любой способ преобразования чертежа.
Дано: чертеж «Сечение комбинированной поверхности плоскостью».
Задание: Построить натуральную величину сечения, применив для этого любой способ преобразования чертежа.
Решение задачи по начертательной геометрии на определение натуральной величины сечения:
Все способы преобразования чертежа представлены в виде практических видеоуроков по НГ/Автокад в разделе «Способы преобразования чертежа».
В этом видеоуроке мы будем использовать способ перемены плоскостей проекций. Мы уже решили несколько задач по начертательной геометрии, используя способ перемены плоскостей проекций, вот некоторые из них:
- Построение натуральной величины сечения.
- Способ замены (перемены) плоскостей проекций для нахождения натуральной величины сечения цилиндра.
Алгоритм решения задачи с использованием способа замены (перемены) плоскостей проекции
- Вводим новую плоскость, которая будет располагаться параллельно отрезка, в который проецируется сечение комбинированной поверхности на горизонтальной плоскости проекции.
- Строим линии связи.
- На линиях проекционной связи откладываем координаты Z точек сечения цилиндра.
Повторим специальную команду Выровнять в Автокад, которая ускорит построение натуральной величины сечения в 3 раза.
Более подробно в видеоуроке по начертательной геометрии в Автокад.
Видео “Определение натуральной величины сечения – Способ перемены плоскостей проекций”
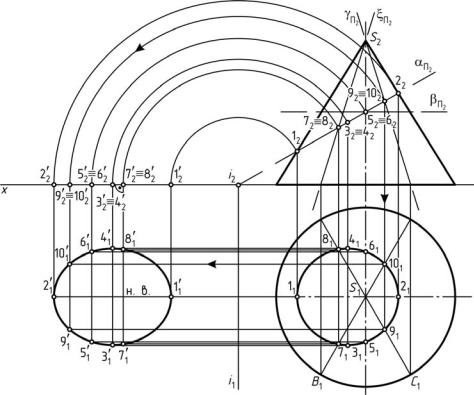
Рис. 80. Пересечение прямого конуса плоскостью частного положения
Сечение поверхностей гранных геометрических тел плоско-
стями общего положения. Построение линии пересечения многогранника плоскостью общего положения сводится к двум этапам. На первом этапе плоскость из общего положения преобразуют в частное (проецирующее) положение. На втором — определяют точки пересечения ребер многогранника с секущей плоскостью.
Рассмотрим некоторые примеры.
З а д а ч а 18
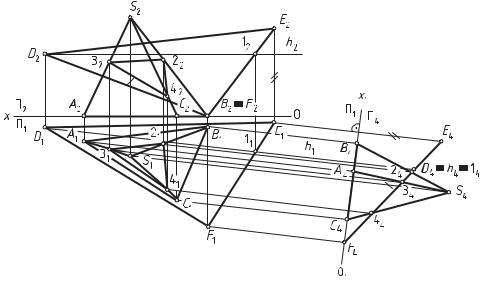
Дано: прямая трехгранная пирамида ABC с вершиной в точке S и плоскость общего положения α, заданная DEF (рис. 81).
Выполнить: 1) построить линию пересечения пирамиды плоскостью; 2) определитьнатуральную величину сеченияпирамидыплоскостью.
Порядок выполнения:
1. Способом замены плоскостей проекций преобразуют плоскость α ( DEF) из общего положения в частное — проецирующее, где αΠ4 ( D4E4F4) — проецирующий след плоскости. В плоскости П4 вы-
страивают проекцию пирамиды (A4B4C4S4).
91
2. След αΠ4 ( D4E4F4) проецирующей плоскости обладает собира-
тельным свойством. Следовательно, пересечение проецирующего следа αΠ4 ( D4E4F4) с ребрами пирамиды образует проекцию сечения
геометрического тела плоскостью — 24344 4.
3.Горизонтальную (213141) и фронтальную (223242) проекции сечения геометрического тела плоскостью определяют из условия принадлежности точки прямой.
4.Натуральную величину сечения поверхности плоскостью можно определить любым известным способом (на примере не показано).
Рис. 81. Пересечение прямой пирамиды плоскостью общего положения α ( DEF)
З а д а ч а 19
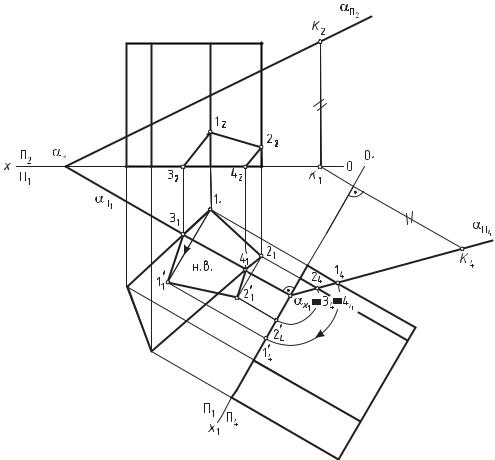
Дано: прямая четырехгранная призма ABCD и плоскость общего положения α, заданная следами (рис. 82).
Выполнить: 1) построить линию пересечения призмы плоскостью; 2) определить натуральную величину сечения призмы плоскостью.
Порядок выполнения:
1. Способом замены плоскостей проекций преобразуют плоскость α из общего положения в частное — проецирующее, где αΠ4 — проеци-
рующий след плоскости. В плоскости П4 выстраивают проекцию приз-
мы (A4B4C4D4).
2. След αΠ4 проецирующей плоскости α обладает собирательным свойством. Следовательно, пересечение проецирующего следа αΠ4
с ребрами призмы образует проекцию сечения геометрического тела плоскостью — 1424344 4.
92
3.Призматическая поверхность является горизонтально проецирующей. Поэтому горизонтальную проекцию сечения геометрического тела плоскостью (11214131) и фронтальную (12224232) определяют из этого условия и условия принадлежности точки прямой.
4.Натуральную величину сечения поверхности плоскостью в данной задаче определяют способом вращения. Однако допустимо применение и любого другого способа.
Рис. 82. Пересечение прямой призмы плоскостью общего положения α, заданной следами
Сечение поверхностей геометрических тел вращения плоско-
стями общего положения. Построение линии пересечения тел вращения плоскостью общего положения также сводится к двум этапам. На первом этапе плоскость из общего положения преобразуют в частное (проецирующее), а затем определяют точки пересечения образующих кривой поверхности с секущей плоскостью.
93
Рассмотрим некоторые примеры. З а д а ч а 20
Дано: прямой круговой цилиндр и плоскость общего положения α, заданная следами (рис. 83).
Выполнить: 1) построить линию пересечения цилиндра плоскостью; 2) определить натуральную величину сечения цилиндра плоскостью.
Рис. 83. Пересечение прямого цилиндра плоскостью общего положения
94
Порядок выполнения:
1. Способом замены плоскостей проекций преобразуют плоскость α из общего положения в частное — проецирующее, где αΠ4 — проеци-
рующий след плоскости. В плоскости П4 выстраивают проекцию цилиндра.
2. След αΠ4 проецирующей плоскости α обладает собирательным
свойством (любой геометрический элемент, принадлежащий фрон- тально-проецирующей плоскости, будет проецироваться в ее фронтальный след). Следовательно, пересечение следа αΠ4 с поверхностью
цилиндра образует проекцию сечения геометрического тела плоско-
стью — 1424344 454.
3.Цилиндрическая поверхность является горизонтально проецирующей. Поэтому горизонтальную проекцию сечения геометрического
тела плоскостью (1121314151) и фронтальную (1222324252) определяют из этого условия и условия принадлежности точки прямой.
4.Натуральную величину сечения поверхности плоскостью в данной задаче определяют способом замены плоскостей проекций.
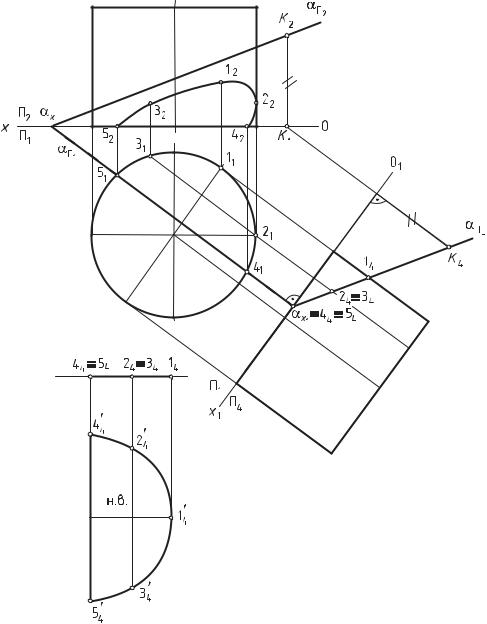
З а д а ч а 21 Дано: прямой круговой конус и плоскость общего положения α,
заданная следами (рис. 84).
Выполнить: 1) построить линию пересечения конуса плоскостью; 2) определить натуральную величину сечения конуса плоскостью.
Порядок выполнения:
1. Способом замены плоскостей проекций преобразуют плоскость α из общего положения в частное — проецирующее, где αΠ4 — проеци-
рующий след плоскости. В плоскости П4 выстраивают проекциюконуса. 2. След αΠ4 обладает собирательным свойством (любой геомет-
рический элемент, принадлежащий фронтально-проецирующей плоскости, в том числе и линия пересечения конуса плоскостью, будет проецироваться в ее фронтальный след). Следовательно, пересечение проецирующего следа αΠ4 с поверхностью конуса образует проекцию
сечения геометрического тела плоскостью — 1424344 454.
3.Горизонтальную проекцию сечения геометрического тела плос-
костью (1121415131) и фронтальную (1222425232) определяют из условия принадлежности точки прямой.
4.Натуральную величину сечения поверхности плоскостью в данной задаче определяют способом вращения, однако допустимо применение и любого другого способа.
95
|
Разделы Уроки по теме Рекомендуем |

Как начертить наклонное сечение Автор: Moroz Дата: 2010-09-21
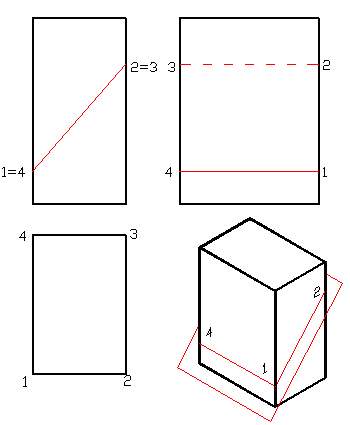
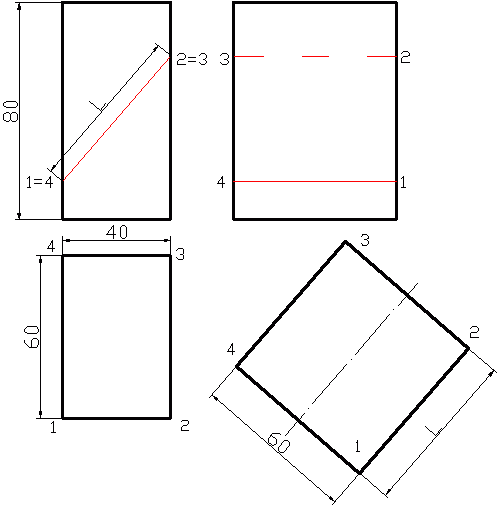
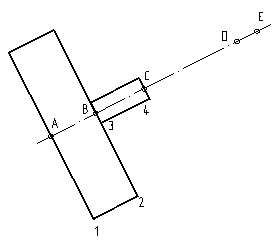
Проанализировав запросы, с которыми вы приходите на наш сайт, мы увидели, что многих интересует вопрос, как начертить наклонное сечение. Само же задание обычно звучит так: “построить натуральный вид фигуры сечения”. Конечно же, мы решили не оставлять этот вопрос в стороне и постараться по возможности объяснить, как происходит построение наклонного сечения. Для того, чтобы объяснить, как строится наклонное сечение, я приведу несколько примеров. Начну конечно же с элементарного, постепенно наращивая сложность примеров. Надеюсь, что проанализировав эти примеры чертежей сечений, вы разберетесь в том, как это делается, и сможете сами выполнить свое учебное задание. Рассмотрим построение наклонного сечения “кирпичика” с размерами 40х60х80 мм произвольной наклонной плоскостью. Секущая плоскость разрезает его по точкам 1-2-3-4. Думаю, тут все понятно.
Перейдем к построению натурального вида фигуры сечения.
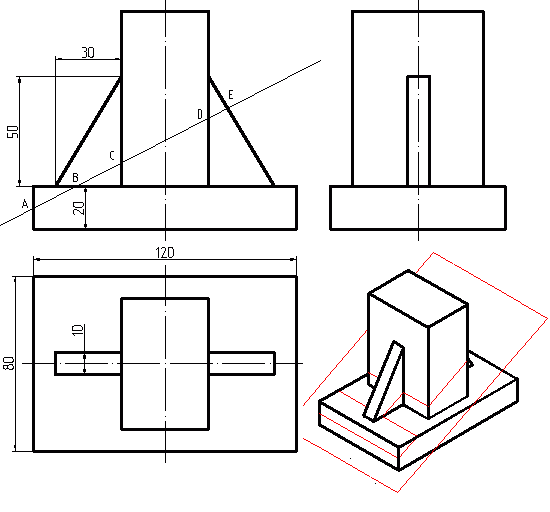
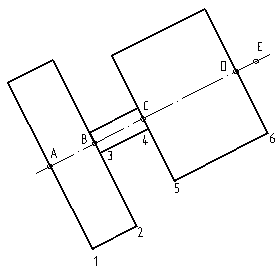
Теперь давайте усложним нашу деталь. Поставим кирпичик на основание 120х80х20 мм и дополним фигуру ребрами жесткости. Проведем секущую плоскость так, чтобы она проходила через все четыре элемента фигуры (через основание, кирпичик и два ребра жесткости). На рисунке ниже вы можете увидеть три вида и реалистичое изображение этой детали
Попробуем построить натуральный вид этого наклонного сечения. Начнем опять с оси сечения: проведем ее параллельно плоскости сечения обозначенного на главном виде. На ней отложим длину сечения равную А-Е. Точка А является точкой входа сечения в деталь, а в частном случае – точкой входа сечения в основание. Точкой выхода из основания является точка В. Отметим точку В на оси сечения. Аналогичным образом отметим и точки входа-выхода в ребро, в “кирпичик” и во второе ребро. Из точек А и В перпендикулярно оси отложим отрезки равные ширине основания (в каждую сторону от оси по 40, всего 80мм). Соединим крайние точки – получим прямоугольник, являющийся натуральным видом сечения основания детали.
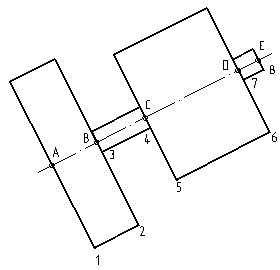
Теперь настал черед построить кусочек сечения, являющийся сечением ребра детали. Из точек В и С отложим перпендикуляры по 5 мм в каждую сторону – получатся отрезки по 10 мм. Соединим крайние точки и получим сечение ребра.
Из точек С и D откладывем перпендикулярные отрезки равные ширине “кирпичика” – полностью аналогично первому примеру этого урока.
Отложив перпендикуляры из точек D и Е равные ширине второго ребра и соединив крайние точки получим натуральный вид его сечения.
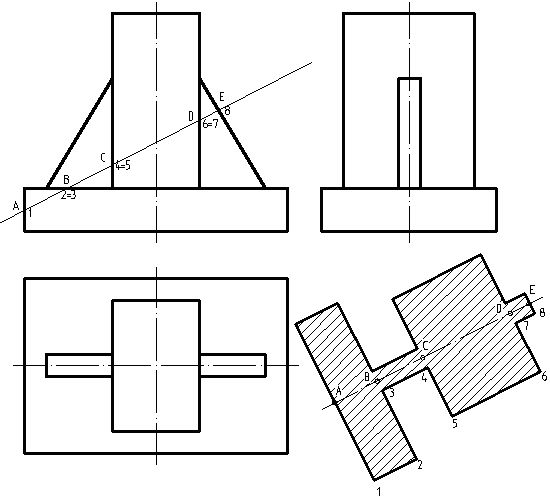
Остается стереть перемычки между отдельными элементами получившегося сечения и нанести штриховку. Должно получиться что-то вроде этого:
Если же по заданному сечению произвести разделение фигуры, то мы увидим следующий вид:
Я надеюсь, что вас не запугали нудные абзацы описания алгоритма. Если вы прочли все вышенаписанное и еще не до конца поняли, как начертить наклонное сечение, я очень советую вам взять в руки лист бумаги и карандаш и попытаться повторить все шаги за мной – это почти 100% поможет вам усвоить материал. Когда-то я пообещал продолжение данной статьи. Наконец-то я готов представить вам пример пошагового построения наклонного сечения детали, более приближенной к уровню домашних заданий. Более того, наклонное сечение задано на третьем виде (наклонное сечение задано на виде слева) Просмотров: 130852 Вы можете сказать “спасибо!” автору статьи: пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект “White Bird. Чертежи Студентам” или или запишите наш телефон и расскажите о нас своим друзьям – кто-то наверняка ищет способ выполнить чертежи или создайте у себя на страничке или в блоге заметку про наши уроки – и кто-то еще сможет освоить черчение.
А вот это – не реклама. Это напоминание, что каждый из нас может сделать. Если хотите – это просьба. Мы действительно им нужны:
Комментарии: огромное спасибо!так бы сама не справилась!!! очень доступно и наглядно.Спасибо за Ваш труд! Да всё хорошо, только хотелось бы увидеть как делаеться тоже самое на более сложной детали, с фасками и конусовидным отверстием например. Спасибо. А разве на разрезах ребра жесткости не штрихуются? Спасибо,очень доступно.Скажите,а наклонное сечение можно выполнить на виде с верху,или на виде слева?Если да,то хотелось бы увидеть простейший пример.Пожалуйста.
Да всё хорошо, только хотелось бы увидеть как делаеться тоже самое, но с отверстиями (сквозными и несквозными), а то в элипс они в голове так и не превращаются помогите мне по комплексной задаче
Хорошо объясняете.
благодарю автора за статью!кратко и доступно пониманию.лет 20 назад сам грыз гранит науки,теперь сыну помогаю. Добавьте свой комментарий: |
Последние уроки Как построить диметрию детали? Построение наклонного сечения, заданного на виде слева Определение линии пересечения двух плоскостей. Метод вспомогательных секущих плоскостей. Наша почта: zakaz@trivida.ru Наша страница в ВК: Случайный комментарий Валерий: Антон, у вас офис только в Москве? или в других городах тоже есть? Валерий, в настоящее время мы не имеем региональных представительств. Хорошо это или нет – не знаю. Сейчас для удаленных пользователей доступны только услуги по выполнению чертежей в электронном виде |
Как найти натуральную величину сечения
Свойствами фигур в пространстве занимается такой раздел геометрии, как стереометрия. Основным методом для решения задач в стереометрии является метод сечения многогранников. Он позволяет правильно строить сечения многогранников и определять вид этих сечений.

Инструкция
Определение вида сечения какой-либо фигуры, то есть натуральной величины этого сечения, часто подразумевается при формулировке задач на построение наклонного сечения. Наклонное сечение правильнее называть фронтально-проецирующей секущей плоскостью. И для построения его натуральной величины достаточно выполнить несколько действий.
С помощью линейки и карандаша начертите фигуру в 3х проекциях – вид спереди, вид сверху и вид сбоку. На главной проекции на виде спереди покажите путь, по которому проходит фронтально-проецирующая секущая плоскость, для чего начертите наклонную прямую.
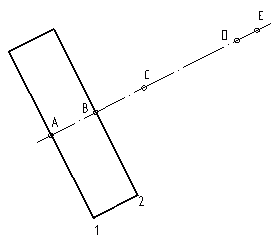
На наклонной прямой отметьте главные точки: точки вхождения сечения и выхода сечения. Если фигурой является прямоугольник, то точек вхождения и выхода будет по одной. Если фигурой является призма, то количество точек удваивается. Две точки определяют вхождение в фигуру и выход. Две другие определяют точки на боках призмы.
На произвольном расстоянии проведите прямую, параллельную фронтально-проецирующей секущей плоскости. Затем из точек, расположенных на оси главного вида, проведите вспомогательные линии перпендикулярно наклонной прямой, пока они не пересекутся с параллельной осью. Тем самым вы получите проекции полученных точек фигуры в новой координатной системе.
Чтобы определить ширину фигуры, опустите прямые из точек главного вида на фигуру вида сверху. Обозначьте соответствующими индексами проекции точек при каждом пересечении прямой и фигуры. Например, если точка А принадлежит главному виду фигуры, то точки А’ и А” принадлежат проецирующим плоскостям.
Отложите в новой координатной системе расстояние, которое образуется между вертикальными проекциями основных точек. Фигура, которая получается в результате построения, и является натуральной величиной наклонного сечения.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.