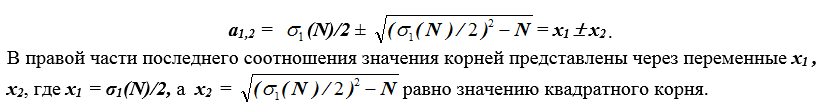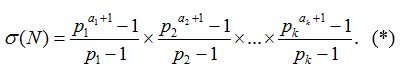Как найти нечетное составное число

Out of all the existing integers, everyone can be classified as one of two types: an Odd Number or an Even Number. This differentiation between odd and even is called the parity of a number, that is even numbers have a parity of 1, and odd numbers have a parity of 0. For example, 1 and 5 have the same parity i.e. 0 as both are Odd Numbers, and 3 and 12 have different parity as one is Odd and the other is Even.

What are Odd Numbers?

For any number when divided by 2, if the reminder is non zero i.e. 1 then it is an Odd Number. In other words, a number is an Odd number if it is not divisible by 2. For example, 1, 3, 5, 7, 9, etc. One intuitive way to understand Odd numbers is to assume you have n number of fruits, if you try to divide those n fruits among two people such that one person ends up with one more fruit than the other person, then you have an odd number of fruits in the beginning.

Note: All integers are either even numbers or odd numbers.

List of Odd Numbers

It is not possible to list out all Odd numbers, as there are an infinite number of them. However, we can list the initial Odd numbers, which include positive Odd numbers such as 1, 3, 5, 7, 9, and so on, extending to infinity, as well as negative odd numbers such as -1, -3, -5, -7, -9, and so on, extending to negative infinity.

Odd Numbers from 1 to 100

Odd numbers from 1 to 100, can be listed as follows:

How to Identify Odd Numbers?

Numbers ending with 1, 3, 5, 7, and 9 are Odd numbers, as only numbers ending with 0, 2, 4, 6, and 8 are divisible by 2.

Example: Which of the following is an odd number?

1123, 3214, 12452, 34824, and 98354

Solution:

1123 is ending with 3, 3214 is ending with 4, 12452 is ending with 2, 34824 is ending with 4 and 98354 is ending with 4. As only number ending with 1, 3, 5, 7, and 9 is 1123, thus 1123 is the odd number ou of all.

Even and Odd Numbers

There are some differences between even and odd numbers, as follows:

Even Numbers	Odd Numbers
Numbers divisible exactly by 2 are even numbers.	When divided by 2, those numbers give 1 as a reminder and are known as Odd numbers.
Some examples, of even numbers, are 2, 4, 6, 8,10, etc.	Some examples of odd numbers are 1, 3, 5, 7, 9, etc.
Even numbers can be represented by 2k, where all k belongs to integers.	Odd numbers can be represented by 2k+1, where all k belongs to integers.

Properties of Odd Numbers

All the Odd numbers can be represented as 2k+1, where all k belongs to integers. For example, 13 can be written as 2×6+1, -11 can be written as 2×(-6)+1, and 21 can be written as 2×10+1, etc.

Other than this, there are some operation-based properties of the Odd Numbers, that are as follows,

Addition Property 

• Addition of two Odd Numbers results in an Even Number.
  • For example, 1+3=4, 5+11=16, and -3+5=2 etc.
• Addition of one Odd and one Even number results in an Odd Number.
  • For example, 2+3=5, -1,4=3, and 11+4=15 etc.

Subtraction Property 

• Subtraction between two Odd numbers always results in an even number.
  • For example, 3-5=-2, 7-1=6, and -5-3=-8 etc.
• Subtraction between one Odd and one Even number always results in an Odd number.
  • For example, 1-4=-3, -1-2=-3, and 2-5=-3, etc.

Multiplication Property

• Multiplication of two Odd numbers always results in an Odd number.
  • For example, 3×5=15, 1×17=17, and 13×5=65 etc.
• Multiplication of one odd and one even number always results in an Even number.
  • For example, 4×5=20, 2×13=26, and 11×4=44 etc.

Types of Odd Numbers

Various types of Odd Numbers are as follows,

• Consecutive Odd Numbers
• Composite Odd Numbers
• Prime Odd Numbers

Now let’s learn about them in detail.

Consecutive Odd Numbers

For any number to be consecutive, they need to follow each other in order, and if numbers are consecutive as well as Odd in nature then those are called consecutive odd numbers. Examples of consecutive odd numbers include 1, 3, 5, 7, and 9 (the first five consecutive odd natural numbers), and 11, 13, 15, 17, and 19. If we have an odd number a, we can determine the next consecutive odd number by adding 2 to it, i.e., a+2. It is important to note that the difference between any two consecutive odd or even numbers is always 2.

Composite Odd Numbers

Positive integers that have factors other than 1 and themselves are called composite numbers. For a number to be considered a composite odd number, a number must be both odd and composite. For instance, 9 is a composite odd number because it is divisible by 3, and when divided by 2, it gives a remainder of 1. Other examples of composite odd numbers include 15, 27, 35, 65, and so on.

Prime Odd Numbers

Except for the number 2, all prime numbers are odd. This is because, except for 2, all even numbers have 2 as a factor, making them composite numbers. However, not all odd numbers are prime since the product of two odd numbers is also an odd number, but it cannot be a prime number because it has two factors. A prime number is defined as an odd number that has no factors other than 1 and itself.

Some examples of prime as well as odd numbers are 3, 5, 7, 11, 13, 17, 19, etc.

Note: All Prime Numbers are Odd Numbers except for 2 which is Even Number

What is the Smallest Odd Composite Number?

The smallest odd composite number is 9, as the list of first odd natural numbers is 1, 3, 5, 7, 9, 11, 13,… and the first composite number is 4 which is not an odd number, a second composite number is 6 which is also not an odd number as it is divisible by 2, third composite number is 8 which is again an even number. So, the fourth composite number which is 9 is the first odd composite number. Thus, 9 is the smallest odd composite number.

Also, Read

• Natural Numbers
• Real Numbers
• Imaginary Numbers

Solved Examples of Odd Numbers

Example 1: How many odd numbers are between 1 and 150(including 1 and 150)?

Solution:

Every other number is an odd number thus half of the all the numbers are odd.

So, between 1 and 150 (including 1 and 150), there are 150 numbers, 

Thus, half of 150 number are odd. 

Thus, there are 75 odd numbers between 1 and 150.

Example 2: Find the units digit of 3²⁰¹.

Solution:

The units digit of any power of 3 is cyclical and follows a pattern. The pattern for 3 is 3, 9, 7, 1. 

Therefore, the units digit of 3²⁰¹ is the same as the units digit of 3^x where x is the remainder when 201 is divided by 4.

and the remainder when 201 is divided by 4 is 1, so the units digit of 3²⁰¹ is the same as the units digit of 3¹, which is 3.

Therefore, the unit digit of 3²⁰¹ is 3.

Example 3: Find the product of all odd numbers between 1 to 9.

Solution:

The odd numbers between 1 to 9 are 1, 3, 5, 7, 9.

The product of all odd numbers between 1 to 9 = 1 * 3 * 5 * 7 * 9 = 945.

Example 4: Determine whether the following numbers are even or odd:

73, 2 + 4 + 6 + 8, and 99 – 67

Solution:

73 is not divisible by 2, so it is an odd number.

The sum of the first four even numbers is 2 + 4 + 6 + 8 = 20. Since 20 is divisible by 2, it is not an odd number, so it is an even number.

99 – 67 = 32. Since 32 is divisible by 2, it is not an odd number, so it is an even number.

Thus, only odd number out of all three is 73.

FAQs on Odd Numbers

Q1: What are Odd Numbers?

Answer:

Those numbers which are exactly not divisible by 2, are called Odd numbers. For example, 3, 5, 7, 15, etc.

Q2: What is the HCF of two consecutive odd numbers?

Answer:

Consecutive number are those number which follow each other in order.

Thus, list consecutive of Odd natural number is 1, 3, 5, 7, 9, 11, 13, . . . 

for 1 and 3, only common factor is 1.

for 3 and 5, only common factor is 1.

for 5 and 7, only common factor is 1.

and so on.

and similarly for each consecutive pair only possible common factor is 1.

So, HCF of two conscutive odd numbers is 1.

Q3: How many odd numbers are between 1 and 100?

Answer:

As every other integer is odd and between 1 and 100 there are 98 number(not including 1 and 100). Thus, half of them must be even and half of them are odd number. Therefore there are 49 Odd numbers between 1 and 100.

Q4: What is the sum of first n odd natural numbers?

Answer:

1+3+5+7+ . . . up to n terms

Consider this Arithmetic Progression, a=1, d=2 and using summation of n terms of A.P. 

Required Sum = dfrac{n}{2}left( 2a+(n-1)dright)

Thus, sum of first n odd natural numbers is n².

Давайте вспомним, как разложить число на простые множители, для этого нам надо разбить число на простые множители:

Все числа, которые заканчиваются на пять, делятся на пять. Поэтому все числа, кратные 5 и больше пяти, являются составными числами.

Возможность единственного представления составного нечетного натурального числа (СННЧ) N в виде произведения степеней простых (кроме 2) чисел составляет существо основной теоремы арифметики (ОТА). Для больших чисел, содержащих в своей записи и более цифр, эта возможность, а точнее задача не получила приемлемого для практики (за обозримое время) решения до наших дней. Кратко эту задачу называют задачей факторизации больших чисел(ЗФБЧ). Ее формулировка проста и известна уже несколько тысячелетий: для заданного натурального числа N = pq найти все его нетривиальные делители.

При заданном значении СННЧ N что можно узнать о его делителях? Практически ни о числе, ни составе делителей в теории чисел нет теорем. Поэтому ЗФБЧ до сегодняшнего дня является практически нерешаемой. Известен переборный алгоритм решения ЗФБЧ методом решета о котором мной написаны прочие статьи цикла под спойлером. Имеется зацепка в виде суммы σ(N) = N +p +q +1 делителей N для подступа к ее решению, минуя решета и связанные с ними проблемы.

Так в Г^2± – модели НРЧ в клетке () всегда лежит сумма делителей N, если само число N помещено в клетке (). Кроме этого, в клетке () лежит значение функции Эйлера СННЧ N, если его собственные делители простые числа.

В теории чисел известны две формы представления (моделей) числа: аддитивная и мультипликативная на основе ОТА. Эти формы (при аддитивном представлении числа суммой членов отрезка непрерывной последовательности нечетных чисел) тесно связаны. Число слагаемых в сумме равно меньшему делителю, а среднее слагаемое — большему. Это не так, если аддитивная форма представляет произвольное разбиение числа на части. Например, в 1-ом случае 105 =33+35+37 =3·35 и 105 = 60+40 +5 ≠3·40 — во 2-ом.

Поводом для написания этой работы послужило стремление автора познакомить читателей с подходом к задаче факторизации чисел на основе факта, открытого автором при изучении модели натурального ряда чисел (НРЧ), а также с результатом Л. Эйлера,
$inline$σ(N) = σ(N-1)+σ(N-2)-σ(N-5)-σ(N-7)+σ(N-12)+σ(N-15)-$inline$
, который состоит в том, что для произвольного СННЧ N можно вычислить сумму σ(N) его делителей, не располагая значениями самих делителей. Это положение граничит с мистикой, но оказывается такое возможно при наличии качественных моделей НРЧ и отдельного числа.

Определенным стимулом явилась также публикация Пшеннова А.В. в Интернете, где приводится некоторый фактический материал по делителям чисел и их суммам. Конечно,
основной причиной является наблюдение, сделанное автором самостоятельно, при изучении созданной и разрабатываемой им оригинальной модели натурального ряда чисел (НРЧ). Приведу краткое описание модели, которая ранее уже рассматривалась здесь.

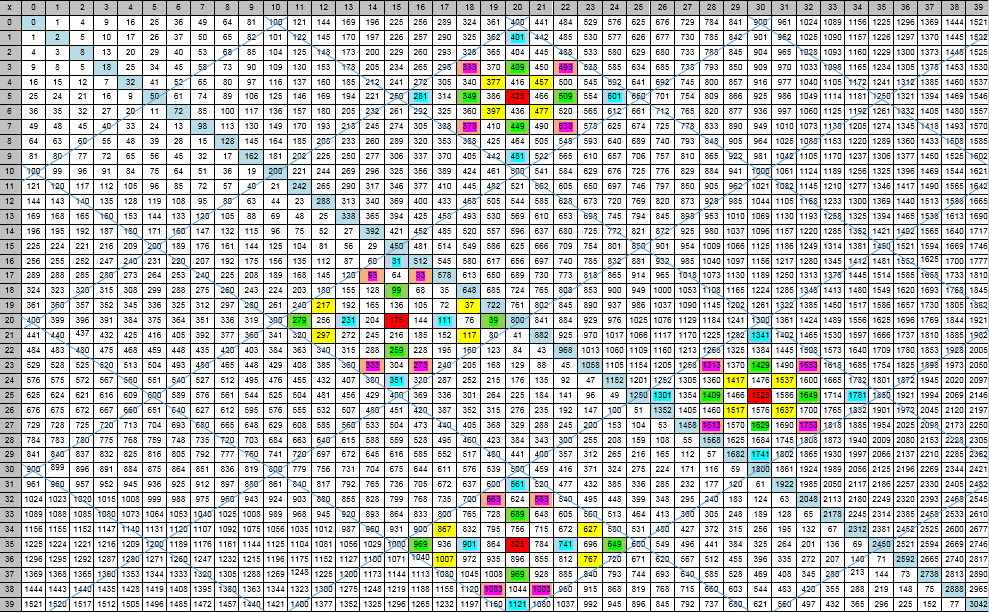
Таблица М — Модель (плоскостная) натурального ряда чисел

символами в модели обозначены соответственно номера строк и столбцов.

В модели использовано известное положение о том, что в любой клетке СННЧ N = а·b представимо разностью квадратов двух целых чисел () разной четности, которые выбираются специальным образом, т.е. и а, b играют роль диагоналей, пересекающихся в этой клетке модели.

Сущность наблюдения в Г^2± – модели НРЧ (таблица М) состоит в следующем. Располагая в модели координатами клетки, легко определяются значения чисел в них, но обратная задача трудно решаемая. Допускаем, что координаты клетки заданного СННЧ N известны.

Сумму делителей числа N из клетки () обозначают σ(N). Cумма σ(N) этих двух (а, b) неизвестных нетривиальных делителей, а также тривиальных делителей 1 и самого N, определяется (вычисляется) в модели, как значение числа в другой клетке с координатами (), в то время как само число N помещается в клетке (), что легко показывается. Установлены, сформулированы и доказаны две новые теоремы.

Теорема 1. Если в клетке () Г^2± – модели НРЧ содержится СННЧ N = а·b, где а,b -собственные делители играют роль номеров короткой и длинной диагоналей, пересекающихся в этой клетке, то в строке ниже под этой клеткой в клетке () содержится сумма σ(N) делителей СННЧ N. (положение N задано, а и b неизвестны).

Доказательство. Значение любой клетки Г^2± – модели НРЧ по основному соотношению модели равно , где в скобках соответственно приведено произведение — номеров диагоналей длинной и короткой, пересекающихся в этой клетке и выполняющих роль делителей N=аb. Под клеткой со значением N помещается клетка, значение в которой равно произведению диагоналей, увеличенных на 1, т.е. (а+1)(b+1)=а·b+а+b+1=σ(N), раскрывая скобки, получаем сумму делителей. Этим доказательство завершается.

В этом равенстве а·b+1=N+1, а разность σ(N)-N-1=а+b — есть сумма только собственных делителей N. Названные зависимости легко могут быть выражены через переменные модели (), так как а = () и b=(), тогда .
Здесь же отметим и еще одно наблюдение для которого справедлива следующая

Теорема 2. Если в клетке () Г^2± – модели НРЧ содержится СННЧ N = а·b, где а,b -собственные делители играют роль номеров короткой и длинной диагоналей, пересекающихся в этой клетке и являющиеся простыми нечетными числами, то в строке выше над этой клеткой в клетке () содержится функция Эйлера φ(N) СННЧ N. Положение N задано, а и b неизвестны.

Доказательство. Здесь повторяется положение предыдущей теоремы, но для клетки выше изменяются знаки. Над клеткой со значением N помещается клетка, значение в которой произведение номеров диагоналей, уменьшенных на 1, т.е. φ(N)=(а-1)(b-1) = а·b -а-b+1. Этим равенством доказательство теоремы завершено.
Результаты обеих теорем (показано ниже) могут быть применены в атаках на шифр RSA.

Из второй теоремы следует, если а и b простые нечетные числа-нетривиальные делители числа N, то произведение φ(N) = (а – 1)( b – 1) и разность являются теоретико-числовой функцией Эйлера для составного числа N.
Приведем вид решетчатой функции σ(N) суммы делителей в зависимости от числа N. По оси ординат расположим числа N, а по оси абсцисс σ(N) сумму их делителей (1≤N≤1000).

На графике отчётливо просматриваются несколько наклонных линий из точек, имеющих сходство с прямыми, например, нижняя линия соответствует суммам делителей простых чисел. Верхняя граница – это наиболее сложные числа (имеющие наибольшее количество делителей) — это не прямая, но и не парабола. Возможно – это показательная функция вида ().

При решении задачи факторизации совсем не обязательно сразу получать все степени простых чисел. Можно пойти путем нахождения вначале лишь одного единственного делителя (второй получается, как частное при выполнении деления). Этот единственный делитель может быть и составным числом, как впрочем, и частное от деления числа N на него. После этого оба найденные делителя (числа меньшей разрядности) подвергаются процедуре дальнейшей факторизации до ее полного завершения.

Процесс продолжается до тех пор, пока это оказывается возможным. Как только все возможности разложения всех делителей N исчерпаны, процесс факторизации прекращается. Найденные простые факторы можно перемножить между собой, что должно дать в результате вновь исходное число N.

Этот факт служит подтверждением правильности найденного решения.
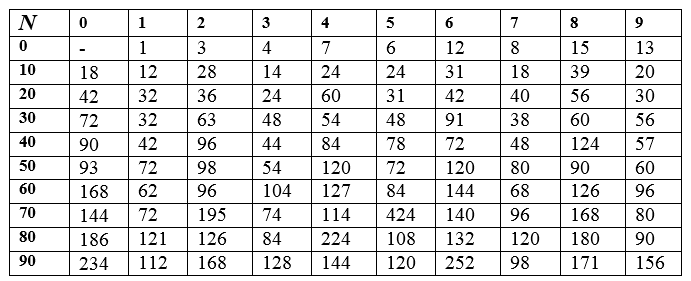
Чтобы количественно почувствовать и оценить зависимость σ(N) – суммы делителей от числа N покажем последовательность таких сумм для первых ста натуральных чисел N (см. таблицу 1):

Таблица 1. Суммы σ(N) делителей натуральных чисел, полученные Эйлером.

Из приведенных весьма ограниченных данных видим, что для простых чисел σ(N)=N+1, что некоторые различные числа (46, 55, 71) имеют совпадающие значения σ(N) = 72, а некоторые N не являются суммами делителей ни одного из натуральных чисел.

В теории чисел известны следующие результаты. Найти сумму всех делителей натурального числа можно с использованием канонического разложения N, если оно известно. Легко найти простым перебором σ(N) для небольших натуральных чисел, например, .

Но при достаточно больших значениях N нахождение всех делителей, а тем более их суммы становится затруднительным. Совсем другое дело, если уже известно, каноническое разложение числа N.
Делителями N являются все числа, для которых $inline$0 ≤ β_s ≤ α_s , s = 1(1)k$inline$. Ясно, что σ(N) представляет собой сумму всех таких чисел при различных значениях показателей .

В работе предлагается один из возможных вариантов построения алгоритма решения за-дачи факторизации, который не зависит или слабо зависит от разрядности факторизуемого числа. В основу алгоритма поиска решения положен принцип использования суммы двух нетривиальных делителей (факторов) натурального числа.

Ясно, что существуют составные натуральные числа, образованные произведением всего лишь двух простых чисел (RSA числа). Это, вообще говоря, частный для теории чисел случай, но очень важный для практики. В общем случае оба делителя а и b – составные числа. Для лучшего понимания идеи такого алгоритма факторизации ниже приведем числовые примеры, рассматриваемые в рамках приведенной Г^2± – модели НРЧ (табл. М).

Пример 1.
Найти разложение заданного составного натурального числа N на множители а и b, если а и b неизвестны, а их сумма σ(N)=а + b известна.
Данная задача может быть сведена к нахождению решения системы двух алгебраических уравнений с двумя неизвестными. Чтобы исключить тривиальные решения (делители) вычтем их из заданной σ(N) суммы делителей .

В рассматриваемом примере решением задачи факторизации числа N являются значения а и b, удовлетворяющие замкнутой системе двух алгебраических уравнений:
,
.

Здесь σ(N) обозначает сумму всех делителей N, которая полагается известной, а вычисляется и представляет собой сумму лишь двух нетривиальных делителей простых или составных чисел. Как находить значения таких сумм σ(N) и будет показано позже.

Выполним преобразование записанной системы двух уравнений путем исключения переменной b. Это приводит к одному квадратному уравнению , корни которого и есть искомые делители числа N. Воспользуемся теоремой Виета. Тогда корни квадратного уравнения определяются соотношением

Таким образом, задача факторизации числа в рассматриваемой ситуации будет успешно решена, если для числа N предварительно будет определена σ(N) сумма делителей.

Пример 2 (числовой с двумя простыми делителями). Задано N = a·b = 301, для которого известна клетка () его размещения в Г^2± – модели НРЧ. Требуется определить cумму всех делителей σ(N) числа N, вычислить функцию Эйлера и факторизовать N.

Решение. Воспользуемся результатом Эйлера для подсчета суммы собственных делителей
$inline$σ(N) = σ(N-1)+σ(N-2)-σ(N-5)-σ(N-7)+σ(N-12)+σ(N-15)-$inline$

$inline$σ(300)+σ(299)-σ(296)-σ(294)+σ(289)+σ(286)-σ(279)-σ(275)+σ(266)+$inline$
$inline$+σ(261)-σ(250)-σ(244)+σ(231)+σ(224)-σ(209)-σ(201)+σ(184)+σ(175)-$inline$
$inline$-σ(156)-σ(146)+σ(125)+σ(114)-σ(91)-σ(70)+σ(54)+σ(41)-σ(14)-σ(0)=$inline$

Уже отмечалось, что для простого числа q сумма σ(q)=q+1 равна сумме делителей q и 1. Поэтому при $inline$N = 301 =7·43, σ(301)=σ(7)·σ(43)=8·44 =352 $inline$

Располагая моделью Г^2± этот результат получается вычислением в одной клетке. Находим , сумма неизвестных а и b делителей Находим делители $inline$а_{1,2}=50/2±(25^2-301)^ ½ =25± 18; а = а_1=43, b=а_2 =7.$inline$Покажем как связаны делители и координаты клетки

Наконец, вычислим значение функции Эйлера
Ответ: корни уравнения-делители N реализуют факторизацию. Проверка N = a∙b = 43∙7 = 301,

Убедимся, что в терминах переменных сумма делителей совпадает с вычисленной

Вычислим при найденных значениях a и b, функцию Эйлера
. Значения функции Эйлера, вычисленные двумя способами, совпали.

Пример 3 (числовой с одним простым и одним составным делителем). Задано N = 147, для которого сумма всех делителей σ(N) = σ(147) = 1+3+7+21+49 +147= 228. Но для четырех делителей числа N сумма равна 1 + а + b + 147, σ(N) = 176. Здесь а=21 и b=7 неизвестные делители, формирующие значение N. Требуется факторизовать число N.

Решение. Находим .
$inline$а_{1,2}=28/2 ±(196 — 147)^ ½= 14 ± 7.$inline$ Корни найдены Установим связь корней с переменными .
Ответ: Корни уравнения . Проверка a∙b = 21∙7 = 147

В этом примере один из делителей а=21 оказался составным числом, но именно это число и является слагаемым в сумме делителей, что видим в модели (табл. М строки 14,15; столб. 7) .

В примерах 2 и 3 рассмотрены задачи, в которых в качестве исходных данных задано число N и клетка его размещения. Требовалось факторизовать число N, т.е. отыскать делители. Для факторизации привлекалась модель НРЧ и в ее клетках отыскивалась сумма делителей σ(N) и функция Эйлера φ(N), когда делителей (собственных) было всего два и они оба были простыми числами.

Существует симметричная относительно исходных данных задача, в которой известна сумма N+1 кратных делителей N = pq и клетка в Г^2± – модели НРЧ с координатами (), в которой лежит кратное целому числу sN произведение . Само число N лежит в последней клетке строки x1 с кратным произведением в Г^2- – модели НРЧ. Требуется факторизовать составное число N.

Пример 4. Заданы составное число N=pq =77, сумма , коэффициенты целые числа, координаты клетки () с кратным произведением числа . Требуется факторизовать N, т.е. определить p и q делители N.

Решение. По координатам клетки легко определяется значение в ней . Далее определяем произведение коэффициентов делителей в сумме . Получаем для двух неизвестных p и q замкнутую систему из двух уравнений:
,
.
Введем новые обозначения неизвестных . Перепишем систему.
,
.
Решение. .
Последнее слагаемое в квадратном уравнении необходимо сделать квадратом числа 39. Для этого добавим в левую и правую части уравнения число . Тогда получаем или и окончательно или

Пример 5. Если – различные простые числа, то σ(N) для различных их комбинаций имеет формулы:

$inline$σ(a·b·c·d) = σ(a)·σ(b)·σ(c)·σ(d),$inline$

, и вообще,
.

Пользуясь этими соотношениями, можно записать
$inline$σ(a^q·b^w·c^e·d^r) = σ(a^q)·σ(b^w)·σ(c^e)·σ(d^r). $inline$
Пусть $inline$N = p_1^{α_1}×…× p_k^{α_k}$inline$ по формуле конечного числа членов геометрической прогрессии приходим к равенству

Следующий результат в виде ряда для σ(N) получил Л. Эйлер, который записал сомножители N в многочленном представлении и раскрыл скобки в произведении многочленов
$inline$σ(N) = σ( p_1^{α_1}×…× p_k^{α_k}))$inline$ =
.

Ряд Эйлера

Этот ряд обеспечивает вычисление суммы делителей составного числа N, не зная ни числа делителей, ни их значений.
$inline$σ(N) = σ(N-1)+σ(N-2)-σ(N-5)-σ(N-7)+σ(N-12)+$inline$

Аналогичный результат получен в рамках исследования Г^2± – модели НРЧ (Теоремы 1 и 2)

Пример 6. Необходимо вычислить σ(360), при известном каноническом разложении на множители числа. По формулам теории чисел это легко вычисляется.
.

Эта задача по формулам не решается, если для N отсутствует каноническое разложение.
Ряд Эйлера позволяет свести задачу к решению системы алгебраических уравнений как в примерах 2 и 3. Но возникает ряд проблем, хотя и преодолимых. Привлечение модели НРЧ (табл. М) снимает часть затруднений, но создает свои.

Описание и использование ряда Эйлера при расчетах σ(N)

Пусть задано нечетное число N, которое требуется факторизовать, и известно, что N = pq, где p и q простые числа. Делителями N кроме p и q являются также 1 и само число N. Если известна сумма p + q = σ(N), то, как показано ранее, задача факторизации легко решается. Далее поясним как находятся значения σ(N) без знания делителей.

Рассмотрим две числовые последовательности: а) натуральных чисел;
б) нечетных чисел.
а)1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 3738…
б) 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49……

вторая последовательность начинается не 1, а числом 3.
Сольем эти две последовательности в одну, обозначив ее s, чередуя числа из последовательностей а) и б), а также выполним нумерацию элементов s сформированного ряда.

Таблица 2 – Совмещенные последовательности ряда нечетных и натуральных чисел.

Нечетные номера получают элементы из натурального ряда, а четные – из ряда нечетных чисел (при начале отсчета элементов s от единицы и наоборот, если начать отсчет номеров от нуля).

Использование ряда s предполагает возможность вычисления любого его элемента по текущему номеру или восстановление текущего номера по известному значению элемента ряда. Анализ ряда s показывает, что для элементов нечетного ряда их значение на единицу больше текущего номера, а значения элементов из натурального ряда равны половине увеличенного на единицу порядкового номера. Следующие примеры проясняют эти утверждения.

Пример 7. Порядковый номер элемента ряда s равен 30. Определить значение s(30).
Так как 30 ≡ 0(mod2), т.е. номер – четное число, то s(30) принадлежит ряду б) нечетных чисел и равно s(30) = 30 + 1 = 31.

Пример 8. Порядковый номер элемента ряда s равен 37. Определить значение s(37).
Определяем четность номера 37 ≡ 1(mod2). Номер нечетный, следовательно, число с этим номером принадлежит натуральному ряду а) и его значение
s(37) = (37 + 1)/2 = 19.

При известном значении s можно определить его порядковый номер. Необходимо только учесть одну особенность ряда s. Нечетные значения в ряде s встречаются дважды и, следовательно, занимают в нем две позиции с разными номерами. Поэтому для нечетных s существуют два порядковых номера, которые требуется определять (находить).

Пример 9. Значение элемента ряда s = 13. Определить порядковые номера для s-1(13).
Если s принадлежит натуральному ряду чисел, то его номер является нечетным числом и большим из двух возможных.
Таким образом, №натур(s) = 2s – 1 = 2∙13 – 1 = 25.

Если s принадлежит ряду нечетных чисел, то его номер – четное число и определяется по формуле № нечетн(s) = s – 1 = 13 – 1 = 12. Это меньший номер из двух. Оба номера связаны простым соотношением
№натур(s) – № нечетн(s) = (2s – 1) – (s –1)= s = 25 – 12 = 13.

Разность номеров равна значению s. Таким образом, поведение элементов ряда s, т.е. значения и занимаемые позиции устанавливаются достаточно простыми соотношениями.
Как этими фактами можно воспользоваться при решении задачи факторизации?
Оказывается, ряд s является рядом разностей смежных элементов другого ряда k(i), открытого Эйлером, и по известному ряду s ряд k(i) можно восстановить.

Таблица 3 – Последовательность нумерованных чисел k(i) ряда Эйлера

k(1) =1, k(2) = k(1) + s(1) = 2, k(3) = k(2) + s(2) = 2 + 3 = 5,
k(4) = k(3) + s(3) = 5 + 2 = 7, k(5) = k(4) + s(4) = 7 + 5 = 12 и т. д… в общем виде
k(i + 1) = k(i) + s(i), i = 1(1)…, k(1) = 1.

Ряд k(i) был открыт Л. Эйлером, который указал на его применимость к решению задачи определения сумм делителей натуральных чисел в формуле:
σ(N)=σ(N-k(1))+σ(N-k(2))-σ(N-k(3))-σ(N-k(4))+σ(N-k(5))+σ(N-k(6))-σ(N-k(7))-
-σ(N–k(8))+= … = σ(N-1)+σ(N-2)-σ(N-5)-σ(N-7)+σ(N-12)+σ(N-15)-σ(N-22)-σ(N–26)+ …

При выполнении расчетов σ(N) для аргумента функции σ(N) вычисляются разности
N — k(i), если σ(N) обозначает любой член этой последовательности, а σ(N — 1),
σ(N — 2), σ(N — 5)… предшествующие члены, то σ(N) всегда можно получить по нескольким предыдущим членам:
σ(N)= σ(N — 1)+ σ(N — 2)- σ(N — 5)- σ(N — 7)+ σ(N — 12)+σ(N — 15)- σ(N — 22)- σ(N – 26)+ …

Знаки «+» и «–» в правой части формулы попарно чередуются.
Возникают еще вопросы. Когда необходимо ограничить бесконечный ряд, остановиться? Как определить значение в точке останова?

Остановка происходит при получении отрицательного или нулевого значения аргумента в некотором слагаемом. Последняя разность при вычислениях N — k(i) может оказаться отрицательной при N < k(i) или нулевой при N = k(i). В первом случае останавливаются на предпоследнем значении аргумента, а во втором – нулевое значение заменяется на N.
Вычисления функции σ(N — k(i)) с аргументами, определяемыми с использованием ряда k(i), с учетом знаков при суммировании обеспечивает нахождение суммы делителей N без знания значений самих делителей. Наличие такой суммы приводит к решению задачи факторизации чисел вида N = ab, где а и b – делители N.
Эйлеру не удалось найти доказательство открытой им закономерности и те, к кому он обращался ничего подсказать ему не смогли, но он был глубоко убежден в правильности открытого закона и опубликовал его. Почитать об этом можно в [10]. В модели (табл. М) я привожу формулировку и доказательство теорем о σ(N) и φ(N), которые несколько перекрывают результат Эйлера (он не говорит ничего о значениях функции φ(N), которая лежит строкой выше).
Закон образования ряда чисел 1, 2, 5, 7, 12, 15…, которые необходимо вычитать из рассматриваемого числа N, станет ясен, если рассмотреть их последовательные разности:
Числа:1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100…
Разности: 1, 3, 2, 5, 3, 7, 4, 9, 5, 11, 6, 13, 7, 15, 8…

В самом деле, в ряде разности обнаруживаются два ряда: поочередно через один элемент все натуральные числа 1, 2, 3, 4, 5, 6, 7… и остаются после этого только нечетные числа 3, 5, 7, 9 11…они выделены жирным шрифтом между числами натурального ряда.

Хотя эта последовательность бесконечна, в каждом случае берутся только те члены, для которых числа, стоящие под знаком σ, еще положительны, и опускаются σ для отрицательных чисел. Если в формуле ряда σ(N) встречается элемент σ(0), то, поскольку его значение само по себе является неопределённым, необходимо подставить вместо σ(0) рассматриваемое число N.

Пример 10. Вычислить сумму делителей числа N = 20. Начальные условия для формулы Эйлера имеют вид: σ(1) = σ(0) =1, σ(2) = σ(1) + σ(0) = 1 + 2 = 3, …
Решение: σ(20) = σ(19) + σ(18) — σ(15) — σ(13) + σ(8) + σ(5) =
=20 + 39 – 24 – 14 + 15 + 6 = 42.

Формула содержит лишь шесть слагаемых, так как в седьмом аргумент 20 – 22 = –2 получает отрицательное значение и процесс вычислений обрывается. Для поиска новых возможностей изучения натуральных чисел мы продолжаем экспериментировать и часть материалов приводим ниже.

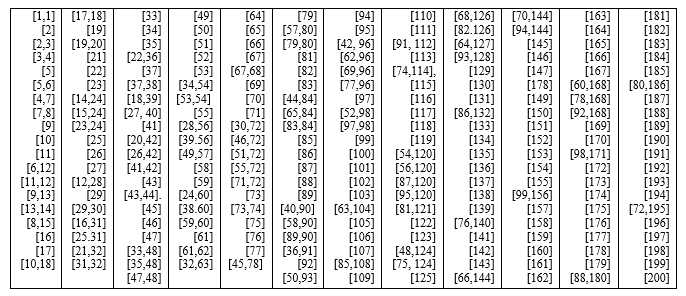
Приведём далее экспериментальный материал (список, который был получен с помощью программы для ЭВМ. Для нахождения делителей числа N, программа делила число N на другое число, не превосходящее корня из N, и, если результат деления был равен целому числу, то оба числа записывались как делители N. Ниже приведен фрагмент (таблица 4) списка чисел в интервале 1 < N < 1000 и их делителей
Таблица 4 – Делители натуральных чисел (фрагмент)

Теперь посмотрим, все ли натуральные числа являются суммой делителей какого-либо числа, и есть ли такие числа, суммы делителей которых равны (в первых двух сотнях) друг другу.

Далее приведена таблица 5: ее элемент [[N, σ(N)]]=[[4, 7]](на втором месте обозначения сумма делителей, а на первом число с данной суммой делителей) … [[1, 1]], [2], [5] (т.е. для чисел 2, 5 нет такого числа с суммой делителей равной двум или пяти). Если несколько чисел имеют одинаковые суммы делителей, то значения для таких сумм повторяются нужное число раз для чисел 14, 15 и 23 сумма делителей равна 24: [14,24]; [15,24]; [23,24].

Таблица 5. Числа от 1 до 200, совпадающие с суммами делителей разных чисел и не являющиеся такими суммами.

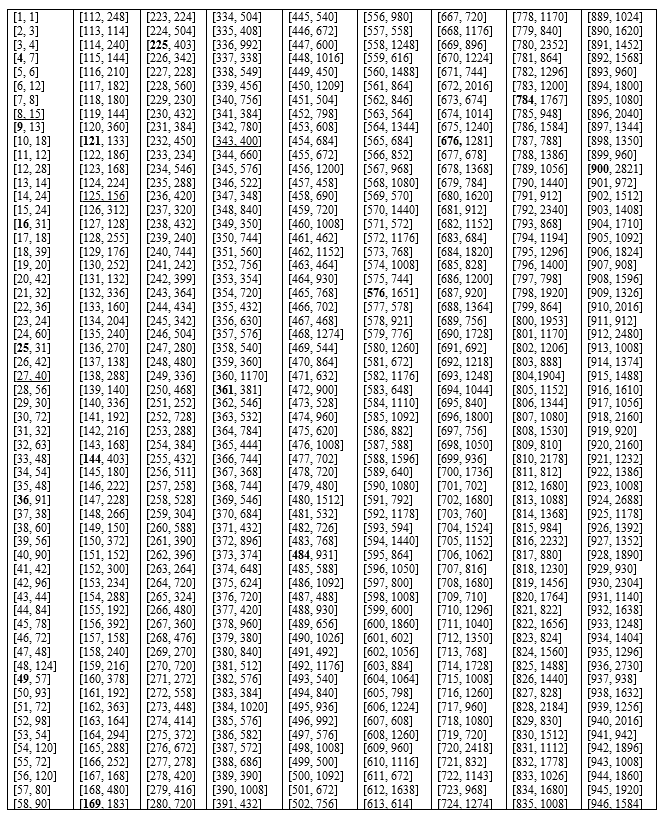
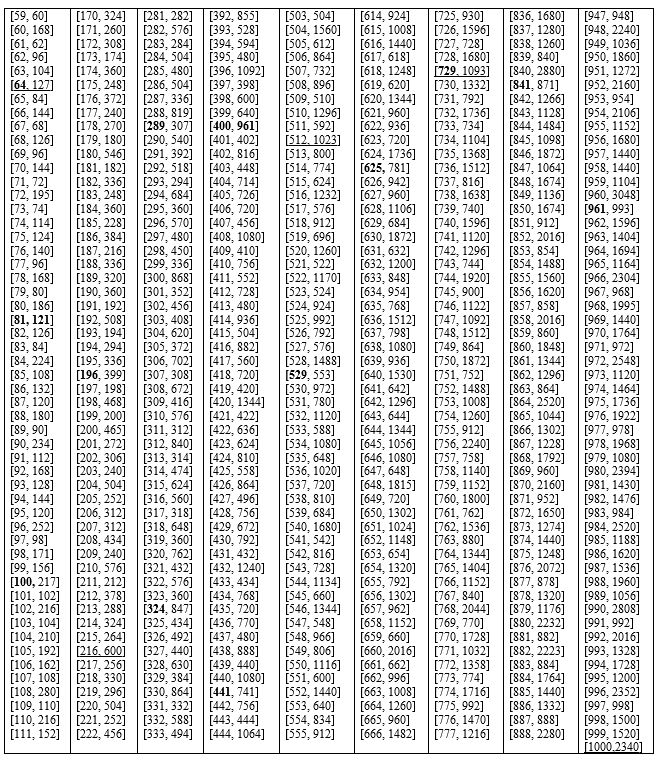
Теперь вычислим σ(N) суммы делителей всех чисел из диапазона
1< N < 1000 (которые тоже были получены с помощью программы, делители N из таблицы 4 просто суммировались). Как можно увидеть в таблице есть такие числа, которые не являются суммой делителей ни одного числа и так же есть такие числа, которые являются суммой делителей не одного, а нескольких чисел.
Таблица 6 – Суммы делителей σ(N) натуральных чисел 1< N<1000.


Жирным шрифтом выделены квадраты чисел. Подчеркиванием выделены кубы чисел.

Список литературы
1. Ферма П. Исследования по теории чисел и диофантову анализу. – М.: Наука, 1992. – 320 с.
2. Евклид, Начала Евклида, т.1–3, М–Л.,1948–1950.
3. Euler, Opera Omnia, ser.1, vol. 2, p. 241-253.
4. Ваулин А.Е. и др. Фундаментальные структуры натурального ряда чисел.//Сб.тр. 7-го Международного симпозиума. – М.: РУСАКИ, 2006. – с.456-459.
5. Ваулин А.Е. Новый метод факторизации больших чисел в задачах анализа и синтеза двух-ключевых криптографических алгоритмов. Ч.1.// Информация и космос .№3, 2005, 74 –78с.
6. Ваулин А.Е. Новый метод факторизации больших чисел в задачах анализа и синтеза двух-ключевых криптографических алгоритмов. Ч.2.//Информация и космос. №4, 2005,104 –112с.
7. Василенко О.Н. Теоретико–числовые алгоритмы в криптографии.–М.: МЦНМО,2003.–328с.
8. Дэвенпорт Г. Высшая арифметика. – М.: Наука, 1966. – 176с.
9. Ноден П., Китте К. Алгебраическая алгоритмика (с упражнениями и решениями). – М.: Мир, 1999. – 720с.
10. Пойя Д. Математика и правдоподобные рассуждения.– М.: Наука, 1975. – 464с.
11. Пойя Д. Математическое открытие. – М.: Наука, 1970.–
12. Эндрюс Г. Теория разбиений. – М.: Наука, 1982. – 256с.
13. Пшеннов А.В.