Up to isomorphism, there are only two groups of order $10$: the cyclic group $mathbb{Z}/10mathbb{Z}$, and the dihedral group $D_{10}$.
One way to see this is to first notice, as you did, that a group $G$ of order $10$ has an element of order $5$ and another of order $2$; the subgroups they generate, say $G_5$ and $G_2$, have order $5$ and $2$, respectively.
Now, since $G_5$ has index $2$, it is a normal subgroup of $G$. Moreover, $G_5$ and $G_2$ have trivial intersection, and $G_5G_2=G$ (this can be seen by looking at the cardinality of $G_5G_2$). Thus $G$ is the semidirect product of those two subgroups: $G=G_5rtimes G_2$.
Now, semidirect products of the form $G_5rtimes G_2$ are determined by an action of $G_2$ on $G_5$, or equivalently, by a homomorphism of groups $G_2to Aut(G_5)$. Since $G_5 cong mathbb{Z}/5mathbb{Z}$, we have $Aut(G_5)cong mathbb{Z}/4mathbb{Z}$, so there are exactly two group homomorphisms $G_2to Aut(G_5)$ (since $G_2 cong mathbb{Z}/2mathbb{Z}$).
Thus there are exactly two semidirect products $G_5rtimes G_2$: the one corresponding to the trivial action of $G_2$ on $G_5$ gives $mathbb{Z}/10mathbb{Z}$, and the only non-trivial action of $G_2$ on $G_5$ gives $D_{10}$.
For your second, more general question, this post seems to provide the answer.
|
n |
… |
k |
. |
||||||
|
p |
1 |
p |
|||||||
|
1 |
k |
||||||||
|
Пример 2. Разложим группу |
вычетов |
360 в прямую сумму |
своих примарных компонент. Поскольку 360 23 32 5 , то
360 8 9 5 .
Для того чтобы разложить абелеву группу
n1 … nm
впрямую сумму примарных циклических групп, нужно разложить каждое слагае-
мое этой группы.
Пример 3. Разложим группу
756 2250 105
в прямую сумму примарных циклических групп. Поскольку 756 22 33 7 ,
2250 2 32 53 , 105 3 5 7 , то
756 4 27 7 ,
2250 2 9 125 ,
105 3 5 7 .
Поэтому
756 2250 105 2 3 4 5 7 7 9 27 125 .
Пример 4. Определим, изоморфны ли группы 15 225 и 75 45 . Поскольку 15 3 5 , 225 9 25 , то
15 225 3 5 9 25 .
Далее, 75 3 25 , 45 5 9 . Поэтому
75 45 3 25 5 9 .
Поскольку разложения совпадают с точностью до перестановки слагаемых, группы изоморфны.
Пример 5. Определим, изоморфны ли группы 9 225 и 15 135 . Находим разложение каждой группы в прямую сумму примарных циклических групп:
9 225 9 9 25 ,15 135 3 5 5 27 .
Примарные циклические группы не совпадают, группы неизоморфны.
Число неизоморфных абелевых групп порядка pn равно числу p(n) разбиений чис-
ла n в сумму нескольких (возможно, одного) натуральных чисел
n n1 n2 … nr , где 1 n1 n2 … nr , 1 r n .
31
|
Например, |
существуют две неизоморфные абелевы группы порядка p2 : |
p |
2 и |
||||
|
p p . |
|||||||
|
p(3) 3 , так как 3 1 2 1 1 1. |
|||||||
|
p(4) 5 , так как 4 1 3 2 |
2 1 1 2 1 1 1 1. |
||||||
|
p(5) 7 , так как 5 1 4 2 |
3 1 1 3 1 2 2 1 1 1 2 1 1 1 1 1. |
||||||
|
Пример 6. Найдѐм число неизоморфных абелевых групп порядка 64. |
|||||||
|
Поскольку |
64 26 |
и |
6 1 5 2 4 3 3 1 1 4 1 2 3 |
2 2 2 1 1 1 3 1 1 2 2 1 1 1 1 2 1 1 1 1 1 1, то p(6) 11. Поэтому сущест-
вует 11 неизоморфных абелевых групп порядка 64.
Пример 7. Найдѐм число неизоморфных абелевых групп порядка 864. 864 33 25 .
Так как p(3) 3, p(5) 7 , то абелевых групп порядка 864 существует 3 7 21.
Задачи
Разложите в прямую сумму примарных циклических групп следующие группы:
1.6 .
2.12 .
3.60 .
Сколько существует неизоморфных абелевых групп порядка:
4.36?
5.100?
6.64?
Выясните, изоморфны ли следующие группы:
7.6 36 и 12 18 ?
8.6 36 и 9 24 ?
9.6 10 10 и 60 10 ?
1.8.Конечные группы до 10-го порядка
Перечислим все конечные группы до 10-го порядка включительно с точностью до изоморфизма.
G 1. Существует одна группа порядка 1, состоящая из одной единицы e . Есте-
ственно, она абелева.
G 2 . Существует одна абелева группа порядка 2 – это 2 .
32
G 3. Существует одна абелева группа порядка 3 – это 3 .
G 4 . Здесь существуют две группы – это 4 и 2 2 . Обе они абелевы.
G 5 . Существует одна абелева группа порядка 5 – это 5 .
G 6 . Здесь существуют две группы, одна из них абелева – это 6 , другая – не-
|
абелева. Это D3 – группа движений треугольника. |
||||||||
|
G |
7 . Существует одна абелева группа порядка 7 – это 7 . |
8 , |
2 4 и |
|||||
|
G |
8 . Существуют 5 групп порядка 8. Три из них абелевы. Это |
|||||||
|
2 2 2 . Кроме них существуют две неабелевы группы. Это D4 – группа движений |
||||||||
|
квадрата и 8 |
– группа кватернионов. |
|||||||
|
G |
9 . |
Существуют две абелевы группы порядка 9. Это 9 и 3 3 . |
||||||
G10 . Существуют две группы порядка 10. Одна из них абелева. Это 10 . Другая
–неабелева. Это D5 – группа движений правильного пятиугольника.
Задачи
1.Докажите, что всякая циклическая группа является абелевой.
2.Докажите, что любая конечная группа простого порядка p изоморфна p –
группе вычетов по модулю p .
3.Докажите, что если в конечной группе каждый элемент, кроме единицы, имеет порядок 2, то эта группа абелева.
4.Докажите, что любая группа порядка 4 изоморфна либо 4 , либо группе движе-
ний ромба.
5. Докажите, что в неабелевой группе порядка 6 должен существовать элемент по-
рядка 3.
6. Пусть G – неабелева группа порядка 6, a G – элемент порядка 3 и b G a, a2 ,e . Докажите, что тогда все элементы a, a2 ,e, ab, a2b,b разные и b имеет поря-
док 2.
7.Докажите, что в обозначениях предыдущей задачи ba ab2 .
8.Докажите, что всякая неабелева группа порядка 6 изоморфна S3 .
33
1.9. Кольцо, тело, поле
Определение 1. Множество A с двумя бинарными операциями ( ) и ( ) называ-
ется ассоциативным кольцом, если
1)относительно операции ( ) множество A является абелевой группой;
2)a,b,c A (ab)c a(bc) ;
3)a,b,c A a(b c) ab ac, (b c)a ba bc .
В случае, если
4) a,b A ab ba , кольцо A называется коммутативным.
В случае, когда
5) 1 A: a A 1 a a 1 a , говорят, что кольцо A имеет единицу.
Неассоциативных колец рассматривать не будем, поэтому в дальнейшем слово
«кольцо» будет обозначать ассоциативное кольцо.
Пример 1. Множество с обычными операциями ( ) и ( ) является коммутатив-
ным кольцом с 1.
Пример 2. Множества , , с обычными операциями ( ) и ( ) являются комму-
тативными кольцами с 1.
Пример 3. Множество n 0,1, 2,…, n 1, операции ( ) и ( ) в котором определя-
ются как остатки от деления на n результатов обычных операций сложения и умножения,
является кольцом. Например, в кольце 9 6 7 5, 6 7 2 .
n – всегда коммутативное кольцо с 1.
Пример 4. Кольцо матриц Mn ( ) размера n n с коэффициентами из и с опе-
рациями сложения и умножения матриц, Mn ( ) является уже некоммутативным кольцом с 1.
Пример 5. Множество C a,b всех непрерывных функций на отрезке a,b с опе-
рациями «поточечного» сложения и умножения функций. Это коммутативное кольцо с 1.
Пример 6. Кольцо многочленов [x] от одной переменной с действительными коэффициентами и с обычными операциями сложения и умножения многочленов. Это также коммутативное кольцо с единицей.
Определение 2. Кольцо с единицей называется телом, если каждый ненулевой элемент имеет обратный.
Определение 3. Коммутативное кольцо с единицей, в котором каждый ненуле-
вой элемент имеет обратный, называется полем.
34
a b a b .
Оказывается, всякое конечное тело является полем. Эта теорема была доказана
Веддербарном в 1905 году.
Определение 4. Пусть B – подмножество в кольце A . Если относительно су-
ществующих в кольце A операций «сложения» и «умножения» B также является коль-
цом, то B называется подкольцом кольца A .
Определение 5. Подкольцо I кольца A называется идеалом, если a A и x I
элементы ax и xa принадлежат I .
Пример 7. Множество n для фиксированного натурального n является идеалом
кольца .
Определение 6. Пусть I – идеал кольца A . Рассмотрим множество смежных классов кольца A по идеалу I , рассматриваемое пока как абелева группа. Смежными классами будут являться подмножества кольца A вида a I , которые будем обозначать
a .
В фактор-группе A / I имеется операция сложения, определѐнная формулой Определим операцию умножения равенством
a b ab .
В силу того что I – идеал, это определение корректно.
Рассмотренное множество смежных классов с определѐнными на нѐм операциями
( ) и ( ) образуют кольцо, которое называется фактор-кольцом кольца A по идеалу I и
обозначается A / I .
Пример 8. / n n .
Определение 7. Пусть A и B – кольца. Отображение f : A B называется го-
моморфизмом колец, если x, y A
f (x y) f (x) f ( y), f (xy) f (x) f ( y) .
Если к тому же f – взаимно однозначное отображение, то f называется изо-
морфизмом.
Среди рассмотренных примеров 1 – 6 примерами полей являются , , . Если же
n p – простое число, то кольцо p вычетов по модулю p также является полем.
Пример 9. Пусть A – кольцо (2 2) -матриц вида
|
a |
b |
a,b . |
|
, |
||
|
b |
a |
|
|
Проверка показывает, что отображение |
||
|
a |
b |
a bi |
|
b |
a |
|
|
35 |
является изоморфизмом, т.е. кольцо A изоморфно полю комплексных чисел.
Пример 10. Рассмотрим кольцо многочленов A x и идеал I , состоящий из всех многочленов, делящихся на x2 1 . В этом случае говорят, что I порождѐн многочле-
ном x2 1. Можно записать I (x2 1) x . В каждом смежном классе можно выбрать представитель в виде многочлена степени не выше первой. Поэтому элементы этого фак-
тор-кольца можно записывать в виде a bx, a,b . Отображение a bx a bi является изоморфизмом, т.е. опять A / I .
Пример 11. Примером тела, не являющегося полем, может служить «тело кватер-
нионов».
Пусть i, j, k – символы, перемножающиеся по правилу
i2 j2 k2 1, ij k ji, jk i k, ki j ik . (1.1)
Множество выражений ai bj ck d , где a,b,c, d , с операцией покомпонентно-
го сложения и умножения, определѐнного с помощью формул (1.1) и закона дистрибутив-
ности, образует тело, называемое телом кватернионов.
Задачи
1.В кольце вычетов 12 найдите все обратимые элементы.
2.Найдите все нетривиальные идеалы в кольце вычетов 12 .
3.Пусть V – множество всех векторов в пространстве. В качестве операции ( )
рассмотрим обычное сложение векторов, а в качестве операции ( ) рассмотрим векторное произведение. Будет ли V с двумя этими операциями ассоциативным кольцом?
1.10. Строение конечных полей
Определение 1. Пусть F – поле. Наименьшее натуральное n , при котором
1 1 … 1 0 , называется характеристикой поля F и обозначается char F . Если такого
n
n не существует, то считается, что char F 0 .
Теорема 1. Характеристика конечного поля – простое число.
Доказательство. Если бы char F n k m , где k, m 1, то в поле F произведение двух ненулевых элементов k и m равнялось бы 0. Это невозможно. Действительно, ра-
венство k m 0 можно было бы умножить на m 1 и тогда k 0 . Противоречие.
36
e1,…,en
Теорема доказана.
Если характеристика поля F равна p , то F содержит подполе из p элементов,
изоморфное p . Элементами этого подполя являются суммы 1 1 … 1 k .
Теорема 2. Число элементов конечного поля характеристики p равно pn для не-
которого натурального n .
Доказательство. Поле F можно рассматривать как векторное пространство над подполем p . Как во всяком векторном пространстве, в F можно выбрать базис
над p . Этот базис конечен в силу конечности поля F . Каждый элемент поля F можно
единственным образом представить в виде 1e1 2e2 … nen , p . Число таких выра-
жений равно pn .
Теорема доказана.
Теорема 3. Для каждого простого p и натурального n существует единствен-
ное с точностью до изоморфизма конечное поле из pn элементов.
Без доказательства.
Определение 2. Конечное поле из pn элементов обозначается GF ( pn ) и называ-
ется полем Галуа.
Определение 3. Если рассматривать все ненулевые элементы конечного поля,
то относительно операции умножения они образуют коммутативную группу. Эта груп-
па называется мультипликативной группой поля.
Имеет место следующий факт.
Теорема 4. Мультипликативная группа конечного поля циклическая.
Без доказательства.
Определение 4. Образующие мультипликативной циклической группы поля на-
|
зываются примитивными элементами этого поля. |
|||||
|
Если |
F |
pn , то примитивными элементами |
a F будут те, для которых |
||
|
o( ) pn 1 . |
Если F – конечное поле, то можно рассматривать кольцо многочленов F[x] над F .
Элементами этого кольца являются многочлены от переменной x с коэффициентами из F
|
. Степенью многочлена f (x) a |
xn a |
xn 1 |
… a x a называется число n (a |
0) . |
||
|
n |
n 1 |
1 |
0 |
n |
||
|
Определение 5. Многочлен |
f (x) |
над полем F |
называется неприводимым, если |
его нельзя представить в виде произведения двух многочленов меньших степеней.
37
Пример 1. Найдѐм неприводимые многочлены над полем 2 степени 2. Всего существует 4 многочлена степени 2:
x2 , x2 1, x2 x, x2 x 1.
Неприводимым среди них является только x2 x 1, так как
x2 x x, x2 1 (x 1)(x 1), x2 x x(x 1) .
Многочлен x2 x 1 неприводим, так как 0 и 1 не являются его корнями, и поэтому
он не может быть разложен в произведение двух линейных многочленов.
Существуют два неприводимых многочлена 3-й степени: x3 x2 1, x3 x 1 .
Теорема 5. Для каждого простого p и натурального n в кольце p [x] сущест-
вуют неприводимые многочлены степени n .
Без доказательства.
Теорема 6. Пусть f (x) – неприводимый многочлен степени n над полем p .
|
Пусть I f (x) p[x] – идеал в кольце многочленов |
A p [x] , порождѐнный многочленом |
|
f (x) . Тогда A / I – конечное поле из pn элементов. |
Доказательство. Фактор-кольцо A / I коммутативно и имеет единицу. Если u (x) A / I , то в кольце A найдутся многочлены s(x) и t(x) такие, что u(x)s(x) f (x)t(x) 1
(это следует из алгоритма Евклида). Тогда u (x) s (x) 1 в кольце A / I , т.е. каждый ненуле-
вой элемент кольца A / I обратим. Значит A / I – поле.
Пример 2. Рассмотрим поле F22 . Его можно представлять как фактор-кольцо A / I
, где A 2 ( ), I ( 2 1) 2[ ] (будет удобнее здесь писать вместо x ). В каждом смежном классе можно выбрать в качестве представителя многочлен степени не выше первой:
a b . Таблица умножений элементов этого поля выглядит так:
|
0 |
1 |
1 |
||
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
|
0 |
1 |
1 |
||
|
1 |
0 |
1 |
1 |
|
Пусть |
F |
pn . |
Каждый |
ненулевой элемент поля является корнем уравнения |
||
|
x pn 1 1 0 . Многочлен |
x pn 1 1 |
в кольце [x] можно разложить в произведение непри- |
p
водимых многочленов:
38
x pn 1 1 p1(x) p2 (x) … pk (x) .
Тогда каждый ненулевой элемент поля является корнем одного из них.
Определение 6. Пусть элемент конечного поля F из pn элементов является корнем многочлена pi (x) – одного из неприводимых многочленов в разложении x pn 1 1 .
Тогда этот многочлен называется минимальным многочленом для .
Среди всех многочленов, одним из корней которых является , этот многочлен имеет наименьшую степень. Каждый элемент поля имеет свой минимальный многочлен.
Пример 2 (продолжение). Минимальным многочленом для 1 является x 1. Ми-
нимальным многочленом для элементов и 1 является многочлен x2 x 1. Разложе-
нием многочлена x22 1 1 в произведении неприводимых в данном случае является
x3 1 (x 1)(x2 x 1)
(в поле 2 имеет место равенство 1 1).
Задачи
Все рассматриваемые многочлены предполагаются принадлежащими кольцу 2[x] .
|
1. |
Разделите с остатком многочлен f (x) x7 x5 x4 1 |
на многочлен g(x) x2 x 1 |
|||
|
. |
|||||
|
2. |
Найдите наибольший общий делитель |
f (x), g(x) d(x) , |
если |
f (x) x5 x4 1, |
|
|
g(x) x6 |
x5 x4 x3 x2 x 1. Далее найдите |
многочлены |
u(x) |
и |
v(x) такие, что |
f (x) u(x) g(x) v(x) d(x) .
3. Найдите все неприводимые многочлены 3, 4 и 5-й степеней в кольце 2[x] .
Разложите следующие многочлены в произведение неприводимых многочленов.
4.x7 1.
5.x15 1.
6.x31 1.
Через f (x) будем обозначать идеал, порождѐнный многочленом f (x) . Этот идеал состоит из всех многочленов, делящихся на f (x) .
7. Выпишите таблицу умножения для элементов фактор-кольца 2[x] / (x2 1) . Бу-
дет ли это кольцо полем?
Найдите наименьший идеал, содержащий многочлены f (x) и g(x) .
39
8.f (x) x2 1, g(x) x3 x2 x 1 .
9.f (x) x2 1, g(x) x3 1.
|
10. |
Выпишите |
таблицу |
умножения |
для |
элементов |
фактор-кольца |
||
|
F |
2 |
[x] / (x3 x 1) , взяв в качестве представителей смежных классов многочлены степе- |
||||||
|
1 |
||||||||
|
ни не выше второй. Будет ли это кольцо полем? |
||||||||
|
11. |
Выпишите |
таблицу |
умножения |
для |
элементов |
фактор-кольца |
||
|
F |
2 |
[ y] / ( y3 y2 1) |
, взяв в качестве представителей смежных классов многочлены сте- |
|||||
|
1 |
||||||||
|
пени не выше второй. Будет ли это кольцо полем? |
||||||||
|
12. |
Задайте явным образом изоморфизм полей |
f : F1 F2 из задач 10 и 11. |
40
Соседние файлы в папке ИФПМ (ПРИТ)
- #
- #
- #
- #
Изоморфизм и гомоморфизм групп Определение. Группы G 1 и G 2 называются гомоморфными, если существует отображение : G 1 G 2, сохраняющее операции, определенные в G 1 и G 2. Т. е. , для и имеем: a, b G 1, (a b) = (a)○ (b). Обозн. : ~ . Если – взаимно-однозначное отображение, то группы называются изоморфными. Обозн. :
Примеры. 1) G 1 = , G 2 = <{ 1}, > : G 1 G 2 так, что (2 n) = 1; (2 n+1) = -1. Проверим сохранение операции: (2 n+2 k) = (2(n+k)) = 1 (2 n) (2 k) = 1 1=1 ((2 n+1)+(2 k+1)) = (2(n+k+1)) = 1 (2 n+1) (2 k+1) = (-1) = 1 1=1 (2 n+(2 k+1)) = (2(n+k)+1) = -1 (2 n) (2 k+1) = 1 (-1) = -1 – гомоморфизм. -1 = -1
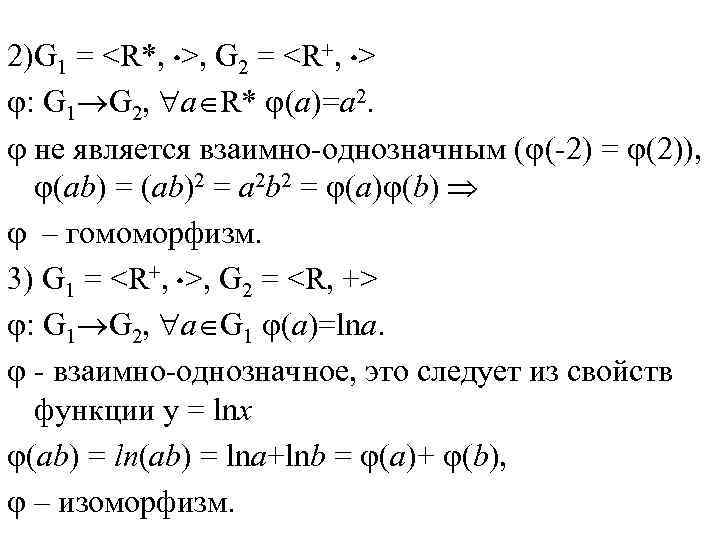
2)G 1 = , G 2 = : G 1 G 2, a R* (a)=a 2. не является взаимно-однозначным ( (-2) = (2)), (ab) = (ab)2 = a 2 b 2 = (a) (b) – гомоморфизм. 3) G 1 = , G 2 = : G 1 G 2, a G 1 (a)=lna. – взаимно-однозначное, это следует из свойств функции y = lnx (ab) = lna+lnb = (a)+ (b), – изоморфизм.
Свойства изоморфизма Т 1. Изоморфный образ группы является группой. Дано: , G 1 – группа. Доказать: G 2 – группа. Доказательство: 1) Выполнимость: Пусть : G 1 G 2 – изоморфизм, b 1, b 2 G 2. Докажем, что b 1○b 2 G 2. Т. к. – изоморфизм, то a 1, a 2 G 1, (a 1) = b 1, (a 2) = b 2. a 1 a 2 G 1; (a 1 a 2) G 2. (a 1 a 2) = (a 1)○ (a 2) = b 1○b 2 G 2. 2) Ассоциативность: b 1, b 2, b 3 G 2, докажем, что (b 1○b 2)○b 3 = b 1○(b 2○b 3). (b 1○b 2)○b 3 = ( (a 1)○ (a 2))○ (a 3) = -изом. (a 1 a 2)○ (a 3) = -изом. ((a 1 a 2) a 3) =G 1–гр. (a 1 (a 2 a 3)) = -изом. (a 1)○ (a 2 a 3)= -изом. = (a )○( (a )○ (a )) = b ○(b ○b ). 1 2 3
3) Существование нейтрального элемента. Пусть e – нейтральный элемент из G 1. Покажем, что (e) – нейтральный элемент G 2. Т. е. b G 2 b○ (e) = (e)○b = b. Т. к. – изоморфизм, то a G 1, (a) = b. b○ (e) = (a)○ (e) = (a) = b (e)○b = (e)○ (a) = (e a) = (a) = b b○ (e) = (e)○b = b, следовательно (e) – нейтральный элемент G 2. 4) Нейтрализующий элемент. b G 2 b-1 G 2, b○b-1 = e’, e’ = (e) – нейтральный элемент G 2. (a) = b. Покажем, что (a-1) = b-1. b○b-1 = (a)○ (a-1) = (a a-1) = (e) = e’ G 2, b-1○b = (a-1)○ (a) = (a-1 a) = (e) = e’.
1) Взаимная однозначность. а) Пусть am 1 = am 2 am 1 -m 2 =e св-ва порядка m 1 = m 2 + nt, t Z. (am 1) = (am 2). б) Пусть (am 1) = (am 2), т. е. тогда
2) Сохранение операций: (am 1 am 2) = (am 1+m 2) =
Т 5 (Кэли). Любая конечная группа порядка n изоморфна некоторой подгруппе подстановок n -ой степени. Дано: G – группа; |G| = n. Доказать: Н Sn такая, что G H. Доказательство: G = {a 1, a 2, …, an, } ai G рассмотрим произведения a 1 ai, a 2 ai, …, an ai G. Все эти произведения будут различными Обозначим: a 1 ai = a 1, a 2 ai = a 2, … an ai = a n. 1, 2, …, n – некоторый набор чисел от 1 до n. Рассмотрим отображение Покажем, что – изоморфизм.
1) Взаимная однозначность. а) Пусть ai = aj из однозначности произведения (ai) = (aj) б) Пусть (ai) = (aj). Тогда k, k=1, 2, …, n ak ai = ak aj ai = aj. 2) Для доказательства сохранения операции будем использовать подстановку: Тогда
![Ядро гомоморфизма (kernel ['kə: nəl]) Пусть : G 1 G 2; –гомоморфизм. Определение. Ядром](https://present5.com/presentation/3/154154717_166247568.pdf-img/154154717_166247568.pdf-13.jpg "Ядро гомоморфизма (kernel ['kə: nəl]) Пусть : G 1 G 2; –гомоморфизм. Определение. Ядром")
Ядро гомоморфизма (kernel [‘kə: nəl]) Пусть : G 1 G 2; –гомоморфизм. Определение. Ядром гомоморфизма называется множество элементов группы G 1, которые отображаются в нейтральный элемент группы G 2. G 1 G 2 e´ Обозн. : Ker = {a G 1 / (a) =e’, e’ G 2}.
Т 1. Ядро гомоморфизма является нормальным делителем группы. Дано: G – группа, H = Ker . Доказать: H G. Доказательство: 1) Покажем, что H G а) a, b H ab H. Пусть a, b H, тогда (a) = (b) = e’. (ab) = – гомоморфизм (a) (b) = e’ e’ = e’ ab H. б) Пусть a H, тогда (a) = e’. Найдем (a-1) = ( (a))-1 = (e’)-1 = e’ a-1 H. 2) Покажем, что H G, т. е. a G a. H = Ha. Пусть ah a. H, покажем, что h 1 a Ha, такой, что ah=h 1 a. Рассмотрим aha-1 и найдем его образ: (aha-1) = (a) (h) (a-1) = (a) e (a-1) = (a a-1) = (e) = e’. Тогда aha-1 H или aha-1=h 1 ah=h 1 a.
Т 2. Любая нормальная подгруппа группы G является ядром некоторого гомоморфизма. Дано: H G Доказать: H – ядро некоторого гомоморфизма. Доказательство: G/H={H, g 1 H, g 2 H, …}. : G G/H g G (g) = g H. Покажем, что – гомоморфизм ( – сохраняет операцию). g 1, g 2 G (g 1 g 2) = (g 1 g 2) H = (g 1 g 2)H H = g 1 H g 2 H = (g 1) (g 2) – гомоморфизм. Покажем, что H = Ker . Пусть h H (h) = h H = H – нейтральный элемент G/H. Следовательно, h Ker и H Ker (1) Пусть h 1 Ker (h 1) = H или h 1 H = H h 1 H Ker H (2). Из (1) и (2) следует ч. т. д. Определение. Гомоморфизм группы G на факторгруппу G/H называется естественным гомоморфизмом группы G.
Т 3. Гомоморфный образ группы изоморфен факторгруппе по ядру этого гомоморфизма. Дано: : G 1 G 2; – гомоморфизм, H = Ker . Доказать: G 1/H G 2. Доказательство: Рассмотрим отображение : G 1/H G 2 такое, что g H G 1/H (g H) = (g); g G 1; (g) G 2. Покажем, что – изоморфизм. 1. Взаимная однозначность. Пусть g 1 H = g 2 H (g 2 -1 g 1)H = H g 2 -1 g 1 H, т. е. g 2 -1 g 1 Ker (g 2 -1 g 1) = e’ G 2. Т. к. – гомоморфизм, (g 2 -1) (g 1) = e’ или ( (g 2))-1 (g 1) = e’ (g 1) = (g 2) (g 1 H) = (g 2 H). Обратно, пусть (g 1 H) = (g 2 H), или (g 1) = (g 2), ( (g 2))-1 (g 1) = e’ G 2 (g 2 -1 g 1) = e’. Тогда g 2 -1 g 1 Ker = H или (g 2 -1 g 1)H = H g 1 H = g 2 H. 2. Сохранение операции. (g 1 H g 2 H) = ((g 1 g 2)H) = (g 1 g 2) = (g 1) (g 2) = (g 1 H) (g 2 H).
Изоморфизм групп — взаимно-однозначное соответствие между элементами двух групп, сохраняющее групповые операции.
Если существует изоморфизм между двумя группами, группы называются изоморфными. С точки зрения теории групп изоморфные группы имеют одни и те же свойства и их можно не различать.
Определение[править | править код]
Если заданы две группы (G, ∗) и (H, 
).
Изоморфизм групп из (G, ∗) в (H, ) — это биективный гомоморфизм групп из G в H.
Другими словами, изоморфизм групп — это биекция 
, такая, что для любых u и v из G выполняется
.
Замечания[править | править код]
- Часто используется более короткая и простая запись. Если групповые операции не приводят к двусмысленности, их опускают:
- (Иногда даже пишут просто G = H. Не приведёт ли такая запись к путанице и двусмысленности, зависит от контекста. Например, употребление знака равно не очень подходит в случае, когда две группы являются подгруппами одной и той же группы.)
- Если H = G и = ∗, биекция является автоморфизмом[⇨].
- Изоморфизм групп можно определить как двусторонний обратимый морфизм в категории групп.
Примеры[править | править код]
-
- посредством изоморфизма
- (смотрите экспонента).
-
- Изоморфизм задаётся выражением
- для любого x из .
- Обобщая, для всех нечётных n, группа Dih2n изоморфна прямому произведению Dihn и Z2.
Для некоторых групп можно доказать изоморфизм, исходя из аксиомы выбора, но такое доказательство не показывает, каким образом сконструировать конкретный изоморфизм. Примеры:
Циклические группы[править | править код]
Если (G, ∗) является бесконечной циклической группой, то (G, ∗) изоморфна целым числам (по сложению). С алгебраической точки зрения это означает, что множество всех целых чисел (по сложению) является единственной бесконечной циклической группой.
Все конечные циклические группы заданного порядка изоморфны 
.
Пусть G — циклическая группа и n — порядок группы G. G является группой, порождённой элементом 
.
Мы покажем, что
Определим
- , так что . Ясно, что биективно.
Таким образом,
- , что доказывает, что .
Свойства[править | править код]
- Ядро изоморфизма из (G, ∗) в (H, ) всегда равно {eG}, где eG — нейтральный элемент группы (G, ∗)
- Если (G, ∗) изоморфна (H,) и если G абелева, то H тоже абелева.
- Если f — изоморфизм между (G, *) и (H, ), тогда, если a принадлежит G и имеет порядок n, то такой же порядок имеет f(a).
Следствия[править | править код]
Из определения следует, что любой изоморфизм отображает нейтральный элемент G в нейтральный элемент H,
- ,
откуда следует, что обратные отображаются в обратные,
![f(u^{{-1}})=left[f(u)right]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1e1fbe22b073103c1a948972449f92413e0bb46)
и n-е степени в n-е степени,
![f(u^{n})=left[f(u)right]^{n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f48b11cde66496951fb09d74eddfef5a0626afba)
для всех u из G,
а также что обратное отображение 
тоже является изоморфизмом.
Отношение «изоморфно» удовлетворяет всем аксиомам отношения эквивалентности. Если f является изоморфизмом двух групп G и H, то все утверждения, верные для G, связанные со структурой группы, можно перенести посредством f на такие же утверждения в H, и наоборот.
Автоморфизмы[править | править код]
Изоморфизм из группы (G, ∗) в себя называется автоморфизмом этой группы. Так как изомофизм 
биективен,
- .
Автоморфизм всегда отображает нейтральный элемент в себя. Образ класса сопряжённости всегда является классом сопряжённости (тем же самым или другим). Образ элемента имеет тот же порядок, что и сам элемент.
Композиция двух автоморфизмов снова является автоморфизмом, и эта операция с множеством всех автоморфизмов группы G, обозначаемая Aut(G), образует группу, группу автоморфизмов G.
Для всех абелевых групп имеется, по меньшей мере, автоморфизм, переводящий элементы группы в их обратные. Однако в группах, где все элементы равны своим обратным, этот автоморфизм является тривиальным, например, в четверной группе Клейна (для этой группы все перестановки трёх, не являющихся нейтральными, элементов группы являются автоморфизмами, так что группа изоморфизмов изоморфна S3 и Dih3).
В Zp для простого числа p, один, не являющийся нейтральным, элемент может быть заменён другим, с соответствующими изменениями в других элементах. Группа автоморфизмов изоморфна Zp − 1. Например, для n = 7, умножение всех элементов Z7 на 3 (по модулю 7), является автоморфизмом порядка 6 в группе автоморфизмов, поскольку 36 ≡ 1 (по модулю 7), а меньшие степени 1 не дают. Таким образом, этот автоморфизм порождает Z6. Имеется ещё один автоморфизм с этим свойством — умножение всех элементов Z7 на 5 (по модулю 7). Таким образом, эти два автоморфизма соответствуют элементам 1 и 5 Z6, в этом порядке или обратном.
Группа автоморфизмов Z6 изоморфна Z2, поскольку только эти два элемента 1 и 5 порождают Z6.
Группа автоморфизмов Z2 × Z2 × Z2 = Dih2 × Z2 имеет порядок 168, что можно показать следующим образом. Все 7 элементов, не являющихся нейтральными, играют одну и ту же роль, так что мы можем выбрать, который играет роль (1,0,0). Любой из оставшихся шести может быть выбран для роли (0,1,0). Эти два определяют, что соответствует (1,1,0). (0,0,1) мы можем выбрать из четырёх, и этот выбор определяет оставшиеся элементы. Таким образом, получим 7 × 6 × 4 = 168 автоморфизмов. Они соответствуют автоморфизмам плоскости Фано, 7 точек которой соответствуют 7 элементам, не являющихся нейтральными. Прямые, соединяющие три точки, соответствуют операции группы: a, b, и c на прямой означают a + b = c, a + c = b, и b + c = a. См. также Полная линейная группа над конечным полем.
Для абелевых групп все автоморфизмы, за исключением тривиального, называются внешними автоморфизмами[en].
Неабелевы группы имеют нетривиальные внутренние автоморфизмы, и, возможно, внешние автоморфизмы.
Примечания[править | править код]
- ↑ Ash. A Consequence of the Axiom of Choice // Journal of the Australian Mathematical Society. — 1973. — Т. 19. — С. 306—308.
Ссылки[править | править код]
Herstein, I. N. Topics in Algebra. — 2 edition. — Wiley, 1975. — ISBN 0-471-01090-1..
|
0 / 0 / 0 Регистрация: 27.11.2019 Сообщений: 6 |
|
|
1 |
|
|
27.11.2019, 17:23. Показов 2111. Ответов 4
Специальные главы алгебры
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
27.11.2019, 17:23 |
|
4 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
28.11.2019, 12:38 |
2 |
|
все неизоморфные группы порядка 180 Их 37 штук. Может быть таки абелевы группы?
0 |
|
0 / 0 / 0 Регистрация: 27.11.2019 Сообщений: 6 |
|
|
28.11.2019, 13:35 [ТС] |
3 |
|
kabenyuk, я извиняюсь и вправду абелевы
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
28.11.2019, 13:44 |
4 |
|
Решение
абелевы А вот абелевых 4 штуки, так как 180=4*9*5, то полный список абелевых групп получается так:
2 |
Сообщение было отмечено Vincent VanGog как решение
|
0 / 0 / 0 Регистрация: 27.11.2019 Сообщений: 6 |
|
|
28.11.2019, 13:47 [ТС] |
5 |
|
kabenyuk, Спасибо большое, разобрался.
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
28.11.2019, 13:47 |
|
5 |
