Как найти неизвестное число матрицы

Как найти неизвестное число матрицы

Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях». 

Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано. 

Краткое содержание прошлых частей: 

  • Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности. 
  • Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел. 
  • Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше). 
  • Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
  • Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми. 
  • Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный. 

И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.

❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.

Что такое матричное уравнение

Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.

Что такое матричное уравнение

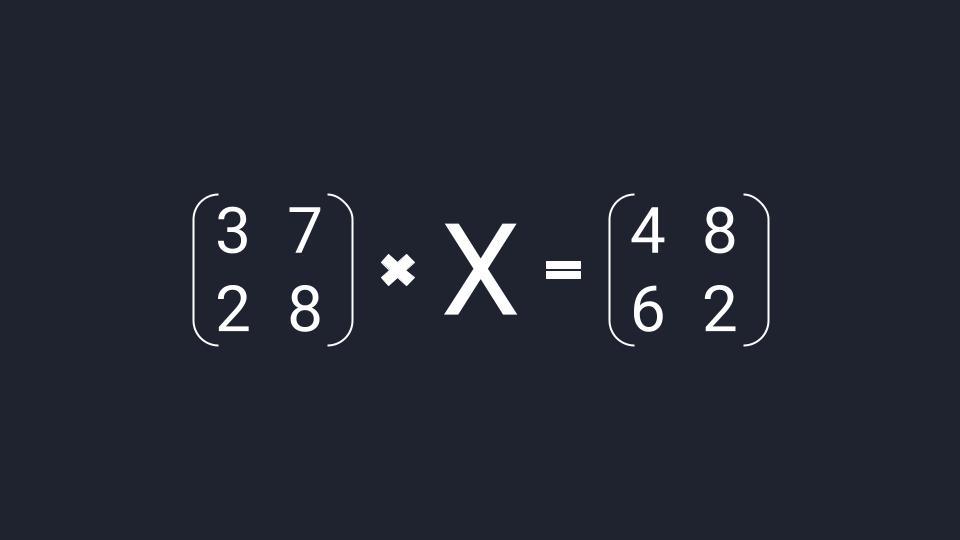
Шаг 1. Упрощаем уравнение 

Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.

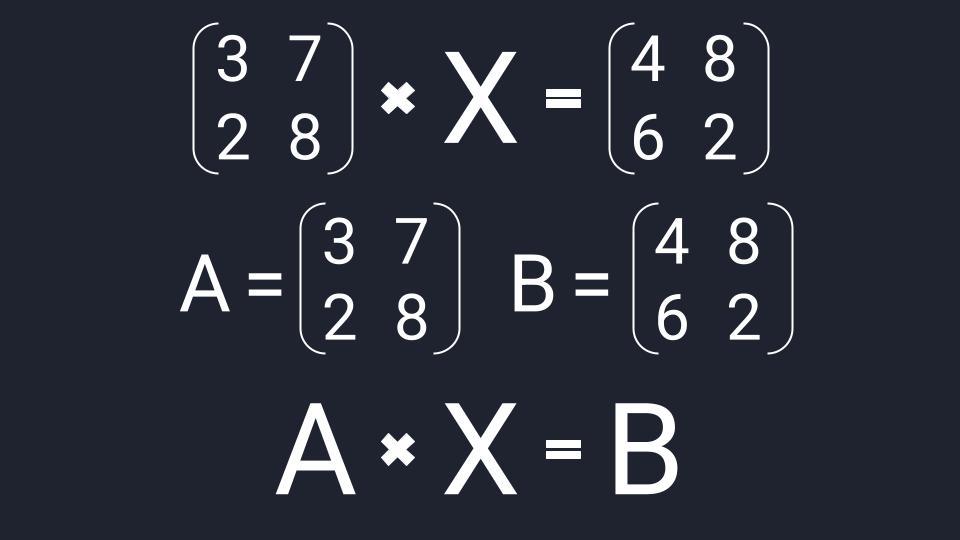
Приводим матричное уравнение к упрощённому виду

Приводим матричное уравнение к упрощённому виду

Шаг 2. Вводим единичную матрицу 

В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу. 

Можно представить, что есть число 100 — это «сто в первой степени», 1001

И есть число 0,01 — это «сто в минус первой степени», 100-1

При перемножении этих двух чисел получится единица:
1001 × 100-1 = 100 × 0,01 = 1. 

Вот такое, только в мире матриц. 

Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А-1. Неизвестную матрицу Х оставляем без изменений и переписываем уравнение: 

А-1 × А × Х = А-1 × В  

Добавляем единичную матрицу и упрощаем запись: 

А-1 × А = E — единичная матрица 

E × Х = А-1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем

Х = А-1 × В — новая запись уравнения 

После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B. 

💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A-1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто. 

Шаг 3. Находим обратную матрицу

Вспоминаем формулу и порядок расчёта обратной матрицы: 

  1. Делим единицу на определитель матрицы A. 
  2. Считаем транспонированную матрицу алгебраических дополнений. 
  3. Перемножаем значения и получаем нужную матрицу.

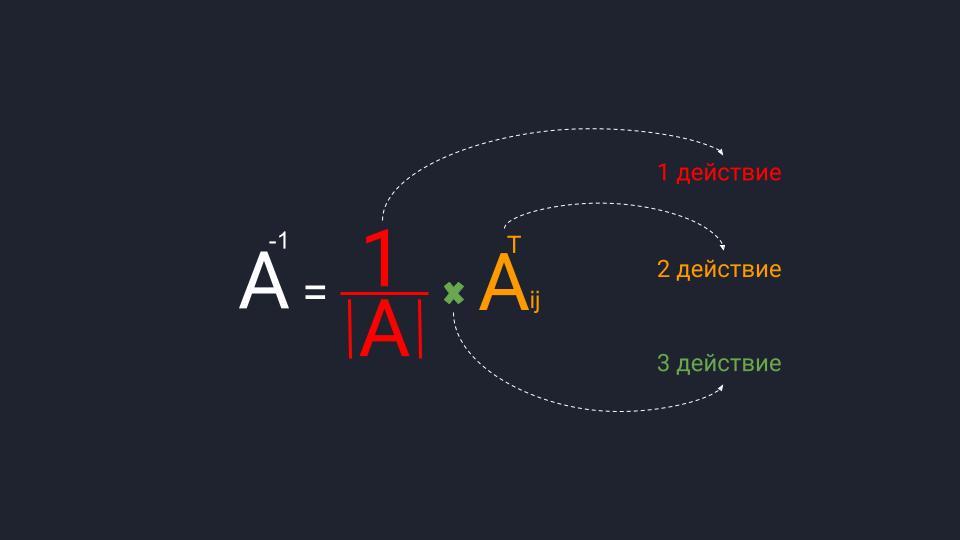
Формула вычисления обратной матрицы

Формула вычисления обратной матрицы
Решение матричных уравнений
Первое действие. Мы посчитали определитель и убедились, что он не равен нулю, — это значит, что у матричного уравнения есть вариант решения и можно продолжать
Решение матричных уравнений
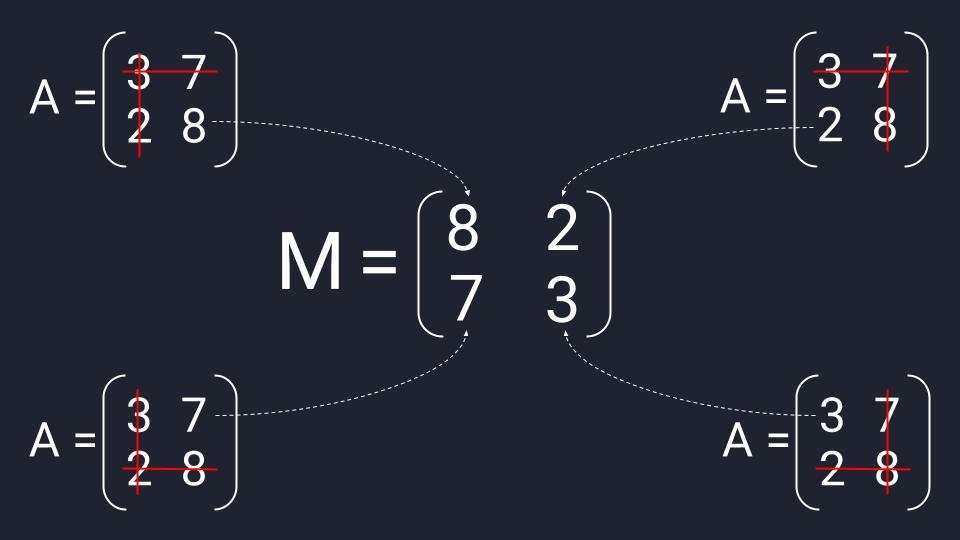
Второе действие, часть 1: получаем матрицу миноров
Решение матричных уравнений
Второе действие, часть 2: переводим матрицу миноров в транспонированную матрицу алгебраических дополнений

Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Решение матричных уравнений

Третье действие: получаем обратную матрицу

Шаг 4. Вычисляем неизвестную матрицу

Нам остаётся посчитать матрицу X: умножаем обратную матрицу А-1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Решение матричных уравнений

Решаем матричное уравнение и находим неизвестную матрицу X. Мы получили кратные числа и внесли дробь в матрицу

Шаг 5. Проверяем уравнение

Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново. 

👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Решение матричных уравнений

Проверяем ответ и получаем матрицу B — наши расчёты верны

Ну и что

Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:

Решение матричных уравнений

Этого котика не существует, а матрицы — существуют. 

Источник

Если вы перешли к изучению данной темы, то уже знаете, что такое матрица и определитель матрицы, умеете находить определители второго, третьего и высших порядков, а также обратные матрицы. Если какая-то из этих тем вам незнакома, то следует изучить сначала ее.

Приступим к рассмотрению понятия матричного уравнения.

Матричные уравнения

Матричные уравнения устроены практически также как и числовые, только вместо чисел в них содержатся числовые матрицы. Как правило, типовое матричное уравнение состоит из нескольких матриц и некоторой неизвестной матрицы XX, которую и требуется найти.

Рассмотрим примеры наиболее простых матричных уравнений и их решения.

Пример 1

Решить матричное уравнение

(1234)+x=(1101)begin{pmatrix}1&2\3&4end{pmatrix}+x=begin{pmatrix}1&1\0&1end{pmatrix}.

Перенесем матрицу из левой части в правую:

x=(1101)−(1234)x=begin{pmatrix}1&1\0&1end{pmatrix}-begin{pmatrix}1&2\3&4end{pmatrix}.

Найдем разность матриц в правой части уравнения:

x=(1−11−20−31−4)x=begin{pmatrix}1-1&1-2\0-3&1-4end{pmatrix}.

Значит, x=(0−1−3−3)x=begin{pmatrix}0&-1\-3&-3end{pmatrix}.

Можно провести проверку:

(1234)+(0−1−3−3)=(1+02−13−34−3)=(1101)begin{pmatrix}1&2\3&4end{pmatrix}+begin{pmatrix}0&-1\-3&-3end{pmatrix}=begin{pmatrix}1+0&2-1\3-3&4-3end{pmatrix}=begin{pmatrix}1&1\0&1end{pmatrix},

(1101)=(1101)begin{pmatrix}1&1\0&1end{pmatrix}=begin{pmatrix}1&1\0&1end{pmatrix}.

Пример 2

Решить матричное уравнение (58−469−5)−12x=(341212)begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-frac{1}{2}x=begin{pmatrix}3&4&1\2&1&2end{pmatrix}.

Перенесем матрицу из левой части в правую:

−12x=(341212)−(58−469−5)-frac{1}{2}x=begin{pmatrix}3&4&1\2&1&2end{pmatrix}-begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}.

Найдем разность матриц в правой части уравнения:

−12x=(3−54−81−(−4)2−61−92−(−5))-frac{1}{2}x=begin{pmatrix}3-5&4-8&1-(-4)\2-6&1-9&2-(-5)end{pmatrix},

−12x=(−2−45−4−87)-frac{1}{2}x=begin{pmatrix}-2&-4&5\-4&-8&7end{pmatrix}.

Умножим обе части уравнения на -2:

x=−2(−2−45−4−87)x=-2begin{pmatrix}-2&-4&5\-4&-8&7end{pmatrix},

x=(48−10816−14)x=begin{pmatrix}4&8&-10\8&16&-14end{pmatrix}.

Можно провести проверку:

(58−469−5)−12(48−10816−14)=(58−469−5)−(24−548−7)=(341212)begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-frac{1}{2}begin{pmatrix}4&8&-10\8&16&-14end{pmatrix}=begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-begin{pmatrix}2&4&-5\4&8&-7end{pmatrix}=begin{pmatrix}3&4&1\2&1&2end{pmatrix},

(341212)=(341212)begin{pmatrix}3&4&1\2&1&2end{pmatrix}=begin{pmatrix}3&4&1\2&1&2end{pmatrix}.

Такие уравнения элементарны, поэтому они довольно редко встречаются на практике.

Простейшие матричные уравнения

Обычно решение матричных уравнений сводится к одному из двух видов:

  1. A⋅X=BAcdot X=B;
  2. X⋅A=BXcdot A=B.

Рассмотрим, как решается каждое из этих уравнений.

Уравнение вида A⋅X=BAcdot X=B Уравнение вида X⋅A=BXcdot A=B
Для того чтобы разрешить данное уравнение относительно XX умножим обе его части на A−1A^{-1} слева: A−1⋅A⋅X=A−1⋅BA^{-1}cdot Acdot X=A^{-1}cdot B.

Так как A−1⋅A=EA^{-1}cdot A=E, то E⋅X=A−1⋅BEcdot X=A^{-1}cdot B, EE — единичная матрица.

Так как E⋅X=XEcdot X=X, то X=A−1⋅BX=A^{-1}cdot B.

 Для того чтобы разрешить данное уравнение относительно XX умножим обе его части на A−1A^{-1} справа: X⋅A⋅A−1=B⋅A−1Xcdot Acdot A^{-1}=Bcdot A^{-1}.

Так как A⋅A−1=EAcdot A^{-1}=E, то X⋅E=B⋅A−1Xcdot E=Bcdot A^{-1}, EE — единичная матрица.

Так как X⋅E=XXcdot E=X, то X=B⋅A−1X=Bcdot A^{-1}.

Рассмотрим примеры решения простейших матричных уравнений вида A⋅X=BAcdot X=B.

Пример 1

Решить матричное уравнение (3728)⋅X=(4862)begin{pmatrix}3&7\2&8end{pmatrix}cdot X=begin{pmatrix}4&8\6&2end{pmatrix}. Выполнить проверку.

Уравнение имеет вид A⋅X=BAcdot X=B, где A=(3728)A=begin{pmatrix}3&7\2&8end{pmatrix}, B=(4862)B=begin{pmatrix}4&8\6&2end{pmatrix}.

Умножим обе части уравнения на A−1A^{-1} слева:

A−1⋅A⋅X=A−1⋅BA^{-1}cdot Acdot X=A^{-1}cdot B,

E⋅X=A−1⋅BEcdot X=A^{-1}cdot B, EE — единичная матрица,

X=A−1⋅BX=A^{-1}cdot B.

Найдем матрицу A−1A^{-1}.

∣3728∣=3⋅8−2⋅7=24−14=10≠0begin{vmatrix}3&7\2&8end{vmatrix}=3cdot8-2cdot7=24-14=10neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.

Составим расширенную матрицу:

(3728∣1001)begin{pmatrix}left.begin{matrix}3&7\2&8end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.

Вычтем из строки №1 строку №2:

(3728∣1001)∼(1−128∣1−101)begin{pmatrix}left.begin{matrix}3&7\2&8end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-1\2&8end{matrix}right|begin{matrix}1&-1\0&1end{matrix}end{pmatrix}.

Прибавим к строке №2 строку №1, умноженную на -2:

(1−128∣1−101)∼(1−1010∣1−1−23)begin{pmatrix}left.begin{matrix}1&-1\2&8end{matrix}right|begin{matrix}1&-1\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-1\0&10end{matrix}right|begin{matrix}1&-1\-2&3end{matrix}end{pmatrix}.

Умножим строку №1 на 10:

(1−1010∣1−1−23)∼(10−10010∣10−10−23)begin{pmatrix}left.begin{matrix}1&-1\0&10end{matrix}right|begin{matrix}1&-1\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}10&-10\0&10end{matrix}right|begin{matrix}10&-10\-2&3end{matrix}end{pmatrix}.

Прибавим к строке №1 строку №2, умноженную на 1:

(10−10010∣10−10−23)∼(100010∣8−7−23)begin{pmatrix}left.begin{matrix}10&-10\0&10end{matrix}right|begin{matrix}10&-10\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}10&0\0&10end{matrix}right|begin{matrix}8&-7\-2&3end{matrix}end{pmatrix}.

Умножим строку №1 и №2 на 110frac{1}{10}:

(100010∣8−7−23)∼(1001∣810−710−210310)begin{pmatrix}left.begin{matrix}10&0\0&10end{matrix}right|begin{matrix}8&-7\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}frac{8}{10}&-frac{7}{10}\-frac{2}{10}&frac{3}{10}end{matrix}end{pmatrix}.

Значит, A−1=(810−710−210310)=110(8−7−23)A^{-1}=begin{pmatrix}frac{8}{10}&-frac{7}{10}\-frac{2}{10}&frac{3}{10}end{pmatrix}=frac{1}{10}begin{pmatrix}8&-7\-2&3end{pmatrix}.

A−1⋅B=110(8−7−23)⋅(4862)=110(−105010−10)=(−151−1)=XA^{-1}cdot B=frac{1}{10}begin{pmatrix}8&-7\-2&3end{pmatrix}cdotbegin{pmatrix}4&8\6&2end{pmatrix}=frac{1}{10}begin{pmatrix}-10&50\10&-10end{pmatrix}=begin{pmatrix}-1&5\1&-1end{pmatrix}=X.

Проверка:

(3728)⋅(−151−1)=(4862)begin{pmatrix}3&7\2&8end{pmatrix}cdotbegin{pmatrix}-1&5\1&-1end{pmatrix}=begin{pmatrix}4&8\6&2end{pmatrix}. — Верно.

Ответ: X=(−151−1)X=begin{pmatrix}-1&5\1&-1end{pmatrix}.

Пример 2

Решить матричное уравнение (0230)⋅X=(243−6)begin{pmatrix}0&2\3&0end{pmatrix}cdot X=begin{pmatrix}2&4\3&-6end{pmatrix}. Выполнить проверку.

Уравнение имеет вид A⋅X=BAcdot X=B, где A=(0230)A=begin{pmatrix}0&2\3&0end{pmatrix}, B=(243−6)B=begin{pmatrix}2&4\3&-6end{pmatrix}.

Умножим обе части уравнения на A−1A^{-1} слева:

A−1⋅A⋅X=A−1⋅BA^{-1}cdot Acdot X=A^{-1}cdot B,

E⋅X=A−1⋅BEcdot X=A^{-1}cdot B, EE — единичная матрица,

X=A−1⋅BX=A^{-1}cdot B.

Найдем матрицу A−1A^{-1}.

∣0230∣=0⋅0−3⋅2=0−6=−6≠0begin{vmatrix}0&2\3&0end{vmatrix}=0cdot0-3cdot2=0-6=-6neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.

Составим расширенную матрицу:

(0230∣1001)begin{pmatrix}left.begin{matrix}0&2\3&0end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.

Поменяем местами строки №1 и №2:

(0230∣1001)∼(3002∣0110)begin{pmatrix}left.begin{matrix}0&2\3&0end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}3&0\0&2end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}.

Умножим строку №1 на 13frac{1}{3}, а строку №2 на 12frac{1}{2}:

(3002∣0110)∼(1001∣013120)begin{pmatrix}left.begin{matrix}3&0\0&2end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}0&frac{1}{3}\frac{1}{2}&0end{matrix}end{pmatrix}.

Значит, A−1=(013120)=16(0230)A^{-1}=begin{pmatrix}0&frac{1}{3}\frac{1}{2}&0end{pmatrix}=frac{1}{6}begin{pmatrix}0&2\3&0end{pmatrix}.

A−1⋅B=16(0230)⋅(243−6)=16(6−12612)=(1−212)=XA^{-1}cdot B=frac{1}{6}begin{pmatrix}0&2\3&0end{pmatrix}cdot begin{pmatrix}2&4\3&-6end{pmatrix}=frac{1}{6}begin{pmatrix}6&-12\6&12end{pmatrix}=begin{pmatrix}1&-2\1&2end{pmatrix}=X.

Проверка:

(0230)⋅(1−212)=(243−6)begin{pmatrix}0&2\3&0end{pmatrix}cdotbegin{pmatrix}1&-2\1&2end{pmatrix}=begin{pmatrix}2&4\3&-6end{pmatrix}. — Верно.

Ответ: X=(1−212)X=begin{pmatrix}1&-2\1&2end{pmatrix}.

Рассмотрим примеры решения простейших матричных уравнений вида X⋅A=BXcdot A=B.

Пример 3

Решить матричное уравнение

X⋅(9711)=(201812)Xcdotbegin{pmatrix}9&7\1&1end{pmatrix}=begin{pmatrix}2&0\18&12end{pmatrix}. Выполнить проверку.

Уравнение имеет вид X⋅A=BXcdot A=B, где A=(9711)A=begin{pmatrix}9&7\1&1end{pmatrix}, B=(201812)B=begin{pmatrix}2&0\18&12end{pmatrix}.

Умножим обе части уравнения на A−1A^{-1} справа:

X⋅A⋅A−1=B⋅A−1Xcdot Acdot A^{-1}=Bcdot A^{-1},

X⋅E=B⋅A−1Xcdot E=Bcdot A^{-1}, EE — единичная матрица,

X=B⋅A−1X=Bcdot A^{-1}.

Найдем матрицу A−1A^{-1}.

∣9711∣=9⋅1−1⋅7=9−7=2≠0begin{vmatrix}9&7\1&1end{vmatrix}=9cdot1-1cdot7=9-7=2neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.

Составим расширенную матрицу:

(9711∣1001)begin{pmatrix}left.begin{matrix}9&7\1&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.

Поменяем строки №1 и №2 местами:

(9711∣1001)∼(1197∣0110)begin{pmatrix}left.begin{matrix}9&7\1&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\9&7end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}.

Прибавим к строке №2 строку №1, умноженную на -9:

(1197∣0110)∼(110−2∣011−9)begin{pmatrix}left.begin{matrix}1&1\9&7end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\0&-2end{matrix}right|begin{matrix}0&1\1&-9end{matrix}end{pmatrix}.

Умножим строку №2 на −12-frac{1}{2}:

(110−2∣011−9)∼(1101∣01−1292)begin{pmatrix}left.begin{matrix}1&1\0&-2end{matrix}right|begin{matrix}0&1\1&-9end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\0&1end{matrix}right|begin{matrix}0&1\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}.

Прибавим к строке №1 строку №2, умноженную на -1:

(1101∣01−1292)∼(1001∣12−72−1292)begin{pmatrix}left.begin{matrix}1&1\0&1end{matrix}right|begin{matrix}0&1\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}frac{1}{2}&-frac{7}{2}\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}.

Значит, A−1=(12−72−1292)=12(1−7−19)A^{-1}=begin{pmatrix}frac{1}{2}&-frac{7}{2}\-frac{1}{2}&frac{9}{2}end{pmatrix}=frac{1}{2}begin{pmatrix}1&-7\-1&9end{pmatrix}.

B⋅A−1=(201812)⋅12⋅(1−7−19)=12(201812)⋅(1−7−19)=12(2−146−18)=(1−73−9)=XBcdot A^{-1}=begin{pmatrix}2&0\18&12end{pmatrix}cdot frac{1}{2}cdot begin{pmatrix}1&-7\-1&9end{pmatrix}=frac{1}{2}begin{pmatrix}2&0\18&12end{pmatrix}cdotbegin{pmatrix}1&-7\-1&9end{pmatrix}=frac{1}{2}begin{pmatrix}2&-14\6&-18end{pmatrix}=begin{pmatrix}1&-7\3&-9end{pmatrix}=X.

Проверка: (1−73−9)⋅(9711)=(201812).begin{pmatrix}1&-7\3&-9end{pmatrix}cdotbegin{pmatrix}9&7\1&1end{pmatrix}=begin{pmatrix}2&0\18&12end{pmatrix}. — Верно.

Ответ: X=(1−73−9)X=begin{pmatrix}1&-7\3&-9end{pmatrix}.

Пример 4

Решить матричное уравнение X⋅(1325)=(4−132)Xcdotbegin{pmatrix}1&3\2&5end{pmatrix}=begin{pmatrix}4&-1\3&2end{pmatrix}. Выполнить проверку.

Уравнение имеет вид X⋅A=BXcdot A=B, где A=(1325)A=begin{pmatrix}1&3\2&5end{pmatrix}, B=(4−132)B=begin{pmatrix}4&-1\3&2end{pmatrix}.

Умножим обе части уравнения на A−1A^{-1} справа:

X⋅A⋅A−1=B⋅A−1Xcdot Acdot A^{-1}=Bcdot A^{-1},

X⋅E=B⋅A−1Xcdot E=Bcdot A^{-1}, EE — единичная матрица,

X=B⋅A−1X=Bcdot A^{-1}.

Найдем матрицу A−1A^{-1}.

∣1325∣=1⋅5−2⋅3=5−6=−1≠0begin{vmatrix}1&3\2&5end{vmatrix}=1cdot5-2cdot3=5-6=-1neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.

Составим расширенную матрицу:

(1325∣1001)begin{pmatrix}left.begin{matrix}1&3\2&5end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.

Прибавим к строке №2 строку №1, умноженную на -2:

(1325∣1001)∼(130−1∣10−21)begin{pmatrix}left.begin{matrix}1&3\2&5end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&3\0&-1end{matrix}right|begin{matrix}1&0\-2&1end{matrix}end{pmatrix}.

Прибавим к строке №1 строку №2, умноженную на 3:

(130−1∣10−21)∼(100−1∣−53−21)begin{pmatrix}left.begin{matrix}1&3\0&-1end{matrix}right|begin{matrix}1&0\-2&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&-1end{matrix}right|begin{matrix}-5&3\-2&1end{matrix}end{pmatrix}.

Умножим строку №2 на -1:

(100−1∣−53−21)∼(1001∣−532−1)begin{pmatrix}left.begin{matrix}1&0\0&-1end{matrix}right|begin{matrix}-5&3\-2&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}-5&3\2&-1end{matrix}end{pmatrix}.

Значит, A−1=(−532−1)A^{-1}=begin{pmatrix}-5&3\2&-1end{pmatrix}.

B⋅A−1=(4−132)⋅(−532−1)=(−2213−117)=XBcdot A^{-1}=begin{pmatrix}4&-1\3&2end{pmatrix}cdotbegin{pmatrix}-5&3\2&-1end{pmatrix}=begin{pmatrix}-22&13\-11&7end{pmatrix}=X.

Проверка:

(−2213−117)⋅(1325)=(4−132)begin{pmatrix}-22&13\-11&7end{pmatrix}cdotbegin{pmatrix}1&3\2&5end{pmatrix}=begin{pmatrix}4&-1\3&2end{pmatrix}. — Верно.

Ответ: X=(−2213−117).X=begin{pmatrix}-22&13\-11&7end{pmatrix}.

Существует третий вид матричных уравнений: A⋅X⋅B=CAcdot Xcdot B=C, но в действительности он встречается редко.

Обе части уравнения умножим на A−1A^{-1} слева: A−1⋅A⋅X⋅B=A−1⋅CA^{-1}cdot Acdot Xcdot B=A^{-1}cdot C.

Зная, что A−1⋅A=EA^{-1}cdot A=E, получим: E⋅X⋅B=A−1⋅CEcdot Xcdot B=A^{-1}cdot C.

Поскольку E⋅X=XEcdot X=X, то X⋅B=A−1⋅CXcdot B=A^{-1}cdot C.

Обе части уравнения умножим на B−1B^{-1} справа: X⋅B⋅B−1=A−1⋅C⋅B−1Xcdot Bcdot B^{-1}=A^{-1}cdot Ccdot B^{-1}.

Зная, что B⋅B−1=EBcdot B^{-1}=E, получим: X⋅E=A−1⋅C⋅B−1Xcdot E=A^{-1}cdot Ccdot B^{-1}.

Поскольку X⋅E=XXcdot E=X, то X=A−1⋅C⋅B−1X=A^{-1}cdot Ccdot B^{-1}.

Источник

Матрица – это своеобразный математический объект, который записывается в виде таблицы элементов. Обычно представлен прямоугольником или квадратом. Математический объект, который записывается в виде таблицы компонентов, состоящей из определенного количества строк и столбцов.

С соответствующими составляющими можно выполнять разные действия. Пример – решать уравнения. Именно об этом пойдет речь далее. Информация пригодится как математикам, так и сотрудникам IT-сферы.

Матричное уравнение – это…

Матричное уравнение – это уравнение, которое напоминает линейный (числовой) аналог. Но в качестве элементов в нем используются матрицы.

Типовое уравнение подобного характера включает себя ранее упомянутые математические объекты, а также некоторую неизвестную матрицу X. Именно ее и необходимо вычислить.

Что потребуется для обнаружения результата

Для того, чтобы найти значение неизвестного, которое содержит уравнение, каждый должен сначала тщательно изучить теорию. Без этого проводить необходимые манипуляции не получится.

Решить матричное уравнение можно, если заучена следующая теория:

  • понятие соответствующего объекта и его составляющих;
  • определитель матрицы;
  • ключевые операции над рассматриваемыми компонентами;
  • определение столбцов матрицы, главной диагонали;
  • что такое транспонированная матрица.

Также человек должен уметь решать линейные числовые уравнения. Без всего этого смысл изначально поставленной задачи теряется.

Сложение и вычитание

Для того, чтобы должным образом можно было решить пример, содержащий матричные компоненты, необходимо хорошо разбираться в элементарных операциях с ними. Первый вариант – сложение и вычитание.

Стоит запомнить – решать задачи по сложению удастся лишь матрицы одного и того же размера. Результатом станет математический объект аналогичного «объема».

Сам процесс вычислений достаточно прост – нужно сложить или вычесть соответствующие элементы в столбцах и строках.

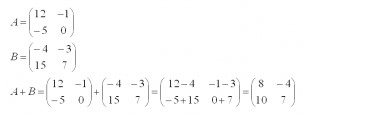
Выше – наглядный пример сложения. Вычитание производится аналогичным образом.

Умножение на число

Матрицы можно умножать на то или иное число. Такая манипуляция с легкостью производится любым математиком. Решение задачи напоминает линейные примеры.

Здесь необходимо запомнить следующие данные:

  • операции подобного плана возможны с матрицами любого размера;
  • для получения результата на необходимое число нужно умножить каждый элемент упомянутого мат объекта;
  • полученный результат – матричный компонент аналогичного размера.

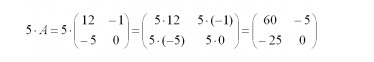
Выше – наглядный пример того, как осуществляется умножение на число 5.

Перемножение друг с другом

Умножение матриц между собой – манипуляция, которую можно осуществлять не всегда. Пример – даны мат объекты A и B. Их удастся перемножить, если количество столбцов матрицы a будет равно строкам матрицы b.

Каждый компонент, получившийся в ходе расчетов, стоящий в i-строке и j-столбце равен сумме произведений соответствующих элементов в i-строчке первого множителя и j-столбце второго.

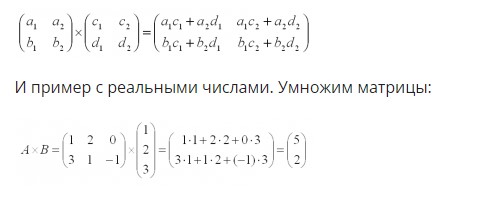
Данный шаблон и наглядный пример помогут найти грамотное решение при перемножении матричных объектов.

Транспонирование

Математика – наука, в которой формулы матриц и иных составляющих играют важную роль. Если не усвоена теория, решить поставленную задачу не получится. Для уравнений может потребоваться транспонированная ма трица.

При транспонировании строки и столбцы будут меняться местами. На письме такие компоненты обознаются как AT.

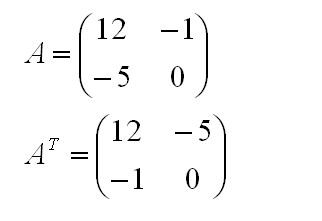
Это – наглядный пример того, как осуществляется соответствующая математическая операция.

Определитель

В случае с определителем необходимо уяснить следующие данные:

  • определитель – это детерминант;
  • представляет собой численную характеристику квадратной матрицы;
  • при помощи определителя удастся решить множество математических задач;
  • для нахождения соответствующего результата необходимо вычислить разность произведение составляющих главной и побочной диагоналей.

Определитель матрицы первого порядка (это – единичные матрицы) будет равен этому самому компоненту. Если речь идет об объекте размером 3×3, ситуация усложняется.

Для нее значение детерминанта будет равно сумме произведений компонентов главной диагонали и произведений составляющих на треугольниках с гранью параллельной главной. От последней нужно отнять произведение элементов побочной диагонали и произведение чисел, лежащих на треугольниках с гранью параллельной побочной диагонали.

На практике вычисление детерминантов больших размеров встречается редко. Некоторые, чтобы не запутаться, для решения поставленной задачи пользуются разнообразными онлайн калькуляторами. Их смысл – объяснение вычислительного процесса, а также выдача грамотных результатов.

Обратная матрица

Для каждого числа a, которое не равно нулю, существует обратное a-1. Оно будет таким, что произведение оных на выходе даст единицу. Формула записи проста: a*a-1=1. Это понятие подходит и для квадратных матриц.

Матрица A-1 будет обратной по отношению к матрице A, если при умножении оной на данную, как справа, так и слева, получится единичная матрица. К таковым относят математические объекты, включающие в себя всего один элемент (то есть, одну строку и столбец).

Не каждый квадратный матричный элемент имеет обратную матрицу. Если a не равно нулю – это достаточное и необходимое условие существования a-1, то для существования A-1 соответствующим требованием будет |A| не равен нулю.

Миноры и дополнения

Для полного понимания теории, связанной с матрицами и уравнениями, нужно разобраться с понятием алгебраических дополнений, а также минором:

  • Если в определителе n-го порядка происходит вычеркивание i-строки и k-столбца, на пересечении которых расположен объект aik, то полученный детерминант (n-1)-порядка будет обозначаться минором Mik.

  • Минор с определенным знаком, который находится в зависимости от четности суммы i+k номеров строчки и столбца, на пересечении которых расположен компонент aik, — это алгебраическое дополнение. Обозначается как Aik=(-1)i+kMik.
  • Когда в детерминанте порядка n все составляющие последней строчки (столбца), за исключением компонента, стоящего в правом нижнем углу, равняются нулю, то определитель – это произведение соответствующего элемента на минор.
  • Если у детерминанта все составляющие строчки/столбца за исключением одного равняются 0, то определитель – это произведение этого самого компонента на алгебраическое дополнение.

Наглядные примеры и доказательства перечисленных утверждений, раскрывающие их смысл, можно обнаружить по этой ссылке.

Уравнения и их решение

Теперь, когда уделено время произведению матрицы на число, а также иным элементарным операциям с рассматриваемыми объектами математики, можно приступать к непосредственному решению уравнений. Это не самый трудный процесс. Математика здесь находится примерно на школьном уровне.

Формула вычислений у матричных уравнений – точно такая же, как и простых алгебраических, в которых есть умножение. Здесь на помощь придет теория относительно обнаружения произведения матриц.

Пусть будут даны: A * X = B или X * A = B, где A и B – это известные матрицы, а X – неизвестная. Далее ситуация будет зависеть от конкретных обстоятельств:

  1. В первом случае, когда речь идет об уравнении A * X = B, обе части требуется умножить на обратную к A матрицу A-1 с левой стороны. Получится E * X = A-1 * B, где E – единичная матрица. Отсюда следует, что E * X = X. Результат вычислений – X = A-1 * B.
  2. Во втором случае, при уравнении X * A = B ситуация будет обстоять аналогичным образом. Но направление умножения на матрицу, обратную матрице A, меняется. Элемент B будет перемножаться с ней с правой стороны. Получится X * A * A-1 = B * A-1. Итог – X = B * A-1.
  3. Есть и третий случай – когда неизвестная матрица в уравнении расположена в середине произведения трех матриц: A * X * B = C. Здесь нужно известную матрицу из левой части умножить на обратную той, что стоит слева в заданном уравнении. И справа на матрицу, обратную той, что была с правой стороны. Итог будет следующим: X = A-1 * C * B-1.

Если же X в заданном примере – это обычное число, то формула обнаружения результата будет точно такой же, как и в линейных уравнениях.

Как лучше разобраться в теме

С формулой матрицы, а также ее основными компонентами теперь все понятно. И с основными операциями тоже удалось познакомиться. Отныне с легкостью найдем матрицу даже в уравнении при необходимости.

Для того, чтобы лучше вникнуть в соответствующую тему, стоит хорошенько изучить школьный курс математики, а также алгебру на 1 курсе обучения в ВУЗах. Информация пригодится как ученым, так и программистам.

Научиться коддить можно на специализированных дистанционных курсах. Они помогут быстро вникнуть в основы математики и информатики, а также создания приложений и игр. Курс рассчитан на срок до года. В процессе даже новичок, далекий от точных наук, сможет разобраться с матрицами и коддингом. А еще человек получит бесценную практику и новые полезные знакомства.

Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!

Также, возможно, вам будет интересен следующий курс:

Источник
    Виды матриц.

  • Матрица A размера m×n — это прямоугольная таблица чисел, расположенных в m строках и n столбцах
    Матрица
    где aij (i =1, …, m; j =1, …, n) — это элементы матрицы A. Первый индекс i — это номер строки, второй индекс j — это номер столбца, на пересечении которых расположен элемент aij.
    Сокращённое обозначение матрицы A=(aij)m×n.
  • Порядок матрицы — это число ее строк или столбцов.
  • Главная диагональ квадратной матрицы — это диагональ, идущая из левого верхнего в правый нижний угол.
  • Прямоугольная матрица — это матрица, у которой число строк не равно числу столбцов.
  • Квадратная матрица — это матрица у которой число строк равно числу столбцов:
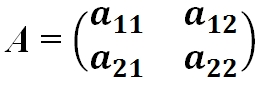
    Квадратная матрица 2х2
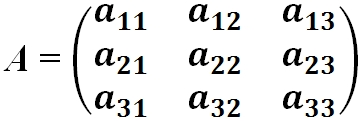
    Квадратная матрица 3х3
  • Матрица-столбец — это матрица, у которой всего один столбец:
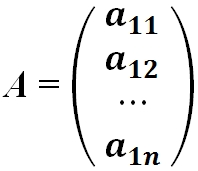
    Матрица-столбец
  • Матрица-строка — это матрица, у которой всего одна строка:
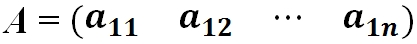
    Матрица-строка
  • Диагональная матрица — это квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю.
  • Единичная матрица — это диагональная матрица, у которой все диагональные элементы равны единице:
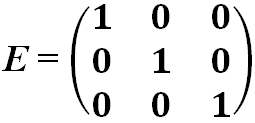
    Единичная матрица
  • Матрица квадратная диагональная:
    Матрица квадратная диагональная
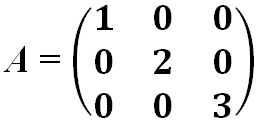
  • Треугольная матрица — это квадратная матрица, у которой все элементы, расположенные по одну сторону главной диагонали, равны нулю.
  • Матрица верхняя треугольная:Матрица верхняя треугольная
  • Матрица нижняя треугольная:
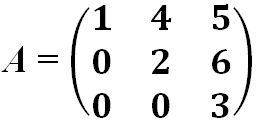
    Матрица нижняя треугольная
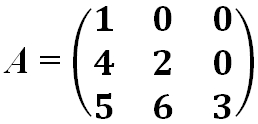
  • Нулевая матрица — это матрица, все элементы которой равны 0:
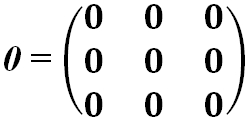
    Нулевая матрица
    Операции над матрицами.

  • Равенство матриц.
    Две матрицы A (aij), B (bij) совпадают |A=B|, если совпадают их размеры и соответствующие элементы равны,
    то есть при всех i, j aij=bij.
  • Сложение матриц.
    Суммой двух матриц A=(aij)m×n и B=(bij) m×n одинаковых размеров называется матрица C=(cij)m×n=A+B тех же размеров, элементы которой определяются равенствами cij=aij+bij. Пример 1.
  • Умножение матрицы на число.
    Произведением матрицы A=(aij)m×n на число λ ∈ R называется матрица B=(bij)m×n=λA, элементы которой определяются равенствами bij=λaij. Пример 2.
  • Умножение матриц.
    Произведением матрицы A=(aij)m×k на матрицу B=(bij)k×n называется матрица C=(cij)m×n=A· B размера m×n, элементы которой cij определяются равенством
    cij=ai1b1j+ai2b2j+ … aikbkj.
    Таким образом, элемент матрицы C=A·B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Пример 3.
  • Транспонированные матрицы.
    Транспонированием матрицы А называется замена строк этой матрицы ее столбцами с сохранением их номеров.
    Полученная матрица обозначается через A’ или AT. Пример 4.
    Квадратная матрица называется симметричной, если A=A’, то есть для элементов выполнены равенства aij=aji.
  • Обратная матрица.
    Квадратная матрица n–го порядка называется вырожденной, если определитель этой матрицы равен нулю, |A| = 0, и невырожденной, если |A| ≠ 0.
    Матрица А-1 называется обратной матрицей для некоторой квадратной матрицы А, если выполняется соотношение:
    A*A^{-1}=A^{-1}*A=E
    Если матрица А-1 не вырождена, то существует, и притом единственная, обратная матрица А-1, равная A^{-1}={1/{detA}}(A^V)^T, где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
    1) (A^{-1})^{-1}=A
    2) {alpha}*A^{-1}={1/{alpha}}*A^{-1}
    3) (A*B)^{-1}=B^{-1}*A^{-1}
    4) (A^{-1})^{T}=(A^{T})^{-1}
  • Алгоритм нахождения А-1 заключается в следующих пунктах:
    1) Находим det A, проверяем det A ≠ 0.
    2) Находим Mij — все миноры матрицы A.
    3) Определяем A_{ij}=(-1)^{i+j}M_{ij}
    4) Строим матрицу алгебраических дополнений A^{V}=(A_{ij}) и транспонируем: (A^{V})^T=(A_{ij})
    5) Делим каждый элемент матрицы на det A: A^{-1}={1/{det A}}(A^V)^T Пример 5.
  • Элементарные преобразования строк (столбцов) матрицы:
    1) перестановка строк (столбцов);
    2) умножение строки (столбца) на число α ≠ 0;
    3) прибавление к элементам строки (столбца) матрицы элементов другой строки (столбца), умноженных на некоторое число.
  • Решение матричных уравнений.
    Матричное уравнение — это уравнение, содержащее неизвестную матрицу X и известные матрицы A, B, …, .
    Простейшие типы матричных уравнений:
    1) A*X=B. Матрица A – квадратная и невырожденная,
    |A| ≠ 0, следовательно, существует обратная матрица A-1.
    Умножим уравнение на A-1 слева: A^{-1}*A*X=A^{-1}*B,~E*X=A^{-1}*B,~X=A^{-1}*B
    2) X*A=B. Матрица A – квадратная, |A| ≠ 0.
    Умножим уравнение на A-1 справа: X*A*A^{-1}=B*A^{-1} {doubleright} X=B*A^{-1}.
    3) A*X*B=C. Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
    Умножим уравнение на A-1 слева: A^{-1}*A*X*B=A^{-1}*C~{doubleright}~X*B=A^{-1}*C
    Умножим уравнение на B-1 справа: X*B*B^{-1}=A^{-1}*C*B^{-1}~{doubleright}~X=A^{-1}*C*B^{-1}.
  • Ранг матрицы.
    Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров.
    Mk этой матрицы: r=r(A)=rang A
    Матрицы называются эквивалентными, что обозначается
    A ∼ B, если r(A)=r(B).
    Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований.
  • Метод окаймляющих миноров.
    Пусть в матрице A элемент aij ≠ 0, тогда M1 ≠ 0 и r(A) ≥ 1. Окаймляем этот элемент элементами соседнего столбца и соседней строки (например, (j+1)–го столбца и (i+1)–й строки), получаем минор 2-го порядка: M_2 = delim{|}{matrix{2}{2}{{a_{i,j}} {a_{i,j+1}} {a_{i+1,j}} {a_{i+1,j+1}}} }{|}.
    Если M2, то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка.
    Если все миноры второго порядка равны нулю, то r(A) = 1; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то r(A) ≥ 1.
    Выбираем отличный от нуля минор 2-го порядка M2 и окаймляем его элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие: Mr ≠ 0, но все Mr+1 = 0. Пример 6.
  • Метод элементарных преобразований.
    Элементарные преобразования матрицы не меняют ее ранга.
    К элементарным преобразованиям матрицы относятся следующие: транспонирование; перестановка строк (столбцов); умножение строки (столбца) на число α ≠ 0; прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число; отбрасывание нулевой строки (столбца) матрицы.
    Для определения ранга матрицы A методом элементарных преобразований следует:
    1) Переставить строки и столбцы так, чтобы в верхнем левом углу матрицы был ненулевой элемент.
    2) Все элементы первого столбца, кроме a11, обратить в ноль с помощью элементарных преобразований строк:
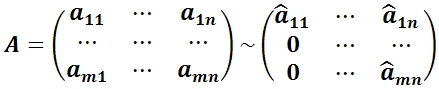
    Рисунок №14 Определение ранга матрицы
    3) Переставить строки со 2–й по m и столбцы со 2–го по n так, чтобы a22 ≠ 0. Повторить операцию (2) со вторым столбцом: во втором столбце все элементы, кроме a12 и a22, обратить в ноль.
    Окончательно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:
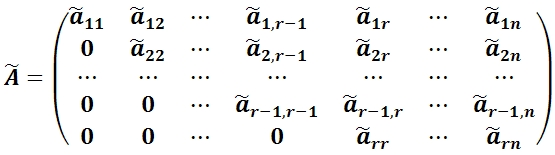
    Рисунок №15 Определение ранга мастера
    Тогда ранг матрицы A равен: rang A = rang Ã.
    Свойства определителей.

  1. Определитель квадратной матрицы А не меняется при транспонировании: |AT|=|A|.
  2. При перестановке местами любых двух строк (столбцов) определитель |A| меняет знак:
    delim{|}{matrix{3}{3}{{a_{11}} {a_{12}} {a_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}= - delim{|}{matrix{3}{3}{{a_{21}} {a_{22}} {a_{23}}{a_{11}} {a_{12}} {a_{13}} {a_{31}} {a_{32}} {a_{33}}} }{|}
  3. Определитель, содержащий две одинаковые строки (столбца), равен нулю.
  4. Умножение всех элементов некоторой строки (столбца) определителя |A| на число k равносильно умножению определителя на это число:
    delim{|}{matrix{3}{3}{{k*a_{11}} {k*a_{12}} {k*a_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|} = k*delim{|}{matrix{3}{3}{{a_{11}} {a_{12}} {a_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|},~k=const
  5. Если все элементы некоторой строки (столбца) определителя |A| равны нулю, то и сам определитель равен нулю (вытекает из предыдущего свойства при (k = 0):
    delim{|}{matrix{3}{3}{{a_{11}} {a_{12}} {a_{13}} {0} {0} {0} {a_{31}} {a_{32}} {a_{33}}} }{|} = 0
  6. Если все элементы двух строк (столбцов) определителя |A| пропорциональны, то определитель равен нулю.
  7. Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей:
    delim{|}{A}{|}=delim{|}{matrix{3}{3}{{{a{prime}}_{11}+{{a{{prime}{prime}}}_{11}}} {{a{prime}}_{12}+{{a{{prime}{prime}}}_{12}}} {{a{prime}}_{13}+{{a{{prime}{prime}}}_{13}}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}=
    {=}delim{|}{matrix{3}{3}{{{a{prime}}_{11}} {{a{prime}}_{12}} {{a{prime}}_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}+delim{|}{matrix{3}{3}{{{a{prime}{prime}}_{11}} {{a{prime}{prime}}_{12}} {{a{prime}{prime}}_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}
  8. Если к элементам какой-нибудь строки (столбца) определителя |A| прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится:
    delim{|}{matrix{3}{3}{{a_{11}+{k*a_{21}}} {a_{12}+{k*a_{22}}} {a_{13}+{k*a_{23}}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}=delim{|}{matrix{3}{3}{{a_{11}} {a_{12}} {a_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}
  9. Определитель |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения:
    delim{|}{A}{|}=delim{|}{matrix{3}{3}{{a_{11}} {a_{12}} {a_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|}={a_{i1}}{A_{i1}}+{a_{i2}}{A_{i2}}+{a_{i3}}{A_{i3}},~i=1,~2,~3
  10. Определитель произведения матриц А и В равен произведению их определителей:
    delim{|}{A*B}{|}=delim{|}{A}{|}*delim{|}{B}{|}.
    Определители n–го порядка.

  • Минор Мij или Δij элемента аij ( иначе – дополнительный минор элемента аij) определителя n-го порядка — это определитель (n–1) порядка, полученный из исходного вычеркиванием i–й строки и j–го столбца, на пересечении которых стоит элемент aij.
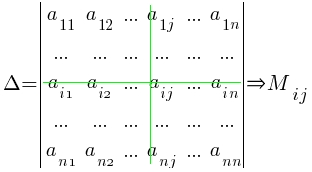
    Минор Мij элемента аij
  • Алгебраическое дополнение Аij элемента аij — это его минор со знаком (-1)i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент aij, Аij=(-1)i+jMij или Аij=(-1)i+jΔij. Пример 8.
    Для определителей n-го порядка имеют место все перечисленные выше свойства определителей.
  • Правило выбора знака перед минором в алгебраическом дополнении: delim{|}{matrix{3}{3}{{+} {-} {+} {-} {+} {-} {+} {-} {+}} }{|}
  • Определитель n-го порядка |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения.
  • Метод сведения к треугольному виду.
    Используя свойства (1–9), определитель преобразуют к виду, когда элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. Преобразованный таким образом определитель равен произведению элементов, лежащих на главной диагонали.

Формулы, уравнения, теоремы, примеры решения задач

Источник

Содержание материала

  1. Алгоритм решения матричных уравнений
  2. Видео
  3. AX = B, где матрица A обратима
  4. Решение матричного уравнения или системы линейных уравнений AX=B онлайн
  5. Вычисление псевдообратной матрицы онлайн
  6. Вычисляем неизвестную матрицу
  7. Вводим единичную матрицу
  8. Вычисление определителя матрицы онлайн
  9. Решение матричных уравнений: примеры
  10. Примеры решения задач

Алгоритм решения матричных уравнений

1. Матричное уравнение приводится к одному из простейших уравнений:

где — известные матрицы, — искомая ( или где — известные матрицы, — искомая (

где ЗАМЕЧАНИЕ Существует также уравнение вида — известные матрицы, ЗАМЕЧАНИЕ Существует также уравнение вида — искомая (неизвестная) матрица.

ЗАМЕЧАНИЕ

Существует также уравнение вида , но оно является комбинацией методов решения двух первых указанных простейших уравнений.

Чтобы привести произвольное матричное уравнение к одному из видов (1), надо все известные матрицы по свойствам уравнений перенести вправо, а неизвестную матрицу в левой части и свести подобные.

2. Разрешаем полученное простейшее уравнение относительно неизвестной матрицы 2.1 Если в результате преобразований получили прос.

2.1 Если в результате преобразований получили простейшее уравнение , то необходимо левую и правую часть этого равенства слева умножить на обратную матрицу к матрице :

ЗАМЕЧАНИЕ Поскольку умножение матриц неком

ЗАМЕЧАНИЕ

Поскольку умножение матриц некоммутативно, то нужно строго соблюдать умножение слева или справа, иначе это влияет на результат.

2.2 Для простейшего уравнения после умножения справа на обратную матрицу получаем:

ЗАМЕЧАНИЕ Обратная матрица находится либо

ЗАМЕЧАНИЕ

Обратная матрица находится либо методом союзной матрицы, либо методом присоединенной матрицы.

3. Далее вычисляется одно из произведений 4. Делаем проверку, для этого подставляем найденну или 4. Делаем проверку, для этого подставляем найденну, что и определяет искомую матрицу.

4. Делаем проверку, для этого подставляем найденную матрицу Видео в исходное уравнение.

Видео

AX = B, где матрица A обратима

Поскольку умножение матриц не всегда коммутативно, умножаем слева обе части уравнения на$ A^<-1>$.

$A^<-1>cdot|Acdot X = B$

$A^<-1>cdot Acdot X = A^<-1>cdot B$

$I_cdot X = A^<-1>cdot B$

Решение уравнения имеет общий вид $colorcdot B>$

Пример 50 Решить уравнение $egin 1 & 3 2 & 5 endcdot X egin 3 & 5 2 & 1 end$

Убедимся, что первая матрица обратима. $left|A ight|=5-6=-1 eq 0$, следовательно, матрица обратима.

Умножаем слева на обратную ей матрицу. $egin 1 & 3 2 & 5 end^<-1>cdot egin 1 & 3 2 & 5 endcdot X= egin 1 & 3 2 & 5 end^<-1>cdot egin 3 & 5 2 & 1 end$

$I_<2>cdot X = egin 1 & 3 2 & 5 end^<-1>cdot egin 3 & 5 2 & 1 end$

$egin 1 & 3 2 & 5 end^<-1>= egin -5 & 3 2 & -1 end ightarrow X= egin -5 & 3 2 & -1 endcdot egin 3 & 5 2 & 1 end= egin -9 & -22 4 & 9 end$

Решение матричного уравнения или системы линейных уравнений AX=B онлайн

Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.

Для решения матричного уравнения:

  1. Введите размерности матриц Введите элементы матриц. и Введите элементы матриц..
  2. Введите элементы матриц.
  3. Нажмите на кнопку “решение AX=B”.

Учтите, что матрицы и должны иметь равное количество строк .

Вычисление псевдообратной матрицы онлайн

Матричным онлайн калькулятором можно вычислить псевдообратную матрицу. Псевдообратная к данной матрице всегда существует.

Для вычисления псевдообратной матрицы:

  1. Выберите матрицу Введите размерность матрицы. или Введите размерность матрицы. с помощью радиокнопки Введите размерность матрицы..
  2. Введите размерность матрицы.
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “псевдообратное “.

Вычисляем неизвестную матрицу

Нам остаётся посчитать матрицу X: умножаем обратную матрицу А-1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Решаем матричное уравнение и находим неизвестную м

Решаем матричное уравнение и находим неизвестную матрицу X. Мы получили кратные числа и внесли дробь в матрицу

Вводим единичную матрицу

В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу. 

Можно представить, что есть число 100 — это «сто в первой степени», 1001

И есть число 0,01 — это «сто в минус первой степени», 100-1

При перемножении этих двух чисел получится единица:1001 × 100-1 = 100 × 0,01 = 1. 

Вот такое, только в мире матриц. 

Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А-1. Неизвестную матрицу Х оставляем без изменений и переписываем уравнение: 

А-1 × А × Х = А-1 × В  

Добавляем единичную матрицу и упрощаем запись: 

А-1 × А = E — единичная матрица 

E × Х = А-1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем

Х = А-1 × В — новая запись уравнения 

После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B. 

💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A-1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто. 

Вычисление определителя матрицы онлайн

Матричным онлайн калькулятором можно вычислить определитель матрицы. Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.

Для вычисления определителя матрицы:

  1. Выберите матрицу Введите размерность матрицы .или Введите размерность матрицы .с помощью радиокнопки .
  2. Введите размерность матрицы .
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “определитель “.

Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы. Теорию вычисления определителя матрицы смотрите здесь.

Решение матричных уравнений: примеры

Пример 1. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X = B , то.

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде B, то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :.

Найдём алгебраические дополнения матрицы A :

Примеры решения задач.

Примеры решения задач

ПРИМЕР 1

Задание Решить уравнение

Решение В левой части оставляем слагаемое с искомой матрицей , в правую часть переносим все известные матрицы и производим умножение матрицы на число 3 (для этого каждый элемент указанной матрицы умножаем на это число):

В правой части полученного уравнения выполняем вычитание матриц (от элементов первой матрицы отнимаем соответствующие элементы второй):

Для нахождения искомой матрицы делим левую и правую части последнего уравнения на (— 2):

Ответ

ПРИМЕР 2

Задание Решить матричное уравнение

Решение Заданное уравнение является простейшим матричным уравнением первого типа. Для нахождения неизвестной матрицы умножим его левую и правую части слева на обратную к матрице :

На данном этапе задача сводится к нахождению обратной матрицы. Ее найдем методом союзной матрицы:

где — определитель матрицы ; — союзная к матрица, то есть матрица, состоящая из алгебраических дополнений к ее элементам; — транспонирование матрицы, то есть операция, состоящая в том, что строки матрицы становятся ее столбцами с теми же номерами.

Для заданной матрицы имеем:

алгебраические дополнения:

Тогда

а обратная матрица

Таким образом, искомая матрица

Ответ

Теги

Источник

Добавить комментарий