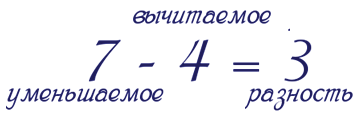Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
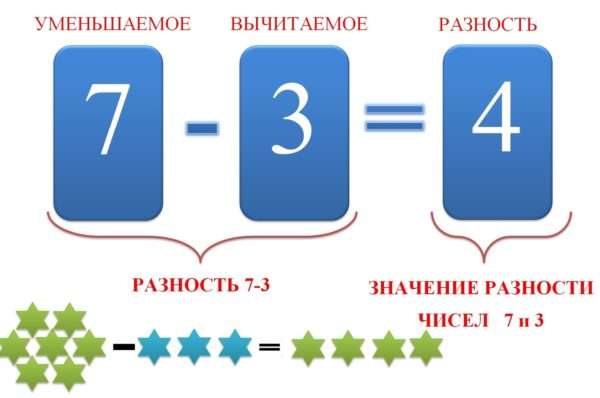
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
- разницу между двумя числами,
- это показатель того, насколько одно количество больше или меньше другого,
- это результат, полученный при выполнении вычитания такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | ||
| 18 | 11 | = | 7 | |
| 14 | 5 | = | 9 | |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Скачать материал

Скачать материал


- Сейчас обучается 26 человек из 13 регионов


- Сейчас обучается 141 человек из 50 регионов


- Сейчас обучается 143 человека из 49 регионов


Описание презентации по отдельным слайдам:
-
-
2 слайд
А что вы хотите узнать на уроке?
Что вы можете узнать?
Скажите, зачем вам эти знания? -
3 слайд
Я задумала число. Если к нему прибавить 3, то получится 84. Какое число было задумано? (81, 87, 80)
В каком числе 4 десятка и 7 единиц? (74, 17, 47)
Какое число меньше, чем 70, на 1? (69, 71, 59) -
4 слайд
Я задумала число. Если к нему прибавить 3, то получится 84. Какое число было задумано? (81, 87, 80)
В каком числе 4 десятка и 7 единиц? (74, 17, 47)
Какое число меньше, чем 70, на 1? (69, 71, 59) -
5 слайд
Я задумала число. Если к нему прибавить 3, то получится 84. Какое число было задумано? (81, 87, 80)
В каком числе 4 десятка и 7 единиц? (74, 17, 47)
Какое число меньше, чем 70, на 1? (69, 71, 59) -
6 слайд
Я задумала число. Если к нему прибавить 3, то получится 84. Какое число было задумано? (81, 87, 80)
В каком числе 4 десятка и 7 единиц? (74, 17, 47)
Какое число меньше, чем 70, на 1? (69, 71, 59) -
7 слайд
4.Найди сумму чисел 8 и 50. (42, 58, 85)
5. Найди разность чисел 94 и 4. (98, 90,54)
6. Найди число, в котором 5 десятков, а единиц на 2 меньше, чем десятков.(52, 35, 53) -
8 слайд
4.Найди сумму чисел 8 и 50. (42, 58, 85)
5. Найди разность чисел 94 и 4. (98, 90,54)
6. Найди число, в котором 5 десятков, а единиц на 2 меньше, чем десятков.(52, 35, 53) -
9 слайд
4.Найди сумму чисел 8 и 50. (42, 58, 85)
5. Найди разность чисел 94 и 4. (98, 90,54)
6. Найди число, в котором 5 десятков, а единиц на 2 меньше, чем десятков.(52, 35, 53) -
10 слайд
4.Найди сумму чисел 8 и 50. (42, 58, 85)
5. Найди разность чисел 94 и 4. (98, 90,54)
6. Найди число, в котором 5 десятков, а единиц на 2 меньше, чем десятков.(52, 35, 53) -
11 слайд
7. Какое число увеличили на 7, если получили 30? (23, 29, 27)
8. Какое число уменьшили на 9, если получили 21? (30, 12, 11)
9. Велосипедист проехал на двухколёсном велосипеде 14 км. Сколько километров проехало каждое колесо? (7 км, 28 км, 14 км) -
12 слайд
7. Какое число увеличили на 7, если получили 30? (23, 29, 27)
8. Какое число уменьшили на 9, если получили 21? (30, 12, 11)
9. Велосипедист проехал на двухколёсном велосипеде 14 км. Сколько километров проехало каждое колесо? (7 км, 28 км, 14 км) -
13 слайд
7. Какое число увеличили на 7, если получили 30? (23, 29, 27)
8. Какое число уменьшили на 9, если получили 21? (30, 12, 11)
9. Велосипедист проехал на двухколёсном велосипеде 14 км. Сколько километров проехало каждое колесо? (7 км, 28 км, 14 км) -
14 слайд
7. Какое число увеличили на 7, если получили 30? (23, 29, 27)
8. Какое число уменьшили на 9, если получили 21? (30, 12, 11)
9. Велосипедист проехал на двухколёсном велосипеде 14 км. Сколько километров проехало каждое колесо? (7 км, 28 км, 14 км) -
15 слайд
3*2+4*1=__
8+10*2*4 =__
4*2*6+2=__ -
16 слайд
3*2+4*1=10
8+10*2*4 =
4*2*6+2= -
17 слайд
3*2+4*1=10
8+10*2*4 =88
4*2*6+2= -
18 слайд
3*2+4*1=10
8+10*2*4 =88
4*2*6+2=50 -
-
-
-
-
-
-
25 слайд
Тема: как найти неизвестное вычитаемое.
Цель: -
26 слайд
Тема: как найти неизвестное вычитаемое.
Цель: научиться находить неизвестное вычитаемое и закрепить навыки по нахождению корня уравнения. -
27 слайд
19 марта.
Классная работа. -
28 слайд
Самостоятельная работа.
-
29 слайд
66-х=10
Х=56
31-х=20
Х=11
80-х=50
Х=30
25-х=15
Х=10
68-х=39
Х=29
74-х=60
Х=14
12-х=8
Х=4
34-х=3
Х=31
51-х=10
Х=41 -
30 слайд
Домашнее задание: рабочая тетрадь стр 36 №3
-
-
32 слайд
Спасибо за урок.
До свидания!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 261 211 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы






- 12.01.2021
- 126
- 0

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Содержание материала
- Предварительный просмотр:
- Видео
- Нахождение неизвестного множителя
- Поиск вычитаемого
- Правила нахождения уменьшаемого
- Свойства сложения
- Общие правила
- Другие методы
- Сложение в столбик многозначных чисел
Предварительный просмотр:
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Видео
Нахождение неизвестного множителя
Посмотрим на два уравнения: x·2=20 и 3·x=12. В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.
Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.
Данное правило базируется на смысле, который является обратным смыслу умножения. Между умножением и делением есть следующая связь: a·b=c при a и b, не равных , c: a=b, c: b=c и наоборот.
Вычислим неизвестный множитель в первом уравнении, разделив известное частное 20 на известный множитель 2. Проводим деление натуральных чисел и получаем 10. Запишем последовательность равенств:
x·2=20x=20:2x=10.
Подставляем десятку в исходное равенство и получаем, что 2·10=20. Значение неизвестного множителя было выполнено правильно.
Уточним, что в случае, если один из множителей нулевой, данное правило применять нельзя. Так, уравнение x·=11 с его помощью решить мы не можем. Эта запись не имеет смысла, поскольку для решения надо разделить 11 на , а деление на нуль не определено. Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.
Когда мы применяем это правило, мы, по сути, делим обе части уравнения на другой множитель, отличный от . Существует отдельное правило, согласно которому можно проводить такое деление, и оно не повлияет на корни уравнения, и то, о чем мы писали в этом пункте, с ним полностью согласовано.
Поиск вычитаемого
Нахождение вычитаемого — это такой же простой процесс, как и поиск уменьшаемого. Уравнение может иметь следующий вид: 7-x=3. Мы имеем разность — результат вычитания, и уменьшаемое число. Формулировка правила: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Так, если мы вычитаем из одного числа неизвестное число и получаем определённый результат (разность), значит, для поиска неизвестного вычитаемого вычтем из известного числа разность. В нашем примере x=7−3, результат равен 4. Для проверки вычтем 4 из 7, и получим 3 — решение верное. Ещё один вариант проверки — сложить 3 и 4. Так как сумма равна 7, решение правильное.
Правила нахождения уменьшаемого

При поиске уменьшаемого уравнение может выглядеть следующим образом: x-2=4. Мы имеем разность — результат вычитания и число, которое вычитаем. Необходимо найти уменьшаемое — самое большое число в примере. Формулировка правила: чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Так, если мы вычитаем из неизвестного числа другое число и получаем результат, известный нам, то для поиска уменьшаемого необходимо сложить разность и вычитаемое. Простейший пример: дома были конфеты. Их количество мы не знаем. После того как Дима съел 2 конфеты, их осталось 4. Вопрос: сколько их всего было изначально? Для того чтобы узнать, прибавим 2 к 4 и получим результат — было 6 конфет. Для проверки вычтем 2 из 6. Получим результат 4 — решение верное.
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
Общие правила
Для того чтобы гораздо быстрее решать элементарные уравнения, необходимо знать некоторые правила математики и логики. Здесь даже навыки арифметики не имеют такого решающего значения, как понимание того, что именно необходимо находить.
В случае с неизвестным слагаемым оно находится очень просто. От перестановки слагаемых сумма не меняется. То есть совершенно неважно, какой вид имеет уравнение x+2=6, или 2+x=6. В любом случае компонент x будет равен 4.

Дело в том, что уравнения с одним неизвестным предусмотрены школьной программой третьего класса. А ученики могут путаться и испытывать трудности в их решении, не зная этого правила.
Первое, с чего стоит начинать развитие навыка решения — это многократное повторение. Достаточно решать 5—10 уравнений в день с одним неизвестным компонентом, и уже через несколько дней ученик будет справляться с подобными заданиями гораздо быстрее. И только потом можно переходить к более сложным заданиям.

А также для улучшения понимания необходимо решать обратные уравнения. Что это значит? Вычитание — процесс, обратный сложению. То есть при сложении 3 и 4 сумма равна 7. А при вычитании 4 из 7 разность равна 3. В первом уравнении можно искать неизвестные слагаемые. При этом решать его с теми же числами, но на поиск уменьшаемого или вычитаемого.
Решение подобных уравнений точно не навредит ученику, это лишь ускорит процесс формирования навыка. При проверке и решении обратных уравнений в голове откладывается взаимосвязь между всеми компонентами примеров, а их решение практически доводит до автоматизма. Главное — постоянно тренировать этот навык.
Другие методы
Правило, которое позволяет быстро найти неизвестное слагаемое, довольно простое. Однако для того, чтобы облегчить его понимание, из него можно вывести правила, связанные с вычитанием.
Так, в примерах со сложением мы имеем два слагаемых и сумму: 3+5=8. Здесь 3 и 5 — слагаемые, а 8 — сумма. А в примерах с вычитанием мы имеем:
- Уменьшаемое.
- Вычитаемое.
- Разность.
Например, 7 — 4=3. В этом случае уменьшаемое — 7, вычитаемое — 3, а разность — 4. Уменьшаемое и вычитаемое также могут быть неизвестными. И крайне важно знать, как их вычислять.
Сложение в столбик многозначных чисел
Сложение в столбик – это способ нахождения суммы чисел путем их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим).
Итак, допустим, что нам нужно найти сумму : 5728+803
Теги
- Главная
- Справочники
- Справочник по математике для начальной школы
- Вычитание
Познакомимся с вычитанием.
Рассмотрим числовой ряд и вспомним, в каком порядке идут числа.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
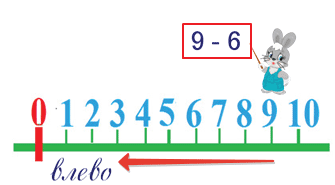
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Вычитает число 6.
Из какого числа он вычитает число 6?
Из числа 9. Мы поставили зайчика на число 9.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 6.
На каком делении он остановится? На числе 3.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
9 – 6 = 3
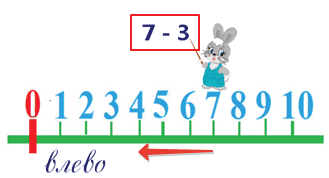
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Вычитает число 3.
Из какого числа он вычитает число 3?
Из числа 7. Мы поставили зайчика на число 7.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 3.
На каком делении он остановится? На числе 4.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
7 – 3 = 4
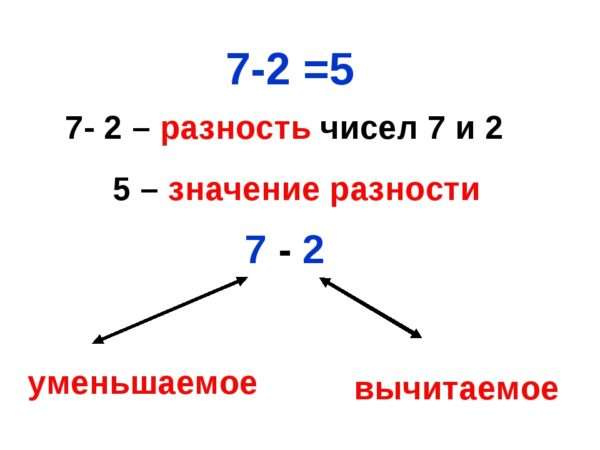
Как называются числа при вычитании?
Число, из которого вычитают, становится МЕНЬШЕ, уменьшается, поэтому его называют “уменьшаемое”.
Число, которое вычитают, называют “вычитаемое”.
Число, которое получается в результате вычитания, называют “разность”.
Рассмотри рисунок.
У жонглёра было 9 шариков.
Когда несколько шариков упало, осталось ещё 5 шариков.
Сколько шариков упало?
Каким действием будем находить? Вычитанием.
9 – 4 = 5
Как называются числа при вычитании?
9 – уменьшаемое
4 – вычитаемое
5 – разность
Как найти неизвестное вычитаемое
Рассмотри рисунок.
У жонглера было 9 шариков. Когда несколько шариков упало, осталось 5. Упали, значит, убрали.
Решаем вычитанием. Что нужно найти?
Нужно найти вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
9 – 5 = 4
Вычитаемое равно 4.
Упало 4 шарика.
Как найти неизвестное уменьшаемое
Что известно?
Вычитаемое – 4.
Разность – 5.
Нужно найти уменьшаемое.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
5 + 4 = 9
Проверка вычитания
Если к разности прибавить вычитаемое, получится уменьшаемое.
Именно эта связь между разностью, уменьшаемым и вычитаемым используют для проверки вычитания.
Например, 35 – 15 = 20.
Правильно ли произведено вычисление? Можно проверить так:
20 + 15 = 35, мы к разности прибавили вычитаемое и получили уменьшаемое. Значит, вычисление произведено верно и пример решен правильно.
Советуем посмотреть:
Табличное вычитание
Письменное вычитание в столбик
Правило встречается в следующих упражнениях:
1 класс
Страница 53,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 56,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 95,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 4,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 5,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 12,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 17,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 28. Урок 17,
Петерсон, Учебник, часть 1
Страница 35. Урок 23,
Петерсон, Учебник, часть 1
Страница 7. Урок 4,
Петерсон, Учебник, часть 2
2 класс
Страница 12,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 34. ПР 4. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 10,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 11,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 18,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 29. Урок 15,
Петерсон, Учебник, часть 1
Страница 33. Урок 17,
Петерсон, Учебник, часть 1
3 класс
Страница 22,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 38,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 39,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 46,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 105,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 11,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 103. Урок 39,
Петерсон, Учебник, часть 1
Страница 42. Урок 16,
Петерсон, Учебник, часть 2
4 класс
Страница 24,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 63,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 25,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 8. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 82. Тест 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
В последнее время Интернет просто ломится от желающих поделиться секретами простого обучения школьников любого возраста. Больше достаётся малышам. Один советует не учить таблицу умножения, а выполнять умножение многозначных чисел диковинным японским способом — при помощи подсчёта точек пересечения прямых.
При этом советующий не думает о последствиях, ведь надо будет учить не только умножению, но и делению, где используется умножение, а также действиям с обыкновенными и десятичными дробями.
https://zen.yandex.ru/media/shevkin/tablica-umnojeniia-bolshe-ne-nujna-5f8dee7cb5e4d5370eefe9f6
Второй предлагает складывать и вычитать обыкновенные дроби по правилу «бабочки».
И при этом не задумывается о громоздкости вычислений даже в простом примере: 5/36 + 7/72.
https://zen.yandex.ru/media/tehno_chtivo/genialnyi-metod-slojeniia-drobei-i-ego-podvodnye-kamni-5f5f94295622142b93db0f92
Разумеется, я прокомментировал и это предложение. Критикуя, предложил, как надо учить сложению и вычитанию дробей самым традиционным способом — без лайфхаков, вызывающих у читателей этих лайфхаков оглушительные восторги.
https://zen.yandex.ru/media/shevkin/sovet-protiv-laifhaka-5f5a36b98279b40946603e1a
Про ролик, прославивший молодого учителя миллионными просмотрами, написала МК (10.09.2020) и блогер, указавший на “подводные камни” метода на примере 4/6 + 2/12 = 60/72. Блогер решил задачу проще: 4/6 + 2/12 = 10/12, но не заметил ещё более простого решения: 4/6 + 2/12 = 4/6 + 1/6 = 5/6.
Хорошо, что у него были внимательные читатели. Вот и решайте, чему надо учить: тупо применять единственный алгоритм, показанный учителем, или учить анализировать ситуацию и поступать по ситуации.
На днях я прочитал на Дзене предложение некоей KUMONo-мамы об упрощении запоминания правил нахождения уменьшаемого и вычитаемого. Вот начало статьи Как находить уменьшаемое и вычитаемое — Простая техника запоминания для малышей.
«Ваши первоклашки уравнения уже решают по Петерсон? Ну второклашки-то уж точно!
Малыши, не знакомые с отрицательными числами, решают уравнения, запоминая адские правила про «сложить разность и вычитаемое».
Ага, осталось только запомнить, что из них что…
Я, кстати, в школе была отличницей и прекрасно знала математику… и до сих пор помню, как чудовищно сложно (и, главное, в 1-2 классе непонятно, ради чего) было запомнить эти слова: вычитаемое, уменьшаемое…»
https://zen.yandex.ru/media/kumon/kak-nahodit-umenshaemoe-i-vychitaemoe-prostaia-tehnika-zapominaniia-dlia-malyshei-5f85864fa144c35a271d1920
Итак, мама видит проблему в том, что ребёнку, не знающему отрицательных чисел, трудно запомнить термины «уменьшаемое» и «вычитаемое». Она старается помочь, называя уменьшаемое, вычитаемое и разность одинаково — «числа».
Неужели так сложно донести до ребёнка, наученного вычитать, что при вычитании первое число уменьшается, его называют уменьшаемое? Это надо делать обязательно, так как развитие понятийного мышления, если хотите, научного мышления, предполагает использования терминов для обозначения изучаемых объектов. Станет ли ребёнку легче учиться, если мы избавим его от заучивания двух терминов из десяти, используемых для обозначения компонентов арифметических действий? Ребёнок и дальше будет обходиться без терминологии и называть словом «числа» каждое из чисел в следующих равенствах?
4 + 3 = 7
6 – 1 = 5
3 ∙ 2 = 6
8 : 4 = 2
Без терминов, которыми советчица пользуется, ребёнку станет легче выражать свои мысли и описывать свои действия? Чем же именно? Или термины знать всё-таки надо, но трудно запомнить, какое действие надо выполнить при поиске неизвестного компонента?
Раскрою секрет: обсуждаемые здесь термины гораздо важнее для развития речи и мышления школьника, чем для изучения математики, так как в старших классах эти правила уже не используются. Там говорят о переносе слагаемого в другую часть уравнения с противоположным знаком, о прибавлении к двум частям уравнения одного и того же числа, об умножении (делении) обеих частей уравнения на одно и то же число. Очевидно, что с этого нельзя начинать в начальной школе. А вот приучать малыша использовать речевые «шаблоны»: «чтобы найти… надо…» полезно именно для развития речи и мышления обучаемого.
В чём суть предложения KUMONo-мамы? Она записывает на листке уравнение х – 6 = 22 «на нахождение уменьшаемого», далее пишет: «Скажите ребенку, что числа стоят рядышком — так просто представить, что они ВМЕСТЕ, так и просят сложиться, чтобы стать ещё поближе друг к другу».
Интересный аргумент! А в уравнении x ∙ 2 = 6 числа 2 и 6 стоят так же близко. Они тоже будут просить сложиться? Ведь основание для выбора действия (они близко) одно и то же. А вот и рисунок, советующий ребёнку действие, а под ним умилительная запись с использованием тех самых терминов, которые детям трудно запомнить.
Что из этого поймёт ребёнок ещё вопрос, и поймёт ли?
Ещё изобретательнее KUMONo-мама объясняет нахождение вычитаемого. Она пишет на листке уравнение 12 – x = 7 «на нахождение вычитаемого». Далее пишет: «Предложите ребенку представить, что минус пытается выыыытянуться и дотянуться до ближайшего числа:
Теперь можно вычесть и получить вычитаемое.
Осталось только запомнить, как искать слагаемые. Если знаете такие же техники про них — обязательно напишите в комментариях».
Наша советчица ещё не придумала, как объяснять поиск неизвестного слагаемого. А там ещё неизвестные множители, делимое и делитель…
Но ещё больше, чем советы блогерши, меня огорчили «лайки» и восторги читателей.
Я оставил краткий комментарий: «Прекрасные примеры того, как не надо учить детей. Пытаясь придумать про “рядышком” и “выыыытянуть” автор хочет дать детям какой-то рецепт, никак не связанный с математикой. Не проще ли показывать связь операций на очевидных примерах?
1 + 2 = 3.
Накроем пальцем (монеткой…) первое слагаемое:
x + 2 = 3.
Каким действием можно найти спрятанное слагаемое?
И вопреки мнению автора, надо формулировать: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Также со вторым слагаемым, уменьшаемым,… всего шесть правил. Это и развитие речи, и развитие наблюдательности, умения замечать закономерности».
Развиваю мысль. В начале 80-х годов прошлого века я недолго увлекался идеей использования опорных конспектов (В.Ф. Шаталов). В 5 классе у меня был такой опорный конспект, возникавший в процессе работы с классом.
Глядя на него, ребята лучше запоминали упомянутые выше термины (первая буква термина стоит над числом), а также действия, с помощью которых находится неизвестная компонента (знак действия под числом). Ребята на отметку сдавали мне зачёт — формулировали каждое правило и приводили пример на его применение, я уточнял: а как называется это число, а это? Первые сдавшие зачёт увлечённо и строго экзаменовали одноклассников…
Может быть, и в начальной школе стоит попробовать применить этот опорный конспект? Только надо двигаться постепенно. Изучили сложение и вычитание — учим правила нахождения неизвестных слагаемого, уменьшаемого и вычитаемого.
Вместо заключения. Говорят, что лечить и учить умеет каждый. Не знаю, как насчёт лечить, но желающих учить — хоть отбавляй. Это явление, к сожалению, подстёгивают наши «учёные», твердящие из каждого утюга: «учитель утратил монополию на знание». Ну и чего хорошего мы дождёмся от этой утраты? От появления новых непрофессиональных желающих “сеять разумное, доброе, вечное”? Чему радуемся? Много ли пользы получим от непрофессионалов?