Как найти неизвестное значение в excel

«Подбор параметра» – ограниченный по функционалу вариант надстройки «Поиск решения». Это часть блока задач инструмента «Анализ «Что-Если»».

В упрощенном виде его назначение можно сформулировать так: найти значения, которые нужно ввести в одиночную формулу, чтобы получить желаемый (известный) результат.

Где находится «Подбор параметра» в Excel

Известен результат некой формулы. Имеются также входные данные. Кроме одного. Неизвестное входное значение мы и будем искать. Рассмотрим функцию «Подбора параметров» в Excel на примере.

Необходимо подобрать процентную ставку по займу, если известна сумма и срок. Заполняем таблицу входными данными.

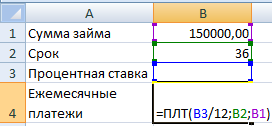
Процентная ставка неизвестна, поэтому ячейка пустая. Для расчета ежемесячных платежей используем функцию ПЛТ.

Когда условия задачи записаны, переходим на вкладку «Данные». «Работа с данными» – «Анализ «Что-Если»» – «Подбор параметра».

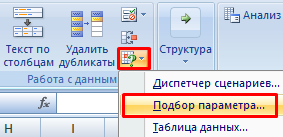
В поле «Установить в ячейке» задаем ссылку на ячейку с расчетной формулой (B4). Поле «Значение» предназначено для введения желаемого результата формулы. В нашем примере это сумма ежемесячных платежей. Допустим, -5 000 (чтобы формула работала правильно, ставим знак «минус», ведь эти деньги будут отдаваться). В поле «Изменяя значение ячейки» – абсолютная ссылка на ячейку с искомым параметром ($B$3).

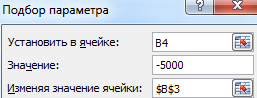
После нажатия ОК на экране появится окно результата.

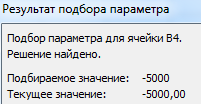
Чтобы сохранить, нажимаем ОК или ВВОД.

Функция «Подбор параметра» изменяет значение в ячейке В3 до тех пор, пока не получит заданный пользователем результат формулы, записанной в ячейке В4. Команда выдает только одно решение задачи.



Решение уравнений методом «Подбора параметров» в Excel

Функция «Подбор параметра» идеально подходит для решения уравнений с одним неизвестным. Возьмем для примера выражение: 20 * х – 20 / х = 25. Аргумент х – искомый параметр. Пусть функция поможет решить уравнение подбором параметра и отобразит найденное значение в ячейке Е2.

В ячейку Е3 введем формулу: = 20 * Е2 – 20 / Е2.

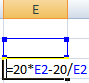
А в ячейку Е2 поставим любое число, которое находится в области определения функции. Пусть это будет 2.

Запускам инструмент и заполняем поля:

«Установить в ячейке» – Е3 (ячейка с формулой);

«Значение» – 25 (результат уравнения);

«Изменяя значение ячейки» – $Е$2 (ячейка, назначенная для аргумента х).

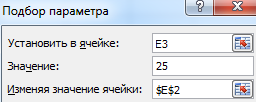
Результат функции:

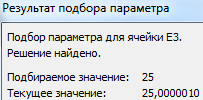
Найденный аргумент отобразится в зарезервированной для него ячейке.

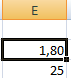
Решение уравнения: х = 1,80.

Функция «Подбор параметра» возвращает в качестве результата поиска первое найденное значение. Вне зависимости от того, сколько уравнение имеет решений.

Если, например, в ячейку Е2 мы поставим начальное число -2, то решение будет иным.

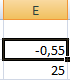
Примеры подбора параметра в Excel

Функция «Подбор параметра» в Excel применяется тогда, когда известен результат формулы, но начальный параметр для получения результата неизвестен. Чтобы не подбирать входные значения, используется встроенная команда.

Пример 1. Метод подбора начальной суммы инвестиций (вклада).

Известные параметры:

• срок – 10 лет;
• доходность – 10%;
• коэффициент наращения – расчетная величина;
• сумма выплат в конце срока – желаемая цифра (500 000 рублей).

Внесем входные данные в таблицу:

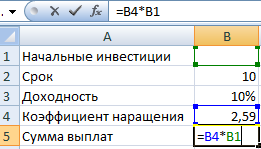
Начальные инвестиции – искомая величина. В ячейке В4 (коэффициент наращения) – формула =(1+B3)^B2.

Вызываем окно команды «Подбор параметра». Заполняем поля:

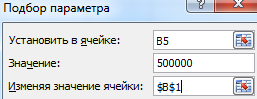
После выполнения команды Excel выдает результат:

Чтобы через 10 лет получить 500 000 рублей при 10% годовых, требуется внести 192 772 рубля.

Пример 2. Рассчитаем возможную прибавку к пенсии по старости за счет участия в государственной программе софинансирования.

Входные данные:

• ежемесячные отчисления – 1000 руб.;
• период уплаты дополнительных страховых взносов – расчетная величина (пенсионный возраст (в примере – для мужчины) минус возраст участника программы на момент вступления);
• пенсионные накопления – расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза);
• ожидаемый период выплаты трудовой пенсии – 228 мес.;
• желаемая прибавка к пенсии – 2000 руб.

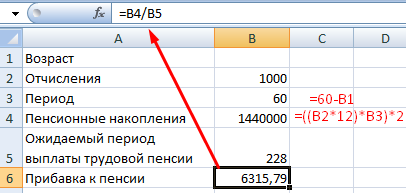
С какого возраста необходимо уплачивать по 1000 рублей в качестве дополнительных страховых взносов, чтобы получить прибавку к пенсии в 2000 рублей:

1. Ячейка с формулой расчета прибавки к пенсии активна – вызываем команду «Подбор параметра». Заполняем поля в открывшемся меню.



2. Нажимаем ОК – получаем результат подбора.

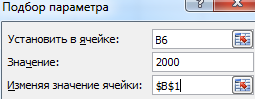
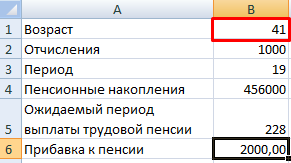
Чтобы получить прибавку в 2000 руб., необходимо ежемесячно переводить на накопительную часть пенсии по 1000 рублей с 41 года.

Функция «Подбор параметра» работает правильно, если:

• значение желаемого результата выражено формулой;
• все формулы написаны полностью и без ошибок.

Предположим, что вы хотите найти расширение телефона сотрудника, используя его номер эмблемы или правильную ставку комиссионных за объем продаж. Вы можете искать данные для быстрого и эффективного поиска определенных данных в списке, а также для автоматической проверки правильности данных. После поиска данных можно выполнить вычисления или отобразить результаты с возвращаемой величиной. Существует несколько способов поиска значений в списке данных и отображения результатов.

Что необходимо сделать

• Точное совпадение значений по вертикали в списке

• Подыыывка значений по вертикали в списке с помощью приблизительного совпадения

• Подстановка значений по вертикали в списке неизвестного размера с использованием точного совпадения

• Точное совпадение значений по горизонтали в списке

• Подыыывка значений по горизонтали в списке с использованием приблизительного совпадения

• Создание формулы подступа с помощью мастера подметок (только в Excel 2007)

Точное совпадение значений по вертикали в списке

Для этого можно использовать функцию ВLOOKUP или сочетание функций ИНДЕКС и НАЙТИПОЗ.

Примеры ВРОТ

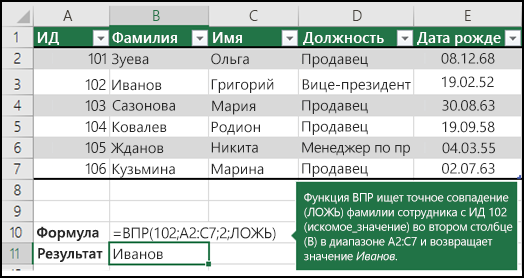
Дополнительные сведения см. в этой информации.

Примеры индексов и совпадений

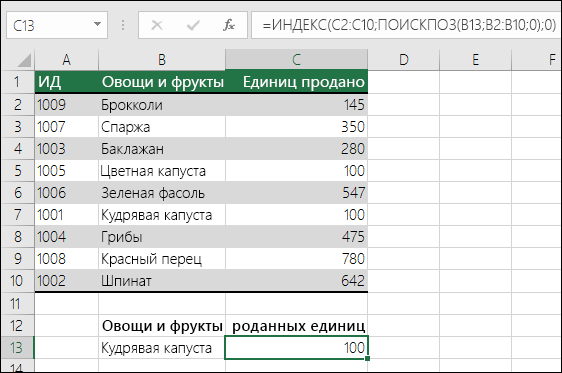
Что означает:

=ИНДЕКС(нужно вернуть значение из C2:C10, которое будет соответствовать ПОИСКПОЗ(первое значение “Капуста” в массиве B2:B10))

Формула ищет в C2:C10 первое значение, соответствующее значению “Ольга” (в B7), и возвращает значение в C7(100),которое является первым значением, которое соответствует значению “Ольга”.

Дополнительные сведения см. в функциях ИНДЕКС иФУНКЦИЯ MATCH.

К началу страницы

Подыыывка значений по вертикали в списке с помощью приблизительного совпадения

Для этого используйте функцию ВЛВП.

Важно:  Убедитесь, что значения в первой строке отсортировали в порядке возрастания.

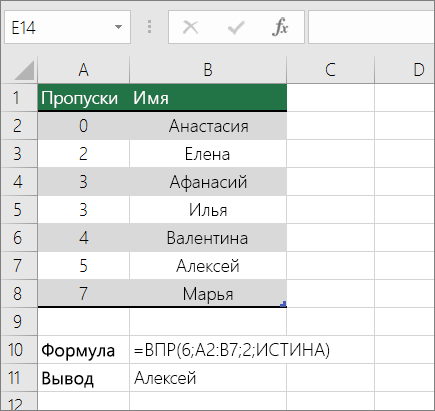
В примере выше ВРОТ ищет имя учащегося, у которого 6 просмотров в диапазоне A2:B7. В таблице нет записи для 6 просмотров, поэтому ВРОТ ищет следующее самое высокое совпадение меньше 6 и находит значение 5, связанное с именем Виктор,и таким образом возвращает Его.

Дополнительные сведения см. в этой информации.

К началу страницы

Подстановка значений по вертикали в списке неизвестного размера с использованием точного совпадения

Для этого используйте функции СМЕЩЕНИЕ и НАЙТИВМЕСЯК.

Примечание: Используйте этот подход, если данные в диапазоне внешних данных обновляются каждый день. Вы знаете, что цена находится в столбце B, но вы не знаете, сколько строк данных возвращает сервер, а первый столбец не отсортировали по алфавиту.

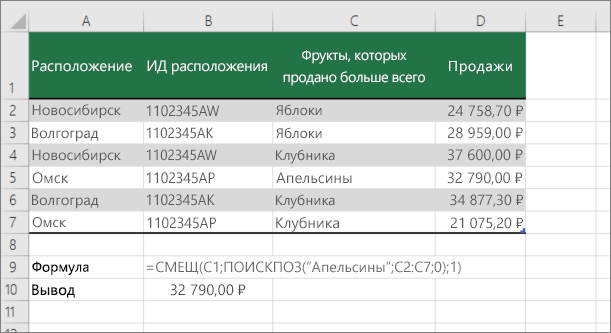
C1 — это левые верхние ячейки диапазона (также называемые начальной).

MATCH(“Оранжевая”;C2:C7;0) ищет “Оранжевые” в диапазоне C2:C7. В диапазон не следует включать запускаемую ячейку.

1 — количество столбцов справа от начальной ячейки, из которых должно быть возвращено значение. В нашем примере возвращается значение из столбца D, Sales.

К началу страницы

Точное совпадение значений по горизонтали в списке

Для этого используйте функцию ГГПУ. См. пример ниже.

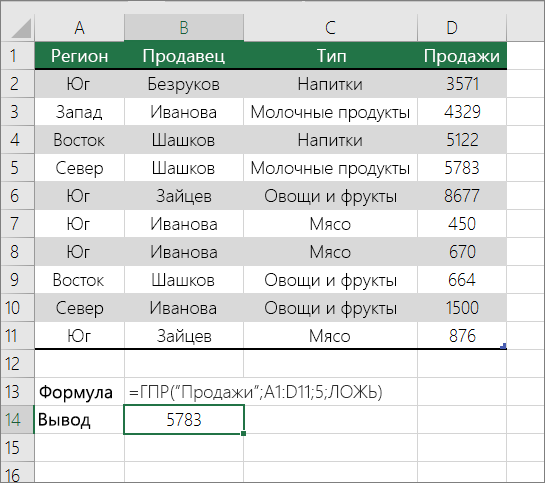
Г ПРОСМОТР ищет столбец “Продажи” и возвращает значение из строки 5 в указанном диапазоне.

Дополнительные сведения см. в сведениях о функции Г ПРОСМОТР.

К началу страницы

Подыыывка значений по горизонтали в списке с использованием приблизительного совпадения

Для этого используйте функцию ГГПУ.

Важно:  Убедитесь, что значения в первой строке отсортировали в порядке возрастания.

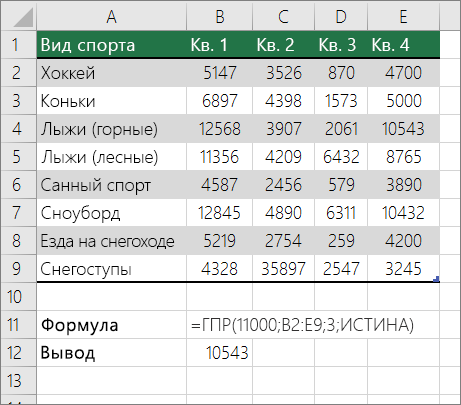
В примере выше ГЛЕБ ищет значение 11000 в строке 3 указанного диапазона. Она не находит 11000, поэтому ищет следующее наибольшее значение меньше 1100 и возвращает значение 10543.

Дополнительные сведения см. в сведениях о функции Г ПРОСМОТР.

К началу страницы

Создание формулы подступа с помощью мастера подметок (толькоExcel 2007 )

Примечание: В Excel 2010 больше не будет надстройки #x0. Эта функция была заменена мастером функций и доступными функциями подменю и справки (справка).

В Excel 2007 создается формула подытов на основе данных на основе данных на основе строк и столбцов. Если вы знаете значение в одном столбце и наоборот, мастер под поисков помогает находить другие значения в строке. В формулах, которые он создает, используются индекс и MATCH.

1. Щелкните ячейку в диапазоне.

2. На вкладке Формулы в группе Решения нажмите кнопку Под поиск.

3. Если команда Подытов недоступна, вам необходимо загрузить мастер под надстройка подытогов.

   Загрузка надстройки “Мастер подстройок”

4. Нажмите кнопку Microsoft Office , выберите Параметры Excel и щелкните категорию Надстройки.

5. В поле Управление выберите элемент Надстройки Excel и нажмите кнопку Перейти.

6. В диалоговом окне Доступные надстройки щелкните рядом с полем Мастер подстрок инажмите кнопку ОК.

7. Следуйте инструкциям мастера.

К началу страницы

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил. Рассказываем, как освоить функцию поиска решений.

---

Основные параметры поиска решений

Найти решение задачи можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый и покажет максимально точное решение, если знать, как использовать функцию.

Итак, мы решаем задачу с помощью поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. К поиску решения вернемся чуть позже, а сейчас разберемся, что входит в каждый из этих типов:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки — переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон. При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения.

Целевая функция — результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом. 

Ограничения — условия, которые необходимо учесть при оптимизации функции, называющейся целевой. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников. 

Пример использования поиска решений

Теперь перейдем к самой функции. 

1) Чтобы включить «Поиск решений», выполните следующие шаги:

• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

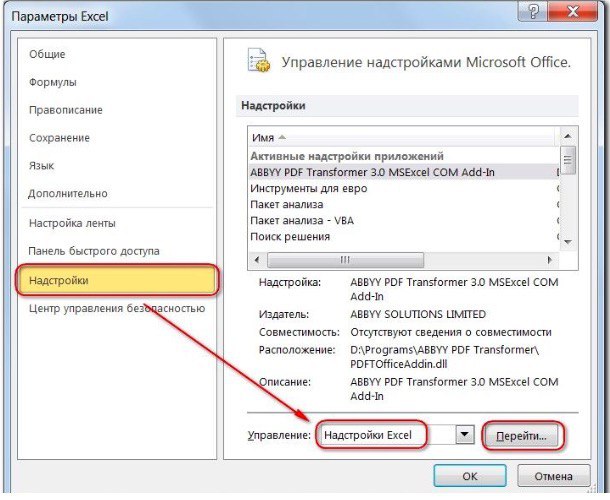
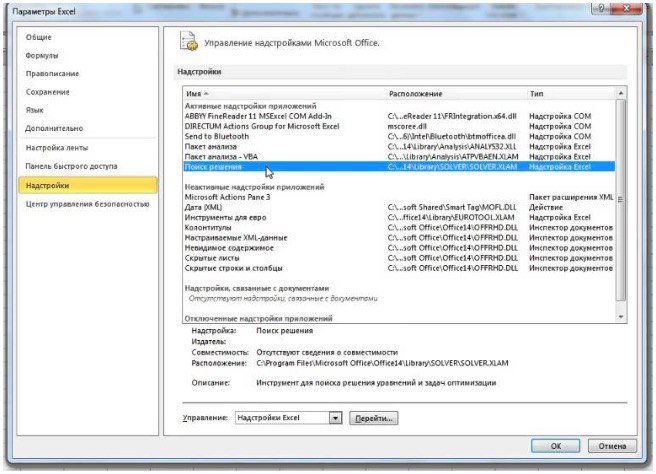
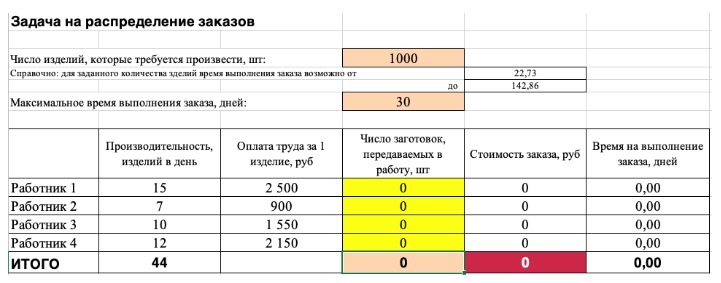
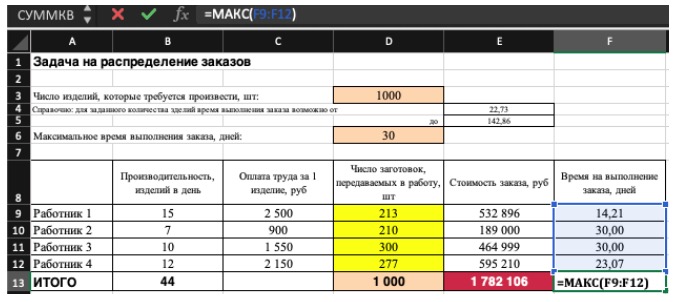
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым – изменяемые ячейки.

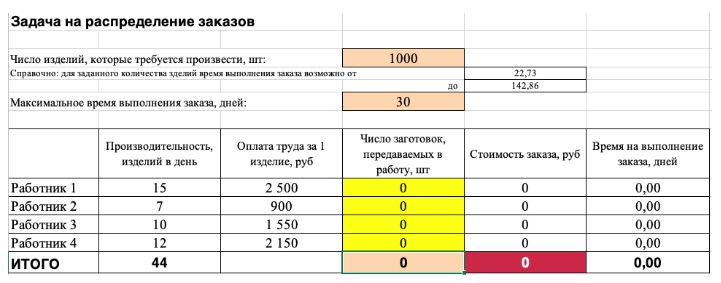
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

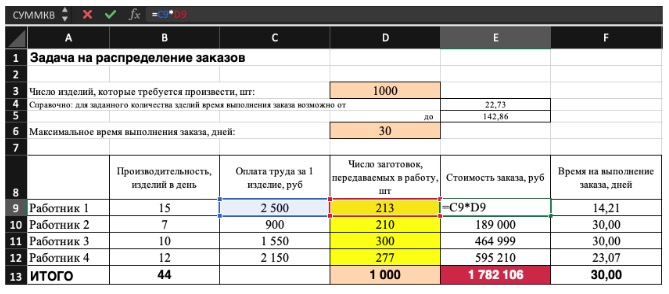
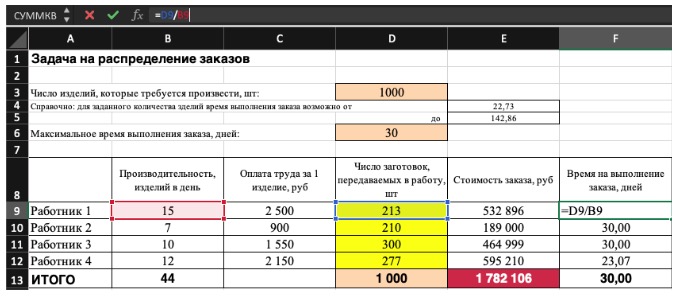
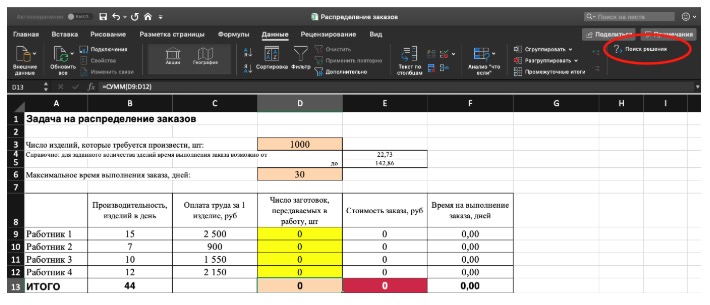
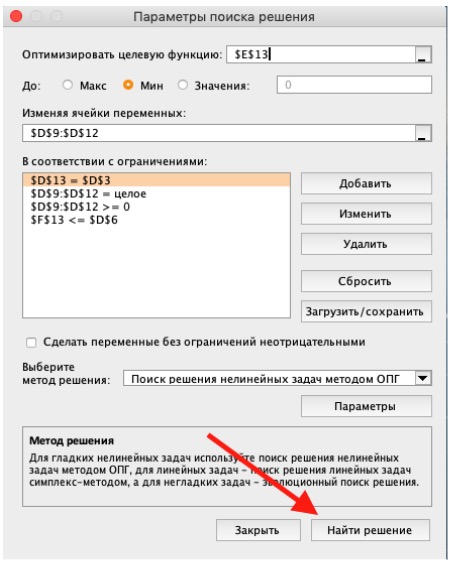
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите  «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

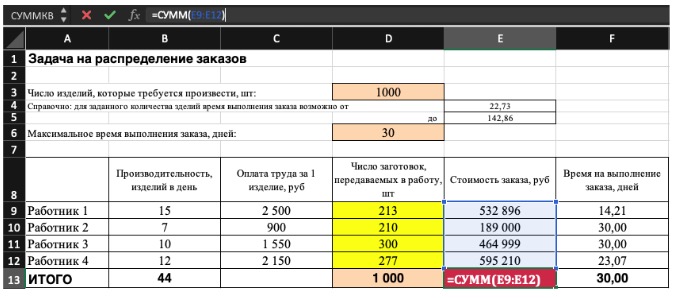
4) Заполните параметры «Поиска решений» и нажмите «Найти решение». 

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения: 

• общее количество изделий 1000 штук ($D$13 = $D$3); 
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0); 
• количество дней меньше либо равно 30 ($F$9:$F$12 < = $D$6, либо как в примере в ячейке F13 задать функцию МАКС(F9:F12) и поставить ограничение $F$13 < = $D$6).

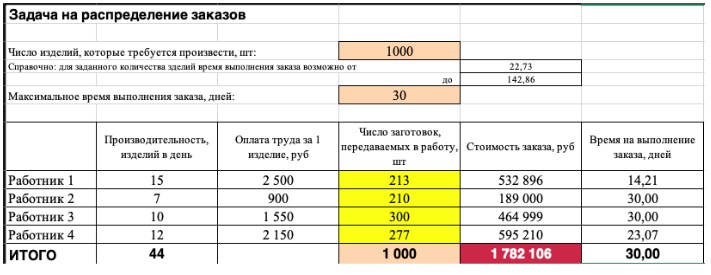
5) В конце проверьте полученные данные на соответствие заданному целевому значению. Если что-то не сходится — нужно пересмотреть исходные данные, введенные формулы и ограничения.

Хотите научиться решать задачи в Excel, как это делают в компаниях-лидерах? Приходите на наш онлайн-курс, на котором вы освоите этот инструмент на уровне профи. Вашими преподавателями будут эксперты-практики, а после обучения вы сможете дополнить резюме весомой строчкой. Регистрируйтесь!

Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную – скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра

.

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке

Данные,

группа

Работа с данным

.

Простейший пример

Найдем значение параметра

b

в уравнении

2*а+3*b=x

, при котором

x=21

, параметр

а=

3

.

Подготовим исходные данные.

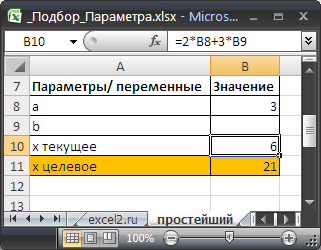
Значения параметров

а

и

b

введены в ячейках

B8

и

B9

. В ячейке

B10

введена формула

=2*B8+3*B9

(т.е. уравнение

2*а+3*b=x

).

Целевое значение x

в ячейке

B11

введено

для информации.

Выделите ячейку с формулой

B10

и вызовите

Подбор параметра (на вкладке

Данные

в группе

Работа с данными

выберите команду

Анализ «что-если?»

, а затем выберите в списке пункт

Подбор параметра

…)

.

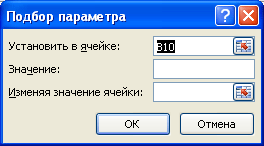
В качестве целевого значения для ячейки

B10

укажите 21, изменять будем ячейку

B9

(параметр

b

).

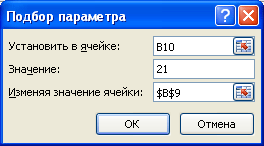
Нажмите ОК.

Инструмент

Подбор параметра

подобрал значение параметра

b

равное 5.

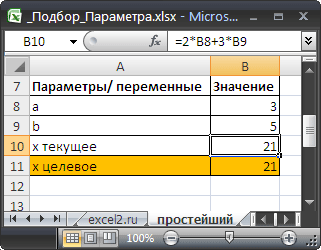
Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку

B9

последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без

Подбора параметра

параметр будет подобрать сложно

.

Примечание

: Уравнение

2*а+3*b=x

является линейным, т.е. при заданных

a

и

х

существует только одно значение

b

, которое ему удовлетворяет. Поэтому инструмент

Подбор параметра

работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то

Подбор параметра

найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в

файле примера

на листе

Простейший

.

Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X – аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).

Калькуляция, подбираем значение прибыли

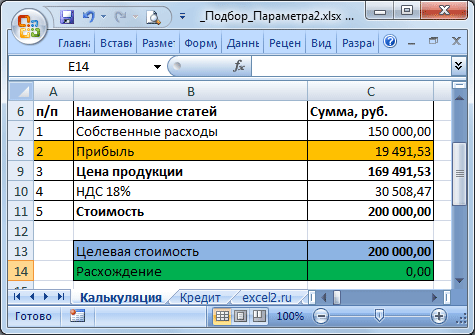
Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.

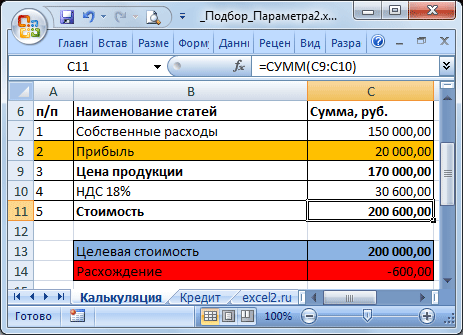
Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка

С13

). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (

С8

), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (

С14

) равно 0.

В структуре цены в ячейке

С9

(Цена продукции) введена формула Собственные расходы + Прибыль (

=С7+С8

). Стоимость договора (ячейка

С11

) вычисляется как Цена продукции + НДС (=

СУММ(С9:C10)

).

Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент

Подбор параметра

.

Выделите ячейку

С14

, вызовите

Подбор параметра

(на вкладке

Данные

в группе

Работа с данными

выберите команду

Анализ «что-если?»

, а затем выберите в списке пункт

Подбор параметра

…). В качестве целевого значения для ячейки

С14

укажите 0, изменять будем ячейку

С8

(Прибыль).

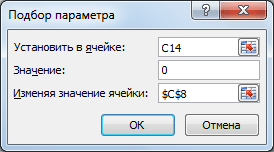
Нажмите ОК.

Теперь, о том когда этот инструмент работает. 1. Изменяемая ячейка не должна содержать формулу, только значение.2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0

Примечание

: В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.

Подбор суммы кредита

Предположим, что нам необходимо

определить максимальную сумму кредита

, которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).

В EXCEL существует функция

ПЛТ()

для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см.

статьи про аннуитет

). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции

ПЛТ()

) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента

Подбор параметра

сумму займа пришлось бы подбирать в ручную с помощью функции

ПЛТ()

или использовать соответствующую формулу.

Введем в ячейку

B

6

ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку

B

7

, % ставку по кредиту введем в ячейку

B8,

а формулу

=ПЛТ(B8/12;B7;B6)

для расчета суммы ежемесячного платежа в ячейку

B9

(см.

файл примера

).

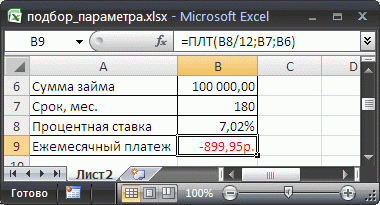
Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:

• на вкладке
  
  Данные
  
  в группе
  
  Работа с данными
  
  выберите команду
  
  Анализ «что-если?»
  
  , а затем выберите в списке пункт
  
  Подбор параметра
  
  …;
• в поле
  
  Установить
  
  введите ссылку на ячейку, содержащую формулу. В данном примере – это ячейка
  
  B9
  
  ;
• введите искомый результат в поле
  
  Значение
  
  . В данном примере он равен
  
  -1800
  
  ;
• В поле
  
  Изменяя значение ячейки
  
  введите ссылку на ячейку, значение которой нужно подобрать. В данном примере – это ячейка
  
  B6
  
  ;
• Нажмите ОК

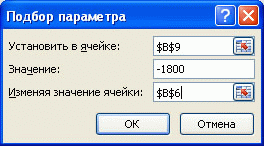
Что же сделал

Подбор параметра

? Инструмент

Подбор параметра

изменял по своему внутреннему алгоритму сумму в ячейке

B6

до тех пор, пока размер платежа в ячейке

B9

не стал равен 1800,00 руб. Был получен результат – 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.

Подбор параметра

подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте

инструмент

Поиск решения

. Точность подбора параметра можно задать через меню

.

Вопросом об единственности найденного решения

Подбор параметра

не занимается, вероятно выводится первое подходящее решение.

Иными словами, инструмент

Подбор параметра

позволяет сэкономить несколько минут по сравнению с ручным перебором.

Программа Excel радует своих пользователей множеством полезных инструментов и функций. К одной из таких, несомненно, можно отнести Подбор параметра. Этот инструмент позволяет найти начальное значение исходя из конечного, которое планируется получить. Давайте разберемся, как работать с данной функцией в Эксель.

Зачем нужна функция

Как было уже выше упомянуто, задача функции Подбор параметра состоит в нахождении начального значения, из которого можно получить заданный конечный результат. В целом, эта функция похожа на Поиск решения (подробно вы можете с ней ознакомиться в нашей статье – “Поиск решения в Excel: пример использования функции”), однако, при этом является более простой.

Применять функцию можно исключительно в одиночных формулах, и если потребуется выполнить вычисления в других ячейках, в них придется все действия выполнить заново. Также функционал ограничен количеством обрабатываемых данных – только одно начальное и конечное значения.

Использование функции

Давайте перейдем к практическому примеру, который позволит наилучшим образом понять, как работает функция.

Итак, у нас есть таблица с перечнем спортивных товаров. Мы знаем только сумму скидки (560 руб. для первой позиции) и ее размер, который для всех наименований одинаковый. Предстоит выяснить полную стоимость товара. При этом важно, чтобы в ячейке, в которой в дальнейшем отразится сумма скидки, была записана формула ее расчета (в нашем случае – умножение полной суммы на размер скидки).

Итак, алгоритм действий следующий:

1. Переходим во вкладку “Данные”, в которой нажимаем на кнопку “Анализ “что если” в группе инструментов “Прогноз”. В раскрывшемся списке выбираем “Подбор параметра” (в ранних версиях кнопка может находиться в группе “Работа с данными”).
2. На экране появится окно для подбора параметра, которе нужно заполнить:
   • в значении поля “Установить в ячейке” пишем адрес с финальными данными, которые нам известны, т.е. это ячейка с суммой скидки. Вместо ручного ввода координат можно просто щелкнуть по нужной ячейке в самой таблице. При этом курсор должен быть в соответствующем поле для ввода информации.
   • В качестве значения указываем сумму скидки, которая нам известна – 560 руб.
   • В поле “Изменяя значение ячейки” вручную или посредством клика мышью указываем координаты ячейки (должна участвовать в формуле расчета суммы скидки), в которой планируем вывести начальное значение.
   • по готовности нажимаем OK.
3. Программа выполнит расчеты и выдаст результат в небольшом окошке, которое можно закрыть, нажав кнопку OK. Также найденные значения автоматически появятся в заданных ячейках таблицы.
4. Аналогичным образом можно посчитать цену без скидки для других товаров, если нам известна точная сумма скидки по каждому из них.

Решение уравнений с помощью подбора параметра

Несмотря на то, что это не основное направление использования функции, в некоторых случаях, когда речь идет про одну неизвестную, она может помочь в решении уравнений.

Например, нам нужно решить уравнение: 7x+17x-9x=75.

1. Пишем выражение в свободной ячейке, заменив символ x на адрес ячейки, значение которой нужно найти. В итоге формула выглядит так: =7*D2+17*D2-9*D2.
2. Щелкаем Enter и получаем результат в виде числа 0, что вполне логично, так как нам только предстоит вычислить значение ячейки D2, которе и является “иксом” в нашем уравнении.
3. Как было описано в первом разделе статьи, во вкладке “Данные” нажимаем кнопку “Анализ “что если” и выбираем “Подбор параметра”.
4. В появившемся окошке заполняем параметры:
   • В значении поля “Установить в ячейке” указываем координаты ячейки, в которой мы написали уравнение (т.е. B4).
   • В значении, согласно уравнению, пишем число 75.
   • В поле “Изменяя значения ячейки” указываем координаты ячейки, значение которой нужно найти. В нашем случае – это D2.
   • Когда все готово, нажимаем OK.
5. Как и в примере, рассмотренном выше, будут произведены вычисления и получен результат, о чем будет свидетельствовать небольшой окошко.
6. Таким образом, нам удалось решить уравнение и найти значение x, которое оказалось равным числу 5.

Заключение

Подбор параметра – функция, которая может помочь в поиске неизвестного числа в таблице или, даже решении уравнения с одной неизвестной. Главное – овладеть навыками использования данного инструмента, и тогда он станет незаменимым помощников во время выполнения различных задач.