|
СЛОЖИТЬ – это значит объединить группы предметов в одно целое. При перестановке слагаемых сумма не меняется. СЛАГАЕМЫЕ – это части, СУММА – это целое. |
ВЫЧЕСТЬ – это значит взять часть и найти оставшуюся часть. УМЕНЬШАЕМОЕ – это целое, ВЫЧИТАЕМОЕ и РАЗНОСТЬ – это части. Если из ЦЕЛОГО вычесть ОДНУ ЧАСТЬ, то останется ДРУГАЯ ЧАСТЬ |
|
Имеется всего 6 перестановок из 3 элементов. Чтобы их получить, надо поочередно фиксировать на первом месте каждый элемент, а два остальных – переставлять. |
ЗАМКНУТУЮ ЛОМАНУЮ ЛИНИЮ называют МНОГОУГОЛЬНИКОМ. В зависимости от числа сторон различают треугольники, четырёхугольники, пятиугольники. |
|
ЛОМАНАЯ ЛИНИЯ состоит из последовательно соединённых друг с другом отрезков Никакие два последовательных отрезка ломаной линии не лежат на одной прямой. |
При увеличении (уменьшении) одного слагаемого на несколько единиц сумма тоже увеличивается (уменьшается) на столько же единиц |
|
Из двух чисел на числовом отрезке меньше то, которое расположено левее, а больше то, которое расположено правее. |
ЗАДАЧА
|
|
РИМСКИЕ ЦИФРЫ I – 1 VII – 7 XIII – 13 XIX – 19 II – 2 VIII – 8 XIV – 14 XX – 20 III – 3 IX – 9 XV – 15 IV – 4 X – 10 XVI – 16 V – 5 XI – 11 XVII – 17 VI – 6 XII – 12 XVIII – 18 |
|
Чем больше единица измерения, тем меньше её значение 2 кг. = 200 гр. Сравнивать, складывать и вычитать массы (объёма, длины) можно только тогда, когда они ИЗМЕРЕНЫ ОДИНАКОВЫМИ МЕРКАМИ |
|
Чтобы измерить МАССУ предмета, надо выбрать мерку (единицу измерения) и узнать, сколько мерок уравновесят этот предмет. 1 КИЛОГРАММ = 100 ГРАММ |
Чтобы измерить ОБЪЁМ сосуда, надо выбрать мерку (единицу измерения) и узнать, сколько мерок содержится в этом сосуде. 1 ЛИТР = 100 МИЛЛИЛИТРОВ |
|
Чтобы измерить ДЛИНУ отрезка, надо выбрать мерку (единицу измерения) и узнать, сколько раз она содержится в измеряемом отрезке. 1 ДЕЦИМЕТР = 10 САНТИМЕТРОВ |
РЕШЕНИЕ СОСТАВНЫХ ЗАДАЧ |
|
РЕШЕНИЕ СОСТАВНЫХ ЗАДАЧ |
АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЯ:
|
|
АЛГОРИТМ КОММЕНТИРОВАНИЯ УРАВНЕНИЯ
|
|
ПЛАН РЕШЕНИЯ ЗАДАЧИ
|
ПЛАН АНАЛИЗА СОСТАВНОЙ ЗАДАЧИ
|
|
ПЛАН АНАЛИЗА ПРОСТОЙ ЗАДАЧИ
|
|
Чтобы сложить (вычесть) КРУГЛЫЕ ЧИСЛА можно сложить (вычесть) ДЕСЯТКИ И ПРИПИСАТЬ СПРАВА 0 20 + 30 = 50 50 – 30 = 20 |
Чтобы вычесть числа, выраженные в десятках и единицах, можно ИЗ ДЕСЯТКОВ ВЫЧЕСТЬ ДЕСЯТКИ, а ИЗ ЕДИНИЦ ВЫЧЕСТЬ ЕДИНИЦЫ. 3 дм 5 см – 1 дм 2 см = 2 дм 4 см |
|
Чтобы сложить числа, выраженные в десятках и единицах, можно к ДЕСЯТКАМ ПРИБАВИТЬ ДЕСЯТКИ, а К ЕДИНИЦАМ ПРИБАВИТЬ ЕДИНИЦЫ. 1 дм 3 см + 2 дм 4 см = 3 дм 7 см |
Натуральный ряд чисел: 1, 2, 3, 4, 5… – служит для счёта предметов. Самое маленькое число – 1, самого большого числа нет. Каждое следующее из чисел на 1 больше предыдущего |
|
АЛГОРИТМ СРАВНЕНИЯ ДВУЗНАЧНЫХ ЧИСЕЛ Если количество десятков разное, то больше число, у которого больше десятков; меньше то число, у которого меньше десятков. 47 > 37 |
9 + 7 = 10 + 6 = 16 |
|
АЛГОРИТМ СРАВНЕНИЯ ДВУЗНАЧНЫХ ЧИСЕЛ Если количество десятков одинаковое, то больше число, у которого больше единиц; меньше то число, у которого меньше единиц. 45 > 41 |
11 – 6 = 10 – 5 = 5 |
|
алгоритм СЛОЖЕНИЯ ОДНОЗНАЧНЫХ ЧИСЕЛ С ПЕРЕХОДОМ ЧЕРЕЗ ДЕСЯТОК
|
ПАМЯТКИ ПО МАТЕМАТИКЕ 1 КЛАСС |
|
алгоритм ВЫЧИТАНИЯ ЧИСЕЛ С ПЕРЕХОДОМ ПО «ЧАСТЯМ»
|
5 + 1 = 6
СЛАГАЕМОЕ
СЛАГАЕМОЕ
СУММА
РАЗНОСТЬ
ВЫЧИТАЕМОЕ
УМЕНЬШАЕМОЕ
6 – 1 = 5
МЕНЬШЕЕ
ЧИСЛО
БОЛЬШЕЕ
ЧИСЛО
?
А
Б
Чтобы найти ЦЕЛОЕ,
надо к ОДНОЙ ЧАСТИ прибавить ДРУГУЮ ЧАСТЬ
Чтобы найти ЧАСТЬ,
надо из ЦЕЛОГО вычесть ИЗВЕСТНУЮ ЧАСТЬ
?
А
В
Чтобы найти ЧАСТЬ,
надо из ЦЕЛОГО вычесть ИЗВЕСТНУЮ ЧАСТЬ
Б
?
В
?
М
Р
М + Р
Чтобы найти БОЛЬШЕЕ число, надо
К МЕНЬШЕМУ ЧИСЛУ ПРИБАВИТЬ РАЗНОСТЬ
Чтобы найти МЕНЬШЕЕ число, надо
ИЗ БОЛЬШЕГО ЧИСЛА ВЫЧЕСТЬ РАЗНОСТЬ
Б – Р
Р
?
Б
Чтобы найти,
НА СКОЛЬКО ОДНО ЧИСЛО БОЛЬШЕ (меньше) другого, надо
ИЗ БОЛЬШЕГО ЧИСЛА ВЫЧЕСТЬ МЕНЬШЕЕ.
Б – М
?
М
Б
Если а = б, то б = а
а
б
б
а
Если а = б, б = с, то а = с
с
с
б
а
Если а > б, то б < а
б
а
Если а > б, б > с, то а > с
- находим меньшую часть
- находим целое – Б + М
?
М
?
Б
?
- находим большую часть
- находим целое – Б + М
М
?
Б
Чтобы найти НЕИЗВЕСТНУЮ ЧАСТЬ, надо из ЦЕЛОГО ЧИСЛА ВЫЧЕСТЬ ИЗВЕСТНУЮ ЧАСТЬ
а – х = б
х = а – б
б
х
а
Чтобы найти ЦЕЛОЕ, надо СЛОЖИТЬ ЧАСТИ,
х – а = б
х = а + б
б
а
х
Чтобы найти НЕИЗВЕСТНУЮ ЧАСТЬ, надо из ЦЕЛОГО ЧИСЛА ВЫЧЕСТЬ ИЗВЕСТНУЮ ЧАСТЬ
а + х = б
х = б – а
х
а
б
- найти неизвестное целое
- найти часть ?
?
+
+
?
=
?
1
6
Чтобы сложить однозначные числа с переходом через десяток, можно сначала дополнить до 10 первое слагаемое, а затем добавить остальные единицы
1
5
Чтобы вычесть числа с переходом через десяток, можно сначала вычесть ту часть числа, которая содержится в разряде единицу уменьшаемого, а затем из десятка вычесть оставшуюся часть.
Помощь родителям: «целое» и «части».

Тема «Целое и части» — одна из важных в математике 1 классе.
Познакомить с этими понятиями очень легко на самом простом примере: возьмите яблоко.
Что можно рассказать о нем? (На самом деле ответов очень много – это цвет, размер, форма).

Что мы видим теперь? Сколько кусков получилось?
Кусок в математике называется – частью.
Сколько получилось частей? А можно по-другому разрезать?
Что больше: целое или его часть?
Если мы соединим эти части, то получим целое яблоко.
Часть всегда меньше целого, а целое всегда больше части.
Целое равно сумме частей.
Чтобы найти часть, надо из целого вычесть другую часть.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 67
ГДЗ учебник по математике 2 класс Петерсон. Часть 2. Урок 28. Решение задач. Номер №9
Как найти целое? Как найти часть? Определи в равенствах части и целое и найди x.
x − a = p
x + b = c
d − x = k
Решение
Чтобы найти целое нужно сложить части.
Чтобы найти часть нужно из целого вычесть другую часть.
x − a = p
x − целое;
a, p − части.
x = a + p
x + b = c
c − целое;
x, b − части.
x = c − b
d − x = k
d − целое;
x, k − части.
x = d − k
Решение уравнений с опорой на отношение «части и целое»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Урок математики в 1 классе
УМК «Классическая программа»
Решение уравнений с опорой на отношение «части и целое»
Автор: Шишкалова Нина Петровна
учитель начальных классов
МБОУ «СОШ№6»
Г. Сосновый Бор

Цель:
учить решать уравнения, используя графические модели (схемы) и отношение «части и целое».

Подготовительный этап к восприятию нового материала.
Задание 1. У данных фигур покажите части и целое.
Задание 2. Найдите лишнюю фигуру.
а)
б)
в)
г)
д)
е)

Задание 2. По данной модели составьте из частей целое. Запишите формулу, применяя правило.
А
М
В
К
А = _____________
Если сложить части, то получится целое.

М
В
К
По этой же модели запишите формулы, как из целого найти части.
А
М = ____________
В = _____________
К = _____________
Если из целого вычесть часть, то останется другая часть.

К = А – М – В
Проверьте правильность выполненного вами задания.
А = М + В + К
М = А – В – К
В = А – М – К

Задание 3. (выполняется устно)
— Вычислить целое по его частям.
+
=
5 и 2 4 и 5
3 и 7 8 и 1
6 и 2 9 и 2
— Вычислить часть по целому и другой части.
=
—
8 и 2 5 и 4
7 и 1 6 и 2
7 и 4 3 и 2

Задание 4.
Обозначьте задуманное число буквой Х, У или Z. Запишите предложения формулами.
К задуманному числу прибавили 2 и получили 4.
Из задуманного числа вычли 3 и получили 2.
Из числа 7 вычли задуманное число и получили 6.

Равенства имеют вид: (проверка)
Х + 2 =4 У – 3 = 2 7 – Z = 6
Равенство, в котором есть неизвестная величина, называется уравнением.
Чтобы решить уравнение, нужно определить, что неизвестно — часть или целое. В этом помогут модели и схемы.

Задание 5.
— Обозначьте в каждом уравнении части и целое и найдите неизвестное число.
Х + 2 = 4 У – 3 = 2 7 – Z = 6
Х = У = Z =
Алгоритм.
Определите, частью или целым является неизвестная величина.
Примените правило и выберите действие.

Проверка выполненного задания.
x + 2 = 4 y — 3 = 2
x = 4 — 2 y = 3 + 2
7 — z = 6
z = 7 — 6

Проблемные и практические задачи по теме.
Задание 1.
Найдите и прочитайте те выражения, которые являются уравнениями.
c = a – b 5 = 6 – x
7 + x = 10 6 + 2 = 9
6 = 4 + 2 x – 4 = 3
Задание 2.
Составьте модели к найденным уравнениям и найдите неизвестное число.

Проверка выполненного задания.
7 + x = 10 5 = 6 — x
10
7
X
6
5
X
x – 4 = 3
x
4
3

Задание 3.
Составьте всевозможные уравнения по данной схеме.
x
c
a

Возможные варианты ответов.
x + c = a
a – x = c
c + x = a
a – c = x

Задание 4. Дано уравнение. x = d – a
— Определите, по какой из схем составлено уравнение.

Задание 5.
Решите задачу, используя модели или схему.
Мама испекла 16 пирожков. Когда несколько пирожков съели, их осталось 10. Сколько пирожков съели?

Проверьте схему и объясните свой выбор решения.
?
10
16
16
?
10


Выводы по теме.
Уравнение – это равенство с одним неизвестным.
Если неизвестна часть, то от целого отнимают другую часть.
Если неизвестно целое, то части складывают.
Уравнение – один из способов решения задачи.


Курс повышения квалификации
Охрана труда
- Сейчас обучается 114 человек из 42 регионов

Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 233 человека из 54 регионов

Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 352 человека из 64 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 586 282 материала в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 27.12.2020
- 1548
- 44
- 27.12.2020
- 1592
- 6
- 27.12.2020
- 574
- 4
- 27.12.2020
- 486
- 0
- 27.12.2020
- 449
- 0
- 27.12.2020
- 356
- 1
- 27.12.2020
- 510
- 3
- 27.12.2020
- 191
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 03.06.2020 618
- PPTX 148 кбайт
- 4 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Софронова Ольга Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
![]()
- На сайте: 1 год и 1 месяц
- Подписчики: 0
- Всего просмотров: 24277
- Всего материалов: 234
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут

В Курганской области дистанционный режим для школьников продлили до конца февраля
Время чтения: 1 минута

Минобрнауки создаст для вузов рекомендации по поддержке молодых семей
Время чтения: 1 минута

Инфоурок стал резидентом Сколково
Время чтения: 2 минуты

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных
Время чтения: 1 минута

Ленобласть распределит в школы прибывающих из Донбасса детей
Время чтения: 1 минута

В школах Хабаровского края введут уроки спортивной борьбы
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Получите новую специальность с дополнительной скидкой 10%
Цена от 4900 740 руб. Промокод (до 23 февраля): Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки
источники:
http://reshalka.com/uchebniki/2-klass/matematika/peterson/753
http://infourok.ru/reshenie-uravnenij-s-oporoj-na-otnoshenie-chasti-i-celoe-4730144.html
Решение задач на нахождение части целого
В этом уроке научимся решать и составлять задачи на нахождение части целого.
Решим такую задачу:
В аквариуме было 7 рыбок, из них 2 больших, остальные маленькие.
Сколько маленьких рыбок в аквариуме?
Что известно в этой задаче? Всего рыбок 7, из них 2 больших, остальные маленькие.
Что нужно узнать? Сколько маленьких рыбок.
Изобразим данные и искомое задачи на схеме.
Общее количество рыбок в аквариуме изобразим отрезком, всего рыбок 7.
Разделим отрезок на две части.
Первая часть – это большие рыбки, их 2.
Вторая часть отрезка – это маленькие рыбки, их количество неизвестно.

Что нужно найти в задаче целое или часть?
Найти нужно часть, значит, из целого нужно вычесть известную часть.
Решим задачу:
7 – 2 = 5.
Ответ: 5 рыбок маленьких.
Сделаем вывод:
если в задаче требуется найти часть, то нужно из целого вычесть известную часть.
Выполним еще одно практическое задание.
Составьте задачу по схеме и решите ее.
По схеме можно сказать, что известно целое – это 9, известны две части целого – 2 и 4. Найти нужно третью часть целого.
Составим задачу:
Таня нарисовала 9 шариков, 2 из них желтых, 4 красных, остальные зеленые.
Сколько зеленых шариков нарисовала Таня?
В этой задаче нужно найти часть целого, значит, выбираем для решения действие вычитание: из целого вычитаем сначала одну известную часть, потом вторую.
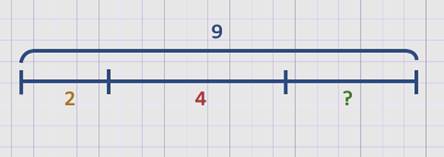
Решение:
9 – 2 – 4 = 3.
Ответ: 3 зеленых шарика нарисовала Таня.
В этом уроке Вы научились решать и составлять задачи на нахождение неизвестной части целого.
Урок математики в 1 классе по теме: “Уравнения”
Цели. Ввести понятие уравнения, научить решать уравнения с неизвестными компонентами-слагаемыми на основе взаимосвязи между частью и целым; обрабатывать навыки быстрого и стабильного счета в пределах 9; развивать логическое мышление, внимание, память, аналитические способности.
Оборудование. Учебник “Математика. 1 класс” (сост. Л.Г. Петерсон). Издательство “С-инфо”.
I. Организационный момент
Учитель: Прочитайте, что написано?
На доске: “Если не лениться…”
У. Как бы вы продолжили? (Ответы детей). Вот как продолжила я: “Можно многого добиться”. Вы готовы не лениться?
II. Актуализация знаний и мотивация.
Проверка устного счета. Учитель диктует числовые выражения:
Дети устно считают, ответ говорят вслух. Учитель на доске записывает ответы.
У. Составьте с помощью чисел 2, 7, 5 четыре равенства. Обозначьте в них целое и части.
Проверка: один ученик на доске записывает суммы (2 + 5 = 7, 5 + 2 =7), другой – разности (7 –5 =2, 7 – 2 =5).
У. Назовите, где целое и части. Почему?
Д. 2 и 5 – это части, т.к. складывать мы можем только части. 7 – это целое, т.к. вычитать мы можем только из целого.
У. Что записано на доске?
Д. Равенства с неизвестным числом.
У. Каким образом будем считать?
Д. Методом подбора.
У. Найдите ошибки. Почему?
III. Постановка проблемы.
У. Рассмотрите вот эту запись. Что это на ваш взгляд?
На доске: Х + 2 = 5
Д. Равенство, в котором есть неизвестный компонент.
У. Такие равенства в математике называются уравнениями. (Учитель на доске вывешивает табличку с надписью “Уравнение”).
Неизвестное число в уравнениях можно обозначить по-разному, но чаще всего используют латинские буквы, например Х.
Давайте решим наше уравнение. Чему равен Х?
Д. Х равен 3.
У. Значение Х называют корнем уравнения.
У. Почему Х равен 3? Как нашли?
Д. 5 – это 2 и 3. Подобрали число.
У. Итак, мы решили уравнение с помощью подбора корней.

У. Чем это уравнение отличается от предыдущего? Сравните их.
Д. В этом уравнении даны геометрические фигуры.
У. Решим уравнение. Чему равен Х?
Д.

У. Как нашли корень уравнения?
Д. Способом подбора.
У. У вас на карточках дано уравнение. Решите его самостоятельно. Каким способом вы будете решать?

Д. Способом подбора.
У. Легко ли найти Х – корень уравнения способом подбора?
Д. Трудно.
У. Удобно подбирать геометрическую фигуру?
Д. Нет.
IV. Поиск решения.
У. Что же нам нужно сделать сегодня на уроке?
Д. Найти новый способ решения уравнения.
У. Есть такой “секрет”, который как “волшебный ключик”, поможет решить любое уравнение. Подумайте, какое действие с “мешками” нужно сделать, чтобы найти Х?
Д. Вычитание.
У. Почему?
Д. Потому, что Х – это часть.
У. А как найти часть?
Д. Из целого вычесть другую часть.
У. Зачеркните в сумме известную часть. Какие фигурки остались? Удобно так считать? Какое правило нам помогло?
Д. Чтобы найти часть, надо из целого вычесть другую часть.
У. Давайте проверим по учебнику.
с. 20 (Дети читают по учебнику правило и убеждаются в правильности своего вывода.)
Чтобы найти часть, надо из целого вычесть другую часть
V. Закрепление изученного материала с проговариванием.

У. Прочитайте уравнение. Что неизвестно?
Д. Из целого вычесть другую часть.

Уравнения можно составлять не только с геометрическими фигурами, но и с буквами.

- Прочитайте уравнение.
- Что неизвестно?
- Как найти?
- Чему равен Х?
Дети отвечают на вопросы.
VI. Самостоятельная работа по выбору.
с. 20, № 3, 4. Проверка в парах.

VII. Включение нового способа действия в систему знаний.

У. Давайте рассмотрим рисунок. Что видите?
Д. Весы в равновесии.
У. Что обозначено за Х?
Д. Масса мешка с крупой.
У. Давайте составим уравнение.
Д. Х + 2 = 4
У. Объясните по образцу как решали уравнение. (Составление алгоритма на доске).
Д.
1. Выделить части и целое.
2. Определить, что неизвестно.
3. Применить правило (как найти).
4. Найти корень уравнения.
№5 (б) – с комментированием (рассмотреть рисунок, составить уравнение, решить по алгоритму);

№5 (в) – самостоятельно с проверкой на доске:
У. Встаньте те ребята, у кого решено уравнение так, как у меня на доске.

VIII. Итог урока. Рефлексия деятельности.
У. Мы начали урок со слов: “Если не лениться, можно многого добиться”.
Кто сегодня не ленился? А чего же вы добились? Что узнали нового? Какое “открытие” сделали?
А вы хотите составить свои уравнения? У вас на столах лежат листочки. Попробуйте сейчас придумать свои уравнения. Они могут быть любые: числовые, буквенные, с использованием геометрических фигур. Пофантазируйте, как можно изобразить неизвестный компонент.
Урок математики в 1-м классе. Тема: “Решение уравнений” (урок рефлексии по учебнику Л.Г.Петерсон “Математика. 1-й класс”)
Класс: 1
Учебник: Л.Г. Петерсон «Математика. 1 класс».
Цели:
- Закрепить умение решать уравнения на вычитание, основанные на взаимодействии части и целого.
- Развивать математическую речь, логическое мышление, умение работать по алгоритму.
- Воспитывать коммуникативные качества, через работу в парах.
Оборудование:
- Карточки для закрепления быстрого правильного счета в пределах 9.
- Карточки для самостоятельной работы №1, №2 с образцом для самопроверки.
- Карточки с алгоритмом комментирования решения уравнений.
- Схемы для составления уравнений.
Ход урока
I. Орг. момент.
- Упражнение для активизации мыслительной деятельности «Ленивые восьмёрки».
Чтобы наша работа на уроке шла успешно, проведём упражнение.
Нарисуйте в воздухе «лежачую восьмёрку» по три раза каждой рукой, а затем обеими руками.
Мы рады приветствовать вас в классе нашем.
Возможно, есть классы и лучше и краше.
Но пусть в нашем классе вам будет светло.
Пусть будет уютно и очень легко.
Поручено нам вас сегодня встречать.
Ну что ж, начнём урок, не будем зря время терять
II. Самоопределение к деятельности.
- Чему вы учитесь на уроках математики?
- Вы сказали правильно писать цифры.
- Зачем? Где вам может пригодиться?
- Сейчас мы поупражняемся в правильном написании чисел.
- Зарядка для пальчиков «Котятки».
У котяток лапки царапки, (сжимание и разжимание кулачков)
Любят котятки лапками царапать (сжали кулачки).
Выпустят один коготок, выпустят второй коготок,
Третий, четвёртый, пятый (поочерёдное разжимание пальчиков, начиная с большёго).
И ну давай царапать (разжимание и сжимание кулачков).

– На доске записан ряд чисел.
– Что вы можете о них сказать? (однозначные, чётные)
– Установите закономерность (увеличиваются на 2).
– Продолжите ряд на 2 числа (8, 10) – проверка . Какое число лишнее? Почему? Самостоятельно повторите ряд 1 раз.
- Чему вы сейчас учились? Где это вам может пригодиться?
- Вы сказали, что на уроках математики учитесь быстро и правильно читать.
- Что для этого необходимо знать? Уметь?
Проверим, как вы быстро и правильно умеете считать в пределах 9.
- Что у вас получилось? (выражения)
- Что записано вместо ответов? (буквы)
Перед вами на партах лежат листочки с табличками (покажите их).
Вы должны найти значение выражений и под ответами записать буквы в клеточки, соответственно ответам.
Если, вы, правильно найдёте значение выражений,у вас получится слово (2 мин).
– Какое слово у вас получилось? (уравнение)
Значит, состав чисел в пределах 9 вы знаете хорошо, и не будете допускать ошибки в вычислениях.
- У кого не получилось слово?
- Почему?
- Над чем нужно поработать?
III. Актуализация знаний.
- Объясните, что такое уравнение?
- Что в уравнении может быть неизвестным?
- Давайте вспомним, как найти целое? Часть?
Какую цель поставите перед собой?
Чему будете учиться на уроке? (решать уравнения на вычитание).
IV. Фиксирование затруднен.


Выделите части и целое.
- Как работаем в паре?
- Как показываем готовность?
Ученики крепят файлы под схемами, объясняют.
Кто помнит, какую цель поставили? Чему будем учиться?
- Чтобы решать уравнения, что необходимо знать? (правила, алгоритм)
Алгоритм решения уравнений:
- Найти в уравнении части и целое.
- Определить, чем является х, частью или целым.
- Применить соответствующее правило.
- Назвать и записать ответ.
- Сделать проверку.
> Правила мы повторили, давайте повторим алгоритм (алгоритм вывешен на доске).
А сейчас, пользуясь алгоритмом, попробуйте решить уравнения самостоятельно по вариантам (ученики на обратной стороне доски)

Объяснение по алгоритму?
Алгоритм комментирования решения уравнений:
- Читаю уравнение:
- В этом уравнении части… и целое – …
- Применяю правило: .
- х равен сумме (разности) . и .
- Ответ: х равен .
- Проверяю: .
Кто не согласен, стукните карандашом.
V. Самостоятельная работа с проверкой по образцу.
Сейчас вы самостоятельно попробуете решить уравнение, будете сами себя проверять и оценивать.
У каждого из вас лежат на партах карточки с самостоятельными работами № 1 и № 2.
- Вы выполняете сначала самостоятельную работу № 1 первое уравнение.
- Затем проверяете себя по образцу, отгибая правый край карточки, если допустили ошибки, выполняете второе уравнение.
- Если нет, переходите к самостоятельной работе № 2, проверяете по образцу.
- Если выполнили, устно составляете задачу по схеме, с помощью которых вы составляли уравнения, эти схемы находятся на доске.
- Проверку выполняете зеленой ручкой, у кого нет, простым карандашом.
– Повторите, как поняли задание.
– Когда можно открывать образец? (когда выполнили задание)
– Почему? (Потому, что каждый должен научиться решать такие уравнения сам).
VI. Рефлексия
- Какую цель ставили перед собой?
- А теперь себя оцените.
- Как оцениваем? (Eсли всё получилось, рисуем себе зелёный кружок; если, я, старался, но у меня не всё получилось, жёлтый; мне нужна помощь – красный.)
- Поставьте себе нужный кружок.
VII. Итог.
- Поднимите руку те, у кого зелёный кружок? Молодцы! Значит уравнения такого вида, вы, научились решать.
- Жёлтый? Как, вы, думаете, почему? Над чем нужно поработать?
- Красный? Как, вы, думаете, почему? Над чем нужно поработать?
Домашнее задание: составить и решить два уравнения на вычитание.
Урок по математике (Л.Г.Петерсон) 1 класс

Урок по математике (Л.Г.Петерсон)
1 класс
Тема: Уравнения.
Цель: Ввести понятие уравнение; сформировать способность к решению уравнений на основе взаимосвязи между частью и целым.
Задачи:
- Актуализировать умение решать простые задачи на сложение и вычитание;
- Тренировать автоматизированный навык счета в пределах9.
- Развивать мыслительные операции необходимые на этапе проектирования: анализ, сравнение, синтез, обобщение.
Оборудование: интерактивная доска, компьютер, проектор, таблички со словами уравнение, корень уравнения, алгоритм комментирования решения уравнений.
Ход урока:
- Организационный момент.
-Проверим готовность к уроку. Я загадываю загадку, а вы показываете отгадку
Я с собой её ношу,
Не макаю, но пишу.
Я то в клетку, то в линейку,
Написать на мне сумей-ка!
Можешь и нарисовать.
Не куст, а с листочками,
Не рубашка, а сшита,
Не человек, а разговаривает.( книга, учебник)
– Итак к уроку вы готовы можем начать работу.
Ребята, сегодняшний урок я хочу начать такими словами:
Слайд 1.
В школу мы пришли учиться,
В жизни это пригодится.
Тот, кто хочет много знать,
Должен сам все постигать.
– Ребята, как Вы понимаете эти строки? Что значит: ученье в жизни пригодится. (Без знаний ничего не сделаешь.)
– Выделите главное слово в последних двух строчках и объясните свой выбор.
Слово “сам”, т.к. мы учимся тогда, когда сами понимаем, чего мы не знаем и сами открываем новые знания.)
II. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.
1.Устный счёт
Для успешной работы предлагаю повторить только самые нужные знания!
Блицтурнир
1.Ася выше Тани. Кто из них ниже? ( Таня)
2. В банке столько же воды, сколько в кастрюле, а в кастрюле столько же воды, сколько в миске. Где больше воды: в банке или в миске? ( Поровну)
3. Лошадь темнее овцы. Овца темнее коровы. Кто светлее всех? ( Корова)
2. Работа с кассой.
Н 1+4 (5) Р 4- 2 (2) И 5+3 (8)
У 6-5 (1) Я 3+6 (9) А 9-6 (3)
Н 4+3 (7) Е 8-2 (6) В 0+4 (4)
Эталон 5 1 7 2 9 6 8 3 4
– Сверьте ответы с доской.
– На какие 2 группы можно распределить примеры?.(1 группа – примеры на сложение, находим целое; 2 группа – примеры на вычитание, находим часть.)
III. Работа по теме урока.
- Знакомство с уравнением.
А сейчас я Вам хочу предложить такое равенство- с окошком.
(…++2=8 4+ =9 НА ДОСКУ
Давайте попробуем его решить.
Кто знает, какое число спряталось в окошке? (6)
(Если к 6 прибавить 2, то получим 8)
Ребята, оказывается, у такого равенства есть своё название.
Может быть кто-нибудь знает, как называется такое равенство?.
Вы сможете его узнать, если справитесь со следующим заданием.
В паре 1 2 3 4 5 6 7 8 9
Вам нужно расположить получившиеся ответы в порядке возрастания, а затем вписать буквы и вы сможете прочитать название таких равенств
Итак, это слово УРАВНЕНИЯ.
Как вы думаете, какая же сегодня тема нашего урока? (Уравнения)
– Какую же цель поставим перед собой?
(Узнать, что такое уравнения и научиться их решать.)
-А может- быть кто-то хочет сформулировать определение, что же такое уравнение? (Равенства с окошками называют уравнениями.)
-А что обозначает окошко? (Неизвестное число)
Неизвестный компонент чаще всего в математике обозначают латинской буквой Х (икс).
Поставим его в “окошко” и получим равенство.
– х+2=8 – это уравнение.
Х=6 – корень уравнения.
Мы решили уравнения с помощью подбора.
Что значит решили?
(Подобрали такое число Х, при котором равенство верно.)
- Решение уравнения методом подбора.
Работа в учебнике на с.20 №1. Как вы думаете, что нужно сделать в этом задании?
– Надо подобрать предметы в мешок – часть, так, чтобы получилось верное равенство.
– Как называются такие равенства?
(Уравнения).
– Верно ли решено первое уравнение? Докажите.
– Подберите решение для второго уравнения.
– Подберите решение для третьего уравнения.
– Молодцы, вы все справились с заданием и теперь решите самостоятельно следующее уравнение.
№2
Проверка: Чему равен х? (Появляются разные ответы.)
(Возникла трудность: много фигур, они разной формы и цвета.)
– А в чем возникло затруднение? (Мы путаемся. Если фигур становится больше – труднее подбирать решение?)
– Значитметод подбора подходит для небольшого количества фигур, а для большого количества нужен другой способ.
Какая же наша задача? (Найти новый способ решения уравнений).
4. Решение уравнений на основе использования взаимосвязи между частью и целым.
Итак, наша цель – придумать, как по – другому найти неизвестную часть в уравнении, который можно использовать для решения любых уравнений.
Какими знаниями для решения можем воспользоваться?
(Знаем части и целое)
Правило1: Целое равно сумме частей.
Правило 2: Чтобы найти часть, надо из целого вычесть часть.
– А теперь каждый из вас должен догадаться какое из этих правил подойдет?
Применение правила (дети предлагают способ).
– Вычтите из обеих частей равенства поровну – фигурки из первого мешка.
Обозначим вычитание зачеркиванием. Удобно так искать неизвестное слагаемое?( Да)
– Какое правило нам помогло.(Нахождение части.)
V. Закрепление изученного.
1. Решение уравнений с комментированием
Тетрадь с 14 №1,2 ПЛАН. Алгоритм
Дети с помощью учителя составляют план для решения уравнений.
Учитель предлагает план проговаривания решения уравнений.
В этом уравнении части -:…и. целое – :.
Неизвестна часть. Чтобы найти неизвестную часть, надо из целого вычесть известную часть.
Х Равен разности::и::
Дети действуют по плану.
– Что было известно?(одна часть, целое.)
– Что требовалось найти?(Другую часть)
– Чему же равна неизвестная часть или х ?
-Смогли преодолеть затруднения?
– Что вам помогло? (Правило нахождения части.)
– Что позволяет вам открытый новый способ?(Решать уравнения)
Физминутка.
- Составление уравнений по рисунку.
-Посмотрим, получится ли применять новый способ нахождения неизвестного в похожих ситуациях.
Ребята, о какой величине идёт речь? (О массе)
У кого есть ошибки? В чем они? Сделайте вывод.
VI. Повторение пройденного.
VII. Итог урока.
Давайте оглянемся назад и вспомним, какую цель перед собой ставили.
(Узнать, что такое уравнение и научиться их решать)
– Достигли своей цели?(Да)
(Уравнение – это равенство с неизвестным числом и чтобы его решить надо следовать плану.Чтобы найти неизвестную часть надо из целого вычесть известную часть)
– Что дает нам новое знание?
(Научились сами и теперь можем научить других.)
Творческое задание: Для своего товарища можете сделать карточку с заданием на решение уравнения.
Просмотр содержимого документа
«Урок по математике (Л.Г.Петерсон) 1 класс»
Урок по математике (Л.Г.Петерсон)
Цель: Ввести понятие уравнение; сформировать способность к решению уравнений на основе взаимосвязи между частью и целым.
Актуализировать умение решать простые задачи на сложение и вычитание;
Тренировать автоматизированный навык счета в пределах9.
Развивать мыслительные операции необходимые на этапе проектирования: анализ, сравнение, синтез, обобщение.
Оборудование: интерактивная доска, компьютер, проектор, таблички со словами уравнение, корень уравнения, алгоритм комментирования решения уравнений.
-Проверим готовность к уроку. Я загадываю загадку, а вы показываете отгадку
Я с собой её ношу,
Не макаю, но пишу.
Я то в клетку, то в линейку,
Написать на мне сумей-ка!
Можешь и нарисовать.
Не куст, а с листочками,
Не рубашка , а сшита,
Не человек , а разговаривает.( книга, учебник)
– Итак к уроку вы готовы можем начать работу.
Ребята, сегодняшний урок я хочу начать такими словами:
В школу мы пришли учиться,
В жизни это пригодится.
Тот, кто хочет много знать,
Должен сам все постигать.
– Ребята, как Вы понимаете эти строки? Что значит: ученье в жизни пригодится. (Без знаний ничего не сделаешь.)
– Выделите главное слово в последних двух строчках и объясните свой выбор.
Слово “сам”, т.к. мы учимся тогда, когда сами понимаем, чего мы не знаем и сами открываем новые знания.)
II. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.
Для успешной работы предлагаю повторить только самые нужные знания!
1.Ася выше Тани. Кто из них ниже? ( Таня)
2. В банке столько же воды, сколько в кастрюле, а в кастрюле столько же воды, сколько в миске. Где больше воды: в банке или в миске? ( Поровну)
3. Лошадь темнее овцы. Овца темнее коровы. Кто светлее всех? ( Корова)
2. Работа с кассой.
Н 1+4 (5) Р 4- 2 (2) И 5+3 (8)
У 6-5 (1) Я 3+6 (9) А 9-6 (3)
Н 4+3 (7) Е 8-2 (6) В 0+4 (4)
Эталон 5 1 7 2 9 6 8 3 4
– Сверьте ответы с доской .
– На какие 2 группы можно распределить примеры?.(1 группа – примеры на сложение, находим целое; 2 группа – примеры на вычитание, находим часть.)
III. Работа по теме урока.
Знакомство с уравнением.
А сейчас я Вам хочу предложить такое равенство- с окошком.


Давайте попробуем его решить.
Кто знает, какое число спряталось в окошке? (6)
(Если к 6 прибавить 2, то получим 8)
Ребята, оказывается, у такого равенства есть своё название.
Может быть кто-нибудь знает, как называется такое равенство.
Вы сможете его узнать, если справитесь со следующим заданием.
В паре 1 2 3 4 5 6 7 8 9
Вам нужно расположить получившиеся ответы в порядке возрастания, а затем вписать буквы и вы сможете прочитать название таких равенств
Итак, это слово УРАВНЕНИЯ.
Как вы думаете, какая же сегодня тема нашего урока? (Уравнения)
– Какую же цель поставим перед собой?
(Узнать, что такое уравнения и научиться их решать.)
-А может- быть кто-то хочет сформулировать определение, что же такое уравнение? (Равенства с окошками называют уравнениями.)
-А что обозначает окошко? (Неизвестное число)
Неизвестный компонент чаще всего в математике обозначают латинской буквой Х (икс).
Поставим его в “окошко” и получим равенство.
– х+2=8 – это уравнение.
Х=6 – корень уравнения.
Мы решили уравнения с помощью подбора.
Что значит решили?
(Подобрали такое число Х, при котором равенство верно.)
Решение уравнения методом подбора.
Работа в учебнике на с.20 №1. Как вы думаете, что нужно сделать в этом задании?
– Надо подобрать предметы в мешок – часть, так, чтобы получилось верное равенство.
– Как называются такие равенства?
– Верно ли решено первое уравнение? Докажите.
– Подберите решение для второго уравнения.
– Подберите решение для третьего уравнения.
– Молодцы, вы все справились с заданием и теперь решите самостоятельно следующее уравнение.
Проверка: Чему равен х? (Появляются разные ответы.)
(Возникла трудность: много фигур, они разной формы и цвета.)
– А в чем возникло затруднение? (Мы путаемся. Если фигур становится больше – труднее подбирать решение?)
– Значитметод подбора подходит для небольшого количества фигур, а для большого количества нужен другой способ.
Какая же наша задача? (Найти новый способ решения уравнений).
4. Решение уравнений на основе использования взаимосвязи между частью и целым.
Итак, наша цель – придумать, как по – другому найти неизвестную часть в уравнении, который можно использовать для решения любых уравнений.
Какими знаниями для решения можем воспользоваться?
(Знаем части и целое)
Правило1: Целое равно сумме частей.
Правило 2: Чтобы найти часть, надо из целого вычесть часть.
– А теперь каждый из вас должен догадаться какое из этих правил подойдет?
Применение правила (дети предлагают способ).
– Вычтите из обеих частей равенства поровну – фигурки из первого мешка.
Обозначим вычитание зачеркиванием. Удобно так искать неизвестное слагаемое?( Да)
– Какое правило нам помогло.(Нахождение части.)
V. Закрепление изученного.
1. Решение уравнений с комментированием
Тетрадь с 14 №1,2 ПЛАН. Алгоритм
Дети с помощью учителя составляют план для решения уравнений.
Учитель предлагает план проговаривания решения уравнений.
В этом уравнении части -:…и. целое – :.
Неизвестна часть. Чтобы найти неизвестную часть, надо из целого вычесть известную часть.
Х Равен разности::и::
Дети действуют по плану.
– Что было известно?(одна часть, целое.)
– Что требовалось найти?(Другую часть)
– Чему же равна неизвестная часть или х ?
-Смогли преодолеть затруднения?
– Что вам помогло? (Правило нахождения части.)
– Что позволяет вам открытый новый способ?(Решать уравнения)
Составление уравнений по рисунку.
-Посмотрим, получится ли применять новый способ нахождения неизвестного в похожих ситуациях.
Ребята, о какой величине идёт речь? (О массе)
У кого есть ошибки? В чем они? Сделайте вывод..
VI. Повторение пройденного.
Давайте оглянемся назад и вспомним, какую цель перед собой ставили.
(Узнать, что такое уравнение и научиться их решать)
– Достигли своей цели?(Да)
(Уравнение – это равенство с неизвестным числом и чтобы его решить надо следовать плану.Чтобы найти неизвестную часть надо из целого вычесть известную часть)
– Что дает нам новое знание?
(Научились сами и теперь можем научить других.)
Творческое задание: Для своего товарища можете сделать карточку с заданием на решение уравнения.
Но сначала отгадайте, кто пришёл к нам в гости.
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/550333
http://kopilkaurokov.ru/nachalniyeKlassi/uroki/urok_po_matiematikie_l_g_pietierson_1_klass
[/spoiler]
|
|
Тема урока: Вычисление части.
Тип урока: Урок закрепления знаний: 1, 3, 4, 5, 6, 7, 14, 15
Цель урока
Закреплять умение находить значение части, закреплять знание о составе чисел
Задачи урока:
Образовательные: Учить находить неизвестную часть по известному целому и другой части
Развивающие: развивать внимание, память, логическое мышление, речь, творческие способности
Воспитательные: воспитывать интерес к предмету, чувство товарищества, взаимопонимания, взаимоуважения
Планируемые результаты
Предметные
Уметь находить неизвестную часть по известному целому и другой части
Личностные
Формирование мотива деятельности. Развитие готовности к сотрудничеству
Метапредметные
Коммуникативные
Умение слушать, получать необходимые сведения. Умение договориться, находить общее решение проблемы.
Регулятивные
Волевая саморегуляция. Корректировка выполнения заданий. Моделирование различные ситуации при решении задач
Познавательные
Умение осознанно строить высказывания. Формирование умений сравнивать, анализировать, обобщать по разным основаниям, моделировать выбор способов деятельности, группировать
Межпредметные связи
Окружающий мир
Ресурсы урока
Презентация
Формы урока
Фронтальная, индивидуальная, парная, групповая, …
УМК
Система Эльконина-Давыдова
Ход урока
Дидактическая
структура урока, с указанием времени
Деятельность
учителя
Деятельность
учеников
Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов
Планируемые результаты
Предметные УУД
Метапредметные УУД
1
Организационный этап, _____ мин
Настраивает учащихся на работу
Организуют рабочее место
Прозвенел звонок веселый.
Мы начать урок готовы.
Будем слушать, рассуждать,
И друг другу помогать.
Личностные
2
Актуализация знаний, _____ мин
Организует работу по устному счету в пределах 10
Находят часть по значению целого и другой части
– Как найти неизвестную часть?
– Найдите неизвестную часть: 10 – это 3 и…, 6 – это 1 и …, 2 – это 2 и …, 8 – это 4 и …, 4 – это 3 и …
Уметь устно считать в пределах 10
Коммуникативные, познавательные, регулятивные
3
Постановка цели и задач урока. Мотивация учебной деятельности учащихся, ____мин
Подводит к формулированию темы урока
Отвечают на вопросы
– Какое действие производили, чтобы найти часть? (вычитание)
-Объявите тему урока.
Уметь обобщать имеющиеся сведения
Регулятивные:
Оценивание: выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению
Познавательные
Формирование умения выдвигать гипотезы
5
Первичное усвоение новых знаний, _____ мин
Организует первичное усвоение знаний
Работают в тетрадях для доп.работ по учебнику
Работа по учебнику
с.101 №5 (письменно, коллективно)
– Прочитайте задание шепотом, скажите, как поняли задание
– Как найти недостающее число?
С.102 №6 (письменно, по цепочке)
– Что нужно узнавать сложением? А что вычитанием?
– Какое правило знаем? (чтобы найти целое надо сложить части; чтобы найти часть нужно из целого вычесть другую часть)
Уметь разбивать целое на части, находить значение целого и частей, решать примеры в пределах 10, знать состав чисел до 10
8
Творческое применение и добывание знаний в новой ситуации, _____ мин
Организует самостоятельную работу
Работают самостоятельно с последующей проверкой
Работа в тетрадях на печатной основе с.27 №1, 2, 5
№1 – узнай длину отрезков
№2 – повтори состав числа 7
№5 – найди значение выражений, которые соответствуют схеме
15
Рефлексия, подведение итогов занятия _____ мин
Подводит учащихся к определению своего уровня знания-незнания по теме урока
Подводят итог
– Чему учились на уроке?
– Что понравилось? В чем затруднялись? Что нового узнали?
– Оцените работу на уроке с помощью веера цифр:
«5» – все понял, «4» – не совсем понял, «3» – почти ничего не понял.
Самооценка
Коммуникативные, личностные
