Как найти неизвестную длину стороны треугольника - Сайт, где вы сможете решить свои вопросы

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a, b, c – стороны произвольного треугольника

α, β, γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), (a):

* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), (a):

Есть следующие формулы для определения катета или гипотенузы

a, b – катеты

c – гипотенуза

α, β – острые углы

Формулы для катета, (a):

Формулы для катета, (b):

Формулы для гипотенузы, (c):

Формулы сторон по теореме Пифагора, (a,b):

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b):

Формулы длины равных сторон , (a):

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β, γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, (H):

Формула длины высоты через сторону и угол, (H):

Формула длины высоты через сторону и площадь, (H):

Формула длины высоты через стороны и радиус, (H):

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.

H – высота из прямого угла

a, b – катеты

с – гипотенуза

c₁, c₂ – отрезки полученные от деления гипотенузы, высотой

α, β – углы при гипотенузе

Формула длины высоты через стороны, (H):

Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через катет и угол, (H):

Формула длины высоты через составные отрезки гипотенузы , (H):

L– биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b – стороны треугольника

с – сторона на которую опущена биссектриса

d, e – отрезки полученные делением биссектрисы

γ – угол ABC , разделенный биссектрисой пополам

p – полупериметр, p=(a+b+c)/2

Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через стороны и отрезки d, e, (L):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

L – биссектриса, отрезок ME , исходящий из прямого угла (90 град)

a, b – катеты прямоугольного треугольника

с – гипотенуза

α – угол прилежащий к гипотенузе

Формула длины биссектрисы через катеты, ( L):

Формула длины биссектрисы через гипотенузу и угол, ( L):

2. Найти по формулам длину биссектрисы из острого угла на катет:

L – биссектриса, отрезок ME , исходящий из острого угла

a, b – катеты прямоугольного треугольника

с – гипотенуза

α, β – углы прилежащие к гипотенузе

Формулы длины биссектрисы через катет и угол, (L):

Формула длины биссектрисы через катет и гипотенузу, (L):

L – высота = биссектриса = медиана

a – одинаковые стороны треугольника

b – основание

α – равные углы при основании

β – угол образованный равными сторонами

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

Формула высоты, биссектрисы и медианы, через стороны, (L):

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L – высота=биссектриса=медиана

a – сторона треугольника

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.

Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M – медиана, отрезок |AO|

c – сторона на которую ложится медиана

a, b – стороны треугольника

γ – угол CAB

Формула длины медианы через три стороны, (M):

Формула длины медианы через две стороны и угол между ними, (M):

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.

Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M – медиана

R – радиус описанной окружности

O – центр описанной окружности

с – гипотенуза

a, b – катеты

α – острый угол CAB

Медиана равна радиусу и половине гипотенузы, (M):

Формула длины через катеты, (M):

Формула длины через катет и острый угол, (M):

Источник

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

Найти все стороны треугольника.
Найти все углы треугольника.
Найти площадь (S) и периметр (P) треугольника.
Найти радиус (r) вписанной окружности.
Найти радиус (R) описанной окружности.
Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.

Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b – катеты, с – гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b – катеты, с – гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.

Для равностороннего треугольника:

1) Найти сторону через площадь

где a – искомая сторона, S – площадь треугольника.

2) Найти сторону через высоту

где a – искомая сторона,h – высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a – искомая сторона,r – радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a – искомая сторона,R – радиус описанной окружности.

Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a – искомая сторона, b – известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word

Источник

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника

α , β , γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b – катеты

c – гипотенуза

α , β – острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β , γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Треугольник. Формулы определения и свойства треугольников.

В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры – треугольника. А также разберем некоторе примеры решения задач на треугольники.

Содержание:

Определение треугольника

Треугольник – это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом – △, после которго пишут названия вершин треугольника напр. △ABC.

Треугольник ABC (△ABC)

Точки A, B и C – вершины треугольника. Принято писать их большими буквами.
Отрезки AB, BC и СА – стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b – β, с – γ.

Углы треугольника, также, можно обозначать специальным символом – ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:

Классификация треугольников

Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.

1.Разносторонний – треугольник, у которого все стороны имеют разную длину.

2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β

3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°

5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).

Свойства треугольника

1.Свойства углов и сторон треугольника.

Сумма всех углов треугольника равна 180°:

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

2.Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c
sin α	sin β	sin γ

3. Теорема косинусов.

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

4. Теорема о проекциях

Для остроугольного треугольника:

Медианы треугольника

Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника:

1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)

2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

AO	=	BO	=	CO	=	2
OD	OE	OF	1

3. Медиана треугольника делит треугольник на две равновеликие по площади части

4. Треугольник делится тремя медианами на шесть равновеликих треугольников.

5. Из векторов, образующих медианы, можно составить треугольник.

Формулы медиан треугольника

Формулы медиан треугольника через стороны:

Как найти третью сторону треугольника — формулы и расчеты

В геометрии первая фигура, которую школьники начинают изучать, это треугольник. Он является одним из самых распространенных и простых замкнутых объектов. Знание свойств фигуры и необходимых теорем позволяет решать разные задачи о том, как найти третью сторону треугольника на плоскости.

Фигура из шести элементов

Под геометрическим элементом полагают какой-либо объект, который имеет определенную меру и является составляющей частью некоторой фигуры. Например, для сферы основными образующими элементами являются радиус и центр.

Как известно, треугольник — это фигура, которая состоит из трех отрезков и такого же количества вершин. При этом все отрезки попарно пересекаются. Из определения фигуры следует, что ее образуют два типа элементов, общее количество которых составляет 6:

сторона (3);
вершина (3).

Обычно треугольник обозначают большими латинскими буквами, например, ABC, PQM и так далее. Каждая буква — это название вершины (точка пересечения двух отрезков). AB, BC и CA, которые являются длинами сторон, принято обозначать маленькими латинскими буквами по названию противоположных им вершин, то есть c, a и b, соответственно.

Дополнительные отрезки

Несмотря на всю простоту построения фигуры, она обладает большим количеством дополнительных элементов, которые ее могут определять. Среди них самыми важными являются следующие:

Медиана — отрезок, который соединяет вершину и середину противоположной стороны. Таких отрезков в треугольнике три. Все они пересекаются в одной точке, которая является центром масс фигуры. Эта точка делит каждую медиану в отношении 2:1, начиная от вершины. Каждый из трех названных отрезков делит треугольник на две аналогичных фигуры равной площади.

Биссектриса — отрезок, который отличается от медианы тем, что он делит пополам соответствующий угол.

Высота — перпендикуляр, который из вершины опускается на сторону фигуры. Его удобно использовать при вычислении площади или при определении его углов через тригонометрические выражения. Для некоторых типов треугольников высота может совпадать со стороной (катет в прямоугольной фигуре).

Радиусы вписанной и описанной окружностей. Эти замкнутые симметричные кривые можно провести для любого треугольника. Указанные радиусы однозначно определяются через стороны и углы фигуры.

Средняя линия — это соединяющий две середины сторон отрезок. Его особенность заключается в том, что он всегда параллелен третьей стороне и равен половине ее длины.

Виды треугольников

Разработана достаточно развитая классификация рассматриваемых фигур. Главными ее пунктами являются значения углов треугольника и взаимоотношение между его отрезками. Так, если в фигуре все углы острые, то она называется остроугольной. Если же один из углов больше 90 °, то треугольник полагается тупоугольным. Чаще всего в задачах рассматривают следующие виды:

Основные свойства и понятия

Треугольник является одной из самых изученных фигур в геометрии. Для него известны многие теоремы, которые с успехом используются при решении задач. Существует два основных свойства фигуры, которые следуют из характеристик евклидового пространства:

Равенство суммы трех углов 180 °, то есть A + B + C = 180 °. Этот факт доказал еще Евклид в своем знаменитом труде «Элементы». По этой причине треугольник не может содержать больше одного прямого или тупого внутреннего угла.

Если известны три отрезка a, b и c такие, что выполняется равенство a + b = c, то из них составить треугольник невозможно. Это фундаментальное свойство говорит о том, что для всякого типа рассматриваемой фигуры сумма длин ее двух любых сторон всегда больше длины третьей.

Помимо названных свойств, следует знать о треугольнике еще такое понятие, как подобие. Его суть состоит в том, что одна из рассматриваемых фигур является точной копией в миниатюре другой. Для подобных треугольников все углы равны попарно, а все три стороны относятся соответственно попарно друг к другу с одним и тем же коэффициентом подобия.

Еще одной полезной характеристикой рассматриваемой фигуры является ее качество (CT). Вычисляется оно по следующей формуле:

CT = (a + b — c)*(b + c — a)*(c + a — b)/(a*b*c).

Величина CT лежит в пределах от 0 до 1. Она показывает степень близости фигуры к равностороннему, то есть к наиболее симметричному объекту. Если CT 0,5, то фигура характеризуется, как имеющая хорошее качество.

Величина CT применяется для алгоритмов, которые разделяют какую-либо изучаемую геометрическую поверхность на сетку треугольников. Если в этой сетке генерируется много низкокачественных фигур, то будет велика ошибка аппроксимации рассматриваемой величины.

Важные теоремы

Знание теорем для рассматриваемой фигуры позволяет понять, как найти сторону, зная 2 стороны треугольника. Прежде всего применяются две базовые теоремы:

Синусов. Как известно, синус — это тригонометрическая функция, которая вводится в прямоугольном треугольнике и определяет отношение противолежащего углу катета к гипотенузе. Теорема синусов для фигуры произвольного типа устанавливает следующее математическое взаимоотношение между отрезками и углами: a/sinA = b/sinB = c/sinC. Это означает, что вычислить длину любой стороны можно, если известен еще какой-нибудь отрезок и два угла.

Косинусов. Как и синус, косинус тоже является тригонометрической функцией, которая определяет отношение катета прилежащего к гипотенузе прямоугольной фигуры. Теорему косинусов удобно записать в виде следующего математического выражения: c 2 = a 2 + b 2 — 2*a*b*cosC. С помощью этого равенства можно найти 3 сторону треугольника по 2 сторонам известным и углу между ними.

К этим двум теоремам следует добавить еще два важных равенства, которые связаны с именами древнегреческих философов.

Первое выражение базируется на знаменитой теореме Пифагора, которая устанавливает связь между длинами двух катетов (меньшие стороны) и гипотенузы (большая сторона) в треугольнике с прямым углом. Если гипотенузу обозначить буквой c, тогда будет выполняться следующее равенство:

Если известные любые две стороны, то для определения третьей достаточно взять под квадратный корень соответствующую сумму или разницу квадратов.

Вторая из дополнительных теорем носит название философа Аполлония Пергского. Соответствующее ей математическое выражение выглядит так:

a 2 + b 2 = ½*c 2 + 2*Mc 2 .

Здесь Mc — это медиана, проведенная к стороне c из вершины C. Это равенство также называют в математике теоремой медианы.

Примеры решения задач

После того как изучены и рассмотрены основные понятия, свойства и теоремы для различного рода треугольников, можно переходить к решению геометрических задач. Поскольку для этого требуется в большинстве случаев знать значения тригонометрических функций, рекомендуется воспользоваться либо соответствующими таблицами, либо инженерным калькулятором.

Задачи школьного курса с треугольниками, как правило, не являются сложными. Они решаются благодаря однократному применению какого-либо свойства или теоремы.

Квадрат и его диагональ

Пусть дан квадрат, сторона которого составляет 11 см. Необходимо определить половину длины его диагонали.

Эту геометрическую задачу проще всего решить, если увидеть, что две смежные стороны исходной фигуры и ее диагональ образуют прямоугольный треугольник, который к тому же является равнобедренным. Каждая из равных сторон в нем имеет длину 11 см и является катетом. Диагональ c — это гипотенуза. Применяя пифагорову теорему, можно получить следующее равенство:

c = (11 2 + 11 2 )^0,5 ≈ 15,556 см.

Поскольку половина диагонали в два раза меньше гипотенузы, то искомым ответом на задачу будет число c/2 ≈ 7,778 см.

Две высоты и угол

Дан треугольник ABC. Известно, что при вершине C угол составляет 37 °. Из вершин A и B проведены высоты к сторонам этого треугольника, их длины составляют h1 = 10 см и h2 = 8 см, соответственно. Необходимо узнать длину стороны фигуры, которая лежит против угла C.

Из условия задачи можно найти длины сторон AC и BC. Для этого следует увидеть, что каждая из высот с двумя другими сторонами треугольника образует прямоугольную фигуру. Воспользовавшись тригонометрическими равенствами, можно получить следующие результаты:

AC = h1/sinC = 10/sin (37 °) ≈ 16,616 см;
BC = h2/sinC = 8/sin (37 °) ≈ 13,293 см.

Против угла C лежит сторона AB, которую следует найти. Получается, что известны две стороны треугольника (AC и BC) и угол между ними. Остается применить теорему косинусов, чтобы получить ответ:

AB = (AC 2 + BC 2 — 2*AC*BC*cosC)^0,5 = (16,616 2 + 13,293 2 — 2* 16,616 * 13,293 *cos (37 °))^0,5 ≈ 10 см.

Полученный результат свидетельствует о том, что высота h1 совпадает со стороной AB с рассчитанной точностью, то есть исходный треугольник являлся прямоугольным.

Таким образом, для нахождения стороны треугольника, если известны две другие его стороны или иные отрезки, следует воспользоваться теоремами. Основными из них являются теорема косинусов и синусов, а также Пифагора и Аполлония.

[spoiler title=”источники:”]

http://binary2hex.ru/triangle.html

http://sprint-olympic.ru/uroki/geometrija/128034-kak-naiti-tretu-storony-treygolnika-formyly-i-raschety.html

[/spoiler]

Источник

Исторический термин «решение треугольников» (лат. solutio triangulorum) обозначает решение следующей тригонометрической задачи: найти остальные стороны и/или углы треугольника по уже известным^[1]. Существуют также обобщения этой задачи на случай, когда заданы другие элементы треугольника (например, медианы, биссектрисы, высоты, площадь и т. д.), а также на случай, когда треугольник располагается не на евклидовой плоскости, а на сфере (сферический треугольник), на гиперболической плоскости (гиперболический треугольник) и т. п. Данная задача часто встречается в тригонометрических приложениях — например, в геодезии, астрономии, строительстве, навигации.

Решение плоских треугольников[править | править код]

Стандартные обозначения в треугольнике

У треугольника^[2] общего вида имеется 6 основных элементов: 3 линейные (длины сторон a,b,c ) и 3 угловые (). Сторону, противолежащую углу при вершине, традиционно обозначают той же буквой, что и эта вершина, но не заглавной, а строчной (см. рисунок). В классической задаче плоской тригонометрии заданы 3 из этих 6 характеристик, и нужно определить 3 остальные. Очевидно, если известны только 2 или 3 угла, однозначного решения не получится, так как любой треугольник, подобный данному, тоже будет решением, поэтому далее предполагается, что хотя бы одна из известных величин — линейная^[3].

Алгоритм решения задачи зависит от того, какие именно характеристики треугольника считаются известными. Поскольку вариант «заданы три угла» исключён из рассмотрения, остаются 5 различных вариантов^[4]:

три стороны;
две стороны и угол между ними;
две стороны и угол напротив одной из них;
сторона и два прилежащих угла;
сторона, противолежащий угол и один из прилежащих.

Основные теоремы[править | править код]

Стандартным методом решения задачи является использование нескольких фундаментальных соотношений, выполняющихся для всех плоских треугольников^[5]:

Теорема косинусов: ${displaystyle a^{2}=b^{2}+c^{2}-2bccdot cos alpha }$; ${displaystyle b^{2}=a^{2}+c^{2}-2accdot cos beta }$; ${displaystyle c^{2}=a^{2}+b^{2}-2abcdot cos gamma }$
Теорема синусов: ${frac {a}{sin alpha }}={frac {b}{sin beta }}={frac {c}{sin gamma }}$
Сумма углов треугольника: $alpha +beta +gamma =180^{circ }$

Из других иногда полезных на практике универсальных соотношений следует упомянуть теорему тангенсов, теорему котангенсов, теорему о проекциях и формулы Мольвейде.

Замечания[править | править код]

Для нахождения неизвестного угла надёжнее использовать теорему косинусов, а не синусов, потому что значение синуса угла при вершине треугольника не определяет однозначно самого угла, поскольку смежные углы имеют один и тот же синус^[6]. Например, если то угол может быть как $30^{circ }$ , так и $150^{circ }$ , потому что синусы этих углов совпадают. Исключением является случай, когда заранее известно, что в данном треугольнике тупых углов быть не может — например, если треугольник прямоугольный. С косинусом такие проблемы не возникают: в интервале от $0^{circ }$ до $180^{circ }$ значение косинуса определяет угол однозначно.
При построении треугольников важно помнить, что зеркальное отражение построенного треугольника тоже будет решением задачи. Например, три стороны однозначно определяют треугольник с точностью до отражения.
Все треугольники подразумеваются невырожденными, то есть длина стороны не может быть нулевой, а величина угла — положительное число, меньшее, чем $180^{circ }$ .

Три стороны[править | править код]

Пусть заданы длины всех трёх сторон a,b,c . Условие разрешимости задачи — выполнение неравенства треугольника, то есть каждая длина должна быть меньше, чем сумма двух других длин:

{displaystyle a<b+c,quad b<a+c,quad c<a+b.}

Чтобы найти углы , надо воспользоваться теоремой косинусов^[7]:

${displaystyle alpha =arccos {frac {b^{2}+c^{2}-a^{2}}{2bc}},quad beta =arccos {frac {a^{2}+c^{2}-b^{2}}{2ac}}.}$

Третий угол сразу находится из правила, что сумма всех трёх углов должна быть равна ${displaystyle 180^{circ }colon }$

${displaystyle gamma =180^{circ }-(alpha +beta ).}$

Не рекомендуется второй угол находить по теореме синусов, потому что, как указано в замечании 1, существует опасность спутать тупой угол с острым. Этой опасности не возникнет, если первым определить, по теореме косинусов, наибольший угол (он лежит против наибольшей из сторон) — два других угла точно являются острыми, и применение к ним теоремы синусов безопасно.

Ещё один метод вычисления углов по известным сторонам — использование теоремы котангенсов.

Заданы две стороны и угол между ними

Две стороны и угол между ними[править | править код]

Пусть для определённости известны длины сторон a,b и угол gamma между ними. Этот вариант задачи всегда имеет единственное решение. Для определения длины стороны применяется теорема косинусов^[8]:

${displaystyle c={sqrt {a^{2}+b^{2}-2abcos gamma }}.}$

Фактически задача сведена к предыдущему случаю. Далее ещё раз применяется теорема косинусов для нахождения второго угла:

${displaystyle alpha =arccos {frac {b^{2}+c^{2}-a^{2}}{2bc}}=arccos {frac {b-acos gamma }{sqrt {a^{2}+b^{2}-2abcos gamma }}}.}$

Третий угол находится из теоремы о сумме углов треугольника: $beta =180^{circ }-alpha -gamma$ .

Заданы две стороны и угол не между ними

Две стороны и угол напротив одной из них[править | править код]

В этом случае решений может быть два, одно или ни одного. Пусть известны две стороны b,c и угол beta . Тогда уравнение для угла gamma находится из теоремы синусов^[9]:

${displaystyle sin gamma ={frac {c}{b}}sin beta .}$

Для краткости обозначим ${displaystyle D={frac {c}{b}}sin beta }$ (правая часть уравнения). Это число всегда положительно. При решении уравнения возможны 4 случая, во многом зависящие от D^[10]^[11].

Задача не имеет решения (сторона «не достаёт» до линии ) в двух случаях: если или если угол $beta geqslant 90^{circ }$ и при этом
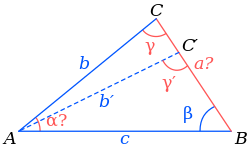
Если существует единственное решение, причём треугольник прямоугольный: ${displaystyle gamma =arcsin D=90^{circ }.}$

Если то возможны 2 варианта.
1. Если , то угол имеет два возможных значения: острый угол и тупой угол ${displaystyle gamma '=180^{circ }-gamma }$ . На рисунке справа первому значению соответствуют точка , сторона и угол , а второму значению — точка , сторона и угол .
2. Если , то (большей стороне треугольника соответствует больший противолежащий угол). Поскольку в треугольнике не может быть двух тупых углов, тупой угол для исключён и решение единственно.

Третий угол определяется по формуле ${displaystyle alpha =180^{circ }-beta -gamma }$ . Третью сторону можно найти по теореме синусов:

$a=b {frac {sin alpha }{sin beta }}$

В данном случае заданы сторона и прилежащие к ней углы. Аналогичные рассуждения имеют смысл, даже если один из известных углов противоположен стороне.

Сторона и два угла[править | править код]

Пусть задана сторона и два угла. Эта задача имеет единственное решение, если сумма двух углов меньше $180^{circ }$ . В противном случае задача решения не имеет.

Вначале определяется третий угол. Например, если даны углы , то ${displaystyle gamma =180^{circ }-alpha -beta }$ . Далее обе неизвестные стороны находятся по теореме синусов^[12]:

${displaystyle a=c {frac {sin alpha }{sin gamma }},quad b=c {frac {sin beta }{sin gamma }}.}$

Решение прямоугольных треугольников[править | править код]

Прямоугольный треугольник

В этом случае известен один из углов — он равен 90°. Необходимо знать ещё два элемента, хотя бы один из которых — сторона. Возможны следующие случаи:

два катета;
катет и гипотенуза;
катет и прилежащий острый угол;
катет и противолежащий острый угол;
гипотенуза и острый угол.

Вершину прямого угла традиционно обозначают буквой , гипотенузу — . Катеты обозначаются и , а величины противолежащих им углов — alpha и beta соответственно.

Расчётные формулы существенно упрощаются, так как вместо теорем синусов и косинусов можно использовать более простые соотношения — теорему Пифагора:

$c^{2}=a^{2}+b^{2}$

и определения основных тригонометрических функций:

$sin alpha =cos beta ={frac {a}{c}},quad cos alpha =sin beta ={frac {b}{c}},$

${displaystyle operatorname {tg} alpha =operatorname {ctg} beta ={frac {a}{b}},quad operatorname {ctg} alpha =operatorname {tg} beta ={frac {b}{a}}.}$

Ясно также, что углы alpha и beta — острые, так как их сумма равна $90^{circ }$ . Поэтому любой из неизвестных углов однозначно определяется по любой из его тригонометрических функций (синусу, косинусу, тангенсу и др.) путём вычисления соответствующей обратной тригонометрической функции.

При корректной постановке задачи (если заданы гипотенуза и катет, то катет должен быть меньше гипотенузы; если задан один из двух непрямых углов, то он должен быть острый) решение всегда существует и единственно.

Два катета[править | править код]

Гипотенуза находится по теореме Пифагора:

$c={sqrt {a^{2}+b^{2}}}.$

Углы могут быть найдены с использованием функции арктангенса:

${displaystyle alpha =operatorname {arctg} {frac {a}{b}},quad beta =operatorname {arctg} {frac {b}{a}}}$

или же по только что найденной гипотенузе:

$alpha =arcsin {frac {a}{c}}=arccos {frac {b}{c}},quad beta =arcsin {frac {b}{c}}=arccos {frac {a}{c}}.$

Катет и гипотенуза[править | править код]

Пусть известны катет и гипотенуза — тогда катет находится из теоремы Пифагора:

$a={sqrt {c^{2}-b^{2}}}.$

После этого углы определяются аналогично предыдущему случаю.

Катет и прилежащий острый угол[править | править код]

Пусть известны катет и прилежащий к нему угол alpha .

Гипотенуза находится из соотношения

$c={frac {b}{cos alpha }}.$

Катет может быть найден либо по теореме Пифагора аналогично предыдущему случаю, либо из соотношения

Острый угол beta может быть найден как

$beta =90^{circ }-alpha .$

Катет и противолежащий острый угол[править | править код]

Пусть известны катет и противолежащий ему угол beta .

Гипотенуза находится из соотношения

$c={frac {b}{sin beta }}.$

Катет и второй острый угол alpha могут быть найдены аналогично предыдущему случаю.

Гипотенуза и острый угол[править | править код]

Пусть известны гипотенуза и острый угол beta .

Острый угол alpha может быть найден как

$alpha =90^{circ }-beta .$

Катеты определяются из соотношений

Решение сферических треугольников[править | править код]

Стороны сферического треугольника a,b,c измеряют величиной опирающихся на них центральных углов

Сферический треугольник общего вида полностью определяется тремя из шести своих характеристик (3 стороны и 3 угла). Стороны сферического треугольника a,b,c принято измерять не линейными единицами, а величиной опирающихся на них центральных углов.

Решение треугольников в сферической геометрии имеет ряд отличий от плоского случая. Например, сумма трёх углов зависит от треугольника; кроме того, на сфере не существует неравных подобных треугольников, и поэтому задача построения треугольника по трём углам имеет единственное решение. Но основные соотношения: две сферические теоремы косинусов и сферическая теорема синусов, — используемые для решения задачи, аналогичны плоскому случаю.

Из других соотношений могут оказаться полезными формулы аналогии Непера^[13] и формула половины стороны^[14].

Три стороны[править | править код]

Если даны (в угловых единицах) стороны a,b,c , то углы треугольника определяются из теоремы косинусов^[15]:

$alpha =arccos left({frac {cos a-cos b cos c}{sin b sin c}}right)$

$beta =arccos left({frac {cos b-cos c cos a}{sin c sin a}}right)$

$gamma =arccos left({frac {cos c-cos a cos b}{sin a sin b}}right)$

Заданы две стороны и угол между ними

Две стороны и угол между ними[править | править код]

Пусть заданы стороны a,b и угол gamma между ними. Сторона находится по теореме косинусов^[15]:

c=arccos left(cos acos b+sin asin bcos gamma right)

Углы можно найти так же, как в предыдущем случае, можно также использовать формулы аналогии Непера:

${displaystyle alpha =operatorname {arctg} {frac {2sin a}{operatorname {tg} ({frac {gamma }{2}})sin(b+a)+operatorname {ctg} ({frac {gamma }{2}})sin(b-a)}},}$

${displaystyle beta =operatorname {arctg} {frac {2sin b}{operatorname {tg} ({frac {gamma }{2}})sin(a+b)+operatorname {ctg} ({frac {gamma }{2}})sin(a-b)}}.}$

Заданы две стороны и угол не между ними

Две стороны и угол не между ними[править | править код]

Пусть заданы стороны b,c и угол beta . Чтобы решение существовало, необходимо выполнение условия:

{displaystyle b>arcsin(sin c,sin beta ).}

Угол gamma получается из теоремы синусов:

${displaystyle gamma =arcsin left({frac {sin c,sin beta }{sin b}}right).}$

Здесь, аналогично плоскому случаю, при b<c получаются два решения: gamma и ${displaystyle 180^{circ }-gamma }$ .

Остальные величины можно найти из формул аналогии Непера^[16]:

$a=2operatorname {arctg} left{operatorname {tg} left({frac {1}{2}}(b-c)right){frac {sin left({frac {1}{2}}(beta +gamma )right)}{sin left({frac {1}{2}}(beta -gamma )right)}}right}$

$alpha =2operatorname {arcctg} left{operatorname {tg} left({frac {1}{2}}(beta -gamma )right){frac {sin left({frac {1}{2}}(b+c)right)}{sin left({frac {1}{2}}(b-c)right)}}right}$

Заданы сторона и прилежащие углы

Сторона и прилежащие углы[править | править код]

В этом варианте задана сторона и углы . Угол gamma определяется по теореме косинусов^[17]:

{displaystyle gamma =arccos(sin alpha sin beta cos c-cos alpha cos beta ).}

Две неизвестные стороны получаются из формул аналогии Непера:

$a=operatorname {arctg} left{{frac {2sin alpha }{operatorname {ctg} (c/2)sin(beta +alpha )+operatorname {tg} (c/2)sin(beta -alpha )}}right}$

$b=operatorname {arctg} left{{frac {2sin beta }{operatorname {ctg} (c/2)sin(alpha +beta )+operatorname {tg} (c/2)sin(alpha -beta )}}right}$

или, если использовать вычисленный угол gamma , по теореме косинусов:

${displaystyle a=arccos left({frac {cos alpha +cos beta cos gamma }{sin beta sin gamma }}right),}$

${displaystyle b=arccos left({frac {cos beta +cos gamma cos alpha }{sin gamma sin alpha }}right).}$

Заданы два угла и сторона не между ними

Два угла и сторона не между ними[править | править код]

В отличие от плоского аналога данная задача может иметь несколько решений.

Пусть заданы сторона и углы . Сторона определяется по теореме синусов^[18]:

${displaystyle b=arcsin left({frac {sin a,sin beta }{sin alpha }}right).}$

Если угол для стороны острый и , существует второе решение:

${displaystyle b=pi -arcsin left({frac {sin a,sin beta }{sin alpha }}right).}$

Остальные величины определяются из формул аналогии Непера:

${displaystyle c=2operatorname {arctg} left{operatorname {tg} left({frac {1}{2}}(a-b)right){frac {sin left({frac {1}{2}}(alpha +beta )right)}{sin left({frac {1}{2}}(alpha -beta )right)}}right}.}$

${displaystyle gamma =2operatorname {arcctg} left{operatorname {tg} left({frac {1}{2}}(alpha -beta )right){frac {sin left({frac {1}{2}}(a+b)right)}{sin left({frac {1}{2}}(a-b)right)}}right}.}$

Три угла[править | править код]

Если заданы три угла, стороны находятся по теореме косинусов:

$a=arccos left({frac {cos alpha +cos beta cos gamma }{sin beta sin gamma }}right)$

$b=arccos left({frac {cos beta +cos gamma cos alpha }{sin gamma sin alpha }}right)$

$c=arccos left({frac {cos gamma +cos alpha cos beta }{sin alpha sin beta }}right)$

Другой вариант: использование формулы половины угла^[19].

Решение прямоугольных сферических треугольников[править | править код]

Изложенные алгоритмы значительно упрощаются, если известно, что один из углов треугольника (например, угол ) прямой. Прямоугольный сферический треугольник полностью определяется двумя элементами, остальные три находятся при помощи мнемонического правила Непера или из нижеприведённых соотношений^[20]:

{displaystyle sin a=sin ccdot sin alpha =operatorname {tg} bcdot operatorname {ctg} beta ,}

{displaystyle sin b=sin ccdot sin beta =operatorname {tg} acdot operatorname {ctg} alpha ,}

{displaystyle cos c=cos acdot cos b=operatorname {ctg} alpha cdot operatorname {ctg} beta ,}

{displaystyle operatorname {tg} a=sin bcdot operatorname {tg} alpha ,}

{displaystyle operatorname {tg} b=operatorname {tg} ccdot cos alpha ,}

{displaystyle cos alpha =cos acdot sin beta =operatorname {tg} bcdot operatorname {ctg} c,}

{displaystyle cos beta =cos bcdot sin alpha =operatorname {tg} acdot operatorname {ctg} c.}

Вариации и обобщения[править | править код]

Во многих практически важных задачах вместо сторон треугольника задаются другие его характеристики — например, длина медианы, высоты, биссектрисы, радиус вписанного или описанного круга и т. д. Аналогично вместо углов при вершинах треугольника в задаче могут фигурировать иные углы. Алгоритмы решения подобных задач чаще всего комбинируются из рассмотренных выше теорем тригонометрии.

Примеры:

Примеры практического применения[править | править код]

Триангуляция[править | править код]

Чтобы определить расстояние от берега до недоступной точки — например, до удалённого корабля,— нужно отметить на берегу две точки, расстояние между которыми известно, и измерить углы alpha и beta между линией, соединяющей эти точки, и направлением на корабль. Из формул варианта «сторона и два угла» можно найти длину высоты треугольника^[23]:

$d={frac {sin alpha ,sin beta }{sin(alpha +beta )}},l={frac {operatorname {tg} alpha ,operatorname {tg} beta }{operatorname {tg} alpha +operatorname {tg} beta }},l$

Этот метод используется в каботажном судоходстве. Углы при этом оцениваются наблюдениями с корабля известных ориентиров на земле. Аналогичная схема используется в астрономии, чтобы определить расстояние до близкой звезды: измеряются углы наблюдения этой звезды с противоположных точек земной орбиты (то есть с интервалом в полгода) и по их разности (параллаксу) вычисляют искомое расстояние^[23].

Другой пример: требуется измерить высоту горы или высокого здания. Известны углы наблюдения вершины из двух точек, расположенных на расстоянии . Из формул того же варианта, что и выше, получается^[24]:

$h={frac {sin alpha ,sin beta }{sin(beta -alpha )}},l={frac {operatorname {tg} alpha ,operatorname {tg} beta }{operatorname {tg} beta -operatorname {tg} alpha }},l$

Расстояние между двумя точками на поверхности земного шара[править | править код]

Надо вычислить расстояние между двумя точками на земном шаре^[25]:

Точка

: широта $lambda _{mathrm {A} },$

долгота $L_{mathrm {A} },$

Точка

: широта $lambda _{mathrm {B} },$

долгота $L_{mathrm {B} },$

Для сферического треугольника ABC , где — северный полюс, известны следующие величины:

${displaystyle a=90^{mathrm {o} }-lambda _{mathrm {B} }}$

${displaystyle b=90^{mathrm {o} }-lambda _{mathrm {A} }}$

${displaystyle gamma =L_{mathrm {A} }-L_{mathrm {B} }}$

Это случай «две стороны и угол между ними». Из приведенных выше формул получается:

$mathrm {AB} =Rarccos left{sin lambda _{mathrm {A} },sin lambda _{mathrm {B} }+cos lambda _{mathrm {A} },cos lambda _{mathrm {B} },cos left(L_{mathrm {A} }-L_{mathrm {B} }right)right}$

где — радиус Земли.

История[править | править код]

Зачатки тригонометрических знаний можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора; Ван дер Варден считает, что вавилоняне открыли его между 2000 и 1786 годами до н. э.^[26]

Общая постановка задачи решения треугольников (как плоских, так и сферических) появилась в древнегреческой геометрии^[27]. Во второй книге «Начал» Евклида теорема 12 представляет собой словесный аналог теоремы косинусов для тупоугольных треугольников^[28]:

В тупоугольных треугольниках квадрат на стороне, стягивающей тупой угол, больше [суммы] квадратов на сторонах, содержащих тупой угол, на дважды взятый прямоугольник, заключённый между одной из сторон при тупом угле, на которую падает перпендикуляр, и отсекаемым этим перпендикуляром снаружи отрезком при тупом угле.

Следующая за ней теорема 13 — вариант теоремы косинусов для остроугольных треугольников. Аналога теоремы синусов у греков не было, это важнейшее открытие было сделано гораздо позднее^[29]: древнейшее из дошедших до нас доказательств теоремы синусов на плоскости описано в книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике», написанной в XIII веке^[30].

Первые тригонометрические таблицы составил, вероятно, Гиппарх в середине II века до н. э. для астрономических расчётов. Позднее астроном II века Клавдий Птолемей в «Альмагесте» дополнил результаты Гиппарха. Первая книга «Альмагеста» — самая значимая тригонометрическая работа всей античности. В частности, «Альмагест» содержит обширные тригонометрические таблицы хорд для острых и тупых углов, с шагом 30 угловых минут. В таблицах Птолемей приводит значение длин хорд с точностью до трех шестидесятиричных знаков^[31]. Такая точность примерно соответствует пятизначной десятичной таблице синусов с шагом 15 угловых минут^[1].

Птолемей явно не формулирует теорему синусов и косинусов для треугольников. Тем не менее он всегда справляется с задачей решения треугольников, разбивая треугольник на два прямоугольных^[32].

Параллельно с развитием тригонометрии плоскости греки, под влиянием астрономии, далеко продвинули сферическую тригонометрию^[33]. Решающим этапом в развитии теории стала монография «Сферика» в трёх книгах, которую написал Менелай Александрийский (около 100 года н. э.). В первой книге он изложил теоремы о сферических треугольниках, аналогичные теоремам Евклида о плоских треугольниках (см. I книгу «Начал»). По сообщению Паппа, Менелай первым ввёл понятие сферического треугольника как фигуры, образованной отрезками больших кругов^[34]. Несколько десятилетий спустя Клавдий Птолемей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике.

В IV веке, после упадка античной науки, центр развития математики переместился в Индию. Сочинения индийских математиков (сиддханты) показывают, что их авторы были хорошо знакомы с трудами греческих астрономов и геометров^[35]. Чистой геометрией индийцы интересовались мало, но их вклад в прикладную астрономию и расчётные аспекты тригонометрии очень значителен. В частности, индийцы первыми ввели в использование косинус^[36]. Кроме того, индийцы знали формулы для кратных углов , для . В «Сурья-сиддханте» и в трудах Брахмагупты при решении задач фактически используется сферический вариант теоремы синусов, однако общая формулировка этой теоремы в Индии так и не появилась^[37].

В VIII веке учёные стран Ближнего и Среднего Востока познакомились с трудами древнегреческих и индийских математиков и астрономов. Их астрономические трактаты, аналогичные индийским сиддхантам, назывались «зиджи»; типичный зидж представлял собой сборник астрономических и тригонометрических таблиц, снабжённый руководством по их использованию и (не всегда) изложением общей теории^[38]. Сравнение зиджей периода VIII—XIII веков показывает быструю эволюцию тригонометрических знаний. Самые ранние из сохранившихся трудов принадлежат ал-Хорезми и ал-Марвази (IX век), которые рассмотрели, наряду с известными ещё индийцам синусом и косинусом, новые тригонометрические функции: тангенс, котангенс, секанс и косеканс^[36].

Сабит ибн Курра (IX век) и ал-Баттани (X век) первыми открыли фундаментальную теорему синусов для частного случая прямоугольного сферического треугольника. Для произвольного сферического треугольника доказательство было найдено (разными способами и, вероятно, независимо друг от друга) Абу-л-Вафой, ал-Худжанди и ибн Ираком в конце X века^[29]. В другом трактате ибн Ирака сформулирована и доказана теорема синусов для плоского треугольника^[39]. Сферическая теорема косинусов в общем виде сформулирована в странах ислама не была, однако в трудах Сабита ибн Курры, ал-Баттани и других астрономов имеются эквивалентные ей утверждения^[40].

Фундаментальное изложение тригонометрии как самостоятельной науки (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году^[41]. Его «Трактат о полном четырёхстороннике» содержит практические способы решения типичных задач, в том числе труднейших, решенных самим ат-Туси — например, построение сторон сферического треугольника по заданным трём углам^[42]. Таким образом, к концу XIII века были открыты базовые теоремы, необходимые для эффективного решения треугольников.

В Европе развитие тригонометрической теории стало чрезвычайно важным в Новое время, в первую очередь для артиллерии, оптики и навигации при дальних морских путешествиях. В 1551 году появились 15-значные тригонометрические таблицы Ретика, ученика Коперника, с шагом 10″^[43]. Потребность в сложных тригонометрических расчётах вызвала в начале XVII века открытие логарифмов, причём первые логарифмические таблицы Джона Непера содержали только логарифмы тригонометрических функций. Среди других открытий Непера — эффективный алгоритм решения сферических треугольников, получивший название «формулы аналогии Непера»^[44]. Алгебраизация тригонометрии, начатая Франсуа Виетом, была завершена Леонардом Эйлером в XVIII веке, после чего алгоритмы решения треугольников приобрели современный вид.

См. также[править | править код]

Признаки подобия треугольников
Площадь треугольника
Сферическая тригонометрия
Сферический треугольник
Триангуляция
Тригонометрические тождества
Тригонометрические функции
Формулы Мольвейде

Примечания[править | править код]

↑ ¹ ² Выгодский М. Я., 1978, с. 266—268.
↑ Плоский треугольник иногда называют прямолинейным.
↑ Элементарная математика, 1976, с. 487.
↑ Solving Triangles. Maths is Fun. Дата обращения: 23 Jule 2012. Архивировано 30 июня 2019 года.
↑ Элементарная математика, 1976, с. 488.
↑ Степанов Н. Н., 1948, с. 133.
↑ Solving SSS Triangles. Maths is Fun. Дата обращения: 23 Jule 2012. Архивировано 30 сентября 2012 года.
↑ Solving SAS Triangles. Maths is Fun. Дата обращения: 24 Jule 2012. Архивировано 30 сентября 2012 года.
↑ Solving SSA Triangles. Maths is Fun. Дата обращения: 24 Jule 2012). Архивировано 30 сентября 2012 года.
↑ Выгодский М. Я., 1978, с. 294.
↑ Элементарная математика, 1976, с. 493—496.
↑ Solving ASA Triangles. Maths is Fun. Дата обращения: 24 Jule 2012. Архивировано 30 сентября 2012 года.
↑ Степанов Н. Н., 1948, с. 87—90.
↑ Степанов Н. Н., 1948, с. 102—104.
↑ ¹ ² Энциклопедия элементарной математики, 1963, с. 545.
↑ Степанов Н. Н., 1948, с. 121—128.
↑ Степанов Н. Н., 1948, с. 115—121.
↑ Степанов Н. Н., 1948, с. 128—133.
↑ Степанов Н. Н., 1948, с. 104—108.
↑ Основные формулы физики, 1957, с. 14—15.
↑ Цейтен Г. Г., 1932, с. 223—224.
↑ Цейтен Г. Г., 1938, с. 126—127.
↑ ¹ ² Геометрия: 7—9 классы, 2009, с. 260—261.
↑ Геометрия: 7—9 классы, 2009, с. 260.
↑ Степанов Н. Н., 1948, с. 136—137.
↑ van der Waerden, Bartel Leendert. Geometry and Algebra in Ancient Civilizations. — Springer, 1983. — ISBN 3-540-12159-5.
↑ Глейзер Г. И., 1982, с. 77.
↑ Глейзер Г. И., 1982, с. 94—95.
↑ ¹ ² Матвиевская Г. П., 2012, с. 92—96.
↑ Berggren, J. Lennart. Mathematics in Medieval Islam // The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook (англ.). — Princeton University Press, 2007. — P. 518. — ISBN 9780691114859.
↑ История математики, том I, 1970, с. 143.
↑ Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. — М.: Наука, 1959. — С. 366. — 456 с.
↑ Матвиевская Г. П., 2012, с. 25—27.
↑ Матвиевская Г. П., 2012, с. 33—36.
↑ Матвиевская Г. П., 2012, с. 40—44.
↑ ¹ ² Сираждинов С. Х., Матвиевская Г. П., 1978, с. 79.
↑ Юшкевич А. П. История математики в Средние века. — М.: ГИФМЛ, 1961. — С. 160. — 448 с.
↑ Матвиевская Г. П., 2012, с. 51—55.
↑ Матвиевская Г. П., 2012, с. 111.
↑ Матвиевская Г. П., 2012, с. 96—98.
↑ Туси Насирэддин. Трактат о полном четырёхстороннике. Баку, Изд. АН АзССР, 1952.
↑ Рыбников К. А., 1960, с. 105.
↑ История математики, том I, 1970, с. 320.
↑ Степанов Н. Н. § 42. Формулы «аналогии Непера» // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 87—90. — 154 с.

Литература[править | править код]

Теория и алгоритмы

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия: 7—9 классы. Учебник для общеобразовательных учреждений. — 19-е изд. — М.: Просвещение, 2009. — 384 с. — ISBN 978-5-09-021136-9.
Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
Гельфанд И. М., Львовский С. М., Тоом А. Л. Тригонометрия, учебник для 10 класса. — М.: МЦНМО, 2002. — ISBN 5-94057-050-X.
Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Мензел Д. (ред.). Основные формулы физики. Глава 1. Основные математические формулы. — М.: Изд. иностранной литературы, 1957. — 658 с.
Основные понятия сферической геометрии и тригонометрии // Энциклопедия элементарной математики (в 5 томах). — М.: Физматгиз, 1963. — Т. 4. — С. 518—557. — 568 с.
Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948.

История

Глейзер Г. И. История математики в школе. VII-VIII классы. Пособие для учителей. — М.: Просвещение, 1982. — С. 76—95. — 240 с.
Глейзер Г. И. История математики в школе. IX-X классы. Пособие для учителей. — М.: Просвещение, 1983. — 352 с.
История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9.
Рыбников К. А. История математики в двух томах. — М.: Изд. МГУ, 1960. — Т. I.
Сираждинов С. Х., Матвиевская Г. П. Абу Райхан Беруни и его математические труды. Пособие для учащихся. — М.: Просвещение, 1978. — 95 с. — (Люди науки).
Цейтен Г. Г. История математики в древности и в средние века. — М.—Л.: ГТТИ, 1932. — 230 с.
Цейтен Г. Г. История математики в XVI и XVII веках. — М.—Л.: ОНТИ, 1938. — 456 с.

Источник

Формул для нахождения стороны треугольника не так уж много, но главное не знать их – а успешно применять при решении задач, ведь далеко не каждую задачу можно решить в лоб.

Сейчас на примере я покажу, как нужно их применять.

Есть произвольный треугольник со стороной 18 см, один угол при нем равен 30 градусам, а площадь равна 36 см.кв. Нужно найти две другие стороны. Сделаем рисунок

Для решения задачи проведем к основанию (с=18см) высоту h и тем самым разделим наш треугольник на два прямоугольных.

Исходя из формулы площади, найдем высоту

S = 1/2h*c откуда h = 2S/c = 2*36/18 = 4 см

Теперь находим сторону b по синусу угла

sin = h/b (отношение противоположного катета к гипотенузе) откуда b = h/(sin 30) = 4/(1/2) = 8 см.

Мы уже знаем две стороны у угол между ними и третью сторону можно найти по формуле из теоремы косинусов, но к сожалению не всегда мы ее помним. В нашем случае ничего страшного – найдем сторону а по формуле Пифагора, но для начала нам нужно найти сторону х.

Можно по формуле Пифагора

откуда х = квадратный корень из (8*8 – 4*4), что равно 4*(кв.к3)

и находим последнюю сторону нашего треугольника

а = кв.к из (c-x)*(c-x) + h*h = кв.к из 18*18-2*18*4*(кв.к3)+4*(кв.к3)*4*(кв.к3)+4*4

здесь стоит обратить внимание, что

18*18 = с*с

4*(кв.к3)*4*(кв.к3)+4*4 = 4*4*3+4*4 = 4*4*4 = 4*2*2*2 = 8*8 = b*b

2*18*4*(кв.к3) = 2*18*4*2*(кв.к3/2) = 2*18*8*(кв.к3/2) = 2*с*b*cos30 и теперь можно записать

а = кв.к из с*с – 2*с*b*cos30 + b*b Что на самом деле есть формулой нахождения стороны треугольника по теореме косинусов (мы ее только что вывели)

Теперь посчитаем и найдем сторону а = 11,772 см.

Источник

Как найти длину стороны треугольника?

Для прямоугольного треугольника: 1) Найти катет через гипотенузу и другой катет

2) Найти гипотенузу по двум катетам

3) Найти катет по гипотенузе и противолежащему углу

4) Найти гипотенузу через катет и противолежащий угол

1) Найти основание через боковые стороны и угол между ними

2) Найти основание через боковые стороны и угол при основании

3) Найти боковые стороны по углу между ними

4) Найти боковые стороны по углу при основании

1) Найти сторону через площадь

2) Найти сторону через высоту

3) Найти сторону через радиус вписанной окружности

4) Найти сторону через радиус описанной окружности

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

2. Как узнать сторону прямоугольного треугольника

3. Формулы сторон равнобедренного треугольника

4. Найти длину высоты треугольника

Треугольник. Формулы определения и свойства треугольников.

Определение треугольника

Классификация треугольников

1.Разносторонний – треугольник, у которого все стороны имеют разную длину.

3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.

4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°

5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.

Свойства треугольника

1.Свойства углов и сторон треугольника.

2.Теорема синусов.

3. Теорема косинусов.

4. Теорема о проекциях

Медианы треугольника

Свойства медиан треугольника:

Формулы медиан треугольника

Как найти третью сторону треугольника — формулы и расчеты

Фигура из шести элементов

Дополнительные отрезки

Виды треугольников

Основные свойства и понятия

Важные теоремы

Примеры решения задач

Квадрат и его диагональ

Две высоты и угол

Решение плоских треугольников[править | править код]

Основные теоремы[править | править код]

Замечания[править | править код]

Три стороны[править | править код]

Две стороны и угол между ними[править | править код]

Две стороны и угол напротив одной из них[править | править код]

Сторона и два угла[править | править код]

Решение прямоугольных треугольников[править | править код]

Два катета[править | править код]

Катет и гипотенуза[править | править код]

Катет и прилежащий острый угол[править | править код]

Катет и противолежащий острый угол[править | править код]

Гипотенуза и острый угол[править | править код]

Решение сферических треугольников[править | править код]

Три стороны[править | править код]

Две стороны и угол между ними[править | править код]

Две стороны и угол не между ними[править | править код]

Сторона и прилежащие углы[править | править код]

Два угла и сторона не между ними[править | править код]

Три угла[править | править код]

Решение прямоугольных сферических треугольников[править | править код]

Вариации и обобщения[править | править код]

Примеры практического применения[править | править код]

Триангуляция[править | править код]

Расстояние между двумя точками на поверхности земного шара[править | править код]

История[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Симс 4 как исправить вылеты в

Видео как найти блокнот

Как найти длину вектора между двумя векторами

Добавить комментарий Отменить ответ

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет