- Учебники
- 2 класс
- Математика 👍
- Петерсон
- №10
авторы: Петерсон.
издательство: Ювента
Раздел:
- ЧАСТЬ 2
- Урок 28. Решение задач
ГДЗ учебник по математике 2 класс Петерсон. Часть 2. Урок 28. Решение задач. Номер №10
- Предыдущее
- Следующее
Определи неизвестную операцию и найди неизвестное число. Какая операция обратна сложению, вычитанию?
reshalka.com
ГДЗ учебник по математике 2 класс Петерсон. Часть 2. Урок 28. Решение задач. Номер №10
Решение

Вычитание обратно сложению.
Сложение обратно вычитанию.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Математика 2 класс учебник Петерсон 2 часть ответы — страница 31

- Тип: ГДЗ, Решебник.
- Автор: Л. Г. Петерсон.
- Год: 2021.
- Серия: Учись Учиться.
- Издательство: Просвещение/Бином.
Подготовили готовое домашнее задание к упражнениям на 31
странице по предмету математика за 2 класс. Ответы на задания: 8, 9, 10, 11 и 12.
Учебник 2 часть – Страница 31.
Ответы 2021 года.
Номер 8.
Маша нашла 13 грибов, Ира – на 2 гриба меньше, чем Маша, а Наташа – столько же грибов, сколько Ира и Маша вместе. Сколько всего грибов нашли девочки? Какие ещё вопросы можно поставить к этому условию?
Ответ:
Чтобы ответить на вопрос задачи, то есть найти целое, нужно сложить все части. Сразу мы этого сделать не можем, так как не знаем, сколько нашли грибов Ира и Наташа. По условию задачи Ира нашла на 2 гриба меньше, чем Маша, то есть 13 – 2. Если сложим грибы, которые нашли Маша и Ира, узнаем, сколько грибов нашла Наташа.
1) 13 – 2 = 11 (гр.) – нашла Ира
2) 13 + 11 = 24 (гр.) – нашла Наташа
3) 13 + 11 + 24 = 48 (гр.)
Ответ: 48 грибов нашли девочки вместе.
Дополнительные вопросы:
• На сколько больше грибов нашла Наташа, чем Маша? 24 – 13 = 11 (гр.)
• На сколько больше грибов нашла Наташа, чем Ира? 24 – 11 = 13 (гр.)
Номер 9.
В одном детском саду 98 детей, а в другом — на 36 детей больше. В младшие группы обоих садов ходят 56 малышей, в средние 74, а остальные дети ходят в старшие группы. На сколько меньше детей в младших группах, чем в старших?
Ответ:
Чтобы ответить на вопрос задачи, нужно от большего числа (количество детей в старших группах) отнять меньшее (число детей в младших группах). Сразу это сделать нельзя, так как не знаем, сколько детей в старших группах. Это часть, которую можно найти, отняв от общего числа детей из младших и средних групп. Сначала нужно узнать число детей во втором саду. Их больше на 36, чем в первом, то есть 98 + 36. Найдем сколько всего детей, сложив детей из двух садов.
1) 98 + 36 = 134 (д.) – во втором саду
2) 134 + 98 = 232 (д.) – всего детей
3) 56 + 74 = 130 (д.) – в младших и средних группах
4) 232 − 130 = 102 (д.) – в старших группах
5) 102 − 56 = 46 (д.)
Ответ: на 46 человек в старших группах детей больше, чем в младших.
II вариант
1) 98 + 36 = 134 (д.) – во втором саду
2) 134 + 98 = 232 (д.) – всего детей
3) 232 − 56 = 176 (д.) – в старших и средних группах
4) 176 − 74 = 102 (д.) – в старших группах
5) 102 − 56 = 46 (д.)
Ответ: на 46 человек в старших группах детей больше, чем в младших.
Номер 10.
а) Что надо записать вместо знака вопроса? Что происходит с числом в результате операций прибавления и вычитания? Как найти неизвестную операцию?
б) Пользуясь полученным выводом, составь и реши уравнения
в) Найди неизвестные операции:
85 – х = 17 14 + х = 70 106 – х = 92 38 + х = 125
Ответ:
а) Операции прибавления и вычитания изменяют данное число (объект операции) на несколько единиц. Значит, чтобы найти неизвестную операцию, надо узнать, на сколько одно из чисел (объект операции) больше или меньше другого числа. Известно, что ответ на этот вопрос находится действием вычитания. Поэтому, чтобы узнать, например, какая операция переводит 24 в 30, надо из 30 вычесть 24 («+ 6» – увеличение на 6), а чтобы узнать, какая операция переводит 73 в 59, надо из 73 вычесть 59 («– 14» — уменьшение на 14).
В обоих случаях из большего числа надо вычесть меньшее число.
б)Неизвестная операция находится действием вычитания
213 + х = 306 952 – х = 573
х = 306 – 213 х = 952 – 573
х = 93 х = 37
в) Неизвестная операция находится действием вычитаниях
85 – х = 17 14 + х = 70 106 – х = 92 38 + х = 125
Х = 85 – 17 Х = 70 – 14 Х = 106 – 92 Х = 125 – 38
Х = 68 Х = 56 Х = 14 Х = 87
Номер 11.
Разрежь прямоугольник со сторонами 3 см и 6 см на 4 равных треугольника и составь из них квадрат.
Ответ:
Номер 12.
Сколько существует двузначных чисел, в записи которых содержится хотя бы одна цифра 5?
Ответ:
Условию удовлетворяют двузначные числа, в записи которых содержится одна или две цифры 5. В разряде единиц цифра 5 встречается 9 раз: это числа 15, 25, … 95. В разряде десятков – 10 раз в числах пятого десятка: 50, 51, 52, … 59.
В указанных числовых рядах число 55 встречается дважды.
Значит, всего существует 9 + 10 – 1 = 18 двузначных чисел, удовлетворяющих заданному условию.
Рейтинг
Страница 37 из 110
Урок 13. Решение задач. Страница 38.
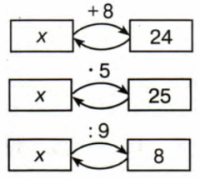
6. Как найти неизвестный объект операции? Составь уравнения по схемами реши их, используя данное правило.
Решение
x + 8 = 24,
x = 24 − 8,
x = 16.
Проверка:
16 + 8 = 24,
24 = 24.x * 5 = 25,
x = 25 : 5,
x = 5.
Проверка:
5 * 5 = 25,
25 = 25.x : 9 = 8,
x = 8 * 9,
x = 72.
Проверка:
72 : 8 = 9,
9 = 9.
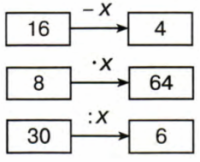
7. Как изменяется число в результате операций прибавления и вычитания? А в результате операций прибавления и вычитания? А в результате операций умножения и деления? Составь и реши уравнения по схемам:
Решение
В результате прибавления число увеличивается, а в результате убавления число уменьшается.
В результате умножения число увеличивается, а в результате деления число уменьшается.16 − x = 4,
x = 16 − 4,
x = 12.
Проверка:
16 − 12 = 4,
4 = 4.8 * x = 64,
x = 64 : 8,
x = 8.
Проверка:
8 * 8 = 64,
64 = 64.30 : x = 6,
x = 30 : 6,
x = 5.
Проверка:
30 : 5 = 6,
6 = 6.
8. Найди уравнения, в которых не известны объект операции, операция. Реши их, используя соответствующие правила.
x − 3 = 5
x : 3 = 5
x + 4 = 12
x * 4 = 12
21 − x = 7
21 : x = 7
9 + x = 36
9 * x = 36
Решение
x − 3 = 5,
x = 5 + 3,
x = 8.
Проверка:
8 − 3 = 5,
5 = 5.x : 3 = 5,
x = 5 * 3,
x = 15.
Проверка:
15 : 3 = 5,
5 = 5.x + 4 = 12,
x = 12 − 4,
x = 8.
Проверка:
8 + 4 = 12,
12 = 12.x * 4 = 12,
x = 12 : 4,
x = 3.
Проверка:
3 * 4 = 12,
12 = 12.21 − x = 7,
x = 21 − 7,
x = 14.
Проверка:
21 − 14 = 7,
7 = 7.21 : x = 7,
x = 21 : 7,
x = 3.
Проверка:
21 : 3 = 7,
7 = 7.9 + x = 36,
x = 36 − 9,
x = 27.
Проверка:
9 + 27 = 36,
36 = 36.9 * x = 36,
x = 36 : 9,
x = 4.
Проверка:
9 * 4 = 36,
36 = 36.
9. Цена пары ботинок x руб., а пары сапог – y руб. Что означают выражения:
x + y y − x y : x x * 2 + y * 3
Решение
x + y (р.) − стоят вместе одна пара ботинок и один сапог;
y − x (р.) − цена сапога больше, чем одна пара ботинок;
y : x (раз) − цена сапога больше, чем одна пара ботинок;
x * 2 + y * 3 − стоимость двух пар ботинок и трех сапог.
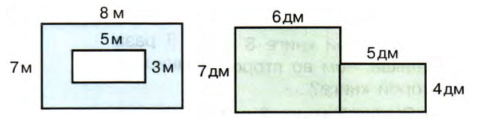
10. Найди площадь закрашенных фигур:
Решение
а. 1) 8 * 7 = 56 $(м^2)$ − площадь всего прямоугольника;
2) 5 * 3 = 15 $(м^2)$ − площадь незакрашенной фигуры;
3) 56 − 15 = 41 $(м^2)$ − площадь закрашенной фигуры.
Ответ: 41 $м^2$б. 1) 7 * 6 = 42 $(дм^2)$ − площадь большого прямоугольника;
2) 5 * 4 = 20 $(дм^2)$ − площадь маленького прямоугольника;
3) 42 + 20 = 62 $(дм^2)$ − площадь закрашенной фигуры.
Ответ: 62 $дм^2$.
11. Сравни с помощью знаков >, <, =:
2 м 4 дм ☐ 206 см
51 дм 8 см ☐ 7 м
9 $дм^2$ ☐ 90 $см^2$
400 $дм^2$ ☐ 6 $м^2$
Решение
2 м 4 дм > 206 см
51 дм 8 см <7м9 дм2 > 90 см2
400 дм2 < 6 м2
Полная запись:
2 м 4 дм = (2 * 100 + 4 * 10) см = 240 см;
240 см > 206 см;
2 м 4 дм > 206 см.7 м = (7 * 10) дм = 70 дм;
51 дм 8 см < 70 дм;
51 дм 8 см < 7 м.9 $дм^2$ = (9 * 100) $см^2$ = 900 $см^2$;
900 $см^2$ > 90 $см^2$;
9 $дм^2$ > 90 $см^2$.6 $м^2$ = (6 * 100) $дм^2$ = 600 $дм^2$;
400 $дм^2$ < 600 $дм^2$;
400 $дм^2$ < 6 $м^2$.
12. Выполни действия.
6 м 3 см – 45 дм +1 м 4 дм 7 см = 603 см – 450 см+147 см = 300 см = 3 м
5 м 32 см + 4 м 1 дм 6 см =532 см + 416 см = 948 см = 9 м 4 дм 8 см4 дм2 58 см2 + 342 см2 = 458 см2 + 342 см2 = 800 см2 = 8 дм2
8 дм2 – 5 дм2 6 см2 = 800 см2 – 506 см2 = 294 см2 = 2 дм2 94 см2
1. На блок−схеме показаны варианты развития событий в сказке «Гуси−лебеди», когда девочка просит печку спрятать ее и братца. Прочитай блок−схему. Что ты замечаешь? Сделай вывод.
Решение
Можно заметить, что существует два варианта развития событий.
От варианта развития событий зависит конечный результат.
2. Пользуясь программой действий, объясни, как заменить стержень в шариковой ручке.
Решение
1) Взять запасной стержень, если его нет, то купить его.
2) Развинтить ручку.
3) Вынуть пустой стержень.
4) Вставить полный стержень.
5) Завинтить ручку.
3. Выполни действия по заданным алгоритмам и запиши значения x в тетради. Какой из этих алгоритмов можно назвать линейным, разветвляющимся, циклическим? Почему?
Решение
Алгоритм линейный, так как в нем нет вопроса и все действия выполняются по порядку.
при a = 5:
5 + 9 = 14
14 − 7 = 7
7 + 38 = 45
x = 45
при a = 12:
12 + 9 = 21
21 − 7 = 14
14 + 38 = 52
x = 52
при a = 20:
20 + 9 = 29
29 − 7 = 22
22 + 38 = 60
x = 60
Алгоритм разветвляющийся, так как после вопроса возможны два варианта событий.
при a = 5:
5 + 7 = 12
12 < 18 − да
12 + 5 = 17
x = 17
при a = 12:
12 + 7 = 19
19 < 18 − нет
19 − 4 = 15
x = 15
при a = 20:
20 + 7 = 27
27 < 18 − нет
27 − 4 = 23
x = 23
Алгоритм циклический, так как при отрицательном ответе на вопрос, будет повторяться действие +3, пока ответ на вопрос не станет положительным.
при a = 5:
5 + 3 = 8
8 > 15 − нет
8 + 3 = 11
11 > 15 − нет
11 + 3 = 14
14 > 15 − нет
14 + 3 = 17
17 > 15 − да
17 − 8 = 9
x = 9
при a = 12:
12 + 3 = 15
15 > 15 − нет
15 + 3 = 18
18 > 15 − да
18 − 8 = 10
x = 10
при a = 20:
20 + 3 = 23
23 > 15 − да
23 − 8 = 15
x = 15
4. Определи порядок действий при входе в метро:
1. Прохожу в метро.
2. Дожидаюсь зеленого сигнала.
3. Покупаю карточку.
4. Иду к кассе.
5. Прикладываю карточку к автомату.
Укажи, каким блок−схемы соответствуют эти действия?
Решение
5. Составь программу пользования лифтом.
Решение
- подхожу к лифту
- нажимаю кнопку вызова лифта
- дожидаюсь когда лифт приедет и двери откроются
- захожу в лифт
- нажимаю кнопку нужного этажа
- дожидаюсь когда лифт поднимется и двери откроются
- выхожу из лифта
6. Маша нашла 13 грибов, Ира − на 2 гриба меньше, чем Маша, а Наташа − столько же грибов, сколько Ира и Маша вместе. Сколько всего грибов нашли девочки? Какие еще вопросы можно поставить к этому условию?
Решение
13 + (13 − 2) + (13 + 13 − 2) = 13 + 11 + 24 = 24 + 24 = 48 (грибов) − всего нашли девочки.
Ответ: 48 грибов
Дополнительные вопросы к условию задачи: На сколько больше грибов собрали Маша и Наташа вместе, чем Ира? На сколько больше грибов собрали Ира и Наташа вместе, чем Маша? Кто из девочек нашел больше всего грибов? Кто из девочек нашел меньше всего грибов? Сколько грибов собрали Маша и Ира вместе (Ира и Наташа, Маша и Наташа)?
7. Найди значения выражений:
Решение
215 − (38 + 169) = 8
(354 + 97) − 263 = 188
500 − (239 + 85) + 457 = 633
(304 − 26) − (72 + 168) =38
8. В одном детском саду 98 детей, а в другом − на 36 детей больше. В младшую группу ходят 56 малышей, в среднюю − 74, а остальные дети ходят в старшую группу. На сколько меньше детей в младшей группе, чем в старшей?
Решение
1) 98 + 36 = 134 (детей) − в другом детском саду;
2) 98 + 134 = 232 (ребенка) − в двух детских садах;
3) 56 + 74 = 130 (детей) − в младшей и средней группе;
4) 232 − 130 = 102 (ребенка) − в старшей группе;
5) 102 − 56 = на 46 (детей) − меньше в младшей группе, чем в старшей.
Ответ: на 46 детей.
9. а) Что надо записать вместо знака вопроса? Как найти неизвестную операцию прибавления, вычитания?
Решение
Чтобы найти неизвестную операцию прибавления, нужно из результата операции (суммы) вычесть объект операции (слагаемое).
Чтобы найти неизвестную операцию вычитания, нужно из объекта операции (уменьшаемого) вычесть результат операции (разность).
9. б) Пользуясь полученным выводом, составь и реши уравнения
Решение
213 + x = 306
x = 306 − 213
x = 93
952 − x = 573
x = 952 − 573
x = 379
9. в) Найди неизвестные операции
Решение
85 − x = 17
x = 85 − 17
x = 68
14 + x = 70
x = 70 − 14
x = 56
106 − x = 92
x = 106 − 92
x = 14
38 + x = 125
x = 125 − 38
x = 87
10. Разрежь прямоугольник со сторонами 3 см и 6 см на 4 равных треугольника и составь из них квадрат.
Решение
11. Сколько существует двузначных чисел, в записи которых содержится хотя бы одна цифра 5?
Решение
15, 25, 35, 45, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 65, 75, 85, 95.
Ответ: 18 чисел.
Назад к содержанию
-
Главная
-
ГДЗ
- 2 класс
- Математика
-
Петерсон. Учебник
- Страница 38. Урок 13. Часть 3
Вернуться к содержанию учебника
Вопрос
Задание № 6. Составь уравнения по схемам. Что в них общего? Как найти неизвестный объект операции?
Подсказка
Ответ
Вопрос
Задание № 7. Как изменяется число в результате операций прибавления и вычитания? А в результате операций умножения и деления? Составь и реши уравнения по схемам.
Подсказка
Ответ
Вопрос
Задание № 8. Найди уравнения, в которых не известен объект операции, и в которых не известна операция. Как их можно решить?
Реши уравнения. Что ты замечаешь?
Подсказка
Ответ
Вопрос
Задание № 9. Цена пары ботинок х руб., а цена пары сапог у руб. Что означают выражения:
| х + у | у – х | у : х | х • 2 + у • 3 |
Подсказка
Ответ
Вопрос
Задание № 10. Найди площадь закрашенных фигур.
Подсказка
Повтори, как найти площадь прямоугольника.
Ответ
Вопрос
Подсказка
Ответ
Вопрос
Задание № 12. Выполни действия:
| 6 м 3 см – 45 дм + 1 м 4 дм 7 см | 4 дм2 58 см2 + 342 см2 |
| 5 м 32 см + 4 м 1 дм 6 см | 8 дм2 – 5 дм2 6 см2 |
Подсказка
Ответ
Вернуться к содержанию учебника



.jpg)