Как найти неизвестную систему исчисления

Это ж всё брутфорс, это ж несерьезно 🙂

На самом деле, конечно, перебор здесь вполне подходит, и можно дать ему границы сразу — по количеству цифр, по максимальной цифре. Но есть же и аналитический метод.

350214_х = 118924₁₀

Это означает, что

3x⁵ + 5x⁴ + 0x³ + 2x² + 1x + 4 = 118924₁₀

или

3x⁵ + 5x⁴ + 2x² + x – 118920 = 0

Классический многочлен пятой степени. И теперь нужно просто решить полиномиальное уравнение. По основной теореме алгебры у него будет пять комплексных корней, нас, правда, интересует только действительный, хорошо бы положительный, и хорошо бы целый 🙂

Из теоремы Абеля-Руффини известно, что аналитически мы такое уравнение не решим в общем случае, но я бы даже и пробовать не стал: на то придуманы численные методы, которых всяких есть многатыщ — выбрать можно по вкусу, начиная хоть с метода товарища Ньютона. Решаем, и получаем:

x = 8

Хорошо и красиво. Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием (-7.07949 – 4.865i) 🙂

Формулировка задания: Запись числа в некоторой системе счисления выглядит так. Найдите основание системы счисления q.

Задание входит в ЕГЭ по информатике для 11 класса под номером 16 (Кодирование чисел. Системы счисления).

Рассмотрим, как решаются подобные задания на примере.

Решить уравнение с неизвестной системой счисления

В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание.

Составим уравнение: где n — основание этой системы счисления. Исходя из уравнения,

Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).

Основание системы счисления равно 6₁₀ = 20₃.

Корни квадратного уравнения: 8 и −10. Следовательно, основание системы счисления равно 8.

Переведём все числа в десятичную систему счисления:

Составим новое уравнение и решим уже его:

Чему равно наименьшее основание позиционной системы счисления x, при котором 225_x = 405_y?

Ответ записать в виде целого числа.

Поскольку в левой и в правой частях есть цифра 5, оба основания больше 5, то есть перебор имеет смысл начинать с

Для каждого x вычисляем значение и решаем уравнение , причем нас интересуют только натуральные

Для и нужных решений нет, а для получаем так что

Ответ:

Задача №16. Поиск основания системы по окончанию числа, уравнения и различные кодировки, арифметические действия в различных системах.

Перед тем, как приступить к решению задач, нам нужно понять несколько несложных моментов.

Рассмотрим десятичное число 875. Последняя цифра числа (5) – это остаток от деления числа 875 на 10. Последние две цифры образуют число 75 – это остаток от деления числа 875 на 100. Аналогичные утверждения справедливы для любой системы счисления:

Последняя цифра числа – это остаток от деления этого числа на основание системы счисления.

Последние две цифры числа – это остаток от деления числа на основание системы счисления в квадрате.

Например, . Разделим 23 на основание системы 3, получим 7 и 2 в остатке (2 – это последняя цифра числа в троичной системе). Разделим 23 на 9 (основание в квадрате), получим 18 и 5 в остатке (5 = ).

Вернемся опять к привычной десятичной системе. Число = 100000. Т.е. 10 в степени k– это единица и k нулей.

Аналогичное утверждение справедливо для любой системы счисления:

Основание системы счисления в степени k в этой системе счисления записывается как единица и k нулей.

1. Поиск основания системы счисления

Пример 1.

В системе счисления с некоторым основанием десятичное число 27 записывается в виде 30. Укажите это основание.

Решение:

Обозначим искомое основание x. Тогда .Т.е. x = 9.

Пример 2.

В системе счисления с некоторым основанием десятичное число 13 записывается в виде 111. Укажите это основание.

Решение:

Обозначим искомое основание x. Тогда

Решаем квадратное уравнение, получаем корни 3 и -4. Поскольку основание системы счисления не может быть отрицательным, ответ 3.

Ответ: 3

Пример 3

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.

Решение:

Если в некоторой системе число 29 оканчивается на 5, то уменьшенное на 5 число (29-5=24) оканчивается на 0. Ранее мы уже говорили, что число оканчивается на 0 в том случае, когда оно без остатка делится на основание системы. Т.е. нам нужно найти все такие числа, которые являются делителями числа 24. Эти числа: 2, 3, 4, 6, 8, 12, 24. Заметим, что в системах счисления с основанием 2, 3, 4 нет числа 5 (а в формулировке задачи число 29 оканчивается на 5), значит остаются системы с основаниями: 6, 8, 12,

Ответ: 6, 8, 12, 24

Пример 4

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.

Если в некоторой системе число оканчивается на 13, то основание этой системы не меньше 4 (иначе там нет цифры 3).

Уменьшенное на 3 число (71-3=68) оканчивается на 10. Т.е. 68 нацело делится на искомое основание системы, а частное от этого при делении на основание системы дает в остатке 0.

Выпишем все целые делители числа 68: 2, 4, 17, 34, 68.

2 не подходит, т.к. основание не меньше 4. Остальные делители проверим:

68:4 = 17; 17:4 = 4 (ост 1) – подходит

68:17 = 4; 4:17 = 0 (ост 4) – не подходит

68:34 = 2; 2:17 = 0 (ост 2) – не подходит

68:68 = 1; 1:68 = 0 (ост 1) – подходит

2. Поиск чисел по условиям

Пример 5

Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?

Решение:

Для начала выясним, как выглядит число 25 в системе счисления с основанием 4.

. Т.е. нам нужно найти все числа, не больше , запись которых оканчивается на 11. По правилу последовательного счета в системе с основанием 4,
получаем числа и . Переводим их в десятичную систему счисления:

3. Решение уравнений

Пример 6

Ответ запишите в троичной системе (основание системы счисления в ответе писать не нужно).

Переведем все числа в десятичную систему счисления:

Квадратное уравнение имеет корни -8 и 6. (т.к. основание системы не может быть отрицательным). .

Ответ: 20

4. Подсчет количества единиц (нулей) в двоичной записи значения выражения

Для решения этого типа задач нам нужно вспомнить, как происходит сложение и вычитание «в столбик»:

При сложении происходит поразрядное суммирование записанных друг под другом цифр, начиная с младших разрядов. В случае, если полученная сумма двух цифр больше или равна основанию системы счисления, под суммируемыми цифрами записывается остаток от деления этой суммы на основание системы, а целая часть от деления этой суммы на основание системы прибавляется к сумме следующих разрядов.

При вычитании происходит поразрядное вычитание записанных друг под другом цифр, начиная с младших разрядов. В случае, если первая цифра меньше второй, мы «занимаем» у соседнего (большего) разряда единицу. Занимаемая единица в текущем разряде равна основанию системы счисления. В десятичной системе это 10, в двоичной 2, в троичной 3 и т.д.

Пример 7

Сколько единиц содержится в двоичной записи значения выражения: ?

Представим все числа выражения, как степени двойки:

В двоичной записи двойка в степени n выглядит, как 1 и n нулей. Тогда суммируя и , получим число, содержащее 2 единицы:

Теперь вычтем из получившегося числа 10000. По правилам вычитания занимаем у следующего разряда.

Теперь прибавляем к получившемуся числу 1:

Видим, что у результата 2013+1+1=2015 единиц.

Решение задач по системе счисления. Часть 2

Главная > Решение

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Решение задач по системе счисления. Часть 2.

Учитель информатики Батракова Л.В.

11. Решите уравнение .
Ответ запишите в четверичной системе счисления. Основание системы счисления указывать не нужно.

Решение: Надо перевести все числа в десятичную систему, решить уравнение и результат перевести в четверичную систему:

1)

из уравнения получаем

переводим 22 в четверичную систему счисления:

12. Запись натурального числа в системах счисления с основанием 4 и 6 заканчивается на 0. Найдите минимальное натуральное число, удовлетворяющее этим условиям.

Решение: если запись числа в системе счисления с основанием N заканчивается на 0, то это число делится на N нацело, поэтому в данной задаче требуется найти наименьшее натуральное число, которое делится одновременно на 4 и на 6, то есть это число12.

13. Укажите, сколько всего раз встречается цифра 3 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 4.

Решение (вариант 1):

При решении задачи надо помнить, что в 4-ой системе счисления самая старшая цифра – 3.

Запишем первое и последнее число в заданном диапазоне в системе счисления с основанием 4:

13 = 31 4 , 23 = 113 4 .

Оба они содержат цифру 3, так что, 2 цифры мы уже нашли.

Между 31 4 и 113 4 есть еще числа:

32 4 , 33 4 , 100 4 , 101 4 , 102 4 , 103 4, 110 4 , 111 4 , 112 4 .

В них 4 цифры 3, поэтому всего цифра 3 встречается 6 раз.

Решение (вариант 2):

Можно перевести все указанные числа в систему счисления с основанием 4 и подсчитать количество 3:

13 =31 4 , 14 =32 4 , 15 =33 4 , 16 =100 4 , 17 =101 4 , 18 =102 4 , 19 =103 4 , 20 =110 4 , 21 = 111 4 , 22=112 4 , 23 = 113 4 .

Получается 6 штук.

14. Укажите наименьшее основание системы счисления, в которой запись числа 50 двузначна.

Решение: Так как число по условию двухзначное, то достаточно найти первое целое число, квадрат которого больше 50; это – 8, так как:

Так как , следовательно, в системе счисления с основанием 7 запись числа 50 будет трехзначна, а в 8-ой системе счисления – двузначной.

15. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием 6 начинается на 4?

Решение: Поскольку , в интересующих нас числах может быть не более 2 цифр. Есть всего одно однозначное число, начинающееся на 4, это 4. Выпишем все числа в шестеричной системе счисления, которые являются двузначными, начинаются с 4 и не превосходят 25 в десятичной системе. Это числа: 40 6 = 24, 41 6 = 25. Ответ: 4, 24, 25

16. Запись числа 65 8 в некоторой системе счисления выглядит так: 311 N . Найдите основание системы счисления N.

Решение: Из условия задачи следует, что 65 8 = 311 N . Переведем 65 8 в десятичную систему счисления:

,

Второе число разложим по основанию счисления N:

Так как что 65 8 = 311 N , то можно записать: .

Решаем это уравнение и получаем, что N = 4.

17. Даны 4 числа, они записаны с использованием различных систем счисления. Укажите среди этих чисел то, в двоичной записи которого содержится ровно 5 единиц. Если таких чисел несколько, укажите наибольшее из них.

1) 31 10 * 8 10 + 1 10 2) F0 16 + 1 10 3) 351 8 4) 11100011 2

Решение: Нужно перевести все заданные числа в двоичную систему, подсчитать число единиц и выбрать наибольшее из чисел, в которых ровно 5 единиц.

Для первого варианта переведем оба сомножителя в двоичную систему:

31­ 10 = 11111­ 2 8 10 = 1000­ 2

В первом числе ровно 5 единиц, умножение на второе добавляет в конец три нуля:

31­ 10 * 8 10 = 11111­ 2 * 1000­ 2 = 111110­00 2

то есть в этом числе 5 единиц, но надо добавить еще одну единицу в конец, получим число 11111001, в котором 6 единиц. Так как нам нужны числа с 5-ю единицами, то это число не рассматриваем.

Для второго варианта воспользуемся двоичным представлением 16-ричных чисел: каждую цифру шестнадцатеричного числа можно переводить отдельно в тетраду (4 двоичных цифры):

F­0 16 = 1111­0000 2

после добавления единицы F0 16 + 1 = 1111 0001 2 получаем число, содержащее ровно 5 единиц.

Для третьего варианта используем связь между восьмеричной и двоичной системами: каждую цифру восьмеричного числа переводим отдельно в триаду (группу из трёх) двоичных цифр:

351 8 = 11101001­ 2

это число тоже содержит 5 единиц, но меньше, чем число во втором варианте ответа.

Последнее число 11100011 2 уже записано в двоичной системе, оно тоже содержит ровно 5 единиц, но меньше второго и третьего числа.

Таким образом, только 3 числа, указанные в вариантах ответов, содержат ровно 5 единиц, но наибольшее из них – второе.

18. Даны 4 целых числа, записанные в двоичной системе:
10001011, 10111000, 10011011, 10110100.
Сколько среди них чисел, больших, чем А4 16 +20 8 ?

1) 1 2) 2 3) 3 4) 4

Решение: Надо перевести А4 16 +20 8 в двоичную систему счисления, разложив их по тетрадам для 16-х чисел и по триадам для 8-х чисел: А4 16 – 10100100 2 и 20 8 – 10000 2 и поразрядно сложить: 10100100 2 + 10000 2 = 10110100 2 .

Сравнив с заданными числами, видим, что только одно число больше полученного, это: 10111000.

19. К записи натурального числа в восьмеричной системе счисления справа приписали два нуля. Во сколько раз увеличилось число? Ответ запишите в десятичной системе счисления.

Решение: Так как приписали 2 нуля, то для решения задачи достаточно вычислить 8 2 =64.

20. Десятичное число 109 в некоторой системе счисления записывается как «214». Определите основание системы счисления.

Решение: Обозначим искомое основание системы счисления через x , тогда можно записать выражение:

109 = 2 x 2 + x +4 или 2 x 2 + x -105 = 0. Решив это уравнение, получим x =7.

Дополнительно (для самых умных):

Запись числа N в системе счисления c основанием 6 содержит две цифры, запись этого числа в системе счисления c основанием 5 содержит три цифры, а запись в системе счисления c основанием 11 заканчивается на 1. Чему равно N? Запишите ответ в десятичной системе счисления.

Решение: Из первых двух условий задачи следует, что 5 2 = 25 ≤ N 2 = 36, следовательно, значение N надо искать из следующего набора чисел: 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35.

Из третьего условия находим число, которое при делении на 11 дает остаток 1, это число 34.

Проверка: 34 = 54 6 =5· 6 1 + 4 · 6 0 , 34 = 114 5 = 1· 5 2 + 1 · 5 1 + 4 · 5 0 , 34 = 31 11 = 3 · 11 1 + 1 · 11 0 .

Найдите основание системы счисления, в которой выполнено сложение: 144 + 24 = 201.

Решение: Так как старшая цифра в выражении 4, то надо рассматривать системы счисления, начиная с 5-ной.

Пятеричная система не подходит, т.к. 4 + 4 в пятеричной системе даст нам последнюю цифру в ответе 3. Шестеричная система так же не подходит – последняя цифра в ответе будет 2. А вот семеричная система подойдет для всех цифр ответа.

Дополнительно (для самых-самых умных):

1. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 11.

неизвестно основание системы счисления, мы обозначим его через

пока будем считать, что запись числа 31 в системе с основанием состоит из трех цифр, причем две младшие (11) нам даны, а одну (обозначим ее через ) нужно найти:

31 = k 1 1 N = k · N 2 + N 1 + N 0 = k· N 2 + N + 1

можно показать, что при большем количестве разрядов эта формула также верна, то есть, число 31 можно представить как при некотором целом ; например, для числа с пятью разрядами получаем:

4 3 2 1 0 ← разряды

31 = k 4 k 3 k 2 1 1 N = k 4 ·N 4 + k 3 · N 3 + k 2 · N 2 + N 1 + N 0

для (из первых трех слагаемых вынесли общий множитель )

Решение: Нужно найти все целые числа , такие что

(**)

где – целое неотрицательное число (0, 1, 2, …).

Сложность в том, что и , и неизвестны, однако здесь нужно «играть» на том, что это натуральные числа.

Из формулы (**) получаем , так что задача сводится к тому, чтобы найти все делители числа 30 и отобрать только те из них, для которых уравнение (**) разрешимо при целом , то есть, – целое число.

Выпишем все делители числа 30, большие или равные 2: 2, 3, 5, 6, 10, 15, 30.

Из всех этих делителей только для 2, 3, 5 и 30 значение – целое число (оно равно соответственно 7, 3, 1 и 0)

Ответ : 2, 3, 5, 30.

Замечание: Можно, конечно, решить задачу и методом подбора.

31 = 2 5 – 1 = 11111 2

2. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 94 начинается на 23.

Решение: Из условия задачи видно, что искомое основание не меньше 4 (в записи есть цифра 3).

Если запись числа 94 в некоторой системе счисления с основанием двузначна (94 = 23 x ), то справедливо равенство .

Нас интересуют натуральные решения этого уравнения, такие что , но таких решений нет.

Предположим, что число четырехзначное. Минимальное допустимое четырехзначное число – 2300 x , где . При минимальном основании () оно равно.

Следовательно, запись нужного нам числа имеет три знака.

Можно записать: , где – целое неотрицательное число, такое что .

Максимальное можно определить как решение уравнения (при ).

Получаем одно из решений – 6,15. Отсюда: 4≤.

определится как: .

Подставим поочередно в эту формулу , пытаясь получить .

Минимальное = 4 будет при , т.е условиевыполняется, а при получается .

[spoiler title=”источники:”]

http://ege-study.ru/ru/ege/materialy/informatika/zadacha-16-razbor-razlichnyx-tipov-zadach/

http://gigabaza.ru/doc/10435.html

[/spoiler]

Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.

Подробная инструкция, как быстро научиться считать в двоичной и шестнадцатеричной системах приведена на сайте https://itvdn.com/ru/blog/article/binary-hexadecimal-system.

В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:

11 – здесь первая единица обозначает десять, а вторая – 1.
II – здесь обе единицы обозначают единицу.

345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.

XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.

Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).

В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.

Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.

Основание системы счисления – это количество знаков, которое используется для записи цифр.

Разряд – это позиция цифры в числе. Разрядность числа – количество цифр, из которых состоит число (например, 264 – трехразрядное число, 00010101 – восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка – третий).

Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)

Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.

Двоичная система счисления

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 – это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

10001001₂ = 13710
Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 1*2 2 + 0*2 1 + 1*2 0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

Восьмеричная система счисления

Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.

В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:

000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7

Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:

1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135

Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 1011101₂ = 1358.

Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.

100₈ = 1 0 0 = 001 000 000 = 001000000 = 10000002

Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:

6728 = 6 * 8 2 + 7 * 8 1 + 2 * 8 0 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 8 2 + 0 * 8 1 + 0 * 8 0 = 6410

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.

В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:

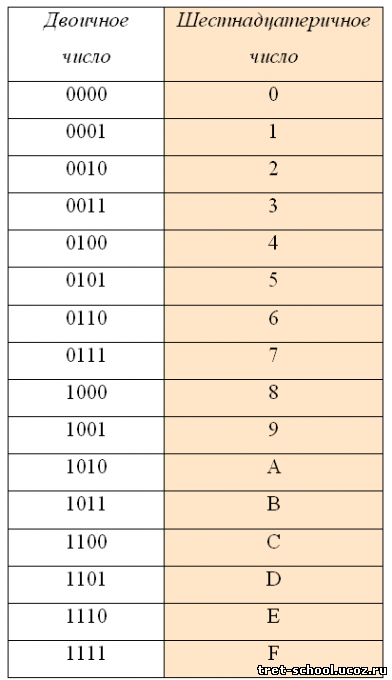
Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5

Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):

4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221

Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи – это FF.

FF = 15 * 161 + 15 * 160 = 240 + 15 = 255

255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние

118924 в 10 системе счисления = 350214 в х системе счисления, как найти х? если можно то попродобнее

5 ответов 5

Это ж всё брутфорс, это ж несерьезно 🙂

На самом деле, конечно, перебор здесь вполне подходит, и можно дать ему границы сразу — по количеству цифр, по максимальной цифре. Но есть же и аналитический метод.

Это означает, что

3x 5 + 5x 4 + 2x 2 + x – 118920 = 0

Классический многочлен пятой степени. И теперь нужно просто решить полиномиальное уравнение. По основной теореме алгебры у него будет пять комплексных корней, нас, правда, интересует только действительный, хорошо бы положительный, и хорошо бы целый 🙂

Из теоремы Абеля-Руффини известно, что аналитически мы такое уравнение не решим в общем случае, но я бы даже и пробовать не стал: на то придуманы численные методы, которых всяких есть многатыщ — выбрать можно по вкусу, начиная хоть с метода товарища Ньютона. Решаем, и получаем:

x = 8

Хорошо и красиво. Ну можете еще добить преподавателя комплексными корнями, сказав, что это же число записывается точно так же в системе счисления с основанием (-7.07949 – 4.865i) 🙂

1) если нужно проверить может ли быть такое число a в данной системе счисления с основанием b, проверьте что все цифры a меньше основания b

т.е. 2358 не может являться числом в 4-ной СС

2)если вы перевели число a из десятичной СС в p-ичную, то для того, чтобы проверить, верно ли вы это сделали, просто переведите ее обратно в десятичную, и проверьте, получится ли то же число а.

Для того чтобы перевести число из p-ичной СС в десятичную, умножьте первую справа цифру на 1, вторую справа на p, третью на p², и т.д. умножая на степени p, а потом найдите сумму всего этого