На этапе подготовки к заключительному тестированию учащимся старших классов необходимо подтянуть знания по теме «Показательные уравнения». Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Готовьтесь к экзаменационному тестированию вместе со «Школково»!
При повторении пройденных материалов многие учащиеся сталкиваются с проблемой поиска нужных для решения уравнений формул. Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.
Образовательный портал «Школково» предлагает ученикам воспользоваться нашей базой знаний. Мы реализуем совершенно новый метод подготовки к итоговому тестированию. Занимаясь на нашем сайте, вы сможете выявить пробелы в знаниях и уделить внимание именно тем заданиям, которые вызывают наибольшие затруднения.
Преподаватели «Школково» собрали, систематизировали и изложили весь необходимый для успешной сдачи ЕГЭ материал в максимально простой и доступной форме.
Основные определения и формулы представлены в разделе «Теоретическая справка».
Для лучшего усвоения материала рекомендуем попрактиковаться в выполнении заданий. Внимательно просмотрите представленные на данной странице примеры показательных уравнений с решением, чтобы понять алгоритм вычисления. После этого приступайте к выполнению задач в разделе «Каталоги». Вы можете начать с самых легких заданий или сразу перейти к решению сложных показательных уравнений с несколькими неизвестными или иррациональным уравнениям со знаком корня. База упражнений на нашем сайте постоянно дополняется и обновляется.
Те примеры с показателями, которые вызвали у вас затруднения, можно добавить в «Избранное». Так вы можете быстро найти их и обсудить решение с преподавателем.
Чтобы успешно сдать ЕГЭ, занимайтесь на портале «Школково» каждый день!
Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Он поможет решить задания №4, 12 и 14 из профильного уровня математики.
Одна из их разновидностей уравнений – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие степеней и переменной (х) не в основании степени, а в самом показателе. Как это выглядит:
$$ a^{f(x)}=b^{g(x)}; $$
Где (a) и (b) – некоторые числа, а (f(x)) и (g(x)) – какие-то выражения, зависящие от (x). Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
$$2^x=8;$$
$$ 2^x=2^{2x+1};$$
$$3^{x^2}=2^{x^2-2x+3};$$
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
$$ 7x+2=16;$$
$$x^2-4x+5=0;$$
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Пример 1
$$ 2^x=8;$$
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
$$ 2^3=2*2*2=8; $$
Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь по-сложнее.
Пример 2
$$ 3^{4x-1}=frac{1}{9};$$
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
$$frac{1}{9}=frac{1}{3^2}=3^{-2};$$
Мы применили свойство отрицательной степени по формуле:
$$ a^{-n}=frac{1}{a^n};$$
Теперь наше уравнение будет выглядеть так:
$$ 3^{4x-1}=3^{-2};$$
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
$$ 4x-1=-2;$$
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
$$4х=-2+1;$$
$$4x=-1;$$
$$x=-frac{1}{4}.$$
Поздравляю, мы нашли корень нашего показательного уравнения.
Пример 3
$$125^x=25;$$
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:
$$ (5^3)^x=5^2;$$
Воспользуемся одним из свойств степеней ((a^n)^m=a^{n*m}):
$$ 5^{3*x}=5^2;$$
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
$$ 3*x=2;$$
$$ x=frac{2}{3};$$
И еще один пример:
Пример 4
$$2^x=-4;$$
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
$$ a^x=b;$$
Где (a,b) какие-то положительные числа. ((a>0, ; b>0)).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:
$$ a^x=a^m;$$
Раз основания одинаковые, то мы можем просто приравнять степени:
$$x=m.$$
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Пример 5
$$2^x=16;$$
Замечаем, что (16=2*2*2*2=2^4) это степень двойки:
$$2^x=2^4$$
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6
$$5^{-x}=125 Rightarrow 5^{-x}=5*5*5 Rightarrow 5^{-x}=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7
$$9^{4x}=81 Rightarrow (3*3)^{4x}=3*3*3*3 Rightarrow(3^2)^{4x}=3^4 Rightarrow 3^{8x}=3^4 Rightarrow 8x=4 Rightarrow x=frac{1}{2}.$$
Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
Пример 8
$$ 3^x=2;$$
(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):
$$ b=a^{log_{a}(b)};$$
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):
$$ 2=3^{log_{3}(2)};$$
Подставим данное преобразование в наш пример:
$$3^x=3^{log_{3}(2)};$$
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
$$x=log_{3}(2).$$
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Пример 9
$$ 7^{2x}=5;$$
$$ 7^{2x}=7^{log_{7}(5)};$$
$$2x=log_{7}(5);$$
$$x=frac{1}{2}*log_{7}(5).$$
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
$$ x=frac{1}{2}*log_{7}(5)=log_{7}(5^{frac{1}{2}})=log_{7}(sqrt{5});$$
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:
Решение показательных уравнений при помощи замены
Рассмотрим уравнение:
Пример 10
$$ 9^x-5*3^x+6=0;$$
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^{2x}=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^{n*m}). Подставим:
$$(3^x)^2-5*3^x+6=0;$$
Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию – (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.
$$t^2-5t+6=0;$$
Квадратное уравнение, которое решается через дискриминант:
$$D=5^2-4*6=25-24=1; Rightarrow t_{1}=frac{5+sqrt{1}}{2}=3; Rightarrow t_{2}=frac{5-sqrt{1}}{2}=2;$$
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
$$ 3^x=3;$$
$$3^x=3^1;$$
$$x=1.$$
И второй корень:
$$ 3^x=2;$$
$$3^x=3^{log_{3}(2)};$$
$$x=log_{3}(2).$$
Ответ: (x_{1}=1; ; x_{2}=log_{3}(2).)
И еще один пример на замену:
Пример 11
$$3^{4x^2-6x+3}-10*3^{2x^2-3x+1}+3=0;$$
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Преобразуем первое слагаемое. Если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):
$$ 3^{4x^2-6x+3}=3^{4x^2-6x+2+1}=3^{2(2x^2-3x+1)+1}=3^{2*(2x^2-3x+1)}*3^1=3*(3^{2x^2-3x+1})^2;$$
Подставим в исходное уравнение:
$$3*(3^{2x^2-3x+1})^2-10*3^{2x^2-3x+1}+3=0;$$
Теперь показательные функции одинаковы и можно сделать замену:
$$t=3^{2x^2-3x+1}; ; t>0;$$
$$3*t^2-10t+3=0;$$
$$D=100-36=64; Rightarrow t_{1}=3; t_{2}=frac{1}{3};$$
Обратная замена, и наше уравнение сводится к простейшему:
$$ 3^{2x^2-3x+1}=3;$$
$$ 2x^2-3x+1=1;$$
$$x(2x-3)=0;$$
$$x=0; ; x=frac{3}{2}.$$
И второе значение (t):
$$3^{2x^2-3x+1}=frac{1}{3};$$
$$3^{2x^2-3x+1}=3^{-1};$$
$$2x^2-3x+1=-1;$$
$$2x^2-3x+2=0;$$
$$D=9-16=-7<0;$$
Раз дискриминант получился меньше нуля, то вторая ветка решений нам корней не дает.
Ответ: (x_{1}=0; ; x_{2}=frac{3}{2}.)
Однородные показательные уравнения
Иногда встречаются такие показательные уравнения, в которых не сразу видно, как сделать одинаковые функции, а именно одинаковые основания, чтобы произвести замену. Посмотрим на такой пример:
Пример 12
$$ 7^{x+1}+3*7^{x}=3^{x+2}+3^{x};$$
Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):
$$ 7^{x+1}+3*7^{x}=3^{x+2}+3^{x} ; ; :3^x$$
$$ frac{7^{x+1}}{3^x}+frac{3*7^{x}}{3^x}=frac{3^{x+2}}{3^x}+frac{3^{x}}{3^x};$$
Здесь нам придется воспользоваться свойствами степеней:
$$frac{a^n}{a^m}=a^{n-m};$$
$$ a^n*a^m=a^{n+m};$$
$$ frac{a^n}{b^n}=(frac{a}{b})^n;$$
Разберем каждое слагаемое:
$$ frac{7^{x+1}}{3^x}=frac{7*7^x}{3^x}=7*frac{7^x}{3^x}=7*(frac{7}{3})^x;$$
$$ frac{3*7^{x}}{3^x}=3*frac{7^x}{3^x}=3*(frac{7}{3})^x;$$
$$ frac{3^{x+2}}{3^x}=3^2*frac{3^x}{3^x}=3^2*1=9;$$
$$ frac{3^{x}}{3^x}=1;$$
Теперь подставим получившееся преобразования в исходное уравнение:
$$ 7*(frac{7}{3})^x+3*(frac{7}{3})^x=9+1;$$
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac{7}{3})^x):
$$7t+3t=10;$$
$$10t=10;$$
$$t=1;$$
Сделаем обратную замену:
$$(frac{7}{3})^x=1;$$
Вспоминаем, что (1=(frac{7}{3})^0):
$$(frac{7}{3})^x=(frac{7}{3})^0;$$
$$x=0.$$
Ответ: (x=0).
И последний пример на замену:
Пример 13
$$2^{x+2}+0,5^{-x-1}+4*2^{x+1}=28;$$
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
$$ a^n*a^m=a^{n+m};$$
$$a^{-n}=frac{1}{a^n};$$
$${(a^n)}^m=a^{n*m};$$
Разберем каждое слагаемое нашего уравнения:
$$2^{x+2}=2^x*2^2=4*2^x;$$
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны – отрицательная степень не имеет никакого отношения к знаку показательной функции!
$$0,5^{-x-1}=0,5^{-(x+1)}={(frac{1}{2})}^{-(x+1)}={(2^{-1})}^{-(x+1)}=2^{x+1}=2^x*2^1=2*2^x;$$
И последнее слагаемое со степенью:
$$ 4*2^{x+1}=4*2^x*2^1=8*2^x;$$
Подставим все наши преобразования в исходное уравнение:
$$4*2^x+2*2^x+8*2^x=28;$$
Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):
$$2^x*(4+2+8)=28;$$
$$14*2^x=28;$$
$$2^x=frac{28}{14}=2;$$
$$2^x=2^1;$$
$$x=1.$$
Ответ: (x=1.)
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера.
Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Пример 14
$$2^{x+1}*5^x=10^{x+1}*5^{x+2};$$
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:
$$2^{x+1}*5^x=(2*5)^{x+1}*5^{x+2};$$
Воспользуемся формулой ((a*b)^n=a^n*b^n):
$$ 2^{x+1}*5^x=2^{x+1}*5^{x+1}*5^{x+2};$$
И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:
$$frac{2^{x+1}}{2^{x+1}}=frac{5^{x+1}*5^{x+2}}{5^x};$$
Сокращаем и воспользуемся формулами (a^n*a^m=a^{n+m}) и (frac{a^n}{a^m}=a^{n-m}):
$$1=frac{5^{x+1+x+2}}{5^x};$$
$$1=frac{5^{2x+3}}{5^x};$$
$$1=5^{2x+3-x};$$
$$1=5^{x+3};$$
$$5^0=5^{x+3};$$
$$x+3=0;$$
$$x=-3.$$
Ответ: (x=-3).
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
На этой странице вы узнаете
- Зачем показательная функция смотрится в зеркало?
- Возможна ли дружба в математике?
- Как поменять знак неравенства всего одним действием?
Оценка за тест зависит от набранных баллов, а они зависят от количества и качества ответов. Цена билета в развлекательный центр может меняться от времени суток или дня недели. Погода в городе напрямую связана со временем года, географическим положением, температурой воздуха, влажностью, осадками и многими другими факторами. Функция в математике показывает нам зависимость одной переменной от другой. Об этом подробнее поговорим в статье.
Показательная функция и её основные свойства
Что же нам дает знание о характере этой зависимости?
Показательная функция — это функция, у которой неизвестная находится в показателе.
Она выглядит следующим образом:
y=ax, где
a > 0 и a ≠ 1
Посмотрим на обозначения элементов в показательной функции:

Рассмотрим промежутки, которым может принадлежать a.
При 0 < a < 1 и a > 1 показательные функции отличаются. Графики функций выглядят зеркально друг другу, если основание степени одной из них b, а второй
Например:

Рассмотрим функции с разными основаниями подробней.
Основные свойства функции:
1) Область определения
D(y)=(-∞;+∞)
2) Множество значений функции
Е(y)=(0;+∞)
3) Нет ни наименьшего, ни наибольшего значения.
4) Функция возрастает.
5) Функция непрерывна.

Рассмотрим функции с разными основаниями подробней.
Основные свойства функции:
1) Область определения
D(y)=(-∞;+∞)
2) Множество значений функции
Е(y)=(0;+∞)
3) Нет ни наименьшего, ни наибольшего значения.
4) Функция убывает.
5) Функция непрерывна.

Повторение свойств степеней
Прежде чем переходить к показательным уравнениям, давайте вспомним свойства степеней. Их можно применять для преобразований во время решения.

Методы решения показательных уравнений
Показательное уравнение – это уравнение, где неизвестная находится в показателе степени.
Если неизвестная содержится и в показателе степени, и в основании, уравнение также считается показательным.
Пример показательного уравнения: 54x-2 = 25.
Методы решения показательных уравнений:
- графический метод;
- метод уравнивания показателей;
- метод введения новой переменной;
- метод вынесения общего множителя;
- метод группировки;
- метод умножения/деления на показательную функцию.
- Графический метод
Этот метод заключается в рассмотрении левой и правой частей уравнения, как отдельных функций, и изображении их на плоскости. Данный метод в некоторых случаях может оказаться неточным. Поэтому его лучше использовать для нахождения количества решений, а сами значения находить другим методом.
Решим следующее уравнение:
0,5x+2 = x+5
Разделим его на отдельные функции:

Изобразим их на плоскости и найдем точку пересечения, именно она и будет решением данного уравнения.

Точка пересечения имеет координаты (-1;4). В ответ выпишем х=-1.
- Метод уравнивания показателей
Этот метод заключается в представлении обеих частей уравнения в виде степени с одинаковыми основаниями и приравниванию показателей степеней

Рассмотрим на примере:
2x⋅3x = 36
Воспользуемся свойством степеней для левой части и приведем к такому виду:
6x = 36
Запишем левую часть как степень с основанием 6:
6x = 62
Перейдем к равенству степеней и найдем х:
x = 2
- Метод введения новой переменной
Чтобы решить уравнение данным методом, нужно принять повторяющееся выражение за переменную и решить относительно нее, а после сделать обратную замену. Нельзя забывать про обратную замену, потому что значение введенной переменной не равно значению изначальной переменной.
Можно представить, что повторяющееся выражение и новая переменная – это лучшие друзья . Когда появляются затруднения с решением уравнения, подружка повторяющегося выражения прибегает и заменяет его до того момента, пока у уравнения не будут найдены корни. Затем они снова меняются.

Решим следующее уравнение:
22x-2⋅2x+6 = 5
Соберем все слагаемые слева
22x-2⋅2x+1 = 0
Разложим каждое слагаемое на множители:
2x⋅2x-2⋅2x+1 = 0
Заметим, что 2x можно заменить. Пусть t = 2x, t > 0, тогда уравнение можно записать следующим образом:
t2-2t+1 = 0
Решим его относительно новой переменной:
(t-1)2 = 0
t = 1
Найденное значение подходит под условие t > 0, сделаем обратную замену:
2x = 1
Представим правую часть в виде степени с основанием 2:
2x = 20
Приравняем показатели степеней и найдем х:
x = 0
- Метод вынесения общего множителя
Этот метод заключается в вынесение общего множителя за скобку.
Рассмотрим на примере:
6x-3x = 0
Разложим первое слагаемое на множители:
3x⋅2x-3x = 0
Вынесем общий множитель за скобку:
3x(2x-1) = 0
Так как произведение равно нулю, один из множителей должен равняться нулю. Перейдем к совокупности уравнений:

Так как показательная функция всегда больше 0, то у первого уравнения не будет решений. Из второго уравнения х = 0, значит, единственным решением данного уравнения будет х = 0.
- Метод группировки
Заключается этот метод во взятии слагаемых в скобки с последующим упрощением.
Давай решим такое уравнение:
x⋅5x-5x-3⋅5x+15 = 0
Заметим, что, сгруппировав 1 и 3 слагаемые и 2 и 4 слагаемые и вынося общий множитель за скобки, получаем одинаковые скобки:
(x⋅5x-3⋅5x)-(5x-15) = 0
5x(x-3)-5(x-3) = 0
Вынесем за скобку общий множитель (х — 3):
(5x-5)(x-3) = 0
Перейдем к совокупности уравнений:

Решим уравнения и получим х = 1 и х = 3.
- Метод умножения/деления на показательную функцию
Данный метод заключается в умножении каждого слагаемого уравнения на определенную показательную функцию.
Рассмотрим следующее уравнение:
Для упрощения уравнения умножим каждое слагаемое на 5x и получим:
2x⋅5x-1 = 0
Воспользуемся свойством степеней для первого слагаемого, а второе перенесем вправо:
10x = 1
Представим справа степень с основанием 10:
10x = 100
Приравняем степени и получим ответ:
x = 0
Также можно делить все слагаемые на показательную функцию для упрощения уравнения. Это допустимо, только если эта функция точно не равна нулю, так как на ноль делить нельзя.
Показательные неравенства и методы их решения
Показательное неравенство – это неравенство, у которого переменная находится в показателе степени.
Самый простой вид показательного неравенства:
ax > y , где a и y – числа
Неравенства видов af(x) > y и af(x) > ag(x) называются простейшими показательными неравенствами.
Особые случаи:
- af(x) < y при y ≤ 0 не имеет решений, так как число больше нуля в степени всегда больше 0;
- af(x)>y при y ≤ 0, в таком неравенстве множеством решений является множество действительных чисел, так как:
- число больше нуля в степени всегда положительное,
- положительное число больше отрицательного.
Давайте вспомним, как сравниваются показатели степеней с основаниями от 0 до 1 и основаниями больше 1.

Если основание от 0 до 1, то при переходе к неравенству степеней знак меняется на противоположный, а если основание больше 1, тогда при переходе знак остается прежним.
При делении или умножении каждой части неравенства на отрицательное число знак неравенства меняется на противоположный.
Например:
2x-1 > -3 | : (-1)
-2x+1 < 3
Методы решения показательных неравенств
Для решения показательных неравенств можно использовать те же методы, что и для решения уравнений, но с некоторыми изменениями. Они коснутся графического метода, метода уравнивания показателей и метода умножения/деления на показательную функцию.
- Графический метод
Теперь используя этот метод нужно закрашивать нужную область.
Рассмотрим такое неравенство:
2x ≥ -x+3
Запишем функции:
y = 2x
y = -x+3
Изобразим их на графике:

Так как первая функция больше или равна второй, выделим промежуток на графике, где график первой функции выше графика второй

В ответ получим промежуток [1;+∞).
- Метод уравнивания показателей
Данный метод будет записан по-разному для возрастающей и убывающей показательных функций.
af(x) < ag(x), где a > 1 ⬄ f(x) < g(x)
af(x) < ag(x), где 0 < a < 1 ⬄ f(x) > g(x)
3, 4, 5 методы работают без изменений.
6) Метод умножения/деления на показательную функцию
Используя данный метод для неравенств, нужно учитывать, что при умножении/делении на отрицательное число знак неравенства меняется на противоположный.
Решим одно неравенство:
(frac{1}{3})^{x+1}+frac{1}{3}^x ≥ 12
- Воспользуемся свойством степеней и преобразуем
(frac{1}{3})^{x}⋅frac{1}{3}+ frac{1}{3}^x ≥ 12
- Вынесем общий множитель
(frac{1}{3})^{x}⋅(frac{1}{3}+ 1) ≥ 12
(frac{1}{3})^{x}⋅frac{3}{4} ≥ 12
- Домножим обе части неравенства на
- Представим правую часть неравенства в виде степени с основанием 13
(frac{1}{3})^x ≥ (frac{1}{3})^{-2}
- Перейдем к неравенству степеней, поменяем знак уравнения, так как основание принадлежит промежутку от 0 до 1
x ≤ -2
Ответ: (-∞; -2].
Фактчек
- Вид показательной функции y=ax, где a > 0 и a ≠ 1.
- При 0 < a < 1 показательная функция убывает, а при a > 1 показательная функция возрастает.
- Показательное уравнение или неравенство – это уравнение или неравенство, где неизвестная находится в показателе степени.
- Методы решения показательных уравнений и неравенств:
- графический метод;
- метод уравнивания показателей;
- метод введения новой переменной;
- метод вынесения общего множителя;
- метод группировки;
- метод умножения/деления на показательную функцию.
- Если основание степени в неравенстве от 0 до 1, то при переходе к неравенству степеней знак меняется на противоположный.
- При умножении/делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный.
Термины
Область определения функции – это множество значений, которые может принимать х.
Множество значений функции – это множество значений, которые можно получить подставляя разные х из области определения функции.
Проверь себя
Задание 1.
Решите уравнение 3x3x+2=9
- 2
- -2
- 0
- 1
Задание 2.
Решите уравнение
5^frac{x-5}{x}-5^frac{1}{x} = 0
- 5
- 6
- 0
- 4
Задание 3.
Решите уравнение 4x⋅2=256
- 3,5
- 0
- 1
- 2,8
Задание 4.
Решите неравенство
- -3
- (-3; 3)
- (-∞; -3]
- [-3; +∞)
Задание 5.
Решите неравенство 3x+2-9x ≥ 0
- [2; +∞)
- (-∞; 2)
- (-∞; 2]
- 2
Ответы: 1. — 3; 2. — 2; 3. — 1; 4. — 4; 5. — 3.
Что такое показательные уравнения
Если ты забыл следующие темы, то для получения наилучшего результата, пожалуйста, повтори:
- Свойства степени и корня
- Решение линейных и квадратных уравнений
- Разложение на множители
Повторил? Замечательно!
Тогда тебе не составит труда заметить, что корнем уравнения ( 3x+5=2{x} -1) является число ( x=-6).
Ты точно понял, как я это сделал? Правда? Тогда продолжаем. Теперь ответь мне на вопрос, чему равно ( 5) в третьей степени? Ты абсолютно прав:
( {{5}^{3}}=5cdot 5cdot 5=125).
А восьмерка – это какая степень двойки? Правильно – третья! Потому что:
( 2cdot 2cdot 2={{2}^{3}}=8).
Ну вот, теперь давай попробуем решить следующую задачку: Пусть я ( x) раз умножаю само на себя число ( 2) и получаю в результате ( 16).
Спрашивается, сколько раз я умножил ( 2) само на себя? Ты, конечно, можешь проверить это непосредственно:
( begin{align} & 2=2 \ & 2cdot 2=4 \ & 2cdot 2cdot 2=8 \ & 2cdot 2cdot 2cdot 2=16 \ end{align} )
Тогда ты можешь сделать вывод, что ( 2) само на себя я умножал ( displaystyle 4) раза.
Как еще это можно проверить?
А вот как: непосредственно по определению степени: ( displaystyle {{2}^{4}}=16).
Но, согласись, если бы я спрашивал, сколько раз два нужно умножить само на себя, чтобы получить, скажем ( displaystyle 1024), ты бы сказал мне: я не буду морочить себе голову и умножать ( displaystyle 2) само на себя до посинения.
И был бы абсолютно прав. Потому как ты можешь записать все действия кратко (а краткость – сестра таланта)
( displaystyle {{2}^{x}}=1024),
где ( displaystyle x) – это и есть те самые «разы», когда ты умножаешь ( displaystyle 2) само на себя.
Я думаю, что ты знаешь ( а если не знаешь, срочно, очень срочно повторяй степени!), что ( displaystyle 1024={{2}^{10}}), тогда моя задачка запишется в виде:
( displaystyle {{2}^{x}}={{2}^{10}}), откуда ты можешь сделать вполне оправданный вывод, что:
( x=10).
Вот так вот незаметно я записал простейшее показательное уравнение:
( {{2}^{x}}={{2}^{10}})
И даже нашел его корень ( x=10). Тебе не кажется, что все совсем тривиально? Вот и я думаю именно так же.
Вот тебе еще один пример:
( {{1000}^{x}}=100).
Но что же делать?
Ведь ( 100) нельзя записать в виде степени (разумной) числа ( 1000).
Давай не будем отчаиваться и заметим, что оба этих числа прекрасно выражаются через степень одного и того же числа.
Какого?
Верно: ( 100={{10}^{2}},~1000={{10}^{3}}).
Тогда исходное уравнение преобразуется к виду:
( {{10}^{3x}}={{10}^{2}}),
откуда, как ты уже понял, ( 3x=2,~x=frac{2}{3}).
Давай более не будем тянуть и запишем определение:
Пример 1 (меркантильный)
Пусть у тебя есть ( displaystyle 1000000) рублей, а тебе хочется превратить его в ( displaystyle 1500000) рублей.
Банк предлагает тебе взять у тебя эти деньги под ( displaystyle 12%) годовых с ежемесячной капитализацией процентов (ежемесячным начислением).
Спрашивается, на сколько месяцев нужно открыть вклад, чтобы набрать нужную конечную сумму?
Вполне приземленная задача, не так ли?
Тем не менее ее решение связано с построением соответствующего показательного уравнения:
Пусть ( Sn) – начальная сумма, ( Sk) – конечная сумма, ( i) – процентная ставка за период, ( x) – количество периодов.
Тогда:
( Sk=Sn{{left( 1+frac{i}{100} right)}^{x}})
В нашем случае ( displaystyle Sn=1000000={{10}^{6}},~Sk=1500000=1.5cdot {{10}^{6}},~i=1) (если ставка ( 12%) годовых, то за месяц начисляют ( 1%)).
А почему ( i) делится на ( 100)? Если не знаешь ответ на этот вопрос, вспоминай тему «Проценты»!
Тогда мы получим вот такое уравнение:
( 1.5cdot {{10}^{6}}={{10}^{6}}{{left( 1+0.01 right)}^{x}})
( 1.5={{1.01}^{x}})
Данное показательное уравнение уже можно решить только при помощи калькулятора (его внешний вид на это намекает, причем для этого требуется знание логарифмов, с которыми мы познакомимся чуть позже), что я и сделаю: ( xtilde{ }40.7489)…
Таким образом, для получения ( 1.5) млн. нам потребуется сделать вклад на ( 41) месяц (не очень быстро, не правда ли?)
Пример 1. Метод простой замены
( {{4}^{x}}+{{2}^{x+1}}-3=0)
Решение:
Это уравнение решается при помощи «простой замены», как ее пренебрежительно называют математики.
В самом деле, замена здесь – самая очевидная. Стоит лишь увидеть, что
( {{4}^{x}}={{2}^{2x}}={{({{2}^{x}})}^{2}})
Тогда исходное уравнение превратится вот в такое:
( {{({{2}^{x}})}^{2}}+{{2}^{x+1}}-3=0)
Если же дополнительно представить ( {{2}^{x+1}}) как ( 2cdot {{2}^{x}}), то совершенно ясно, что надо заменять: конечно же, ( t={{2}^{x}}). Во что тогда превратится исходное уравнение? А вот во что:
( {{t}^{2}}+2t-3=0)
Ты без проблем самостоятельно отыщешь его корни: ( {{t}_{1}}=-3,~{{t}_{2}}=1).
Что нам делать теперь?
Пришло время возвращаться к исходной переменной ( displaystyle x).
А что я забыл указать? Именно: при замене некоторой степени на новую переменную (то есть при замене вида ( t={{a}^{x}})), меня будут интересовать только положительные корни!
Ты и сам без труда ответишь, почему.
Таким образом, ( {{t}_{1}}=-3) нас с тобой не интересует, а вот второй корень нам вполне подходит:
( {{t}_{2}}=1), тогда ( {{2}^{x}}=1), откуда ( x=0).
Ответ: ( x=0)
Как видишь, в предыдущем примере, замена так и просилась к нам в руки. К сожалению, так бывает далеко не всегда.
Однако давай не будем переходить сразу к грустному, а потренируемся еще на одном примере с достаточно простой заменой.
Пример 2. Метод простой замены
( {{3}^{3x+1}}-4cdot {{9}^{x}}=17cdot {{3}^{x}}-6)
Решение:
Ясно, что скорее всего заменять придется ( {{3}^{x}}) (это наименьшая из степеней, входящая в наше уравнение).
Однако прежде чем вводить замену, наше уравнение нужно к ней «подготовить», а именно:
( {{3}^{3x+1}}=3cdot {{left( {{3}^{x}} right)}^{3}}), ( {{9}^{x}}={{({{3}^{x}})}^{2}}).
Тогда можно заменять ( t={{3}^{x}}), в результате я получу следующее выражение:
( 3{{t}^{3}}-4{{t}^{2}}=17t-6)
( 3{{t}^{3}}-4{{t}^{2}}-17t+6=0)
О ужас: кубическое уравнение с совершенно жуткими формулами его решения (ну если говорить в общем виде). Но давай не будем сразу отчаиваться, а подумаем, что нам делать.
Я предложу смошенничать: мы знаем, что для получения «красивого» ответа, нам нужно получить ( t) в виде некоторой степени тройки (с чего бы это, а?).
А давай попробуем угадать хотя бы один корень нашего уравнения (я начну гадать со степеней тройки).
Первое предположение ( displaystyle t=1). Не является корнем. Увы и ах! Хорошо, а теперь возьмем…
Как видишь, отбор корней показательных уравнений требует достаточно глубокого знания свойств логарифмов, так что я советую тебе быть как можно внимательнее, когда решаешь показательные уравнения.
Как ты понимаешь, в математике все взаимосвязано! Как говорила моя учительница по математике, математику, как историю, за ночь не прочитаешь.
Как правило, всю сложность при решении задач повышенной сложности составляет именно отбор корней уравнения.
Еще один пример для тренировки
( {{9}^{x+1}}-2cdot {{3}^{x+2}}+5=0,~) при ( ~xin (lo{{g}_{3}}frac{3}{2};sqrt{5}))
Решение:
Ясно, что само уравнение решается довольно просто. Сделав замену ( t={{3}^{x}}) мы сведем наше исходное уравнение к следующему:
( {{t}^{2}}-18t+5=0)
( {{t}_{1}}=frac{1}{3},~{{t}_{2}}=frac{5~}{3})
Тогда ( {{x}_{1}}=-1,~{{x}_{2}}=mathbf{lo}{{mathbf{g}}_{3}}left( frac{5}{3} right)~~~)
Вначале давай рассмотрим первый корень.
Сравним ( -1) и ( lo{{g}_{3}}left( frac{3}{2} right)):
так как ( frac{3}{2}>1), то ( lo{{g}_{3}}left( frac{3}{2} right)>0). (свойство логарифмической функции ( y=lo{{g}_{a}}x) при ( a>1)).
Тогда ясно, что( lo{{g}_{3}}left( frac{3}{2} right)>-1) и первый корень не принадлежит нашему промежутку.
Теперь второй корень:
Пример уравнения с нестандартной заменой!
( displaystyle 4sqrt[x]{81}-12sqrt[x]{36}+9sqrt[x]{16}=0)
Решение:
Давай сразу начнем с того, что делать можно, а что – в принципе можно, но лучше не делать.
Можно – представить все через степени тройки, двойки и шестерки. К чему это приведет?
Да ни к чему и не приведет: мешанина степеней, причем от некоторых будет довольно сложно избавиться.
А что же тогда нужно?
Давай заметим, что ( 81={{9}^{2}},~16={{4}^{2}},~) а ( 36=4cdot 9.)
И что нам это даст? А то, что мы можем свести решение данного примера к решению достаточно простого показательного уравнения!
Вначале давай перепишем наше уравнение в виде:
( displaystyle 4cdot {{9}^{frac{2}{x}}}~-12cdot {{4}^{frac{1}{x}}}{{9}^{frac{1}{x}}}+9cdot {{4}^{frac{2}{x}}}=0)
Такие уравнения называются однородными (подробнее читай в теме «Однородные уравнения»).
Теперь разделим обе части получившегося уравнения на ( {{4}^{frac{2}{x}}}):
Например, уравнение вида:
( {{a}^{F(x)}}=b(x)), причем ( b(x)ne {{a}^{i}}), ( i)( in R/Q)
В общем случае можно решить только логарифмированием обеих частей (например по основанию ( a)), при котором исходное уравнение превратится в следующее:
( F(x)=lo{{g}_{a}}b(x))
Давай рассмотрим следующий пример:
( {{x}^{1+lgx}}=10x)
Ясно, что по ОДЗ логарифмической функции, нас интересуют только ( x>0). Однако, это следует не только из ОДЗ логарифма, а еще по одной причине. Я думаю, что тебе не будет трудно угадать, по какой же именно.
Давай прологарифмируем обе части нашего уравнения по основанию ( 10):
( lg({{x}^{1+lgx}})=lg(10x))
( (1+lg(x))cdot lg(x)=1+lg(x))
( (1+lg(x))(lg(x)-1)=0)
( lg(x)=1,~lg(x)=-1)
( {{x}_{1}}=10,~{{x}_{2}}=0,1)
Как видишь, логарифмирование нашего исходного уравнения достаточно быстро привело нас к правильному (и красивому!) ответу.
Давай потренируемся еще на одном примере:
( {{x}^{lo{{g}_{4}}x-2}}={{2}^{2(lo{{g}_{4}}x-1)}})
Здесь тоже нет ничего страшного: прологарифмируем обе стороны уравнения по основанию ( 4), тогда получим:
( lo{{g}_{4}}({{x}^{lo{{g}_{4}}x-2}})=lo{{g}_{4}}({{2}^{2(lo{{g}_{4}}x-1)}});)
( left( lo{{g}_{4}}x-2 right)text{lo}{{text{g}}_{4}}x=2left( text{lo}{{text{g}}_{4}}x-1 right)text{lo}{{text{g}}_{4}}2;)
( (lo{{g}_{4}}x-2)lo{{g}_{4}}x=(lo{{g}_{4}}x-1);)
Сделаем замену: ( t=lo{{g}_{4}}x)
( {{t}_{1}}=frac{3+sqrt{5}}{2},~{{t}_{2}}=frac{3-sqrt{5}}{2})
Тогда ( {{x}_{1}}=lo{{g}_{4}}left( frac{3+sqrt{5}}{2} right),~{{x}_{2}}=lo{{g}_{4}}left( frac{3-sqrt{5}}{2} right),~)
Однако мы кое-что упустили! Ты заметил, где я сделал промах?
Ведь ( frac{3-sqrt{5}}{2}<1,~) тогда:
( {{x}_{2}}=lo{{g}_{4}}left( frac{3-sqrt{5}}{2} right)<0,~~) что не удовлетворяет требованию ( x>0) (подумай откуда оно взялось!)
Ответ: ( lo{{g}_{4}}left( frac{3+sqrt{5}}{2} right))
Попробуй самостоятельно записать решение показательных уравнений, приведенных ниже
- ( {{x}^{2l{{g}^{3}}x-1.5lgx}}=sqrt{10})
- ( {{(x+5)}^{lo{{g}_{7}}(x+5)}}=7)
А теперь сверь свое решение с этим:
1. Логарифмируем обе части по основанию ( 10), учитывая, что ( x>0):
( lg left( {{x}^{2l{{g}^{3}}x-1.5lgx}} right)=lgsqrt{10})
( left( 2l{{g}^{3}}x-1.5lgx right)lgx=frac{1}{2},~), замена ( ~t=l{{g}^{2}}xge 0)
( 4{{t}^{2}}-3t-1=0)
( 4{{t}^{2}}-3t-1=0) (второй корень нам не подходит ввиду замены)
( l{{g}^{2}}x=1,~{{x}_{1}}=1,~{{x}_{2}}=0.1~)
2. Логарифмируем по основанию ( displaystyle 7):
( displaystyle lo{{g}_{7}}{{left( x+5 right)}^{lo{{g}_{7}}left( x+5 right)}}=lo{{g}_{7}}7)
Преобразуем полученное выражение к следующему виду:
( displaystyle left( lo{{g}_{7}}left( x+5 right)+1 right)left( lo{{g}_{7}}left( x+5 right)-1 right)=0)
( displaystyle {{x}_{1}}=2,~{{x}_{2}}=-frac{34}{7})
Содержание:
Показательно-степенные уравнения:
Показательно степенными уравнениями обычно называют уравнения, содержащие выражения вида 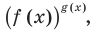
Основные способы решения уравнения вида 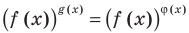
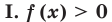
Ориентир
Используем (если возможно) основное логарифмическое тождество в виде
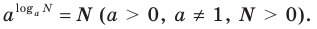
Логарифмируем (если возможно) обе части уравнения по числовому основанию или представляем все степени как степени с одним и тем же числовым основанием по формуле
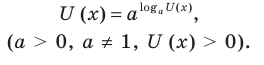
Пример:
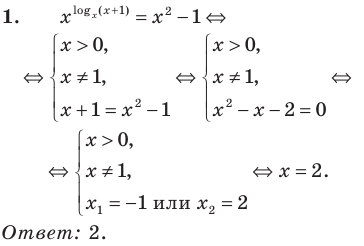
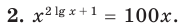
На ОДЗ (х > 0) обе части уравнения положительны, поэтому после логарифмирования по основанию 10 получаем уравнение, равносильное данному:
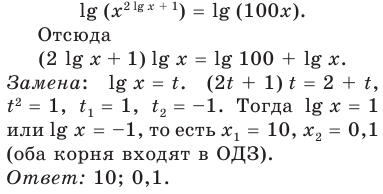
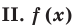 — произвольное выражение
— произвольное выражение
Ориентир:
Две степени с одинаковыми основаниям и 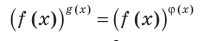 могут быть равными в одном из четырех случаев:
могут быть равными в одном из четырех случаев:
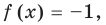 для корней, этого уравнения
для корней, этого уравнения 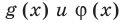 — целые, числа одинаковой четности;
— целые, числа одинаковой четности;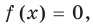 для корней этого уравнения
для корней этого уравнения 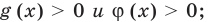
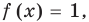 для корней этого уравнения
для корней этого уравнения 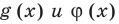 существуют;
существуют;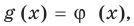 для корней этого уравнения существуют
для корней этого уравнения существуют 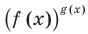 и
и 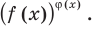
Пример:
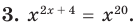
Если предположить, что основание степени 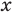 является числом, то сначала рассмотрим три особых случая (основание степени равно
является числом, то сначала рассмотрим три особых случая (основание степени равно 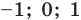 а затем приравняем показатели степеней:
а затем приравняем показатели степеней:
- при
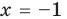 получаем верное равенство
получаем верное равенство 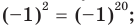
- при
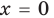 то
то 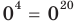 — верное равенство;
— верное равенство; - при
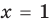 то
то 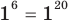 — верное равенство;
— верное равенство; - при
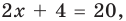 то есть
то есть 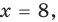 то
то 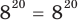 — верное равенство.
— верное равенство.
Ответ: 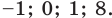
Замечание. Если предположить, что основание 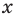 является переменной, то функция
является переменной, то функция 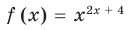 считается определенной только при
считается определенной только при 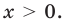 В этом случае данное уравнение имеет только корни 1 и 8, и получаем ответ:
В этом случае данное уравнение имеет только корни 1 и 8, и получаем ответ: 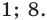
Таким образом, ответ к такому уравнению нельзя записать однозначно.
Объяснение и обоснование
Показательно степенными уравнениями и неравенствами обычно называют уравнения и неравенства, содержащие выражения вида 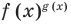 (в которых переменная входит и в основание, и в показатель степени).
(в которых переменная входит и в основание, и в показатель степени).
Анализируя показательно-степенные уравнения, представленные в табл. 26, следует помнить, что в школьном курсе математики понятие уравнения на разных этапах вводилось по-разному. В 4 -5 классах уравнением называлось числовое равенство, содержащее неизвестное число, обозначенное буквой. Значение неизвестного, при котором уравнение обращается в верное числовое равенство, называлось корнем, или решением этого уравнения. Например, для уравнения 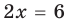 корнем является значение
корнем является значение 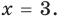
С точки зрения приведенного определения, в уравнении 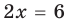 буквой
буквой 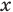 обозначено хотя и неизвестное нам, но конкретное число, поэтому
обозначено хотя и неизвестное нам, но конкретное число, поэтому 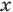 может принимать единственное значение
может принимать единственное значение 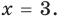 Но такое определение затрудняет в дальнейшем работу с уравнением. Когда
Но такое определение затрудняет в дальнейшем работу с уравнением. Когда 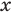 принимает единственное значение, мы не можем применять, например, графическое решение уравнения (имея только одно значение
принимает единственное значение, мы не можем применять, например, графическое решение уравнения (имея только одно значение 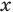 , невозможно получить график
, невозможно получить график 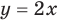 как прямую линию на плоскости). Поэтому, начиная с 6-7 классов, уравнение определяется как равенство с переменной (а корнем, или решением уравнения соответственно называется такое значение переменной, при котором это уравнение обращается в верное числовое равенство). Тогда
как прямую линию на плоскости). Поэтому, начиная с 6-7 классов, уравнение определяется как равенство с переменной (а корнем, или решением уравнения соответственно называется такое значение переменной, при котором это уравнение обращается в верное числовое равенство). Тогда 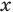 в уравнении
в уравнении 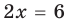 — это переменная, для которой нет ни одного ограничения, и поэтому
— это переменная, для которой нет ни одного ограничения, и поэтому 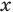 может быть любым числом (ОДЗ уравнения:
может быть любым числом (ОДЗ уравнения: 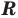 ). При таком подходе каждому значению переменной
). При таком подходе каждому значению переменной 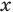 соответствует единственное значение переменной
соответствует единственное значение переменной 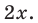 Таким образом, это уравнение можно решить графически, построив графики функций
Таким образом, это уравнение можно решить графически, построив графики функций 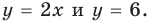 Кроме того, можно записать уравнение в общем виде как равенство
Кроме того, можно записать уравнение в общем виде как равенство 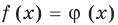 и обоснованно применить свойства функций для решения уравнений.
и обоснованно применить свойства функций для решения уравнений.
Для всех видов уравнений, которые рассматривались в курсе алгебры или алгебры и начал анализа, приведенные два определения уравнения приводят к одному и тому же результату при решении уравнений. Но в случае показательно-степенного уравнения иногда можно получить разные ответы, используя разные подходы к определению уравнения. Например, решим уравнение 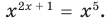
Если рассматривать такое уравнение как числовое равенство, то две степени с одинаковым основанием 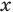 могут быть равными только в одном из четырех случаев. А именно: если основанием степени является одно из значений
могут быть равными только в одном из четырех случаев. А именно: если основанием степени является одно из значений 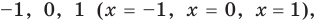 то степени могут быть равными даже тогда, когда их показатели будут разными (при условии, что эти степени существуют). Во всех остальных случаях степени с одинаковым основанием будут равными только тогда, когда показатели этих степеней будут равными (
то степени могут быть равными даже тогда, когда их показатели будут разными (при условии, что эти степени существуют). Во всех остальных случаях степени с одинаковым основанием будут равными только тогда, когда показатели этих степеней будут равными (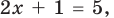 то есть
то есть 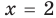 ). Следовательно, для получения всех корней данного уравнения достаточно проверить значения
). Следовательно, для получения всех корней данного уравнения достаточно проверить значения 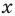 , равные
, равные 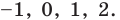 Все эти числа являются корнями, так как при подстановке каждого из них в данное уравнение оно обращается в верное числовое равенство.
Все эти числа являются корнями, так как при подстановке каждого из них в данное уравнение оно обращается в верное числовое равенство.
Если же рассматривать это уравнение как равенство с переменной и встать на функциональную точку зрения, то функция 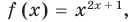 как правило, считается определенной только при
как правило, считается определенной только при 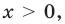 тогда данное уравнение имеет только два корня: 1 и 2.
тогда данное уравнение имеет только два корня: 1 и 2.
Таким образом, в рассмотренном уравнении ответ нельзя записать однозначно (поскольку каждый из указанных подходов к определению уравнения имеет право на существование и реально используется в математике). Поэтому в подобных ситуациях приходится приводить оба варианта ответа. Аналогичный пример приведен в табл. 26.
Обобщая приведенные выше рассуждения, заметим, что в том слу чае, когда при решении уравнения вида 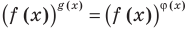 из условия не следует, что основание степени
из условия не следует, что основание степени 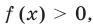 необходимо рассмотреть три особых случая: основание
необходимо рассмотреть три особых случая: основание 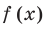 равно -1 , 0, 1 (при этом степени
равно -1 , 0, 1 (при этом степени 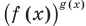 и
и 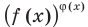 могут быть равными даже тогда, когда показатели
могут быть равными даже тогда, когда показатели 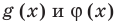 разные), а затем приравнять показатели
разные), а затем приравнять показатели 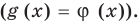 Если же из условия следует, что
Если же из условия следует, что 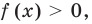 то рассматриваем только один особый случай — основание степени равно
то рассматриваем только один особый случай — основание степени равно 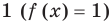 — и приравниваем показатели степеней
— и приравниваем показатели степеней 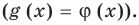
Например, решим уравнение 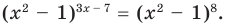
Из условия не следует, что основание степени 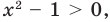 следовательно, приходится рассматривать все случаи.
следовательно, приходится рассматривать все случаи.
Объединяя полученные результаты, получаем ответ.
Ответ: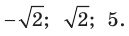
Замечание. При 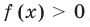 для решения уравнения
для решения уравнения 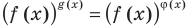 можно прологарифмировать обе его части по любому числовому основанию, получить равносильное уравнение, в котором уже не придется рассматривать особый случай — он будет учтен автоматически. Это связано с тем, что функция
можно прологарифмировать обе его части по любому числовому основанию, получить равносильное уравнение, в котором уже не придется рассматривать особый случай — он будет учтен автоматически. Это связано с тем, что функция 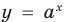 при
при 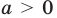 имеет особый случай, если
имеет особый случай, если 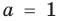 (см. график функции
(см. график функции 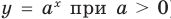 ), а функция
), а функция 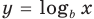 (где
(где 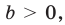
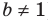 ) особых случаев не имеет.
) особых случаев не имеет.
Также отметим, что при решении неравенств вида 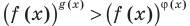 обычно используют функциональный подход и считают, что
обычно используют функциональный подход и считают, что 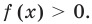 Когда в показательно-степенное уравнение входят выражения вида
Когда в показательно-степенное уравнение входят выражения вида 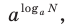 для его решения можно воспользоваться основным логарифмическим тождеством, В этом случае следует учитывать ОДЗ данного уравнения (см. пример 1 в табл. 26).
для его решения можно воспользоваться основным логарифмическим тождеством, В этом случае следует учитывать ОДЗ данного уравнения (см. пример 1 в табл. 26).
Достаточно часто при решении показательно-степенных уравнений логарифмируют обе его части. Это можно сделать только тогда, когда обе части уравнения положительны на его ОДЗ (см. пример 2 в табл. 26). Приведем еще несколько примеров решения показательно-степенных уравнений и неравенств.
Примеры с решениями
Пример №1
Решите уравнение 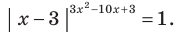
Решение:
Поскольку 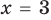 не является корнем данного уравнения (
не является корнем данного уравнения (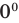 не существует), то при
не существует), то при 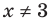 обе его части положительны. После логарифмирования (по основанию 10) обеих частей данного уравнения получаем равносильные ему уравнения:
обе его части положительны. После логарифмирования (по основанию 10) обеих частей данного уравнения получаем равносильные ему уравнения:
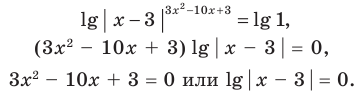
Из первого полученного уравнения имеем 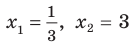 (не является корнем), а из второго —
(не является корнем), а из второго — 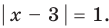 Тогда
Тогда 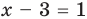 или
или 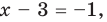 то есть
то есть 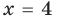 или
или 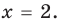 Ответ:
Ответ: 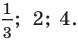
Комментарий:
Поскольку 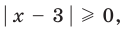 то из особых случаев можно рассмотреть только один — основание равно 0 (
то из особых случаев можно рассмотреть только один — основание равно 0 ( 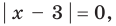 то есть
то есть 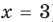 ). Чтобы не рассматривать случай, когда основание равно 1, достаточно при
). Чтобы не рассматривать случай, когда основание равно 1, достаточно при 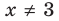 прологарифмировать обе части уравнения по числовому основанию (например, по основанию 10). При
прологарифмировать обе части уравнения по числовому основанию (например, по основанию 10). При 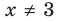 обе части данного уравнения положительны, поэтому после логарифмирования получаем уравнение, равносильное данному. Поскольку все дальнейшие преобразования равносильны (при
обе части данного уравнения положительны, поэтому после логарифмирования получаем уравнение, равносильное данному. Поскольку все дальнейшие преобразования равносильны (при 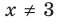 ), то все полученные решения (не равные 3) являются корнями данного уравнения.
), то все полученные решения (не равные 3) являются корнями данного уравнения.
Пример №2
Решите уравнение 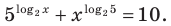
Комментарий:
Прологарифмировать обе части данного уравнения не удается (в левой части стоит сумма), поэтому попытаемся представить все степени в виде степеней с одним и тем же числовым основанием. Так как в уравнении есть логарифм по основанию 2, представим все данные степени в виде степеней с основанием 2 по формуле 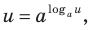 где
где 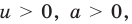
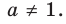 Тогда
Тогда
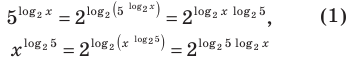
(то есть слагаемые, стоящие в левой части данного уравнения, одинаковы). После получения уравнения (2) (см. решение) можно использовать равенство (1) справа налево, а также записать правую часть уравнения (2) как степень числа 2 или прологарифмировать обе его части по основанию 2.
Решение:
ОДЗ: 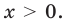 На этой ОДЗ данное уравнение равносильно уравнениям:
На этой ОДЗ данное уравнение равносильно уравнениям:
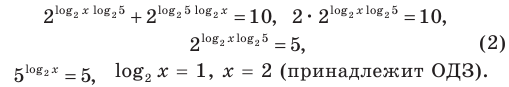
Ответ: 2.
Пример №3
Решите систему уравнений: 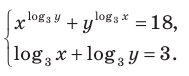
Комментарий :
Используем равносильные преобразования системы. Для этого учтем ОДЗ и проследим, чтобы на этой ОДЗ преобразования уравнений как в прямом, так и в обратном направлениях сохраняли верные равенства. В первом уравнении данной системы запишем все степени как степени с основанием 3 (см. комментарий к задаче 2). После равносильных (на ОДЗ) преобразований первого уравнения получаем систему (1) (см. решение), в которую переменные входят только в виде 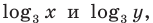 поэтому удобно произвести замену переменных. После обратной замены применяем определение логарифма.
поэтому удобно произвести замену переменных. После обратной замены применяем определение логарифма.
Решение:
ОДЗ: 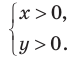 На этой ОДЗ первое уравнение данной системы равносильно уравнениям:
На этой ОДЗ первое уравнение данной системы равносильно уравнениям: 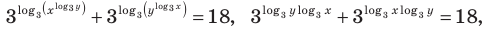
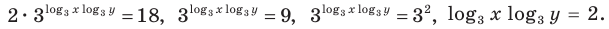
Тогда данная система уравнений равносильна системе
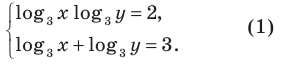
Замена 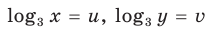 дает систему уравнений
дает систему уравнений 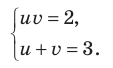 Из второго уравнения последней системы
Из второго уравнения последней системы 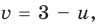 из первого уравнения получаем
из первого уравнения получаем 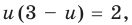 то есть
то есть 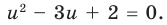 Отсюда
Отсюда 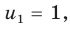
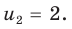 Тогда
Тогда 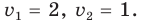 Обратная замена дает
Обратная замена дает
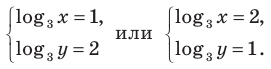
Тогда

(найденные решения входят в ОДЗ). Ответ: 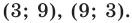
Пример №4
Решите неравенство 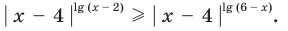
I способ
Комментарий:
Попытаемся выполнить равносильные преобразования данного неравенства, применив рассуждения, аналогичные тем, что приводились при решении показательно-степенных уравнений (см. пункт II табл. 60). Поскольку 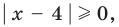 то из особых случаев следует рассмотреть только два: основание равно
то из особых случаев следует рассмотреть только два: основание равно 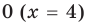 и основание равно
и основание равно 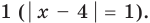 При других значениях
При других значениях 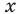 основание — положительное число, не равное 1.
основание — положительное число, не равное 1.
Рассмотрим два случая:
- 1) основание больше 1 (при переходе от степеней к показателям в данном неравенстве знак неравенства не меняется);
- 2) основание меньше 1, но больше 0 (при переходе от степеней к показателям знак неравенства меняется на противоположный). При таких преобразованиях получаем неравенства, равносильные данному (на его ОДЗ), поскольку можем гарантировать правильность не только прямых, но и обратных переходов.
При решении полученных простейших логарифмических неравенств учитываем, что функция 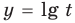 возрастающая. В ответ следует включить все решения полученных систем неравенств и все особые значения, которые являются решениями данного неравенства.
возрастающая. В ответ следует включить все решения полученных систем неравенств и все особые значения, которые являются решениями данного неравенства.
Решение:
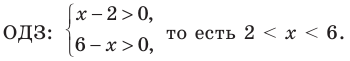
При 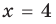 данное неравенство выполняется
данное неравенство выполняется 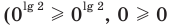 — верное неравенство), таким образом,
— верное неравенство), таким образом, 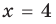 — одно из его решений. Если
— одно из его решений. Если 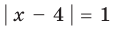 (то есть
(то есть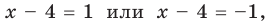 тогда
тогда 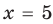 или
или 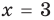 — эти значения входят в ОДЗ), то данное неравенство также выполняется. При
— эти значения входят в ОДЗ), то данное неравенство также выполняется. При 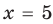 и
и 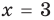 получаем верное неравенство
получаем верное неравенство  Таким образом , эти числа также являются решениями данного неравенства. При
Таким образом , эти числа также являются решениями данного неравенства. При 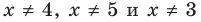 на ОДЗ данное неравенство равносильно следующей совокупности систем:
на ОДЗ данное неравенство равносильно следующей совокупности систем:
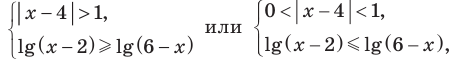
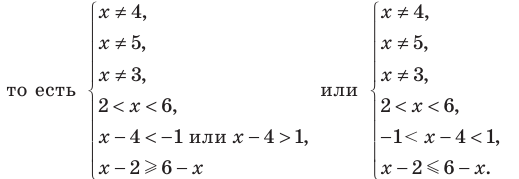
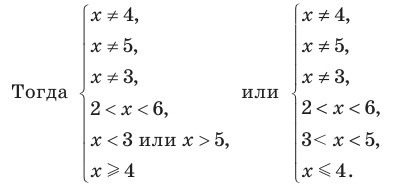
Таким образом, 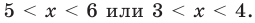 Учитывая особые значения , которые являются решениями, получаем:
Учитывая особые значения , которые являются решениями, получаем: 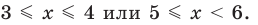 Ответ:
Ответ: 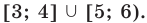
II способ
Комментарий:
Решим данное неравенство методом интервалов, для этого приведем его к виду 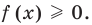 Для нахождения нулей
Для нахождения нулей 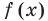 необходимо решить показательно-степенное уравнение (2) (см . решение ниже). Поскольку
необходимо решить показательно-степенное уравнение (2) (см . решение ниже). Поскольку 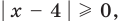 то из особых случаев необходимо рассмотреть только два — основание равно 0
то из особых случаев необходимо рассмотреть только два — основание равно 0 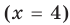 или основание равно
или основание равно 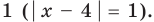 При других значениях
При других значениях 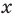 из ОДЗ в уравнении (3) (см. решение ниже) основание — положительное число, не равное 1. Тогда можно приравнять показатели степеней (получаем уравнение, равносильное данному). Для нахождения знаков
из ОДЗ в уравнении (3) (см. решение ниже) основание — положительное число, не равное 1. Тогда можно приравнять показатели степеней (получаем уравнение, равносильное данному). Для нахождения знаков 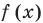 удобно использовать график функции
удобно использовать график функции 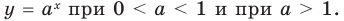
Решение:
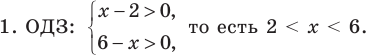
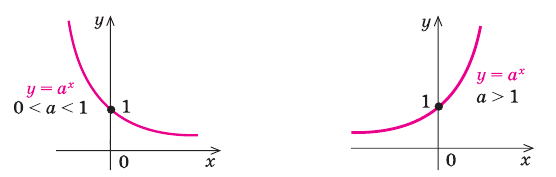
На этой ОДЗ данное неравенство равносильно неравенству
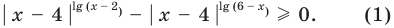
2. Пусть 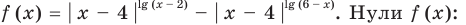
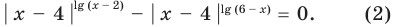
На ОДЗ уравнение (2) равносильно уравнению
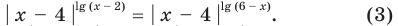
При 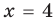 равенство (3) выполняется
равенство (3) выполняется 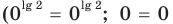 — верное равенство), таким образом,
— верное равенство), таким образом, 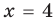 — корень уравнения (3). Если
— корень уравнения (3). Если 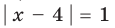 (то есть
(то есть 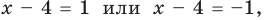 тогда
тогда 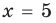 или
или 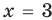 ), то равенство (3) также выполняется. При
), то равенство (3) также выполняется. При 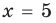 и
и 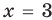 получаем верное равенство
получаем верное равенство 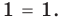 Таким образом, эти числа также являются корнями уравнения (3). При
Таким образом, эти числа также являются корнями уравнения (3). При 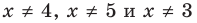 на ОДЗ уравнение (3) равносильно уравнению
на ОДЗ уравнение (3) равносильно уравнению 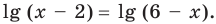 Тогда
Тогда 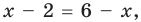 то есть
то есть 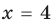 — не удовлетворяет условию
— не удовлетворяет условию 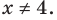 Следовательно, на последнем множестве уравнение (3) корней не имеет.
Следовательно, на последнем множестве уравнение (3) корней не имеет.
3. Отмечаем нули функции на ОДЗ и находим знак 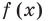 на каждом из промежутков, на которые разбивается ОДЗ (см. рисунок).
на каждом из промежутков, на которые разбивается ОДЗ (см. рисунок).

Ответ: 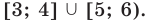
Пример №5
Решите неравенство 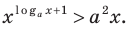
Комментарий:
На ОДЗ обе части неравенства положительны, поэтому попытаемся прологарифмировать обе его части. Поскольку в данное неравенство уже входит 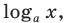 то удобно прологарифмировать по основанию
то удобно прологарифмировать по основанию 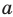 . Но при логарифмировании по основанию больше 1 знак неравенства не меняется, а при логарифмировании по основанию меньше 1 — меняется. Необходимо рассмотреть два случая (в каждом из них получаем неравенство, равносильное данному на его ОДЗ).
. Но при логарифмировании по основанию больше 1 знак неравенства не меняется, а при логарифмировании по основанию меньше 1 — меняется. Необходимо рассмотреть два случая (в каждом из них получаем неравенство, равносильное данному на его ОДЗ).
Решение:
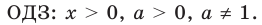
Прологарифмируем обе части неравенства.
1) При 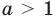 данное неравенство на его ОДЗ равносильно неравенствам:
данное неравенство на его ОДЗ равносильно неравенствам:
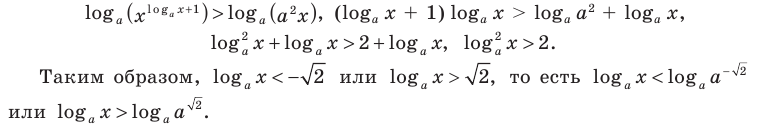
Учитывая ОДЗ  и то, что
и то, что получаем
получаем 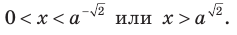 2) При
2) При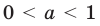 данное неравенство на его ОДЗ равносильно неравенствам:
данное неравенство на его ОДЗ равносильно неравенствам:
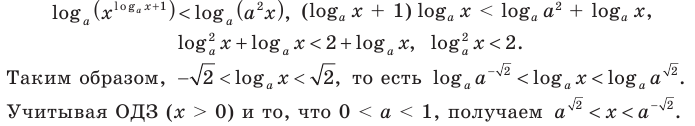
Ответ: 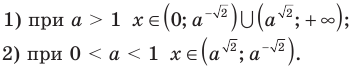
Показательно-степенные уравнения
Показательно-степенные уравнения:
Показательно-степенными уравнениями обычно называют уравнения, содержащие выражения вида 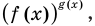 то есть уравнения вида
то есть уравнения вида 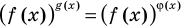 (основанием степеней, стоящих в левой и правой частях показательно степенного уравнения, является
(основанием степеней, стоящих в левой и правой частях показательно степенного уравнения, является 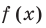 — выражение с переменной).
— выражение с переменной).
Основные способы решения уравнения вида 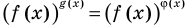
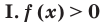
Используем (если возможно) основное логарифмическое тождество в виде 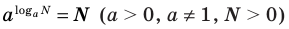
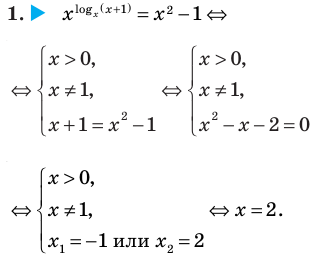
Ответ: 2
Логарифмируем (если возможно) обе части уравнения по числовому основанию или представляем все степени как степени с одним и тем же числовым основанием по формуле
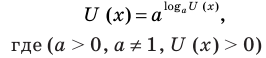
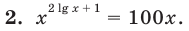
На ОДЗ 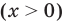 обе части уравнения положительны, поэтому после логарифмирования по основанию 10 получаем уравнение, равносильное данному:
обе части уравнения положительны, поэтому после логарифмирования по основанию 10 получаем уравнение, равносильное данному: 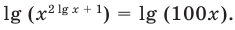
Отсюда 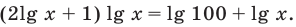
Замена: 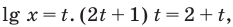
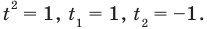 Тогда
Тогда 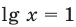 или
или 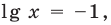 то есть
то есть 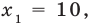
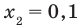 (оба корня входят в ОДЗ). Ответ: 10; 0,1.
(оба корня входят в ОДЗ). Ответ: 10; 0,1.
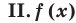 — произвольное выражение
— произвольное выражение
Две степени с одинаковыми основаниями 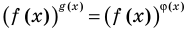 могут быть равными в одном из четырех случаев:
могут быть равными в одном из четырех случаев:
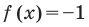 и для корней этого уравнения
и для корней этого уравнения 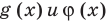 — целые числа одинаковой четности.
— целые числа одинаковой четности.-
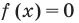 и для корней этого уравнения
и для корней этого уравнения 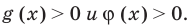
-
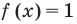 и для корней этого уравнения
и для корней этого уравнения 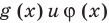 существуют.
существуют. -
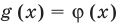 и для корней этого уравнения существуют
и для корней этого уравнения существуют 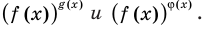
Пример:
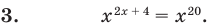
Если предположить, что основание степени 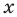 является числом, то сначала рассмотрим три особых случая (основание степени равно –
является числом, то сначала рассмотрим три особых случая (основание степени равно –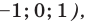 а затем приравняем показатели степеней:
а затем приравняем показатели степеней:
- при
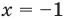 получаем верное равенство
получаем верное равенство 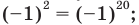
- при
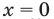
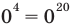 — верное равенство;
— верное равенство; - при
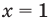
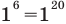 — верное равенство;
— верное равенство; - при
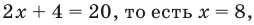 — верное равенство.
— верное равенство.
Ответ: 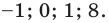
Замечание. Если предположить, что основание 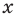 является переменной, то функция
является переменной, то функция 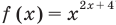 считается определенной только при
считается определенной только при 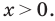 В этом случае данное уравнение имеет только корни 1 и 8, и получаем ответ: 1; 8. Таким образом, ответ к такому уравнению нельзя записать однозначно.
В этом случае данное уравнение имеет только корни 1 и 8, и получаем ответ: 1; 8. Таким образом, ответ к такому уравнению нельзя записать однозначно.
Объяснение и обоснование:
Показательно-степенными уравнениями и неравенствами обычно называют уравнения и неравенства, содержащие выражения вида 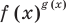 (в которых переменная входит и в основание, и в показатель степени).
(в которых переменная входит и в основание, и в показатель степени).
Анализируя показательно-степенные уравнения, представленные в таблице 57, следует помнить, что в школьном курсе математики понятие уравнения на разных этапах вводилось по-разному. А именно: в 4-5 классах уравнением называлось числовое равенство, содержащее неизвестное число, обозначенное буквой. Значение неизвестного, при котором уравнение обращается в верное числовое равенство, называлось корнем или решением этого уравнения. Например, для уравнения 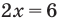 корнем является значение
корнем является значение 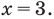
С точки зрения приведенного определения в уравнении 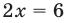 буквой
буквой 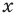 обозначено хотя и неизвестное нам, но конкретное число, поэтому
обозначено хотя и неизвестное нам, но конкретное число, поэтому 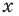 может принимать единственное значение
может принимать единственное значение 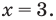 Но такое определение затрудняет в дальнейшем работу с уравнением. Когда
Но такое определение затрудняет в дальнейшем работу с уравнением. Когда 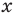 принимает единственное значение, мы не можем применять, например, графическое решение уравнения (имея только одно значение
принимает единственное значение, мы не можем применять, например, графическое решение уравнения (имея только одно значение 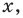 невозможно получить график
невозможно получить график 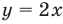 как прямую линию на плоскости). Поэтому, начиная с 6-7 классов, уравнение определяется как равенство с переменной (а корнем или решением уравнения соответственно называется такое значение переменной, при котором это уравнение обращается в верное числовое равенство). Тогда
как прямую линию на плоскости). Поэтому, начиная с 6-7 классов, уравнение определяется как равенство с переменной (а корнем или решением уравнения соответственно называется такое значение переменной, при котором это уравнение обращается в верное числовое равенство). Тогда 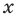 в уравнении
в уравнении 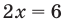 — это переменная, для которой нет ни одного ограничения, и поэтому
— это переменная, для которой нет ни одного ограничения, и поэтому 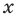 может быть любым числом (ОДЗ уравнения:
может быть любым числом (ОДЗ уравнения: 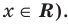 При таком подходе каждому значению переменной
При таком подходе каждому значению переменной 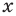 соответствует единственное значение переменной
соответствует единственное значение переменной 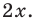 Таким образом, это уравнение можно решить графически, построить графики функций
Таким образом, это уравнение можно решить графически, построить графики функций 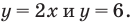 Кроме того, при таком подходе можно записать уравнение в общем виде как равенство
Кроме того, при таком подходе можно записать уравнение в общем виде как равенство 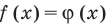 и обоснованно применить свойства функций для решения уравнений.
и обоснованно применить свойства функций для решения уравнений.
Для всех видов уравнений, которые рассматривались в курсе алгебры или алгебры и начал анализа, приведенные два определения уравнения приводят к одному тому же результату при решении уравнений. Но в случае показательно-степенного уравнения иногда можно получить разные ответы, используя разные подходы к определению уравнения.
Например, решим уравнение 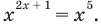
Если рассматривать такое уравнение как числовое равенство, то две степени с одинаковым основанием 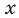 могут быть равными только в одном из четырех случаев. А именно: если основанием степени является одно из значений
могут быть равными только в одном из четырех случаев. А именно: если основанием степени является одно из значений 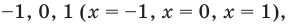 то степени могут быть равными даже тогда, когда их показатели будут разными (при условии, что эти степени существуют). Во всех остальных случаях степени с одинаковым основанием будут равными только тогда, когда показатели этих степеней будут равными
то степени могут быть равными даже тогда, когда их показатели будут разными (при условии, что эти степени существуют). Во всех остальных случаях степени с одинаковым основанием будут равными только тогда, когда показатели этих степеней будут равными 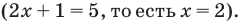 Следовательно, для получения всех корней данного уравнения достаточно проверить значения
Следовательно, для получения всех корней данного уравнения достаточно проверить значения 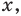 равные-1, 0,1, 2. Все эти числа являются корнями, так как при подстановке каждого из них в данное уравнение оно обращается в верное числовое равенство. Если же рассматривать это уравнение как равенство с переменной и встать на функциональную точку зрения, то функция
равные-1, 0,1, 2. Все эти числа являются корнями, так как при подстановке каждого из них в данное уравнение оно обращается в верное числовое равенство. Если же рассматривать это уравнение как равенство с переменной и встать на функциональную точку зрения, то функция 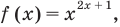 как правило, считается определенной только при
как правило, считается определенной только при 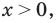 и тогда данное уравнение имеет только два корня:1 и 2.
и тогда данное уравнение имеет только два корня:1 и 2.
Таким образом, в рассмотренном уравнении ответ нельзя записать однозначно (поскольку каждый из указанных подходов к определению уравнения имеет право на существование и реально используется в математике). Поэтому в подобных ситуациях приходится приводить оба варианта ответа. Аналогичный пример приведен в таблице 57.
Обобщая приведенные выше рассуждения, заметим, что в том случае, когда при решении уравнения вида 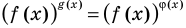 из условия не следует, что основание степени
из условия не следует, что основание степени 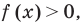 необходимо рассматреть три особых случая: основание
необходимо рассматреть три особых случая: основание 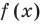 равно-1, 0, 1 (понятно, что в этих случаях степени
равно-1, 0, 1 (понятно, что в этих случаях степени 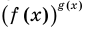 и
и 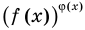 могут быть равными даже тогда, когда показатели
могут быть равными даже тогда, когда показатели 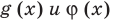 разные), а затем приравнять показатели
разные), а затем приравнять показатели 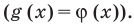 Если же из условия следует, что
Если же из условия следует, что 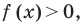 то рассматриваем только один особый случай — основание степени равно
то рассматриваем только один особый случай — основание степени равно 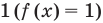 — и приравниваем показатели степеней
— и приравниваем показатели степеней 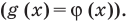
Например, решим уравнение 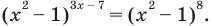
Из условия не следует, что основание степени 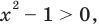 следовательно, приходится рассматривать все случаи. 2 2
следовательно, приходится рассматривать все случаи. 2 2
1) Если 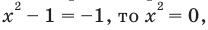 и тогда
и тогда 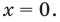
Подставляя это значение в данное уравнение, имеем 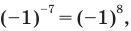 то есть
то есть 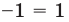 (неверное равенство). Таким образом,
(неверное равенство). Таким образом, 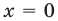 не является корнем данного уравнения.
не является корнем данного уравнения.
2) Если 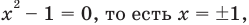 то при этих значениях
то при этих значениях 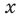 данное уравнение обращается в неверное числовое равенство (поскольку значения выражений
данное уравнение обращается в неверное числовое равенство (поскольку значения выражений 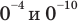 не существуют). Таким образом, числа 1 и -1 не являются корнями данного уравнения.
не существуют). Таким образом, числа 1 и -1 не являются корнями данного уравнения.
3) Если 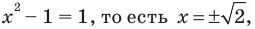 данное уравнение обращается в верное равенство
данное уравнение обращается в верное равенство 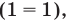 следовательно,
следовательно, 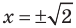 —корни данного уравнения.
—корни данного уравнения.
4) Приравняем показатели степеней данного уравнения (основания степеней в левой и правой частях уравнения одинаковые):  тогда
тогда 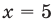 (при подстановке получаем верное равенство
(при подстановке получаем верное равенство 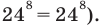
Объединяя полученные результаты, получаем ответ.
Ответ: 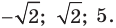
Замечание. При 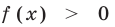 для решения уравнения вида
для решения уравнения вида 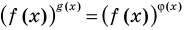 можно прологарифмировать обе его части по любому числовому основанию, получить равносильное уравнение, в котором уже не придется рассматривать особый случай — он будет учтен автоматически. Это связано с тем, что функция
можно прологарифмировать обе его части по любому числовому основанию, получить равносильное уравнение, в котором уже не придется рассматривать особый случай — он будет учтен автоматически. Это связано с тем, что функция 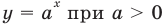 имеет особый случай, если
имеет особый случай, если 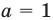 (см. график функции
(см. график функции 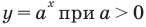 на с. 338), а функция
на с. 338), а функция 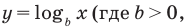
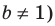 особых случаев не имеет.
особых случаев не имеет.
Также отметим, что при решении неравенств вида 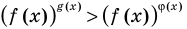 обычно используют функциональный подход и считают, что
обычно используют функциональный подход и считают, что 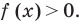
Заметим, что в тех случаях, когда в показательно-степенное уравнение входят выражения вида 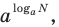 то для решения такого уравнения может использоваться основное логарифмическое тождество. В этом случае следует учитывать ОДЗ данного уравнения (см. пример 1 в табл. 57).
то для решения такого уравнения может использоваться основное логарифмическое тождество. В этом случае следует учитывать ОДЗ данного уравнения (см. пример 1 в табл. 57).
Достаточно часто для решения показательно-степенных уравнений используется логарифмирование обеих частей. Конечно, это можно сделать только тогда, когда на ОДЗ данного уравнения обе части уравнения положительны (см. пример 2 в табл. 57).
Приведем еще несколько примеров решения показательно-степенных уравнений и неравенств.
- Заказать решение задач по высшей математике
Пример №6
Решите уравнение 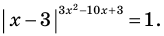
Решение:
Поскольку 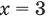 не является корнем данного уравнения
не является корнем данного уравнения 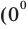 не существует), то при
не существует), то при 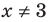 обе его части положительны . После логарифмирования (по основанию 10) обеих частей данного уравнения получаем равносильные ему уравнения:
обе его части положительны . После логарифмирования (по основанию 10) обеих частей данного уравнения получаем равносильные ему уравнения:
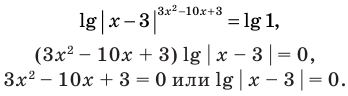
Из первого полученного уравнения имеем 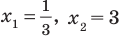 (не является корнем), а из второго
(не является корнем), а из второго 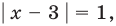 тогда
тогда 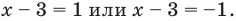 То есть
То есть 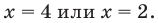
Ответ: 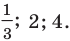
Комментарий:
Поскольку 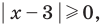 то из особых случаев можно рассмотреть только один — основание равно
то из особых случаев можно рассмотреть только один — основание равно 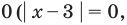 то есть
то есть 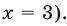 Чтобы не рассматривать случай, когда основание равно 1, достаточно при
Чтобы не рассматривать случай, когда основание равно 1, достаточно при 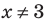 прологарифмировать обе части уравнения по числовому основанию (например, по основанию 10).
прологарифмировать обе части уравнения по числовому основанию (например, по основанию 10).
При 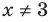 обе части данного уравнения положительны, поэтому после логарифмирования получаем уравнение, равносильное данному. Поскольку все дальнейшие преобразования являются равносильными (при
обе части данного уравнения положительны, поэтому после логарифмирования получаем уравнение, равносильное данному. Поскольку все дальнейшие преобразования являются равносильными (при 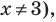 то все полученные решения (не равные 3) являются корнями данного уравнения.
то все полученные решения (не равные 3) являются корнями данного уравнения.
Пример №7
Решите уравнение 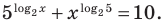
Комментарий:
Прологарифмировать обе части данного уравнения не удается (в левой части стоит сумма), поэтому попытаемся все степени представить в виде степеней с одним и тем же числовым основанием. Учитывая, что в данном уравнении есть логарифм по основанию 2, представим все данные степени как степени с основанием 2 по формуле 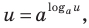 где
где 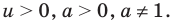 Тогда
Тогда
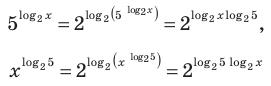
(то есть слагаемые, стоящие в левой части данного уравнения, одинаковы). После получения уравнения (2) (см. решение) можно использовать равенство (1) справа налево. Можно также записать правую часть уравнения (2) как степень числа 2 или прологарифмировать обе его части по основанию 2.
Решение:
► ОДЗ: х > 0. На этой ОДЗ данное уравнение равносильно уравнениям:
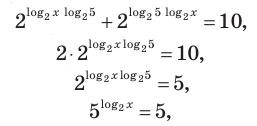
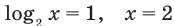 (принадлежит ОДЗ).
(принадлежит ОДЗ).
Ответ: 2.
Комментарий:
Используем равносильные преобразования системы. Для этого учтем ОДЗ и проследим за тем, чтобы на этой ОДЗ все преобразования уравнений как в прямом, так и в обратном направлении сохраняли верные равенства.
В первом уравнении данной системы запишем все степени как степени с основанием 3 (см. выше комментарий к задаче 2). После равносильных (на ОДЗ) преобразований первого уравнения получаем систему (1) (см. решение), в которую переменные входят только в виде 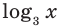 и
и 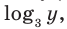 поэтому удобно использовать замену переменных. После обратной замены применяем определение логарифма.
поэтому удобно использовать замену переменных. После обратной замены применяем определение логарифма.
Решение:
ОДЗ: 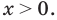 На этой ОДЗ первое уравнение заданной системы равносильно уравнениям:
На этой ОДЗ первое уравнение заданной системы равносильно уравнениям:
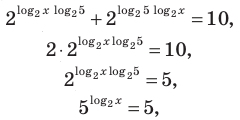
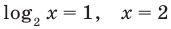 принадлежит ОДЗ.
принадлежит ОДЗ.
Пример №8
Решите систему уравнений 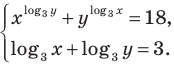
Комментарий:
Используем равносильные преобразования системы. Для этого учтем ОДЗ и проследим за тем, чтобы на этой ОДЗ все преобразования уравнений как в прямом, так и в обратном направлении сохраняли верные равенства.
В первом уравнении данной системы запишем все степени как степени с основанием 3 (см. выше комментарий к задаче 2). После равносильных (на ОДЗ) преобразований первого уравнения получаем систему (1) (см. решение), в которую переменные входят только в виде 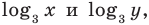 поэтому удобно использовать замену переменных. После обратной замены применяем определение логарифма.
поэтому удобно использовать замену переменных. После обратной замены применяем определение логарифма.
Решение:
ОДЗ: 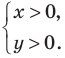 На этой ОДЗ первое уравнение заданной системы равносильно уравнениям:
На этой ОДЗ первое уравнение заданной системы равносильно уравнениям: 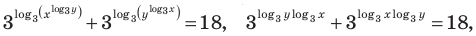
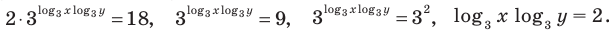
Тогда заданная система равносильна системе
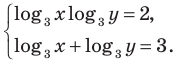
Замена 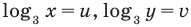 дает систему
дает систему 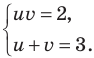
Из второго уравнения последней системы 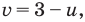 тогда из первого уравнения
тогда из первого уравнения 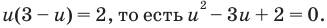 Отсюда
Отсюда 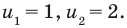 Тогда
Тогда 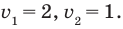
Обратная замена дает
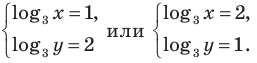
Тогда 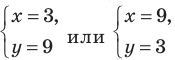 (найденные решения входят ОДЗ)
(найденные решения входят ОДЗ)
Ответ: 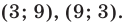
Пример №9
Решите неравенство 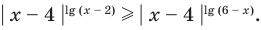
I способ
Комментарий:
Попытаемся выполнить равносильные преобразования данного неравенства, применив рассуждения, аналогичные тем, что приводились при решении показательно-степенных уравнений (см. пункт II табл. 57). Поскольку 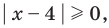 то из особых случаев необходимо рассмотреть только два: основание равно 0 (то есть
то из особых случаев необходимо рассмотреть только два: основание равно 0 (то есть 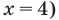 и основание равно 1 (то есть
и основание равно 1 (то есть 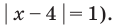 При других значениях
При других значениях 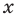 основание — положительное число, не равное 1. Рассмотрим два случая: 1) основание больше 1 (при переходе от степеней к показателям в данном неравенстве знак неравенства не меняется); 2) основание меньше 1, но больше 0 (при переходе от степеней к показателям в данном неравенстве знак неравенства меняется на противоположный). При таких преобразованиях получаем неравенства, равносильные данному (на его ОДЗ), поскольку можем гарантировать правильность не только прямых, но и обратных переходов.
основание — положительное число, не равное 1. Рассмотрим два случая: 1) основание больше 1 (при переходе от степеней к показателям в данном неравенстве знак неравенства не меняется); 2) основание меньше 1, но больше 0 (при переходе от степеней к показателям в данном неравенстве знак неравенства меняется на противоположный). При таких преобразованиях получаем неравенства, равносильные данному (на его ОДЗ), поскольку можем гарантировать правильность не только прямых, но и обратных переходов.
При решении полученных простейших логарифмических неравенств учитываем, что функция 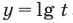 является возрастающей.
является возрастающей.
В ответ следует включить все решения полученных систем неравенств и все особые значения, которые являются решениями данного неравенства.
Решение:
ОДЗ: 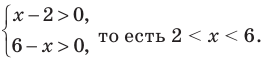 При
При 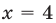 данное неравенство выполняется
данное неравенство выполняется 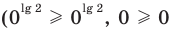 — верное неравенство), таким образом,
— верное неравенство), таким образом, 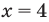 — одно из решений этого неравенства.
— одно из решений этого неравенства.
Если 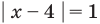 (то есть
(то есть 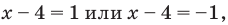 тогда
тогда 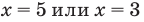 — эти значения входят в ОДЗ), то данное неравенство также выполняется. При
— эти значения входят в ОДЗ), то данное неравенство также выполняется. При 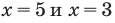 получаем верное неравенство
получаем верное неравенство 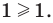 Таким образом, эти числа также являются решениями данного неравенства.
Таким образом, эти числа также являются решениями данного неравенства.
При 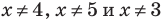 на ОДЗ данное неравенство равносильно следующей совокупности систем:
на ОДЗ данное неравенство равносильно следующей совокупности систем: 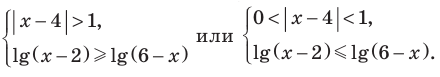 То есть
То есть 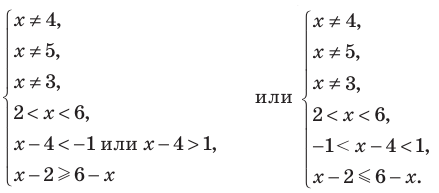
Тогда: 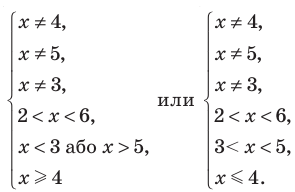
Таким образом, 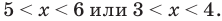 Учитывая особые значения, которые являются решениями, получаем:
Учитывая особые значения, которые являются решениями, получаем: 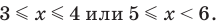
Ответ: 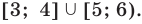
II способ решения неравенства 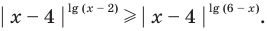
Комментарий:
Решим данное неравенство методом интервалов, для этого приведем его к виду 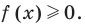
Для нахождения нулей 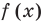 необходимо решить показательно-степенное уравнение (2). Поскольку
необходимо решить показательно-степенное уравнение (2). Поскольку 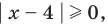 то из особых случаев необходимо рассмотреть только два — основание равно 0 (то есть
то из особых случаев необходимо рассмотреть только два — основание равно 0 (то есть 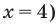 или основание равно 1 (то есть
или основание равно 1 (то есть 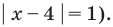 При других значениях
При других значениях 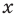 из ОДЗ в уравнении (3) основание — положительное число, не равное 1. Тогда можно приравнять показатели степеней (получаем уравнение, равносильное данному).
из ОДЗ в уравнении (3) основание — положительное число, не равное 1. Тогда можно приравнять показатели степеней (получаем уравнение, равносильное данному).
Для нахождения знаков 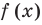 удобно использовать графики функции
удобно использовать графики функции 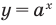 при
при 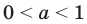 и при
и при 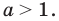
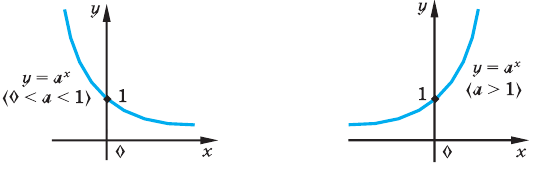
Решение:
1. ОДЗ 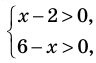 то есть
то есть 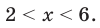
На этой ОДЗ данное неравенство равносильно неравенству
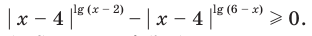
2. Пусть 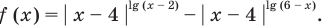 Нули
Нули 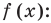
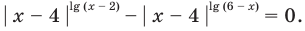
На ОДЗ уравнение (2) равносильно уравнению
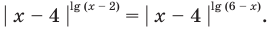
При 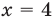 равенство (3) выполняется
равенство (3) выполняется 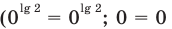 — верное равенство), таким образом,
— верное равенство), таким образом, 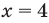 — корень уравнения (3).
— корень уравнения (3).
Если 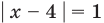 (то есть
(то есть 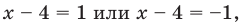 тогда
тогда 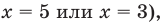 то равенство (3) также выполняется. При
то равенство (3) также выполняется. При 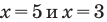 получаем верное равенство
получаем верное равенство 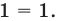 Таким образом, эти числа также являются корнями уравнения (3). При
Таким образом, эти числа также являются корнями уравнения (3). При 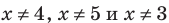 на ОДЗ уравнение (3) равносильно уравнению
на ОДЗ уравнение (3) равносильно уравнению 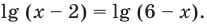 Тогда
Тогда 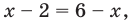 то есть
то есть 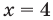 — не удовлетворяет условию
— не удовлетворяет условию 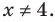 Следовательно, на последнем множестве уравнение (3) корней не имеет.
Следовательно, на последнем множестве уравнение (3) корней не имеет.
3. Отмечаем нули функции на ОДЗ и находим знак 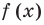 на каждом из промежутков, на которые разбивается ОДЗ (см. рисунок).
на каждом из промежутков, на которые разбивается ОДЗ (см. рисунок).
Ответ: 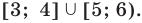

Пример №10
Решите неравенство 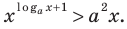
Комментарий:
На ОДЗ обе части неравенства положительны, поэтому попытаемся прологарифмировать обе части неравенства. Поскольку в данное неравенство уже входит 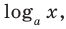 то удобно прологарифмировать по основанию
то удобно прологарифмировать по основанию 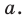 Но при логарифмировании по основанию больше 1 знак неравенства не меняется, а при логарифмировании по основанию меньше 1 знак неравенства меняется. Приходится рассматривать два случая (в каждом из них получаем неравенство, равносильное данному на его ОДЗ).
Но при логарифмировании по основанию больше 1 знак неравенства не меняется, а при логарифмировании по основанию меньше 1 знак неравенства меняется. Приходится рассматривать два случая (в каждом из них получаем неравенство, равносильное данному на его ОДЗ).
Решение:
ОДЗ: 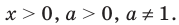
Прологарифмируем обе части неравенства.
1) При 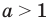 данное неравенство на его ОДЗ равносильно неравенствам:
данное неравенство на его ОДЗ равносильно неравенствам:
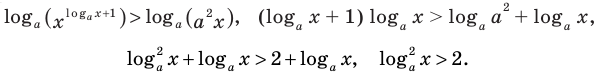
Таким образом, 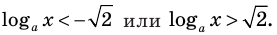
To есть 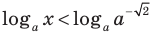 или
или 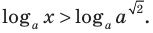
Учитывая ОДЗ 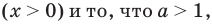 получаем
получаем 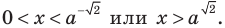
2) При 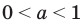 данное неравенство на его ОДЗ равносильно неравенствам:
данное неравенство на его ОДЗ равносильно неравенствам:
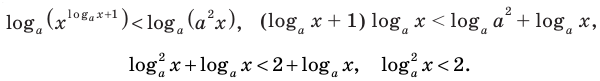
Таким образом,
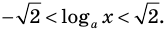
То есть 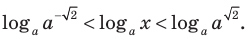
Учитывая ОДЗ 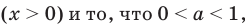 получаем
получаем 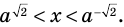
Ответ: 1)при 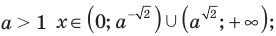 2) при
2) при 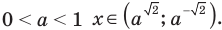
- Показательные уравнения и неравенства
- Логарифмические уравнения и неравенства
- Степенная функция – определение и вычисление
- Степень с целым показателем
- Логарифмическая функция, её свойства и график
- Логарифмические выражения
- Показательная функция, её график и свойства
- Производные показательной и логарифмической функций
