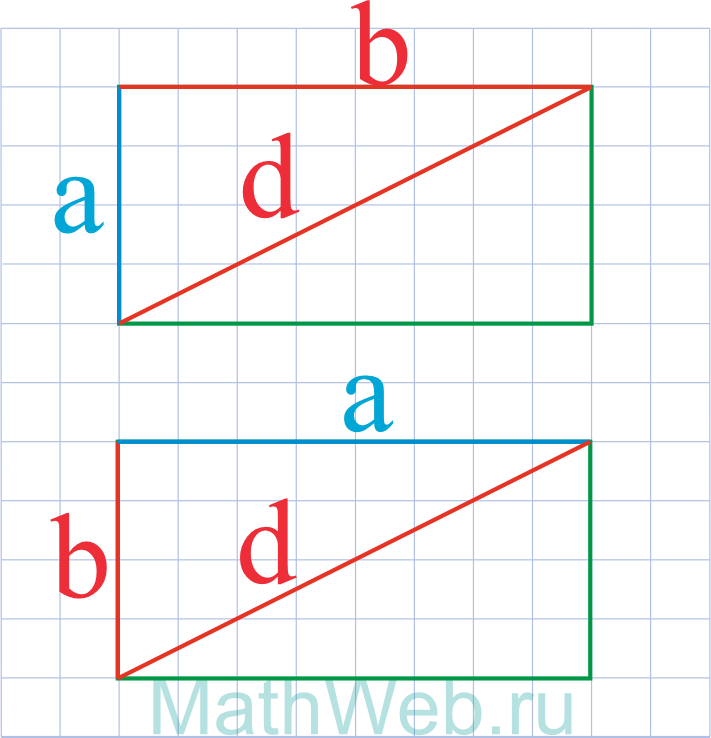
Где d – диагональ,b – сторона.
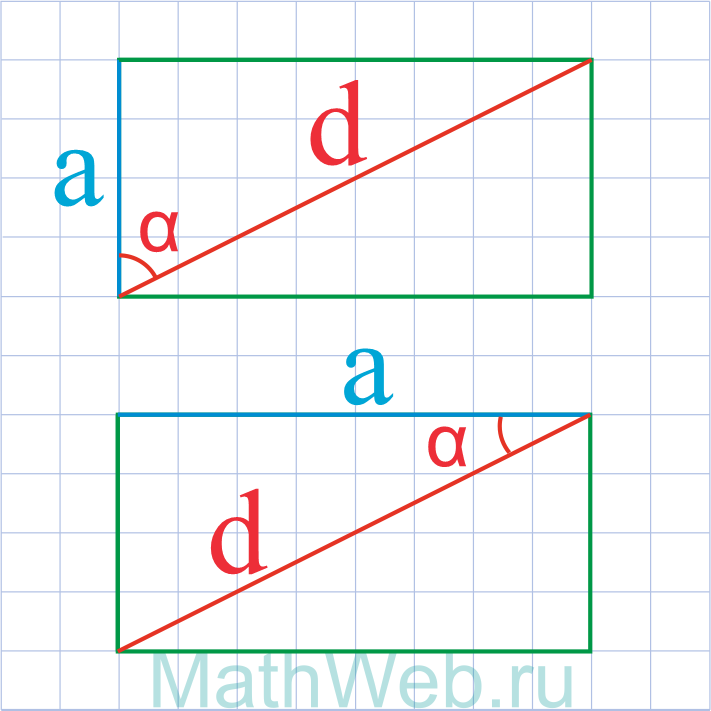
Где d – диагональ,α – угол между диагональю и искомой стороной.
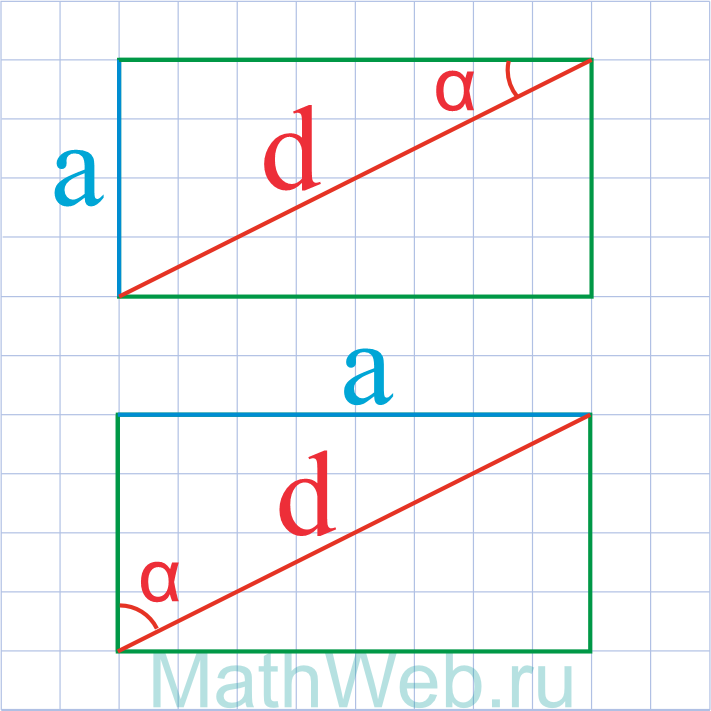
Где d – диагональ,α – угол между диагональю и другой стороной.
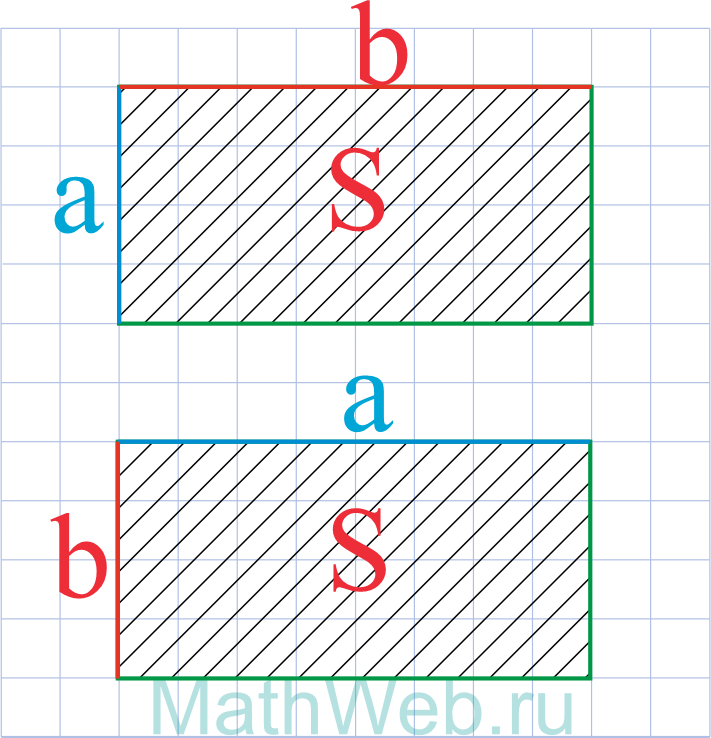
Где S – площадь, b– известная сторона.
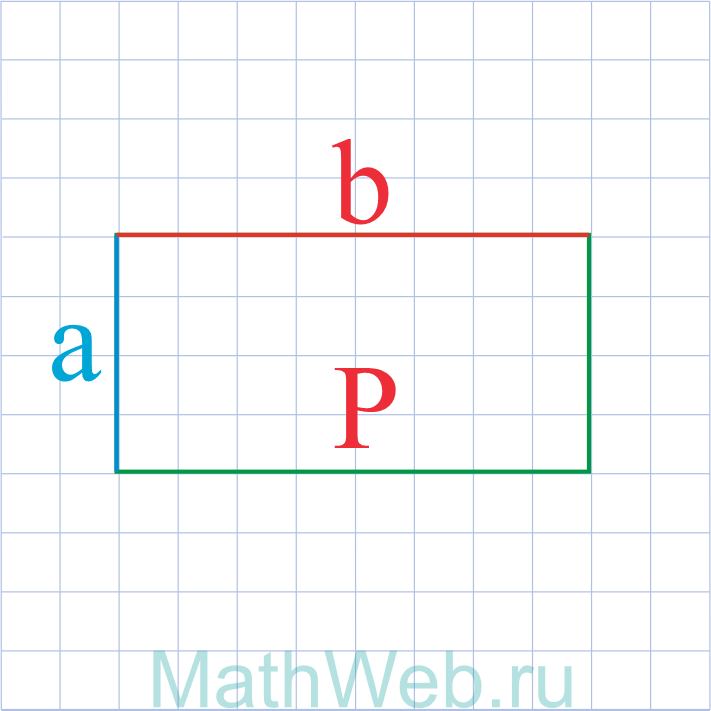
Где P – периметр, b – известная сторона.
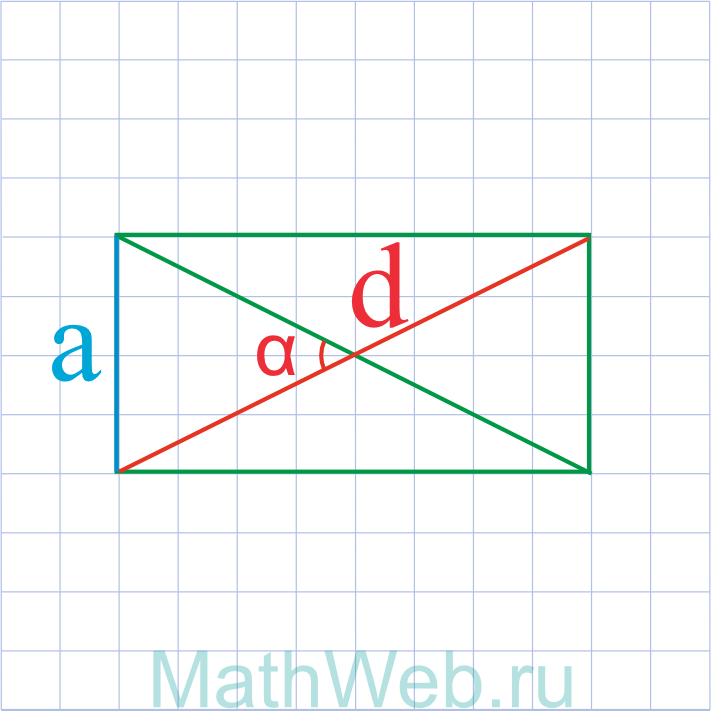
Где d – диагональ, α – угол между диагоналями.
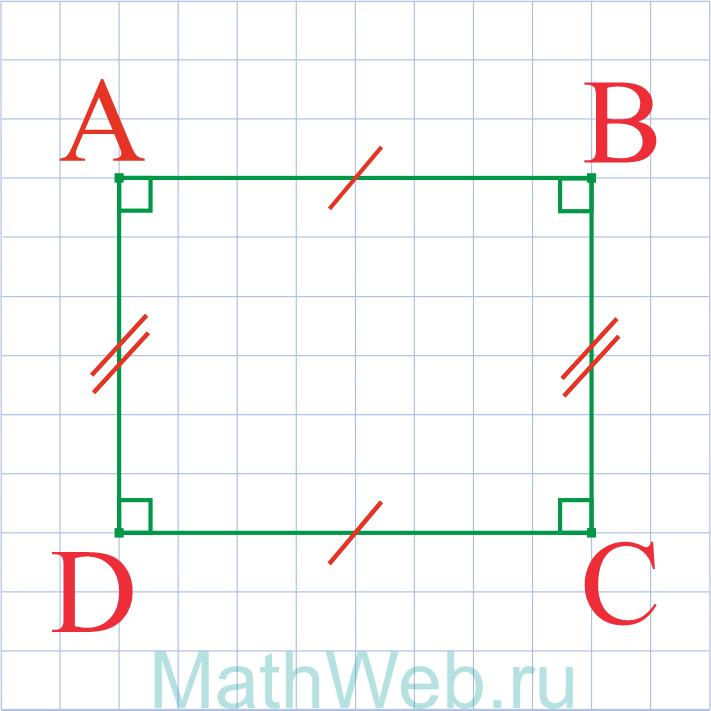
- Прямоугольник – это четырехугольник у которого противоположные стороны равны и параллельны AB = CD и BC = DA.
- Стороны прямоугольника являются его высотами.
- Между прилегающими сторонами угол всегда 90°.
Как найти длину стороны прямоугольника?
Сторона прямоугольника может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = √d2 ― b2 |
 |
a = d·cos(α) |
 |
a = d·sin(α) |
 |
a = S b |
 |
a = P – 2b 2 |
 |
a = d·sin(0.5·α) |
Как найти сторону прямоугольника если известна одна сторона?
Ирина Д.
4 декабря 2018 · 8,8 K
Родилась в Нижнем Новгороде, волей судьбы оказалась в Москве. Мама двоих детей… · 4 дек 2018
Никак. Поскольку для поиска второй стороны Вам как минимум нужна длина гипотенузы. В противном случае вторая сторона может быть любой длины.
6,1 K
А если в задаче по геометрии Дона только одна сторона и маленькая часть диогонали
Комментировать ответ…Комментировать…
Что-найти одну сторону нам нужно знать не только сторону “А” но и площадь или периметр.!!!!!!!
Пример как должно быть:
Дано:
А=120см.
Б=?см.
S(или P) =140см.
Решение:
Б=140-120
Б=20см. Читать далее
5,3 K
Не бывает прямоугольников со стороной 120 и периметром 140
Комментировать ответ…Комментировать…
Прямоугольник — это двухмерная продолговатая фигура, которая имеет 4 стороны и 4 прямых угла.
Находящиеся друг напротив друга стороны имеют одну длину, причем одна пара сторон длиннее другой.
Если все стороны прямоугольника одинакового размера, то он является квадратом. Другими словами,
квадрат — это особенный случай прямоугольника.
- Сторона прямоугольника через диагональ и угол между
диагональю и стороной - Сторона прямоугольника через диагональ и известную
сторону - Сторона прямоугольника через площадь и другую известную
сторону - Сторона прямоугольника через периметр и другую известную
сторону - Сторона прямоугольника через диагональ и угол между
диагоналями
Через диагональ и угол между диагональю и стороной
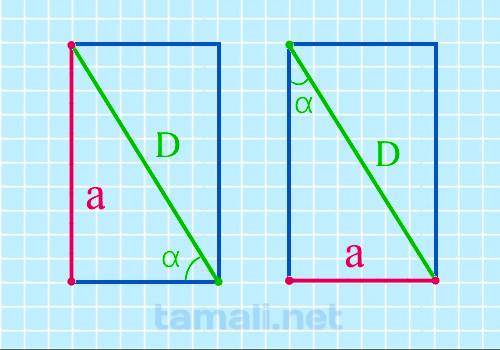
Определить неизвестную сторону прямоугольника можно в том случае, если знаешь длину диагонали и угол
средь ней и стороной. Такая конструкция образует пару прямоугольных треугольников, поэтому можно
воспользоваться следующей формулой:
a = d * sinα
где d — это диагональ, а, b — одна из сторон фигуры.
Цифр после
запятой:
Результат в:
Пример. Найти сторону прямоугольника, если диагональ равна 16 см, а угол между диагональю и этой
стороной — 60º.
Решение.
D = 16, β = 60º, b = ?
b = 16 cos 60º
b = 16 * 0.5 = 8 см.
Через его площадь и известную сторону
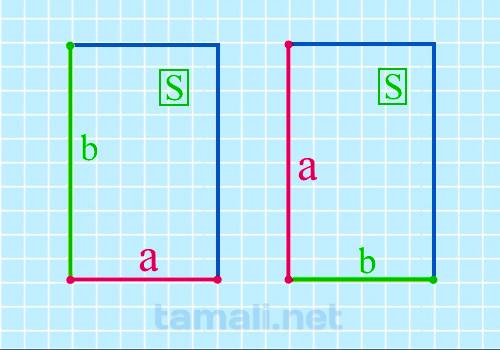
Площадь прямоугольника вычисляется по формуле: S = ab. Следовательно
a = S / b
где S — площадь прямоугольника, b — известная сторона.
Цифр после
запятой:
Результат в:
Пример. Площадь прямоугольника равна 60 единицам, а его длина равна 12 единицам. Подставляем
известные значения в формулу, Вычислив, получим ширину = 60/12, значит ширина равна 5.
Через диагональ и известную сторону
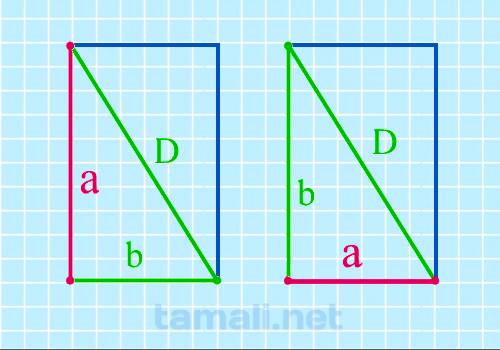
Сторону прямоугольника можно вычислить, если известны его диагональ и другая сторона.
Диагональ
— это отрезок прямой, соединяющий любые две несмежные вершины. Диагонали AC и BD равны. Одна из них
разрезает прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а
две соседние стороны — остальные стороны треугольника. Отсюда :
a = √(d² — b²)
где d — диагональ, а, b — стороны.
Цифр после
запятой:
Результат в:
Пример. Найти сторону прямоугольника, если диагональ равна 5 см, а другая сторона — 4 см.
Решение.
D=5, b=4, a=?
a = √(25 – 16) = √9 = 3 см.
Через диагональ и угол между диагоналями
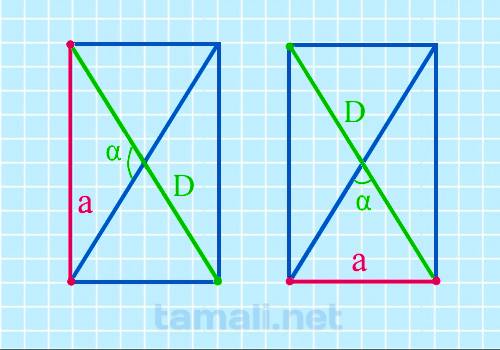
Зная значение угла между двумя диагоналями и длину по крайней мере одной из них, можем рассчитать
сторону прямоугольника, зная следующую формулу:
a = D • sin(α/2)
где D — диагональ, α — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Длина диагонали прямоугольника равна 20 см, а угол между диагоналями — 30º. Найти
сторону.
Решение.
a = 20 * (sin 30º / 2)
a = 20 * 0, 5 / 2 = 5 см.
Через периметр и другую известную сторону
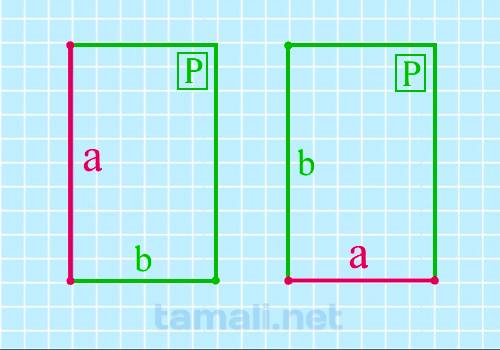
Длину же мы можем вычислить, если известны периметр и ширина. Мы можем использовать формулу периметра
для получения длины. P = 2 (a + b).
a = (P — 2b) / 2
где P — периметр прямоугольника, b — другая известная сторона.
Цифр после
запятой:
Результат в:
Так, если P — 32 см, а b — 4 см, Подставим известные нам значения, получим a = (32 — 2*4).Вычислив,
получим 12 см.
Другие примеры по решению задач на прямоугольник с использованием длины и ширины
- Длина и ширина прямоугольника равны 7 дюймам и 21 дюйму. Найдите его периметр.
Результат: P
прямоугольника = 2 (длина + ширина) = 2 (7 + 21) дюйма = 2 (28) дюймов = 56 дюймов - Длина и ширина прямоугольника равны 0,3 м и 15 см. Найдите его площадь. Результат: Длина = 0,3
м, ширина = 15 см. Длина и ширина прямоугольника находятся в различных значениях, поэтому мы
преобразуем одно из них. Переведем длину в сантиметры, умножив ее на 100, так как 1 м = 100 см.
Итак, длина = 0,3 100 см = 30 см. Площадь = длина ширина = 30 см 15 см = 450 см². - Одна сторона прямоугольника меньше другой на 7 см, а диагональ прямоугольника равна 17 см. Найти
периметр прямоугольника. Решение. Пусть АВ=х. Тогда AD=х+7. Зная, что диагональ BD=17,
используем теорему Пифагора и составим уравнение: AB² +AD² =BD².
Получаем: х² +(х+7)² =17² ⇒ х² +х² +14х+49=289; 2х² +14х-240=0; х² +7х-120=0,
отсюда по теореме Виета х1 =-15; х2 =8.Следовательно, АВ=8 см, AD=8+7=15 см. Периметр прямоугольника: P = 2∙ (AB+AD); P = 2∙ (8+15); P = 46 см.
Ответ: 46 см.
Прямоугольник обладает широким спектром свойств. Некоторые из важных свойств прямоугольника приведены
ниже.
- Прямоугольник — это четырехугольник.
- Противоположные стороны прямоугольника являются равными и параллельны друг другу.
- Внутренний угол прямоугольника при каждой вершине равен 90°.
- Сумма внутренних углов равна 360°.
- Диагонали пересекаются друг с другом.
- Длина диагоналей равна.
- Длина диагоналей может быть получена с помощью теоремы Пифагора. Длина диагонали со сторонами a
и b равна, диагональ = ( a2 + b2). - Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
- Все прямоугольники являются параллелограммами, но все параллелограммы не являются
прямоугольниками.
как найти сторону прямоугольника, если известен периметр и другая сторона?
Профи
(698),
закрыт
13 лет назад
maxim wolf
Новичок
(0)
13 лет назад
вычитаешь из периметра удвоенное произведение известной стороны а затем получившийся результат делишь пополам…. вот и сторона прямоугольника
Екатерина ***
Знаток
(277)
13 лет назад
периметр прямоугольника равен 2(A+B)=>
допустим одна сторона будет 10, периметр будет 40 (так нагляднее объяснить) , а другую сторону мы обозначим за х, тогда
2(х+5)=40
2х+10=40
2х=30
х=15
ффффф ффффффф
Ученик
(102)
2 года назад
9000000000000000000000000000000000000000000000000000000000000000000+1111111111111111111111111111111111111111111111111111111111=112345678963214879076+1212313123123-124135236135326345321-123141123421/4444444444444444444444444444444444444444444444+9999999999999999999999999999999999999999999999999999999999999999999999999999=
сколько будет ???
Прямоугольник — это геометрическая фигура, имеющая две параллельные стороны и соответствующие углы, равные по значению. Эта фигура чрезвычайно распространена в повседневной жизни, поэтому важно уметь определять и вычислять свойства прямоугольника. Одним из способов является нахождение недостающих сторон при известных двух.
Первым шагом в решении этой задачи является знание формулы для вычисления площади прямоугольника. Формула площади прямоугольника — это произведение его двух сторон, т.е. S=ab. Эту формулу можно использовать для вычисления недостающей стороны при известной площади и одной из сторон.
Для нахождения другой недостающей стороны нужно использовать теорему Пифагора. Теорема Пифагора гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Т.е. a²+b²=c². Эту формулу можно использовать для нахождения недостающей стороны прямоугольника при известных двух других сторонах, если одна из них является диагональю.
Как определить длину недостающей стороны прямоугольника?
Прямоугольник — это фигура, состоящая из четырех прямых углов и двух параллельных сторон. В прямоугольнике есть две основные стороны — ширина и длина. Иногда необходимо найти длину дополнительной стороны прямоугольника, используя известные размеры двух сторон.
Если известны длины двух сторон прямоугольника, можно вычислить длину недостающей стороны, используя формулу Пифагора. Для этого нужно возвести в квадрат известные длины сторон, сложить полученные числа и вычислить квадратный корень от суммы. Обозначим длину первой известной стороны буквой a, а второй — буквой b:
- Длина недостающей стороны = √(a² + b²).
Например, если ширина прямоугольника равна 3 см, а длина — 4 см, то длину недостающей стороны можно найти следующим образом:
| a = ширина = 3 см | |
| b = длина = 4 см | |
| √(a² + b²) = √(3² + 4²) ≈ 5 | см |
Иными словами, длина недостающей стороны прямоугольника составляет примерно 5 см.
Подробное объяснение: как найти недостающие стороны прямоугольника при известных 2-х сторонах
Шаг 1: Определить, какую сторону ищем
Первым шагом необходимо определить, какую сторону прямоугольника мы ищем. Для этого нужно взглянуть на задачу и определить, какие стороны мы знаем, а какие нет.
Шаг 2: Использовать формулу для нахождения недостающей стороны
Для нахождения недостающей стороны можно использовать следующую формулу:
S = P — K
Где S — искомая сторона, P — периметр прямоугольника, K — сумма известных сторон.
Например, если известны стороны А и В, нужно вычесть сумму этих сторон из периметра прямоугольника, чтобы получить длину недостающей стороны С: С = P — (А + В).
Шаг 3: Проверить результаты
После нахождения недостающей стороны необходимо проверить результаты, чтобы убедиться в их правильности. Для этого можно воспользоваться формулой для нахождения площади прямоугольника: S = A * B. Если результат сходится с данными из условия задачи, значит мы нашли правильный ответ.
Пример решения задачи
| Условие задачи | Решение |
|---|---|
| Известны стороны А (длина) и В (ширина) прямоугольника, равные соответственно 5 м и 10 м. Найдите длину стороны С (высота). | Периметр прямоугольника равен P = 2 * (А + В) = 2 * (5 м + 10 м) = 30 м. Сумма известных сторон равна К = А + В = 5 м + 10 м = 15 м. Длина недостающей стороны С равна: С = P — K = 30 м — 15 м = 15 м. Проверим результат: S = A * B = 5 м * 10 м = 50 м². Ответ: длина стороны С (высоты) равна 15 м. |
Решение задачи на нахождение недостающих сторон прямоугольника
Начало решения
Если известны две стороны прямоугольника, требуется найти недостающие стороны. Для этого нужно использовать формулу для расчета площади прямоугольника. Формула для расчета площади прямоугольника S=ab, где a и b — это длины сторон прямоугольника. Если известно значение одной стороны и площади, то другую сторону можно найти по формуле b=S/a.
В случае, если известны две стороны А и В прямоугольника, недостающая сторона найдется по формуле C²=A²+B², где С — это гипотенуза прямоугольного треугольника, который является диагональю прямоугольника, а А и В — катеты. Таким образом, чтобы найти недостающие стороны, нужно подставить известные значения в формулу и вычислить недостающие стороны.
Другой способ нахождения недостающих сторон прямоугольника — использование свойств прямоугольников. Прямоугольник имеет четыре прямых угла и противоположные стороны равны между собой. Если известны длины двух сторон прямоугольника, можно использовать эти свойства для нахождения длин других сторон. Например, если известны длины сторон А и В, то можно найти длины сторон С и D, где С=А и D=В.
Формула для нахождения площади прямоугольника
Площадь прямоугольника — это величина, которая показывает, сколько квадратных единиц занимает фигура на плоскости. Она вычисляется по формуле S=a*b, где a и b — это длины двух смежных сторон прямоугольника.
Другими словами, чтобы найти площадь прямоугольника, нужно умножить длину одной стороны на длину другой стороны. Например, если у нас есть прямоугольник со сторонами 5 и 8 метров, то его площадь будет равна 40 квадратных метров: 5 м * 8 м = 40 м².
Формула для нахождения площади прямоугольника является одной из основных формул геометрии. Она широко используется в различных областях, таких как строительство, архитектура, дизайн и технические науки.
Формула нахождения периметра прямоугольника
Периметр прямоугольника — это сумма длин всех его сторон. Для нахождения периметра прямоугольника существует простая формула, которая зависит от значений его сторон. В прямоугольнике две пары сторон, которые друг к другу параллельны и равны между собой. Обозначим эти стороны как ‘a’ и ‘b’.
Формула нахождения периметра прямоугольника:
- Периметр (P) = 2a + 2b
Это означает, что для того, чтобы найти периметр прямоугольника, нужно умножить одну его сторону ‘a’ на 2, затем умножить другую его сторону ‘b’ на 2 и сложить результаты.
| Длина стороны а | Длина стороны b | Периметр |
|---|---|---|
| 5 | 7 | 24 |
| 8 | 12 | 40 |
| 3 | 9 | 24 |
Теперь вы знаете, как находить периметр прямоугольника по его сторонам, используя простую формулу.
Примеры решения задач
Рассмотрим несколько примеров, как можно найти недостающую сторону прямоугольника, зная две другие:
- Пример 1: Известны стороны прямоугольника длиной 9 см и шириной 6 см, необходимо найти длину диагонали прямоугольника.
- Используя теорему Пифагора, найдем длину диагонали: √(9²+6²) ≈ 10,8 см.
- Пример 2: Известны стороны прямоугольника длиной 5 см и диагональю 13 см, необходимо найти длину второй стороны прямоугольника.
- Используя теорему Пифагора, найдем длину второй стороны: √(13²-5²) ≈ 12 см.
- Пример 3: Известны стороны прямоугольника длиной 12 см и шириной 8 см, необходимо найти площадь прямоугольника.
- Одним из способов является умножение длины на ширину: 12 см * 8 см = 96 см².
