Как найти неизвестные компоненты действий по математике

Памятка по нахождению неизвестных компонентов действий.
учебно-методический материал по математике на тему

Памятка по нахождению неизвестных компонентов действий.

Скачать:

Вложение	Размер
pravila_nakhozhdeniya_komponentov.doc	31 КБ

Предварительный просмотр:

Выучи названия компонентов действий и правила нахождения неизвестных компонентов:

1. Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

1. Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

1. Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.

1. Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.

Выучи названия компонентов действий и правила нахождения неизвестных компонентов:

1. Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

1. Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

1. Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.

1. Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.

Памятка для обучающегося “Правила нахождения компонентов при решении уравнений”, 5 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

ПРАВИЛА НАХОЖДЕНИЯ КОМПОНЕНТОВ

ПРАВИЛА НАХОЖДЕНИЯ КОМПОНЕНТОВ

Компоненты при сложении:

I слагаемое, II слагаемое.

Результат сложения: Сумма.

I сл + II сл = Сум

I сл = Сум – II сл

II сл = Сум – I сл

Компоненты при вычитании:

Результат вычитания: Разность.

Ум = Разн + Вычит

Вычит = Ум – Разн

Компоненты при сложении:

I слагаемое, II слагаемое.

Результат сложения: Сумма.

I сл + II сл = Сум

I сл = Сум – II сл

II сл = Сум – I сл

Компоненты при вычитании:

Результат вычитания: Разность.

Ум = Разн + Вычит

Вычит = Ум – Разн

Сложение показывает сумму всех слагаемых

Вычитание показывает на сколько уменьшаемое больше вычитаемого

Сложение показывает сумму всех слагаемых

Вычитание показывает на сколько уменьшаемое больше вычитаемого

Компоненты при умножении:

I множитель, II множитель.

Результат умножения: Произведение.

I мн · II мн = Произвед

I мн = Произвед : II мн

II мн = Произвед : I мн

Компоненты при делении:

Результат деления: Частное .

Делим : делит = Частное

Делим = Част · делит

делит = Делим : Част

Компоненты при умножении:

I множитель, II множитель.

Результат умножения: Произведение.

I мн · II мн = Произвед

I мн = Произвед : II мн

II мн = Произвед : I мн

Компоненты при делении:

Результат деления: Частное .

Делим : делит = Частное

Делим = Част · делит

делит = Делим : Част

Умножение показывает сумму нескольких одинаковых слагаемых

Деление показывает во сколько раз делимое больше делителя

Умножение показывает сумму нескольких одинаковых слагаемых

Деление показывает во сколько раз делимое больше делителя

Компоненты при сложении:

I слагаемое, II слагаемое.

Результат сложения: Сумма.

I сл + II сл = Сум

I сл = Сум – II сл

II сл = Сум – I сл

Компоненты при вычитании:

Результат вычитания: Разность.

Ум = Разн + Вычит

Вычит = Ум – Разн

Компоненты при сложении:

I слагаемое, II слагаемое.

Результат сложения: Сумма.

I сл + II сл = Сум

I сл = Сум – II сл

II сл = Сум – I сл

Компоненты при вычитании:

Результат вычитания: Разность.

Ум = Разн + Вычит

Вычит = Ум – Разн

Сложение показывает сумму всех слагаемых

Вычитание показывает на сколько уменьшаемое больше вычитаемого

Сложение показывает сумму всех слагаемых

Вычитание показывает на сколько уменьшаемое больше вычитаемого

Компоненты при умножении:

I множитель, II множитель.

Результат умножения: Произведение.

I мн · II мн = Произвед

I мн = Произвед : II мн

II мн = Произвед : I мн

Компоненты при делении:

Результат деления: Частное .

Делим : делит = Частное

Делим = Част · делит

делит = Делим : Част

Компоненты при умножении:

I множитель, II множитель.

Результат умножения: Произведение.

I мн · II мн = Произвед

I мн = Произвед : II мн

II мн = Произвед : I мн

Компоненты при делении:

Результат деления: Частное .

Делим : делит = Частное

Делим = Част · делит

делит = Делим : Част

Умножение показывает сумму нескольких одинаковых слагаемых

Деление показывает во сколько раз делимое больше делителя

Умножение показывает сумму нескольких одинаковых слагаемых

Деление показывает во сколько раз делимое больше делителя

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 939 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 686 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 313 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 590 237 материалов в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 04.02.2016
• 12579
• 45

• 04.02.2016
• 1388
• 0

• 04.02.2016
• 4410
• 9

• 04.02.2016
• 5236
• 122

• 04.02.2016
• 7376
• 558

• 04.02.2016
• 1815
• 12

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 04.02.2016 6290
• DOCX 43.5 кбайт
• 49 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Чеснокова Светлана Андреевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет
• Подписчики: 0
• Всего просмотров: 28398
• Всего материалов: 9

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Минпросвещения упростит процедуру подачи документов в детский сад

Время чтения: 1 минута

Каждый второй ребенок в школе подвергался психической агрессии

Время чтения: 3 минуты

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных

Время чтения: 1 минута

В Ленобласти школьники 5-11-х классов вернутся к очному обучению с 21 февраля

Время чтения: 1 минута

Школьник из Сочи выиграл международный турнир по шахматам в Сербии

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Как найти компоненты уравнения 5 класс

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число меньше любого натурального числа.

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

Свойства сложения

Переместительный закон:

Сочетательный закон:

Формула пути

= 50км, = 2ч, = 25км/ч

, 50км = 25км/ч· 2ч

, 25км/ч = 50км : 2ч

, 2ч = 50км : 25км/ч

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

Что значит «Решить уравнение»

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений

• Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

• Чтобы найти неизвестное уменьшаемое, надо к разности при­бавить вычитаемое.

• Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

• Чтобы найти неизвестный множитель, надо произведение раз­делить на известный множитель.

• Чтобы найти неизвестное делимое, надо делитель умножить на частное.

• Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Отрезок, прямая, луч

Отрезок

Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

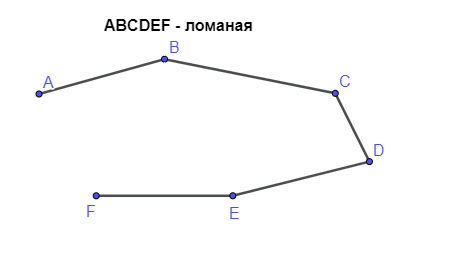
Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.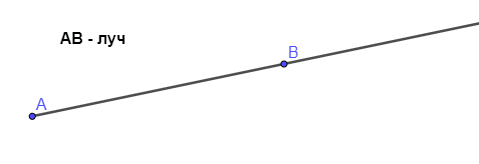

Угол, биссектриса угла

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

Свойство величины угла

Если между сторонами угла ∠ провести луч , то градусная мера ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.

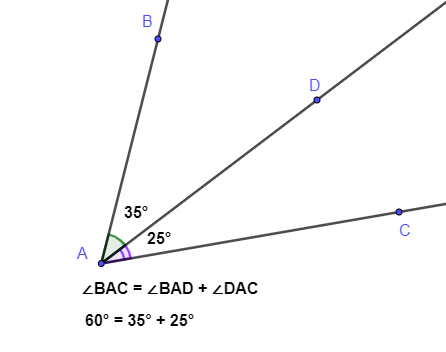
Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой

Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

Многоугольники. Равные фигуры

Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный

Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.

Треугольники: равнобедренный, равносторонний, разносторонний

Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр

Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле .

Умножение. Свойства умножения

Умножение

• Произведением числа на натуральное число , которое не равно 1, называют сумму, состоящую из слагаемых, каждый из которых равен . В равенства числа и называют множителями, а число и запись — произведением.

• Если один из двух множителей равен 1, то произведение равно второму множителю.

• Если один из множителей равен нулю, то произведение равно нулю.

• Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Свойства умножения

• Переместительный закон умножения:

• Сочетательный закон умножения:

• Распределительное свойство умножения относительно сложения:

• Распределительное свойство умножения относительно вычитания:

Деление. Деление с остатком

Деление

Для натуральных чисел равенство является правильным, если является правильным равенство

В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа правильными являются равенства:

,

Деление с остатком

, где — делимое, — делитель, — неполное частное, — остаток, .

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника

Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

,

где — площадь квадрата, — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба

Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

• ,

где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;

, где — площадь поверхности прямоугольного параллелепипеда.

• ,

где — площадь основания параллелепипеда, — его высота.

Объем куба

,

где — объем куба, — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей

Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

Сравнение дробей

• Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.

• Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.

• Все правильные дроби меньше единицы, а неправильные — больше или равны единице.

• Любая неправильная дробь больше любой правильной дроби.

Сложение и вычитание дробей с одинаковыми знаменателями

• Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

• Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.

Сложение и вычитание смешанных чисел

• Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

• Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

• числитель разделить на знаменатель;
• полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

• целую часть числа умножить на знаменатель дробной части;
• к полученному произведению прибавить числитель дробной части;
• эту сумму записать как числитель неправильной дроби;
• в его знаменателе записать знаменатель дробной части смешанного числа.

Десятичные дроби: свойства, сравнение, округление

Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

• с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
• после чего сравнить полученные дроби поразрядно.

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

• все следующие за этим разрядом цифры отбросить.
• если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4 , то последнюю из цифр, которые оставляют, не меняют ;
• если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9 , то последнюю из цифр, которые оставляют, увеличивают на единицу.

Десятичные дроби: сложение, вычитание

Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

• уравнять количество цифр после запятых;
• записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
• сложить полученные числа так, как складывают натуральные числа;
• поставить в полученной сумме запятую под запятыми.

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

• уравнять количество цифр после запятых;
• записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
• выполнить вычитание так, как вычитают натуральные числа;
• поставить в полученной разности запятую под запятыми.

Десятичные дроби: умножение, деление

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

• перемножить их как натуральные числа, не обращая внимания на запятые;
• в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

• перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
• выполнить деление на натуральное число.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Найти среднее арифметическое чисел 15, 25 и 20.

15 + 25 + 20 ⏞ с у м м а ч и с е л 3 ⏟ к о л и ч е с т в о ч и с е л = 60 3 = 20

Примечание:

Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.

V с р е д н я я = S о б щ t о б щ .

1) 200 + 120 = 320(км) -весь путь;

2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;

3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;

4) 4 + 4 = 8(ч) — все время;

5) 320 : 8 = 40(км/ч) — средняя скорость.

Процент

Процентом называют сотую часть величины или числа 1%=

Основные правила математики с примерами. 5 класс: 22 комментария

Спасибо большое! Я решил вспомнить материал по математике и вы мне с этим помогли

Уважаемая Наталья Владимировна! По структуре и подаче материала — это лучшее, что мне удалось найти на просторах интернета. Спасибо вам за труд!

Пожалуйста! Я очень рада, что Вы высоко оценили мой труд.

Спасибо огромное ! У меня завтра впр , и я надеюсь я получу 5 😇💖

[spoiler title=”источники:”]

http://infourok.ru/pamyatka-dlya-obuchayuschegosya-pravila-nahozhdeniya-komponentov-pri-reshenii-uravneniy-klass-842407.html

[/spoiler]