Как найти неизвестный член пропорции видео

§ 1  Понятие пропорции

В этом уроке Вы узнаете, что такое пропорция, познакомитесь с основным ее свойством. А также научитесь составлять пропорции и находить неизвестный член пропорции.

Давайте вспомним, что такое отношение двух чисел.

Частное двух чисел называют отношением этих чисел.

Читают так: отношение пяти к семи или отношение чисел пять и семь.

Рассмотрим отношение 1 : 2 и отношение 5 : 10. Как частные они имеют значения. Значение первого отношения – 0,5 и второго – 0,5.

Значит, они равны, и можно записать:

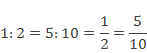
Равенство двух отношений называют пропорцией.

Читается так: «Отношение а к b равно отношению с к d» или «а так относится к b, как с относится к d».

В пропорции числа а и d называют крайними членами пропорции, а b и с называют средними членами пропорции.

§ 2  Основное свойство пропорции

Давайте в нашей пропорции 1 : 2=5 : 10 найдем произведение её крайних и средних членов.

Получим 1 ∙ 10=10; 2 ∙ 5=10. Значит, 1 ∙ 10=2∙5

Таким образом, можно сделать вывод:

В верной пропорции произведение крайних членов пропорции равно произведению её средних членов. А в буквенном выражении: а, умноженное на d, равно в, умноженное на с.

Верно и обратное утверждение:

Если произведение крайних членов пропорции равно произведению средних членов пропорции, то пропорция верна.

Именно это свойство называют основным свойством пропорции.

Это утверждение можно использовать при доказательствах.

Например, пропорция 15 : 3=25 : 5 верна, так как 15 ∙ 5=3 ∙ 25=75.

§ 3  Нахождение неизвестного члена пропорции

Используя основное свойство пропорции, можно найти неизвестный член пропорции, но при условии, что все остальные её члены известны.

Например: найдем неизвестный средний член пропорции 7 : а = 3 : 6, воспользуемся основным свойством пропорции, 7 ∙ 6 = а ∙ 3, а = 7 ∙ 6 : 3 = 14, т.е. неизвестный член пропорции а равен 14.

Отметим, что если в верной пропорции поменять местами средние члены пропорции или крайние члены пропорции, то новые пропорции, которые у нас получатся, будут тоже верными.

Например: 24 : 12 = 8 : 4

Воспользуемся основным свойством пропорции, получим 24 ∙ 4 = 12 ∙ 8 = 96.

Поменяем в пропорции средние члены, получим 24 : 8 = 12 : 4, воспользуемся основным свойством пропорции, получим 24 ∙ 4 = 8 ∙ 12 = 96.

Теперь поменяем местами крайние члены пропорции, получим 4 : 12 = 8 : 24, воспользуемся основным свойством пропорции, получаем 4 ∙ 24 = 12 ∙ 8 = 96.

Видим, что получившиеся пропорции тоже верны, так как при таких перестановках произведение крайних и средних членов пропорции не изменилось.

Итак, на этом уроке Вы узнали, что такое пропорция, познакомились с основным её свойством. А также научились составлять пропорции и находить неизвестный член пропорции.

Список использованной литературы:

1. Математика. 6 класс. Учебник. Виленкин Н.Я., Жохов В.И. и др. 2013.-288 с.
2. Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор – Минаева С.С. – 2014.
3. Математика. 6 класс (И.И. Зубарева, А.Г. Мордкович). 2009.