Как найти неизвестный коэффициент в матрице

Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.

Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.

Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.   

Матричный метод решения – метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.

Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A^-1 · B, где A^-1 – обратная матрица.

Матричный метод решения состоит в следующем.

Пусть дана система линейных уравнений с nнеизвестными:

Её можно переписать в матричной форме: AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A^-1 — матрицу, обратную к матрице A:  A^-1 (AX) = A^-1 B

Так как A^-1A = E, получаем X = A^-1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: detA≠ 0.

Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Пример решения неоднородной системы линейных алгебраических уравнений.

Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.

Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они  понадобятся для нахождения обратной матрицы.

Теперь найдём союзную матрицу и транспонируем  её, потом подставим в формулу для нахождения обратной матрицы.

Подставляя переменные в формулу, получаем:

Найдем неизвестные. Для этого перемножим обратную матрицу  и столбец свободных членов.

Итак, x=2; y=1; z=4.

Если у Вас есть вопросы или Вам нужна помощь в решении линейных уравнений или систем, записывайтесь на мои занятия. Буду рад Вам помочь.  

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Матричный метод решения систем линейных уравнений

Матричный метод может применяться в решении систем линейных уравнений, в которых число неизвестных равно числу уравнений, то есть систем линейных уравнений с квадратной матрицей коэффициентов при неизвестных.

Другое условие применимости матричного метода – невырожденность матрицы коэффициентов при неизвестных, то есть неравенство нулю определителя этой матрицы.

Систему линейных уравнений, при выполнении вышеназванных условий, можно представить в матричном виде, а затем решить её путём отыскания обратной матрицы к матрице системы.

Решение систем линейных уравнений матричным методом основано на следующем свойстве обратной матрицы: произведение обратной матрицы и исходной матрицы равно единичной матрице. Обратная матрица обозначается символом .

Пусть нужно решить систему линейных уравнений:

Запишем эту систему уравнений в матричном виде:

Обозначим отдельно как A матрицу коэффициентов при неизвестных и как B матрицу неизвестных и матрицу свободных членов

.

То есть, для нахождения решений системы нужно обе части уравнения умножить на матрицу, обратную матрице коэффициентов при неизвестных и приравнять соответствующие элементы полученных матриц.

Алгоритм решения системы линейных уравнений матричным методом разберём на следующем примере системы линейных уравнений второго порядка.

Пример 1. Решить матричным методом систему линейных уравнений:

Решение состоит из следующих шагов.

Шаг 1. Составляем следующие матрицы.

Матрица коэффициентов при неизвестных:

Матрица свободных членов:

Это сделано для того, чтобы применить в решении уже записанные закономерности, основанные на свойстве обратной матрицы:

По выведенному выше последнему равенству и будем вычислять решения данной системы.

Но сначала проверим, не является ли матрица коэффициентов при неизвестных вырожденной, то есть можем ли вообще применять матричный метод:

.

Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.

Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:

.

Шаг 3. Находим матрицу неизвестных:

Итак, получили решение:

.

Следовательно, ответ правильный.

Для второго примера выберем систему линейных уравнений третьего порядка.

Пример 2. Решить матричным методом систему линейных уравнений:

Шаг 1. Составляем следующие матрицы.

Матрица коэффициентов при неизвестных:

Матрица свободных членов:

Проверим, не является ли матрица коэффициентов при неизвестных вырожденной:

.

Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.

Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:

.

Шаг 3. Находим матрицу неизвестных:

Итак, получили решение:

.

Следовательно, ответ правильный.

Решить систему уравнений матричным методом самостоятельно, а затем посмотреть решение

Пример 3. Решить матричным методом систему линейных уравнений:

Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы

В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.

Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.

Найти решение системы n линейных уравнений с n неизвестными:

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n

Матричный вид записи: А × X = B

где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n – матрица системы.

X = x 1 x 2 ⋮ x n – столбец неизвестных,

B = b 1 b 2 ⋮ b n – столбец свободных коэффициентов.

Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A – 1 :

A – 1 × A × X = A – 1 × B .

Так как А – 1 × А = Е , то Е × X = А – 1 × В или X = А – 1 × В .

Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .

В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.

Пример решения системы линейных уравнений с помощью метода обратной матрицы

Решаем СЛАУ методом обратной матрицы:

2 x 1 – 4 x 2 + 3 x 3 = 1 x 1 – 2 x 2 + 4 x 3 = 3 3 x 1 – x 2 + 5 x 3 = 2

• Записываем систему в виде матричного уравнения А X = B , где

А = 2 – 4 3 1 – 2 4 3 – 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .

• Выражаем из этого уравнения X :

• Находим определитель матрицы А :

d e t A = 2 – 4 3 1 – 2 4 3 – 1 5 = 2 × ( – 2 ) × 5 + 3 × ( – 4 ) × 4 + 3 × ( – 1 ) × 1 – 3 × ( – 2 ) × 3 – – 1 × ( – 4 ) × 5 – 2 × 4 – ( – 1 ) = – 20 – 48 – 3 + 18 + 20 + 8 = – 25

d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.

• Находим обратную матрицу А – 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :

А 11 = ( – 1 ) ( 1 + 1 ) – 2 4 – 1 5 = – 10 + 4 = – 6 ,

А 12 = ( – 1 ) 1 + 2 1 4 3 5 = – ( 5 – 12 ) = 7 ,

А 13 = ( – 1 ) 1 + 3 1 – 2 3 – 1 = – 1 + 6 = 5 ,

А 21 = ( – 1 ) 2 + 1 – 4 3 – 1 5 = – ( – 20 + 3 ) = 17 ,

А 22 = ( – 1 ) 2 + 2 2 3 3 5 – 10 – 9 = 1 ,

А 23 = ( – 1 ) 2 + 3 2 – 4 3 – 1 = – ( – 2 + 12 ) = – 10 ,

А 31 = ( – 1 ) 3 + 1 – 4 3 – 2 4 = – 16 + 6 = – 10 ,

А 32 = ( – 1 ) 3 + 2 2 3 1 4 = – ( 8 – 3 ) = – 5 ,

А 33 = ( – 1 ) 3 + 3 2 – 4 1 – 2 = – 4 + 4 = 0 .

• Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :

А * = – 6 7 5 17 1 – 10 – 10 – 5 0

• Записываем обратную матрицу согласно формуле:

A – 1 = 1 d e t A ( A * ) T : А – 1 = – 1 25 – 6 17 – 10 7 1 – 5 5 – 10 0 ,

• Умножаем обратную матрицу А – 1 на столбец свободных членов В и получаем решение системы:

X = A – 1 × B = – 1 25 – 6 17 – 10 7 1 – 5 5 – 10 0 1 3 2 = – 1 25 – 6 + 51 – 20 7 + 3 – 10 5 – 30 + 0 = – 1 0 1

Ответ: x 1 = – 1 ; x 2 = 0 ; x 3 = 1

Конспект на тему: “Решение системы линейных уравнений матричным методом”

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Решение систем линейных уравнений матричным методом

Пусть дана система уравнений

Рассмотрим матрицу, составленную из коэффициентов при неизвестных .

Свободные члены и неизвестные можно записать в виде матриц-столбцов:

Тогда используя правило умножения матриц, эту систему уравнений можно записать так:

Это равенство называется простейшим матричным уравнением .

Чтобы решить матричное уравнение, нужно:

Найти обратную матрицу .

Найти произведение обратной матрицы на матрицу – столбец свободных членов В, т.е..

Пользуясь определением равных матриц, записать ответ.

Решить систему уравнений

Представим уравнение в виде матричного уравнения.

Решение . Перепишем систему в виде АХ=В, где

Решение матричного уравнения имеет вид .

Найдем обратную матрицу :

Следовательно, х=2, y =3, z =-2.

Решить систему уравнений матричным методом

Найдем обратную матрицу А -1 .

 = det A = 20 – 12 – 3 + 8 – 45+2= -30.

Находим матрицу Х.

Итого решения системы: x =1; y = 2; z = 3

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 932 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 682 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 308 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 575 831 материал в базе

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 10.06.2020
• 440
• 28

• 10.06.2020
• 433
• 16

• 10.06.2020
• 346
• 4

• 10.06.2020
• 113
• 1

• 10.06.2020
• 110
• 0

• 10.06.2020
• 380
• 8

• 10.06.2020
• 97
• 0

• 10.06.2020
• 291
• 8

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 10.06.2020 489
• DOCX 77.3 кбайт
• 24 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Ажулаева Патимат Магомедрасуловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет
• Подписчики: 0
• Всего просмотров: 134080
• Всего материалов: 69

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

В Ленобласти школьники 5-11-х классов вернутся к очному обучению с 21 февраля

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Минпросвещения подключит студотряды к обновлению школьной инфраструктуры

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/issledovanie-slau/matrichnyj-metod-reshenija-slau/

http://infourok.ru/konspekt-na-temu-reshenie-sistemy-linejnyh-uravnenij-matrichnym-metodom-4353951.html

[/spoiler]

Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:

, где  — основная матрица системы, и  — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на  — матрицу, обратную к матрице :

Так как , получаем . Правая часть этого уравнения даст столбец решений исходной системы.
Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

.

Для однородной системы линейных уравнений, то есть когда вектор , действительно обратное правило: система имеет нетривиальное (то есть ненулевое) решение только если . Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Пример решения неоднородной СЛАУ[править | править код]

Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.

Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.

Далее найдём присоединённую матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.

Подставляя переменные в формулу, получаем:

Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.

Итак, x = 2; y = 1; z = 4.

Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях». 

Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано. 

Краткое содержание прошлых частей: 

И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.

Что такое матричное уравнение

Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.

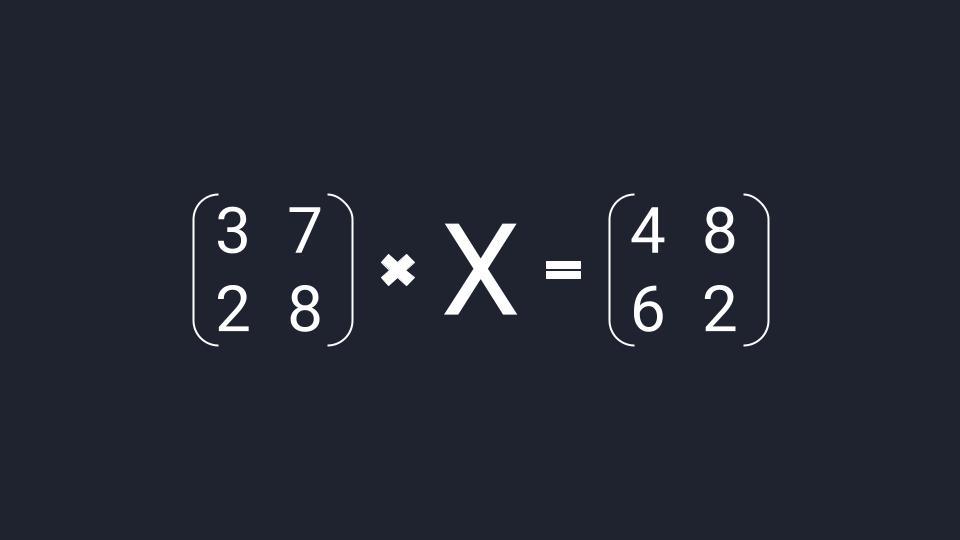
Шаг 1. Упрощаем уравнение 

Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.

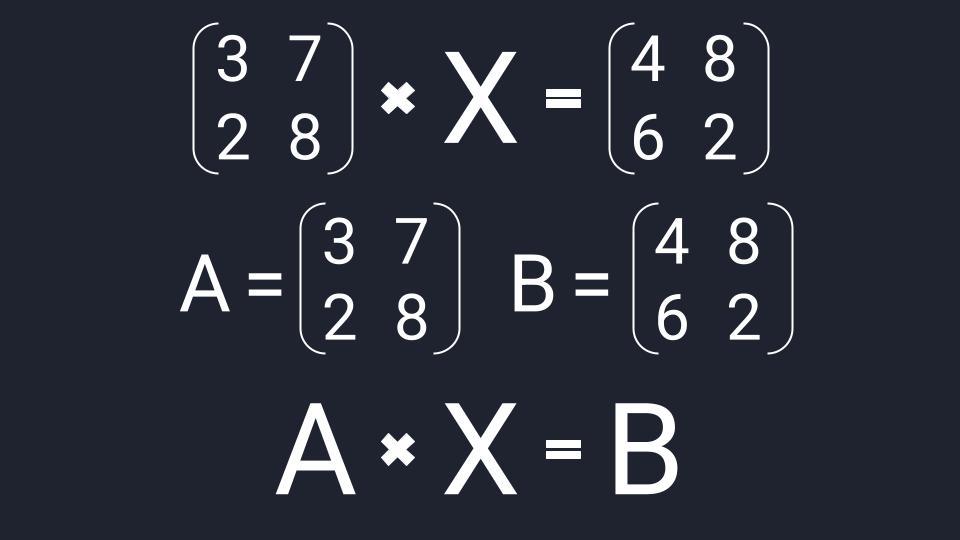
Шаг 2. Вводим единичную матрицу 

В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу. 

Можно представить, что есть число 100 — это «сто в первой степени», 100¹

И есть число 0,01 — это «сто в минус первой степени», 100^-1

При перемножении этих двух чисел получится единица:
100¹ × 100^-1 = 100 × 0,01 = 1. 

Вот такое, только в мире матриц. 

Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А^-1. Неизвестную матрицу Х оставляем без изменений и переписываем уравнение: 

А-1 × А × Х = А-1 × В  

Добавляем единичную матрицу и упрощаем запись: 

А-1 × А = E — единичная матрица 

E × Х = А-1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем

Х = А-1 × В — новая запись уравнения 

После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B. 

💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A^-1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто. 

Шаг 3. Находим обратную матрицу

Вспоминаем формулу и порядок расчёта обратной матрицы: 

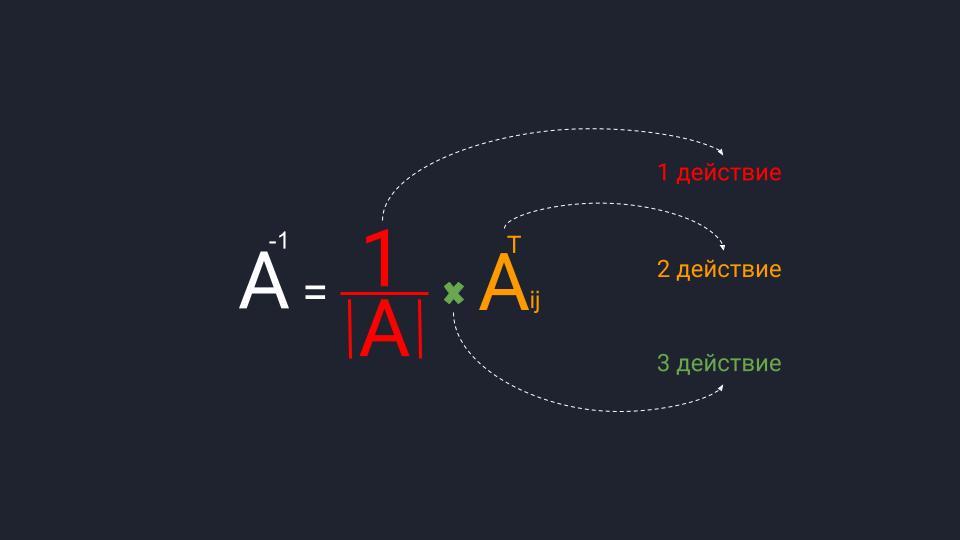
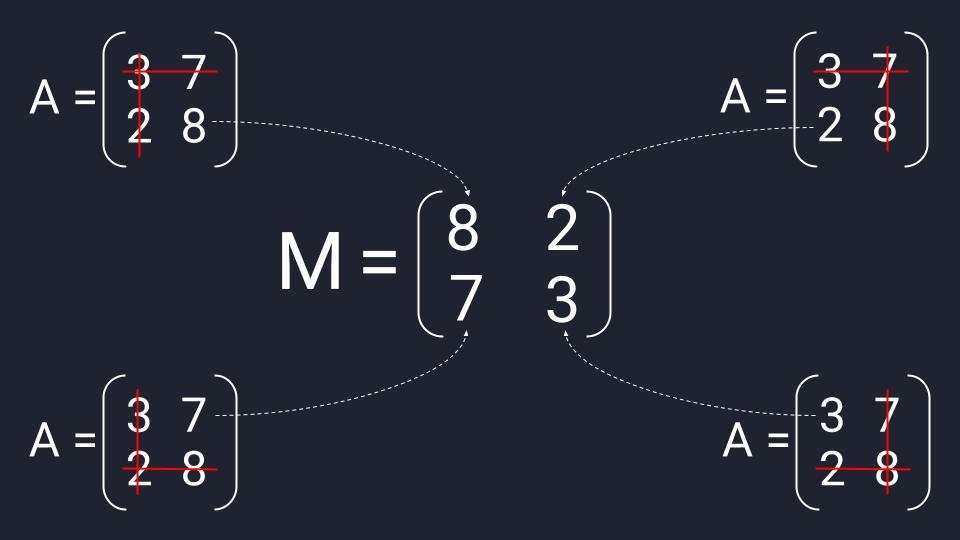
Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Шаг 4. Вычисляем неизвестную матрицу

Нам остаётся посчитать матрицу X: умножаем обратную матрицу А^-1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Шаг 5. Проверяем уравнение

Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново. 

👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Ну и что

Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:

Этого котика не существует, а матрицы — существуют. 

Содержание:

• Матричный метод решения
• Примеры решения систем уравнений

Матричный метод решения

Запишем заданную систему в матричном виде:

$$AX=B$$

Если матрица $$A$$ невырождена, то тогда с помощью
операций над матрицами
выразим неизвестную матрицу $$X$$ . Операция деления на множестве
матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу $A^{-1}$ слева:

$$A^{-1} A X=A^{-1} B Rightarrow E X=A^{-1} B Rightarrow$$
$$X=A^{-1} B$$

Поэтому, чтобы найти неизвестную матрицу $$X$$ надо найти обратную матрицу
к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.

Примеры решения систем уравнений

Читать дальше: метод Крамера.