Составь уравнения по схемам. Что в них общего? Как найти неизвестный объект операции?




reshalka.com
ГДЗ учебник по математике 2 класс Петерсон. Урок 13. Решение задач. Номер №6
Решение
![]() Получай решения и ответы с помощью нашего бота
Получай решения и ответы с помощью нашего бота
![]() Посмотреть калькулятор Вычисления в столбик
Посмотреть калькулятор Вычисления в столбик
x + 8 = 24
x = 24 − 8
x = 16
Проверка:
16 + 8 = 24
24 = 24
x * 5 = 25
x = 25 : 5
x = 5
Проверка:
5 * 5 = 25
25 = 25
x : 9 = 8
x = 8 * 9
x = 72
Проверка:
72 : 8 = 9
9 = 9
-
Главная
-
ГДЗ
- 2 класс
- Математика
-
Петерсон. Учебник
-
Страница 38. Урок 13. Часть 3
Вернуться к содержанию учебника
Вопрос
Задание № 6. Составь уравнения по схемам. Что в них общего? Как найти неизвестный объект операции?
Подсказка
Ответ

Вопрос
Задание № 7. Как изменяется число в результате операций прибавления и вычитания? А в результате операций умножения и деления? Составь и реши уравнения по схемам.
Подсказка
Ответ

Вопрос
Задание № 8. Найди уравнения, в которых не известен объект операции, и в которых не известна операция. Как их можно решить?
Реши уравнения. Что ты замечаешь?
Подсказка
Ответ


Вопрос
Задание № 9. Цена пары ботинок х руб., а цена пары сапог у руб. Что означают выражения:
| х + у | у – х | у : х | х • 2 + у • 3 |
Подсказка
Ответ

Вопрос
Задание № 10. Найди площадь закрашенных фигур.
Подсказка
Повтори, как найти площадь прямоугольника.
Ответ

Вопрос
Подсказка
Ответ

Вопрос
Задание № 12. Выполни действия:
| 6 м 3 см – 45 дм + 1 м 4 дм 7 см | 4 дм2 58 см2 + 342 см2 |
| 5 м 32 см + 4 м 1 дм 6 см | 8 дм2 – 5 дм2 6 см2 |
Подсказка
Ответ


Вернуться к содержанию учебника
Страница 37 из 110
Урок 13. Решение задач. Страница 38.
6. Как найти неизвестный объект операции? Составь уравнения по схемами реши их, используя данное правило.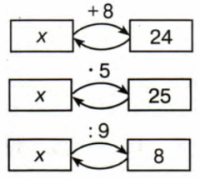
Решение
x + 8 = 24,
x = 24 − 8,
x = 16.
Проверка:
16 + 8 = 24,
24 = 24.x * 5 = 25,
x = 25 : 5,
x = 5.
Проверка:
5 * 5 = 25,
25 = 25.x : 9 = 8,
x = 8 * 9,
x = 72.
Проверка:
72 : 8 = 9,
9 = 9.
7. Как изменяется число в результате операций прибавления и вычитания? А в результате операций прибавления и вычитания? А в результате операций умножения и деления? Составь и реши уравнения по схемам: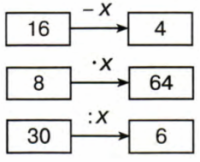
Решение
В результате прибавления число увеличивается, а в результате убавления число уменьшается.
В результате умножения число увеличивается, а в результате деления число уменьшается.16 − x = 4,
x = 16 − 4,
x = 12.
Проверка:
16 − 12 = 4,
4 = 4.8 * x = 64,
x = 64 : 8,
x = 8.
Проверка:
8 * 8 = 64,
64 = 64.30 : x = 6,
x = 30 : 6,
x = 5.
Проверка:
30 : 5 = 6,
6 = 6.
8. Найди уравнения, в которых не известны объект операции, операция. Реши их, используя соответствующие правила.
x − 3 = 5
x : 3 = 5
x + 4 = 12
x * 4 = 12
21 − x = 7
21 : x = 7
9 + x = 36
9 * x = 36
Решение
x − 3 = 5,
x = 5 + 3,
x = 8.
Проверка:
8 − 3 = 5,
5 = 5.x : 3 = 5,
x = 5 * 3,
x = 15.
Проверка:
15 : 3 = 5,
5 = 5.x + 4 = 12,
x = 12 − 4,
x = 8.
Проверка:
8 + 4 = 12,
12 = 12.x * 4 = 12,
x = 12 : 4,
x = 3.
Проверка:
3 * 4 = 12,
12 = 12.21 − x = 7,
x = 21 − 7,
x = 14.
Проверка:
21 − 14 = 7,
7 = 7.21 : x = 7,
x = 21 : 7,
x = 3.
Проверка:
21 : 3 = 7,
7 = 7.9 + x = 36,
x = 36 − 9,
x = 27.
Проверка:
9 + 27 = 36,
36 = 36.9 * x = 36,
x = 36 : 9,
x = 4.
Проверка:
9 * 4 = 36,
36 = 36.
9. Цена пары ботинок x руб., а пары сапог – y руб. Что означают выражения:
x + y y − x y : x x * 2 + y * 3
Решение
x + y (р.) − стоят вместе одна пара ботинок и один сапог;
y − x (р.) − цена сапога больше, чем одна пара ботинок;
y : x (раз) − цена сапога больше, чем одна пара ботинок;
x * 2 + y * 3 − стоимость двух пар ботинок и трех сапог.
10. Найди площадь закрашенных фигур: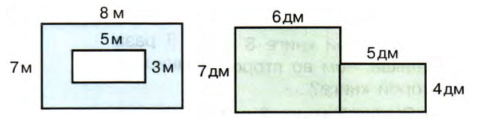
Решение
а. 1) 8 * 7 = 56 $(м^2)$ − площадь всего прямоугольника;
2) 5 * 3 = 15 $(м^2)$ − площадь незакрашенной фигуры;
3) 56 − 15 = 41 $(м^2)$ − площадь закрашенной фигуры.
Ответ: 41 $м^2$б. 1) 7 * 6 = 42 $(дм^2)$ − площадь большого прямоугольника;
2) 5 * 4 = 20 $(дм^2)$ − площадь маленького прямоугольника;
3) 42 + 20 = 62 $(дм^2)$ − площадь закрашенной фигуры.
Ответ: 62 $дм^2$.
11. Сравни с помощью знаков >, <, =:
2 м 4 дм ☐ 206 см
51 дм 8 см ☐ 7 м
9 $дм^2$ ☐ 90 $см^2$
400 $дм^2$ ☐ 6 $м^2$
Решение
2 м 4 дм > 206 см
51 дм 8 см <7м9 дм2 > 90 см2
400 дм2 < 6 м2
Полная запись:
2 м 4 дм = (2 * 100 + 4 * 10) см = 240 см;
240 см > 206 см;
2 м 4 дм > 206 см.7 м = (7 * 10) дм = 70 дм;
51 дм 8 см < 70 дм;
51 дм 8 см < 7 м.9 $дм^2$ = (9 * 100) $см^2$ = 900 $см^2$;
900 $см^2$ > 90 $см^2$;
9 $дм^2$ > 90 $см^2$.6 $м^2$ = (6 * 100) $дм^2$ = 600 $дм^2$;
400 $дм^2$ < 600 $дм^2$;
400 $дм^2$ < 6 $м^2$.
12. Выполни действия.
6 м 3 см – 45 дм +1 м 4 дм 7 см = 603 см – 450 см+147 см = 300 см = 3 м
5 м 32 см + 4 м 1 дм 6 см =532 см + 416 см = 948 см = 9 м 4 дм 8 см4 дм2 58 см2 + 342 см2 = 458 см2 + 342 см2 = 800 см2 = 8 дм2
8 дм2 – 5 дм2 6 см2 = 800 см2 – 506 см2 = 294 см2 = 2 дм2 94 см2
Математика 2 класс учебник Петерсон 3 часть ответы — страница 52

- Тип: ГДЗ, Решебник.
- Автор: Л. Г. Петерсон.
- Год: 2021.
- Серия: Учись Учиться.
- Издательство: Просвещение/Бином.
Подготовили готовое домашнее задание к упражнениям на 52
странице по предмету математика за 2 класс. Ответы на задания: 4, 5, 6, 7, 8, 9 и 10.
.jpg)
Учебник 3 часть – Страница 52.
Ответы 2021 года.
Номер 4.
Отметь цветным карандашом последнее действие. Прочитай выражение и найди его значение:
2 х 8 − 6 = 2 х (8 − 6) = (6 + 9) : 3 =
6 + 9 : 3 = 9 х 8 + 6 х 3 = 9 х 8 − 6 : 3 =
Ответ:
2 х 8 − 6 — разность произведения чисел 2 и 8 и числа 6
2 х (8 − 6) — произведение числа 2 и разности чисел 8 и 6
(6 + 9) : 3 — частное суммы чисел 6 и 9 и числа 3
6 + 9 : 3 — сумма числа 6 и частного чисел 9 и 3
9 х 8 + 6 х 3 — сумма произведений чисел 9 и 8 и чисел 6 и 3
9 х 8 − 6 : 3 — разность произведения чисел 9 и 8 и частного чисел 6 и 3
Номер 5.
Цена пары ботинок х руб., а цена пары сапог у руб. Что означают выражения:
х + у у − х у : х X х 2 + у х 3
Ответ:
х + у — стоимость пары ботинок и пары сапог
у − х — на сколько сапоги дороже ботинок
у : х — во сколько раз сапоги дороже ботинок
X х 2 + у х 3 — стоимость 2 пар ботинок и 3 пар сапог
Номер 6.
Найди площадь закрашенных фигур:

Ответ:
а) Площадь заштрихованной фигуры равна разности площадей большого и маленького прямоугольников: 7 х 8 − 3 х 5 = 41 (м2).
б) Площадь всей фигуры равна сумме площадей двух прямоугольников: 7 х 6 + 5 х 4 = 62 (дм2).
Номер 7.
Нарисуй прямоугольник со сторонами 4 см и 3 см. Проведи диагонали и обозначь их точку пересечения О. Построй окружность с центром в точке О, проходящую через одну из вершин прямоугольника. Что ты замечаешь? Чем это объяснить?
Ответ:

Окружность проходит через все вершины. Диагонали прямоугольника являются диаметрами. Радиус окружности – это половина диагонали.
Номер 8.
Составь уравнения по схемам. Что в них общего? Как найти неизвестный объект операции?

Ответ:
В этом номере происходит повторением понятий «операции» и «обратной операции».
Кроме этого, в уравнениях ищутся неизвестные объекты операций. Поэтому алгоритм решения всех этих уравнений одинаков: чтобы найти неизвестное число, нужно выполнить обратную операцию.
х + 8 = 24 X х 5 = 25 х : 9 = 8
х = 24 − 8 х = 25 : 5 х = 9 х 8
х = 16 х = 5 х = 72
Номер 9.
Как изменяется число в результате операций прибавления и вычитания? А в результате операций умножения и деления? Составь и реши уравнения по схемам:

Ответ:
В этом номере происходит повторением понятий «операции» и «обратной операции».
Кроме этого, в уравнениях ищется неизвестна операция. Поскольку операции прибавления или вычитания некоторого числа изменяют число на несколько единиц, а умножения или деления — в несколько раз, то неизвестное число в них находится по соответствующим правилам сравнения чисел: либо по правилу разностного сравнения — вычесть из большего числа меньшее, либо кратного сравнения — разделить большее число на меньшее.
16 − х = 4 8 х X = 64 30 : х = 6
х = 16 − 4 х = 64 : 8 х = 30 : 6
х = 12 х = 8 х = 5
Номер 10.
Реши уравнения. На какие группы их можно разбить?
х − 3 = 5 х + 4 = 12 21 − х = 7 9 + х = 36
х : 3 = 5 X х 4 = 12 21 : х = 7 9 х X = 36
Ответ:

Уравнения можно разбить на группы разными способами. Первый способ очевиден: по числам, их можно разделить на 4 группы по столбикам.
По методам решения уравнений их можно разбить на группы двумя способами:
1) уравнения первой строки решаются на основе взаимосвязи между частью и целым, а второй — на основе взаимосвязи между сторонами и площадью прямоугольника;
2) в первых двух столбиках даны уравнения с неизвестным объектом операции, а в последних двух — с неизвестной операцией.
Рейтинг
- Вычисли:
1000 – 700 1000 – 7 1000 – 70 1000 – 777
Решение:
1000 –
700 = 300 1000 – 7 = 993 1000 – 70 = 930
1000 – 777 = 223
2. Найди пропущенные числа:

Решение:

3. Составь программу действий и вычисли:

4. Сравни задачи. Чем они похожи и чем различаются? Реши каждую задачу.
а) С первой грядки собрали 45 клубничек, а со
второй – в 5 раз меньше. Сколько клубничек собрали со второй грядки?
б) С первой грядки собрали 45 клубничек, а со
второй – в 5 раз меньше. Сколько клубничек собрали с двух грядок?
Решение:
Задачи о клубнике, условие одинаковое. Во второй
задаче добавляется одно действие, потому что вопросы в задачах разные.
а) 45 : 5 =
9 (кл.) — собрали со второй грядки.
Ответ: 9 клубничек.
б) 1) 45 :
5 = 9 (кл.) — собрали со второй грядки.
2) 45 + 9 = 54 (кл.) –собрали с двух
грядок.
Ответ: 54 клубничек.
5. БЛИЦтурнир
|
а) В книге 56 страниц. Коля читал каждый день по 7 страниц. За сколько дней он прочитал эту книгу? |
56 : 7 = 8 (д.) |
|
б) В первой книге 8 страниц. Это в 3 раза меньше, чем во второй. Сколько страниц во второй книге? |
8 ∙ 3 = 24 (стр.) |
|
в) в одной книге 8 страниц, а в другой – в 4 раза больше. Сколько страниц в этих двух книгах? |
8 ∙ 4 + 8 =40 (стр.) |
|
г) в одной книге 40 страниц, а в другой – в 5 раз меньше. Сколько страниц в этих двух книгах? |
40 : 5 + 40 = 48 (стр.) |
|
д) В первой книге 48 страниц, а во второй – в 6 раз меньше. На сколько страниц в первой книге больше, чем во второй? |
48 — 48 : 6 =40 (стр.) |
6. Составь уравнения по схемам. Что в них общего? Как найти неизвестный объект операции?
![]()
Решение:
х + 8 =
24 х ∙ 5 =
25 х : 9 = 8
х = 24 –
8 х= 25 :
5 х = 8 ∙ 9
х
= 16 х = 5 х = 72
Чтобы найти
неизвестный объект операции, надо по стрелке выполнить обратное действие.
7. Как изменяется число в результате операций прибавления и вычитания? А в результате операций умножения и деления? Составь и реши уравнения по схемам:
![]()
Решение:
В
результате прибавления число увеличивается на то число, которое прибавляем.
В
результате вычитания число уменьшается
на то число, которое вычитаем.
В
результате умножения число увеличивается в несколько раз, а при делении
уменьшается в несколько раз.
16 – х =
4 8 ∙ х = 64 30 : х = 6
х = 16 –
4 х = 64 : 8 х = 30 : 6
Х = 12 х = 8 х = 5
8. Найди уравнения, в которых не известен объект операции, и в которых не известна операция. Как их можно решить?
х – 3 = 5
х + 4 = 12 21 – х = 7 9 + х = 36
х : 3 = 5 х * 4 = 12 21 : х =7 9 * х = 36
Решение:
Чтобы найти
объект операции, надо над результатом провести обратную операцию.
Уравнения,
в которых не известен объект операции:
х – 3 =
5 х + 4
= 12 х : 3
= 5 х
4 = 12
х = 5 +
3 х = 12 – 4 х = 5 ∙ 3 х = 12 : 4
х
= 8
х = 8 х
= 15 х = 3
8 – 3 =
5 8 + 4
= 12 15 :
3 = 5 3 4 = 12
5 = 5 12 = 12 5 = 5 12 = 12
Уравнения,
в которых не известна операция:
21 – х =
7 9 + х = 36 21 : х =7 9 х = 36
х = 21 –
7 х = 36 – 9 х = 21 : 7 х = 36 : 9
х
= 14
х = 27 х
= 3 х = 4
21 – 14 =
7 9 + 27 = 36 21 : 3 =7 9 4 = 36
7
= 7 36 = 36 7 = 7 36 = 36
9. Цена пары ботинок х руб., а цена пары сапог у руб. Что означают выражения:
х + у у – х
у : х х 2 + у 3
Решение:
х + у (руб.) – стоимость пары ботинок и пары
сапог вместе
у – х (руб.) – на сколько сапоги дороже ботинок
у : х (раз.) – во сколько раз сапоги дороже
ботинок
х
2 + у 3 ( руб.) – стоимость 2 пар ботинок и трёх пар
сапог вместе
10. Найди площадь закрашенных фигур:

Решение:
а) 1) 8 ∙ 7 = 56 (м²) – площадь большого прямоугольника
2) 5 ∙ 3 =
15 (м²) – площадь маленького прямоугольника
3) 56 – 15
= 41 (м²) – площадь закрашенной фигуры. Ответ: 41 м²
б) 1) 6 ∙ 7 = 42 (дм²) – площадь большого прямоугольника
2) 5 ∙ 4 = 20
(дм²) – площадь маленького прямоугольника
3) 42 + 20
= 62 (дм²) – площадь закрашенной фигуры. Ответ: 62 дм²
11. Сравни:
2 м 4 дм … 206 см 9 дм2 … 90 см2
51 дм 8 см … 7 см 400 дм2 … 6 м2
Решение:
2 м 4 дм > 206 см 9 дм2 > 90 см2
2 м 4 дм =
240 см 9
дм2 = 900 cм²
240 см > 206 см 900 cм² > 90 cм²
51 дм 8 см > 7 см 400 дм2
< 6 м2
51 дм 8 см = 518 cм
6 м2= 600 дм2
518 см > 7 см 400
дм2 < 600 дм2
12. Выполни действия:
6 м 3 см – 45 дм + 1 м 4 дм 7 см 4 дм2 58 см2
+ 342 см2
5 м 32 см + 4 м 1 дм 6 см 8 дм2 – 5
дм2 6 см2
Решение:
6 м 3 см –
45 дм + 1 м 4 дм 7 см = 603 см — 450 см
+ 147 см = 300 см = = 3 м
4 дм2 58 см2 + 342 см2=
458 см2 + 342 см2 = 800см² = 8дм²
5 м 32 см +
4 м 1 дм 6 см = 532 см + 416см = 948 см = 9 м 4 дм 8 см
8 дм2 – 5 дм2 6 см2=
800 см² — 506 см² = 294 см² = 2 дм² 94 см²
13. Покажи на модели прямоугольного параллелепипеда равные грани и равные рёбра. Измерь длину, ширину и высоту своей модели.

Решение:

14. Длина прямоугольного параллелепипеда равна 4 см, ширина – 2 см, а высота – 3 см. Найди: а) площадь каждой грани параллелепипеда; б) сумму площадей всех граней (площадь полной поверхности).
Решение:
а)1) 4 ∙ 3
= 12 (см²) – площадь передней и задней граней.
2) 4 ∙ 2 = 8 (см²) – площадь верхней и
нижней граней.
3) 2 ∙ 3 = 6 (см²) – площадь боковых граней.
б) 2 ∙ 12 +
2 ∙ 8 + 2 ∙ 6 = 24 + 16 + 12 = 52 (см²) – площадь полной поверхности.
Ответ: а)12
см², 8 см², 6 см²; б) 52 см².
15. Расшифруй предложение:
Р 906
– 538 = 368 Б 156 – 87 = 69 Л 844 – 764 = 80
И 532
– 79 = 453 А 525 – 478 = 47 О 284 – 196 = 88
Г 763 – 274 = 489 Й 600 – 502 = 98 Я
507 – 294 = 213
Т 700 – 364 = 336 Ю 350 – 54 = 296 С 815 – 426 = 389

16. Отметь на клетчатой бумаге точки в ряд через 1 см. Проведи последовательно окружности с центрами в данных точках и радиусом 2 см. Раскрась получившийся узор.

Решение:

Назад к содержанию
