Тема: Найдите нейтральный элемент (Прочитано 3206 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Как найти нейтральный элемент для следующей операции *
х*у = ху+7х+7у+42
Знаю, что нейтральный элемент – это элемент Е удовлетворяющий условию А*Е=Е*А=А
Ну и как же найти этот нейтральный элемент?
« Последнее редактирование: 24 Мая 2011, 23:35:43 от NELL »

Не знаком с нейтральными элементами, но хорошо знаю алгебру. Чтобы выполнялось тождество, должно быть: 7х+7у+42=0 и, следовательно,
y=-x-6

За жизнью надо тщательно следить, все время избегая с ней разлуки.

xy сокращаются и остается 7х+7у+42=0. Отсюда y=-x-6

За жизнью надо тщательно следить, все время избегая с ней разлуки.
нееет! Вы не поняли.
В условии дается такая бинарная операция ” * ” (умножения), которая определяется выражением
х*у = ху+7х+7у+42
т.е. х * у – это не такое обычное умножение, а это операция, которая определяется этим вот большим выражением
« Последнее редактирование: 25 Мая 2011, 02:03:00 от NELL »

Тишина… 

ex=e*x+7x+7e+42=x
e(x+7)=-42-6x
e = -(42+6x)/(x+7)
e = -6(x+7)/(x+7)
e = -6

Ого! Спасибо большое! 

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 июля 2021 года; проверки требуют 3 правки.
Запрос «Единичный элемент» перенаправляется сюда; про элемент «1» в кольцах и алгебрах см. единица (алгебра).
Нейтра́льный элеме́нт бинарной операции — элемент, который оставляет любой другой элемент неизменным при применении этой бинарной операции к этим двум элементам.
Определение[править | править код]
Пусть 




.
В случаях некоммутативных операций, вводят левый нейтральный элемент 
,
и правый нейтральный элемент 
.
В общем случае может существовать произвольное количество элементов, нейтральных слева или справа. Если одновременно существуют и нейтральный слева элемент 


Примеры[править | править код]
| Множество | Бинарная операция | Нейтральный элемент |
|---|---|---|
| Вещественные числа |  (сложение) (сложение) |
число 0 |
| Вещественные числа |  (умножение) (умножение) |
число 1 |
| Вещественные числа |  (вычитание) (вычитание) |
число 0 (нейтральный справа) |
| Вещественные числа |  (возведение в степень) (возведение в степень) |
число 1 (нейтральный справа) |
| Расширенная числовая прямая |  (деление) (деление) |
число 1 (нейтральный справа) |
| Векторное пространство |  (сложение векторов) (сложение векторов) |
 (нуль-вектор) (нуль-вектор)
|
Матрицы размера  |
 (матричное сложение) (матричное сложение) |
нулевая матрица |
Матрицы размера  |
 (матричное произведение) (матричное произведение) |
единичная матрица |
Функции вида  |
 (композиция функций) (композиция функций) |
тождественное отображение |
| Символьные строки | конкатенация | пустая строка |
| Расширенная числовая прямая |  (минимум) или (минимум) или  (инфимум) (инфимум) |

|
| Расширенная числовая прямая |  (максимум) или (максимум) или  (супремум) (супремум) |

|
Подмножества множества  |
 (пересечение множеств) (пересечение множеств) |

|
| Множества |  (объединение множеств) (объединение множеств) |
 (пустое множество) (пустое множество)
|
| Исчисление высказываний |  (конъюнкция) (конъюнкция) |
 (истина) (истина)
|
| Исчисление высказываний |  (дизъюнкция) (дизъюнкция) |
 (ложь) (ложь)
|
Терминология[править | править код]
В алгебре[править | править код]
В приведённой в определении мультипликативной нотации нейтральный элемент принято называть единичным элементом или просто единицей по аналогии с одноимённым числом. См. статью «единица (алгебра)» о двусторонних нейтральных элементах умножения в кольцах, полях, и алгебрах над ними.
Если речь идёт о нейтральном элементе операции, обозначаемой (и называемой) сложением, то нейтральный элемент называют нулём, опять-таки по аналогии с одноимённым числом. Сложением называют не только операцию в теории колец и линейной алгебре, но, обычно, и групповую операцию в абелевых группах в аддитивной нотации.
В теории решёток[править | править код]
В теории решёток нейтральный элемент операции «∨» обозначается «0», а нейтральный элемент операции «∧» обозначается «1».
См. также[править | править код]
- Поглощающий элемент
- Обратный элемент
- Моноид
- Группа
Ссылки[править | править код]
- Куликов Л.Я. Алгебра и теория чисел: Учеб. пособие для педагогических институтов. — М.: Высш. школа, 1979. — 559 с. стр 77 “Нейтральные элементы”
- http://www.algebraical.info/doku.php?id=glossary:element:groupoid:identity (рус.)
- http://mathforum.org/library/drmath/view/56032.html (рус.)
- https://brilliant.org/wiki/identity-element/ (англ.)
- Weisstein, Eric W. “Identity Element.” From MathWorld–A Wolfram Web Resource (англ.)
Группы, кольца, поля в математике
Группа: определение и примеры групп
Множество с алгебраической операцией
называется группой, если выполняются следующие условия:
1) операция в
ассоциативна:
;
2) в существует нейтральный элемент
;
3) для каждого элемента существует обратный ему элемент
.
Если операция коммутативна, то группа называется коммутативной, или абелевой. В противном случае группа называется некоммутативной.
Относительно операции сложения группами являются множества . Относительно операции умножения группами являются множества
и
отличных от нуля рациональных и действительных чисел, поскольку для нуля не существует обратного элемента. Все эти группы коммутативные.
В группах по сложению нейтральный элемент называют нулевым (или просто нулем), а обратный элемент
— противоположным
. В группах по умножению нейтральный элемент
называют единичным (или просто единицей) и обозначают
, для обратного элемента
название и обозначение сохраняется.
Пример В.4. Доказать, что множество , состоящее из одного числа нуль, образует коммутативную группу по сложению.
Решение. Действительно, операция сложения определена на указанном множестве, так как . Из этого равенства следует, что этот единственный элемент множества служит нулевым (нейтральным) элементом, а также противоположным (обратным) для себя. Ассоциативность сложения очевидна:
. Следовательно, все (три) условия в определении группы выполняются. Учитывая коммутативность сложения, заключаем, что рассматриваемое множество — коммутативная группа.
Пример В.5. Доказать, что множество , состоящее из двух чисел, образует коммутативную группу по умножению.
Решение. Действительно, операция умножения определена на указанном множестве, так как
(B.1)
Следовательно, произведение элементов есть элемент того же множества. Ассоциативность умножения очевидна. Из равенств (В.1) следует, что существует единичный элемент . Кроме того, каждый элемент имеет обратный:
. Таким образом, все (три) условия в определении группы выполняются. Из (В.1) следует, что умножение коммутативно, поэтому данная группа коммутативная.
Кольцо
Множество , на котором заданы две операции — сложение
и умножение
, называется кольцом, если выполняются следующие условия:
1) относительно операции сложения множество — коммутативная группа, т.е.
а) операция сложения коммутативна: ;
б) операция сложения ассоциативна: ;
в) существует нулевой элемент ;
г) для каждого элемента существует противоположный ему элемент
;
2) операция умножения в множестве ассоциативна:
3) операции сложения и умножения связаны законами дистрибутивности:
Если операция умножения коммутативна: , то кольцо называется коммутативным, в противном случае кольцо называется некоммутативным. Если для операции умножения существует единичный элемент
, то говорят, что кольцо
— есть кольцо с единицей.
Кольцами являются множества целых, рациональных, действительных чисел, причем все они — коммутативные кольца с единицей. Примеры других колец, в том числе и некоммутативных, встретятся в дальнейшем. Как видим, кольцо — это множество, в котором определены три операции: сложение, умножение и вычитание.
Рассмотрим подробнее законы дистрибутивности. Пусть на множестве заданы две операции
и
. Операция
называется дистрибутивной слева относительно операции
, если для любых
из
справедливо равенство:
и дистрибутивной справа относительно операции , если для любых
из
справедливо равенство:
Если операция коммутативна, то дистрибутивность слева операции
относительно операции
влечет дистрибутивность справа, так как
В этом случае говорят, что операция дистрибутивна относительно операции
. Например, операция умножения чисел дистрибутивна (слева и справа) относительно операции сложения чисел. Следующий пример показывает, что имеются операции с “односторонней” дистрибутивностью.
Пример В.6. Рассмотрим множество положительных действительных чисел. На этом множестве определим две операции: умножения
и возведения в положительную степень
. Доказать, что операция
возведения в степень дистрибутивна справа относительно умножения, но не дистрибутивна слева.
Решение. В самом деле, для любых положительных действительных чисел справедливы равенства
Следовательно, операция дистрибутивна справа относительно операции умножения чисел. Дистрибутивность
слева относительно умножения опровергается примером
Пример В.7. Доказать, что множество чисел вида, где и
— целые числа, является кольцом:
(B.2)
Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.2) имеют тоже самое представление:
Числа , очевидно, целые для любых целых
. Законы коммутативности, ассоциативности и дистрибутивности не нуждаются в проверке, так как речь идет о сложении и умножении действительных чисел. Нулевым элементом служит число
. Для каждого числа
l противоположным элементом является число
, так как
Таким образом, рассматриваемое множество удовлетворяет всем условиям определения кольца.
Поле: определение и примеры полей
Множество , на котором заданы две операции: сложение
и умножение
, называется полем, если выполняются следующие условия:
1) — коммутативное кольцо с единицей
;
2) для каждого элемента , отличного от нулевого
, существует обратный элемент
.
Как видим, поле — это множество, в котором определены четыре операции: сложение, умножение, вычитание и деление. Полями, например, являются множества рациональных и действительных чисел.
Пример В.8. На множестве трех целых чисел определим две операции:
1) “сложение по модулю 3” — остаток от деления суммы на 3 (обозначим через
);
2) “умножение по модулю 3” — остаток от деления произведения на 3 (обозначим через
).
Доказать, что множество является полем относительно введенных операций.
Решение. В этом примере остаток от деления целого числа на 3 будем обозначать через
. Напомним простые свойства деления целых чисел с остатком:
– остаток от деления на 3 суммы не изменится, если слагаемое (или не сколько слагаемых) заменить его остатком при делении на 3:
– остаток от деления на 3 произведения не изменится, если множитель (или несколько множителей) заменить его остатком при делении на 3:
Рассматриваемые в примере операции “сложения по модулю 3” и “умножения по модулю 3” можно представить в виде
и
а указанные свойства остатков записать так .
Перейдем теперь к решению задачи. Отметим, что введенные операции и
определены на
. Составим таблицы “сложения по модулю 3” и “умножения по модулю 3” (рис.В.2). Как видим, результаты этих операций принадлежат
. Следовательно, операции действительно определены на
.
Таблица “сложения по модулю” . Таблица “умножения по модулю”
.
Покажем, что множество является коммутативным кольцом с единицей. В самом деле, операция “сложения по модулю 3” коммутативна и ассоциативна. Это следует из коммутативности и ассоциативности сложения чисел. Действительно, из равенства
следует, что
Коммутативность доказана. Заметим, впрочем, что коммутативность “сложения по модулю 3” видна непосредственно по таблице (см. рис.В.2): слагаемые и
в таблице можно поменять местами, при этом таблица не изменится.
Из равенства следует, что
Ассоциативность “сложения по модулю 3” доказана.
Нулевым элементом служит число 0. По таблице “сложения по модулю 3” определяем, что для каждого элемента
из
имеется противоположный элемент
. Действительно, по таблице “сложения по модулю 3” получаем
Итак, множество относительно операции “сложения по модулю 3” является коммутативной группой.
Операция “умножение по модулю 3” ассоциативна и коммутативна, что следует из ассоциативности и коммутативности умножения целых чисел, а также свойств остатков:
Проверим дистрибутивность:
Следовательно, операция “умножения по модулю 3” дистрибутивна слева относительно операции “сложения по модулю 3”. Дистрибутивность справа можно не проверять, так как обе операции коммутативны.
Единичным элементом служит число 1 (что видно по таблице “умножения по модулю 3”). Следовательно, — коммутативное кольцо с единицей.
Осталось показать существование обратных элементов. Для любого , отличного от нуля, существует обратный элемент
;
. В самом деле, по таблице “умножения по модулю 3”
и
. Таким образом, множество
с введенными операциями является полем.
Замечание В.2. Можно доказать, что числовое множество с операциями “сложения по модулю
” и “умножения по модулю
” является полем для любого простого числа
.
Пример В.9. Доказать, что множество чисел вида, где и
— рациональные числа, является полем:
(B.3))
Решение. Действительно, операции сложения и умножения определены на рассматриваемом множестве, так как сумма и произведение двух чисел вида (В.З) имеют тоже самое представление:
Числа очевидно, рациональные для любых рациональных
. Законы коммутативности, ассоциативности и дистрибутивности не нуждаются в проверке, так как речь идет о сложении и умножении действительных чисел. Нулевым элементом служит число
. Для каждого числа
противоположным элементом является число
, так как
Единичным элементом служит число . В самом деле, для любого числа
имеет место равенство:
Таким образом, рассматриваемое множество является коммутативным кольцом с единицей . Осталось показать, что любое число
, отличное от нулевого элемента
, имеет обратный. В самом деле, учитывая, что
определим обратный элемент равенством . Тогда
Заметим, что знаменатель отличен от нуля для любых рациональных чисел
и
, не равных нулю одновременно. Действительно, равенство
равносильно равенству
, а это означает, что
— рациональное число. Поскольку число
— иррациональное, значит
, т.е. обратный элемент существует для любого
.
Так как рассматриваемое множество является коммутативным кольцом с единицей и каждый элемент, отличный от нуля, имеет обратный, то оно является полем.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание
Нейтральный элемент
Единица
Пусть задан группоид  .
.
Определение 1. Элемент  называется нейтральным слева, или левой единицей1), если выполнено условие
называется нейтральным слева, или левой единицей1), если выполнено условие  для любого
для любого  .
.
Определение 2. Элемент  называется нейтральным справа, или правой единицей2), если выполнено условие
называется нейтральным справа, или правой единицей2), если выполнено условие  для любого
для любого  .
.
Определение 3. Элемент  называется нейтральным, или единицей3), если он нейтральный слева и нейтральный справа, то есть
называется нейтральным, или единицей3), если он нейтральный слева и нейтральный справа, то есть  для любого
для любого  .
.
Замечание 1. Обычно термин единица употребляют, если операция  мультипликативна, при этом часто вместо обозначения
мультипликативна, при этом часто вместо обозначения  используют символ
используют символ  .
.
Пример 1. Единичный элемент  в группе невырожденных матриц
в группе невырожденных матриц  порядка
порядка  над полем
над полем  иногда обозначается символом
иногда обозначается символом  .
.
Предложение 1. Если в группоиде  существуют левая единица и правая единица, то они совпадают.
существуют левая единица и правая единица, то они совпадают.
Нулевой элемент
Определение 5. Если операция  аддитивна, то нейтральный элемент обычно обозначают символом
аддитивна, то нейтральный элемент обычно обозначают символом  и называют нулевым4).
и называют нулевым4).
Пример 2. Нулевой элемент 0 абелевой группы  .
.
См. также
Литература
Наверх
Пусть
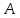
— конечное множество из

элементов:
 .
.
Симметрическая
группа
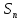
степени
 —
—
группа всех биекций (взаимно-однозначных
отображений)

множества

в себя:
 .
.
Число элементов (подстановок) симметрической
группы:

(число перестановок из
 ).
).
Каждая биекция называется подстановкой
(перестановкой) и записывается (природа
элементов множества

нас не интересует, значит можно считать,
что элементы

— числа):

Во
второй строке записаны номера тех
элементов, которым сопоставляются
элементы из первой строки:
 .
.
Поэтому в написанной матрице столбцы
можно как угодно переставлять, подстановка
останется той же.
Произведение
двух подстановок

и

— результат проведения сначала первой
из них, а затем второй (композиция
отображений):
 .
.
Для
этого представляют столбцы

так, чтобы её первая строка совпадала
со второй строкой
 ;
;
тогда 1-ая строка

есть первая строка
 ,
,
а вторая строка

— есть вторая строка
 .
.
Некоторые
математики иначе определяют произведение
двух подстановок:
 .
.
(Это связано с тем, что произведение
подстановок, по существу, означает
композицию отображений, а математики
не пришли к общему соглашению насчёт
обозначения композиции отображений.)
Соответственно, из-за этого меняется
порядок умножения, в итоге результаты
разнятся. Поэтому необходимо заранее
обозначать композицию так, как
будете её использовать.
Пример.
В данном примере показывается сама суть
умножения подстановок.
Первая
строка первой подстановки «взаимно-однозначно
отображается на» вторую строку второй
подстановки.
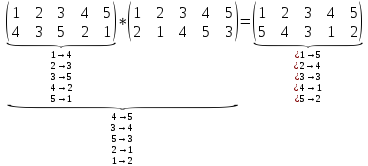
Пример.

Очевидно,
что умножение перестановок ассоциативно,
но не коммутативно.
Нейтральный
элемент — это тождественная подстановка
 .
.
Обратный
к

это
 ,
,
так как
 .
.
Таким
образом, множество подстановок
 -го
-го
порядка — множество, на котором введена
замкнутая ассоциативная бинарная
операция «умножение», на этом множестве
есть нейтральный элемент, и все элементы
этого множества обратимы, следовательно,
множество подстановок образует
мультипликативную группу. Эта группа
называется симметрической группой
степени

и обозначается
 .
.
Очевидно, что это конечная группа, и что
порядок этой группы (число её элементов)
равен
 .
.
Примеры.
-
Запишем все

элементов (подстановок) симметрической
группы
 :
:
 ;
;

-
Найти

и
 :
:


Как
видим
 ,
,
то есть умножение подстановок
некоммутативно.
-
Найти обратную подстановку к

и проверить:


7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа Цикл
Цикл
длины

— симметрическая группа степени
 ,
,
в которой элементы перемещены так, что

(или, что то же самое,
 ),
),
где все числа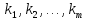
— разные,
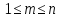 .
.
Цикл обозначается следующим образом:

или

Причём
набор таких элементов

называется

орбитой любого из чисел
 .
.
Цикл
независим, если у него нет общих чисел.
Цикл длины 1 — это, очевидно, тождественная
подстановка
 ;
;
в произведениях подстановок их можно
не записывать.
Теорема.
Любую подстановку в

можно записать в виде произведения
независимых циклов. Разложение подстановки
в произведение циклов длины

определено однозначно с точностью до
порядка циклов.
Доказательство.
Очевидно,
что отношение между числами «принадлежность
одной
 -орбите»
-орбите»
есть отношение эквивалентности:
-
Рефлексивно, то есть
 .
. -
Симметрично, то есть
 .
. -
Транзитивно, то есть
 .
.
Данное
отношение разбивает множество на классы
эквивалентности по этому отношению.
Каждый элемент принадлежит одному и
только одному классу эквивалентности.
Поэтому все числа

однозначно разбиваются на непересекающиеся
классы эквивалентных между собой орбит,
а подстановка

представляется как произведение
соответствующих циклов. Теорема доказана.
Пример.
 .
.
Транспозиция
— подстановка вида
 ,
,
где
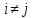 ,
,
сводящаяся к перестановке двух чисел
между собой, или, что тоже самое, цикл
длины 2.
Любой
цикл можно написать в виде произведения
транспозиций:

Замечание.
Транспозиции не коммутируют (как и
перестановки).
Пример.
 .
.
Пример.
 .
.
Пример.
 .
.
Пример.
 .
.
Нетрудно
показать, что любую подстановку можно
представить в виде произведения
транспозиций. Такое представление
не единственно (например, в примерах
выше
 ).
).
Все
подстановки подразделяются на 2 класса:
чётные и нечётные.
Если
в матрице подстановки есть 2 столбца
 ,
,
для которых

и

или
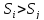
и
 ,
,
то такая пара столбцов называется
инверсией подстановки.
Подстановка
называется чётной или нечётной в
зависимости от того, чётно или нечётно
число инверсий в ней.
Очевидно,
что любая транспозиция является
нечётной подстановкой:

одна инверсия

нечётная
Теорема.
Если подстановка чётная, то при любом
способе разложения её в произведение
транспозиций число множителей (то есть
транспозиций) чётно, а если нечётная —
то число этих транспозиций нечётно.
Следствие.
Так как при перемножении чётных
подстановок, очевидно, снова получается
чётная подстановка, то множество всех
чётных подстановок является подгруппой
симметрической группы

и называется знакопеременной группой
и обозначается
 .
.
Причём порядок

равен
 .
.

состоит из одной подстановки:
 .
.
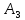
состоит из

подстановок и т. д.
Пример.
Подгруппа

симметрической группы

состоит из 3-х подстановок:

Произведение
двух нечётных подстановок, очевидно,
есть чётная подстановка, поэтому нечётные
подстановки не образуют группу.
Порядок
подстановки — это наименьшее целое
положительное число

такое, что
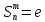 .
.
Пример.
Докажем, что порядок подстановки
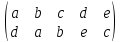
равен 5:


Теорема.
Порядок подстановки равен НОК длин всех
её независимых циклов.
Также
нетрудно показать, что порядок цикла
равен длине цикла.
Пример.
Определить, является ли подстановка
чётной или нечётной и разложить её в
произведение транспозиций:

Сосчитаем
число инверсий
 .
.
Инверсии — это пары столбцов
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Поэтому
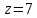
(подстановка нечётная).
Разложим
её на циклы:

Как
видим, число транспозиций в произведении
равно 5, то есть нечётно.
Обратная
операция:
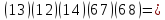





добавлена в середину только потому, что
она равна
 .
.
Другие подстановки (не равные
 )
)
в любое место добавлять нельзя, так как
коммутативности нет.
Порядок
подстановки:
 .
.
То есть
 .
.
Проверим это.


