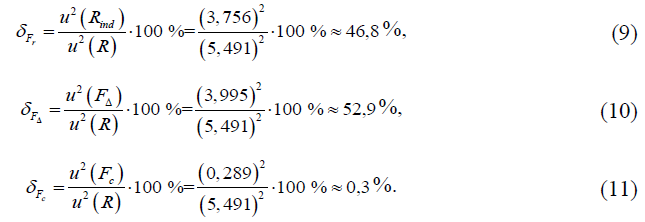Как найти неопределенность измерений

Неопределенность измерений в метрологии

• Неопределенность измерения – история возникновения.
• Термины используемые при расчете неопределенности.
• Оценка результата измерений в терминах «погрешность измерений».
• Оценка результата измерений в терминах «неопределенность измерений».
• Расчёт неопределённости с применением приборов.
• Выводы.

Определения погрешности и неопределенности измерений.

Погрешность измерения – это отклонение измеренного значения величины от ее «истинного» значения. По своей природе или характеру проявления погрешность может быть «случайной» и «систематической». Метод выражения погрешности измерений – а ± Δа, где а – измеренная величина, Δа – суммарная абсолютная погрешность, определяемая методикой выполнения измерений.
Неопределенность измерения – это «сомнения в истинности полученного результата». Т.е. параметр, связанный с результатом измерения, характеризующий разброс значений, которые могли бы быть обосновано приписаны к измеряемой величине. Метод выражения неопределенности – а ± U_а , где а – измеренная величина, U_а – расширенная неопределенность, определяемая измерителем.

История возникновения термина “неопределенность измерений”.

Сразу заметим, что, по сути, оба термина – «погрешность» и «неопределенность» – это выражение в разных терминах, одного и того же понятия – «точность измерений».
В России исторически сложилось так, что при оценке достоверности произведенного измерения использовали погрешность.
За рубежом исходно существовало понятие «error of measurement» – «ошибка измерения». Одной из целей при разработке стандарта качества ISO 9000 было обеспечение безошибочного выполнения всех производственных функций. В рамках ISO 9000 было разработано «Руководство по вычислению неопределенности в измерении» – «Guide to the expression of uncertainty in measurement», в котором описано понятие неопределенности измерений и способы ее вычисления.
Сейчас все чаще требуется оценивать точность проведения измерений (например, такое требование предъявляется при аккредитации лабораторий) в терминах «неопределенности». В связи с вступлением России в ВТО, принято решение перевести правила проведения и оценки качества работ (в том числе и метрологических) в соответствие с международными стандартами ИСО. Все измерительные лаборатории стран-членов ВТО должны оценивать точность результатов измерений в терминах неопределенности. В России о необходимости расчета неопределенности измерений в соответствии с ГОСТ Р ИСО 10576-1-2006 говорится в письме Роспотребнадзора 01/6620-12-32 от 13.06.2012.
«Неопределенность измерений стоило выдумать хотя бы для того, чтобы теперь разъяснять, чем погрешность отличается от неопределенности». Понятие «uncertainty» возникло из дословного перевода документа «Guide to the expression of uncertainty in measurement», ISO-1993. Документ вызвал множество споров и разделил общественность на три лагеря – сторонники «Guide…», противники «Guide…» и специалисты-практики, ожидающие «чем все это закончится».
В итоге, «все закончилось тем», что был выпущен документ РМГ 91-2009 «Совместное использование понятий «погрешность измерения» и «неопределенность измерения» детально разъясняющий соответствие терминов «погрешность» и «неопределенность».

Термины используемые при расчете неопределенности.

Соотношение терминов теории неопределенности с терминами классической теории точности (в скобках):

• Неопределенность результата измерения (погрешность результата измерения),
• Неопределенность типа А (случайная погрешность),
• Неопределенность типа Б (систематическая погрешность),
• Стандартная неопределенность (стандартное отклонение погрешности) результата измерения,
• Расширенная неопределенность (доверительные границы) результата измерения,
• Вероятность охвата, вероятность покрытия (доверительная вероятность),
• Коэффициент охвата, коэффициент покрытия (коэффициент распределения погрешности) 

Подробно о типах определённости и их расчётах рассказано в статье «Понятие и типы неопределенностей. ГОСТ 34100.3-2017»

Оценка результата измерений в терминах «погрешность измерений».

Как уже упоминалось выше, термин «погрешность» привязан к истинному значению измеряемой величины. Однако, это исходное «истинное значение» неизвестно. И при проведении измерений указывают интервал, в котором это «истинное значение» находится с определенным уровнем вероятности – Х = А ± Δ , Р = 0,95 (где Р – доверительная вероятность).
То есть, интервал от (А – Δ) до (А + Δ) с вероятностью Р содержит в себе:
1) «истинное» значение измеряемой величины.
2) погрешность измерений величины

Рис.1.  Диапазон возможных значений при погрешности

Оценка результата измерений в терминах «неопределенность измерений».

Термин «неопределенность» привязан к измеренному значению величины А, а не к ее абстрактному «истинному» значению. Также, как для «погрешности», результат измерения записывается в виде интервала Х = А ± Δ , Р = 0,95 (Р – вероятность охвата).
То есть, интервал от (A – U) до (A + U) содержит бОльшую долю ( Р ) значений, которые могли бы быть приписаны к измеряемой величине.

Рис.2.  Диапазон возможных значений при неопределенности

При оценке точности измерений в терминах “неопределенности” считается, что измеренная величина принадлежит к указанному интервалу значений (например, диапазон оптимальных или допустимых уровней), если она с учетом указанной неопределенности («величина – неопределенность» и «величина + неопределенность») не выходит за пределы этого диапазона.

Рис.3. Интервал значений при расчете неопределенности

Расчёт неопределённости с применением приборов.

В следующей статье “Расчет неопределенности результатов измерений | пример для люксметра “еЛайт”” мы рассмотрим практический пример как вручную вычислить неопределенность измерений освещенности, используя люксметр-пульсметр-яркомер еЛайт02. В некоторых современных приборах такой расчёт неопределённости уже осуществляется автоматически, как, например, в самом доступном люксметре с поверкой еЛайт-мини.

Рис.4. Профессиональный измеритель освещённости еЛайт01 с функцией автоматического расчёта неопределённости измерений.

Рис.5. Термоанемометр-гигрометр-барометр ЭкоТерма Максима 01 с функцией автоматического расчёта неопределённости измерений.

Выводы.

Отличие понятия «погрешности» от «неопределенности»:

• «погрешность» привязана к некоторому «истинному» значению, которое точно неизвестно;
• «неопределенность» привязана к измеренному значению;
• «погрешность» относится к конкретному измерению, сделанному конкретным средством измерения;
• «неопределенность» – это степень сомнения в истинности полученного результата измерения;
• «погрешностью» характеризуются параметры точности средств измерений.

Примеры расчета неопределенности измерений

Оценивание неопределенности измерений (количественных величин) – одна из важных задач, стоящих перед каждой лабораторией. Требование к оцениванию неопределенности измерений заложено в межгосударственном стандарте ГОСТ ISO/IEC 17025-2019, а также политике ILAC-G17:2002.

Чтобы получить предварительную информацию по теме Неопределенность измерений, посмотрите, пожалуйста, наше обучающее видео:

Международное метрологическое сообщество давно уже разработало и приняло основные принципы концепции неопределенности, закрепив их в серии международных документов JCGM (Joint Committee for Guides in Metrology), а также документах ISO/IEC Guide 98. Разработано много дополнительных руководств по различных подходам оценивания неопределенности измерений в конкретных областях испытаний/измерений (EA, EURACHEM, Nordtest, EUROLAB и т.д.).

---

---

Несмотря на хорошо разработанные и представленные в документах свободного доступа теоретические принципы и подходы оценивания, и даже наличия конкретных примеров, у специалистов лабораторий все еще остаются вопросы по практической реализации этих принципов и подходов для измерений, проводимых в их лаборатории.

С целью наглядного представления основных принципов концепции неопределенности измерений и подхода моделирования предлагаем Вашему вниманию решение нескольких несложных, но часто встречающейся в практике многих испытательных лабораторий, задач:

---

Пример 1. Оценивание неопределенности измерений массовой доли влаги

---

Пример 2. Оценивание неопределенности измерений сопротивления изоляции

---

Пример 3. Оценивание неопределенности измерений коэффициента поправки титрованного раствора

---

Пример 4. Оценивание неопределенности измерений pH воды

---

Пример 5. Оценивание неопределенности измерений относительного удлинения эластичного герметика

---

Пример 6. Оценивание неопределенности измерений прочности бетона на растяжение при изгибе

---

Пример 7. Оценивание неопределенности измерений твердости по Бриннелю

---

---

Пример 1. Оценивание неопределенности измерений массовой доли влаги

---

Исходные данные:

1. Объект измерений – углекислый барий
2. Измеряемая величина – массовая доля влаги
3. Единицы измерений – процент (%)
4. Методика выполнения измерения – ГОСТ 2149-75 «Барий углекислый технический. Технические условия»
5. Метод измерений – метод высушивания пробы до постоянной массы

Этап 1. Составление функции измерений

Функция измерений для измеряемой величины составляется на основании принципа измерений, заложенного в методе измерений, и описанного для реализации в методике выполнения измерений.

Массовую долю влаги бария углекислого Х в процентах вычисляют на основании ГОСТ 2149 (п.3.5) в соответствии с функцией измерений:

где Х_i – массовая доля влаги i-ой пробы углекислого бария, %;

m₁ – масса стаканчика для взвешивания с навеской до высушивания, г;

m₂ – масса стаканчика для взвешивания с навеской после высушивания, г;

m – масса навески углекислого бария, г;

m_cт – масса стаканчика для взвешивания, г;

i – номер параллельной пробы, i = 1, 2;

F – поправочный множитель, учитывающий допускаемое расхождение между параллельными определениями.

Этап 2. Анализ входных величин

1) Масса стаканчика для взвешивания с навеской до высушивания, m₁

Масса стаканчика для взвешивания с навеской до высушивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:

• для первой пробы m₁₍₁₎ = 41,0055 г,
• для второй пробы m₁₍₂₎ = 41,3842 г.

Неопределенность, связанную с величиной m₁, оцениваем, используя данные производителя на весы. В паспорте на весы лабораторные AV264C для диапазона измерений до 50 г указаны пределы погрешности взвешивания ± 0,001 г. Поскольку значение дано без доверительной вероятности, принимаем прямоугольное распределение значений погрешности взвешивания в этих границах. Стандартная неопределенность массы стаканчика для взвешивания с навеской до высушивания m₁ оценивается по типу В и составляет:

2) Масса стаканчика для взвешивания, m_cт

Масса стаканчика для взвешивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:

• для первой пробы m_ст(1) = 21,0034 г,
• для второй пробы m_ст(2) = 21,3822 г.

Неопределенность массы стаканчика для взвешивания после высушивания обусловлена двумя факторами:

• погрешностью взвешивания стаканчика на весах;
• возможными отклонениями массы стаканчика после высушивания вследствие нечеткого определения в методике выполнения измерений момента, в который масса стаканчика после высушивания будет являться постоянной величиной.

Стандартная неопределенность u₁(m_cт), связанная с погрешностью взвешивания, оценивается на основании данных производителя на весы лабораторные AV264C, определяется аналогично неопределенности величины m₁ и составляет u₁(m_cт) = 0,00058 г.

Стандартную неопределенность u₂(m_cт), обусловленную отклонениями массы стаканчика для взвешивания после высушивания, можно определить на основании информации о том, что разность между двумя последующими взвешиваниями стаканчика для взвешивания после сушки не должна превышать 0,002 г (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает момент, в который масса стаканчика после высушивания будет являться постоянной величиной). Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u₂(m_cт) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:

Суммарную стандартную неопределенность величины mcт находим путем суммирования квадратов стандартных неопределенностей перечисленных выше двух вкладов:

3) Масса стаканчика для взвешивания с навеской после высушивания, m₂

Масса стаканчика для взвешивания с навеской после высушивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:

• для первой пробы m₂₍₁₎ = 40,9850 г,
• для второй пробы m₂₍₂₎ = 41,3638 г.

Неопределенность массы стаканчика для взвешивания с навеской после высушивания обусловлена двумя факторами:

• погрешностью взвешивания пробы на весах;
• возможными отклонениями массы пробы после высушивания вследствие нечеткого определения в методе испытаний момента, в который масса пробы после высушивания будет являться постоянной величиной.

Стандартная неопределенность u₁(m₂), связанная с погрешностью взвешивания, оценивается на основании данных производителя на весы лабораторные AV264C, определяется аналогично неопределенности величины m₂ и составляет u₁(m₂) = 0,00058 г.

Стандартную неопределенность u₂(m₂), обусловленную отклонениями массы стаканчика для взвешивания с навеской после высушивания, можно определить на основании информации о том, что разность между двумя последующими взвешиваниями стаканчика для взвешивания с навеской пробы бария углекислого после сушки не должна превышать 0,002 г (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает момент, в который масса пробы после высушивания будет являться постоянной величиной). Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u₂(m₂) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:

Суммарную стандартную неопределенность величины m₂ находим путем суммирования квадратов стандартных неопределенностей перечисленных выше двух вкладов:

4) Поправочный множитель, учитывающий допускаемое расхождение между параллельными определениями, F

Значение оценки величины принимается равным единице: F = 1.

Стандартная неопределенность поправочного множителя рассчитывается на основании информации о допускаемом расхождении между параллельными определениями влажности, приведенными в ГОСТ 2149-75 (п.3.5.2). Приведенное допускаемое относительное расхождение составляет r = 20 % и рассматривается как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения. Стандартная неопределенность поправочного множителя будет равна стандартному отклонению, рассчитанному на основании указанного интервала, с учетом того, что за результат измерения принимают среднее арифметические определений двух параллельных проб, по типу В по формуле:

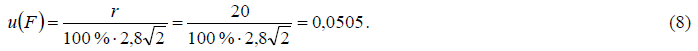
Этап 3. Анализ корреляций

Все входные величины рассматриваются как некоррелированные, поскольку получены независимо друг от друга в различных экспериментах.

Этап 4. Измеренное значение величины

Массовая доля влаги i-ой пробы углекислого бария рассчитывается по формуле (2):

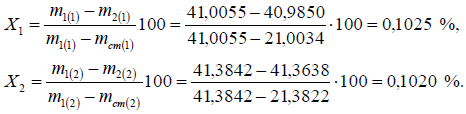
Расхождение между результатами измерений двух параллельных проб не превышает допускаемого значения, установленного в ГОСТ 2149-75 (п.3.5.2):

Массовая доля влаги бария углекислого Х в процентах вычисляется в соответствии с функцией измерений (1):

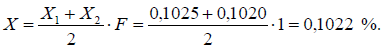
Измеренное значение (оценку измеряемой величины) округляют до четырех знаков после запятой (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает требования к округлению результата измерения).

Этап 5. Суммарная стандартная неопределенность

Стандартную неопределенность измеряемой величины Х получаем по закону распространения неопределенностей путем суммирования квадратов произведений стандартных неопределенностей всех влияющих величин, входящих в функции измерений (1) и (2), на соответствующие коэффициенты чувствительности:

где коэффициенты чувствительности рассчитываются как частные производные функции измерений по входным величинам:

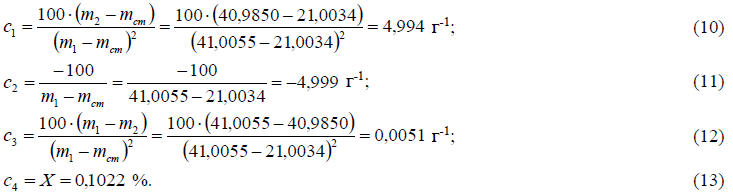
Примечание – Для вычисления коэффициентов чувствительности можно использовать либо минимальные значения масс, полученные при измерении массовой доли влаги i-ой пробы бария углекислого, либо результаты измерений масс, полученные на определенной пробе бария углекислого. В данном примере коэффициенты чувствительности рассчитываются на основании результатов измерений масс для первой пробы.

Суммарная стандартная неопределенность составит

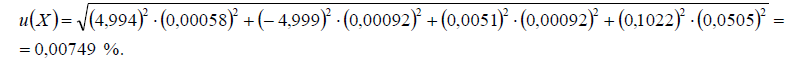
Этап 6. Бюджет неопределенности

В таблице представлен бюджет неопределенности для измеряемой величины.

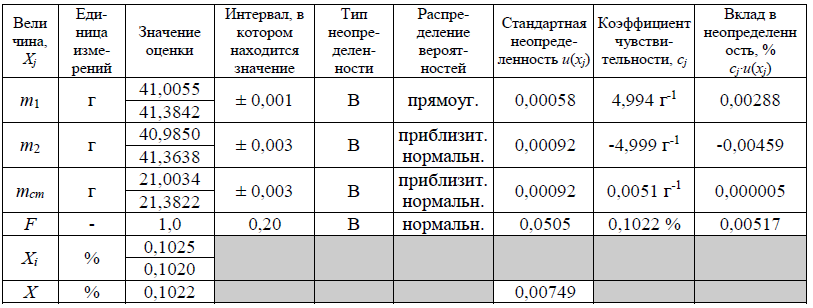
Вклад в неопределенность от j-ой входной величины рассчитывается как произведение стандартной неопределенности этой величины на соответствующий коэффициент чувствительности.

Этап 7. Расширенная неопределенность

Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k, который выбирается равным 2 при уровне доверия приблизительно 95 % в предположении нормального распределения вероятностей измеряемой величины:

Этап 8. Представление результата измерения

Результат измерения массовой доли влаги углекислого бария представляют в виде:

«Массовая доля влаги бария углекислого составила (0,1022 ± 0,0150) %, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %».

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, рекомендуем посетить наш семинар по данной теме, где вы сможете найти ответы на свои вопросы, а также пообщаться с лектором.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

---

---

Пример 2. Оценивание неопределенности измерений сопротивления изоляции

---

Исходные данные:

1. Объект измерений – кабель силовой АВБбШв
2. Измеряемая величина – сопротивления изоляции
3. Единицы измерений – МОм
4. Измерение сопротивления изоляции выполняется методом непосредственной оценки с помощью мегаомметра Е6-24

Измерения проведены в диапазоне измерений мегаомметра Е6-24 от 100 до 999 МОм при температуре окружающего воздуха 22 °С и относительной влажности воздуха 65 %.

Этап 1. Составление функции измерений

Сопротивление изоляции определяется в соответствии со следующей функцией измерений

где R – сопротивление изоляции, МОм;

R_ind – среднее арифметическое повторных измерений сопротивления изоляции, МОм;

F_Δ – поправка, учитывающая допускаемую основную погрешность измерения сопротивления мегаомметра Е6-24, МОм;

F_с – поправка, учитывающая единицу младшего разряда, выдаваемых мегаомметром Е6-24 показаний сопротивления, МОм.

Примечание – В функции измерений не учитываются поправки F_Δt и F_Δφ на дополнительные погрешности измерения сопротивления мегаомметра Е6-24, вызванные отклонением соответственно температуры и влажности окружающей среды от нормальных условий в рабочем диапазоне. Поправки будут вводиться только в случае, если измеренные значения температуры и/или относительной влажности окружающей среды находятся в рабочем диапазоне, но выходят за диапазон нормальных условий эксплуатации мегаомметра Е6-24 (значения нормальных и рабочих условий эксплуатации указаны в руководстве по эксплуатации мегаомметра Е6-24).

Этап 2. Анализ входных величин

1) Среднее арифметическое повторных измерений сопротивления изоляции R_ind, МОм.

При проведении измерений сопротивления изоляции кабеля силового АВБбШв получены следующие результаты повторных измерений: R₁ = 124 МОм; R₂ = 131 МОм; R₃ = 137 МОм.

Значение оценки величины R_ind определяется по формуле

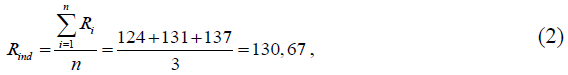
где R_i – результат i-го повторного измерения сопротивления изоляции, определяемый как показание, снимаемое с дисплея мегаомметра Е6-24, МОм;

n – количество повторных измерений, n = 3.

Стандартная неопределенность измерений величины R_ind, МОм, рассчитывается в предположении нормального распределения вероятностей по формуле

2) Поправка, учитывающая допускаемую основную погрешность измерения сопротивления мегаомметра Е6-24, F_Δ

Значение оценки величины F_Δ принимается равным 0,0 МОм.

Стандартная неопределенность u(F_Δ), МОм, оценивается на основании информации о пределах допускаемой основной абсолютной погрешности измерения сопротивления мегаомметра Е6-24 ± Δ, МОм. В предположении прямоугольного распределения вероятностей значений погрешности в границах ± Δ определяется по формуле

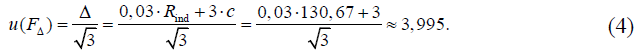
Примечание — согласно [1] пределы допускаемой основной погрешности измерения сопротивления приведены в виде ± (% + е.м.р.) т. е. для получения пределов абсолютной погрешности измерения Δ нужно воспользоваться формулой

где δ» – допускаемая относительная погрешность измерения сопротивления, которая принимается равной первому числу, стоящему в [1] в записи пределов допускаемой основной погрешности измерения сопротивления, %;

100 – коэффициент перехода от долей к процентам, %;

m – второе число стоящее в [1] в записи пределов допускаемой основной погрешности измерения сопротивления, определяющее количество единиц младшего разряда;

с – единица младшего разряда выдаваемого мегаомметром Е6-24 показания сопротивления, МОм.

3) Поправка, учитывающая единицу младшего разряда выдаваемых мегаомметром Е6-24 показаний сопротивления, Fс

Значение оценки величины F_c принимается равным 0,0 МОм.

Стандартная неопределенность u(F_c), МОм, определяется на основании информации о единице младшего разряда выдаваемого мегаомметром Е6-24 показания сопротивления c = 1 МОм (для диапазона измерений мегаомметра Е6-24 от 100 до 999 МОм). В предположении прямоугольного распределения вероятностей значений величины c в границах ± c/2 определяется по формуле

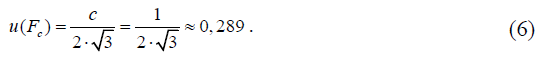
Этап 3. Анализ корреляций

Все величины, входящие в функцию измерений (1), рассматриваются как некоррелированные.

Этап 4. Оценка измеряемой величины

Значение оценки величины R, МОм, «сопротивление изоляции» рассчитывается по формуле (1)

Значение сопротивления изоляции (МОм) округляют до одного знака после запятой.

Этап 5. Суммарная стандартная неопределенность

Суммарная стандартная неопределенность измерений сопротивления изоляции силового кабеля u(R), МОм, определяется по формуле

Процентные вклады неопределенностей влияющих величин в суммарную стандартную неопределенность u(R) определяются по формулам

Этап 6. Бюджет неопределенности

Бюджет неопределенности измерений сопротивления изоляции силового кабеля представлен в таблице 1.

Таблица 1 – Бюджет неопределенности измерений сопротивления изоляции силового кабеля

Этап 7. Расширенная неопределенность

Расширенная неопределенность измерений сопротивления изоляции силового кабеля U(R), МОм, определяется для вероятности 95 % в предположении распределения Стьюдента по формуле

где коэффициент охвата k = 2,26, выбирается в зависимости от числа эффективных степеней свободы v_eff, которое рассчитывается по формуле

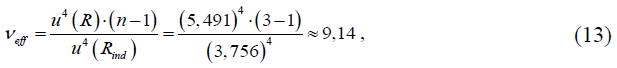
Этап 8. Результат измерения

Сопротивление изоляции силового кабеля АВБбШв составило

(130,7 ± 12,5) МОм (k = 2,26, v_eff = 9,14, Р = 95 %).

Библиография

[1] РЛПА 411218.001 РЭ Руководство по эксплуатации. Мегаомметры Е6-24, E6-24/1 и E6-24/2.

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, рекомендуем посетить наш семинар по данной теме, где вы сможете найти ответы на свои вопросы, а также пообщаться с лектором.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

---

---

Пример 3. Оценивание неопределенности измерений коэффициента поправки титрованного раствора

---

Исходные данные:

1. Объект измерений – раствор серной кислоты концентрации моль/дм3
2. Измеряемая величина – коэффициента поправки 0,1 моль/дм3 раствора серной кислоты
3. Единицы измерений – безразмерная величина
4. Методика измерений – ГОСТ 25794.1 83 «Реактивы. Методы приготовления титрованных растворов для кислотно-основного титрования»
5. Метод измерений – титриметрический по безводному углекислому натрию

Этап 1. Составление функции измерений

Значение оценки коэффициента поправки 0,1 моль/дм3 раствора серной кислоты Ki, при единичном определении рассчитывается по формуле:

где m – масса навески безводного углекислого натрия, г;

P – чистота реактива безводного углекислого натрия, P = 1;

M – молярная масса эквивалента безводного углекислого натрия, г/моль;

с – заданная молярная концентрация серной кислоты в 0,1 моль/дм³ растворе серной кислоты, с = 0,1 моль/дм³, рассматривается как постоянная и не учитывается при расчете неопределенности измерений коэффициента K;

V – объем 0,1 моль/дм³ раствора серной кислоты, израсходованный на титрование, см³.

1000 – коэффициент перехода единицы измерения объема см³ в дм³.

Значение оценки коэффициента K вычисляется как среднее арифметическое трех повторных определений коэффициента поправки раствора серной кислоты по формуле:

где F – поправочный коэффициент, учитывающий расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, F = 1.

Расхождение между результатами трех повторных определений коэффициента поправки раствора серной кислоты не должно превышать значения 0,001, установленного ГОСТ 25794.1 (п. 1.11).

Этап 2. Анализ входных величин

2.1 Масса навески безводного углекислого натрия, m

Значение массы навески безводного углекислого натрия, m, г, определяется как разность показаний весов при взвешивании стаканчика с навеской установочного вещества и пустого стаканчика. При выполнении измерения были получены следующие значения выходной величины для трех повторных определений коэффициента поправки: m₁ = 0,1648 г; m₂ = 0,1643 г; m₃ = 0,1649 г.

Стандартная неопределенность измерений массы навески установочного вещества, u(m), г, оценивается на основании информации о пределах допускаемой погрешности используемых весов ВСЛ-200/0,1А ± Δm = ± 0,001 г в диапазоне измерений от 0,01 до 50 г, и дискретности отсчета весов d = 0,0001 г, установленных в технической документации на весы. В предположении прямоугольного распределения вероятностей значений погрешности и дискретности в границах ± Δm и ± d/2 соответственно и учитывая двойное взвешивание (пустого стаканчика и стаканчика с навеской установочного вещества) стандартная неопределенность u(m) рассчитывается по формуле:

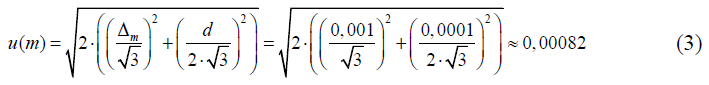
2.2 Чистота реактива безводного углекислого натрия, P

Значение оценки величины P принимается равным 1.

Стандартная неопределенность измерений степени чистоты реактива углекислого натрия u(P) оценивается на основании информации о том, что согласно ГОСТ 83-79 «Реактивы. Натрий углекислый. Технические условия» массовая доля углекислого натрия в реактиве безводного углекислого натрия составляет не менее 99,8 %. Неопределенность измерений u(P) рассчитывается исходя из отклонения значения чистоты реактива от 1 в предположении прямоугольного распределения величины Р в границах ± (1 – 0,998) по формуле:

2.3 Молярная масса эквивалента безводного углекислого натрия, M

Значение оценки величины M, г/моль, определяется как произведение фактора эквивалентности безводного углекислого натрия f_э = 1/2 на молярную массу установочного вещества M₀, г/моль, по формуле:

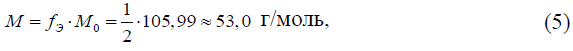
где молярная масса безводного углекислого натрия (Na2CO3) рассчитывается на основании значений атомных масс натрия, углерода и кислорода A, взятых из таблиц атомных масс IUPAC (//www.sbcs.qmul.ac.uk/iupac/AtWt/), и количества атомов этих элементов в молекуле безводного углекислого натрия n (A_Na ≈ 22,98976928, A_с = 12,011, A₀ = 15,999, n_Na= 2, n_с = 1, n₀ = 3):

Стандартная неопределенность измерений молярной массы эквивалента безводного углекислого натрия, u(M), г/моль, определяется на основании возможных разбросов значений атомных масс углерода и кислорода ΔА = A_max – A_min и неопределенности последней цифры атомной массы натрия ΔA, а также количества атомов этих элементов в молекуле безводного углекислого натрия n. Данные по разбросам значений атомных масс углерода и кислорода и неопределенности последней цифры атомной массы натрия выбираются из таблиц атомных масс IUPAC (//www.sbcs.qmul.ac.uk/iupac/AtWt/). Стандартная неопределенность значений атомных масс химических элементов рассчитывается в предположении прямоугольного распределения вероятностей атомных масс элементов в границах ± ΔА/2 (для углерода и кислорода) и в границах ± ΔA (для натрия). Неопределенность для вклада атомов одного элемента рассчитывается умножением стандартной неопределенности атомной массы элемента на количество атомов элемента. Стандартная неопределенность измерений молярной массы эквивалента безводного углекислого натрия, u(M), г/моль, определяется по формуле:

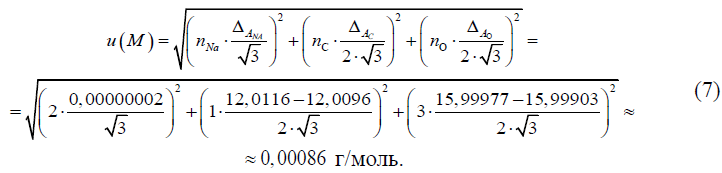
2.4 Объем раствора серной кислоты, израсходованный на титрование, V

Значение оценки величины V, см³, определяется по шкале бюретки номинальной вместимостью 25 см3 2-го класса точности по ГОСТ 29251-91 «Посуда лабораторная стеклянная. Бюретки. Часть 1. Общие требования». При выполнении измерения были получены следующие значения выходной величины для трех повторных определений коэффициента поправки: V₁= 31,1 см³; V₂= 31,0  см³; V₃= 31,1 см³.

Стандартная неопределенность измерений объема 0,1 моль/дм³ раствора серной кислоты, израсходованного на титрование, u(V), см³, состоит из следующих основных вкладов:

• стандартная неопределенность, обусловленная погрешностью измерения объема сливаемой жидкости используемой бюретки, u(V_Δ), см³;
• стандартная неопределенность, обусловленная ценой наименьшего деления шкалы используемой бюретки, u(V_c), см³;
• стандартная неопределенность, обусловленная отличием температуры, при которой проводятся измерения, от температуры, при которой нормируется погрешность измерения объема сливаемой жидкости бюретки, u(V_t), см3.

Стандартная неопределенность u(V_Δ), см3, рассчитывается на основании информации о пределах погрешности измерения сливаемой жидкости бюреткой ± ΔV = 0,1 см³, установленных ГОСТ 29251 в предположении треугольного распределения погрешности в установленных пределах по формуле:

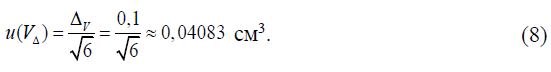
Стандартная неопределенность u(V_c), см3, рассчитывается на основании информации о цене наименьшего деления шкалы используемой бюретки см3, в предположении прямоугольного распределения вероятностей цены деления в пределах ± dV/2 по формуле:

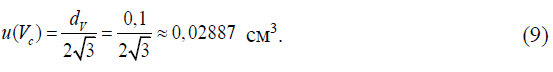
Стандартная неопределенность u(V_t), см3, рассчитывается в предположении прямоугольного распределения исходя из возможных пределов изменения объема жидкости при условии колебания температуры в лаборатории при измерении в пределах (20 ± 5) °С (Δt = 5 °С) и коэффициента объемного расширения жидкости kV, ºС^-1, равного 0,00021 ºС^-1 для воды (основное вещество в растворе) по формуле:

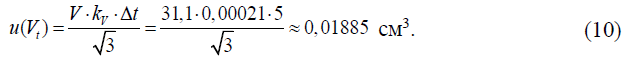
Примечание – Для оценивания стандартной неопределенности u(V_t) используется измеренное значение объема раствора серной кислоты, пошедшего на титрование, полученное для первой навески безводного углекислого натрия.

Суммарная стандартная неопределенность измерений объема 0,1 моль/дм³ раствора серной кислоты, израсходованного на титрование, u(V), см³ вычисляется путем суммирования стандартных неопределенностей перечисленных выше вкладов по формуле:

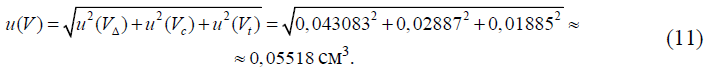
2.5 Поправочный коэффициент, учитывающий расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, F

Значение оценки величины F принимается равным 1.

Стандартная неопределенность измерений поправочного коэффициента, учитывающего расхождение между результатами повторных определений коэффициента поправки раствора серной кислоты, u(F), определяется на основании установленного ГОСТ 25794.1 (п. 1.11) допускаемого расхождения между результатами повторных определений коэффициента поправки r = 0,001, которое рассматривается как предел повторяемости согласно СТБ ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике». С учетом того, что за результат измерения принимается среднее арифметическое трех определений, стандартная неопределенность u(F) определяется по формуле:

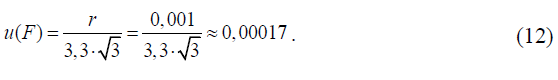
Этап 3. Анализ корреляций

Все входные величины рассматриваются как некоррелированные, поскольку получены независимо друг от друга в различных экспериментах.

Этап 4. Оценка измеряемой величины

Значения коэффициента поправки раствора серной кислоты при i-ом определении согласно формуле (1) составляют:

Максимальное расхождение между результатами трех определений не превышает допускаемого значения, установленного ГОСТ 25794.1:
Значение коэффициента поправки раствора серной кислоты определяется по формуле (2) на основании результатов параллельных определений, которые рассчитываются по формуле (1):

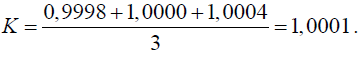
Коэффициент поправки вычисляют с точностью до четвертого десятичного знака. Полученное значение коэффициента поправки раствора серной кислоты удовлетворяет требованию ГОСТ 25794.1 (п. 1.11) о том, что значение коэффициента поправки должно соответствовать диапазону .

Этап 5. Суммарная стандартная неопределенность

Суммарная стандартная неопределенность измерений коэффициента поправки K определяется по закону распространения неопределенностей путем суммирования относительных стандартных неопределенностей всех влияющих величин, входящих в функции измерений (1) и (2), по формуле:

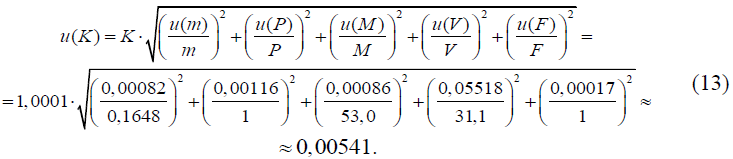
Примечание — Для оценивания суммарной стандартной неопределенности u(K) используются значения оценок влияющих величин (измеренные значения), полученные для первой навески безводного углекислого натрия.

Значения относительных стандартных неопределенностей влияющих величин рассчитываются как отношение стандартной неопределенности влияющей величины к значению оценки влияющей величины.

Значения процентных вкладов неопределенностей влияющих величин в суммарную стандартную неопределенность рассчитываются как умноженное на 100 % отношение квадрата относительной стандартной неопределенности влияющей величины к квадрату относительной суммарной стандартной неопределенности.

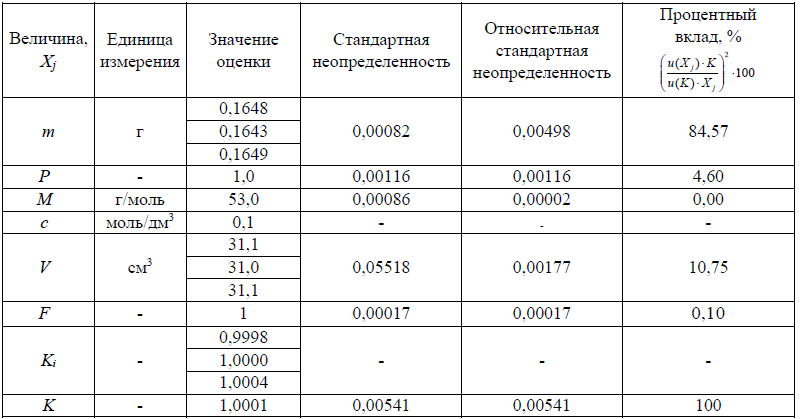
Этап 6. Бюджет неопределенности

В таблице представлен бюджет неопределенности измерений коэффициента поправки серной кислоты.

Этап 7. Расширенная неопределенность

Расширенная неопределенность измерений коэффициента поправки серной кислоты, U(K), получается умножением суммарной стандартной неопределенности, u(K), на коэффициент охвата k, который выбирается равным 2 при уровне доверия приблизительно 95 % в предположении нормального распределения вероятностей измеряемой величины:

Этап 8. Результат измерения

Коэффициент поправки раствора серной кислоты концентрации c(H₂SO₄) = 0,1 моль/дм³ составляет (1,0001 ± 0,0108), где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %.

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, рекомендуем посетить наш семинар по данной теме, где вы сможете найти ответы на свои вопросы, а также пообщаться с лектором.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

---

---

Пример 4. Оценивание неопределенности измерений pH воды

---

Измерительная задача

Метод основан на измерении разности потенциалов гальванического элемента с использованием соответствующего рН-метра. Измерения проводят рН-метром/иономером ИТАН. Перед измерением пробы воды про-водится двухточечная калибровка по буферным растворам. Температура пробы питьевой воды и температура буферных растворов измеряется термодатчиком, встроенным в рН-метр. рН-метр автоматически учитывает разность температур буферных растворов и пробы питьевой воды в выдаваемых показаниях.

Этап 1. Составление функции измерений

Измеряемой величиной является рН пробы питьевой воды, ед. рН, которая определяется согласно функции измерений:

где рНизм – показания рН-метра, ед. рН;
δкал – поправка на погрешность калибровки рН-метра, ед. рН;
δсх – поправка на повторяемость измерений, ед. рН.
Измеренное значение величины округляют до одного десятичного знака.

Результаты измерений

Температура пробы питьевой воды, измеренная термодатчиком рН-метра, составила 10 °С. При измерении пробы питьевой воды с цифрового дисплея рН-метра было снято показание рН равное 6,52 ед. рН.

Этап 2. Анализ входных величин

2.1 Показания рН-метра (рНизм)

Показание рН-метра составило рНизм = 6,52 ед. рН.
Стандартная неопределенность величины рНизм рассчитывается на основании информации о пределах основной допускаемой абсолютной погрешности рН-метра в предположении прямоугольного распределения вероятностей. В паспорте на рН-метр/иономер ИТАН указаны пределы основной допускаемой абсолютной погрешности измерения рН (измерительным преобразователем в комплекте с электродной системой в растворах с температурой от 10 °С до 60 °С) ± Δ = ± 0,050 ед. рН. Стандартная неопределенность величины рНизм рассчитывается по формуле:

Примечание – Неопределенностью измерений, обусловленной разрешающей способностью цифрового дисплея рН-метра пренебрегаем, поскольку данная составляющая неопределенности значительно ниже составляющей, обусловленной основной допускаемой абсолютной погрешностью рН-метра.

2.2 Поправка на погрешность калибровки рН-метра (δкал)

Поправка на погрешность калибровки рН-метра оценивается значением «нуль»
δкал = 0 ед. рН.
Стандартная неопределенность измерений величины δкал рассчитывается на основании информации о допускаемом отклонении значений рН, при проверке калибровки, от значений рН буферных растворов в контрольных точках ± Δк = ± 0,03 ед. рН. Стандартная неопределенность величины δкал рассчитывается в предположении прямо-угольного распределения вероятностей в указанных границах по формуле:

Примечание – Неопределенностью измерений рН буферных растворов пренебрегаем, т.к. значения расширенных неопределенностей измерений рН буферных растворов не превышают 1/3 от допускаемого отклонения Δк.

2.3 Поправка на повторяемость измерений (δсх)

Поправка на повторяемость измерений рН оценивается значением «нуль» δсх = 0 ед. рН.
Стандартная неопределенность измерений величины δсх рассчитывается на основании информации о стандартном отклонении повторяемости в предположении нормального распределения вероятностей. Для питьевой воды в диапазоне рН от 6,35 до 6,46 ед. рН при межлабораторном исследовании метода измерений рН было установлено значение стандартного отклонения повторяемости σr = 0,011 ед. рН. В лаборатории при внедрении метода измерений установленное значение показателя повторяемости было подтверждено и распространено на диапазон измерений, содержащий измеренное значение рН в исследуемой пробе питьевой воды. Стандартная неопределенность величины δсх рассчитывается по формуле:

Этап 3. Анализ корреляций

Все входные величины рассматриваются как некоррелированные.

Этап 4. Измеренное значение величины

рН пробы питьевой воды будет оцениваться в соответствии с выражением (1) и составит:

Этап 5. Суммарная стандартная неопределенность

Суммарная стандартная неопределенность измерений величины рН рассчитывается по формуле:

Коэффициенты чувствительности для всех влияющих величин, входящих в функцию измерений (1), будут равны 1.

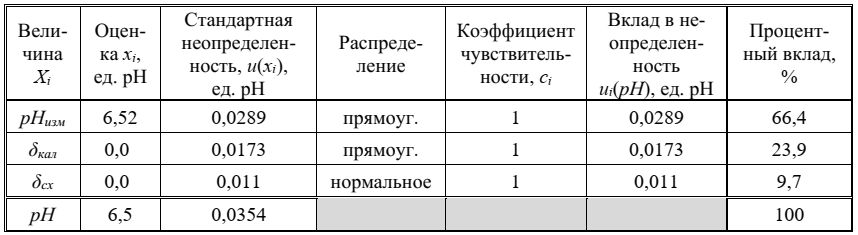
Этап 6. Бюджет неопределенности

В таблице представлен бюджет неопределенности для измеряемой величины и произведены соответствующие расчеты для нахождения ее стандартной неопределенности.

Таблица – Бюджет неопределенности для рН пробы питьевой воды

Этап 7. Расширенная неопределенность

Расширенная неопределенность U получается умножением суммарной стандартной неопределенности на коэффициент охвата k, который выбирается равным 2 при уровне доверия 95 % в предположении нормального распределения вероятностей измеряемой величины:

Этап 8. Представление результата измерения

Результат измерения записывается в виде:
«рН пробы воды составила (6,5 ± 0,1) ед. рН, k = 2, P = 95 %».

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, рекомендуем посетить наш семинар по данной теме, где вы сможете найти ответы на свои вопросы, а также пообщаться с лектором.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

---

Пример 5. Оценивание неопределенности измерений относительного удлинения эластичного герметика

---

Измерительная задача

Относительное удлинение герметика полиуретанового определяется по ГОСТ 21751-76 «Герметики. Метод определения условной прочности относительного удлинения при разрыве и относительной остаточной деформации после разрыва» с применением разрывной машины РМ-30-1 методом растяжения образцов с постоянной скоростью при заданной температуре до разрыва с последующим измерением геометрических параметров образца. Длина рабочего участка образца до и после приложения нагрузки измеряется линейкой металлической по ГОСТ 427-75 с пределом измерений 300 мм и ценой деления 1 мм.
Образцы герметика для испытаний типа 1 вырезают длиной (115 ± 1) мм специальным ножом согласно ГОСТ 21751 (пп. 1.3, 2.1-2.4). Общее количество испытываемых образцов – 5. Испытания проводят при температуре окружающего воздуха (20 ± 3) ºС и относительной влажности (65 ± 5) %.

Этап 1. Составление функции измерений

Относительное удлинение каждого испытываемого образца, εрi, в процентах рассчитывается на основании функции измерений:

где lpi – длина рабочего участка образца в момент разрыва, мм;
l0 – первоначальная длина рабочего участка образца, мм.
Относительное удлинение герметика полиуретанового  рассчитывается как среднее арифметическое относительных удлинений, εрi, полученных для каждого из испытываемых образцов:

где  – среднее арифметическое измерений относительного удлинения пяти образцах, %;
t – количество испытанных образцов герметика;
Fr – поправка на рассеяние результатов измерений относительных удлинений, полученных на всех испытанных образцах, %.
Результат измерения округляется до целых чисел.

Результаты измерений

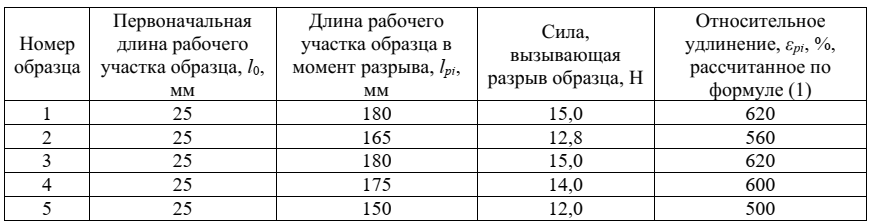
При определении относительного удлинение герметика полиуретанового было испытано 5 образцов. Результаты испытаний представлены в таблице 1.

Таблица 1 – Результаты испытаний образов герметика полиуретанового на относительное удлинение

Этап 2. Анализ входных величин

2.1 Среднее арифметическое измерений относительного удлинения пяти образцах ()

Значение оценки рассчитывается по формуле

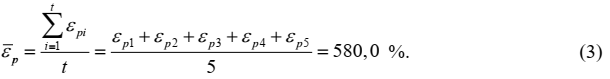
Возможное рассеяние результатов измерений относительного удлинения на пяти единичных образцах герметика учитывается через влияющую величину F.

2.2 Первоначальная длина рабочего участка образца (l0i)

Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Значение оценки: получают путем снятия показаний со шкалы линейки при прямых измерениях длины рабочего участка образца до проведения испытаний, мм; значения для каждого образца представлены в таблице 1
Стандартная неопределенность: u(l0i) = 0,294 мм
Неопределенность, связанная с величиной l0i, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 300 мм ±Δl = ±0,10 мм и цене деления линейки d = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

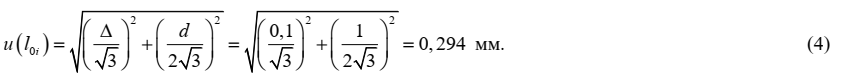
2.3 Длина рабочего участка образца в момент разрыва (lpi)

Вид распределения: трапецеидальное
Значение оценки: получают путем снятия показаний со шкалы линейки при прямых измерениях длины рабочего участка образца после проведения испытаний, мм; значения для каждого образца представлены в таблице 1
Стандартная неопределенность: u(lpi) = 0,294 мм
Неопределенность, связанная с величиной lpi, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 300 мм ±Δl = ±0,10 мм и цене деления линейки d = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

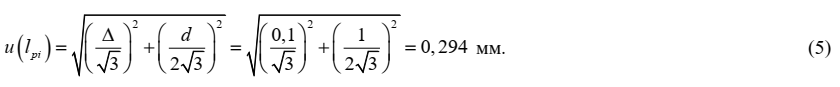
2.4 Поправка на рассеяние результатов измерений относительных удлинений, полученных на всех испытанных образцах (Fr )

Тип оценивания неопределенности: А
Вид распределения: нормальное
Значение оценки: Fr = 0,0 %
Стандартная неопределенность: u(Fr) = 22,80 %
Стандартная неопределенность поправки рассчитывается как стандартное отклонение среднего арифметического измерений относительного удлинения пяти образцах по типу А в предположении нормального распределения и составляет:

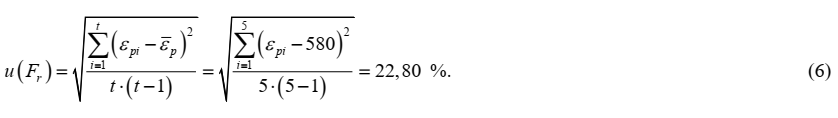
Этап 3. Анализ корреляций

Все входные величины рассматриваются как некоррелированные.

Этап 4. Измеренное значение величины

Оценка измеряемой величины – относительное удлинение герметика, εр, в процентах, рассчитывается по формуле (1) используя полученные в Этапе 2 значения оценок входных величин:

Этап 5. Суммарная стандартная неопределенность

Стандартную неопределенность измеряемой величины εр, %, рассчитываем по закону распространения неопределенностей путем суммирования квадратов произведений стандартных неопределенностей влияющих величин, входящих в функции измерений (1) и (2), на соответствующие коэффициенты чувствительности:

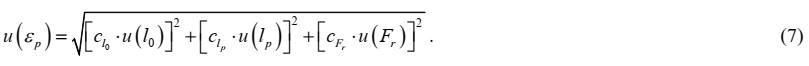
Коэффициенты чувствительности рассчитываются как частные производные функции измерений (1) по входным величинам:

Примечание – Для расчета коэффициентов чувствительности используются значения параметров, полученные при испытаниях первого образца герметика.

Вклад в неопределенность от j-ой входной величины рассчитывается как произведение стандартной неопределенности этой величины на соответствующий коэффициент чувствительности. Процентный вклад рассчитывается как отношение квадрата вклада входной величины к квадрату суммарной стандартной неопределенности (выражается в процентах):

Этап 6. Бюджет неопределенности

Бюджет неопределенности для относительного удлинения герметика представлен в таблице 3.

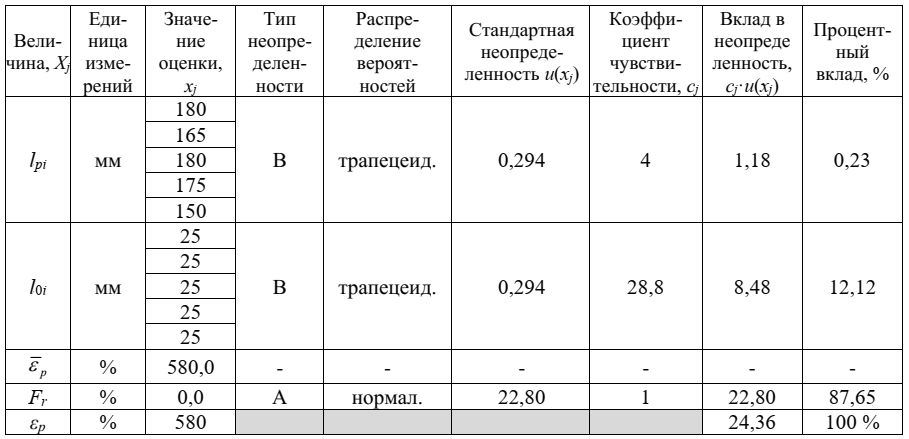
Таблица 3 – Бюджет неопределенности для относительного удлинения

Этап 7. Расширенная неопределенность

Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k. Поскольку в бюджете неопределенности доминирует составляющая, распределенная по нормальному закону распределения и рассчитанная на малом объеме экспериментальных данных (менее 10), то значение коэффициента охвата выбирается в предположении распределения Стьюдента для измеряемой величины как квантиль распределения Стьюдента при вероятности 95 % и числе эффективных степеней свободы, которые рассчитываются по формуле Уэлча-Саттертуэта

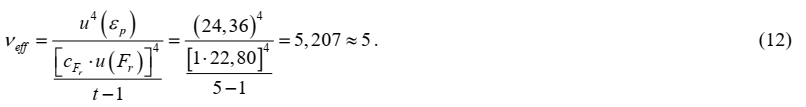
Значение коэффициента охвата принимается равным k = 2,57. Расширенная неопределенность будет рассчитываться по формуле:

Этап 8. Представление результата измерения

Результат измерения представляют в виде:
«Относительное удлинение герметика полиуретанового  составило (580 ±63) %, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2,78, основанный на предполагаемом распределении Стьюдента и числе эффективных степеней свободы νeff = 5, и определяет интервал, соответствующий вероятности охвата 95 %».

Библиография
ГОСТ 21751-76 Герметики. Метод определения условной прочности относительного удлинения при разрыве и относительной остаточной деформации после разрыва
ГОСТ 427-75 Линейки измерительные металлические. Технические условия

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, Вы можете задать их нашим специалистам посредством обратной связи или по телефонам, указанным в контактных данных на сайте.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

---

Пример 6. Оценивание неопределенности измерений прочности бетона на растяжение при изгибе

---

Измерительная задача
Прочность на растяжение при изгибе бетона класса прочности на растяжение при изгибе Вtb3,6 определяется по ГОСТ 10180-2012 «Бетоны. Методы определения прочности по контрольным образцам» путем разрушающих кратковременных статических испытаний специально изготовленных контрольных образцов бетона. В качестве контрольных образцов используются изготовленные согласно ГОСТ 10180 (п. 4) образцы бетона в форме призмы квадратного сечения 100×100×400 мм. Количество контрольных образцов в серии – три.
Испытания контрольных образцов на прочность на растяжение при изгибе проводят на универсальной испытательной машине C093-03A. Линейные размеры образцов измеряют линейкой металлической по ГОСТ 427-75 с пределом измерений 500 мм и ценой деления 1 мм.

Этап 1. Составление функции измерений

Прочность бетона на растяжение при изгибе для i-го образца в серии Rtb,i, МПа, вычисляется в соответствии со следующей функцией измерений:

где δ – масштабный коэффициент для приведения прочности бетона к прочности бетона в образцах базовых размера и формы;
Fi – разрушающая нагрузка для i-го контрольного образца, Н;
ai – ширина поперечного сечения призмы для i-го контрольного образца, мм;
bi – высота поперечного сечения призмы для i-го контрольного образца, мм;
l – расстояние между опорами, мм.
Прочность бетона на растяжение при изгибе Rtb, МПа, вычисляется в соответствии со следующей функцией измерений:

где Fr – поправочный коэффициент, учитывающий расхождение между результатами измерений прочности n образцов, Fr = 1;
n – количество образцов в серии, n = 3.
Измеренное значение прочности бетона на растяжение при изгибе округляется с точностью до 0,01 МПа.

Результаты измерений
При проведении испытаний трех контрольных образцов бетона на растяжение при изгибе были получены значения параметров, представленные в таблице 1.

Таблица 1 – Результаты испытаний контрольных образцов бетона на прочность на растяжение при изгибе

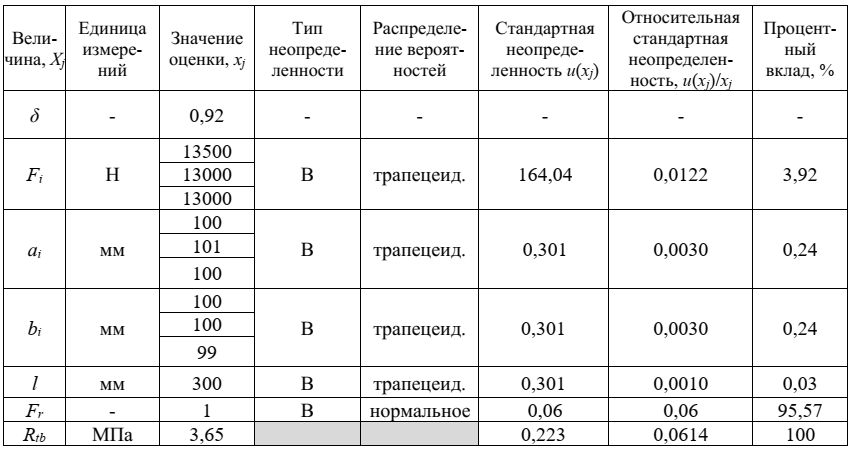
Этап 2. Анализ входных величин

2.1 Масштабный коэффициент для приведения прочности бетона к прочности бетона в образцах базовых размера и формы (δ)

Значение оценки выбирается согласно ГОСТ 10180 (таблица 1) и составляет δ = 0,92.
Величина рассматривается как постоянная.

2.2 Разрушающая нагрузка для i-го контрольного образца (Fi)

Значение оценки величины Fi для каждого контрольного образца определяется по шкале отсчетного устройства испытательной машины и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(F) = 164,04 Н
Неопределенность, связанная с величиной F, оценивается на основании информации о пределах допускаемой относительной погрешности показания силы ± δF = ± 1 % и цене деления шкалы стрелочного индикатора d = 500 Н. Поскольку значения приведены без вероятности, принимаем прямоугольное распределение значений погрешности показаний силы и ошибки оператора при снятии показаний со шкалы индикатора в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

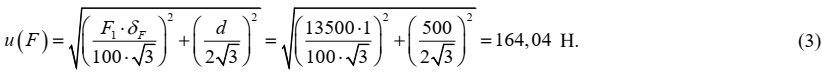
Примечание – Для расчета стандартной неопределенности разрушающей нагрузки используется значение параметра, полученное при испытаниях первого контрольного образца.

2.3 Ширина поперечного сечения призмы для i-го контрольного образца (ai)

Значение оценки величины аi для каждого контрольного образца определяется по шкале линейки металлической и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(а) = 0,301 мм
Неопределенность, связанная с величиной а, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

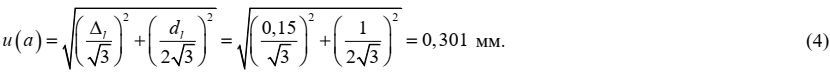
2.4 Высота поперечного сечения призмы для i-го контрольного образца (bi)

Значение оценки величины bi для каждого контрольного образца определяется по шкале линейки металлической и представлено в таблице 1
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(b) = 0,301 мм
Неопределенность, связанная с величиной b, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

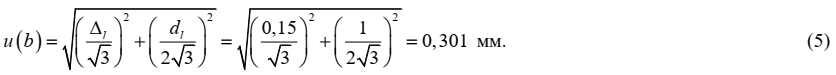
2.5 Расстояние между опорами (l)

Значение оценки величины l = 300 мм и определяется по шкале линейки металлической
Тип оценивания неопределенности: В
Вид распределения: трапецеидальное
Стандартная неопределенность: u(l) = 0,301 мм
Неопределенность, связанная с величиной l, оценивается на основании информации о допускаемом отклонении от номинальных значений длины шкалы используемой линейки с пределом измерений 500 мм ±Δl = ±0,15 мм и цене деления линейки dl = 1 мм. Поскольку значения приведено без вероятности, принимаем прямоугольное распределение значений погрешности линейки и ошибки оператора при снятии показаний со шкалы линейки в соответствующих границах. Стандартная неопределенность оценивается по типу В и составляет:

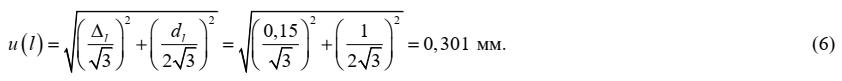
2.6 Поправочный коэффициент, учитывающий расхождение между результатами измерений прочности n образцов (Fr)

Значение оценки: Fr = 1
Тип оценивания неопределенности: B
Вид распределения: нормальное
Стандартная неопределенность: u(Fr) = 0,06
Стандартная неопределенность поправки рассчитывается на основании среднего внутрисерийного коэффициента вариации прочности бетона, установленного в лаборатории согласно ГОСТ 10180 (Приложение А) и равного 6 %. Стандартная неопределенность оценивается по типу В в предположении нормального распределения и составляет:

Примечание – Для использования в расчетах установленного в лаборатории среднего внутрисерийного коэффициента вариации следует проверить соответствие реального разброса результатов измерений прочности бетона на растяжение при изгибе, полученного на испытанных контрольных образцах, установленному среднему внутрисерийному коэффициенту вариации используя положения СТБ ИСО 5725-6 и следующее неравенство:

где f(n) – коэффициент критического размаха, выбирается в зависимости от количества контрольных образцов в серии n по СТБ ИСО 5725-6 (таблица 1).
Для нашего примера f(n=3) = 3,3 и неравенство (8) выполняется:

Этап 3. Анализ корреляций

При измерении величин а и b, близких по измеренным значением, присутствуют корреляционные эффекты, связанные с применением одного средства измерений (линейки металлической) в одной точке диапазона измерений (узком диапазоне измерений) и вызванные погрешностью применяемого средства измерений. Однако, учитывая, что вклад этой составляющей в стандартные неопределенности величин а и b незначителен (в процентном выражении составляет 8,3 %), существующей корреляцией пренебрегаем и не учитываем при расчете суммарной стандартной неопределенности измеряемой величины: прочности бетона на растяжение при изгибе.
Все остальные входные величины рассматриваются как некоррелированные.

Этап 4. Измеренное значение величины

Оценка измеряемой величины – прочности бетона на растяжение при изгибе, Rtb, МПа, рассчитывается по формуле (2) используя полученные в таблице 1 значения оценок входных величин:

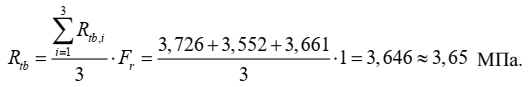
Этап 5. Суммарная стандартная неопределенность

Стандартную неопределенность измеряемой величины Rtb, МПа, рассчитываем по закону распространения неопределенностей путем суммирования квадратов относительных стандартных неопределенностей влияющих величин, входящих в функции измерений (1) и (2):

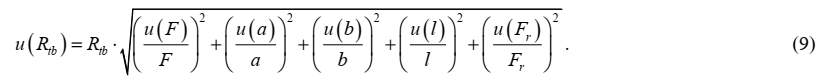
и составляет для нашего примера

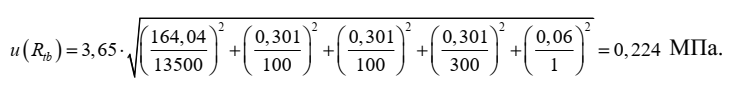
Примечание – Для расчета относительных стандартных неопределенностей входных величин используются значения величин, полученные для первого контрольного образца.
Значения процентных вкладов неопределенностей влияющих величин в суммарную стандартную неопределенность рассчитываются как умноженное на 100 % квадрат отношения относительной стандартной неопределенности влияющей величины к относительной суммарной стандартной неопределенности:

Этап 6. Бюджет неопределенности

Бюджет неопределенности для прочности бетона на растяжение при изгибе представлен в таблице 3.

Таблица 3 – Бюджет неопределенности для прочности бетона на растяжение при изгибе

Этап 7. Расширенная неопределенность

Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k = 2 в предположении нормального распределения при уровне доверия приблизительно 95 %:

Этап 8. Представление результата измерения

Результат измерения представляют в виде:
«Прочность бетона на растяжение при изгибе бетона класса прочности на растяжение при изгибе Вtb3,6 составила (3,65  0,45) МПа, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %».

Библиография
ГОСТ 10180-2012 Бетоны. Методы определения прочности по контрольным образцам
ГОСТ 427-75 Линейки измерительные металлические. Технические условия
СТБ ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, рекомендуем посетить наш семинар по данной теме, где вы сможете найти ответы на свои вопросы, а также пообщаться с лектором.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

---

Пример 7. Оценивание неопределенности измерений твердости по Бриннелю

---

Измерительная задача
Измерение твердости трубопровода из Стали 10Г2СД по шкале Бриннеля выполняется твердомером ТКМ-459

Условия проведения измерений:

• температура окружающего воздуха +15 ºС;
• относительная влажность 60 %;
• толщина контролируемого участка детали 10 мм;
• шероховатость поверхности, на которой производится измерение Rа 1,2.

Этап 1. Составление функции измерений

Измеряемой величиной является твердость контролируемого участка объекта контроля по шкале Бринелля, Н, которая определяется как:

где Низм – показания твердомера, НВ;
δт – поправка на погрешность твердомера, НВ;
δр – поправка на разрешающую способность дисплея твердомера, НВ.

Результаты измерений
На контролируемом участке были получены следующие единичные результаты наблюдения твердости по шкале Бринелля:
H1 = 180 НВ
H2 = 184 НВ
H3 = 175 НВ
H4 = 172 НВ
H5 = 183 НВ

Этап 2. Анализ входных величин

2.1 Показания твердомера (Низм)

Показания твердомера оцениваются как среднее арифметическое из 5 единичных результатов наблюдений твердости контролируемого участка объекта контроля по формуле:

Стандартная неопределенность величины Низм рассчитывается как среднее квадратическое отклонение среднего арифметического из 5 единичных результатов наблюдений по формуле:

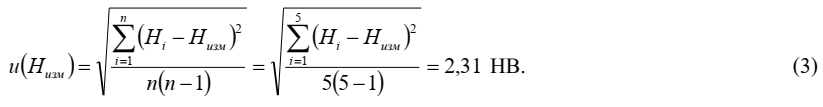
Примечание – Данная составляющая может не учитываться, если отклонение максимального единичного показания твердости от минимального не превышает предела основной допускаемой погрешности твердомера.

2.2 Поправка на погрешность твердомера (δт)

Поправка на погрешность твердомера оценивается значением «нуль». В паспорте на твердомер установлены пределы абсолютной погрешности ± Δ = ± 15 НВ при измерении по шкале Бринелля (НВ). Стандартная неопределенность поправки определяется по типу В на основании установленных пределов абсолютной погрешности твердомера в предположении прямоугольного закона распределения: 2.3 Поправка на разрешающую способность дисплея твердомера (δр)

Поправка на разрешающую способность дисплея твердомера оценивается значением «нуль». Стандартная неопределенность поправки определяется через величину единицы наименьшего разряда дисплея (а = 1 НВ).
Стандартная неопределенность поправки на разрешающую способность дисплея твердо-мера оценивается по типу В в предположении прямоугольного распределения из выражения:

Этап 3. Анализ корреляций

Все входные величины рассматриваются как некоррелированные.

Этап 4. Измеренное значение величины

Твердость контролируемого участка трубопровода будет оцениваться в соответствии с выражением (1) и составит:

Этап 5. Суммарная стандартная неопределенность

Суммарная стандартная неопределенность, приписываемая результату измерения Н, рас-считывается по формуле:

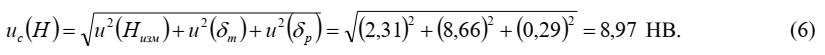
Коэффициенты чувствительности для всех влияющих величин, входящих в функцию измерений (1), будут равны 1.

Этап 6. Бюджет неопределенности

В таблице представлен бюджет неопределенности для измеряемой величины и произведены соответствующие расчеты для нахождения ее стандартной неопределенности.

Таблица – Бюджет неопределенности для твердости по шкале Бриннеля Н

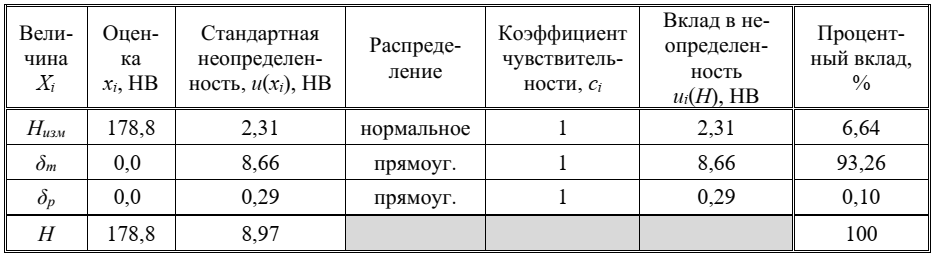
Этап 7. Расширенная неопределенность

Суммарное распределение измеряемой величины предполагаем прямоугольным (по-скольку доминирует составляющая неопределенности от величины δт, процентный вклад составляет более 90 %). Коэффициент охвата для уровня доверия 95 % принимается равным k = 1,65. Расширенную неопределенность рассчитываем по формуле:

Этап 8. Представление результата измерения

Результат измерения записывается в виде:
«Твердость по Бринеллю контролируемого участка трубопровода из Стали 10Г2СД со-ставила (180 ± 15) НВ, k = 1,65, P = 95 %».

Уважаемые коллеги! Если у Вас возникли вопросы по представленному примеру, рекомендуем посетить наш семинар по данной теме, где вы сможете найти ответы на свои вопросы, а также пообщаться с лектором.

Если у Вас есть необходимость разработать методику оценивания неопределенности, Вы можете заказать разработку у нас. Чтобы узнать стоимость и сроки работ, заполните форму обратной связи ниже.

Основные положения

Неопределенность
измерений
– параметр, связанный с результатом
измерений и характеризующий рассеяние
значений, которые могут быть обоснованно
приписаны измеряемой величине.

В
соответствии со способом оценивания
(рис. 9.1)
все составляющие неопределенности
можно сгруппировать в две категории:

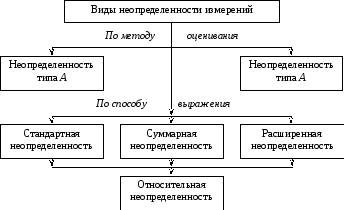
Рисунок 9.1 –
Классификация неопределенностей
измерений

А
– составляющие, оцениваемые путем
применения статистических методов
(обработкой результатов многократных
наблюдений). Составляющие типа А
оцениваются как стандартные отклонения
средних арифметических многократных
наблюдений (неопределенности
типа А –
).
Эти составляющие характеризуются
числами степеней свободы.
Если между составляющими типаА
наблюдается статистическая взаимосвязь
(корреляция), то необходимо указывать
коэффициенты корреляции
;

В
– составляющие, оцениваемые другим
способом (по характеристикам, взятым
из предыдущих экспериментов, из паспорта
на прибор, методик выполнения измерений,
справочников и т.д.)..К источникам этих
неопределенностей относятся: случайные
погрешности однократных измерений;
поправки, вводимые в результат измерения;
неисключенные систематические
погрешности, погрешности справочных
данных и т.д. Составляющие типа В
также оцениваются как предполагаемые
стандартные отклонения, получаемые из
известных границ, в которых могут
находиться значения этих составляющих
(неопределенности
типа В –
).
Между составляющими типаВ
может существовать взаимосвязь, тогда
следует указывать коэффициенты
предполагаемой корреляции.

Суммарная
стандартная неопределенность
рассчитывается по правилу суммирования
дисперсий.

Интервальной
оценкой неопределенности является
расширенная
неопределенность
,
получаемая путем умножения стандартной
суммарной неопределенностина коэффициент охвата.
При указании расширенной неопределенности
указывают уровень доверия – вероятность,
которая обычно принимается равной 0,95.

По
способу выражения неопределенность
может быть стандартной, суммарной и
расширенной. Все виды неопределенности
могут выражаться в относительном виде.

Базовый
алгоритм оценивания неопределенности
измерений
заключается в выполнении таких операций:

1) составление
модельного уравнения;

2)
оценивание значений входных величин,
внесение поправок на известные
систематические эффекты в результаты
их измерений;

3) вычисление оценки
результата измерений;

4)
оценивание стандартных неопределенностей
входных величин;

5) определение
коэффициентов чувствительности;

6)
вычисление вклада неопределенности
каждой входной величины в неопределенность
измеряемой величины;

7) определение
попарной корреляции входных величин;

8)
вычисление суммарной стандартной
неопределенности измеряемой величины;

9) вычисление
коэффициента охвата;

10)
вычисление расширенной неопределенности
измеряемой величины.

1. Составление модельного уравнения

Модельное
уравнение выражает зависимость между
выходной (измеряемой) величиной
и входными величинами

.

В
качестве входных величин в модельное
уравнение, кроме непосредственно
измеряемых величин, входят переменные,
значения и неопределенности которых
известны из внешних источников, а также
поправки к результату измерения на
известные систематические эффекты,
основные и дополнительные абсолютные
погрешности используемых средств
измерительной техники.

Пример:
При измерении напряжения постоянного
тока с помощью вольтметра модельное
уравнение имеет вид

,

где
– индицируемое напряжение;– поправка на основную погрешность
вольтметра;– поправка на температурную погрешность
вольтметра;– поправка на погрешность отсчета
вольтметра.

Соседние файлы в папке KI

• #
• #

При измерении мы имеем случайно меняющуюся величину, и наилучшей оценкой математического ожидания измеренного значения является среднее арифметическое.

Абсолютно точных измерений не существует. При проведении измерения его результат зависит от измерительной системы, методики измерения, квалификации оператора, внешних условий и других факторов. Так, если измерять одну и ту же величину несколько раз одним способом и в одинаковых условиях, то, как правило, полученные значения измеряемой величины всякий раз будут разными. Их среднее должно обеспечить значение оценки истинного значения величины, которая будет более достоверной, чем отдельное показание. Разброс показаний и их число дают некоторую информацию в отношении среднего значения как оценки истинного значения величины, однако, этого недостаточно. В руководстве по оценке неопределенности измерений (GUM) предложено выражать результат измерения как наилучшую оценку измеряемой величины вместе с соответствующей неопределенностью измерения. Неопределенность измерения можно представить через степень уверенности. Такая неопределенность будет отражать неполноту знания об измеряемой величине. Понятие «уверенности» очень важно, т. к. оно перемещает метрологию в сферу, где результат измерения должен рассматриваться и численно определяться в терминах вероятностей, которые выражают степень доверия. Неопределенность измерения — «неотрицательный параметр, характеризующий рассеяние значений, приписываемых измеряемой величине на основании используемой информации».

Сравнительный анализ двух подходов к выражению характеристик точности измерений

Понятие погрешности измерений как разности между результатом измерений и истинным (действительным) значением измеряемой величины используется для описания точности измерений в НД ГСИ по метрологии. Неопределенность измерений понимают как неполное знание значения измеряемой величины и для количественного выражения этой неполноты вводят распределение вероятностей возможных (обоснованно приписанных) значений измеряемой величины.

Таким образом, параметр этого распределения (также называемый — неопределенность) количественно характеризует точность результата измерений. Сходными для обоих подходов являются последовательности действий при оценивании характеристик погрешности и вычислении неопределенности измерений: Методы вычисления неопределенности, так же как и методы оценивания характеристик погрешности, заимствованы из математической статистики, однако при этом используются различные интерпретации закона распределения вероятностей случайных величин.
Из рассмотренных метрологических ситуаций можно предложить общее правило: результаты измерений в большинстве метрологических ситуаций характеризуются неопределенностью, а нормативы точности средств измерений, измерительных и контрольных процедур характеризуются погрешностью. Таким образом, понятия «неопределенность» и «погрешность» рекомендуется гармонично использовать без взаимного противопоставления и исключения одного из них.

Необходимость учета неопределенности при оценке результатов измерений

Измерения выполняются ради оценки результата, сравнения его с нормативами и правила оценки результатов обуславливают требования к выполнению измерений.

Нормативные документы, определяющие требования к оценке результатов измерений.

• ГОСТ Р ИСО 10576-1-2006 «РУКОВОДСТВО ПО ОЦЕНКЕ СООТВЕТСТВИЯ УСТАНОВЛЕННЫМ ТРЕБОВАНИЯМ»
• ГОСТ 34100.1-2017/ISO/IEC Guide 98-1:2009 “Неопределенность измерения. Часть 1. Введение в руководства по выражению неопределенности измерения”
• Межгосударственный стандарт ГОСТ ИСО МЭК 17025-2009
• Письмо Роспотребнадзора от 13.06.2012 г. №01/6620-12-32

Ключевые моменты из документов

ГОСТ Р ИСО 10576-1— 2006 «РУКОВОДСТВО ПО ОЦЕНКЕ СООТВЕТСТВИЯ УСТАНОВЛЕННЫМ ТРЕБОВАНИЯМ»

ГОСТ 34100.1-2017/ISO/IEC Guide 98-1:2009 “Неопределенность измерения. Часть 1. Введение в руководства по выражению неопределенности измерения” (Введен с 01.09.2018)

ФЕДЕРАЛЬНАЯ СЛУЖБА ПО НАДЗОРУ В СФЕРЕ ЗАЩИТЫ ПРАВ ПОТРЕБИТЕЛЕЙ И БЛАГОПОЛУЧИЯ ЧЕЛОВЕКА ПИСЬМО от 13 июня 2012 года N 01/6620-12-32 Об оценке данных, получаемых при инструментальных измерениях физических факторов неионизирующей природы

СанПиН 2.2.4.3359-16 “Санитарно-эпидемиологические требования к физическим факторам на рабочих местах” (Общие положения)

Межгосударственный стандарт ГОСТ ИСО/МЭК 17025-2009 “Общие требования к компетентности испытательных и калибровочных лабораторий” (введен в действие приказом Федерального агентства по техническому регулированию и метрологии от 4 апреля 2011 г. N 41-ст)

Порядок оценки неопределенности измерений

• ГОСТ 34100.1-2017/ISO/IEC Guide 98-1:2009 “Неопределенность измерения. Часть 1. Введение в руководства по выражению неопределенности измерения”
• Межгосударственный стандарт ГОСТ 34100.3-2017/ISO/IEC Guide 98-3:2008 “Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения”
• Рекомендации по метрологии Р 50.2.038-2004 “Государственная система обеспечения единства измерений. Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений”

Разновидности неопределенности измерений

Тип A

Тип B

Стандартная неопределенность

Расширенная неопределенность

Суммарная неопределенность

Погрешность и неопределенность

СКО, характеризующее случайную погрешность <=> Стандартная неопределенность, вычисленная по типу А
СКО, характеризующее неисключенную систематическую погрешность (погрешность СИ) <=> Стандартная неопределенность, вычисленная по типу В
СКО, характеризующее суммарную погрешность <=> Стандартная неопределенность, вычисленная по типу В
Доверительные границы погрешности <=> Расширенная неопределенность

Погрешности (составляющие неопределенности) при выполнении измерений

• инструментальная (приборная) — определяется конструкцией СИ; (основная, дополнительная; предел допускаемой погрешности)
• систематическая — обусловлена методом измерения;
• случайная — разброс результатов, обусловленный совокупностью различных факторов;
• «промах» — грубая ошибка

Вычисление неопределенности прямых измерений

1. Выявление «промахов» и исключение их из выборки
2. Учет систематической погрешности измерения (например, умножение освещенности, измеренной люксметром Ю-116 на поправочный коэффициент для данного типа источника света)
3. Вычисление стандартной неопределенности по типу А — среднего квадратического отклонения (Аналогично вычислению случайной погрешности)
4. Вычисление стандартной неопределенности по типу В (Аналогично вычислению неисключенной погрешности)
5. Определение Расширенной неопределенности (Аналогично суммарной погрешности с доверительными границами)

Метод исключения «промахов» по Q-критерию: (см также ГОСТ Р 8.736-2011)
Q=(X₁-X₂)/R

где X₁ — подозрительно выделяющийся результат измерения; X₂ — результат единичного измерения, ближайший по значению к X₁; R — размах варьирования (разница между наибольшим и наименьшим значением ряда измерений) Вычисленное значение Q сопоставляют с табличным значением Q (Р, ni).

Значения Q-критерия в доверительной вероятности в зависимости от числа измерений (ni)

Наличие грубой погрешности доказано, если Q > Q (Р, n_i).

Пример

Оценка интервала неопределённости при выполнении прямых измерений, для которых отсутствуют показатели точности в методиках измерений

Вычисление стандартной неопределённости измерений.

Стандартная неопределенность измерений (u) включает два компонента:

• среднее квадратическое отклонение, обусловленное случайными колебаниями результата последовательных измерений, соответствует стандартной неопределенности типа А при отсутствии других составляющих, не связанных со статистически случайными процессами (SX);
• среднее квадратическое отклонение неисключенной систематической погрешности (НСП) измерения (как правило, погрешность средства измерений — СИ) (SΘ)

u = √ S ²_Θ + S²_x

ПРИМЕЧАНИЕ: данный способ оценивания неопределённости измерений в терминологии ГОСТ Р 54500.3 является оцениванием по типу В. (настоящий ГОСТ отменен с 1 сентября 2018 г. в связи с принятием и введением в действие ГОСТ 34100.3-2017/ISO/IEC Guide 98-3:2008)

Среднеквадратическое отклонение: (синонимы: среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение; близкие термины: стандартное отклонение, стандартный разброс) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок.

S_Θ= √(Θ₊ – Θ _–)²/ 12 = Θ/√3

где
Θ – граница НСП симметричного доверительного интервала (выражена как абсолютная погрешность СИ);

Θ+, Θ– верхняя и нижняя граница НСП для несимметричных доверительных интервалов, например, когда погрешность СИ несимметрична в положительную и отрицательную сторону (при измерении плотности потока энергии).

где
X_i — результат i-ro наблюдения (единичного замера),
X̅ — среднее арифметическое значение оценки величины X (результат измерения),
n — количество наблюдений (замеров); для многократных измерений количество замеров должно быть не менее 4.

Встречаются ситуации, когда измерения проводятся с однократным наблюдением, и в этом случае стандартная неопределённость измерений оценивается только как Sθ., которая рассчитывается на основе погрешностей СИ.

Выполнение однократных измерений может быть обусловлено следующими факторами:

• производственной необходимостью (невозможность повторения измерений, экономическая целесообразность и т. д.);
• возможностью пренебрежения случайными погрешностями (SX).

Примечание 1 — Если Θ/S_X> 8, то величиной SX при расчёте u можно пренебречь (Р 50.2.038).
Примечание 2 — Если Θ/S_X < 0,8, то величиной SΘ при расчёте u можно пренебречь (Р 50.2.038)

Таким образом, при вычислении стандартной неопределенности сначала вычисляется S_X, затем S_θ для основной погрешности или предела допускаемой погрешности. Если необходимо учесть дополнительную погрешность, то вычисляется также величина стандартной неопределенности, обусловленной дополнительной погрешностью S_ΘД также как S_Θ. После этого вычисляется величина суммарной стандартной неопределенности.

u = √(S²_Θ + S²_ΘД + S²_x

При измерениях с 1 — кратным наблюдением S_Х не вычисляется и не учитывается

Вычисление расширенной неопределённости измерений

Расширенная неопределенность измерений (U) определяется как суммарная стандартная неопределенность (u), умноженная на коэффициент охвата (k):

U=k×u

Коэффициент охвата для уровня доверия 95% для двухстороннего интервала охвата можно принять равным 2, а для одностороннего интервала охвата равным 1,64 при условии, что количество замеров будет не менее 11, что соответствует числу степеней свободы, равному 10 (ГОСТ 54500.3, п. 6.3.3, G6.6 (настоящий ГОСТ отменен с 1 сентября 2018 г. в связи с принятием и введением в действие ГОСТ 34100.3-2017/ISO/IEC Guide 98-3:2008). Таким образом, чем больше измерений в выборке, тем меньше ожидаемая неопределенность измерений.

Одно и двусторонний интервал охвата

Интервал охвата = интервал неопределённости (плохой перевод: ГОСТ Р 54500.3-2011/Руководство ИСО/МЭК 98-3:2008 (п. 6.2.2) Раньше использовались термины «одно — и двусторонние доверительные интервалы».

Если неопределённость оценивается по типу А, то интервал охвата=интервалу неопределённости

К чему ведет недостаточное количество измерений?

Коэффициент охвата для уровня доверия 95% для двухстороннего интервала охвата можно принять равным 2, а для одностороннего интервала охвата равным 1,64 при условии, что количество замеров будет не менее 11, что соответствует числу степеней свободы, равному 10 (ГОСТ 54500.3, п. 6.3.3, G6.6 ). Таким образом, чем больше измерений в выборке, тем меньше ожидаемая неопределенность измерений.

Расширенную неопределенность U вычисляют по формуле: U=k×uc

Если число измерений > 11, то k можно принять равным 2 для двухстороннего коэффициента охвата и 1,64 для одностороннего коэффициента охвата При меньшем числе измерений k зависит от числа измерений (n) В таблице представлены его величины при доверительной вероятности 95%

Оценка интервала неопределённости при использовании аттестованных методик измерений с установленными показателями точности

Аттестованная методика измерений (МИ) должна содержать значения установленной точности измерений в виде расширенной неопределённости.

При наличии установленного МИ диапазона расширенной неопределённости (U), приведенного в используемой аттестованной МИ, в протоколе измерений следует указывать ее значение, если целью исследования является оценка значения величины с некоторой точностью. Как правило, аттестованные МИ содержат установленные значения расширенной неопределённости измерений для двухстороннего охвата при уровне доверия 95%: ±U(95%), при этом используется коэффициент охвата (k), равный 2. В этом случае результат измерений приводится в протоколе как:

<среднее значение> ± U(95%)

Если целью исследования является сопоставление результата измерений с предельным значением (нормативом), когда область допустимых значений располагается ниже (или выше) норматива, то можно оценить диапазон расширенной неопределённости, используя односторонний интервал охвата, который меньше двухстороннего. Для его оценки необходимо значение стандартной неопределённости измерений (u), которое можно найти в МИ, либо рассчитать по формуле (п.4.3.3 ГОСТ Р 54500.3 (настоящий ГОСТ отменен с 1 сентября 2018 г. в связи с принятием и введением в действие ГОСТ 34100.3-2017/ISO/IEC Guide 98-3:2008):

u = U/k = U/2

Верхняя (нижняя) граница одностороннего интервала неопределённости для уровня доверия 95% (Y̅) рассчитывается как среднее значение (Y̅), к которому прибавлен односторонний интервал охвата (1,64*u) с плюсом или минусом:

Y̅+1,64×u или Y̅-1,64×u

Решение о соответствии может быть принято, если односторонний интервал охвата:

(-∞; Y̅+1,64×u] или [Y̅-1,64×u; +∞)

находится в области допустимых значений (то есть ниже или, соответственно, выше предельного значения).

Представление результатов оценивания неопределенности

Если мерой неопределенности результата измерения является расширенная неопределенность U = kи_с(у), то при представлении результата измерения следует: a) дать подробное определение измеряемой величины У; b) указать результат измерения в виде Y = у ± U с указанием единиц измерений для у и U; c) при необходимости указать относительную расширенную неопределенность; d) указать использованное для получения расширенной неопределенности значение k; e) указать приблизительный уровень доверия для интервала у ± У и пояснить, как он был определен;

Форма представления результата измерения

à ± U(Р)

Возможно введение в форму протокола колонки ” неопределенность измерений” и/или «результат с учетом неопределенности измерений»